重庆市2018学年七年级数学下学期第一次月考试题 新人

重庆市第一中学校2023-2024学年七年级下学期第一次月考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．若一个数的倒数是0.25-，则这个数是（ ）A ．4-B ．4C ．0.25-D ．0.25 2．如图是由5个相同的小正方体组成的几何体，该几何体从左面看得到的平面图形是（ ）A ．B ．C ．D ． 3．计算33x x ⋅的结果是（ ）A ．32xB ．62xC ．6xD ．9x 4．如图，AB CD P ，50C ∠=︒，则1∠的度数为（ ）A ．120︒B ．130︒C ．140︒D ．150︒ 5．下列选项中，最适合采用普查方式的是（ ）A ．为保证“神舟十三号”载人航天飞船的成功发射，对其零部件进行检查B ．调查一批灯泡的使用寿命C ．调查全国中学生对“天宫课堂”的了解情况D ．调查嘉陵江水质污染情况6．如果等腰三角形的两边长分别3和6，则它的周长为（ ）A ．9B ．12C ．15D ．12或15 7．小谢去学校，先从家匀速步行到集合点，等几分钟后坐校车匀速去学校，已知小谢家、集合点、学校在同一直线路段上，且集合点在小谢家与学校之间，小谢从家到学校所走的路程()m S 与时间()min t 关系的大致图象是（ ）A ．B ．C ．D ．8．如图是一个运算程序的示意图，如果第一次输入x 的值为1024；那么第2024次输出的结果为（ ）A ．64B ．16C ．4D ．19．将一副三角板按如图叠加放置，其中45BAC ∠=︒，30E ∠=︒，211ABD DBC ∠=∠． 则EOC ∠的度数为（ ）A ．30︒B ．31︒C ．34︒D ．35︒10．如图，若干个相同小三角形按照某种规律进行摆放，则第7个图中小三角形的个数是（ ）A ．55B ．56C ．71D ．7211．已知25a b -=，()()32310a b -+=，则2274a ab b -+的值为（ ）A ．2B ．19C ．25D ．3112．已知a b c d e >>>>，从a 、b 、c 、d 中随机取两个字母作差后取绝对值，记为A ；将剩下两个字母作差后取绝对值，记为B ；再对A B e --进行化简运算，称为“绝差操作”，例如：()()d a c b e a d b c e a b c d e ----=----=-+--为一次“绝差操作”，a b c d e -+--为“绝差操作”的一种运算结果．下列说法：其中正确的个数是（ ） ①存在“绝差操作”的两种运算结果的和为2e -；②存在“绝差操作”的两种运算结果的差为22a b +；③所有的“绝差操作”共有4种不同运算结果．A ．3B ．2C ．1D ．0二、填空题13．电子和质子都是原子的基本组成部分，它们的质量比在原子物理学和量子力学中非常重要，它帮助我们理解原子内部的结构和相互作用，电子与质子的质量比大约是0.00054，将数据0.00054用科学记数法表示为．14．如图，ABC V 中AD BC ⊥，28ACB ∠=︒，ACB ∠的角平分线CE 与AD 交于点F ，与AB 交于点E ，则EFD ∠的度数为．15．若219x mx ++是关于x 的完全平方式，则常数m 的值为． 16．若一个角的余角的2倍比这个角的补角小20︒，则这个角的度数为．17．如图，一张长方形纸片ABCD ，它的四个内角都是直角，将其分别沿EF EM 、折叠后，点B 落在点H 处，点A 落在EH 上点N 处，若BEH α=∠，则DFE ∠的角度用含α的代数式表示为．18．如图，在ABC V 中，D 、H 分别是边BC AC 、的中点，E 、G 是AD 上的点，且::1:2:1AE EG GD =，F 是BE 的中点，若四边形GHCD 的面积为20，则图中阴影部分面积为．19．关于x 的方程()1412632mx x -=-的解为整数，则整数m 的所有可能的取值之和为． 20．若一个四位正整数M abcd =（39a ≤≤，14b ≤≤，14c ≤≤，17d ≤≤），各个数位上的数字均不为0，满足千位与个位数字之差等于百位与十位数字之和，则称这个四位数M 为“分层数”． 另定义对于一个四位正整数N ，分别按顺序取千位数字与百位数字组成两位数，百位数字与十位数字组成两位数，十位数字与个位数字组成两位数，将3个两位数之和记为()F N ，例如()134213344289F =++=． 则当()237F M dk +=（k为整数）时，代数式3a d -所有可能值的和为． 按上述条件，满足1b c -=时M 的值为．三、解答题21．（1）计算：()()02241 3.1439π----+-÷ （2）解方程：121323x x --=- 22．先化简，再求值：()()()()()222235x y x y x y x x y y ⎡⎤+-+-+-÷-⎣⎦，其中()2750y x -++=． 23．如图，在ABC V 中，点D 在边BA 的延长线上，过点D 作射线DM BC ∥，点E 是射线DM 上一个定点．(1)用尺规完成以下基本作图：在射线DM 上方作DEF C ∠=∠，与BA 的延长线交于点F ．（保留作图痕迹）(2)在（1）问条件下，若BD AF =，求证：AC FE ∥请把以下的解题过程补充完整．证明：DM BC ∥Q （已知）B FDE ∴∠=∠（①）BD AF =Q （已知）BD AD ∴-=②（等式的性质）AB FD ∴=在ABC V 和FDE V 中B FDEC DEF AB FD ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ABC FDE ∴V V ≌BAC ∴∠=③（全等三角形的对应角相等）AC FE ∴∥（④）24．四月有着最绚烂的春光和心情，在和煦的阳光下，游览公园、湖泊、山川，感受大自然的清新与美妙，享受春天所带来的愉悦和舒适，某校七年级对．“同学们最愿意选择的春游方式”随机抽取了．部分同学进行了调查，设置了4种选项，分别是A “景点观光”，B “野炊露营”，C “自行车骑行”，D “徒步登山”． 统计并整理调查数据后，绘制了如下不完整的统计图，请根据图中的信息解答下列问题：抽取的学生选择春游方式扇形统计图抽取的学生选择春游方式条形统计图(1)参与此次调查的学生总人数为人，扇形统计图中选项B “野炊露营”人数占总人数的百分比是．(2)请补全条形统计图．(3)该校七年级学生总人数1200人，根据本次调查估计该校初一年级学生选择A “景点观光”和B “野炊露营”的共有多少人．25．如图，已知AB CD P ，1180A ∠+∠=︒．(1)求证：AE BD P ；(2)若80E ∠=︒，ABD ∠的角平分线BF 与CDE ∠的角平分线DF 交于点F ，BF 与CD 交于点M ，1116∠=︒，求F ∠的度数．26．如图，ABC V 、CDE V 中，点D 在AB 上，AC 与DE 交于点F ，AB CE P ．(1)如图1，若47A ∠=︒，82DCE ∠=︒，CD 平分ACB ∠，求B ∠的度数．(2)如图2，若点F 为AC 中点，作DM DA ⊥，DN DC ⊥且DM DA =，DN DC =，连接MN ．求证：2MN EF =．27．春天的周末，阳光明媚，微风和煦，小聪和小明相约去运动公园玩，他们两人的家与公园在同一条笔直的路线上，小明家在小聪家与公园之间，小聪家距离公园1200米，两人同时从家匀速同向出发前往，小聪追上小明时想到自己给小明的礼物忘带了，于是立即原速原路调头回家去取（找礼物时间忽略不计），与此同时小明在相遇地点休息了5分钟才继续前往公园，小聪拿上礼物马上以原速的43倍原路匀速赶往公园，两人最终在公园汇合，若两人的距离y （单位：米）与出发时间x （单位：分钟）的关系如图所示． 请根据图中信息解决下列问题：(1)填空：小聪变速前的速度是米/分钟，小明的速度是米/分钟；(2)小聪返回到家时，小明距离公园还有多少米？(3)当x 为何值时，两人相距360米？28．如图，已知直线PQ MN ∥，点A 在直线MN 上，点B 、C 在直线PQ 上，射线AD 是CAN ∠的三等分线，即3CAN DAN ∠=∠，AC 平分BAE ∠，40BAC ∠︒=．(1)如图1，若30BAD ∠=︒，求AEC ∠的度数；(2)如图2，在AE 上有一点F ，满足CF AD ∥，且FG 平分AFC ∠交AB 于点G ，试探究AGF ∠与ACB ∠的数量关系，并说明理由；(3)如图3，若80ABC ∠=︒，BAC ∠绕点A 顺时针旋转，速度为6︒每秒，记旋转中的BAC ∠为B AC ''∠，C AN '∠的三等分线为AD '，即3C AN D AN ''∠=∠，同时BA 绕点B 逆时针旋转至BA '，速度始终为4︒每秒，当AC '与射线AM 重合时，B AC ''∠立即以原来速度的一半逆时针旋转，当AC '运动到与射线AN 重合时，整个运动停止，设旋转时间为t 秒，在旋转过程中，当AD BA ''∥时，请直接写出t 的值．。

重庆市第七十一中学校2017-2018学年七年级下学期第一次月考数学试题学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. 在方程3x﹣y=2，，，x2﹣2x﹣3=0中一元一次方程的个数为（）A．1个B．2个C．3个D．4个2. 下列方程中，解是x=1的是（）D．A．B．C．3. 解方程，去分母正确的是（）A．3(x+1)-2x-3=6 B．3(x+1)-2x-3=1C．3(x+1)-(2x-3)=12 D．3(x+1)-(2x-3)=64. 儿子今年12岁，父亲今年39岁，（）父亲的年龄是儿子的年龄的4倍. A．3年后B．3年前C．9年后D．不可能5. 根据“的3倍与5的和比的少2”列出的方程是（）A．B．C．D．6. 解方程，得为（）A．2 B．4 C．6 D．87. 某牧场,放养的鸵鸟和奶牛一共70只, 已知鸵鸟和奶牛的腿数之和为196条,则鸵鸟的头数比奶牛多( )A．20只B．14只C．15只D．13只8. 若关于的方程是一元一次方程，则= （）A．2 B．1 C．4 D．69. 用一根72cm的铁丝可围成一个长方形,则这个长方形的最大面积是（）A．81 B．18 C．324 D．32610. 甲、乙两同学从学校出发到县城去，甲每小时走4千米，乙每小时走6千米，甲先出发1小时，结果乙还比甲早到1小时．若设学校与县城间的距离为s千米，则以下方程正确的是（）A．B．D．C．11. 一家商店把某商品按标价的九折出售仍可获利15%，若该商品的进价是35元，若设标价为x元，则可列得方程（）A．B．C．D．12. 某商店有两个进价不同的计算器都卖了135元，其中一个盈利25%，另一个亏本25%，在这次买卖中，这家商店( )A．不赔不赚B．赚了9元C．赚了18元D．赔了18元二、填空题13. 方程的解是___________________________14. 若是关于x的方程的解，则=_________.15. 已知(2－4)2 + =0，则___________.16. 当＝___________时，代数式的值是－1.17. 学校组织植树活动，已知在甲处植树的有27人，在乙处植树的有18人．如果要使在甲处植树的人数是乙处植树人数的2倍，需要从乙队调___人到甲队．18. 某水池有甲进水管和乙出水管，已知单开甲注满水池需6h，单开乙管放完全池水需要9h，当同时开放甲、乙两管时需要_____h水池水量达全池的．三、解答题19. 解下列方程：（1）4＋3＝2(－1)＋1 （2）20. 解下列方程：(1) . (2)21. 解方程：x﹣=解：去分母，得6x﹣3x+1=4﹣2x+4…①即﹣3x+1=﹣2x+8…②移项，得﹣3x+2x=8﹣1…③合并同类项，得﹣x=7…④∴x=﹣7…⑤上述解方程的过程中，是否有错误？答：；如果有错误，则错在步．如果上述解方程有错误，请你给出正确的解题过程．22. 某城市与省会城市相距390千米，客车与轿车分别从该城市和省会城市同时出发，相向而行．已知客车每小时行80千米，轿车每小时行100千米，问经过多少小时后，客车与轿车相距30千米．23. 已知，，求当x取何值时，的值比的值小1？24. 某天，一蔬菜经营户用60元钱从蔬菜批发市场批发了西红柿和豆角共40品名西红柿豆角1.2 1.6批发价（单位：元/千克）零售价（单位：元/千1.82.5克）25. 如果把一个自然数各数位上数字从最高位到个位依次排出一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数叫做“和谐数”．例如：自然数64746从最高位到个位排出的一串数字是：6、4、7、4、6，从个位到最高排出的一串数字也是：6、4、7、4、6，所64746是“和谐数”．再如：33，181，212，4664，…，都是“和谐数”．（1）请你直接写出3个四位“和谐数”，猜想任意一个四位“和谐数”能否被11整除，并说明理由；（2）已知一个能被11整除的三位“和谐数”，设个位上的数字为x（，x为自然数），十位上的数字为y，求y与x的函数关系式．26. 某中学库存若干套桌椅，准备修理后支援贫困山区学校．现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费．(1)该中学库存多少套桌椅？(2)在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案:a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理．你认为哪种方案省时又省钱？为什么？。

第1页，共3页订……号：________订……2018--2019七年级数学试卷第一次阶段测试试卷考试时间：100分钟；满分：150分；命题人： 龙注意：本试卷包含Ⅰ、Ⅱ两卷。

第Ⅰ卷为试题卷，第Ⅱ卷为答题卷，所有答案必须填在答题卷的相应位置。

答案写在试卷上均无效，不予记分。

一、选择题（本大题共10小题，共40分） 1. ﹣（﹣2）等于（ ）A ．﹣2B ．2C ．D ．±22. 最大的负整数和绝对值最小的有理数分别是（ ）A ．0 ，﹣1B ．0 , 0C ．﹣1 , 0D ．﹣1 ，﹣13. 如果|x-1|+(y+2)2=0，那么x+y 的值是（ ）A ．0B ．-1C ．1D ．-24. 下列运算正确的是（ ）A ．（﹣a 2）3=﹣a 5B ．a 3•a 5=a 15C ．（﹣a 2b 3）2=a 4b 6D ．3a 2﹣2a 2=15. 为计算简便，把（﹣2.4）﹣（﹣4.7）﹣（+0.5）+（+3.4）+（﹣3.5）写成省略加号的和的形式，并按要求交换加数的位置正确的是（ ） A ．﹣2.4+3.4﹣4.7﹣0.5﹣3.5 B ．﹣2.4+3.4+4.7+0.5﹣3.5 C ．﹣2.4+3.4+4.7﹣0.5﹣3.5D ．﹣2.4+3.4+4.7﹣0.5+3.56. 我市2018年的最高气温为39℃，最低气温为-3℃，则计算2018年温差列式正确的（ ）A ．（+39）﹣（﹣3）B ．（+39）+（+3）C ．（+39）+（﹣3）D ．（+39）﹣（+3）7. 如图，乐乐将 ， ， ，0，1，2，3，4，5分别填入九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在a 、b 、c 分别标上其中的一个数，则 的值为 A.B. 0C. 1D. 38. 下列说法： 所有有理数都能用数轴上的点表示； 符号不同的两个数互为相反数； 有理数包括整数和分数； 两数相加，和一定大于任意一个加数 正确的有A. 3个B. 2个C. 1个D. 0个9. 有这样的一列数，第一个数为 ，第二个数为 ，从第三个数开始，每个数都等于它相邻两个数之和的一半 如：，则 等于A.B.C.D.10. 数学活动中，王老师给同学们出了一道题：规定一种新运算“@”，对于任意有理数a 和b ，有a @b=a-b+1，请你根据新运算，计算(2@3)@2的值是( )A. 0B.C.D. 1二、填空题（本大题共4小题，共20分）11. 三个连续奇数中，最小的一个是2n ﹣1，则这三个连续奇数的和是 ． 12. 观察一组数2，5，10，17，26，37，…，则第n 个数是 ．13. 目前世界上能制造的芯片最小工艺水平是5纳米，而我国能制造芯片的最小工艺水平是16纳米，已知1纳米=10﹣9米，用科学记数法将16纳米表示为 米． 14. 已知：，，， ，观察上面的计算过程，寻找规律并计算： ______． 三、计算题（本大题共4题，15-18题每题8分，共32分） 15. 直接写出计算结果：；；； ．16. 计算下列各题：第2页，共3页（1）27 + 18﹣﹙﹣3﹚﹣18 （2）15+（﹣5）+ 7﹣（﹣3）17. 运用简便方法计算：()2123（1）3-23⨯1142（2）-1.54 2.75（-5）+++18. 观察图形，解答问题：按下表已填写的形式完成表中的空格：(2) 请用你发现的规律求出图 中的数x ．四、解答题（本大题共5小题，共58分，其中19-20题每题10分，21-22题每题12分，23题14分）19. 在学习绝对值后，我们知道，|a|表示数a 在数轴上的对应点与原点的距离．如：|5|表示5在数轴上的对应点到原点的距离．而|5|=|5﹣0|，即|5﹣0|表示5、0在数轴上对应的两点之间的距离．类似的，有：|5﹣3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5﹣（﹣3）|，所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离．一般地，点A 、B 在数轴上分别表示有理数a 、b ，那么A 、B 之间的距离可表示为|a ﹣b|．请根据绝对值的意义并结合数轴解答下列问题：（1）数轴上表示2和3的两点之间的距离是；数轴上P 、Q 两点的距离为3，点P表示的数是2，则点Q 表示的数是 ．（2）点A 、B 、C 在数轴上分别表示有理数x 、﹣3、1，那么A 到B 的距离与A 到C 的距离之和可表示为 （用含绝对值的式子表示）；满足|x ﹣3|+|x+2|=7的x 的值为 ．（3）试求|x ﹣1|+|x ﹣2|+|x ﹣3|+…+|x ﹣100|的最小值．20. 在1， ，3， ， 中任取两个数相乘，最大的积是a ，最小的积是b ．求ab 的值；若 ，求 的值．第3页，共3页21.已知有理数a，b，c在数轴上的位置如图所示，且．________，；判断，，的符号；判断的符号．22.某出租车司机从西湖大道的汽车站出发在西湖大道西湖大道看作一条直线上来回载客假定向南行驶的路程记为正数，向北行驶的路程记为负数，行驶的各段路程依次为单位：：，，，，，，出租车最后是否回到出发点汽车站？出租车离汽车站最远是多少km？(3)在行程中，如果每行驶4km载到一个顾客，则出租车一共载到多少顾客？23.有一个n位自然数能被整除，依次轮换个位数字得到的新数能被整除，再依次轮换个位数字得到的新数能被整除，按此规律轮换后，能被整除，，能被整除，则称这个n 位数是的一个“轮换数”。

2017-2018学年下期第一次月考初一数学试题总分150分120分钟完卷一、选择题：（每题4分，共48分）1. 9的算术平方根是（）A．3B．±3C．3 D．±32．如图，直线a，b被直线c所截，则下列说法中错误的是（）A.∠1与∠2是邻补角B.∠1与∠3是对顶角C.∠2与∠4是同位角D.∠3与∠4是内错角3．在下面五幅图案中，(2)、(3)、(4)、(5)中哪一幅图案可以通过图案(1)平移得到（）A．(2) B．(3) C．(4) D．(5)4．如图1所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）A．∠3=∠4 B．∠D=∠DCE C．∠1=∠2 D．∠D+∠ACD=180°5．（-11）2的平方根是（）A．121 B．11 C．±11 D﹣116．估计的值在（）A．2到3之间B．3到4之间C．4到5之间D．5到6之间7．如图2，AB∥CD，AD、BC相交于点O，若∠A=20°，∠COD=100°，则∠C的度数是（）A．80°B．70°C．60°D．50°8. 如图3所示，CD ⊥AB ，AC ⊥BC ，图中能表示点A到直线BC的距离的是（）A．线段AC的长度；B．线段BC的长度；B．C．线段AB的长度D．线段CD的长度abc1234图1 图2 图39. 下列命题是真命题的是（ ）A ．两直线被第三条直线所截得的同位角相等B ．两直线被第三条直线所截得的同旁内角互补C ．两平行线被第三条直线所截得的同位角的平分线互相垂直D ．两平行线被第三条直线所截得的同旁内角的平分线互相垂直10.如图，是用棋子摆成的“上”字：如果按照此规律继续摆下去，那么通过观察，可以发现：第10个“上”字需用多少枚棋子（ ）图① 图② 图③ A ．36 B ．38C ．42D ．5011．将一张长方形纸片沿EF 折叠，折叠后的位置 如图所示，若∠EFB =65°，则∠AED ′等于（ ）A ．70°B ．65°C ．50°D ．25° 12．如图，AB ∥EF ，∠C =90°，则α、β、γ的关系是( ) A ．β+γ﹣α=90°B ． α+β﹣γ=90°C ．α+β+γ=180°D ．β=α+γ二、填空题：（每题4分，共24分）13． -8的立方根是 ；14．如图4，把小河里的水引到田地A 处就作AB ，垂足为B ，沿AB 挖水沟，水沟最短．理由是： . 15．把命题“对顶角相等”写成“如果…那么…”的形式为：__ . 16．已知b a ,满足011=-++b a ，则()8201ab 的值是 ；17．若36.25＝5.036，6.253＝15.906，则253600＝__________.18、如果∠α的两边分别平行于∠β的两边,且∠α比∠β的2倍少30°,则∠α,∠β的度数分别是 .D三、解答题:(本大题共2个小题，每小题8分，共16分)19．计算（8分）(1)2)1(25-- (2)33364631125.041027-++---20．（8分）求下列各式中x 的值(1)01642=-x (2)()327364x -=-四、解答题：(本大题共5个小题，每小题10分，共50分)21.如图，在边长为1的小正方形组成的网格中，△ABC 的顶点均在格点上，请按要求完成下列各题：（1）平移△ABC ，使得点A 与点D 重合，在网格中作出平移后的△DEF . （2）求△DEF 的面积.22.若正数m的平方根是5a＋1和a－19，求m的值及m的平方根.23.完成下列推理说明：如图，已知∠1 ＝∠2，∠B＝∠C，可推得AB∥C D．理由如下：∵∠1 ＝∠2（已知），且∠1 ＝∠CGD（______________ _________），∴∠2 ＝∠CGD（等量代换）．∴CE∥BF（___________________ ________）．∴∠＝∠C（__________________________）．又∵∠B＝∠C（已知），∴∠＝∠B（等量代换）．∴AB∥CD（________________________________）．24. 已知：如图，∠AEH＝130°，∠EFD＝50°，∠SMB＝120°．求∠DNG的度数．F25. 如图所示，已知∠1＋∠2＝180°，∠B ＝∠3， （1）求证：BD ∥EF （2）求证：∠AED ＝∠ACB五、解答题：(本大题共1个小题，共12分)26．如图，已知AB ∥CD ，CE ，BE 的交点为E ，现作如下操作：第一次操作，分别作∠ABE 和∠DCE 的平分线，交点为E 1， 第二次操作，分别作∠ABE 1和∠DCE 1的平分线，交点为E 2， 第三次操作，分别作∠ABE 2和∠DCE 2的平分线，交点为E 3…… 第n 次操作，分别作∠ABE n －1和∠DCE n －1的平分线，交点为E n .(1)如图①，求证：∠E ＝∠B ＋∠C ； (2)如图②，求证：∠E 1＝21∠E ； (3)猜想：若∠E n ＝b °，求∠BEC 的度数．2017-2018学年下期第一次月考初一数学试题数学试题参考答案一、选择题：CDBCC BCADC CB二、填空题：13、-2 14、垂线段最短 15、如果两个角是对顶角，那么这两个角相等 16、1 17、503.6 18、110°，70° 三、解答题：19．(1)解：原式=5-1=4……3分(2) 解：原式=-3-0- 12 + 12 + 14 ……6分= -243……8分 20．(1)解：1642=x (2)解：()276433-=-x42=x 343-=-x2±=x ……4分 35=x ……8分四、解答题：21、（1）略 ……5分 （2）3s =∆DEF ……10分 22、解：由题意得：5a ＋1+ a －19=0解得： a=3 ……5分m=5a ＋1=5×3+1=1616的平方根是±4 ……10分 23.完成下列推理说明：如图，已知∠1 ＝∠2，∠B ＝∠C ，可推得AB ∥C D ．理由如下： ∵∠1 ＝∠2（已知），且∠1 ＝∠CGD （对等角相等）， ∴∠2 ＝∠CGD （等量代换）．∴CE ∥BF （同位角相等，两直线平行）． ∴∠BFD ＝∠C （两直线平行，同位角相等）． 又∵∠B ＝∠C （已知），∴∠BFD ＝∠B （等量代换 ）． ∴AB ∥CD （内错角相等，两直线平行）．24、解：∵∠AEH ＝130°，∠EFD ＝50° ∴∠MEF =∠AEH ＝130° ∴∠MEF +∠EFD =130°+50°=180°∴AB ∥CD ∴∠MND =∠SMB ＝120°∴∠DNG =180°-∠MND =180°-120°=60° ……10分 25. （1）∵∠1＋∠2＝180°，∠1＋∠4＝180°，∴∠2＝∠4.∴BD ∥FE ……4分 （2）∵BD ∥FE （已证）∴∠3＝∠ADE . ∵∠3＝∠B ， ∴∠B ＝∠ADE . ∴DE ∥B C.∴∠AED ＝∠AC B. ……10分26. (1)证明：如图，过E 作EF ∥A B.∵AB ∥CD ，∴AB ∥EF ∥CD ， ∴∠B ＝∠1，∠C ＝∠2. ∵∠BEC ＝∠1＋∠2， ∴∠BEC ＝∠B ＋∠C.(4分)（2）证明：由(1)可得∠E 1＝∠ABE 1＋∠DCE 1∵∠ABE 和∠DCE 的平分线交点为E 1∴∠E 1＝12∠ABE ＋12∠DCE=12(∠ABE+∠DCE)又∵由（1）得∠E ＝∠ABE ＋∠DCE∴∠E 1＝21∠E ；(8分)(3)解：当∠E n＝b°时，∠BEC＝2n b°.( 12分)。

尾相接，不能做成三角形框架的是( )8A．x与y都是变量，x是自变量，y是因变量 B．所挂物体为6 kg，弹簧长度为11 cm8. 在下列条件：①A B C ∠+∠=∠；②::1:2:3A B C ∠∠∠=；③1123A B C ∠=∠=∠；④2A B C ∠=∠=∠；⑤12A B C ∠=∠=∠中，能确定ABC △为直角三角形的条件是（ ）A ．5个B ．4个C ．3个D ．2个9. 若M ＝(a ＋3)(a －4)，N ＝(a ＋2)(2a －5)，其中a 为有理数，则M 、N 的大小关系是( )A ．M ＞NB ．M ＜NC ．M ＝ND ．无法确定10. 如图，直线a ∥b ∥c ，直角三角板的直角顶点落在直线b 上，若∠1=38°，则∠2等于（ ）A ．38°B ．42°C ．52°D ．62°11. 端午节三天假期的某一天，小明全家上午8时自架小汽车从家里出发，到某著名旅游景点游玩．该小汽车离家的距离S （千米）与时间t （小时）的关系如图所示．根据图象提供的有关信息，下列说法中错误的是（ ）A ．景点离小明家180千米B ．小明到家的时间为17点C ．返程的速度为60千米每小时D ．10点至14点，汽车匀速行驶12. 下列说法正确的是（ ）①若直线AB 与CD 没有交点，则AB CD ∥；②平行于同一条直线的两条直线平行；③不相等的角一定不是对顶角；④过一点有且只有一条直线与已知直线平行；⑤过直线外一点作直线的垂线段，叫做点到直线的距离。

A ．①③④B ．③⑤C ．②③D ．②④二．填空题：(每小题4分,共32分)13. 人体中成熟的红细胞的平均直径为0.000 007 7 m ，用科学记数法表示为________ m 14. 如图，已知∠1＝∠2，则图中互相平行的线段是 ______________.15. 用一张包装纸包一本长、宽、厚如图所示的书(单位：cm)．若将封面和封底每一边都包进去3cm ，则需长方形的包装纸____________cm 2.16. 如图：AD∥BC，∠DAC=60°，∠ACF=25°，∠EFC=145°，∠B=54°，则∠BEF= °．17. 如图所示是关于变量x ，y 的程序计算，若开始输入的x 值为6，则最后输出因变量y 的值为___________.18. 若2(1)|2|0a b -+-=，则以a 、b 为边长的等腰三角形的周长是 。

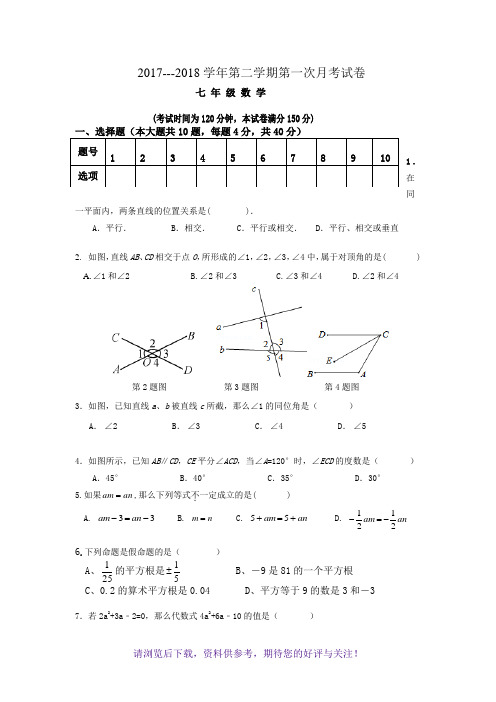
2017---2018学年第二学期第一次月考试卷七年级数学(考试时间为120分钟，本试卷满分150分)1．在同一平面内，两条直线的位置关系是( )．A．平行． B．相交． C．平行或相交． D．平行、相交或垂直2.如图，直线AB、CD相交于点O，所形成的∠1，∠2，∠3，∠4中，属于对顶角的是( )A.∠1和∠2B.∠2和∠3C.∠3和∠4D.∠2和∠4第2题图第3题图第4题图3．如图，已知直线a、b被直线c所截，那么∠1的同位角是（）A．∠2B．∠3C．∠4D．∠54．如图所示，已知AB∥CD，CE平分∠ACD，当∠A=120°时，∠ECD的度数是（）A．45° B．40° C．35° D．30°5.如果anam=,那么下列等式不．一定成立的是( )A. 33-=-anam B. nm= C. anam+=+55 D. anam2121-=-6.下列命题是假命题的是（）A、251的平方根是15± B、－9是81的一个平方根C、0.2的算术平方根是0.04D、平方等于9的数是3和－37．若2a2+3a﹣2=0，那么代数式4a2+6a﹣10的值是（）题号12345678910选项A．1 B．4 C．-4 D．-68．如图，下列条件中：（1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．能判定AB∥CD 的条件个数有（）A．1 B．2 C．3 D．4第8题图第9题图第10题图9 ．有理数数x在数轴上的位置如图所示，则x，的大小关系是（）．A．B．C ．D ．10．如图所示，AB ∥EF ，∠C 90=︒，则α、β、γ的关系是（ ） A ．90αβγ+-=︒ B ．180αβγ++=︒ C ．90βγα+-=︒ D ．βαγ=+二、填空题（本大题共4题，每题5分，共20分）11．94=______． 12．把命题“等角的余角相等”写成“如果……，那么……。

南岸初中2018-2019学年七年级下学期数学第一次月考试卷班级__________ 座号_____ 姓名__________ 分数__________一、选择题1．（2分）若不等式组有三个非负整数解，则m的取值范围是（）A.3＜m＜4B.2＜m＜3C.3＜m≤4D.2＜m≤3【答案】D【考点】一元一次不等式的特殊解【解析】【解答】解不等式组，可得，，即-3≤x＜m，该不等式组有三个非负整数解，分析可知，这三个非负整数为0、1、2，由此可知2≤m＜3.【分析】首先确定不等式组非负整数解，然后根据不等式的非负整数解得到一个关于m的不等式组，从而求解.解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到.2．（2分）如果关于x的不等式x＞2a﹣1的最小整数解为x=3，则a的取值范围是（）A. 0＜a＜2B. a＜2C. ≤a＜2D. a≤2【答案】C【考点】解一元一次不等式组，一元一次不等式组的应用【解析】【解答】解：∵关于x的不等式x＞2a﹣1的最小整数解为x=3，∴2≤2a﹣1＜3，解得：≤a＜2．故答案为：C．【分析】由题意可得不等式组2≤2a﹣1＜3，解这个不等式组即可求解。

3．（2分）下列说法中，不正确的个数有（）．①所有的正数都是整数. ②一定是正数. ③无限小数一定是无理数.④没有平方根. ⑤不是正数的数一定是负数. ⑥带根号的一定是无理数.A. 3个B. 4个C. 5个D. 6个【答案】D【考点】平方根，实数及其分类，有理数及其分类，无理数的认识【解析】【解答】解：①如是正数，但不是整数，故①说法错误.②当a=0时，，不是正数，故②说法错误.③无限小数包括无限循环小数和无限不循环小数，其中无限循环小数是有理数，无限不循环小数是无理数，故③说法错误.④的结果是正数，有平方根，故④说法错误.⑤0既不是正数，也不是负数，故⑤说法错误.⑥带根号且开不尽的数一定是无理数，故⑥说法错误.故不正确的说法有6个.故答案为：D.【分析】本题主要考查有理数和无理数的相关定义，熟记以下几点：（1）实数包括有理数和无理数；（2）有理数包括正数（正整数和正分数）、0和负数（负整数、负分数）；（3）无理数：无限不循环小数；（4）小数分为：有限小数和无限小数（无限不循环小数，无限循环小数）；（5）无限循环小数是有理数，无限不循环小数是无理数.4．（2分）如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图（两图都不完整），则下列结论中错误的是（）A. 该班总人数为50人B. 骑车人数占总人数的20%C. 步行人数为30人D. 乘车人数是骑车人数的2.5倍【答案】C【考点】频数（率）分布直方图，扇形统计图【解析】【解答】解：由条形图中可知乘车的人有25人，骑车的人有10人，在扇形图中分析可知，乘车的占总数的50%，所以总数有25÷50%=50人，所以骑车人数占总人数的20%；步行人数为30%×50=15人；乘车人数是骑车人数的2.5倍．故答案为：C【分析】根据直方图和扇形统计图对应的乘车人数与百分比可得某班的人数，即可判断A，根据扇形统计图可得骑车人数的百分比，即可判断B，根据总人数减去乘车人数再减去骑车人数即可得出步行人数，从而判断C，最后根据直方图的乘车人数与骑车人数即可判断D.5．（2分）如果方程组的解中与的值相等，那么的值是（）A.1B.2C.3D.4【答案】C【考点】解二元一次方程组【解析】【解答】解：∵方程组的解中与的值相等，∴x=y∴3x+7x=10解之：x=1∴y=1∴a+a-1=5解之：a=3故答案为：C【分析】根据已知可得出x=y，将x=y代入第1个方程可求出x、y的值，再将x、y的值代入第2个方程，解方程求出a的值。

重庆市万州区岩口复兴学校2018-2018学年七年级数学下学期第一次月考试题（无答案） 新人教版（时间：120分钟 总分：150分 ）温馨提示：亲爱的同学，这份试卷将再次记录你的自信、沉着、智慧和收获。

我们一直投给你信任的目光。

答题前，请你先通览全卷；答题时，请你认真审题，做到先易后难；答题后，要注意检查．预祝你取得好成绩！一、精心选一选（每小题3分，共45分）1、下列方程中是一元一次方程的是（ ）A 、错误！未找到引用源。

B 、错误！未找到引用源。

+4=3xC 、y 2+3y=0D 、9x ﹣y=22．下列方程组，解为⎩⎨⎧-=-=21y x 是（ ）．A ．⎩⎨⎧=+=-531y x y xB ．⎩⎨⎧-=+=-531y x y xC ．⎩⎨⎧=-=-133y x y xD ．⎩⎨⎧=+-=-533y x y x 3、解方程1﹣错误！未找到引用源。

，去分母，得（ ）A 、1﹣x ﹣3=3xB 、6﹣x ﹣3=3xC 、6﹣x+3=3xD 、1﹣x+3=3x4．下列方程组中，是二元一次方程组的有（ ）①1,23()2;x y x x y y -⎧+=⎪⎨⎪-=-⎩ ②,2;x y xy x y -=⎧⎨+=⎩ ③21,2;x y y z +=⎧⎨+=⎩ ④3;2;x y =⎧⎨=⎩ ⑤3;2;x y x =⎧⎨=+⎩ A ．5个 B ．4个 C ．3个 D ．2个5．用代入法解方程组2335x y x y +=⎧⎨-=⎩（1）由①得x=832y - ③； （2）把③代入②得3×832y --5y=5； （3）去分母得24-9y-10y=5；（4）解之得y=1，再由③得x=2．5，其中错误的一步是（ ）A ．（1）B ．（ 2）C ．（3）D ．（4）6．已知方程组4,2ax by ax by -=⎧⎨+=⎩的解为2,1,x y =⎧⎨=⎩，则2a-3b 的值为（ ）C B A A ．6 B ．4 C ．-4D ．-67．如果方程组326,322x y x y +=⎧⎨-=⎩的解也是方程4x+2a+y=0的解，则a 的值是（ ）A ．-913B ．-196C ．-2D ．2 8．（2018，杭州，3分）已知1,1x y =⎧⎨=-⎩是方程2x-ay=3的一个解，那么a 的值是（ ） A ．1 B ．3 C ．-3 D ．-19．（科内交叉题）如图，射线OC 的端点O 在直线AB 上，∠AOC 的度数比∠BOC 的2倍多10°，设∠AOC 和∠BOC 的度数分别为x °，y °，则可列方程组为（ ）A ．180,10x y x y +=⎧⎨=+⎩B ．180,210x y x y +=⎧⎨=+⎩C ．180,102x y x y +=⎧⎨=-⎩D ．90,210x y y x +=⎧⎨=-⎩10．小明今年12岁，他爷爷60岁，经过（ ）年以后，爷爷的年龄是小明的4倍.A.2B.4C.6D.811．为解决老百姓看病难的问题，•卫生部门决定大幅度降低药价，•某种药品降价40%后的价格为a 元，则降价前此药品的价格为（ ）A ．52a 元 B ．53a 元 C ．40%a 元 D ．60%a 元 12．某个体商贩在一次买卖中同时卖出两件上衣，每件都以135元的价格出售，•若按成本计算其中的一件赢利25%，另一件亏本25%，则在这次买卖中，商贩（ ）A ．赚了9元B ．赔了18元C ．赚了18元D ．不赚不赔13．古尔邦节，6位朋友均匀地围坐在圆桌旁共度佳节．圆桌半径为60cm ，每人离圆桌的距离均为10cm ，现又来了两名客人，每人向后挪动了相同的距离，再左右调整位置，使8人都坐下，并且8人之间的距离与原来6人之间的距离（即在圆周上两人之间的圆弧的长）相等．设每人向后挪动的距离为x ，•根据题意，可列方程（ ）A ．22(6010)(6010)68x ππ++=+B ．228(60)606x ππ=+ c ．2π（60+10）·6=2π（60+x ）·8D ．2π（60-10）·8=2π（60+x ）·614、方程4x+5y=98的正整数解的个数是（ ）A 4 B.5 C.6 D.715.植树节时，某班平均每人植树6棵，如果只由女同学完成，每人应植树15棵；如果只由男同学完成，每人应植树（ ）棵。

2018—2019学年度第一学期第一次月考七年级数学试卷一、选择题（本大题共10小题，每小题3分，共30分）1、下面的几何体中，属于棱柱的有（）A．1个B．2个 C．3个D．4个2、把图1所示的正方体的展开图围成正方体（文字露在外面），再将这个正方体按照图2，依次翻滚到第1格，第2格，第3格，第4格，此时正方体朝上一面的文字为（）A.富B.强C.文D.民3、用一个平面去截一个正方体，截面的形状不可能是（）A．梯形B．五边形C．六边形D．七边形4、下列几何体是由4个相同的小正方体搭成的，其中主视图和左视图相同的是（）A. B. C. D.5、中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入1000元记作＋1000元，那么－600元表示( )A．收入600元 B．支出600元 C．收入400元 D．支出400元6、下面所画数轴正确的是( )7、5的相反数是( )A ．－5B ．5C ．－15 D.158、若绝对值相等的两个数在数轴上的对应点的距离为6，则这两个数为( )A ．＋6和－6B ．－3和＋3C ．－3和＋6D ．－6和＋39、若两个有理数的和为负数，那么这两个有理数( )A ．一定都是负数B ．一正一负，且负数的绝对值大C ．一个为零，另一个为负数D ．至少有一个是负数10、已知|x |＝3，y ＝2，而且x ＜y ，则x －y 等于( )A ．1B ．－5C ．1或－5D ．5二、填空题（本大题共6小题，每小题4分，共24分）11、一个平面去截球，截面的形状一定是． 12、在－6，－23，0，－35，2.5这5个数中，负数有________个．13、小明写作业时不慎将墨水滴在数轴上，墨迹盖住部分的整数共有________个．14、在数轴上距原点3个单位长度的点表示的数是___________.15、谜语：正看三条边，侧看三条边，上看圆圈圈，就是没直边。

巴南初中2018-2019学年七年级下学期数学第一次月考试卷班级__________ 座号_____ 姓名__________ 分数__________一、选择题1．（2分）已知是方程组的解，则a+b+c的值是（）A. 3B. 2C. 1D. 无法确定【答案】A【考点】三元一次方程组解法及应用【解析】【解答】解：将代入方程得，①+②+③得4（a+b+c）=12，∴a+b+c=3，故答案为：A.【分析】将x、y、z的值代入方程组中，再观察方程组中各未知数的系数特点：相同字母的系数之和都为4，因此由（①+②+③）÷4，就可求得a+b+c的值。

2．（2分）如图，在数轴上表示无理数的点落在（）A.线段AB上B.线段BC上C.线段CD上D.线段DE上【答案】C【考点】估算无理数的大小【解析】【解答】解：∵=2≈2×1.414≈2.828，∴2.8＜2.828＜2.9，∴在线段CD上.故答案为：C.【分析】根据无理数大概的范围，即可得出答案.3．（2分）已知是二元一次方程组的解，则的值为（）A.B.C.D.【答案】B【考点】二元一次方程的解，解二元一次方程组【解析】【解答】解：∵是二元一次方程组的解，∴，∴∴a-b=故答案为：B【分析】将已知x、y的值分别代入方程组，建立关于a、b的方程组，解方程组求出a、b的值，然后将a、b的值代入代数式计算即可。

4．（2分）如图，已知∠B＋∠DAB＝180°，AC平分∠DAB，如果∠C＝50°，那么∠B等于（）A.50°B.60°D.80°【答案】D【考点】平行线的判定与性质，三角形内角和定理【解析】【解答】解：∵∠B+∠DAB=180°，∴AD∥BC，∵∠C=50°，∴∠C=∠DAC=50°，又∵AC平分∠DAB，∴∠DAC=∠BAC=∠DAB=50°，∴∠DAB=100°，∴∠B=180°-∠DAB=80°.故答案为：D.【分析】根据平行线的判定得AD∥BC，再由平行线性质得∠C=∠DAC=50°，由角平分线定义得∠DAB=100°，根据补角定义即可得出答案.5．（2分）方程2x+3y=15的正整数解有（）A.0个B.1个C.2个D.无数个【答案】C【考点】二元一次方程的解【解析】【解答】解：方程2x+3y=15，解得：x= ，当y=3时，x=3；当y=1时，x=6，∴方程2x+3y=15的正整数解有2个，故答案为：C．【分析】将方程用含y的代数式表示x，再根据原方程的正整数解，因此分别求出当y=3时；当y=1时的x的值，就可得出此方程的正整数解的个数。