湖南省衡阳八中2017届高三上学期第二次月考试题 数学(文)

2017-2018学年湖南省衡阳八中高三（上）第二次月考数学试卷（文科）一、选择题（每小题5分，共60分）1．（5分）已知x∈R，则“x＜﹣1”是“x2﹣1＞0”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件2．（5分）已知向量=（λ+1，1），=（2，2），若（+）⊥，则λ=（）A．0 B．6 C．﹣6 D．﹣123．（5分）已知i为虚数单位，复数z=i（2﹣i）的模|z|=（）A．1 B．C．D．34．（5分）已知函数f（x）=x2+（2a﹣1）x+b是偶函数，那么函数的定义域为（）A．B． C．（0，2]D．[2，+∞）5．（5分）已知角α的终点经过点（﹣3，4），则cos（π﹣α）=（）A．B．﹣ C．D．﹣6．（5分）已知﹣9，a1，a2，﹣1四个实数成等差数列，﹣9，b1，b2，b3，﹣1五个实数成等比数列，则b2（a2﹣a1）=（）A．8 B．﹣8 C．±8 D．7．（5分）已知两圆x2+y2=1和x2+y2﹣6x﹣8y+9=0，那么这两个圆的位置关系是（）A．相离B．相交C．外切D．内切8．（5分）某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，若这200名学生中每周的自习时间不超过m小时的人数为164，则m的值约为（）A．26.25 B．26.5 C．26.75 D．279．（5分）若y关于x的线性回归方程是由表中提供的数据求出，那么表中m的值为（）A．3.5 B．3 C．2.5 D．210．（5分）函数f（x）=x2﹣8lnx的单调递减区间为（）A．[2，+∞）B．（﹣∞，2]C．（0，2]D．（﹣2，2）11．（5分）已知三棱锥A﹣BCD中，，，且各顶点均在同一个球面上，则该球的体积为（）A．B．4πC．2πD．12．（5分）设函数f（x）=ln（x+）+x3（﹣1＜x＜1），则使得f（x）＞f （3x﹣1）成立的x的取值范围是（）A．（0，）B．（﹣∞，） C．（﹣1，）D．（，）二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）函数y=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，且函数图象关于点对称，则函数的解析式为．14．（5分）两条平行直线l1：x+（1+m）y﹣2=0和l2：mx+2y+4=0之间的距离为．15．（5分）设x，y是满2x+y=4的正数，则lgx+lgy的最大值是．16．（5分）已知函数f（x）=（m＜﹣1），对于任意s∈R，且s≠0，均存在唯一实数t（t≠s），使得f（s）=f（t），若关于x的方程|f（x）|=f （）有4个不相等的实数根，则a的取值范围是．三、解答题（共70分）17．（12分）已知袋中放有形状大小相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个，从袋中随机抽取一个小球，取到标号为2的小球的概率为，现从袋中不放回地随机取出2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．（1）记“a+b=2”为事件A，求事件A发生的概率．（2）在区间[0，2]上任取两个实数x，y，求事件B“x2+y2＞（a﹣b）2恒成立”的概率．18．（12分）如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，PA=AB，底面ABCD为直角梯形，∠ABC=∠BAD=90°，PA=BC=．（1）求证：平面PAC⊥平面PCD；（2）在棱PD上是否存在一点E，使CE∥平面PAB？若存在，请确定E点的位置；若不存在，请说明理由．19．（12分）已知各项均为正数的数列{a n}的前n项和为S n，对∀n∈N*，有2S n=a n2+a n．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）令b n=，设{b n}的前n项和为T n，求证：T n＜1．20．（12分）如图，在平面直角坐标系xOy中，已知椭圆过点A（2，1），离心率为．（1）求椭圆的方程；（2）若直线l：y=kx+m（k≠0）与椭圆相交于B，C两点（异于点A），线段BC 被y轴平分，且AB⊥AC，求直线l的方程．21．（12分）已知函数f（x）=xlnx．（1）求f（x）在[，3]上的最大值与最小值；（2）求证：f（x）﹣（x+1）2≤﹣3x﹣1．[选修4-4：坐标系与参数方程选讲]22．（10分）以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，已知点P的直角坐标为（1，2），点M的极坐标为，若直线l过点P，且倾斜角为，圆C以M为圆心，3为半径．（Ⅰ）求直线l的参数方程和圆C的极坐标方程；（Ⅱ）设直线l与圆C相交于A，B两点，求|PA|•|PB|．[选修4-5：不等式选讲]23．已知函数f（x）=x2+bx+c的顶点为（1，﹣1）．（1）解不等式|f（x）|≥3；（2）若实数a满足|x﹣a|＜，求证：|f（x）﹣f（a）|＜|a|+．2017-2018学年湖南省衡阳八中高三（上）第二次月考数学试卷（文科）参考答案与试题解析一、选择题（每小题5分，共60分）1．（5分）已知x∈R，则“x＜﹣1”是“x2﹣1＞0”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：由x2﹣1＞0得x＞1或x＜﹣1，则“x＜﹣1”是“x2﹣1＞0”的充分不必要条件，故选：A．2．（5分）已知向量=（λ+1，1），=（2，2），若（+）⊥，则λ=（）A．0 B．6 C．﹣6 D．﹣12【解答】解：∵=（λ+1，1），=（2，2），∴=（λ+3，3），若（+）⊥，则2（λ+3）+6=0，解得λ=﹣6．故选：C．3．（5分）已知i为虚数单位，复数z=i（2﹣i）的模|z|=（）A．1 B．C．D．3【解答】解：∵z=i（2﹣i）=2i+1，∴|z|=，故选：C．4．（5分）已知函数f（x）=x2+（2a﹣1）x+b是偶函数，那么函数的定义域为（）A．B． C．（0，2]D．[2，+∞）【解答】解：∵f（x）=x2+（2a﹣1）x+b是偶函数，∴f（﹣x）=x2﹣（2a﹣1）x+b=x2+（2a﹣1）x+b，即2a﹣1=0，解得a=．要使函数有意义，则log a x﹣1≥0，即log，∴log，解得0．即函数的定义域为（0，．故选：B5．（5分）已知角α的终点经过点（﹣3，4），则cos（π﹣α）=（）A．B．﹣ C．D．﹣【解答】解：∵角α的终点经过点（﹣3，4），∴x=﹣3，y=4，r=|OP|=5，则cos（π﹣α）=﹣cosα=﹣=，故选：A．6．（5分）已知﹣9，a1，a2，﹣1四个实数成等差数列，﹣9，b1，b2，b3，﹣1五个实数成等比数列，则b2（a2﹣a1）=（）A．8 B．﹣8 C．±8 D．【解答】解：由题得，又因为b2是等比数列中的第三项，所以与第一项同号，即b2=﹣3∴b2（a2﹣a1）=﹣8．故选B．7．（5分）已知两圆x2+y2=1和x2+y2﹣6x﹣8y+9=0，那么这两个圆的位置关系是（）A．相离B．相交C．外切D．内切【解答】解：∵x2+y2﹣6x﹣8y+9=0化成标准方程，得（x﹣3）2+（y﹣4）2=16，∴圆x2+y2﹣6x﹣8y+9=0的圆心为C1（3，4），半径r1=4．同理可得圆x2+y2=1的圆心为C2（0，0），半径r2=1．∵两圆的圆心距为|C1C2|==5，r1+r2=5，∴|C1C2|=r1+r2，可得两圆相外切．故选：C8．（5分）某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，若这200名学生中每周的自习时间不超过m小时的人数为164，则m的值约为（）A．26.25 B．26.5 C．26.75 D．27【解答】解：因为200名学生中每周的自习时间不超过m小时的人数为164，则自习时间不超过m小时的频率为：=0.82，第一组的频率为0.05，第二组的频率为0.25，第三组的频率为0.4，第四组的频率为0.2，第五组的频率为0.1，其中前三组的频率之和0.05+0.25+0.4=0.7，其中前四组的频率之和0.7+0.2=0.9，则0.82落在第四组，m=25+×2.5=26.59．（5分）若y关于x的线性回归方程是由表中提供的数据求出，那么表中m的值为（）A．3.5 B．3 C．2.5 D．2【解答】解：根据表中数据，计算=×（3+4+5+6）=4.5，=×（3+m+4.5+4）=；代入线性回归直线得，=0.7×4.5+0.35，解得m=2.5．故选：C．10．（5分）函数f（x）=x2﹣8lnx的单调递减区间为（）A．[2，+∞）B．（﹣∞，2]C．（0，2]D．（﹣2，2）【解答】解：f′（x）=2x﹣=（x＞0）．由f′（x）≤0，解得0＜x≤2．∴函数f（x）=x2﹣8lnx的单调递减区间为（0，2]．故选：C．11．（5分）已知三棱锥A﹣BCD中，，，且各顶点均在同一个球面上，则该球的体积为（）A．B．4πC．2πD．【解答】解：补体为底面边长为1，高为的长方体，外接球的球心为长方体体对角线中点，所以球的半径r=1，球的体积，12．（5分）设函数f（x）=ln（x+）+x3（﹣1＜x＜1），则使得f（x）＞f （3x﹣1）成立的x的取值范围是（）A．（0，）B．（﹣∞，） C．（﹣1，）D．（，）【解答】解：显然f（x）是奇函数，而x＞0时，f（x）递增，故x＜0时，f（x）递增，故f（x）在（﹣1，1）递增，若f（x）＞f（3x﹣1），则，解得：0＜x＜，故选：A．二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）函数y=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，且函数图象关于点对称，则函数的解析式为．【解答】解：函数y=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，所以：ω=2，且函数图象关于点对称，则：（k∈Z），解得：（k∈Z），由于0＜φ＜π，当k=0时，，所以函数的解析式为：．故答案为：．14．（5分）两条平行直线l1：x+（1+m）y﹣2=0和l2：mx+2y+4=0之间的距离为．【解答】解：由于两条直线l1：x+（1+m）y﹣2=0和l2：mx+2y+4=0平行，直线的斜率存在，且=≠，求得m=1，∴两条平行直线l1：x+2y﹣2=0和l2：x+2y+4=0，故它们之间的距离为=，故答案为：．15．（5分）设x，y是满2x+y=4的正数，则lgx+lgy的最大值是lg2．【解答】解：∵x，y是满2x+y=4的正数∴2x+y=4≥2即xy≤2∴lgx+lgy=lgxy≤lg2即最大值为lg2故答案为lg216．（5分）已知函数f（x）=（m＜﹣1），对于任意s∈R，且s≠0，均存在唯一实数t（t≠s），使得f（s）=f（t），若关于x的方程|f（x）|=f （）有4个不相等的实数根，则a的取值范围是（﹣4，﹣2）．【解答】解：由题意可知f（x）在[0，+∞）上单调递增，值域为[m，+∞），∵对于任意s∈R，且s≠0，均存在唯一实数t，使得f（s）=f（t），且s≠t，∴f（x）在（﹣∞，0）上是减函数，值域为（m，+∞），∴a＜0，∵|f（x）|=f（）有4个不相等的实数根，∴0＜f（）＜﹣m，又m＜﹣1，∴0＜＜﹣m，即0＜（+1）m＜﹣m，∴﹣4＜a＜﹣2，故答案为：（﹣4，﹣2），三、解答题（共70分）17．（12分）已知袋中放有形状大小相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个，从袋中随机抽取一个小球，取到标号为2的小球的概率为，现从袋中不放回地随机取出2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．（1）记“a+b=2”为事件A，求事件A发生的概率．（2）在区间[0，2]上任取两个实数x，y，求事件B“x2+y2＞（a﹣b）2恒成立”的概率．【解答】解：（1）根据从袋子随机抽取1个小球，取到标号为2的小球的概率是，可得=，解得n=2．从袋子中不放回地随机抽取2个球，共有基本事件12个，其中“a+b=2”为事件A 的基本事件有4个，则P（A）==．（2）“x2+y2＞（a﹣b）2恒成立”为事件B，则事件B等价于“x2+y2＞4恒成立，（x，y）可以看成平面中的点，则全部结果所构成的区域为Ω={（x，y）|0≤x≤2，0≤y≤2，x，y∈R}，而事件B构成的区域B={（x，y）|x2+y2＞4，（x，y）∈Ω}，所以P（B）==1﹣．18．（12分）如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，PA=AB，底面ABCD为直角梯形，∠ABC=∠BAD=90°，PA=BC=．（1）求证：平面PAC⊥平面PCD；（2）在棱PD上是否存在一点E，使CE∥平面PAB？若存在，请确定E点的位置；若不存在，请说明理由．【解答】解：（1）设PA=1．由题意PA=BC=1，AD=2．（2分）∵AB=1，，由∠ABC=∠BAD=90°．易得CD=AC=．由勾股定理逆定理得AC⊥CD．（3分）又∵PA⊥面ABCD，CD⊂面ABCD，∴PA⊥CD．又PA∩AC=A，∴CD⊥面PAC．（5分）又CD⊂面PCD，∴面PAC⊥面PCD．（6分）（2）作CF∥AB交于AD于F，作EF∥AP交于PD于E，连接CE．（8分）∵CF∥AB，EF∥PA，CF∩EF=F，PA∩AB=A，∴平面EFC∥平面PAB．（10分）又CE⊂平面EFC，∴CE∥平面PAB．∵BC=，AF=BC，∴F为AD的中点，∴E为PD中点．故棱PD上存在点E，且E为PD中点，使CE∥面PAB．（12分）19．（12分）已知各项均为正数的数列{a n}的前n项和为S n，对∀n∈N*，有2S n=a n2+a n．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）令b n=，设{b n}的前n项和为T n，求证：T n＜1．【解答】解：（I）当n=1时，2a1=，得a1=1或0（舍去）．=1（n≥2），当n≥2时，，，两式相减得a n﹣a n﹣1所以数列{a n}是以1为首相，1为公差的等差数列，．（Ⅱ）证明：b n====，=．20．（12分）如图，在平面直角坐标系xOy中，已知椭圆过点A（2，1），离心率为．（1）求椭圆的方程；（2）若直线l：y=kx+m（k≠0）与椭圆相交于B，C两点（异于点A），线段BC 被y轴平分，且AB⊥AC，求直线l的方程．【解答】解：（1）由条件知椭圆离线率e==，∴b2=a2﹣c2=a2，将点A（2，1），代入椭圆方程得解得，故椭圆方程为：；（2）将直线l：y=kx+m（k≠0）代入椭圆方程，x2+4（kx+m）2﹣8=0，整理得：（1+4k2）x2+8mkx+4m2﹣8=0，线段BC被y平分得：x B+x C=﹣=0，k≠0，m=0，∴B，C关于原点对称，设B（x，kx），C（﹣x，﹣kx），∴x2=，又∵AB⊥AC，A（2，1），∴•=（x﹣2）（﹣x﹣2）+（kx﹣1）（﹣kx﹣1）=5﹣（1+k2）x2=5﹣=0，解得k=±，由k=，直线y=x过点A（2，1）故k=不符合题意，所以，此时直线l的直线方程y=﹣x．21．（12分）已知函数f（x）=xlnx．（1）求f（x）在[，3]上的最大值与最小值；（2）求证：f（x）﹣（x+1）2≤﹣3x﹣1．【解答】解：（1）f（x）的定义域是（0，+∞），f′（x）=lnx+1，令f′（x）＞0，解得：x＞，令f′（x）＜0，解得：0＜x＜，故f（x）在[，）递减，在（，3]递增，故f（x）min=f（）=﹣，f（x）max=3ln3；（2）要证f（x）﹣（x+1）2≤﹣3x﹣1，即证lnx﹣x+1≤0，令h（x）=lnx﹣x+1，（x＞0），h′（x）=﹣1=，令h′（x）＞0，即1﹣x＞0，解得：0＜x＜1，令h′（x）＜0，解得：x＞1，故h（x）在（0，1）递增，在（1，+∞）递减，故h（x）max=h（1）=0，故h（x）≤0，问题得证．[选修4-4：坐标系与参数方程选讲]22．（10分）以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，已知点P的直角坐标为（1，2），点M的极坐标为，若直线l过点P，且倾斜角为，圆C以M为圆心，3为半径．（Ⅰ）求直线l的参数方程和圆C的极坐标方程；（Ⅱ）设直线l与圆C相交于A，B两点，求|PA|•|PB|．【解答】解：（Ⅰ）直线l的参数方程为（t为参数），（答案不唯一，可酌情给分）圆的极坐标方程为ρ=6sinθ．（5分）（Ⅱ）把代入x2+（y﹣3）2=9，得，设点A，B对应的参数分别为t1，t2，∴t1t2=﹣7，则|PA|=|t1|，|PB|=|t2|，∴|PA|•|PB|=7．（10分）[选修4-5：不等式选讲]23．已知函数f（x）=x2+bx+c的顶点为（1，﹣1）．（1）解不等式|f（x）|≥3；（2）若实数a满足|x﹣a|＜，求证：|f（x）﹣f（a）|＜|a|+．【解答】（1）解：函数f（x）=x2+bx+c的顶点为（1，﹣1），故，解得：b=﹣2，c=0，∴f（x）=x2﹣2x，∵|f（x）|≥3，∴f（x）≥3，或f（x）≤﹣3，∴x2﹣2x≥3，或x2﹣2x≤﹣3，解得x≤﹣1或x≥3，故不等式的解集为（﹣∞，﹣1]∪[3，+∞）（2）证明：|f（x）﹣f（a）|=|x2﹣2x﹣a2+2a|，=|（x﹣a）（x+a﹣2）|，=|x﹣a|•|x+a﹣2|，≤|x+a﹣2|，=|a﹣a+2a﹣2|，≤（|x﹣a|+2|a|+2），=（+2|a|+2）=|a|+．。

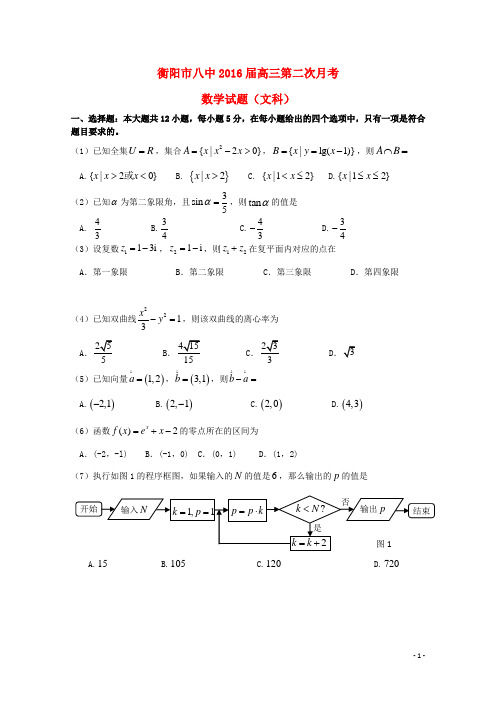
衡阳市八中2016届高三第二次月考数学试题（文科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知全集U R =，集合2{|20}A x x x =->，{|lg(1)}B x y x ==-，则A B ⋂= A.{|20}x x x ><或 B. {}|2x x > C. {|12}x x <≤ D.{|12}≤≤x x（2）已知α为第二象限角，且3sin 5α=，则tan α的值是 A. 43 B.34 C.43- D.34-（3）设复数113i z =-，21i z =-，则12z z +在复平面内对应的点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限（4）已知双曲线2213x y -=，则该双曲线的离心率为 ABCD（5）已知向量()1,2a =，()3,1b =，则b a -=A.()2,1-B.()2,1-C.()2,0D.()4,3 （6）函数()2xf x e x =+-的零点所在的区间为A ．(-2，-l)B ．(-1，0)C ．(0，1)D ．(1，2)（7）执行如图1的程序框图，如果输入的N 的值是6，那么输出的p 的值是A.15B.105C.120D.720（8）在三角形ABC 中，角,,A B C 对应的边分别为,,a b c ，若0120A ∠=，2a =，b =，则B ＝ A.3π B. 56π C. 566ππ或 D. 6π（9）如图所示的三棱柱，其正视图是一个边长为2的正方形，其俯视图是一个正三角形，该三棱柱侧视图的面积为 A ．32B ．3C ．22D ．4（10）若实数,x y 满足y x y x y -2≤0⎧⎪+≥1⎨⎪-≤1⎩则Z=x y 3+的最小值是A .-2B .1C .-1D .3（11）抛物线2y ax =的准线方程是1x =-，则实数a 的值为A .-2B .2C . 4-D .4（12）已知正方形OABC 的四个顶点O(0, 0), A(1, 0), B(1, 1), C(0, 1)，设u ＝2xy,v ＝x 2－y 2，是一个由平面xOy 到平面uO v 上的变换，则正方形OABC 在这个变换下的图形是二.填空题：本大题共4小题，每小题5分（13）命题2:,10P x R x x ∃∈-+>“” 的否定P ⌝为_______ ___（14）已知函数f （x ）＝232,1,,1,x x x ax x +<⎧⎨+≥⎩若f （f （0））＝4a ，则实数a ＝ .（15）若数列{}n a 满足：111,2()n n a a a n N *+==∈，则前6项的和6S = .（用数字作答）（16）定义在R 上的函数f(x)及其导函数f ' (x)的图像都是连续不断的曲线，且对于实数a, b (a ＜b)有f ' (a)＞0, f ' (b)＜0，现给出如下结论：∈[a, b], f(x 0)＝0；0∈[a, b], f(x 0)＞f(b)；∈[a, b], f(x 0)＞f(a)；∈[a, b], f(a)－f(b)＞f ' (x 0)(a －b).其中结论正确的有。

衡阳市八中2015届高三第二次月考试题数 学 （理）【试卷综析】试题考查的知识涉及到函数、三角函数、数列、导数等几章知识，重视学科基础知识和基本技能的考察，同时侧重考察了学生的学习方法和思维能力的考察，知识点综合与迁移。

试卷的整体水准应该说比较高，综合知识、创新题目的题考的有点少,试题适合阶段性质考试.注意事项：请本卷共21道小题，满分150分，时间120分钟。

选择题（每小题5分，共10小题，满分50分） 1．设集合{0,1}M =，{|N x Z y =∈=, 则（ ）A. M N =∅IB. {0}M N =IC. {1}M N =ID. M N M =I 【知识点】交集.A1【答案解析】D 解析：解：因为N 集合表示大于等于-1的整数，所以D 选项正确. 【思路点拨】根据题意求出集合N ，再利用交集求出结果.2.“33a b >”是“33log log a b>”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 【知识点】充要条件.A2【答案解析】B 解析：解：33a b a b >⇒>Q ，但a,b 属于实数，而33log log 0a b a b >⇒>>，所以“33a b >”是“33log log a b >”的必要不充分条件，所以B 选项正确.【思路点拨】根据题意可得两个条件的关系，利用充要关系可推得B 正确.3. 已知2510a b==, 则3222a b ⎛⎫+= ⎪⎝⎭( )A．- B． C．2-D．2【知识点】指数与对数.B6,B7 【答案解析】B解析：解：由题意可得()33222522log 10,log 102lg 2lg 5a b a b ⎛⎫==∴+=+==⎡⎤ ⎪⎣⎦⎝⎭，所以只有B 正确.【思路点拨】根据指数与对数的关系直接代入求出结果.4. 已知函数21(0)()cos (0)x x f x x x ⎧+>=⎨≤⎩, 则下列结论正确的是 ( ) A ．()f x 是偶函数 B. ()f x 是增函数C．()f x的值域为[－1，＋∞) D. ()f x是周期函数【知识点】函数的单调性与奇偶性.B4【答案解析】D 解析：解：由分段函数的图像可知函数是不是偶函数，不是单调增函数，在整个定义域上不是周期函数，计算可知()f x的值域为[－1，＋∞)，所以C正确.【思路点拨】由函数的性质可知函数的值域为[－1，＋∞)5. 已知命题tan1p x R x∃∈=：，使，命题q:0,2>∈∀xRx.下面结论正确的是（）A．命题“p q∧”是真命题 B. 命题“p q∧⌝”是假命题C．命题“p q⌝∨”是真命题 D．命题“qp⌝∧⌝”是假命题【知识点】命题.A2【答案解析】D 解析：解：由题意可知p为真命题，q为假命题，所以根据命题的真假可知D为正确选项.【思路点拨】根据已知命题的真假可以找出正确选项.6.曲线2 yx =与直线1y x=-及4x=所围成的封闭图形的面积为（ )A．2ln2 B. 2ln2- C．4ln2- D．42ln2-【知识点】定积分与面积.B13【答案解析】D 解析：解：由曲线2yx=与直线y=x-1联立，解得，x=-1，x=2，故所求图形的面积为424222112ln|42ln22S x dx x x xx⎛⎫⎛⎫=--=--=-⎪ ⎪⎝⎭⎝⎭⎰故答案为：4-2ln2．【思路点拨】利用函数的定积分求出所围成图形的面积.7.已知函数2siny x=的定义域为[,]a b ,值域为[2,1]-，则b a-的值不可能是( )A. 2πB. 76πC. 56πD. π【知识点】函数的性质.B1【答案解析】A 解析：解：函数y=2sinx 的定义域为[a ，b]，值域为[-2，1]，∴x ∈[a ，b]时，11sin 2x -≤≤∴定义域的区间长度b-a 最小为23π，最大为43π故选 D ．【思路点拨】由定义域的区间长度可直接求出结果.8.若函数2()(,,,)df x a b c d R ax bx c =∈++的图象如图所示，则:::a b c d 等于（ ） A ．1:6:5:(8)- B. 1:(6):5:(8)-- C ．1:(6):5:8- D ．1:6:5:8【知识点】函数的图像.B1,B5【答案解析】B 解析： 解：由题可知20ax bx c ++=的两根为1,5x x ==，所以12126,5b c x x x x a a +=-===在[]1,52y ax bx c =++的最大值时，()f x 最得最小值22244dac b a ∴=-，所以可得:::a b c d =1:(6):5:(8)--【思路点拨】根据已知条件与图像可知函数的取值，再列出关系式求出比值. 9．已知定义在R上的奇函数()x f 和偶函数()x g 满足()()2+-=+-x x a a x g x f ()1,0≠>a a 且，若(2014)g a =，则(2015)f -=（ ）A ．2 B. 2015201522-- C ． 2015201522-- D ． 2a【知识点】函数的奇偶性.B4 【答案解析】B解析：解：由题可知()()()()()22x x f x g x f x g x a a g x --+-=-+=-+∴=，2a ∴=()()2015201522201522x x f x f --∴=-∴-=-所以B 正确. 【思路点拨】根据函数的奇偶性可知函数()22x xf x -=-，代入可得结果.10. 已知方程|2|10x kx --+=有两个不相等的实根，则实数k 的取值范围是( )A.1(0,)2 B. 1(,1)2 C. (1,2) D. (2,)+∞ 【知识点】数形结合；直线斜率.H1【答案解析】B 解析：解：令f （x ）=|x-2|+1，g （x ）=kx ， 将方程|x-2|-kx+1=0有两个不相等的实根， 转化为函数f （x ），g （x ）有2个交点， 由题意可得函数f （x ）的图象（蓝线） 和函数g （x ）的图象（红线）有两个交点，如图所示：12OA k =数形结合可得112k <<，故选：B ．【思路点拨】由函数的图像可以满足条件的k 的取值范围. 二、选择题（每小题5分，共7小题，满分35分） 11. sin600︒= . 【知识点】三角函数的诱导公式.C2【答案解析】3解析：解：由诱导公式可得()3sin 600sin 120sin120︒=-︒=-︒=【思路点拨】由三角函数的诱导公式可直接求出结果.12. 已知幂函数223()(1)m m f x m m x +-=--在0x =处有定义，则实数m = .【知识点】幂函数的定义，函数的性质.B8【答案解析】 2 解析：解：因为函数为幂函数，所以223021,302m m m m m m m +-=∴==-+->∴=或又因为 .【思路点拨】根据函数的定义可列出条件，结合题目中的条件可求出结果.13．曲线11x y x -=+在点(1,0)M 处的切线的斜率为 .【知识点】导数.B11【答案解析】12 解析：解：()()()2211121111x x x y y x x x x +---'=∴==∴=+++Q 时12y '= 【思路点拨】由复合函数的导数可求出M 点处的导数值即切线的斜率.14．若函数3()63f x x bx b =-+在(0,1)内有极小值，则实数b 的取值范围是 . 【知识点】导数与极值.B11【答案解析】1(0,)2 解析：解：由题意得，函数f （x ）=x3-6bx+3b 的导数为()f x ' =3x2-6b在（0，1）内有零点，且 f （0）＜0，()1f '＞0． 即-6b ＜0，且 （3-6b ）＞0．102b <<故答案为：10,2⎛⎫ ⎪⎝⎭【思路点拨】利用导数和已知条件可直接求出b 的取值范围.15. 已知函数()f x 是定义在R 上的奇函数，当0>x 时，),1()(-=-x e x f x给出以下命题： ①当x 0<时，)1()(+=x e x f x； ②函数)(x f 有五个零点；③若关于x 的方程m x f =)(有解，则实数m 的取值范围是)2()2(f m f ≤≤-； ④1221,,()()2x x R f x f x ∀∈-<恒成立.其中，正确命题的序号是 .【知识点】函数的性质.B10【答案解析】①④ 解析：解：令z<0,所以-x>0,所以()()()1x f x e x f x -=--=-，所以()()1x f x e x =+，所以①正确；观察()f x 在x<0时的图像，令()()10x x f x e x e '=++=，x=-2,()()--2f x ∴∞在，上单调递减，在()2,0-上单调递增，而在(),1-∞-上，()0f x <，在()1,0-，()0f x > ，所以()f x 在(),0-∞上仅有一个零点，由对称性可知，()f x 在()0,+∞上也有一个零点，又因为()00f =，所以该函数有三个零点，做出它的图像可知源:]由图可知，若关于x 的方程m x f =)(有解，则11m -<<，且对1221,,()()2x x R f x f x ∀∈-<恒成立.【思路点拨】利用数形结合方法，我们可以逐一进行分析判断即可. 三、解答题（本大题共6小题,满分75分）16、(本题满分12分)设A 是单位圆和x 轴正半轴的交点，P ，Q 是单位圆上两点，O 是坐标原点，且AOP β∠=，(0,)2πβ∈, [)παα,0,∈=∠AOQ .（1）若点Q 的坐标是4(,),5m 其中0m <，求cos()sin()παα-+-的值. （2）设31(,)2P , 函数()sin()f ααβ=+，求()αf 的值域．【知识点】单位圆与三角函数的定义.C1【答案解析】(1)cos()sin()cos sin παααα-+-=--=15-.(2)()αf 的值域是1(,1]2-解析： 解：（1）由224()13550m m m ⎧+=⎪⇒=-⎨⎪<⎩，∴34cos ,sin 55m αα==-=. …..3分所以cos()sin()cos sin παααα-+-=--=15-. …..6分（2）由已知有6πβ=, …..8分因为[0,)απ∈，则7[,)666πππα+∈，所以1sin()126πα-<+≤.故()αf 的值域是1(,1]2-. …..12分【思路点拨】根据单位圆的性质可求出三角函数值，再根据三角函数的性质求出值域. 17、(本题满分12分)已知函数2()(0)f x ax bx c a =++≠满足(0)1f =-，对任意x R ∈都有1()x f x -≤，且11()()22f x f x -+=--．（1）求函数()f x 的解析式.（2）是否存在实数a ，使函数12()log [()]xg x f a =在(,)-∞+∞上为减函数？若存在，求出实数a 的取值范围；若不存在，说明理由． 【知识点】函数解析式.B1,B7【答案解析】(1)()21f x x x =+-(2) 21a a <->或解析：解：（1）由2()(0)f x ax bx c a =++≠满足(0)1f =-，对任意x R ∈都有1()x f x -≤，且11()()22f x f x -+=--，所以函数的图像对称轴为直线11,,222b x a ba =-=-∴=则-，任意x R ∈都有()1f x x ≥-即()210ax b x +-≥对任意x R ∈成立，()()2201110a a b f x x x b >⎧⎪∴∴==∴=+-⎨∆=-≤⎪⎩(2)由（1）知()()()21122log log 1xg x f a a a ==+-⎡⎤⎣⎦，其定义域为R 令()()21xu x a a =+-要使函数()()212log 1xg x a a =+-在(),-∞+∞上为减函数，只需要函数()()21xu x a a =+-在(),-∞+∞上为增函数，由指数函数的单调性，有211a a +->，解得21a a <->或，故存在实数a,当21a a <->或时，函数()()12log xg x f a =⎡⎤⎣⎦在(),-∞+∞上为减函数【思路点拨】由已知条件可求出函数，再由复合函数的关系可证明函数的单调性.18、(本题满分12分) 如图，已知在直四棱柱1111ABCD A B C D -（侧棱垂直底面的棱柱）中，AD DC⊥，AB DC∥，122DC DD AD AB ===2=．（1）求证：⊥DB 平面11BCC B . （2）求1BC 与平面1A BD所成的角的的正弦值．【知识点】直线与平面垂直；直线与平面所成角.G4,G5 【答案解析】D 解析： 解法一：（1）设E 是DC 的中点，连结BE ，则四边形DABE 为正方形，CD BE ⊥∴．故2=BD ，2C =B ，2CD =，90DBC ∴=o ∠，即BD BC ⊥．……….. 2分又1BD BB ⊥，1.B B BC B =I ……..3分BD ∴⊥平面11BCC B ， …….5分 （2）由（1）知⊥DB 平面11BCC B ， 又1BC ⊂平面11BCC B ，1BD BC ∴⊥，取DB 的中点F , 连结1A F ，又11A D A B=，则1A F BD ⊥．取1DC 的中点M ，连结FM ，则1FM BC ∥,FM BD ∴⊥.BD ∴⊥平面1A FM ，E BCDA1A1D1C1BFMH则过M 向平面1A FM引垂线,垂足必落在1A F上1A FM∴∠为直线1BC 与平面1A BD所成的角……8分连结1A M，在1A FM△中，1322A F =2211116222FM BC BC CC ==+=， 取11D C 的中点H ，连结1A H，HM ，在1Rt A HM△中，12A H =Q ，1HM =，13A M ∴=． ………..10分2221111933322cos 233262A F FM A M A FM A F FM +-+-∴∠===⋅⋅⋅．∴1BC 与平面1A BD 所成的角的的正弦值为63． ………..12分解法二： （1）以D 为原点，1DA DC DD ，，所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，则(000)D ，，，(110)B ，，，(0,2,2)C 1，1(102)A ，，， 1(112)B ，，,(0,2,0)C . ….. 2分(110)DB =u u u r ，，(1,1,0)BC =-u u u r,1(0,0,2)BB =u u u r …..3分110BD BC BD BC BD BC ⋅=-+=⇒⊥⇒⊥u u u r u u u r u u u r u u u r1110BD BB BD BB BD BB ⋅=⇒⊥⇒⊥u u u r u u u r u u u r u u u r又因为1.B B BC B =I所以，⊥DB 平面11BCC B . ………..5分 （2）设()x y z =，，n 为平面1A BD的一个法向量．由1DA ⊥u u u u r n ，DB ⊥u u u r n ，1(1,0,2),DA =u u u r (110)DB =u u u r ，，得200.x z x y +=⎧⎨+=⎩， 取1z =，则(221)=-，，n ． ……….8分 又1(1,1,2)BC =-u u u u r…….9分 设1BC 与平面1A BD所成的角为θ，则111||6sin |,|69BC cos BC BC θ⋅=<>===⨯u u u u ru u u u r u u u u r n n n ||||, 即1BC 与平面1A BD 所成的角的的正弦值6． ………..12分【思路点拨】建立空间直角坐标系，利用向量的关系可直接求出结果. 19、(本题满分13分)如图所示,一座小岛距离海岸线上最近的点P 的距离是2km ，从点P 沿海岸正东12km 处有一个城镇。

衡阳市八中2017届高三第二次月考数学试题答案 （考试内容：集合与逻辑用语、函数、导数、三角函数） 共150分，考试用时120分钟。

一 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.设R b a ∈,,则“4>+b a ”是“2,2>>b a 且”的（ ）（A ）充分不必要条件 （B ）必要不充分条件 （C ）充分必要条件 （D ）既非充分又非必要条件 答案：B2.已知a 函数3()12f x x x =-的极小值点，则a =( ) (A)-16 (B) -2 (C)16 (D)2 【答案】D3.设232555322555a b c ===（）,（），（），则a ， b ，c 的大小关系是（A ）A 、a ＞c ＞bB 、a ＞b ＞cC 、c ＞a ＞bD 、b ＞c ＞a4．函数y=sin(2x+π6 )的图象可看成是把函数y=sin2x 的图象作以下平移得到（ D ）A. 向右平移π6B. 向左平移π6C. 向右平移 π12D. 向左平移 π125．已知函数31(),3(),(2log 2)3(1),3xx f x f f x x ⎧≥⎪=+⎨⎪+<⎩则的值为（ B ）A ．227-B ．154C ．227D ．54-6. 已知函数sin cos 1212y x x ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭，则下列判断正确的是（B ） A ．此函数的最小正周期为2π，其图像的一个对称中心是,012π⎛⎫⎪⎝⎭B ．此函数的最小正周期为π，其图像的一个对称中心是,012π⎛⎫⎪⎝⎭ C ．此函数的最小正周期为2π，其图像的一个对称中心是,06π⎛⎫⎪⎝⎭D ．此函数的最小正周期为π，其图像的一个对称中心是,06π⎛⎫⎪⎝⎭7．若316sin =⎪⎭⎫⎝⎛-απ，则⎪⎭⎫⎝⎛+απ232cos = （ A ） A ．97-B ．31- C ．31 D ．978.已知函数()()()f x x a x b =--（其中a b >）的图象如右图所示，则函数()x g x a b =+的图象是（ A )【解析】：由题意得，x a =，x b =为()f x 的零点，由图可知，01a <<，1b <-，∴()g x 的图象可由xy a =向下平移b -个单位得到，∵01a <<，由于1-<b ，1->∴b 故可知A符合题意，故选A ．9．设12322()log (1)2x ex f x x x -⎧<⎪=⎨-≥⎪⎩，则不等式()2f x >的解集为 （ C ） A ．(1,2)(3,)⋃+∞ B ．(10,)+∞C ．(1,2)(10,)⋃+∞D ．（1，2）10. 已知函数1()()2ln ()f x a x x a R x =--∈，()ag x x=-，若至少存在一个0[1,e]x ∈，使00()()f x g x >成立，则实数a 的范围为( B )A ．[2e ，+∞) B ．(0，+∞) C ．[0，+∞) D ．(2e，+∞) 【答案】B11．已知函数()224|log |02151222x x f x x x x <<⎧⎪=⎨-+≥⎪⎩，若存在实数,,,a b c d 满足()()()()f a f b f c f d ===其中0d c b a >>>>，则abcd 的取值范围是（ B ）. A ．()16,21 B ．()16,24 C ．()17,21 D ．()18,24 【答案】B.1,0log 2=∴=∴ab ab 从而的两根是方程则记,12521,,log 422t x x d c t b =+-=2416,2416,40),12(2<<∴<<∴<<-=abcd cd t t cd 而512π 3π-xy 2O12．已知定义在R 上的奇函数f (x )的导函数为)(x f '，当x <0时，f （x ）满足()()2 ') (f x xf x xf x +<，则f (x )在R 上的零点个数为( A )A .1B .3C . 5D .1或3 【答案】A仅一个零点又时时)(,0)0(.0)()(0.0)(,0x f f x f x f x x f x ∴=>--=>∴<<二 填空题：本大题共4小题，每小题5分．13．已知集合{1,2,3,4},{|32},A B y y x x A ===-∈，则A B = 【答案】{1,4}14.以曲线x y 2cos =为曲边的曲边形(如下图阴影部分)面积为45|2sin 21|2sin 212cos 2cos :434412434412=-=-=⎰⎰ππππππππx x xdxxdx S 解15．函数f (x )＝2sin(ωx ＋φ)(ω>0，－π2<φ<π2)的部分图象如图所示，则(0)f 的值是 .解：353(),,241234T T ππππω=--=∴=∴=把5(,2)12π代入，得552sin()22662k ππϕπϕπ+=⇒+=+ 2,,3223k k Z ππππϕπϕϕ∴=-+∈-<<∴=-()2sin(2)(0)2sin()333f x x f ππ∴=-∴=-=-16. 已知()f x 为偶函数，当0x ≤ 时，1()x f x ex --=-，则曲线()y f x =在(1,2)处的切线方程式为_____________________________. 【答案】2y x = 【解析】试题分析：当0x >时，0x -<，则1()x f x ex --=+．又因为()f x 为偶函数，所以1()()x f x f x e x -=-=+，所以1()1x f x e -'=+，则切线斜率为(1)2f '=，所以切线方程为22(1)y x -=-，即2y x =．三 解答题: 解答应写出文字说明，证明过程或演算步骤．17. （本小题满分10分）设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x 。

一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知集合{}|5A x N x =∈<，则下列关系式错误的是（ ）A ．5A ∈B ．1.5A ∉C ．1A -∉D ．0A ∈ 【答案】A【解析】试题分析：因为{}|5A x N x =∈< ，而1.5,1,.5,1N N A A ∉-∉∴∉-∉，即B 、C 正确，又因为0N ∈且05<，所以0A ∈，即D 正确，故选A. 考点：集合与元素的关系. 2．已知命题1:0,2p x x x∀>+≥，则p ⌝为（ ） A ．10,2x x x ∀>+< B ．10,2x x x ∀≤+< C ．10,2x x x ∃≤+< D ．10,2x x x∃>+<【答案】D考点：全称命题的否定.3．下列函数中，定义域是R 且为增函数的是（ ） A.xy e -= B.3y x = C.ln y x =D.y x = 【答案】B【解析】试题分析：对于A ，xy e =为增函数，y x =-为减函数，故xy e -=为减函数，对于B ，2'30y x =>，故3y x =为增函数，对于C ，函数定义域为0x >，不为R ，对于D ，函数y x=为偶函数，在(),0-∞上单调递减，在()0,∞上单调递增，故选B. 考点：1、函数的定义域；2、函数的单调性. 4．集合{}{}2|ln 0,|9A x x B x x =≥=<,则AB =（ ）A ．()1,3B ．[)1,3C ．[]1,+∞D ．[],3e 【答案】B【解析】试题分析：因为{}{}|ln 0|1A x x A x x =≥==≥,{}{}2|9|33B x x B x x =<==-<<,所以AB ={}|13x x ≤<，故选B.考点：1、对数函数的性质及不等式的解法；2、集合交集的应用.5．若函数()y f x =的定义域是[]1,2016，则函数()()1g x f x =+的定义域是（ ）A ．(]0,2016B ．[]0,2015C ．(]1,2016D ．[]1,2017 【答案】B【解析】6．“p q ∨为真”是“p ⌝为假”的（ ）条件A ．充分不必要B ．必要不充分C ．充要D ．既不充分也不必要 【答案】B 【解析】试题分析：因为p 假q 真时，p q ∨真，此时p ⌝为真，所以，“p q ∨ 真”不能得“p ⌝为假”，而“p ⌝为假”时p 为真，必有“p q ∨ 真”，故选B. 考点：1、充分条件与必要条件；2、真值表的应用.7.若()f x 是定义在(),-∞+∞上的偶函数，[)()1212,0,x x x x ∀∈+∞≠，有()()21210f x f x x x -<-，则 （ ）A ．()()()213f f f -<<B ．()()()123f f f <-<C ．()()()312f f f <<D ．()()()321f f f <-< 【答案】D 【解析】8．函数()[]()cos 2,x f x x ππ=∈-的图象大致为（ ）A ．B ．C ．D ．【答案】C 【解析】试题分析：A 、当0x =时，()cos022f x ==，所以不正确；B 、当x π=时，()cos 11222f x π-===，所以不正确；D 、当0x =时，()cos022f x ==，所以不正确；综上所述，故选C.考点：函数的图象与性质.【方法点晴】本题通过对多个图象的选择考察函数的解析式、定义域、值域、单调性以及数学化归思想，属于难题.这类题型也是近年高考常见的命题方向，该题型的特点是综合性较强较强、考查知识点较多，但是并不是无路可循.解答这类题型可以从多方面入手，根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势，利用排除法，将不合题意选项一一排除.本题主要是利用特殊点排除法解答的.9．已知()x f 在R 上是奇函数，且满足()()x f x f -=+5，当()5,0∈x 时，()x x x f -=2，则()=2016f （ ）A 、-12B 、-16C 、-20D 、0 【答案】A 【解析】试题分析：因为()()5f x f x +=-，所以()()()105f x f x f x +=-+=，()f x 的周期为10，因此 ()()()()20164416412f f f =-=-=--=-，故选A.考点：1、函数的奇偶性；2、函数的解析式及单调性. 10．定义运算：,,a a ba b b a b≤⎧*=⎨>⎩．例如121*=，则函数()sin cos f x x x =*的值域为（ ）A ．⎡⎢⎣⎦B ．[]1,1-C ．⎤⎥⎣⎦D ．⎡-⎢⎣⎦【答案】D 【解析】考点：1、分段函数的解析式；2、三角函数的最值及新定义问题.11．函数()log 1xa f x a x =-有两个不同的零点，则实数的取值范围是（ ）A ．()1,10B ．()1,+∞C ．()0,1D ．()10,+∞ 【答案】B 【解析】试题分析：函数()f x 有两个零点等价于1xy a ⎛⎫= ⎪⎝⎭与log a y x =的图象有两个交点，当01a <<时同一坐标系中做出两函数图象如图（2），由图知有一个交点，符合题意；当1a >时同一坐标系中做出两函数图象如图（1），由图知有两个交点，不符合题意,故选B.x（1） （2）考点：1、指数函数与对数函数的图象；2、函数的零点与函数交点之间的关系.【方法点睛】本题主要考查指数函数与对数函数的图象、函数的零点与函数交点之间的关系.属于难题.判断方程()y f x =零点个数的常用方法：①直接法：可利用判别式的正负直接判定一元二次方程根的个数；②转化法：函数()y f x =零点个数就是方程()0f x =根的个数，结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数；③数形结合法：一是转化为两个函数()(),y g x y h x ==的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为(),y a y g x ==的交点个数的图象的交点个数问题.本题的解答就利用了方法③.12．设函数()''y f x =是()'y f x =的导数.某同学经过探究发现，任意一个三次函数()()320f x ax bx cx d a =+++≠都有对称中心()()00,x f x ，其中0x 满足()0''0f x =.已知函数()3211533212f x x x x =-+-，则1232016...2017201720172017f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（ ） A ．2013 B ．2014 C ．2015 D ．2016 【答案】D 【解析】1120142201520161...2201720172017201720172017f f f f f f ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++++⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦()12201620162=⨯⨯=，故选D. 考点：1、转化与划归思想及导数的运算；2、函数对称的性质及求和问题. 【方法点睛】本题通过 “三次函数()()320f x ax bx cx d a =+++≠都有对称中心()()0,x f x ”这一探索性结论考查转化与划归思想及导数的运算、函数对称的性质及求和问题，属于难题.遇到探索性结论问题，应耐心读题，分析新结论的特点，弄清新结论的性质，按新结论的要求，“照章办事”，逐条分析、验证、运算，使问题得以解决.本题的解答就是根据新结论性质求出()311533212f x x x x =-+-的对称中心后再利用对称性和的. 第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每题5分，满分20分．）13．已知函数()22,0,1log ,0,x x f x x x ⎧≤=⎨->⎩则()()2f f -=______．【答案】3考点：1、分段函数的解析式；2、指数函数、对数函数的性质.14．函数()x f x xe =在点()()1,1f 处的切线的斜率是 . 【答案】2e 【解析】 试题分析：()(),'x x x f x xe f x e xe =∴=+，则()'12f e =，故答案为2e .考点：利用导数求曲线上某点切线斜率. 15．幂函数1222)33)(+-+-=m m x m m x f （在区间()+∞,0上是增函数，则=m ．【答案】2【解析】【方法点睛】本题主要考查幂函数的定义与性质,属于中档题.幂函数定义与性质应用的三个关注点：(1)若幂函数()y xR αα=∈是偶函数，则α必为偶数．当α是分数时，一般将其先化为根式，再判断；(2)若幂函数()y xR αα=∈在()0,+∞上单调递增，则α0>，若在()0,+∞上单调递减，则0α<；(3)在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较.16．函数()y f x =图象上不同两点()()1122,,,A x y B x y 处的切线的斜率分别是A B k k ，，规定(),A B k k A B ABϕ-=（AB 为线段AB 的长度）叫做曲线()y f x =在点A 与点B 之间的“弯曲度”，给出以下命题：①函数321y x x =-+图象上两点A 与B 的横坐标分别为1和2，则(),A B ϕ>②存在这样的函数，图象上任意两点之间的“弯曲度”为常数； ③设点A,B 是抛物线21y x =+上不同的两点，则(),2A B ϕ≤；④设曲线xy e =（e 是自然对数的底数）上不同两点()()112212,,,,1A x y B x y x x -=且，若(),1t A B ϕ⋅<恒成立，则实数t 的取值范围是(),1-∞.其中真命题的序号为________.（将所有真命题的序号都填上） 【答案】②③【解析】试题分析：①错：(1,1),(2,5),|||7,A B A B AB k k =-=(,)A B ϕ∴=<②对：如1y =；③对；(,)2A B ϕ==≤；④错；1212(,)x x x x A B ϕ==1211,(,)A B ϕ==>因为1(,)t A B ϕ<恒成立，故1t ≤.故答案为②③.考点：1、利用导数求曲线的切线斜率；2、两点间的距离公式、最值问题、不等式恒成立问题.【方法点晴】本题通过新定义“弯曲度”对多个命题真假的判断考查利用导数求曲线的切线斜率、两点间的距离公式、最值问题、不等式恒成立问题以及及数学化归思想，属于难题.该题型往往出现在在填空题最后两题，综合性较强，同学们往往因为某一点知识掌握不牢就导致本题“全盘皆输”，解答这类问题首先不能慌乱更不能因贪快而审题不清，其次先从最有把握的命题入手，最后集中力量攻坚最不好理解的命题.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17．设集合{}{}2|8150,|10A x x x B x ax =-+==-=． （1）若15a =，判断集合A 与B 的关系； （2）若AB B =，求实数a 组成的集合C ．【答案】（1）A B ⊆；（2）{}5,3,0=C . 【解析】考点：1、集合的表示；2、子集的性质.18．衡阳市为增强市民的环境保护意识，面向全市征召义务宣传志愿者，现从符合条件的志愿者中随机抽取100名后按年龄分组：第1组[20,25)，第2组[25,30)，第3组[30,35)，第4组[35,40)，第5组[40,45]，得到的频率分布直方图如图所示.（1）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动，则应从第3，4，5组各抽取多少名志愿者？（2）在（1）的条件下，该市决定在第3，4组的志愿者中随机抽取2名志愿者介绍宣传经验，求第4组至少有一名志愿者被抽中的概率.【答案】（1）3,2,1；（2）710. 【解析】试题分析：（1）根据分层抽样方法按比例抽取即可；（2）列举出从5名志愿者中抽取2名志愿者有10种情况，其中第4组的2名志愿者12,B B 至少有一名志愿者被抽中的有7种，进而根据古典概型概率公式可得结果.（2）记第3组的3名志愿者为123,,A A A ，第4组的2名志愿者为12,B B ，则从5名志愿者中抽取2名志愿者有12(,)A A ，13(,)A A ，11(,)A B ，12(,)A B ，23(,)A A ，21(,)A B ，22(,)A B ，31(,)A B ，32(,)A B ，12(,)B B ，共10种，其中第4组的2名志愿者12,B B 至少有一名志愿者被抽中的有11(,)A B ，12(,)A B ，21(,)A B ，22(,)A B ，31(,)A B ，32(,)A B ，12(,)B B ，共7种，所以第4组至少有一名志愿都被抽中的概率为710. 考点：1、分层抽样的应用；2、古典概型概率公式.19．如图，在三棱柱111ABC A B C -中，111,A A AB CB A ABB =⊥． （1）求证：1AB ⊥平面1A BC ；（2）若15,3,60AC BC A AB ==∠=，求三棱锥1C AA B -的体积．【答案】（1）证明见解析；（2）【解析】试题分析：（1）有线面垂直的性质可得1BC AB ⊥，再由菱形的性质可得11AB A B ⊥，进而有线面垂直的判定定理可得结论；（2）先证三角形1A AB 为正三角形，再由于勾股定理求得AB 的值，进而的三角形1A AB 的面积，又知三棱锥的高为3BC =，利用棱锥的体积公式可得结果.考点：1、线面垂直的判定定理；2、勾股定理及棱锥的体积公式.20．2()sin 22f x x x =+. （1）求函数()f x 的单调递减区间；（2）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，若()12A f =，ABC ∆的面积为求a 的最小值.【答案】（1）5,36k k ππππ⎡⎤++⎢⎥⎣⎦（k ∈Z ）；（2）【解析】试题分析：（1）根据3222262k x k πππππ+≤-≤+可求得函数()f x 的单调递减区间；（2）由12A f ⎛⎫= ⎪⎝⎭可得3A π=，再由三角形面积公式可得12bc =，根据余弦定理及基本不等式可得a 的最小值.试题解析:（1）111()cos 22sin(2)22262f x x x x π=-+=-+， 令3222262k x k πππππ+≤-≤+，解得536k x k ππππ+≤≤+，k Z ∈， ∴()f x 的单调递减区间为5[,]36k k ππππ++（k Z ∈）.考点：1、正弦函数的图象和性质；2、余弦定理、基本不等式等知识的综合运用．21．已知条件4:11p x ≤--，条件22:q x x a a +<-，且p 是q 的一个必要不充分条件，求实数a的取值范围．【答案】[]1,2-．【解析】试题分析：先化简条件p 得31x -≤<，分三种情况化简条件q ，由p 是q 的一个必要不充分条件，可分三种情况列不等组，分别求解后求并集即可求得符合题意的实数a 的取值范围. 试题解析：由411x ≤--得:31p x -≤<，由22x x a a +<-得()()10x a x a +--<⎡⎤⎣⎦，当12a =时，:q ∅；当12a <时，():1,q a a --；当12a >时，():,1q a a -- 由题意得，p 是q 的一个必要不充分条件， 当12a =时，满足条件；当12a <时，()[)1,3,1a a --⊆-得11,2a ⎡⎫∈-⎪⎢⎣⎭， 当12a >时，()[),13,1a a --⊆-得1,22a ⎛⎤∈ ⎥⎝⎦ 综上，[]1,2a ∈-． 考点：1、充分条件与必要条件；2、子集的性质及不等式的解法.【方法点睛】本题主要考查子集的性质及不等式的解法、充分条件与必要条件，属于中档题,判断p 是q 的什么条件，需要从两方面分析：一是由条件p 能否推得条件q ，二是由条件q 能否推得条件p .对于带有否定性的命题或比较难判断的命题，除借助集合思想把抽象、复杂问题形象化、直观化外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题．本题的解答是根据集合思想解不等式求解的.22．已知函数()2ln f x x bx a x =+-. （1）当函数()f x 在点()()1,1f 处的切线方程为550y x +-=，求函数()f x 的解析式；（2）在（1）的条件下，若0x 是函数()f x 的零点，且()*0,1,x n n n N ∈+∈，求n 的值； （3）当1a =时，函数()f x 有两个零点()1212,x x x x <，且1202x x x +=，求证：()00f x '>． 【答案】（1）()26ln f x x x x =--；（2）3n =；（3）证明见解析.【解析】试题解析： （1）()2a f'x x b x =+-，所以(1)251(1)106f'b a b f b a =+-=-=-⎧⎧⇒⎨⎨=+==⎩⎩， ∴函数()f x 的解析式为2()6ln (0)f x x x x x =-->；（2）22626()6ln '()21x x f x x x x f x x x x --=--⇒=--=， 因为函数()f x 的定义域为0x >， 令(23)(2)3'()02x x f x x x +-==⇒=-或2x =， 当(0,2)x ∈时，'()0f x <，()f x 单调递减，当(2,)x ∈+∞时，'()0f x >，函数()f x 单调递增，且函数()f x 的定义域为0x >，（3）当1a =时，函数2()ln f x x bx x =+-，21111()ln 0f x x bx x =+-=，22222()ln 0f x x bx x =+-=， 两式相减可得22121212()ln ln 0x x b x x x x -+--+=，121212ln ln ()x x b x x x x -=-+-． 1'()2f x x b x =+-，0001'()2f x x b x =+-，因为1202x x x +=， 所以12120121212ln ln 2'()2()2x x x x f x x x x x x x +-=⋅+-+--+212121221221122112211121ln ln 2()211ln ln ln 1x x x x x x x x x x x x x x x x x x x x x x ⎡⎤⎛⎫-⎢⎥ ⎪⎡⎤--⎝⎭⎢⎥=-=--=-⎢⎥⎢⎥-+-+-⎣⎦+⎢⎥⎢⎥⎣⎦设211x t x =>，2(1)()ln 1t h t t t -=-+， ∴2222214(1)4(1)'()0(1)(1)(1)t t t h t t t t t t t +--=-==>+++， 所以()h t 在(1,)+∞上为增函数，且(1)0h =，∴()0h t >，又2110x x >-，所以0'()0f x >． 考点：1、导数几何意义及零点存在定理；2、构造函数证明不等式.【方法点睛】本题主要考查导数几何意义及零点存在定理、构造函数证明不等式，属于难题.涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题，一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路.。

2017-2018学年下学期衡阳市八中高三第二次月考试卷文科数学一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知集合{}|5A x N x =∈<，则下列关系式错误的是（ ） A ．5A ∈ B ．1.5A ∉ C ．1A -∉ D ．0A ∈ 【答案】A2．已知1:0,2p x x x∀>+≥，则p ⌝为（ ） A ．10,2x x x ∀>+< B ．10,2x x x ∀≤+<C ．10,2x x x ∃≤+<D ．10,2x x x∃>+<【答案】D3．下列函数中，定义域是R 且为增函数的是（ ）A.x y e -=B.3y x = C.ln y x = D.y x = 【答案】B4．集合{}{}2|ln 0,|9A x x B x x =≥=≤,则A B =（ ）A ．()1,3B ．[]1,3C ．[]1,+∞D ．[],3e 【答案】B5．若函数()y f x =的定义域是[]1,2016，则函数()()1g x f x =+的定义域是（ ） A ．(]0,2016 B ．[]0,2015 C ．(]1,2016 D ．[]1,2017【答案】B 6．“p q ∨为真”是“p ⌝为假”的（ ）条件A ．充分不必要B ．必要不充分C ．充要D ．既不充分也不必要 【答案】B7．若()f x 是定义在(),-∞+∞上的偶函数，[)()1212,0,x x x x ∀∈+∞≠，有()()21210f x f x x x -<-，则（ ）A ．()()()213f f f -<<B ．()()()123f f f <-<C ．()()()312f f f <<D ．()()()321f f f <-< 【答案】D8．函数()[]()cos 2,xf x x ππ=∈-的图象大致为（ ）A ．B ．C ．D ．【答案】C9．已知()x f 在R 上是奇函数，且满足()()x f x f -=+5，当()5,0∈x 时，()x x x f -=2，则()=2016f （ ） A 、-12 B 、-16 C 、-20 D 、0【答案】A10．定义运算：,,a a ba b b a b ≤⎧*=⎨>⎩．例如121*=，则函数()sin cos f x x x =*的值域为（ ）A．⎡⎢⎣⎦ B ．[]1,1- C．⎤⎥⎣⎦ D．⎡-⎢⎣⎦ 【答案】D11．函数()log 1xa f x a x =-有两个不同的零点，则实数的取值范围是（ ） A ．()1,10 B ．()1,+∞ C ．()0,1 D ．()10,+∞ 【答案】B12．设函数()''y f x =是()'y f x =的导数.某同学经过探究发现，任意一个三次函数()()320f x ax bx cx d a =+++≠都有对称中心()()00,x f x ，其中0x 满足()0''0f x =.已知函数()3211533212f x x x x =-+-，则1232016...2017201720172017f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（ ） A ．2013 B ．2014 C ．2015 D ．2016【答案】D二、填空题（本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.）13．已知函数()22,0,1log ,0,x x f x x x ⎧≤=⎨->⎩则()()2f f -=______．【答案】314．函数()x f x xe =在点()()1,1f 处的切线的斜率是 .【答案】2e 15．幂函数1222)33)(+-+-=m m xm m x f （在区间()+∞,0上是增函数，则=m 【答案】216．函数()y f x =图象上不同两点()()1122,,,A x y B x y 处的切线的斜率分别是A B k k ，，规定(),A Bk k A B ABϕ-=（AB 为线段AB 的长度）叫做曲线()y f x =在点A 与点B 之间的“弯曲度”，给出以下：①函数321y x x =-+图象上两点A 与B 的横坐标分别为1和2，则(),A B ϕ> ②存在这样的函数，图象上任意两点之间的“弯曲度”为常数； ③设点A,B 是抛物线21y x =+上不同的两点，则(),2A B ϕ≤；④设曲线xy e =（e 是自然对数的底数）上不同两点()()112212,,,,1A x y B x y x x -=且，若(),1t A B ϕ⋅<恒成立，则实数t 的取值范围是(),1-∞.其中真的序号为________.（将所有真的序号都填上）【答案】②③ 【解析】：①错：(1,1),(2,5),|||7,A B A B AB k k =-=(,)A B ϕ∴=< ②对：如1y =；③对；(,)2A B ϕ==≤；④错；1212(,)x x x x A B ϕ==，1211,(,)A B ϕ==因为1(,)t A B ϕ<恒成立，故1t ≤. 三、解答题（本大题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤.）17．设集合{}{}2|8150,|10A x x x B x ax =-+==-=．（1）若15a =，判断集合A 与B 的关系； （2）若A B B =，求实数的组成的集合C ．【答案】{}5,3=A （1）若51=a ，则{}5=B ，于是A B ⊆（2）若B B A = ，则A B ⊆，分如下两种情形讨论：①当a=0时，A B ⊆=φ符合题意②当0≠a 时，由{}5,31⊆⎭⎬⎫⎩⎨⎧=a B ，则a=3或5. 故实数a 组成集合{}5,3,0=C .18．衡阳市为增强市民的环境保护意识，面向全市征召义务宣传志愿者，现从符合条件的志愿者中随机抽取100名后按年龄分组：第1组[20,25)，第2组[25,30)，第3组[30,35)，第4组[35,40)，第5组[40,45]，得到的频率分布直方图如图所示.（1）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动，则应从第3，4，5组各抽取多少名志愿者？（2）在（1）的条件下，该市决定在第3，4组的志愿者中随机抽取2名志愿者介绍宣传经验，求第4组至少有一名志愿者被抽中的概率.【答案】（1）第3组的人数为0.310030⨯=，第4组的人数为0.210020⨯=，第5组的人数为0.110010⨯=，因为第3，4，5组共有60名志愿者，所以利用分层抽样的方法在60名志愿者中抽取6名志愿者，每组抽取的人数分别为第3组：306360⨯=；第4组：206260⨯=；第5组：106160⨯=. 所以应从第3，4，5组中分别抽取3人，2人，1人.（2）记第3组的3名志愿者为123,,A A A ，第4组的2名志愿者为12,B B ，则从5名志愿者中抽取2名志愿者有12(,)A A ，13(,)A A ，11(,)A B ，12(,)A B ，23(,)A A ，21(,)A B ，22(,)A B ，31(,)A B ，32(,)A B ，12(,)B B ，共10种，其中第4组的2名志愿者12,B B 至少有一名志愿者被抽中的有11(,)A B ，12(,)A B ，21(,)A B ，22(,)A B ，31(,)A B ，32(,)A B ，12(,)B B ，共7种，所以第4组至少有一名志愿都被抽中的概率为710.19．如图，在三棱柱111ABC A B C -中，111,A A AB CB A ABB =⊥．（1）求证：1AB ⊥平面1A BC ；（2）若15,3,60AC BC A AB ==∠=，求三棱锥1C AA B -的体积．【答案】（1）在侧面11A ABB 中，因为1A A AB =，所以四边形11A ABB 为菱形，所以11AB A B ⊥，因为CB ⊥平面111,A A B B A B ⊂平面11A ABB ，所以1C B A B⊥，又因为11,A B BC B AB =∴⊥平面1A BC ．（2）因为CB ⊥平面11,A ABB AB ⊂平面11A ABB ，AB ⊂平面11A ABB ，CB AB ∴⊥，在Rt ABC ∆中，5,3AC BC ==，所以由勾股定理，得4AB =，又在菱形11A ABB 中，160A AB ∠=，所以1A AB ∆为正三角形，则11111443332C AA B AA B V S CB -∆=⨯=⨯⨯⨯=三棱锥20．2()sin 22f x x x =+. （1）求函数()f x 的单调递减区间；（2）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，若()12Af =，ABC ∆的面积为的最小值.【答案】（1）111()cos 22sin(2)2262f x x x x π=-=-+， 令3222262k x k πππππ+≤-≤+，解得536k x k ππππ+≤≤+，k Z ∈，∴()f x 的单调递减区间为5[,]36k k ππππ++（k Z ∈）. （2）∵1()sin()1262A f A π=-+=，∴1sin()62A π-=，∴3A π=.又∵1sin 23bc π=，∴12bc =，∵222222cos 12a b c bc A b c bc bc =+-=+-≥=，∴a ≥（当且仅当b c ===”）∴的最小值是考点：正弦函数的图象和性质、余弦定理、基本不等式等知识的综合运用． 21．已知条件4:11p x ≤--，条件22:q x x a a +<-，且p 是的一个必要不充分条件，求实数的取值范围．【答案】由411x ≤--得:31p x -≤<，由22x x a a +<-得()()10x a x a +--<⎡⎤⎣⎦，当12a =时，:q ∅；当12a <时，():1,q a a --；当12a >时，():,1q a a --由题意得，p 是的一个必要不充分条件，当12a =时，满足条件；当12a <时，()[)1,3,1a a --⊆-得11,2a ⎡⎫∈-⎪⎢⎣⎭，当12a >时，()[),13,1a a --⊆-得1,22a ⎛⎤∈ ⎥⎝⎦综上，[]1,2a ∈-．已知函数 22．已知函数()2ln f x x bx a x =+-.（1）当函数()f x 在点()()1,1f 处的切线方程为550y x +-=，求函数()f x 的解析式； （2）在（1）的条件下，若0x 是函数()f x 的零点，且()*0,1,x n n n N ∈+∈，求的值；（3）当1a =时，函数()f x 有两个零点()1212,x x x x <，且1202x x x +=，求证：()0f x '>． 【答案】（1）()2a f x x b x '=+-，所以()()12511106f b a b f b a '=+-=-⎧=-⎧⎪⇒⎨⎨=+==⎪⎩⎩， ∴函数()f x 的解析式为()()26ln 0f x x x x x =-->；（2）()()226266ln 21x x f x x x x f x x x x --'=--⇒=--=，因为函数()f x 的定义域为0x >，令()()()2323022x x f x x x x+-'==⇒=-=或，当()0,2x ∈时，()0f x '<，()f x 单调递减，当()2,x ∈+∞时，()0f x '>，函数()f x 单调递增，且函数()f x 的定义域为0x >，令()()()2323022x x f x x x x+-'==⇒=-=或，且()0,2x ∈时，()()0,f x f x '<单调递减，当()2,x ∈+∞时，()0f x '>，()f x 单调递增，且函数()f x 至少有1个零点，而()10f =，不符合要求，()()()()2361ln 30,462ln 46ln 04e f f =-<=-=>，∴()03,4x ∈，故3n =．（3）当1a =时，函数()2ln f x x bx x =+-，()()2211112222ln 0,ln 0f x x bx x f x x bx x =+-==+-=，两式相减可得()()22121212121212ln ln ln ln 0,x x x x b x x x x b x x x x --+--+==-+-．()()000112,2f x x b f x x b x x ''=+-=+-，因为1202x x x +=，所以()()12120121212ln ln 222x x x x f x x x x x x x +-'=⨯+-+--+()21212121122112212221112ln ln 21ln ln 211ln 1x x x x x x x x x x x x x x x x x x x x x x -⎡⎤-=-=--⎢⎥-+-+⎣⎦⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥=-⎢⎥-+⎢⎥⎢⎥⎣⎦设()()21211,ln 1t x t h t t x t -=>=-+， ∴()()()()()()22222141140111t t t h t t t t t t t +--'=-==>+++，所以()h t 在()1,+∞上为增函数，且()10h =，∴()0h t >，又211x x >-，所以()00f x '>．考点：导数几何意义，零点存在定理，构造函数证明不等式【思路点睛】涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题，一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路.。

2017-2018学年湖南省衡阳八中高二（上）第二次月考数学试卷（文科）一、选择题：（本大题共12小题，每小题5分，共60分）1．已知命题p：∀x∈R，2x2+1＞0，则￢p是（）A．∀x∈R，2x2+1≤0 B．∃x0∈R，2x02+1＞0C．∃x0∈R，2x02+1＜0 D．∃x0∈R，2x02+1≤02．问题：①某地区10000名中小学生，其中高中生2000名，初中生4500名，小学生3500名，现从中抽取容量为200的样本；②从1002件同一生产线生产的产品中抽取20件产品进行质量检查．方法：Ⅰ、随机抽样法Ⅱ、分层抽样法Ⅲ、系统抽样法．其中问题与方法配对较适宜的是（）A．①Ⅰ，②ⅡB．①Ⅲ，②ⅠC．①Ⅱ，②ⅢD．①Ⅲ，②Ⅱ3．某小组有3名男生和2名女生，从中任选2名同学去参加演讲比赛，事件“至少1名女生”与事件“全是男生”（）A．是互斥事件，不是对立事件B．是对立事件，不是互斥事件C．既是互斥事件，也是对立事件D．既不是互斥事件也不是对立事件4．双曲线=1的焦距为（）A．2B．4C．2D．45．若函数f（x）=x3﹣x2+1，则（）A．最大值为1，最小值为B．最大值为1，无最小值C．最小值为，无最大值D．既无最大值也无最小值6．若f′（x0）=2，则等于（）A．﹣1 B．﹣2 C．1 D．7．有5个不同的社团，甲、乙两名同学各自参加其中1个社团，每位同学参加各个社团的可能性相同，则这两位同学参加的社团不同的概率为（）A．B．C．D．已求得关于y与x的线性回归方程为=2.1x+0.85，则m的值为（）A．1 B．0.85 C．0.7 D．0.59．如图是某电视台综艺节目举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（）A．84，4.84 B．84，1.6 C．85，4 D．85，1.610．春节期间，“厉行节约，反对浪费”之风悄然吹开，某市通过随机询问100名性别不同的“”附：参照附表，得到的正确结论是（）A．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别有关”B．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别无关”C．有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”D．有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”11．函数f（x）=ax2+bx（a＞0，b＞0）在点（1，f（1））处的切线斜率为2，则的最小值是（）A．10 B．9 C．8 D．12．设双曲线=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，与双曲线的其中一个交点为P，设O为坐标原点，若（m，n∈R），且mn=，则该双曲线的离心率为（）A．B．C．D．二、填空题：（本大题共4小题，每小题5分，共20分）13．甲、乙两人下棋，两人下成和棋的概率为，乙获胜的概率为，甲获胜的概率是，甲不输的概率．14．在区间[﹣2，2]上任取一个实数，则该数是不等式x2＜1的解的概率为．15．抛物线y2=﹣4x的准线方程是．5]，部分对应值如下表．下列关于f（x）的命题：①函数f（x）是周期函数；②函数f（x）在[0，2]是减函数；③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；④当1＜a＜2时，函数y=f（x）﹣a有4个零点；⑤函数y=f（x）﹣a的零点个数可能为0、1、2、3、4个．其中正确命题的序号是．三、解答题（本大题共6小题，共70分，应写出必要的文字说明、证明过程或演算步骤）17．已知函数f（x）=x3+．求函数f（x）在点P（2，4）处的切线方程．18．已知p：（x+2）（x﹣6）≤0，q：|x﹣2|＜5，命题“p∨q”为真，“¬p”为真，求实数x的取值范围．19．2012年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：（60，65），[65，70），[70，75），[80，85），[85，90）后得到如图的频率分布直方图．（1）某调查公司在采样中，用到的是什么抽样方法？（2）求这40辆小型车辆车速的众数和中位数的估计值．（3）若从车速在[60，70）的车辆中任抽取2辆，求车速在[65，70）的车辆至少有一辆的概率．20．已知关于x的一元二次方程x2﹣2ax+b2=0，其中a，b∈R．若a随机选自区间[0，4]，b随机选自区间[0，3]，求方程有实根的概率．21．已知椭圆=1（a＞b＞0）上任意一点到两焦点F1，F2距离之和为4，离心率为．（1）求椭圆的标准方程；（2）若直线l的斜率为，直线l与椭圆C交于A，B两点．点P（2，1）为椭圆上一点，求△PAB的面积的最大值．22．已知函数f（x）=a（x﹣1）2+lnx，a∈R．（Ⅰ）当a=﹣时，求函数y=f（x）的单调区间；（Ⅱ）a=时，令h（x）=f（x）﹣3lnx+x﹣．求h（x）在[1，e]上的最大值和最小值；（Ⅲ）若函数f（x）≤x﹣1对∀x∈[1，+∞）恒成立，求实数a的取值范围．2015-2016学年湖南省衡阳八中高二（上）第二次月考数学试卷（文科）参考答案与试题解析一、选择题：（本大题共12小题，每小题5分，共60分）1．已知命题p：∀x∈R，2x2+1＞0，则￢p是（）A．∀x∈R，2x2+1≤0 B．∃x0∈R，2x02+1＞0C．∃x0∈R，2x02+1＜0 D．∃x0∈R，2x02+1≤0【考点】命题的否定．【分析】利用全称命题的否定是特称命题，写出结果即可．【解答】解：因为全称命题的否定是特称命题，所以命题p：∀x∈R，2x2+1＞0，则￢p是：∃x0∈R，2x02+1≤0．故选：D．2．问题：①某地区10000名中小学生，其中高中生2000名，初中生4500名，小学生3500名，现从中抽取容量为200的样本；②从1002件同一生产线生产的产品中抽取20件产品进行质量检查．方法：Ⅰ、随机抽样法Ⅱ、分层抽样法Ⅲ、系统抽样法．其中问题与方法配对较适宜的是（）A．①Ⅰ，②ⅡB．①Ⅲ，②ⅠC．①Ⅱ，②ⅢD．①Ⅲ，②Ⅱ【考点】收集数据的方法．【分析】根据分层抽样和系统抽样的定义即可得到结论【解答】解：对于①因为地区10000名中小学生，分为高中，初中，小学，所以应该采用分层抽样，故①Ⅱ搭配，对于②，从1002件同一生产线生产的产品中抽取20件产品，应该根据系统抽样法，故②Ⅲ搭配．故选：C3．某小组有3名男生和2名女生，从中任选2名同学去参加演讲比赛，事件“至少1名女生”与事件“全是男生”（）A．是互斥事件，不是对立事件B．是对立事件，不是互斥事件C．既是互斥事件，也是对立事件D．既不是互斥事件也不是对立事件【考点】随机事件．【分析】互斥事件是两个事件不包括共同的事件，对立事件首先是互斥事件，再就是两个事件的和事件是全集，本题所给的两个事件不可能同时发生，且和是全集．【解答】解：“至少有一名女生”包括“一男一女”和“两个女生”两种情况，这两种情况再加上“全是男生”构成全集，且不能同时发生，故互为对立事件，故选C．4．双曲线=1的焦距为（）A．2B．4C．2D．4【考点】双曲线的简单性质．【分析】直接利用双曲线方程，求出c，即可得到双曲线的焦距．【解答】解：双曲线=1，可知a2=10，b2=2，c2=12，∴c=2，2c=4．双曲线=1的焦距为：4．故选：D．5．若函数f（x）=x3﹣x2+1，则（）A．最大值为1，最小值为B．最大值为1，无最小值C．最小值为，无最大值D．既无最大值也无最小值【考点】函数的最值及其几何意义．【分析】求函数的导数，利用导数研究函数的极值和最值，即可得到结论．【解答】解：∵f（x）=x3﹣x2+1，∴f′（x）=3x2﹣3x=3x（x﹣1），则由f′（x）=3x（x﹣1）＞0，解得x＞1或x＜0，此时函数单调递增，由f′（x）=3x（x﹣1）＜0，解得0＜x＜1，此时函数单调递减，即函数在x=0处取得极大值，在x=1处取得极小值，无最大值和最小值．故选：D．6．若f′（x0）=2，则等于（）A．﹣1 B．﹣2 C．1 D．【考点】极限及其运算．【分析】首先应该紧扣函数在一点导数的概念，由概念的应用直接列出等式，与式子对比求解．【解答】解析：因为f′（x0）=2，由导数的定义即=2⇒=﹣1所以答案选择A．7．有5个不同的社团，甲、乙两名同学各自参加其中1个社团，每位同学参加各个社团的可能性相同，则这两位同学参加的社团不同的概率为（）A．B．C．D．【考点】列举法计算基本事件数及事件发生的概率．【分析】分别求出甲、乙两名同学各自参加其中1个社团的总事件个数，及这两位同学参加的社团不同的事件个数，代入古典概型概率计算公式，可得答案．【解答】解：有5个不同的社团，甲、乙两名同学各自参加其中1个社团，共有5×5=25种不同的情况；其中这两位同学参加的社团共有5×4=20不同的情况；故这两位同学参加的社团不同的概率P==，故选：D．已求得关于y与x的线性回归方程为=2.1x+0.85，则m的值为（）A．1 B．0.85 C．0.7 D．0.5【考点】线性回归方程．【分析】求出这组数据的横标和纵标的平均数，写出这组数据的样本中心点，把样本中心点代入线性回归方程求出m的值．【解答】解：∵==，=，∴这组数据的样本中心点是（，），∵关于y与x的线性回归方程=2.1x+0.85，∴=2.1×+0.85，解得m=0.5，∴m的值为0.5．故选：D．9．如图是某电视台综艺节目举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（）A．84，4.84 B．84，1.6 C．85，4 D．85，1.6【考点】茎叶图；众数、中位数、平均数；极差、方差与标准差．【分析】由茎叶图可知评委打出的最低分为79，最高分为93，去掉最高分和最低分，其余得分为84，84，86，84，87，求出平均数，再求出方差．【解答】解：由茎叶图可知评委打出的最低分为79，最高分为93，其余得分为84，84，86，84，87，故平均分为=85，方差为 [3×（84﹣85）2+（86﹣85）2+（87﹣85）2]=1.6．故选D．10．春节期间，“厉行节约，反对浪费”之风悄然吹开，某市通过随机询问100名性别不同的附：参照附表，得到的正确结论是（）A．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别有关”B．在犯错误的概率不超过l%的前提下，认为“该市居民能否做到‘光盘’与性别无关”C．有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”D．有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”【考点】独立性检验．【分析】通过图表读取数据，代入观测值公式计算，然后参照临界值表即可得到正确结论．【解答】解：由2×2列联表得到a=45，b=10，c=30，d=15．则a+b=55，c+d=45，a+c=75，b+d=25，ad=675，bc=300，n=100．代入，得k2的观测值k=．因为2.706＜3.030＜3.841．所以有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”．故选C．11．函数f（x）=ax2+bx（a＞0，b＞0）在点（1，f（1））处的切线斜率为2，则的最小值是（）A．10 B．9 C．8 D．【考点】导数的运算；基本不等式．【分析】求出原函数的导函数，由f′（1）=2a+b=2，得，把变形为后整体乘以1，展开后利用基本不等式求最小值．【解答】解：由f（x）=ax2+bx，得f′（x）=2ax+b，又f（x）=ax2+bx（a＞0，b＞0）在点（1，f（1））处的切线斜率为2，所以f′（1）=2a+b=2，即．则=．当且仅当，即时“=”成立．所以的最小值是9．故选B．12．设双曲线=1（a＞0，b＞0）的右焦点为F，过点F作与x轴垂直的直线l交两渐近线于A、B两点，与双曲线的其中一个交点为P，设O为坐标原点，若（m，n∈R），且mn=，则该双曲线的离心率为（）A．B．C．D．【考点】双曲线的简单性质；平面向量的基本定理及其意义．【分析】求出A、C坐标，然后求出P的坐标，代入双曲线方程，利用，即可求出双曲线的离心率．【解答】解：由题意可知，代入=，得，代入双曲线方程，得，所以4e2mn=1，因为，即可得；故选C．二、填空题：（本大题共4小题，每小题5分，共20分）13．甲、乙两人下棋，两人下成和棋的概率为，乙获胜的概率为，甲获胜的概率是，甲不输的概率．【考点】互斥事件的概率加法公式．【分析】甲获胜和乙不输是对立互斥事件，甲不输与乙获胜对立互斥事件，根据概率公式计算即可．【解答】解：甲获胜和乙不输是对立互斥事件，∴甲获胜的概率是1﹣（）=，甲不输与乙获胜对立互斥事件．∴甲不输的概率是1﹣=，故答案为：，．14．在区间[﹣2，2]上任取一个实数，则该数是不等式x2＜1的解的概率为．【考点】几何概型．【分析】由题意，本题符合几何概型，只要求出对应区间的长度，利用长度比得到概率．【解答】解：由已知，区间[﹣2，2]长度为4，而不等式x2＜1的解是（﹣1，1），区间长度为2，由几何概型公式得到在区间[﹣2，2]上任取一个实数，则该数是不等式x2＜1的解的概率为；故答案为：．15．抛物线y2=﹣4x的准线方程是x=1．【考点】抛物线的简单性质．【分析】根据抛物线的标准方程及基本概念，结合题中数据加以计算，可得答案．【解答】解：∵抛物线的方程y2=﹣4x，∴2p=4，得=1，因此，抛物线的焦点为F（﹣1，0），准线方程为x=1．故答案为：x=15]，部分对应值如下表．下列关于f（x）的命题：①函数f（x）是周期函数；②函数f（x）在[0，2]是减函数；③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；④当1＜a＜2时，函数y=f（x）﹣a有4个零点；⑤函数y=f（x）﹣a的零点个数可能为0、1、2、3、4个．其中正确命题的序号是②⑤．【考点】利用导数求闭区间上函数的最值；函数的周期性；函数的零点；利用导数研究函数的单调性．【分析】先由导函数的图象和原函数的关系画出原函数的大致图象，再借助与图象和导函数的图象，对五个命题，一一进行验证，对于假命题采用举反例的方法进行排除即可得到答案．【解答】解：由导函数的图象和原函数的关系得，原函数的大致图象可由以下两种代表形式，如图：由图得：①为假命题．函数f（x）不能断定为是周期函数．②为真命题，因为在[0，2]上导函数为负，故原函数递减；③为假命题，当t=5时，也满足x∈[﹣1，t]时，f（x）的最大值是2；④为假命题，当a离1非常接近时，对于第二个图，y=f（x）﹣a有2个零点，也可以是3个零点．⑤为真命题，动直线y=a与y=f（x）图象交点个数可以为0、1、2、3、4个，故函数y=f （x）﹣a的零点个数可能为0、1、2、3、4个．综上得：真命题只有②⑤．故答案为：②⑤三、解答题（本大题共6小题，共70分，应写出必要的文字说明、证明过程或演算步骤）17．已知函数f（x）=x3+．求函数f（x）在点P（2，4）处的切线方程．【考点】利用导数研究曲线上某点切线方程．【分析】求得函数的导数，求得切线的斜率，由点斜式方程，即可得到所求切线方程．【解答】解：函数f（x）=x3+的导数为f′（x）=x2，则函数f（x）在点P（2，4）处的切线斜率为k=f′（2）=4，即有函数f（x）在点P（2，4）处的切线方程为y﹣4=4（x﹣2），即为4x﹣y﹣4=0．18．已知p：（x+2）（x﹣6）≤0，q：|x﹣2|＜5，命题“p∨q”为真，“¬p”为真，求实数x的取值范围．【考点】复合命题的真假．【分析】利用不等式的解法分别化简命题p，q，由命题“p∨q”为真，“¬p”为真，可知：p假q真，即可得出．【解答】解：p：由（x+2）（x﹣6）≤0，解得﹣2≤x≤6，q：由|x﹣2|＜5，解得﹣3≤x≤7．由命题“p∨q”为真，“¬p”为真，可知：p假q真，由，∴实数x的取值范围是[﹣3，﹣2）∪（6，7]．19．2012年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：（60，65），[65，70），[70，75），[80，85），[85，90）后得到如图的频率分布直方图．（1）某调查公司在采样中，用到的是什么抽样方法？（2）求这40辆小型车辆车速的众数和中位数的估计值．（3）若从车速在[60，70）的车辆中任抽取2辆，求车速在[65，70）的车辆至少有一辆的概率．【考点】等可能事件的概率；用样本的频率分布估计总体分布．【分析】（1）这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，是一个具有相同间隔的抽样，并且总体的个数比较多，这是一个系统抽样；（2）选出直方图中最高的矩形求出其底边的中点即为众数；求出从左边开始小矩形的面积和为0.5对应的横轴的左边即为中位数；利用各个小矩形的面积乘以对应矩形的底边的中点的和为数据的平均数．（3）从图中可知，车速在[60，65）的车辆数和车速在[65，70）的车辆数．从车速在（60，70）的车辆中任抽取2辆，设车速在[60，65）的车辆设为a，b，车速在[65，70）的车辆设为c，d，e，f，列出各自的基本事件数，从而求出相应的概率即可．【解答】解：（1）由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，是一个具有相同间隔的抽样，并且总体的个数比较多，这是一个系统抽样．故调查公司在采样中，用到的是系统抽样，（2）众数的估计值为最高的矩形的中点，即众数的估计值等于77.5设图中虚线所对应的车速为x，则中位数的估计值为：0.01×5+0.02×5+0.04×5+0.06×（x﹣75）=0.5，解得x=77.5，即中位数的估计值为77.5（3）从图中可知，车速在[60，65）的车辆数为：m1=0.01×5×40=2（辆），车速在[65，70）的车辆数为：m2=0.02×5×40=4（辆）设车速在[60，65）的车辆设为a，b，车速在[65，70）的车辆设为c，d，e，f，则所有基本事件有：（a，b），（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b，f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）共15种其中车速在[65，70）的车辆至少有一辆的事件有：（a，c），（a，d），（a，e），（a，f），（b，c），（b，d），（b，e），（b，f），（c，d），（c，e），（c，f），（d，e），（d，f），（e，f）共14种所以，车速在[65，70）的车辆至少有一辆的概率为．20．已知关于x的一元二次方程x2﹣2ax+b2=0，其中a，b∈R．若a随机选自区间[0，4]，b随机选自区间[0，3]，求方程有实根的概率．【考点】列举法计算基本事件数及事件发生的概率．【分析】由a∈[0，4]，b∈[0，3]，求出试验的全部结果构成区域Ω的面积为μΩ=3×4=12，事件A所构成的区域Ω={（a，b）|0≤a≤4，0≤b≤3，a≥b}，由此能示出方程有实根的概率．【解答】解：设事件A表示“方程有实根”，因为a∈[0，4]，b∈[0，3]，则试验的全部结果构成区域Ω={（a，b）|0≤a≤4，0≤b≤3}，Ω的面积为μΩ=3×4=12，事件A所构成的区域Ω={（a，b）|0≤a≤4，0≤b≤3，a≥b}，A的面积为，所以方程有实根的概率．21．已知椭圆=1（a＞b＞0）上任意一点到两焦点F1，F2距离之和为4，离心率为．（1）求椭圆的标准方程；（2）若直线l的斜率为，直线l与椭圆C交于A，B两点．点P（2，1）为椭圆上一点，求△PAB的面积的最大值．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．【分析】（1）由椭圆定义，椭圆上任意一点到两焦点距离之和为常数2a=，得，离心率，于是，从而可得椭圆的标准方程；（2）设直线l的方程为，把其与椭圆的方程联立，求出弦长，即为△PAB的底，由点线距离公式求出△PAB的高，然后用基本不等式求最值．【解答】解：（1）由条件得：，解得，所以椭圆的方程为（2）设l的方程为，点A（x1，y1），B（x2，y2），由消去y得x2+2mx+2m2﹣4=0．令△=4m2﹣8m2+16＞0，解得|m|＜2，由韦达定理得．则由弦长公式得|AB|=•=•．又点P到直线l的距离，∴，当且仅当m2=2，即时取得最大值．∴△PAB面积的最大值为2．22．已知函数f（x）=a（x﹣1）2+lnx，a∈R．（Ⅰ）当a=﹣时，求函数y=f（x）的单调区间；（Ⅱ）a=时，令h（x）=f（x）﹣3lnx+x﹣．求h（x）在[1，e]上的最大值和最小值；（Ⅲ）若函数f（x）≤x﹣1对∀x∈[1，+∞）恒成立，求实数a的取值范围．【考点】利用导数研究函数的单调性；利用导数求闭区间上函数的最值；导数在最大值、最小值问题中的应用．【分析】（Ⅰ）先求导，根据导数和函数的单调性即可求出单调区间；（Ⅱ）先求导，根据导数和函数的最值的关系即可求出；（Ⅲ）构造函数，转化为设g（x）=a（x﹣1）2+lnx﹣x+1，x∈[1，+∞），则g（x）max≤0，x∈[1，+∞），根据导数和函数最值的关系分类讨论即可．【解答】解：（Ⅰ）当a=﹣时，f（x）=﹣（x﹣1）2+lnx，（x＞0）…f'（x）=﹣x++=﹣，…①当0＜x＜2时，f'（x）＞0，f（x）在（0，2）单调递增；②当x＞2时，f'（x）＜0，f（x）在（2，+∞）单调递减；所以函数的单调递增区间是（0，2），单调递减区间是（2，+∞）．…（Ⅱ）当a=时，h（x）=f（x）﹣3lnx+x﹣=x2﹣2lnx，∴h′（x）=x﹣令h′（x）=0解得x=，…当x∈[1，]时，h′（x）＜0，当x∈[，e）时，h′（x）＞0，故x=是函数h（x）在[1，e]上唯一的极小值点，…故h（x）min=h（）=1﹣ln2，又h（1）=，h（e）=e2﹣2，所以h（x）max=e2﹣2．…（Ⅲ）由题意得a（x﹣1）2+lnx≤x﹣1对x∈[1，+∞）恒成立，…设g（x）=a（x﹣1）2+lnx﹣x+1，x∈[1，+∞），则g（x）max≤0，x∈[1，+∞），∴，…①当a≤0时，若x＞1，则g′（x）＜0，所以g（x）在[1，+∞）单调递减，∴g（x）max=g（1）=0≤0成立，得a≤0；…②当时，，g（x）在[1，+∞）单调递增，所以存在x＞1，使g（x）＞g（1）=0，则不成立；…③当时，x=＞1，则f（x）在[1，]上单调递减，[，+∞）单调递增，则存在∈[，+∞），有g（）=a（﹣1）2+ln﹣+1=﹣lna+a﹣1＞0，所以不成立，…综上得a≤0．…2016年11月15日。

湖南省衡阳市第八中学2017届高三数学上学期第三次（10月）月考试题文（扫描版）衡阳市八中2017届高三第二次月考试卷文科数学命题人： 审题人：一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1、已知i 是虚数单位，则i i -+在复平面上对应的点是（ C ） A.(1，0) B.(0，1) C.(1，1) D.（1，-1） 2. 函数)0(2)(>+=x xx x f 的单调减区间是 ( D ) A.(2,+∞)B.(0,2)C.(2,+∞)D.(0, 2)3.判断下列四个命题：①若b a ρρ//则b a ρρ=；②若b a ρρ=，则b a ρρ=；③若b a ρρ=，则b a ρρ//；④若b a ρρ=，则b a ρρ=.其中正确的个数是( A )A ．1B ．2C ．3D ．44．如图是函数y=f （x ）的导函数y=f′（x ）的图象，则下列判断正确的是（ C ）A ．在区间（﹣3，1）上y=f （x ）是增函数B ．在区间（1，3）上y=f （x ）是减函数C ．在区间（4，5）上y=f （x ）是增函数D ．在x=2时y=f （x ）取到极小值 【解答】解：由图象可知， 当﹣3≤x＜﹣时，f′（x ）＜0； 当﹣＜x ＜2时，f′（x ）＞0； 当2＜x ＜4时，f′（x ）＜0； 当4＜x ＜5时，f′（x ）＞0；故函数y=f （x ）在（﹣3，﹣），（2，4）上是减函数， 在（﹣，2），（4，5）上是增函数； 在x=2时取得极大值；故选：C ．5、若1tan 3θ=，则cos 2θ= ( D ) A.45-B. 15-C.15D.456、已知单位向量=-==||,23,31cos ,,2121a e e a e e ρρρρρρ则若向量且的夹角为αα（ B ） A ．2 B ．3C ．9D ．13【答案】3试题分析：因为22221211221||(32)9124912cos 413129,3a e e e e e e α=-=-⋅+=-⨯+=-⨯=r r r r r r r 所以|| 3.a =r7 ．函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是（B ）A ．2,6π-B ．2,3π-C ．4,6π-D ．4,3π8．已知ABC ∆中，内角,,A B C 的对边分别为,,a b c ，若222a b c bc =+-，3=a ，则ABC ∆ 的周长的最大值为（ D ）A. 32B. 6C. 3D. 9 9、已知ABC △的三个内角为A B C 、、，若函数2cos cos cos )(22CB A x x x f -⋅-=有一零点为1， 则ABC △一定是（ A ）A ．等腰三角形B ．直角三角形C ．锐角三角形D ．钝角三角形10、已知命题:p []1,2x ∀∈-，函数()2f x x x =-的值大于0．若p q ∨是真命题，则命题q 可以是（ C ）A ．()1,1x ∃∈-，使得1cos 2x <B ．“30m -<<”是“函数()2log f x x x m =++在区间1,22⎛⎫⎪⎝⎭上有零点”的必要不充分条件.C ．6x π=是曲线()3sin 2cos2f x x x =+的一条对称轴D ．若()0,2x ∈，则在曲线()()2xf x e x =-上任意一点处的切线的斜率不小于1e-11、 函数x x x y sin cos +=的图象大致为（ D ）12、若实数m 的取值使函数)(x f 在定义域上有两个极值点，则叫做函数)(x f 具有 “凹凸趋向性”，已知)(x f '是函数)(x f 的导数，且x xmx f ln 2)(-='，当函数)(x f 具有“凹凸趋向性”时，m 的取值范围是（ ） A 、⎪⎭⎫ ⎝⎛+∞-,2e B 、⎪⎭⎫ ⎝⎛-0,2e C 、⎪⎭⎫ ⎝⎛-∞-e 2, D 、⎪⎭⎫⎝⎛-e e 2,2二、填空题：13.若函数52)(23-++=mx x x x f 是R 上的单调递增函数，则m 的取值范围是____34≥m __________. 14.若直线l 与曲线C 满足下列两个条件：)(i 直线l 在点()00,y x P 处与曲线C 相切；)(ii 曲线C 在P 附近位于直线l 的两侧，则称直线l 在点P 处“切过”曲线C .下列命题正确的是____ _____(写出所有正确命题的编号) ①直线0:=y l 在点()0,0P 处“切过”曲线C ：3yx =②直线1:-=x l 在点()0,1-P 处“切过”曲线C ：2)1(+=x y ③直线x y l =:在点()0,0P 处“切过”曲线C ：x y sin = ④直线x y l =:在点()0,0P 处“切过”曲线C ：x y tan =⑤直线1:-=x y l 在点()0,1P 处“切过”曲线C ：x y ln =15、若函数()()R x x f ∈是周期为4的奇函数，且在[]2,0上的解析式为()⎩⎨⎧≤<≤≤-=21,sin 10),1(x x x x x x f π，则_______641429=⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛f f .考点：1.函数的奇偶性与周期性；2.分段函数求值.16.如图，边长为2的正方形CD AB 的顶点A ，B 分别在两条互相垂直的射线OP ，Q O 上滑动，则C D O ⋅O u u u r u u u r的最大值为 8三、解答题（本大题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤.）17.在ABC ∆中，角A,B,C 的对边分别为,,a b c ,且2cos 2a B c b =-. （1）求A 的大小（2）若2,4,a b c ABC =+=∆求的面积.2222222222cos 2,2221=2220,3a cb a Bc b a c bacb c a bcb c a bc bc bc A A ππ+-=-⋅=-+-=+-==<<=Q 解法一：由余弦定理得即根据余弦定理，有cosA 又故解法二，由正弦定理得：2sinAcosB=2sinC-sinB=2sin(A+B)-sinB 即：2cosAsinB=sinB 1sin 0,cos ,23B A A π≠∴==Q (2)222,43a Abc bc π==+-=Q 由余弦定理得2b+c 34,4,4bc b c bc ∴-=+=∴=（）又1sin 32ABC S bc A ∆∴==18.为了促进人口的均衡发展，我国从2016年1月1日起，全国统一实施全面放开两孩政策.为了解适龄国民对放开生育二胎政策的态度，某部门选对70后和80后年龄的人作为调查对象，进行了问卷调查，其中，持“支持生二胎”“不支持生二胎”和“保留意见”态度的人数如下表所示.支持 保留 不支持 80后 780 420 200 70后120180300（1）在所有参与调查的人中，用分层抽样的方法抽取n 个人，其中持“支持”态度的有36人，求n 的值；（2）在持“不支持”态度的人中，仍用分层抽样的方法抽取5人，并将其看成一个总体，从这5人中任意选取2人，求至少有一个80后的概率.解：（1）所有参与调查的人数为780+120+420+180+200+300=2000由分层抽样的特点知 36200080900n =⨯= (2) 710P =19．如图所示，在正三棱柱111ABC A B C -中，1AB AA =，D 是BC 上的一点，且1AD C D ⊥. （1）求证：1//A B 平面1AC D ；（2）在棱1CC 上是否存在一点P ，使直线1PB ⊥平面1AC D ？若存在，找出这个点，并加以证明，若不存在，请说明理由.试题解析：（1）证明：因为111ABC A B C -是正三棱柱，所以1CC ⊥平面ABC ，所以1CC AD ⊥，又1AD C D ⊥，111CC C D C =I ,所以AD ⊥平面1BCC B ，所以AD BC ⊥，所以D 是BC 的中点.如图，连接1A C ，设与1AC 相交于点E ，则点E 为1A C 的中点，连接DE ，则在1A BC ∆中，因为,D E 分别是1,BC A C 的中点，所以1//A B DE ，又DE 在平面1AC D 内，1A B 不在平面1AC D 内，所以1//A B 平面1AC D .（2）存在这样的点P ，且点P 为1CC 的中点，下面证明：由（1）知AD ⊥平面1BCC B ，故1B P AD ⊥，设1PB 与1C D 相交于点Q ，由于1DC C ∆≌11PB C ∆，故111QB C CC D ∠=∠,因为111QC B CDC ∠=∠，从而11QC B ∆∽1CDC ∆，所以011190C QB DCC ∠=∠=，所以11B P C D ⊥.因为1AD C D D =I ，所以1B P ⊥平面1AC D20．已知向量a r ＝⎝ ⎛⎭⎪⎫sin x ，34，b r ＝(cos x ，－1)． (1)当a r ∥b r 时，求cos 2x －sin 2x 的值；(2)设函数f (x )＝2(a r ＋b r )·b r ，已知在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若a ＝3，b ＝2，sin B ＝63，求f (x )＋4cos ⎝⎛⎭⎪⎫2A ＋π6⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π3的取值范围． 解 (1)因为a ∥b ，所以34cos x ＋sin x ＝0， 所以tan x ＝－34. cos 2x －sin 2x ＝cos 2x －2sin x cos x sin 2x ＋cos 2x ＝1－2tan x 1＋tan 2x ＝85. (2)f (x )＝2(a ＋b )·b ＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋32. 由正弦定理a sin A ＝bsin B ，得sin A ＝22，所以A ＝π4，或A ＝3π4. 因为b ＞a ，所以A ＝π4. f (x )＋4cos ⎝ ⎛⎭⎪⎫2A ＋π6＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4－12， 因为[0,]2x π∈，所以2x ＋π4∈5[,]44ππ， 32-≤f (x )＋4cos ⎝ ⎛⎭⎪⎫2A ＋π6≤2－12. ∴所求范围是3212⎡⎤-⎢⎥⎣⎦.21.设函数()(1)(0,1)x x f x a k a a a -=-->≠且是定义域为R 的奇函数.（1）求k 的值；（2）若(1)0f <，试判断函数的单调性，并求使不等式2()(4)0f x tx f x ++-<恒成立 的t 的取值范围；（3）若223(1),()2()[1,)2x x f g x a a mf x -==+-+∞且在上的最小值为2-，求m 的值. 解：（1）00(0)(1)1(1)0f a k a k =--=--=，k=2（2）由（1）知()(0,1).x x f x a a a a -=->≠且1(1)0,0,0,1,01f a a a a a <∴-<>≠∴<<Q 又且 x y a R ∴=在上是减函数，x y a -=在R 上是增函数， 故f(x)在R 上是单调递减，不等式22()(4)0()(-4)f x tx f x f x tx f x ++-<+<可化为 224,(1)40x tx x x t x ∴+>-+-+>即恒成立，2(1)160,t ∴∆=--<解得-3<t<5(3)3131(1)=,2(222f a a a a ∴-=∴==-Q ，或舍去）2222222min min ()222(22)(22)2(22)2()22,3()221,(1)23()=22()2()23,2,223317253,-32=224122x x x x x x x x x x x x g x m m n k x k x x n k h n n mn n m m n m m m n m m ------∴=+--=---+==-=-≥∴≥=-+=-+-≥≥=-∴=<==->Q 令为增函数，令若则当n=m 时，h (n)=2-m 若则当时，h (n)=，（舍去） 综上可知，m=222．设函数21()()ln 2f x x a b x ab x =-++【答案】（1）b e =；（2）实数a 的取值范围为2212(]2(1+)e e e --∞,. 【解析】试题分析：（1）求导()()()()ab x a x b f x x a b x x--'=-++=，再由条件'()0f e =，从而可求得b e =；（2）由（1）得21()()ln 2f x x a e x ae x =-++，()()()x a x e f x x --'=，因此需对a 的取值分以下三种情况分类讨论：①当1a e≤时，要使得()f x 在1[,)e +∞上有且只有两个零点，只需 2111()ln 2a e f ae e e e e+=-+222(12)2(1)02e e e a e --+=≥， ②当1a e e<<时，求导确定零点个数， ③当a e >时，求导确定零点个数.试题解析：（1）()()()()ab x a x b f x x a b x x--'=-++=， 2分 ∵()0f e '=，a e ≠，∴b e =； 3分（2）由（1）得21()()ln 2f x x a e x ae x =-++，()()()x a x e f x x --'=，①当1a e ≤时，由()>0f x '得x e >，由()0f x '<得1x e e <<，此时()f x 在1(,)e e 上单调递减，在()e +∞，上单调递增，∵2211()()ln 022f e e a e e ae e e =-++=-<， 242221112()()2(2)(2)(2)()0222f e e a e e ae e e e a e e e e=-++=--≥--> （或当x →+∞时，()0f x >亦可）∴要使得()f x 在1[,)e +∞上有且只有两个零点， 则只需2111()ln 2a e f ae e e e e +=-+222(12)2(1)02e e e a e --+=≥，即22122(1+)e a e e -≤， 6分 ②当1a e e<<时，由()>0f x '得1x a e <<或x e >；由()0f x '<得a x e <<.此时()f x 在(,)a e 上单调递减，在1(,)a e和()e +∞，上单调递增， 此时222111()ln ln 0222f a a ae ae a a ae ae e a =--+<--+=-<，∴此时()f x 在[)e +∞，至多只有一个零点，不合题意， 9分③当a e >时，由()0f x '>得1x e e<<或x a >，由()0f x '<得e x a <<，此时()f x 在1(,)e e 和()a +∞，上单调递增，在(,)e a 上单调递减，且21()02f e e =-<，∴()f x 在1[,)e+∞至多只有一个零点，不合题意.综上所述，实数a 的取值范围为2212(]2(1+)e e e --∞,. 12分 考点：1.利用导数研究曲线上某点切线方程；2.函数的零点；3.分类讨论的数学思想.。

衡阳八中2017年下期高三年级第二次月考试卷理数（试题卷）注意事项：1.本卷为衡阳八中高三年级实验班第二次月考试卷，分两卷。

其中共22题，满分150分，考试时间为120分钟。

2.考生领取到试卷后，应检查试卷是否有缺页漏页，重影模糊等妨碍答题现象，如有请立即向监考老师通报。

开考15分钟后，考生禁止入场，监考老师处理余卷。

3.请考生将答案填写在答题卡上，选择题部分请用2B铅笔填涂，非选择题部分请用黑色0.5mm 签字笔书写。

考试结束后，试题卷与答题卡一并交回。

★预祝考生考试顺利★第I卷选择题（每题5分，共60分）本卷共12题，每题5分，共60分，在每题后面所给的四个选项中，只有一个是正确的。

1.已知全集N=Z，集合A={﹣1，1，2，3，4}，B={﹣2，﹣1，0，1，2}，则（∁U A）∩B=（）A．{3，4} B．{﹣2，3} C．{﹣2，4} D．{﹣2，0}2.设i为虚数单位，复数（2﹣i）z=1+i，则z的共轭复数在复平面中对应的点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3.已知α为锐角，cos（α+）=，则sinα=（）A．B．C．D．4.已知0＜a＜1，x=log a+log a，y=log a5，z=log a﹣log a，则（）A．x＞y＞z B．z＞y＞x C．y＞x＞z D．z＞x＞y5.若函数f（x）=x2+x﹣lnx+1在其定义域的一个子区间（2k﹣1，k+2）内不是单调函数，则实数k的取值范围是（）A．（﹣，）B．[，3）C．（﹣，3）D．[，）6.成书于公元五世纪的《张邱建算经》是中国古代数学史上的杰作，该书中记载有很多数列问题，如“今有女善织，日益功疾．初日织五尺，今一月日织九匹三丈．问日益几何．”意思是：某女子善于织布，一天比一天织得快，而且每天增加的数量相同．已知第一天织布5尺，30天共织布390尺，则该女子织布每天增加（）（其中1匹=4丈，1丈=10尺，1尺=10寸）A．5寸另寸B．5寸另寸C．5寸另寸D．5寸另寸7.设点P（x，y）在不等式组表示的平面区域上，则z=的最小值为（）A．1 B．C．2 D．8.若某几何体的三视图（单位：cm）如图所示，其中左视图是一个边长为2的正三角形，则这个几何体的体积是（）A．2cm2B． cm3C．3cm3D．3cm39.已知对任意实数k＞1，关于x的不等式在（0，+∞）上恒成立，则a的最大整数值为（）A．0 B．﹣1 C．﹣2 D．﹣310.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）A．2 B．3 C．4 D．511.直线l与抛物线y2=6x交于A，B两点，圆（x﹣6）2+y2=r2与直线l相切于点M，且M为线段AB的中点．若这样的直线l恰有4条，则r的取值范围是（）A．（，2）B．（，3）C．（3，）D．（3，3）12.函数y=4cosx﹣e|x|（e为自然对数的底数）的图象可能是（）A．B．C． D．第II卷非选择题（共90分）二.填空题（每题5分，共20分）13.二项式的展开式中常数项是．14.在△ABC中，∠C=45°，O是△ABC的外心，若=m+n(m，n∈R)，则m+n的取值范围为．15.在三棱柱ABC﹣A1B1C1中侧棱垂直于底面，∠ACB=90°，∠BAC=30°，BC=1，且三棱柱ABC ﹣A1B1C1的体积为3，则三棱柱ABC﹣A1B1C1的外接球的表面积为．16.设F1，F2分别是双曲线的左、右焦点，A为双曲线的左顶点，以线段F1，F2为直径的圆O与双曲线的一个交点为P，与y轴交于B，D两点，且与双曲线的一条渐近线交于M，N两点，则下列命题正确的是．（写出所有正确的命题编号）①线段BD是双曲线的虚轴；②△PF1F2的面积为b2；③若∠MAN=120°，则双曲线C的离心率为；④△PF1F2的内切圆的圆心到y轴的距离为a．三.解答题（共6题，共70分）17.（本题满分12分）设函数f（x）=sinx（cosx﹣sinx）．（1）求函数f（x）在[0，π]上的单调递增区间；（2）设△ABC的三个角A、B、C所对的边分别为a、b、c，且f（B）=0，a、b、c成公差大于零的等差数列，求的值．18.（本题满分12分）如图，边长为3的正方形ABCD所在平面与等腰直角三角形ABE所在平面互相垂直，AE⊥AB，且，．（Ⅰ）求证：MN∥平面BEC；（Ⅱ）求二面角N﹣ME﹣C的大小．19.（本题满分12分）微信是腾讯公司推出的一种手机通讯软件，它支持发送语音短信、视频、图片和文字，一经推出便风靡全国，甚至涌现出一批在微信的朋友圈内销售商品的人（被称为微商）．为了调查每天微信用户使用微信的时间情况，某经销化妆品的微商在一广场随机采访男性、女性微信用户各50名．其中每天玩微信时间超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如表：（1）根据以上数据，能否有60%的把握认为“微信控”与“性别”有关？（2）现从参与调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份，求所抽取的5人中“微信控”和“非微信控”的人数；（3）从（2）中抽选取的5人中再随机抽取3人赠送价值200元的护肤品套装，记这3人中“微信控”的人数为X ，试求X 的分布列及数学期望． 参考公式：，其中n=a+b+c+d ．20.（本题满分12分） 已知椭圆C ：=1（a ＞b ＞0），定义椭圆C 上的点M （x 0，y 0）的“伴随点”为．（1）求椭圆C 上的点M 的“伴随点”N 的轨迹方程； （2）如果椭圆C 上的点（1，）的“伴随点”为（，），对于椭圆C 上的任意点M 及它的“伴随点”N，求的取值范围；（3）当a=2，b=时，直线l交椭圆C于A，B两点，若点A，B的“伴随点”分别是P，Q，且以PQ为直径的圆经过坐标原点O，求△OAB的面积．21.（本题满分12分）已知函数f（x）=x2﹣ax（a≠0），g（x）=lnx，f（x）的图象在它与x轴异于原点的交点M处的切线为l1，g（x﹣1）的图象在它与x轴的交点N处的切线为l2，且l1与l2平行．（1）求a的值；（2）已知t∈R，求函数y=f（xg（x）+t）在x∈[1，e]上的最小值h（t）；（3）令F（x）=g（x）+g′（x），给定x1，x2∈（1，+∞），x1＜x2，对于两个大于1的正数α，β，存在实数m满足：α=mx1+（1﹣m）x2，β=（1﹣m）x1+mx2，并且使得不等式|F（α）﹣F（β）|＜|F（x1）﹣F（x2）|恒成立，求实数m的取值范围．选做题请考生从22、23题中任选一题作答，并将所选题号在答题卡上填涂，共10分。

2017年下期高三年级第二次月考试卷理数（试题卷）注意事项：1.本卷为衡阳八中高三年级实验班第二次月考试卷，分两卷。

其中共22题，满分150分，考试时间为120分钟。

2.考生领取到试卷后，应检查试卷是否有缺页漏页，重影模糊等妨碍答题现象，如有请立即向监考老师通报。

开考15分钟后，考生禁止入场，监考老师处理余卷。

3.请考生将答案填写在答题卡上，选择题部分请用2B铅笔填涂，非选择题部分请用黑色0.5mm 签字笔书写。

考试结束后，试题卷与答题卡一并交回。

★预祝考生考试顺利★第I卷选择题（每题5分，共60分）本卷共12题，每题5分，共60分，在每题后面所给的四个选项中，只有一个是正确的。

1.已知全集N=Z，集合A={﹣1，1，2，3，4}，B={﹣2，﹣1，0，1，2}，则（∁U A）∩B=（）A．{3，4} B．{﹣2，3} C．{﹣2，4} D．{﹣2，0}2.设i为虚数单位，复数（2﹣i）z=1+i，则z的共轭复数在复平面中对应的点在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3.已知α为锐角，cos（α+）=，则sinα=（）A．B．C．D．4.已知0＜a＜1，x=log a+log a，y=log a5，z=log a﹣log a，则（）A．x＞y＞z B．z＞y＞x C．y＞x＞z D．z＞x＞y5.若函数f（x）=x2+x﹣lnx+1在其定义域的一个子区间（2k﹣1，k+2）内不是单调函数，则实数k的取值范围是（）A．（﹣，）B．[，3）C．（﹣，3）D．[，）6.成书于公元五世纪的《张邱建算经》是中国古代数学史上的杰作，该书中记载有很多数列问题，如“今有女善织，日益功疾．初日织五尺，今一月日织九匹三丈．问日益几何．”意思是：某女子善于织布，一天比一天织得快，而且每天增加的数量相同．已知第一天织布5尺，30天共织布390尺，则该女子织布每天增加（）（其中1匹=4丈，1丈=10尺，1尺=10寸）A．5寸另寸B．5寸另寸C．5寸另寸D．5寸另寸7.设点P（x，y）在不等式组表示的平面区域上，则z=的最小值为（）A．1 B．C．2 D．8.若某几何体的三视图（单位：cm）如图所示，其中左视图是一个边长为2的正三角形，则这个几何体的体积是（）A．2cm2B． cm3C．3cm3D．3cm39.已知对任意实数k＞1，关于x的不等式在（0，+∞）上恒成立，则a的最大整数值为（）A．0 B．﹣1 C．﹣2 D．﹣310.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）A．2 B．3 C．4 D．511.直线l与抛物线y2=6x交于A，B两点，圆（x﹣6）2+y2=r2与直线l相切于点M，且M为线段AB的中点．若这样的直线l恰有4条，则r的取值范围是（）A．（，2）B．（，3）C．（3，）D．（3，3）12.函数y=4cosx﹣e|x|（e为自然对数的底数）的图象可能是（）A．B．C． D．第II卷非选择题（共90分）二.填空题（每题5分，共20分）13.二项式的展开式中常数项是．14.在△ABC中，∠C=45°，O是△ABC的外心，若OC=m OA+n OB(m，n∈R)，则m+n的取值范围为．15.在三棱柱ABC﹣A1B1C1中侧棱垂直于底面，∠ACB=90°，∠BAC=30°，BC=1，且三棱柱ABC ﹣A1B1C1的体积为3，则三棱柱ABC﹣A1B1C1的外接球的表面积为．16.设F1，F2分别是双曲线的左、右焦点，A为双曲线的左顶点，以线段F1，F2为直径的圆O与双曲线的一个交点为P，与y轴交于B，D两点，且与双曲线的一条渐近线交于M，N两点，则下列命题正确的是．（写出所有正确的命题编号）①线段BD是双曲线的虚轴；②△PF1F2的面积为b2；③若∠MAN=120°，则双曲线C的离心率为；④△PF1F2的内切圆的圆心到y轴的距离为a．三.解答题（共6题，共70分）17.（本题满分12分）设函数f（x）=sinx（cosx﹣sinx）．（1）求函数f（x）在[0，π]上的单调递增区间；（2）设△ABC的三个角A、B、C所对的边分别为a、b、c，且f（B）=0，a、b、c成公差大于零的等差数列，求的值．18.（本题满分12分）如图，边长为3的正方形ABCD所在平面与等腰直角三角形ABE所在平面互相垂直，AE⊥AB，且，．（Ⅰ）求证：MN∥平面BEC；（Ⅱ）求二面角N﹣ME﹣C的大小．19.（本题满分12分）微信是腾讯公司推出的一种手机通讯软件，它支持发送语音短信、视频、图片和文字，一经推出便风靡全国，甚至涌现出一批在微信的朋友圈内销售商品的人（被称为微商）．为了调查每天微信用户使用微信的时间情况，某经销化妆品的微商在一广场随机采访男性、女性微信用户各50名．其中每天玩微信时间超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如表：（1）根据以上数据，能否有60%的把握认为“微信控”与“性别”有关？（2）现从参与调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份，求所抽取的5人中“微信控”和“非微信控”的人数；（3）从（2）中抽选取的5人中再随机抽取3人赠送价值200元的护肤品套装，记这3人中“微信控”的人数为X ，试求X 的分布列及数学期望． 参考公式：，其中n=a+b+c+d ．20.（本题满分12分） 已知椭圆C ：=1（a ＞b ＞0），定义椭圆C 上的点M （x 0，y 0）的“伴随点”为．（1）求椭圆C 上的点M 的“伴随点”N 的轨迹方程； （2）如果椭圆C 上的点（1，）的“伴随点”为（，），对于椭圆C 上的任意点M 及它的“伴随点”N，求的取值范围；（3）当a=2，b=时，直线l交椭圆C于A，B两点，若点A，B的“伴随点”分别是P，Q，且以PQ为直径的圆经过坐标原点O，求△OAB的面积．21.（本题满分12分）已知函数f（x）=x2﹣ax（a≠0），g（x）=lnx，f（x）的图象在它与x轴异于原点的交点M处的切线为l1，g（x﹣1）的图象在它与x轴的交点N处的切线为l2，且l1与l2平行．（1）求a的值；（2）已知t∈R，求函数y=f（xg（x）+t）在x∈[1，e]上的最小值h（t）；（3）令F（x）=g（x）+g′（x），给定x1，x2∈（1，+∞），x1＜x2，对于两个大于1的正数α，β，存在实数m满足：α=mx1+（1﹣m）x2，β=（1﹣m）x1+mx2，并且使得不等式|F（α）﹣F（β）|＜|F（x1）﹣F（x2）|恒成立，求实数m的取值范围．选做题请考生从22、23题中任选一题作答，并将所选题号在答题卡上填涂，共10分。