当前位置：文档之家 › 第三章 词法分析作业

第三章 词法分析作业

  • 格式：doc
  • 大小：101.00 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

西安理工大学《编译原理》编译原理作业集－第三章－修订版

西安理工大学《编译原理》编译原理作业集－第三章－修订版

第三章词法分析本章要点１．词法分析器设计，２．正规表达式与有限自动机，３．词法分析器自动生成。

本章目标：１．理解对词法分析器的任务，掌握词法分析器的设计；２．掌握正规表达式与有限自动机；３．掌握词法分析器的自动产生。

本章重点：1．词法分析器的作用和接口，用高级语言编写词法分析器等内容，它们与词法分析器的实现有关。

应重点掌握词法分析器的任务与设计，状态转换图等内容。

2．掌握下面涉及的一些概念，它们之间转换的技巧、方法或算法。

（1）非形式描述的语言↔正规式（2）正规式→ NFA（非确定的有限自动机）（3）NFA→ DFA（确定的有限自动机）（4）DFA→最简DFA本章难点（1）非形式描述的语言↔正规式（2）正规式→ NFA（非确定的有限自动机）（3）NFA→ DFA（确定的有限自动机）（4）DFA→最简DFA作业题一、单项选择题（按照组卷方案，至少15道）1. 程序语言下面的单词符号中，一般不需要超前搜索a. 关键字b. 标识符c. 常数d. 算符和界符2. 在状态转换图的实现中，一般对应一个循环语句a. 不含回路的分叉结点b. 含回路的状态结点c. 终态结点d. 都不是3. 用了表示字母，d表示数字， ={l，d}，则定义标识符的正则表达式可以是：。

(a)ld*(b)ll*(c)l(l | d)*(d)ll* | d*4. 正规表达式(ε|a|b)2表示的集合是(a){ε，ab，ba，aa，bb} (b){ab，ba，aa，bb}(c){a，b，ab，aa，ba，bb} (d){ε，a，b，aa，bb，ab，ba}5. 有限状态自动机可用五元组（V T，Q，δ，q0，Q f）来描述，设有一有限状态自动机M的定义如下：V T={0，1}，Q={q0，q1，q2}，Q f={q2}，δ的定义为：δ（q0，0）=q1δ（q1，0）=q2δ（q2，1）=q2δ（q2，0）=q2M所对应的状态转换图为。

6. 有限状态自动机可用五元组（V T，Q，δ，q0，Q f）来描述，设有一有限状态自动机M的定义如下：V T={0，1}，Q={q0，q1，q2}，Q f={q2}，δ的定义为：δ（q0，0）=q1δ（q1，0）=q2δ（q2，1）=q2δ（q2，0）=q2M所能接受的语言可以用正则表达式表示为。

第三章 词法分析及词法分析程序 课后答案【khdaw_lxywyl】

第三章 词法分析及词法分析程序 课后答案【khdaw_lxywyl】

课 后 答 案 网
第三章 词法分析及词法分析程序 1 试用某种高级语言编写一个 FORTRAN 源程序的预处理子程序，其功能是： 每调用它一次， 即把源程序中的一个完整语句送入扫描缓冲区。要求删去语句中的注释行；删去续行标记字 符，把语句中的各行连接起来，并在语句的末端加上语句结束符。此外，还要求此程序具有 组织源程序列表输出的功能。 2 画出用来识别如下三个关键字的状态转移图。 STEP STRING SWITCH 3 假定有一个猎人带着一只狼、一头山羊和一棵白菜来到一条河的左岸，拟摆渡过河，而岸 边只有一条小船，其 大小仅能装载人和其余三件东西中的一件，也就是说，每一次猎人只 能将随行者中的一件带到彼岸。若猎人将狼和山羊留在同一岸上而无人照管，那么，狼就会 将羊吃掉；如果猎人把山羊和白菜留在同一岸，山羊也会把白菜吃掉。现在，请你用状态转
试找出一个长度最小的输入串，使得：
h (1) 在识别此输入串的过程中，每一状态至少经历一次；
(2) 每一状态转换至少经历一次。 9 对于下列的状态转换矩阵：[]a[]bS[]A[]SA[]A[]BB[]B[]B(i) 初态：S
k 终态：B[][][]a[]bS[]A[]BA[]B[]AB[]B[]B(ii) 初态：S
26 指出下列 LEX 正规式所匹配的字符串：
. (1) "{" ［^{］*"}"
(2) ^［^a-z］［A-Z］［0-9］$ (3) ［^0-9］|［＼r＼n］
w (4) ＼′(［^′＼n］|＼′＼′)+＼′
(5) ＼"(［^"＼n］|＼＼［"＼n］)*＼"
a 27 写出一个 LEX 正规式，它能匹配 C 语言的所有无符号整数 (例如：OX89ab，0123，45，

编译原理与实现03第3章 词法分析

编译原理与实现03第3章 词法分析

利用状态图识别句子的方法是一种自底向上的分析方法。开始时，处于开 始状态，此时句柄是随后扫描的字符，即输入串的的第一个符号，所要归 约的符号就是从开始状态经过标记有句柄符号的弧到达的下一个状态的名 字。以后每一步（除第一步外）的句柄是当前状态的名字和随后扫描的字 符，而句柄所要归约的符号就是下一个状态的名字。
3.3.2 状态图的用法
例3.2，对句子0110进行的分析。 解：根据上面介绍的状态图使用方法，我们在图3.5（a）列出分析的每一步。 由于这些规则很简单，所以分析也非常简单。首先，在开始状态S下扫描的第 一个符号是0，转到状态V，表示0是句柄，归约到V。接下来，在状态V扫描1， 转到状态Z，此时句柄为V1，归约成Z。再往下扫描1，由状态Z转到状态U，表 示句柄为Z1归约为U。最后，扫描0，转到状态Z，此时句柄为U0，归约为Z， 从而形成图3.5（b）所示的语法树。 步骤 1 2 状态 S V 扫描的字符 0 1 余留部分 110 10
3.3.2 状态图的用法
状态图画好后，就可以利用状态图来分析和识别字符串，其方法如下： 1.首先设置初始状态S为当前状态。从输入串的最左字符开始重复步骤2，直 到到达输入串的右端为止。 2.扫描输入串的下一个字符，在当前状态所射出的弧中，找出标记有该字符 的弧，并沿此弧前进，过渡到下一个状态。如果找不到标记有该字符的弧， 则说明输入串不是合法的句子，分析过程失败结束；如果我们扫描输入串 的最后一个字符，并从当前状态出发沿着标记有该字符的弧到达终结状态， 则表示输入串是该文法的合法句子，识别过程成功结束；如果扫描输入串 的最后一个符号后到达的状态不是状态图的终结状态，则表示输入串不是 该文法的合法句子，识别过程失败结束。
3.3 正则文法及状态图
程序设计语言的单词符号可用3型文法来描述，3型文法也称为正 则文法。对于正则文法所描述的语言可以用一种有穷自动机来识 别。我们的目的是实现词法分析程序，所以为了简化问题，我们 直接介绍这种自动机的非形式表示，即状态图。

编译原理第三章练习题答案

编译原理第三章练习题答案

编译原理第三章练习题答案编译原理第三章练习题答案编译原理是计算机科学中的重要课程之一，它研究的是将高级语言程序转化为机器语言的过程。

在编译原理的学习过程中，练习题是提高理解和应用能力的重要途径。

本文将为大家提供编译原理第三章的练习题答案，希望能够对大家的学习有所帮助。

1. 什么是词法分析？请简要描述词法分析的过程。

词法分析是编译过程中的第一个阶段，它的主要任务是将源程序中的字符序列划分为有意义的词素（token）序列。

词法分析的过程包括以下几个步骤：1）扫描：从源程序中读取字符序列，并将其转化为内部表示形式。

2）识别：根据预先定义的词法规则，将字符序列划分为不同的词素。

3）分类：将识别出的词素进行分类，如关键字、标识符、常量等。

4）输出：将分类后的词素输出给语法分析器进行进一步处理。

2. 什么是正则表达式？请给出一个简单的正则表达式示例。

正则表达式是一种用于描述字符串模式的工具，它由一系列字符和操作符组成。

正则表达式可以用于词法分析中的词法规则定义。

以下是一个简单的正则表达式示例：[a-z]+该正则表达式表示匹配一个或多个小写字母。

3. 请简要描述DFA和NFA的区别。

DFA（Deterministic Finite Automaton）和NFA（Nondeterministic Finite Automaton）是有限状态自动机的两种形式。

它们在词法分析中常用于构建词法分析器。

DFA是一种确定性有限状态自动机，它的状态转换是确定的，每个输入符号只能对应一个状态转换。

相比之下，NFA是一种非确定性有限状态自动机，它的状态转换是非确定的，每个输入符号可以对应多个状态转换。

4. 请简要描述词法分析器的实现过程。

词法分析器的实现过程包括以下几个步骤：1）定义词法规则：根据编程语言的语法规范，定义词法规则，如关键字、标识符、常量等。

2）构建正则表达式：根据词法规则，使用正则表达式描述不同类型的词素。

3）构建有限状态自动机：根据正则表达式，构建DFA或NFA来识别词素。

第3章 词法分析 (编译原理 陈火旺)

第3章 词法分析 (编译原理 陈火旺)

标识符的符号表入口地址作为其单词符号的属性值,常
每个基本字占一个单词种别，单词符号的属性值缺省。
对于界符，运算符通常一个符号一个种别，单词符号的
属性值缺省
例: 参见P42.表3.1 单词符号及种别编码
10
3.1.3 词法分析器作为独立子程序

词法分析可采用如下两种处理结构：
把词法分析程序作为主程序。将词法分析作为
19
3.2.1 正规文法、正规式与正规集

正规集：由正规文法产生的语言所构成的集合。
注：正规集是集合，可有穷也可无穷。 可通过正规式来形式化表示。

对于一个正规文法的语言提炼出一个简洁的公式，用这个
式子来对它进行形式化的表示，这个式子叫正规式。

正规式：也称正则表达式,是说明单词的模式的一种重要的 表示法（记号）；是定义正规集的数学工具；用来描述单词 符号。
在设计一个编译程序时，通常是把对源程序的结构分析分为词 法分析和语法分析两个相对独立的阶段来完成。
第一，描述单词的结构比描述源程序的其它语法结构要简单

得多，仅使用3型文法也就基本够用了。
第二，由于把词法分析和语法分析分开，可使编译程序各部

分的功能更为单一，整个编译程序的结构也更加清晰，从而 有利于编译程序的编写和调整。 上述词法分析和语法分析两个阶段的划分，仅仅是对整个编译 程序的逻辑功能而言，而不一定指的是编译程序的执行流程。
25
例3.2 判断下述正规式之间是否等价： (1)b(ab)*与(ba)*b (2)(ab)*与a*b* 解: (1) b(ab)*对应的正规集是b后面出现任意多个ab对
L(b(ab)*)={b,bab,babab, ……}

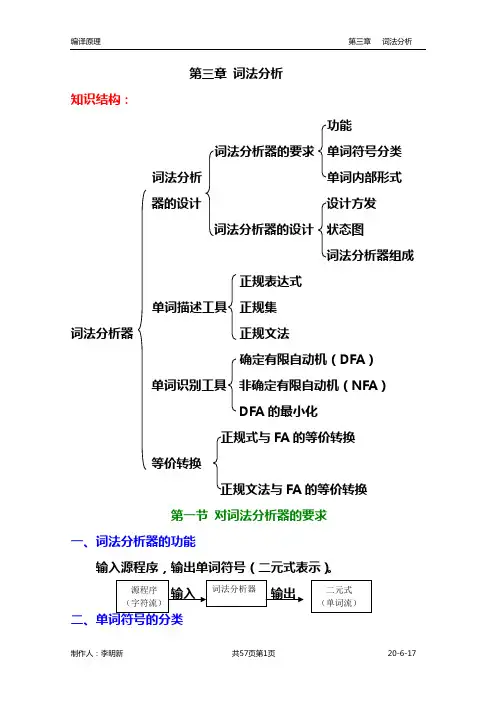
第3章词法分析1

第3章词法分析1

第三章 词法分析知识结构：功能 词法分析器的要求 单词符号分类 词法分析 单词内部形式器的设计 设计方发词法分析器的设计 状态图词法分析器组成正规表达式单词描述工具 正规集词法分析器 正规文法确定有限自动机（DFA ）单词识别工具 非确定有限自动机（NFA ）DFA 的最小化FA 的等价转换等价转换FA 的等价转换第一节 对词法分析器的要求一、词法分析器的功能输入源程序，输出单词符号（二元式表示）。

关键字：是由程序语言定义的具有固定意义的标识符。

标识符：用来表示各种名字，如变量等。

常数：常数的类型有整型，实型等。

运算符：算术运算符，关系运算符，逻辑运算符。

界限符：逗号，分号等。

三、单词符号内部的表示形式内部的单词符号TOKEN字（二元式），TOKEN字占用机器字的长度，依据信息量的多少而定。

1、TOKEN字结构CLASS：用整数表示。

VALUE：表示单词符号的属性（符号表指针）。

2、TOKEN的作用CLASS：用于语法分析器对源程序结构的分析。

VALUE：用于语义分析器对源程序具体操作的分析。

3、单词种别码划分原则CLASS：关键字，运算符，界限符（编译程序定义的符号）使用一字一种编码。

VALUE值省略。

VALUE：标识符，常数（用户定义的符号），存放符号表常数表的指针。

标识符，常数每一类为一种编码。

例：BEGIN A：= B END；词法分析结果：符号表（BEGIN，---- ）Array（A ，K1 ） K1（：= ，--- ）（B ，K3 ） K3（END ，--- ）（；，--- ）四、词法分析器的结构1、一遍扫描（交互式结构）。

2、多遍扫描（独立式结构）。

第二节词法分析器的设计一、设计步骤1、确定词法分析器的接口关系；2、确定单词分类和TOKEN字的结构；3、对每一类单词构造状态转换图；4、根据状态转换图设计算法。

二、功能描述1、组织源程序输入；2、按词法规则拼读单词符号，并转换成二元式；3、删除注解行，空格和无用符号；4、检查词法错误。

03第3章 词法分析2


2014年1月4日
15
【例】求正则表达式(a|b)(a|b|0|1)*对应的正则文法（左线性） A→A(a|b|0|1)|(a|b) 正则表达式 A=yx* A=x|y
(a|b)(a|b|0|1)* 文法产生式
规则1
规则2
A→Ax|y A→x,A→y
G[A]: A→Aa|Ab|A0|A1|a|b
该文法是左线性正则文法
B →bC
C →aC|a
文法产生式 规则1 规则2 规则3
2014年1月4日
正则表达式 A=xy A=x*y A=x|y
最终转成正则表达式 S=a*aba*a
A→xB,B→y A→xA|y A→x,A→y
步骤1 构造 S→R（正则表达式） 步骤2 不断利用规则做变换,直到每个产生式最多含有 一个终结符为止 文法产生式 规则1 规则2 A→xB,B→y A→xA|y 正则表达式 A=xy A=x*y
2014年1月4日
16
练习：给出正则表达式(a|b)*a(a|b)(a|b)的正则文法 （左线性和右线性） 正则文法（左线性）： S→A(a|b) S→ (a|b)*a(a|b)(a|b) A→B(a|b) A→(a|b)*a(a|b) B→(a|b)*a B→Ca C→C(a|b)|ε A→Ba|Bb C→Ca|Cb|ε
22
3.6.1 确定的有穷自动机
3、确定的有穷自动机状态转换矩阵
∑ a 1 3 1 3
a b a 2 1 a 3 a,b
23
状态转换矩阵： 确定的有穷自动机M= S （ Q， Σ， q0，F，δ）可用状态转换矩阵 0 表示。 矩阵的第一列元素与自动机M的状态集 合Q一一对应，且初始状态q0是第一列的 第一个元素，右上角标记*的元素对应终 结状态。 矩阵的第一行元素与Σ的每个符号对应。 矩阵中的元素对应每个状态转换函数。 如果有状态转换函数δ（q，a）=q’，则在 矩阵中状态q对应的行和符号a对应的列单 元中填入q’。

第三章 词法分析 习题讲解


③状态空间重新命名，得到的状态转换矩阵为:
④将其最小化，首先划分状态{1，2，3，4}，{5}两个 状态由于状态2和状态4输入a后都达到状态3，输入b 后都达到4，所以状态2和状态4等价。
1
a
2 3 (4) 3 4 4
b
2 2 2 2
⑤所以最小DFA的初态集是0，终态集为{4}， 状态集为{1，2，3，4}，字母表为{a,b} ， 状态转换矩阵如上。
a {X} {1,2,3} {2,3,4} {} {2,3,4} {2,3,4,Y}
b 1 ε
b {1,2,3} {2,3} {2,3}
a 2
ε
b
3
a
4
a
Y
{2,3}
{2,3,4,{Y}}
{2,3,4}
{2,3,4,Y}
{2,3}
{2,3} a 1 2 3 4 (5) 3 5 3 5 b 2 4 4 4 4
2.1，2.5 2.6 2.8 2.9 2.10 2.13
1 构造与正规式（a|b|c）*a等价的DFA: 答：（1）与此正规式对应的NFA为 a
0
（2）状态转换矩阵为：
a {0，1，2}
ε
b
1
cபைடு நூலகம்
b
ε
2
c
a
3
{1,2,3}
{1,2}
{1,2}
{1，2，(3)}
{1，2}
{1,2,3}
{1,2,3}
⑤所以最小DFA的初态为1，终态集为{3}，状态集为 {1，2，3}，字母表为{a,b},状态转换矩阵如上。
{3}
2
3
4 写出在字母表{a,b}上，不是a开头，但以aa结尾的字符串集合的正规表达式？并

编译原理chapter3 词法分析


一 设计一个奇偶校验器
DFA是由集合，序列和函数定义的数学模型， 它对于 上的w，判定是可接受的还是不可 接受的。例如，设计一个DFA m ，奇偶校验 器，首先，w是由0，1组成的字符串，因此， 1. ={0 ,1}且w在一条输入带上。
0 1 0 1 1$
读头
精品文档
11
2. 状态集：它记忆已读入w子串的状态,m是 奇偶校验器，它应该记住，初始序列是奇数 个1还是偶数个1。因此，m有even和odd两个 状态. 3 .even为开始状态。
词法分析器
‘while’，‘i’，‘＜＞’，‘j’， ‘do’， ‘if’，‘i’，‘＞’，‘j’,‘then’, 'i', ':=’ , 'i', ’-’ , 'j', 'else', 'j', ':=', 'j', '-', ‘i'
精品文档
4
词类和属性
computator n. Calcculating machine.
3.1.1 词法分析程序的功能 源程序 单词词序法列分析器
3.1.2 单词的词类和属性 （词类符号，单词的属性值）
3.1.3 词法分析程序作为一个独立子程序 （1）语法分析程序的子程序； （2）组 织成一遍扫描。
精品文档
3
While i＜＞j do if i＞j then i:＝i-j else j:=j－I
三 一个ＤＦＡ有三种表示：
（1）象上面，用转换函数；
精品文档
14
转移矩阵
状态转换图
a
b
0
1
2
a

第三章 词法分析终


1
ε
a
3 4
a
5
35
ε-closure（I）={1，3}
定义2: 令I是NFA M‟的状态集的一个子集, a∈Σ 定义: Ia=ε-closure(J) 其中J = ∪δ(s,a) S∈I
f是一个从K * 到K的子集的映像，即：K* * →2 K SK是一个非空初态集 ZK是一个终态集
30
例3.7：一个NFA M=（{0，1，2，3，4}，{a，b}，f，
{0}，{2,4}）其中 f(0,a)={0,3} f(2,b)={2}
f(0,b)={0,1}
f(1,b)={2} f(2,a)={2}
(R2)对形如A
A xB，A
x*y的正规产生式，重写为：
y，B xB，B y
(R3)对形如A A
xy的正规产生式，重写为: x，A y
17
不断应用R做变换，直到每个产生式右端只含一个VN
例3.4
将 r=a(a|d)*转换成相应的正规文法 a(a|d)*： (a|d)*
令S是文法的开始符号，形成S R1 R2 S S aA aA A
L(e1)L(e2)和(L(e1))
仅由有限词使用上述三步骤而定义的表达式才是上的 正规式，仅由这些正规式所表示的字集才是上的正规 集
12
其中的“”读为“或”（也有使用“+”代替 “” 的 ）；“ ”读为“连接”；“”读为“闭包”（即，任 意有限次的自重复连接）。在不致混淆时，括号可省去， 但规定算符的优先顺序为“”、“”、“”、“ ”、 “” 。连接符“ ”一般可省略不写。“”、“ ”和
令I是一个状态集的子集，定义ε-closure（I）为： 1）若s∈I，则s∈ε-closure（I）； 2）若s∈I，则从s出发经过任意条ε弧能够到达的 任何状态都属于ε-closure（I）。 状态集ε-closure（I）称为I的ε-闭包 ε a 2 6 例：如图所示的状态图：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章词法分析(作业)
1、求正则式（a|b)(a|b|0|1)*对应的正则文法（右线性文法），画状态转换图。

解:(a|b):S—>a|b
(a|b|0|1)*:A—>aA|bA|0A|1A
合并: S—>a|b
A—>aA|bA|0A|1A| ε
2、已知正则文法 G[Z]：Z0Z|1Z|0A
A0B
B0
（1）求对应的正则式？
（2）G[Z]所描述的语言？
解:
1)(0|1)*000
2)G[Z]所描述的语言是L(G[Z])={x|x∈(0|1|000)}
3、已知有限自动机如图
(1)以上状态转换图表示的语言有什么特征？
(2)写出其正规式与正规文法.
(3)构造识别该语言的有限自动机 DFA.
解：
（1）L={W |W {0,1},并且W至少有两个连续的1}
（2）正则式为（0|1)*11(0|1)*
正则文法G(Z)为:
Z—>0Z|1Z|1A
A—>1B|1
B—>0B|1B|0|1
（3）将图中有限自动机确定化：
首先从处态A出发：
I I0 I1
(1){A} (1){A} (2){A,B}
(2){A,B} (1){A} (3){A,B,C}
(3){A,B,C} (4){A,C} (3){A,B,C}
(4){A,C} (4){A,C} (3){A,B,C}
其相应的DFA如下图：
将这个DFA最小化：
首先分终态和非终态两个集K1={1,2} 和 K2={3,4}。

由于状态1输入1到达状态K1集，而状态2输入1到达K2集故将k1分为K11={1}, K12={2}。

由于状态3，和 4 输入1，或0 都到达k2集，所以状态3，4等价。

则可以分割成三个子集:{1}，{2}，{3，4}
所以将DFA最小化的状态图如下：
4、请构造与正则式 R=(a*b)*ba(a|b)* 等价的状态最少的 DFA（确定有限自动机）
解：
（1）首先构造转换系统图：
（2）由系统转换图构造DFA（NFA确定化）设初态为[S, A, B, G,F]
NFA确定化为DFA的过程：
I Ia Ib
(1)[S,A,B,G,F] (2)[G,F] (3)[A,B,C,G,F]
(2)[G,F] (2)[G,F] (4)[A,B,G,F]
(3)[A,B,C,G,F] (5)[D,F,G,E,Z] (3)[A,B,C,G,F]
(4)[A,B,G,F] (2)[G,F] (3)[A,B,C,G,F]
(5)[D,F,G,E,Z] (6)[G,F,E,Z] (7)[A,B,E,Z,G,F]
(6)[G,F,E,Z] (6)[G,F,E,Z] (7)[A,B,E,Z,G,F]
(7)[A,B,E,Z,G,F] (6)[G,F,E,Z] (8)[A,B,C,E,Z,G,F]
(8)[A,B,C,E,Z,G,F] (5)[D,F,G,E,Z] (8)[A,B,C,E,Z,G,F]
DFA确定有限自动机状态图如下：
（3）将DFA最小化：
先将终态和非终态分成两个集: K1={1,2,3,4} , K2={5,6,7,8}。

对于K1中的3态输入a则进入K2集，而1，2，4态输入a仍然在K1中，故K1可一分为二K11={1,2,4}和K12={3}；考察K11对于1，4态输入b到达3态而2态输入b到达4态，故K11可一分为二K111={1,4}； K112={2}最后考
察K2输入a或b都到达K2集，则DFA化简为{1，4}，{2}，{3}，{5，6，7，8}四个子集。

其状态图如下：。