圆锥曲线方程 公式总结
- 格式:doc
- 大小:119.50 KB
- 文档页数:3

圆锥曲线的切线与切点弦方程圆锥曲线的切线与切点弦方程说明:(1)以上方程可以通过局部分割曲线,利用导数求得.(2)切点弦方程可以通过两切点具有相同结构方程式且切线有公共交点推导而得.1.过点(M 且与圆224x y +=相切的直线方程为2.由点()2,2P 向圆221x y +=引两切线,PA PB ,其中切点为,A B ,则AOB S ∆=3.设抛物线24y x =在()00,P x y 处的切线为l ,则点(2,0)A 到直线l 的距离的最小值为 4.设椭圆2214x y +=在()00,P x y 处的切线为l ,直线l 与两坐标轴交点分别为,A B ,则AOB S ∆最小值为 ;AB 最小值为 .二、抛物线的切线与切点弦方程1.已知抛物线24x y =在1(1,),(2,1)4A B -两点处的切线分别为12,l l ,且1l 与2l 相交于点P(1)求点P 的坐标.(2)求直线AB 的方程.2.已知抛物线22(0)x py p =>,过M 引抛物线的两条切线,切点分别为,A B .(1)证明:,,A M B 三点的横坐标成等差数列.(2)若(2,2)M p -且AB =.3.已知抛物线24x y =,过点P 的直线l 交抛物线于,A B 两点,分别以,A B 为切点的两切线12,l l .(1)若(2,2)P ,求1l 与2l 交点M 的轨迹方程.(2)若点P 为抛物线的焦点F ,证明:(i )MF AB ⊥; (ii )MA MB ⊥.4.已知抛物线C :22x py =的焦点(0,)F c (0)c >到直线l :20x y --=,设P 为直线l 上点,过点P 作抛物线的两条切线12,l l ,求切点分别为,A B .(1)求抛物线C 的方程;(2)当00(,)P x y 为定点时,求直线AB 的方程;(3)当P 在直线上运动时,求FA FB ⋅的最小值. 5.已知椭圆1C :22221x y a b+=的两个焦点1(2,0)F -,2(2,0)F ,点(2,3)A 在椭圆上,过点A 的直线l 与抛物线2C :24x y =交于,B C 两点,抛物线2C 在,B C 两点处的切线分别为12,l l 且1l 与2l 相交于点P .(1)求椭圆1C 的方程;(2)是否存在满足1212PF PF AF AF +=+的点P ,若存在,请指出个数?若不存在说明理由.。

2011年圆锥曲线方程知识点总结1.圆锥曲线的两个定义:(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F 1,F 2的距离的和等于常数2a ,且此常数2a 一定要大于21F F ,当常数等于21F F 时,轨迹是线段F 1F 2,当常数小于21F F 时,无轨迹;双曲线中,与两定点F 1,F 2的距离的差的绝对值等于常数2a ,且此常数2a 一定要小于|F 1F 2|,定义中的“绝对值”与2a <|F 1F 2|不可忽视。
若2a =|F 1F 2|,则轨迹是以F 1,F 2为端点的两条射线,若2a ﹥|F 1F 2|,则轨迹不存在。
若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
如(1)已知定点)0,3(),0,3(21F F -,在满足下列条件的平面上动点P 的轨迹中是椭圆的是 A .421=+PF PF B .621=+PF PF C .1021=+PF PF D .122221=+PF PF (答:C );(2)方程8=表示的曲线是_____(答:双曲线的左支)(2)第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母”,其商即是离心率e 。
圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。
如 (08宣武一模) 已知P 为抛物线221x y =上的动点,点P 在x 轴上的射影为M ,点A 的坐标是)217,6(,则PM PA +的最小值是 _____ (答:219)2.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):(1)椭圆:焦点在x 轴上时12222=+b y a x (0a b >>)⇔{cos sin x a y b ϕϕ==(参数方程,其中ϕ为参数),焦点在y 轴上时2222b x a y +=1(0a b >>)。

圆锥曲线是一个在三维空间中由一个固定点(焦点)和一个固定直线(直角方向线)确定的曲线。
根据焦点和直角方向线的位置关系,圆锥曲线可以分为四种类型:椭圆、双曲线、抛物线和直线。
下面是各种圆锥曲线的基本方程:
1. 椭圆(Ellipse)的方程:
(x/a)² + (y/b)² = 1
其中,a为椭圆的长轴(长半径)长度,b为椭圆的短轴(短半径)长度。
2. 双曲线(Hyperbola)的方程:
(x/a)² - (y/b)² = 1 (右开口)
或
-(x/a)² + (y/b)² = 1 (左开口)
其中,a为双曲线的实轴(长半轴)长度,b为双曲线的虚轴(短半轴)长度。
3. 抛物线(Parabola)的方程:
y = ax² + bx + c
其中,a、b、c为抛物线方程的系数,确定了抛物线的形状和位置。
4. 直线(Line)的方程:
y = mx + c
其中,m为直线的斜率,c为直线的纵截距。
这些方程仅涵盖了基本形态的圆锥曲线方程。
在实际应用中,还可以根据具体情况进行方程的变形和扩展。

圆锥曲线全总结及全题型解析1.圆锥曲线的两定义:第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F ,F 的距离的和等于常,且此常数一定要大于,当常数等时,轨迹是线段 F F ,当常数小时,无轨迹;双曲线中,与两定点F ,F 的距离的差的绝对值等于常数,且此常数一定要小于F |,定义中的“绝对值”与<|F F|不可忽视。
若=|F F|,则轨迹是以F,F为端点的两条射线,若﹥|F F |,则轨迹不存在。
若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
2.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):(1)椭圆:焦点在轴上时(),焦点在轴上时=1()。
方程表示椭圆的充要条件是什么?(A B C≠0,且A,B,C同号,A≠B)。
(2)双曲线:焦点在轴上=1,焦点在轴上=1()。
方表示双曲线的充要条件是什么?(ABC≠0,且A,B 异号)。
(3)抛物线:开口向右时,开口向左,开口向上时,开口向下时。
3.圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):(1)椭圆:由, 分母的大小决定,焦点在分母大的坐标轴上。
(2)双曲线:由, 项系数的正负决定,焦点在系数为正的坐标轴上;(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
提醒:在椭圆中,最大,在双曲线中,最大。
4.圆锥曲线的几何性质:(1)椭圆(以()为例):①范围:;②焦点:两个焦点;③对称性:两条对称轴,一个对称中心(0,0),四个顶点,其中长轴长为,短轴长为;④准线:两条准线;⑤离心率:,椭圆,越小,椭圆越圆;越大,椭圆越扁。
(2)双曲线(以()为例):①范围:或;②焦点:两个焦点;③对称性:两条对称轴,一个对称中心(0,0),两个顶点,其中实轴长为2 ,虚轴长为,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为;④准线:两条准线;⑤离心率:,双曲线,等轴双曲线在椭圆外, 越小,开口越小, 越大,开口越大;⑥两条渐近线。
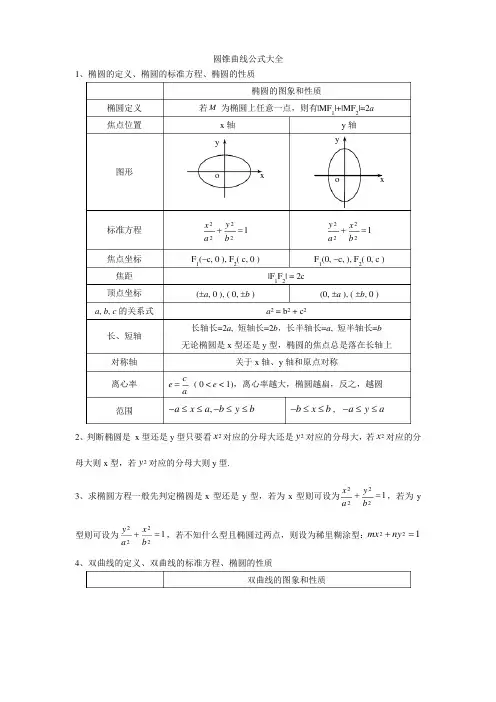
圆锥曲线公式大全1、椭圆的定义、椭圆的标准方程、椭圆的性质椭圆定义焦点位置椭圆的图象和性质若M 为椭圆上任意一点,则有|MF 1|+|MF 2|=2ax 轴y图形o xy 轴y o x标准方程焦点坐标焦距顶点坐标a ,b ,c 的关系式长、短轴对称轴离心率范围x 2y 2+2=12a b F 1(-c, 0 ), F 2( c, 0 )|F 1F 2| = 2c(±a , 0 ), ( 0,±b )a 2 =b 2 +c 2y 2x 2+2=12a b F 1(0,-c, ), F 2( 0, c )(0,±a ), (±b , 0 )长轴长=2a ,短轴长=2b ,长半轴长=a ,短半轴长=b 无论椭圆是x 型还是y 型,椭圆的焦点总是落在长轴上关于x 轴、y 轴和原点对称e =c ( 0 <e < 1),离心率越大,椭圆越扁,反之,越圆a-a ≤x ≤a ,-b ≤y ≤b 2-b ≤x ≤b ,-a ≤y ≤a22、判断椭圆是x 型还是y 型只要看x 对应的分母大还是y 对应的分母大,若x 对应的分母大则x 型,若y 对应的分母大则y 型.22x 2y 23、求椭圆方程一般先判定椭圆是x 型还是y 型,若为x 型则可设为2+2=1,若为y a b y 2x 222型则可设为2+2=1,若不知什么型且椭圆过两点,则设为稀里糊涂型:mx +ny =1a b 4、双曲线的定义、双曲线的标准方程、椭圆的性质双曲线的图象和性质若M为双曲线上任意一点,则有MF1-MF2=2a(2a<2c)双曲线定义若MF1-MF2=2a=2c,则点M的轨迹为两条射线若MF1-MF2=2a>2c,则点M无轨迹焦点位置x轴y轴图形标准方程焦点坐标焦距顶点坐标(±a, 0 )x2y2-2=12a bF1(-c, 0 ), F2( c, 0 )|F1F2| = 2cy2x2-2=12a bF1(0,-c, ), F2( 0, c )(0,±a )a,b,c的关系式椭圆形状长的像a,所以a是老大,a2 = b2 + c2;双曲线形状长的像c,所以c是老大,c2 = a2 + b2实轴、虚轴对称轴离心率范围渐近线实轴长=2a,虚轴长=2b,实半轴长=a,虚半轴长=b无论双曲线是x型还是y型,双曲线的焦点总是落在实轴上关于x轴、y轴和原点对称e=c(e >1)aa≤x或x≤-a,y∈R a≤y或y≤-a,x∈Ry=±bxay=±axb2、判断双曲线是x 型还是y 型只要看x 前的符号是正还是y 前的符号是正,若x 前的符号为正则x 型,若y 前的符号为正则y 型,同样的,哪个分母前的符号为正,则哪个分母就为a 22222x 2y 23、求双曲线方程一般先判定双曲线是x 型还是y 型,若为x 型则可设为2-2=1,若a b y 2x 2为y 型则可设为2-2=1,若不知什么型且双曲线过两点,则设为稀里糊涂型:a b mx 2-ny 2=1(mn <0)6、若已知双曲线一点坐标和渐近线方程y =mx ,则可设双曲线方程为y 2-m 2x 2=λ(λ≠0),而后把点坐标代入求解7、椭圆、双曲线、抛物线与直线l :y =kx +b 的弦长公式:AB =(k 2+1)(x 1-x 2)2=(12+1)(y -y )122k 8、椭圆、双曲线、抛物线与直线问题出现弦的中点往往考虑用点差法9、椭圆、双曲线、抛物线与直线问题的解题步骤:(1)假化成整(把分式型的椭圆方程化为整式型的椭圆方程),联立消y 或x (2)求出判别式,并设点使用伟大定理(3)使用弦长公式1、抛物线的定义:平面内有一定点F 及一定直线l (F 不在l 上)P 点是该平面内一动点,当且仅当点P 到F 的距离与点P 到直线l 距离相等时,那么P 的轨迹是以F 为焦点,l 为准线的一条抛物线.————见距离想定义!!!2、(1)抛物线标准方程左边一定是x 或y 的平方(系数为1),右边一定是关于x 和y 的一次项,如果抛物线方程不标准,立即化为标准方程!(2)抛物线的一次项为x 即为x 型,一次项为y 即为y 型!(3)抛物线的焦点坐标为一次项系数的四分之一,准线与焦点坐标互为相反数!一次项为x ,则准线为”x=多少”,一次项为y ,则准线为”y=多少”!(4)抛物线的开口看一次项的符号,一次项为正,则开口朝着正半轴,一次项为负,则开口朝着负半轴!(5)抛物线的题目强烈建议画图,有图有真相,无图无真相!3、求抛物线方程,如果只知x 型,则设它为y =ax (a ≠0),a>o,开口朝右;a<0,开口朝左;如果只知y 型,则设它为x =ay (a ≠0),a>o,开口朝上;a<0,开口朝下。


最全圆锥曲线知识点总结的定义是指平面内一个动点P到两个定点F1,F2的距离之和等于常数(PF1+PF2=2a>F1F2),那么这个动点P的轨迹就是椭圆。
这两个定点被称为椭圆的焦点,两焦点的距离被称为椭圆的焦距。
注意:如果PF1+PF2=F1F2,则动点P的轨迹是线段F1F2;如果PF1+PF2<F1F2,则动点P的轨迹无图形。
2)对于椭圆,如果焦点在x轴上,那么它的参数方程是x=acosθ,y=bsinθ(其中θ为参数),如果焦点在y轴上,那么它的参数方程是y=acosθ,x=bsinθ。
如果椭圆的标准方程是x2/a2+y2/b2=1(a>b>0),那么它的范围是−a≤x≤a,−b≤y≤b,焦点是两个点(±c,0),对称中心是(0,0),顶点是(±a,0)和(0,±b),长轴长为2a,短轴长为2b,离心率为e=c/a,椭圆即为0<e<1的情况。
3)关于直线与椭圆的位置关系,如果点P(x,y)在椭圆外,那么a2+b2>1;如果点P(x,y)在椭圆上,那么a2+b2=1;如果点P(x,y)在椭圆内,那么a2+b2<1.4)焦点三角形是指椭圆上的一点与两个焦点构成的三角形。
5)弦长公式是指如果直线y=kx+b与圆锥曲线相交于两点A、B,且x1、x2分别为A、B的横坐标,那么AB=√[1+k2(x1−x2)2]。
如果y1、y2分别为A、B的纵坐标,则AB=√[1+k2(y1−y2)2]。
如果弦AB所在直线方程设为x=ky+b,则AB=√[1+k2(y1−y2)2]。
6)圆锥曲线的中点弦问题可以用“韦达定理”或“点差法”求解。
在椭圆中,以P(x,b2x,y)为中点的弦所在直线的斜率k=−a2y。
1.已知椭圆 $m x^2 + n y^2 = 1$ 与直线 $x+y=1$ 相交于$A,B$ 两点,点 $C$ 是 $AB$ 的中点,且 $AB=2\sqrt{2}$,求椭圆的方程,若 $OC$ 的斜率为 $\frac{1}{2}$,求 $m,n$ 的值。

圆锥曲线知识点总结圆锥曲线是高中数学中的重要内容,包括椭圆、双曲线和抛物线。
掌握圆锥曲线的相关知识对于解决数学问题和理解数学的应用具有重要意义。
一、椭圆1、定义平面内与两个定点 F1、F2 的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2、标准方程(1)焦点在 x 轴上:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)(\(a > b > 0\)),其中\(a\)为长半轴长,\(b\)为短半轴长,\(c\)为半焦距,满足\(c^2 = a^2 b^2\)。
(2)焦点在 y 轴上:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1\)(\(a > b > 0\))。
3、椭圆的性质(1)对称性:椭圆关于 x 轴、y 轴和原点对称。
(2)范围:\(a \leq x \leq a\),\(b \leq y \leq b\)。
点为\((\pm a, 0)\),\((0, \pm b)\);焦点在 y 轴上时,顶点为\((0, \pm a)\),\((\pm b, 0)\)。
(4)离心率:椭圆的离心率\(e =\frac{c}{a}\)(\(0 < e < 1\)),它反映了椭圆的扁平程度,\(e\)越接近 0,椭圆越接近于圆;\(e\)越接近 1,椭圆越扁。
二、双曲线1、定义平面内与两个定点 F1、F2 的距离之差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距。
2、标准方程(1)焦点在 x 轴上:\(\frac{x^2}{a^2} \frac{y^2}{b^2} =1\),其中\(a\)为实半轴长,\(b\)为虚半轴长,\(c\)为半焦距,满足\(c^2 = a^2 + b^2\)。
(2)焦点在 y 轴上:\(\frac{y^2}{a^2} \frac{x^2}{b^2} =1\)。

高考数学圆锥曲线部分知识点梳理一、方程的曲线:在平面直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:(1)曲线上的点的坐标都是这个方程的解;(2)以这个方程的解为坐标的点都是曲线上的点,那么这个方程叫做曲线的方程;这条曲线叫做方程的曲线。
点与曲线的关系:若曲线C 的方程是f(x,y)=0,则点P 0(x 0,y 0)在曲线C 上⇔f(x 0,y 0)=0;点P 0(x 0,y 0)不在曲线C 上⇔f(x 0,y 0)≠0。
两条曲线的交点:若曲线C 1,C 2的方程分别为f 1(x,y)=0,f 2(x,y)=0,则点P 0(x 0,y 0)是C 1,C 2的交点⇔{),(0),(002001==y x f y x f 方程组有n 个不同的实数解,两条曲线就有n 个不同的交点;方程组没有实数解,曲线就没有交点。
二、圆:1、定义:点集{M ||OM |=r },其中定点O 为圆心,定长r 为半径.2、方程:(1)标准方程:圆心在c(a,b),半径为r 的圆方程是(x-a)2+(y-b)2=r 2圆心在坐标原点,半径为r 的圆方程是x 2+y 2=r 2 (2)一般方程:①当D 2+E 2-4F >0时,一元二次方程x 2+y 2+Dx+Ey+F=0叫做圆的一般方程,圆心为)2,2(E D--半径是2422FE D -+。
配方,将方程x 2+y 2+Dx+Ey+F=0化为(x+2D )2+(y+2E)2=44F-E D 22+②当D 2+E 2-4F=0时,方程表示一个点(-2D ,-2E); ③当D 2+E 2-4F <0时,方程不表示任何图形.(3)点与圆的位置关系 已知圆心C(a,b),半径为r,点M 的坐标为(x 0,y 0),则|MC |<r ⇔点M 在圆C 内,|MC |=r ⇔点M 在圆C 上,|MC |>r ⇔点M 在圆C 内,其中|MC |=2020b)-(y a)-(x +。

圆锥曲线极坐标方程一、知识总结:1、标准形式:1cos epe ρθ=-,其中p 为焦准距(焦点到准线的距离),对于椭圆和双曲线2b p c=,对于抛物线就是那个p ,其实抛物线中p 也表示焦准距。
2、过程:取圆锥曲线的一个焦点(椭圆取左焦点,双曲线取右焦点,抛物线右焦点)为极点,极轴垂直于相应的准线,但与其不相交,建立极坐标系。
注意,该极坐标方程,仅表示双曲线的右支,如果允许0ρ<,则表示两支。
3、关于ρ的正负问题:通常情况下规定0ρ≥,首先,ρ是极径,是长度,小于0没意义,其次,当0ρ>,02θπ≤<时,除极点外,平面上的点就与它的极坐标构成一一对应关系。
二、推广形式: 1、推广1:1cos epe ρθ=+:1)当01e <<时,方程表示极点在右焦点的椭圆; 2)当1e =时,方程表示开口向左的抛物线;3)当1e >时,方程表示极点在左焦点的抛物线。
2、推广2:1sin epe ρθ=-:1)当01e <<时,方程表示极点在下焦点的椭圆; 2)当1e =时,方程表示开口向上的抛物线;3)当1e >时,方程表示极点在上焦点的双曲线。
3、推广3:1sin epe ρθ=+:1)当01e <<时,方程表示极点在上焦点的椭圆;2)当1e =时,方程表示开口向下的抛物线;3)当1e >时,方程表示极点在下焦点的双曲线。
三、几点性质:1、当原点与极点重合,极轴与x 轴正半轴重合,单位长度相同时,对于圆锥曲线标准极坐标方程:1cos epe ρθ=-,与之对应的直角坐标方程为:1)当01e <<时,()22221x c y a b-+= ; 2)当1e =时,222p y p x ⎛⎫=+⎪⎝⎭;3)当1e >时,()22221x c y a b+-= 。
2、记圆锥曲线的标准形式:1cos epe ρθ=-时:1)公式1:()()20a ρρπ=+;公式2:()()20c ρρπ=-;公式3:b =2)过圆锥曲线的标准极坐标方程易求得过焦点且倾斜角为θ的弦长AB : 2221cos epAB e θ=-,特别地,对于抛物线,22sin p AB θ=. 四、焦半径公式:1、椭圆:已知(),P x y 在椭圆上,则:12,PF a ex PF a ex =+=-;2、双曲线:1)已知(),P x y 在双曲线右支上,则12,PF ex a PF ex a =+=-; 2)已知(),P x y 在双曲线左支上,则()()12,PF ex a PF ex a =-+=--; 综上,12,PF ex a PF ex a =+=-。

极点极线定义已知圆锥曲线С: Ax +By +Cx+Dy+E=0与一点P(x0,y 0) [ 其中 A +B x0+x≠0,点.P.不.在.曲.线.中.心.和.渐.近.线.上.]. 则称点P 和直线L:A?x0x+B?y0y+C? 2 +D?y2+y+E=0是圆锥曲线С的一对极点和极线x0+x y0+y 即在圆锥曲线方程中, 以x0x 替换x ,以2替换x,以y0y 替换y , 以2替换y 则可得到极点P(x0,y 0) 的极线方程L.特别地:(1) 对于圆(x-a) +(y-b) =r , 与点P(x 0 ,y 0) 对应的极线方程为(x 0-a)(x-a)+(y 0-b)(y-b)=r ;x y x0x y0y(2) 对于椭圆+ =1,与点P(x0,y 0)对应的极线方程为0 + 0 =1 ;a b a bx y x 0x y 0y(3) 对于双曲线 a -b =1,与点 P(x 0,y 0)对应的极线方程为 a 0 -b 0 =1 ;(4) 对于抛物线 y =2px ,与点 P(x 0,y 0) 对应的极线方程为 y 0y=p(x 0+x) ; 性质 一般地,有如下性质 [焦.点.所.在.区.域.为.曲.线.内.部. ]: ① 若极点 P 在曲线С上,则极线 L 是曲线С在P 点的切线;② 若极点 P 在曲线С外,则极线 L 是过极点 P 作曲线С的两条切线的切点连线;③ 若极点 P 在曲线С内,则极线 L 在曲线С外且与以极点 P 为中点的弦平行 [仅是 斜率相 等 ]( 若是 圆 , 则此时中 点 弦的 方程 为(x 0-a)(x-a)+(y 0-b)(y-b)=x 0x y 0y x 0 y 0;若是椭圆,则此时中点弦的方程为 a x x +b y y =x a +y bx 0x y 0y x 0 y 0双曲线,则此时中点弦的方程为 a x0x -b y0y =x a 0 -y b 0 ;若是抛物线 ,则此时中点弦的 方程为 y 0y-p(x 0+x)=y 0 -2px 0) ;(x 0-a) +(y 0-b) 若是④当P(x0,y 0)为圆锥曲线的焦点F(c,0) 时,极线恰为该圆锥曲线的准线..;⑤极点极线的对偶性:Ⅰ.已知点P和直线L是关于曲线С的一对极点和极线,则L上任一点Pn对应的极线Ln必过点P,反之亦然,任意过点P的直线Ln对应的极点Pn必在直线L上[图.Ⅱ.过点P作曲线C的两条割线L1、L2,L1交曲线C于AB,L2交曲线C于MN,则直线AM、BN的交点T,直线AN、BM的交点S必都落在点P 关于曲线C的极线L 上[ 图.中.点.P.与.直.线.S..T是.一.对.极.点.极.线.;.点.T.与.直.线.S..P是.一.对.极.点.极.线.] ;即OP = OR OROQⅢ. 点 P 是曲线 C 的极点,它对应的极线为 L ,则有 :1)若C 为椭圆或双曲线,O 是C 的中心,直线 OP 交C 与R ,交L 于Q ,则OP?OQ=OR如图中学数学中极点与极线知识的现状与应用虽然中学数学中没有提到极点极线,但事实上,它的身影随处可见,只是没有点破而已.教材内改名换姓,“视”而不“见” .由④可知椭圆x a +y b =1的焦点的极a线方程为: x= . 焦点与准线是圆锥曲线一章中的核心内容, 它揭示了圆锥曲线c的统一定义, 更是高考的必考知识点. 正是因为它太常见了, 反而往往使我们“视”而不“见” .圆锥曲线基础必备1、长轴短轴与焦距,形似勾股弦定理长轴=2“,短轴= 2b,焦距= 2c.则:a2 =b2 -^c2 1、准线方程准焦距.〃方、"方涂以r..& 0・ 刁2sm —cos — sm 0_ 2 2 1 +cos0 2 cos 2—2 & 所以:椭圆的焦点三角形的面积为S 胚恶=b tail-.4.焦三角形计面积"半角正切進乘焦三角形:以椭圆的两个焦点巧・耳为顶点,另一个顶点」 在椭圆上的三角形称为焦三角形•半角是指—Z 与P 巧的一半. 则焦三角形的面积为: 证明:设阿| =小|昭| = S 由余弦定理:m 2 +n 2 - 2mn cos^= 4c 2=4a即:-2mn - = 2mn - 4b 2,故: Sgf =-m n sin0 =-』+ cos& l + cos0又:0 =tan —三、椭圆的相关公式 切线平分焦周角, 切点连线求方程, 弦与中线斜率积, 细看中点弦方程,称为弦切角定理① 极线屯理须牢记② 准线去除准焦距③ 恰似弦中点轨迹④艮卩:2D = (1+ cos0)mn .1、 切线平分焦周角,称为弦切角定理弦切角定理:切线平分椭圆焦周角的外角,平分双 曲线的焦周角.焦周角是焦点三角形中,焦距所对应的角.弦切角是指椭圆的弦与其切线相交于椭圆上时它 们的夹角,当弦为焦点弦时(过焦点的弦),那么切 线是两个焦点弦的角平 分线.第6页2. 切点连线求方程,圾线定理须牢记若旳(X05)在椭圆卡+$ = 1外,则过昨作椭圆的两 条切线,切点、为P 』,巧,则点耳和切点弦马•勺分别称 为椭圆的极点和极线.切点弦耳乃的直线方程即极线方程是笫?页3、弦与中线斜■率积.准线去涂准焦距|弦指椭圆内的一弦•中线指弦AB 的中点M 与 原点O 的连线,即2AB 得中线•这两条直线的斜率的VY - Q 2於乘积,等于准线距离去除准焦^p= — .其k k_ p 结杲是:0M = T =~V第8页(称为极线定理)4、细看中点弦方程,恰似弦中点、轨迹|中点、弦AB 的方程:在椭圆中,若弦的中点、为弦仙称为中点弦,则中点弦的方程就是弦中点M 的轨迹方程:在椭圆中,过椭圆内点 p 皿、m 的弦AB , 其中点、M 的方程就是 S . y o y … /( y 2. 一7*+矿二正+歹,仍为椭圆.这两个方程有些相似,要擦亮眼睛,千万不要搞 混了.第9页是直线方程.圆锥曲线必背口诀(红字为口诀)-双曲线一、双曲线定义双曲线有四定义.差比交线反比何1、定义1:(差)平面内,到两个定点唇码的距离之差的绝对值为定值2“(小于这两个定点间的距离冈砂)的点的轨迹称为双曲线。
双曲线知识点一、 双曲线的定义:1. 第一定义:到两个定点F 1与F 2的距离之差的绝对值等于定长〔<|F 1F 2|〕的点的轨迹〔21212F F a PF PF <=-〔a 为常数〕〕这两个定点叫双曲线的焦点.要注意两点:〔1〕距离之差的绝对值.〔2〕2a <|F 1F 2|.当|MF 1|-|MF 2|=2a 时,曲线仅表示焦点F 2所对应的一支; 当|MF 1|-|MF 2|=-2a 时,曲线仅表示焦点F 1所对应的一支;当2a =|F 1F 2|时,轨迹是一直线上以F 1、F 2为端点向外的两条射线;当2a >|F 1F 2|时,动点轨迹不存在.2. 第二定义:动点到一定点F 的距离与它到一条定直线l 的距离之比是常数e (e >1)时,这个动点的轨迹是双曲线这定点叫做双曲线的焦点,定直线l 叫做双曲线的准线二、双曲线的标准方程:12222=-b y a x 〔a >0,b >0〕(焦点在x 轴上);12222=-bx a y 〔a >0,b >0〕(焦点在y 轴上);1. 如果2x 项的系数是正数,那么焦点在x 轴上;如果2y 项的系数是正数,那么焦点在y 轴上. a 不一定大于b.2. 与双曲线12222=-by a x 共焦点的双曲线系方程是12222=--+k b y k a x 3. 双曲线方程也可设为:221(0)x y mn m n-=> 例题:双曲线C 和椭圆221169x y +=有相同的焦点,且过(3,4)P 点,求双曲线C 的轨迹方程。
三、点与双曲线的位置关系,直线与双曲线的位置关系: 1 点与双曲线:点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的内部2200221x y a b ⇔->点00(,)P x y 在双曲线22221(0,0)x y a b a b -=>>的外部2200221x y a b ⇔-<点00(,)P x y 在双曲线22221(0,0)x y a b a b-=>>上220022-=1x y a b ⇔2 直线与双曲线:〔代数法〕设直线:l y kx m =+,双曲线)0,0(12222>>=-b a by a x 联立解得02)(222222222=----b a m a mkx a x k a b1) 0m =时,b bk a a-<<直线与双曲线交于两点〔左支一个点右支一个点〕;b k a ≥,bk a≤-,或k 不存在时直线与双曲线没有交点;2) 0m ≠时,k 存在时,假设0222=-k a babk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;假设2220b a k -≠,222222222(2)4()()a mk b a k a m a b ∆=-----2222224()a b m b a k =+-0∆>时,22220m b a k +->,直线与双曲线相交于两点; 0∆<时,22220m b a k +-<,直线与双曲线相离,没有交点;0∆=时22220m b a k +-=,2222m b k a +=直线与双曲线有一个交点;假设k 不存在,a m a -<<时,直线与双曲线没有交点; m a m a ><-或直线与双曲线相交于两点; 3. 过定点的直线与双曲线的位置关系:设直线:l y kx m =+过定点00(,)P x y ,双曲线)0,0(12222>>=-b a by a x1).当点00(,)P x y 在双曲线内部时:b bk a a-<<,直线与双曲线两支各有一个交点; a bk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;b k a >或bk a<-或k 不存在时直线与双曲线的一支有两个交点;2).当点00(,)P x y 在双曲线上时:bk a =±或2020b x k a y =,直线与双曲线只交于点00(,)P x y ;b bk a a-<<直线与双曲线交于两点〔左支一个点右支一个点〕; 2020b x k a y >〔00y ≠〕或2020b x bk a a y << 〔00y ≠〕或b k a <-或k 不存在,直线与双曲线在一支上有两个交点;当00y ≠时,bk a =±或k 不存在,直线与双曲线只交于点00(,)P x y ;b k a >或bk a <-时直线与双曲线的一支有两个交点;b bk a a-<<直线与双曲线交于两点〔左支一个点右支一个点〕; 3).当点00(,)P x y 在双曲线外部时: 当()0,0P 时,b bk a a -<<,直线与双曲线两支各有一个交点; b k a ≥或bk a≤或k 不存在,直线与双曲线没有交点;当点0m ≠时,k =时,过点00(,)P x y 的直线与双曲线相切 bk a=±时,直线与双曲线只交于一点;几何法:直线与渐近线的位置关系例:过点(0,3)P 的直线l 和双曲线22:14y C x -=,仅有一个公共点,求直线l 的方程。
2019高考数学复习常用圆锥曲线公式总结圆锥曲线包括圆,椭圆,双曲线,抛物线。
以下是常用圆锥曲线公式总结,请考生及时学习。
抛物线:y = ax *+ bx + c就是y等于ax 的平方加上bx再加上ca 0时开口向上a 0时开口向下c = 0时抛物线经过原点b = 0时抛物线对称轴为y轴还有顶点式y = a(x+h)* + k就是y等于a乘以(x+h)的平方+k-h是顶点坐标的xk是顶点坐标的y一般用于求最大值与最小值抛物线标准方程:y^2=2px它表示抛物线的焦点在x的正半轴上,焦点坐标为(p/2,0) 准线方程为x=-p/2由于抛物线的焦点可在任意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py圆:体积=4/3(pi)(r^3)面积=(pi)(r^2)周长=2(pi)r圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F0语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。
如果有选择循序渐进地让学生背诵一些优秀篇目、精彩段落,对提高学生的水平会大有裨益。
现在,不少语文教师在分析课文时,把文章解体的支离破碎,总在文章的技巧方面下功夫。
结果教师费劲,学生头疼。
分析完之后,学生收效甚微,没过几天便忘的一干二净。
造成这种事倍功半的尴尬局面的关键就是对文章读的不熟。
常言道“书读百遍,其义自见”,如果有目的、有计划地引导学生反复阅读课文,或细读、默读、跳读,或听读、范读、轮读、分角色朗读,学生便可以在读中自然领悟文章的思想内容和写作技巧,可以在读中自然加强语感,增强语言的感受力。
久而久之,这种思想内容、写作技巧和语感就会自然渗透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创造和发展。
常用圆锥曲线公式总结的全部内容就是这些,查字典数学网预祝考生取得优异的成绩。
宋以后,京师所设小学馆和武学堂中的教师称谓皆称之为“教谕”。
圆锥曲线推导过程要推导圆锥曲线,我们首先需要了解什么是圆锥。
圆锥是由一个圆在一个点上沿着一条直线平移而生成的曲面。
在数学中,圆锥曲线是圆锥与一个平面的交线。
现在我们来推导圆锥曲线的具体过程。
1.圆锥的定义:假设我们有一个圆心为O,半径为r的圆C以及一个点V,且OV的长度为h,V在与圆C不在同一平面上。
接下来,我们沿着OV的方向以圆C为基准,平移V点,从而生成圆锥曲线。
2.圆锥曲线的参数方程:设V点的坐标为(x,y,z)。
由于平移是沿着OV的方向进行的,所以可以得到以下关系式:x=k*ry=k*rz=k*h其中,k为比例因子。
3.圆锥曲线的一般方程:将参数方程转化为一般方程。
我们可以用x,y和z来代替r和h的关系,从而得到一般方程:(x/a)^2+(y/b)^2=(z/c)^2其中,a=r^2/h,b=r^2/h,c=r。
4.圆锥曲线的分类:根据参数方程或一般方程的形式,我们将圆锥曲线分为四类:椭圆、抛物线、双曲线和直线。
当a=b=c时,我们得到的方程为x^2+y^2=z^2,这是一个圆锥面。
当a=b≠c时,我们得到的方程为x^2+y^2=kz^2,这是一个椭圆锥面。
当a=b≠c时,我们得到的方程为x^2y^2=kz^2,这是一个双曲线锥面。
当a=0或b=0时,我们得到的方程为y=kx^2,这是一个抛物线。
5.圆锥曲线在平面上的投影:将圆锥曲线投影到平面上可以得到不同的曲线。
椭圆的投影是一个椭圆或一个圆,抛物线的投影是一个抛物线,双曲线的投影是一个双曲线或两个直线,直线的投影仍然是一条直线。
6.圆锥曲线在几何中的应用:圆锥曲线在几何学中有着广泛的应用。
椭圆轨道用于描述行星在太阳系中的运动,抛物线轨道用于描述天体的抛物运动,双曲线轨道用于描述一些天文现象,如彗星的路径等。
以上就是推导圆锥曲线的过程。
通过了解圆锥的定义和参数方程,我们可以得到一般方程,并根据方程的形式将圆锥曲线进行分类。
圆锥曲线在几何学中有着重要的应用,我们可以通过研究它们的特性来更好地理解和描述各种现象。
圆 锥 曲 线一、基本思想和基本方法⒈基本思想:运动与联系、特殊与一般、函数与方程、转化与类比 ⒉基本方法:代数方法、几何方法、向量方法、三角代换 ⒊基本问题:①由性质求轨迹方程 ②由方程研究性质二、常见的几种题型 ⒈ 求轨迹方程⒉ 弦长公式极其应用 ⒊ 垂直半径的问题⒋ 弦的中点与斜率的关系⒌ 圆锥曲线上关于直线的对称点问题 ⒍ 圆锥曲线的切线问题⒎ 圆锥曲线中的不等式问题三、几组公式:㈠三类弦长(e 表示离心率,p 表示焦准距,α弦所在直线的倾斜角):? 1.焦点弦的弦长:椭圆: |AB|=α22cos12e ep -;双曲线:|AB|=|cos 1|222αe ep -;当α22cos1e ->0时,AB 是内点弦,当α22cos 1e -<0时,AB 是外点弦. 抛物线:|AB|=α2sin2p .说明:利用圆锥曲线的统一定义证明. 2.中心弦的弦长:椭圆: |AB|=α22cos 12e b -; 双曲线:|AB|=1cos 222-αe b .说明:可结合圆锥曲线的参数方程证明.3.顶点弦的弦长(这里的顶点在长轴、实轴上): 椭圆: |AB|=α22cos12e ep -|cos α|; 双曲线: |AB|=|cos 1|222αe ep -|cos α|;抛物线: |AB|=α2sin2p |cos α|.说明:可利用直线、圆锥曲线的参数方程证明.㈡ 与圆锥曲线离心率相关的几个角(以椭圆为例): ⒈ 命题1:设P (x ,y )是椭圆2222by ax +=1(a >b >0)上一点,F 1、F 2是椭圆的两个焦点,∠F 1PF 2=α,则y=±b 时,max α=2arctg bc ,简证:由△PF 1F 2的面积为S=b 2 tg 2α =c|y|,所以tg 2α =2by c .(或由均值定理).2.命题2.设P (x ,y )是椭圆2222by ax +=1(a >b >0)上一点。