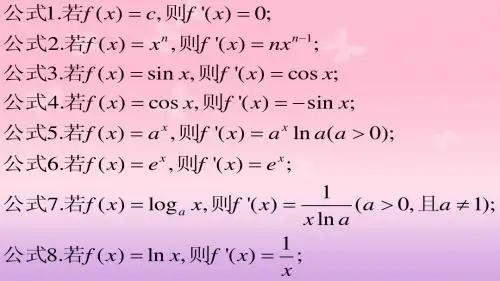复合函数的导数PPT优秀课件

复合函数的导数
目 录
• 复合函数简介 • 复合函数的导数 • 复合函数导数的计算 • 复合函数导数的应用 • 习题与答案
01
CATALOGUE
复合函数简介
复合函数的定义
复合函数是由两个或多个函数通过复 合运算得到的函数。
设$u = f(x)$是一个函数，$y = g(u)$是另一个函数，则复合函数$y = g(f(x))$是由$f(x)$和$g(u)$复合而 成。
复合函数导数的计算
链式法则
总结词
链式法则是复合函数求导的核心，它描述了函数内部自变量对外部自变量的导数关系。
详细描述
链式法则指出，如果一个函数y是另一个函数u的复合函数，即y=f(u)，那么dy/dx等于dy/du乘以du/dx。具体 地，假设y=f(u)和u=g(x)，则dy/dx=(dy/du)*(du/dx)。
$f'(x) = 3x^2 + 4x + 1$
$f'(frac{pi}{2}) = cos(frac{pi}{2}) cdot frac{pi}{2} = 0$
$f'(e) = frac{2}{e}$
THANKS
感谢观看
复合函数导数的应用 利用导数研究函数的单调性
总结词
利用导数研究曲线的凹凸性。
详细描述
通过求二阶导数并分析其符号，可以判断曲线的凹凸性 。二阶导数大于0的区间内，曲线为凹；二阶导数小于0 的区间内，曲线为凸。这一性质在几何和工程领域中有 重要的应用。
05
CATALOGUE
习题与答案
习题
计算复合函数$f(x) = (x^2 + 1)(x + 3)$的导数 。
乘积法则

THANKS
THANK YOU FOR YOUR WATCHING
边际分析
在经济学中，导数可以用来进行边际分析，帮助理解经济变量的 变化对总体的影响。
弹性分析
导数可以用来计算弹性，帮助理解经济变量之间的相对变化。
最优化问题
通过导数，可以找到使经济效用最大的最优解。
导数在物理学中的应用
速度和加速度
在物理学中，导数可以用来计算速度和加速度，从而更好地理解 物体的运动状态。
03
复合函数求导的应用
ห้องสมุดไป่ตู้
导数在几何中的应用
切线斜率计算
在几何中，导数可以用来计算曲线的切线斜率， 从而了解曲线在某一点的增减性。
极值问题
通过导数，可以确定曲线的极值点，从而确定曲 线的最大值和最小值。
曲线的凹凸性
导数的符号可以用来判断曲线的凹凸性，从而更 好地理解曲线的形状。
导数在经济学中的应用
商式法则是指对复合函数的商式形式进行求导，即对分子和分母分别进行求导，然后将结果相除。
详细描述
商式法则用于处理复合函数中多个函数的商式形式。其基本思想是将复合函数分解为两个基本初等函 数的商，然后分别对分子和分母进行求导。具体地，对于复合函数$frac{f(u)}{g(u)}$，商式法则可以 表示为$frac{f'(u) cdot g(u) - f(u) cdot g'(u)}{[g(u)]^2}$。
《复合函数求导》ppt课件
目录 CONTENTS
• 引言 • 复合函数求导法则 • 复合函数求导的应用 • 复合函数求导的注意事项 • 习题与解答
01
引言
课程背景
01
复合函数求导是微积分中的重要概念，是学习微积分的基础。

i
n1 x
co
s1(1)
usinv,
xx
s
e
i
n1
x.c
o1sx(x12)

1 x2
sin1
ex
co
1 s x
目录
练习. 求导数 (1).ysin22x
(2)ycoe sx
解 (1).y[(s2in x)2]2sin 2x(si2nx) 2sin 2xco2sx(2x) 4sin 2xco2sx2sin 4x
2 （ [six n ） （ cox） s （ six n ） （ cox） s ] （求导
（ 2coxscoxssix n（ six n） ] （导数公
（ 2co2x ss i2nx） 2co2x s
目录
(s2 ix n )2co 2x s
思考 因为 ysin2x是由 ysinu u2x复合而成的复合函数，
x
1 ln
a
1 8.(lnx)
x
9.(sixn)coxs
1.0(cxo)ssinx
1.1(tax)ns
e
c2
x

1 cos2
x
1.2(cxo)tcs2cx s
1 in2 x
目录
导数的四则运算法则
(1) 函数和的导数等于函数 导数的和
(u v ) u v;

s
1 inx

cosx
coxt.
错误写法
错解 y(lቤተ መጻሕፍቲ ባይዱn ixn )(sx i)n
一般按 “由外向里层层求导” 法求导
目录
例 求函y数 e12x的导. 数 解 y euu (e 1 2 x)1 ( 2 x)

我们遇到的许多函数都 可以看成是由两个函数 经过 " 复合" 得到的, 例如, 函数y 2 x 3 由y u 2和u 2 x 3
2
" 复合" 而成, 等等.
一般地, 对于两个函数 y f u 和u g x , 如果通过变量 u, y可以表示成 x的函数, 那么称这个函数为函数 y f u 和 u g x 的复合函数 (com posite fun ction), 记作y f g x .
' ' ' yx yu ux ln u 3x 2 ' '
即y对x的导数等于 y对u的导数与 u对x的导数的乘积 .
1 3 3 . u 3x 2
例4
求下列函数的导数
2
1 y 2 x 3 ; 2 y e 0.05 x 1 ; 3 y sin x 其中 , 均为常数.
复合函数y f g x 的导数和函数 y f u , u g x 的
' ' ' 导数间的关系为 yx yu ux .

' yx 表示y对x的导数
由此可得 , y ln3 x 2 对x的导数等于 y ln u对u的 导数与u 3x 2对x的导数的乘积 ,即
练习2、求下列函数的导数。
1、y=x5+sinx-7x 2、y=6x-cosx+log7x 3、y=ex+lnx+9x7 4、y=4ex-2cosx+7sinx
一、复习与引入：
求函数y=(3x-2)2的导数. 可以把平方式展开,利用导数的四则运算法则,再 求导. 思考: 能否用其它的办法求导呢? 又如函数 f x ln x 的导数是什么 ？ 函数 f x ln 3x 2 的导数又是什么呢?

y 2 u
y
u 1 (u u )
x 2
2u x 2

1 2
[(
2u
2

1 2

2u 1)
2
( 2u

1 2
2u
2

1)] 2

1 4
(2u2

2
2u


2u
2
)
x y, x2 y
y
解
求 uxx , uxy , uxz .
ux
f1
1 y

f2 z
f3 0
1 y
f1
zf2
uxx
1( y
f11

1 y

f12 z)
f

z(
f21
1 y

f22 z)
1x
2y 3z

1 y2
f11

2
z y
f12

z2
f

,
f21

2 f vu
,
f22

2 f v 2
例1 z f ( xy, x2 y2 ), f 有二阶连续偏导，
求 z xy . 解 zx f1 y f2 2x
1x
f
2y
f1
1 2
x y
f2
1 2
x y
zxy f1 y( f11 x f12 (2 y)) 2x( f21 x f22 (2 y))
第4节 多元复合函数微分法
一、多元复合函数的求导法则
一元函数：y f (u), u ( x) 都可导，则

（2）函数 = −.+ 可以看作函数 = 和 = −. + 的复合函数.根
据复合函数的求导法则，有
′ = ′ ∙ ′ = ′ ∙ −. + ′ = −. = −. −.+
（3）函数 = ln(2 − 1) 可以看作函数 = ln 和 = 2 − 1 的复合函数.根据
(2)令 u＝ex＋x2，则 y＝ln u，
ex＋2x
1 x 2
1
x
y′x＝y'u·u′x＝u·(e ＋x )′＝ x
·
(e
＋2x)＝ x
.
2
2
e ＋x
e ＋x
例3 某个弹簧振子在振动过程中的位移y（单位：mm）关于时间t（单位：
s）的函数满足关系式为 = (





− ) . 求函数y在t=3s 时的导数，并解
个函数为函数y＝f(u)和u＝g(x)的复合函数，记作y＝f(g(x)). 且 ˊ = ˊ · ˊ .
复
合
函
数
求
导
分层——选择中间变量，写出
构成它的内、外层函数
求导——分别求内、外层函数对
应变量的导数
代回——把中间变量回代
相乘——把上述求导的结果相乘
课后提升
3



1．下列求导运算正确的是（ B）A．( + )′ = +
5.2 导数的运算
思 考


=
(1
+
)
的导数呢？
如何求函数 = (1 + ) 的导数呢？
3
= (1 + )3 = 3 + 3 2 + 3 + 1

1 － 2a = 2b －4
ab 5. 2
解(2): ab a b
ab (a b)2 25 .
2
2
16
16
再见!
17
eu (0.05) 0.05e0.05x1.
10
例2 求下列函数的导数
1 y 2x 32 ; 2 y e0.05x1 ; 3 y sin x 其中 ,均为常数 .
(3)函数 y sin x 可以看作函数 y sin u
13
例4.求过点P(－2,0)且与曲线y=x2＋x＋1相切的直线方程.
b=a2＋a＋1 …………(1)
y' 2x 1
kPA 2a 1
kPA

a
b
2
b
P(－2,0)
2a 1
a2
b=2a2＋5a＋2 …………(2)
A(a,b)
2a2＋5a＋2 =a2＋a＋1 a2＋4a＋1=0
和 u x 的复合函数. 由复合函数求导法则有:
y'x yu' u'x (sin u)' x ' cos u cos x .
11
4 y 2x 3 ; 5 y ln(2x 1);
(6) y ( x 2)3(3x 1)2
解出a即可。
15
例5.设抛物线C1 : y x2 - 2x 2与抛物线 C2 : y - x2 ax b在它们的交点处的切线互相垂直. (1)求a, b之间的关系.
(2)若a 0, b 0,求ab的最大值.
解(1): 设C1与C2交点P(m,n),

tt
z z u z v o( ) ( (u)2 (v)2 )
t u t v t t
则有u 0, v 0,
z
u du , v dv t dt t dt
uv
o( )
tt
(△t＜0 时,根式前加“–”号)
d z z d u z dv ( 全导数公式 ) d t u d t v d t
t tt
z f (u,v) , u (x, y), v (x, y)
z x
z u z v u x v x
f11
f21
z
uv
z z u z v y u y v y
f12 f2 2
x yx y
又如, z f (x,v), v (x, y)
当它们都具有可微条件时, 有
w x
f2 yz
x y zx y z
y z f2 (x y z, xyz)
2w xz
f12 xy
f22 x y
为简便 起f11见
,y引(x入 z记) f号12
xfy12z
f2f2, u
fy12f
2
2 f u v
,
例5. 设
二阶偏导数连续,求下列表达式在
极坐标系下的形式
解: 已知
,则
一、多元复合函数求导的链式法则
定理. 若函数
z f (u,v)
处偏导连续, 则复合函数
在点 t 可导, 且有链式法则
d z z d u z dv d t u d t v d t
z
uv
证: 设 t 取增量△t , 则相应中间变量 有增量△u ,△v ,
z z u z v o ( )
u v
说明: 若定理中

1.2.3 复合函数的导数
苏教版选修2-2 高中数学
一、学习目标： 1、了解简单复合函数的求导法则; 2、会运用上述法则求简单复合函数的导数。
二、学习重点： 简单复合函数的求导法则的应用。
三、 学习难点： 将复合函数分解为两个简单函数。
知识回顾：
求 下 列 函 数 的 导 数 ：
1fxx29x3x
和 函 数 u2x复 合 而 成 .
求导
相乘
回代
复合函数的求导法则：
一般地，若 yfu,uaxb，则
函数 f22fxx的 f导 x数是？
对于一般的复合函数，结论也成立 。
例题讲解
课堂练习 1、求下列函数的导数：
课堂练习 1、求下列函数的导数：
课堂练习 1、求下列函数的导数：
课堂练习
2 、 求 曲 线 y s in 2 x 6 在 x 1 2 处 的 切 线 方 程 .
解 ： ysinu,u2x.
切 y 线 的 sin 斜 u 率 ku 2 6c o c o ss u 2 1 2 2 2 6 c o s 1 2 .x 6 .
而切点坐标为12，23，
切 线 的 方 程 为 y 2 3 1 x 1 2 ,即 y x 2 3 1 2 .

小结 ： • ⑴复合函数的求导，要注意分析复合函数的结 构，引入中间变量，将复合函数分解成为较简单的 函数，然后再用复合函数的求导法则求导； • ⑵复合函数求导的基本步骤是：
分解——求导——相乘——回代
懂得如何避开问题的人，胜过知道怎样解决问题的人。在这个世界上，不知道怎么办的时候，就选择学习，也许是最佳选择。胜出者往往不是能力而是观念！在家里看到的 永远是家，走出去看到的才是世界。把钱放在眼前，看到的永远是钱，把钱放在有用的地方，看到的是金钱的世界。给人金钱是下策，给人能力是中策，给人观念是上策。 财富买不来好观念，好观念能换来亿万财富。世界上最大的市场，是在人的脑海里！要用行动控制情绪，不要让情绪控制行动；要让心灵启迪智慧，不能让耳朵支配心灵。 人与人之间的差别，主要差在两耳之间的那块地方！人无远虑，必有近忧。人好的时候要找一条备胎，人不好的时候要找一条退路；人得意的时候要找一条退路，人失意的 时候要找一条出路！孩子贫穷是与父母的有一定的关系，因为他小的时候，父母没给他足够正确的人生观。家长的观念是孩子人生的起跑线！有什么信念，就选择什么态度； 有什么态度，就会有什么行为；有什么行为，就产生什么结果。要想结果变得好，必须选择好的信念。播下一个行动，收获一种习惯；播下一种习惯，收获一种性格；播下 一种性格，收获一种命运。思想会变成语言，语言会变成行动，行动会变成习惯，习惯会变成性格。性格会影响人生！习惯不加以抑制，会变成生活的必需品，不良的习惯 随时改变人生走向。人往往难以改变习惯，因为造习惯的就是自己，结果人又成为习惯的奴隶！人生重要的不是你从哪里来，而是你到哪里去。当你在埋头工作的时侯，一 定要抬头看看你去的方向。方向不对，努力白费！你来自何处并不重要，重要的是你要去往何方，人生最重要的不是所站的位置，而是所去的方向。人只要不失去方向，就 永远不会失去自己！这个世界唯一不变的真理就是变化，任何优势都是暂时的。当你在占有这个优势时，必须争取主动，再占据下一个优势，这需要前瞻的决断力，需要的 是智慧！世上本无移山之术，惟一能移山的方法就是：山不过来，我就过去。人生最聪明的态度就是：改变可以改变的一切，适应不能改变的一切！学一分退让，讨一分便 宜；增一分享受，减一分福泽。念头端正，福星临，念头不正，善人行善，从乐入乐，从明入明；行恶，从苦入苦，骨宜刚，气宜柔，志宜大，胆宜小，心宜虚，言宜实， 慧宜增，福宜惜，虑不远，忧亦近。人之所以痛苦，在于追求错误的东西。你目前拥有的，都将随着你的而成为他人的。那为何不现在就给真正需要的人呢？如得意不宜重 往，凡做事应有余步。我们最值得自豪的不在于从不跌倒，而在于每次跌倒之后都爬得起来。见己不是，万善之门。见人不是，诸恶之根。为了向别人、向世界证明自己而 努力拼搏，而一旦你真的取得了成绩，才会明白：人无须向别人证明什么，只要你能超越自己。没有哪种教育能及得上逆境。如果你想成功，那么请记住：遗产为零、诚实 第一、学习第二、礼貌第三、刻苦第四、精明第五。任何的限制，都是从自己的内心开始的。失败只是暂时停止成功，假如我不能，我就一定要；假如我要，我就一定能！ 无论你如何为他人着想，烦你的人眼里，你就是居心叵测；不管你怎样据理力争，不懂你的人心里，你就是胡搅蛮缠。最后你会发现，有些事不是你做错了，而是你遇错了 人；有些人不是不理解你，而是根本不想懂你。不管怎样，生活还是要继续向前走去。有的时候伤害和失败不见得是一件坏事，它会让你变得更好，孤单和失落亦是如此。 每件事到最后一定会变成一件好事，只要你能够走到最后。工资是发给日常工作的人，高薪是发给承担责任的人，奖金是发给做出成绩的人，股权是分给能干忠诚的人，荣 誉是颁给有理想抱负的人，辞退信将送给没结果还耍个性的人，这里一定有个你。内心想成为什么样的人，就会努力成为这样的人，做你想做的那种人。与其指望遇到一个 谁，不如指望自己能够吸引那样的人；与其指望每次失落的时候会有正能量出现温暖自己，不如指望自己变成一个正能量满满的人；与其担心未来，不如现在好好努力。彩 虹绚烂多姿，是在与狂风暴雨争斗之后；枫叶似火燃烧，是在与秋叶的寒霜争斗之后；雄鹰的展翅高飞，是在与坠崖的危险争斗之后。他们保持着奋斗的姿态，才铸就了他 们的成功。有能力的人影响别人，没能力的人受人影响；不是某人使自己烦恼不安，而是自己拿某人的言行来烦恼自己；树一个目标，一步步前行，做好自己就好。雄鹰， 不需鼓掌，也在飞翔；小草，没人心疼，也在成长；野花，没人欣赏，也在芬芳；做事不需人人都理解，只需尽心尽力；做人不需人人都喜欢，只需坦坦荡荡。努力到无能 为力，拼搏到感动自己；吃过的苦，受过的累，会照亮未来的路；没有年少轻狂，只有胜者为王。真正成功的人生，不在于成就的大小，而在于你是否努力地去实现自我， 喊出自己的声音，走出属于自己的道路。选一个方向，定一个时间；剩下的只管努力与坚持，时间会给我们最后的答案。许多人企求着生活的完美结局，殊不知美根本不在 结局，而在于追求的过程。慢慢的才知道：坚持未必就是胜利，放弃未必就是认输，。给自己一个迂回的空间，学会思索，学会等待，学会调整。人生没有假设，当下即是 全部。背不动的，放下了；伤不起的，看淡了；想不通的，不想了；恨不过的，抚平了。在比夜更深的地方，一定有比夜更黑的眼睛。一切伟大的行动和思想，都有一个微 不足道的开始。从来不跌倒不算光彩，每次跌倒后能再站起来，才是最大的荣耀。这个世界到处充满着不公平，我们能做的不仅仅是接受，还要试着做一些反抗。一个最困 苦、最卑贱、最为命运所屈辱的人，只要还抱有希望，便无所怨惧。有些人，因为陪你走的时间长了，你便淡然了，其实是他们给你撑起了生命的天空；有些人，分开了， 就忘了吧，残缺是一种大美。照自己的意思去理解自己，不要小看自己，被别人的意见引入歧途。没人能让我输，除非我不想赢！花开不是为了花落，而是为了开的更加灿 烂。随随便便浪费的时间，再也不能赢回来。不管从什么时候开始，重要的是开始以后不要停止；不管在什么时候结束，重要的是结束以后不要后悔。当你决定坚持一件事 情，全世界都会为你让路。只有在开水里，茶叶才能展开生命浓郁的香气。别想一下造出大海，必须先由小河川开始。不要让未来的你，讨厌现在的自己，困惑谁都有，但 成功只配得上勇敢的行动派。人生最大的喜悦是每个人都说你做不到，你却完成它了！如果你真的愿意为自己的梦想去努力，最差的结果，不过是大器晚成。不忘初心，方 得始终。每个人都有潜在的能量，只是很容易：被习惯所掩盖，被时间所迷离，被惰性所消磨。不论你在什么时候开始，重要的是开始之后就不要轻言放弃。恨别人，痛苦 的却是自己。每天醒来，敲醒自己的不是钟声，而是梦想。你不能拼爹的时候，你就只能去拼命！、如果人生的旅程上没有障碍，人还有什么可做的呢。我们无法选择自己 的出身，可是我们的未来是自己去改变的。励志名言：比别人多一点执着，你就会创造奇迹伟人之所以伟大，是因为他与别人共处逆境时，别人失去了信心，他却下决心实 现自己的目标。人生就像一道漫长的阶梯，任何人也无法逆向而行，只能在急促而繁忙的进程中，偶尔转过头来，回望自己留下的蹒跚脚印。时间，带不走真正的朋友；岁 月，留不住虚幻的拥有。时光转换，体会到缘分善变；平淡无语，感受了人情冷暖。有心的人，不管你在与不在，都会惦念；无心的情，无论你好与不好，只是漠然。走过 一段路，总能有一次领悟；经历一些事，才能看清一些人。我们无法选择自己的出身，可是我们的未来是自己去改变的。

5.2.3
简单复合函数的导数
课标阐释
思维脉络
1.了解复合函数的概念.(数学抽象) 简 单 复 合 函 数 的 导 数
2.理解复合函数的求导法则,并能求
概念
简单的复合函数的导数.(逻辑推理、
求导法则——应用
数学运算)
激趣诱思
知识点拨
我们学习过基本初等函数,如指数函数、对数函数、幂函数、三角
函数、常数函数,我们可以把这些函数进行加、减、乘、除、乘方、
a=
.
分析:(1)设 P(x0,y0)→由 y'| = =2
0
求P(x0,y0)→由点到直线的距离求最小值
(2)求y'→由y'|x=0=2求a的值
)
探究一
探究二
探究三
素养形成
当堂检测
解析:(1)设曲线y=ln(2x-1)在点(x0,y0)处的切线与直线2x-y+3=0平行.
2
,∴y'| =
f'(x)=(
)
A.2cos 2x+2e2x
B.cos 2x+e2x
C.2sin 2x+2e2x
D.sin 2x+e2x
解析:因为f(x)=sin 2x+e2x,所以f'(x)=2cos 2x+2e2x.故选A.
答案:A
探究一
探究二
探究三
素养形成
当堂检测
3.(2020福建高二期末)已知f(x)=ln(2x+1)-ax,且f'(2)=-1,则a=(
(1)中间变量的选择应是基本函数结构;
(2)关键是正确分析函数的复合层次;
(3)一般是从最外层开始,由外及里,一层层地求导;

小结 ： • ⑴复合函数的求导，要注意分析复合函数的结 构，引入中间变量，将复合函数分解成为较简单的 函数，然后再用复合函数的求导法则求导； • ⑵复合函数求导的基本步骤是：
分解——求导——相乘——回代
播下一个行动，收获一种习惯；播下一种习惯，收获一种性格；播下一种性格，收获一种命运。思想会变成语言，语言会变成行动，行动会变成习惯，习惯会变成性格。性格会影响人生！习惯不加以抑 制，会变成生活的必需品，不良的习惯随时改变人生走向。人往往难以改变习惯，因为造习惯的就是自己，结果人又成为习惯的奴隶！人生重要的不是你从哪里来，而是你到哪里去。当你在埋头工作的 时侯，一定要抬头看看你去的方向。方向不对，努力白费！你来自何处并不重要，重要的是你要去往何方，人生最重要的不是所站的位置，而是所去的方向。人只要不失去方向，就永远不会失去自己！ 这个世界唯一不变的真理就是变化，任何优势都是暂时的。当你在占有这个优势时，必须争取主动，再占据下一个优势，这需要前瞻的决断力，需要的是智慧！世上本无移山之术，惟一能移山的方法就 是：山不过来，我就过去。人生最聪明的态度就是：改变可以改变的一切，适应不能改变的一切！亿万财富不是存在银行里，而是产生在人的思想里。你没找到路，不等于没有路，你想知道将来要得到 什么，你必须知道现在应该先放弃什么！命运把人抛入最低谷时，往往是人生转折的最佳期。谁能积累能量，谁就能获得回报；谁若自怨自艾，必会坐失良机人人都有两个门：一个是家门，成长的地方； 一个是心门，成功的地方。能赶走门中的小人，就会唤醒心中的巨人！要想事情改变，首先自己改变，只有自己改变，才可改变世界。人最大的敌人不是别人，而是自己，只有战胜自己，才能战胜困难！ 1、烦恼的时候，想一想到底为什么烦恼，你会发现其实都不是很大的事，计较了，就烦恼。我们要知道，所有发生的一切都是该发生的，都是因缘。顺利的就感恩，不顺利的就忏悔，然后放下。“雁渡 寒潭，雁过而潭不留影；风吹疏竹，风过而竹不留声。”修行者的心境，就是“过而不留”。忍得住孤独；耐得住寂寞；挺得住痛苦；顶得住压力；挡得住诱惑；经得起折腾；受得起打击；丢得起面子；担 得起责任；1提得起精神。闲时多读书，博览凝才气；众前慎言行，低调养清气；交友重情义，慷慨有人气；困中善负重，忍辱蓄志气；处事宜平易，不争添和气；对已讲原则，坚持守底气；淡泊且致 远，修身立正气；居低少卑怯，坦然见骨气；卓而能合群，品高养浩气淡然于心，自在于世间。云淡得悠闲，水淡育万物。世间之事，纷纷扰扰，对错得失，难求完美。若一心想要事事求顺意，反而深 陷于计较的泥潭，不能自拔。若凡事但求无愧于心，得失荣辱不介怀，自然落得清闲自在。人活一世，心态比什么都重要。财富名利毕竟如云烟，心情快乐才是人生的至宝。我们的梦想在哪里？在路上， 在脚踏实地的道路上；我们的期待在哪里？在路上，在勤劳勇敢的心路上；我们的快乐在哪里？在路上，在健康阳光的大道上；我们的朋友在哪里？在心里，在真诚友谊的宽道上！珍惜每一分钟，对自 己负责；善于发现看问题的角度；不满足于现状，别自我设限；勇于承认错误；不断反省自己，向周围的成功者学习；不轻言放弃。做事要有恒心；珍惜你所拥有的，不要感叹你失去或未得到；学会赞 美；不找任何借口。与贤人相近，则可重用；与小人为伍，则要当心；只满足私欲，贪图享乐者，则不可用；处显赫之位，任人唯贤，秉公办事者，是有为之人；身处困境之人，不做苟且之事，则可重 任；贫困潦倒时，不取不义之财者，品行高洁；见钱眼开者，则不可用。人最大的魅力，是有一颗阳光的心态。韶华易逝，容颜易老，浮华终是云烟。拥抱一颗阳光的心态，得失了无忧，来去都随缘。 心无所求，便不受万象牵绊；心无牵绊，坐也从容，行也从容，故生优雅。一个优雅的人，养眼又养心，才是魅力十足的人。容貌乃天成，浮华在身外，心里满是阳光，才是永恒的美。意逐白云飞，心 随流水宁。心无牵挂起，开阔空净明。幸福并不复杂，饿时，饭是幸福，够饱即可；渴时，水是幸福，够饮即可；裸时，衣是幸福，够穿即可；穷时，钱是幸福，够用即可；累时，闲是幸福，够畅即可； 困时，眠是幸福，够时即可。爱时，牵挂是幸福，离时，回忆是幸福。人生，由我不由天，幸福，由心不由境。心是一个人的翅膀，心有多大，世界就有多大。很多时候限制我们的，不是周遭的环境， 也不是他人的言行，而是我们自己。人心如江河，窄处水花四溅，宽时水波不兴。世间太大，一颗心承载不起。生活的最高境界，一是痛而不言，二是笑而不语。无论有多少委屈，一笑而泯之。人生的 幸福在于祥和，生命的祥和在于宁静，宁静的心境在于少欲。无意于得，就无所谓失去，无所谓失去，得失皆安谧。闹市间虽见繁华，却有名利争抢；田园间无争，却有柴米之忧烦；世外桃源祥和升平， 最终不过梦一场。心静，则万象皆静。知足者常在静中邂逅幸福。顺利人生，善于处理关系；普通人生，只会使用关系；不顺人生，只会弄僵关系。为人要心底坦荡，不为虚名所累；做事要头脑清醒， 不为假象所惑。智者，以别人惨痛的教训警示自己；愚者，用自己沉重的代价唤醒别人。对人多一份宽容，多一份爱心；对事多一份认真，多一份责任；对己多一点要求，多一点警醒。傲不可长，志不 可满，乐不可极，警醒自己。静能生慧。让心静下来，你才能看淡一切。静中，你才会反观自己，知道哪些行为还需要修正，哪些地方还需要精进，在静中让生命得到升华洗礼，在自观中走向觉悟。让 心静下来，你才能学会放下。你放下了，你的心也就静了。心不静，是你没有放下。静，通一切境界。人与人的差距，表面上看是财富的差距，实际上是福报的差距；表面上看是人脉的差距，实际上是 人品的差距；表面上看是气质的差距，实际上是涵养的差距；表面上看是容貌的差距，实际上是心地的差距；表面上看是人与人都差不多，内心境界却大不相同，心态决定命运。知恩感恩，是很重要的 一件事。因为当一个人具有感恩的心，心会常常欢喜，总是觉得很满足，一个不感恩不满足的人，总是会觉得欠缺、饥渴。一个常感恩的人，会觉得自己很幸运，有时候其实没什么道理，但他这样一想、 一感恩，就变得很快乐。这种感恩的心，对自己其实是有很大利益。压力最大的时候，效率可能最高；最忙碌的时候，学的东西可能最多；最惬意的时候，往往是失败的开始；寒冷到了极致，太阳就要 光临。成长不是靠时间，而是靠勤奋；时间不是靠虚度，而是靠利用；感情不是靠缘分，而是靠珍惜；金钱不是靠积攒，而是靠投资；事业不是靠满足，而是靠踏实。知恩感恩，是很重要的一件事。因 为当一个人具有感恩的心，心会常常欢喜，总是觉得很满足，一个不感恩不满足的人，总是会觉得欠缺、饥渴。一个常感恩的人，会觉得自己很幸运，有时候其实没什么道理，但他这样一想、一感恩， 就变得很快乐。这种感恩的心，对自己其实是有很大利益。压力最大的时候，效率可能最高；最忙碌的时候，学的东西可能最多；最惬意的时候，往往是失败的开始；寒冷到了极致，太阳就要光临。成 长不是靠时间，而是靠勤奋；时间不是靠虚度，而是靠利用；感情不是靠缘分，而是靠珍惜；金钱不是靠积攒，而是靠投资；事业不是靠满足，而是靠踏实。以平常心观不平常事，则事事平常。在危险 面前，平常心就是勇敢；在利诱面前，平常心就是纯洁；在复杂的环境面前，平常心就是保持清醒智慧。平常心不是消极遁世，而是一种境界，一种积极的人生。不仅要为成功而努力，更要为做一个有 价值的人而努力。命运不是机遇，而是选择；命运不靠等待，全靠争取。成熟就是学会在逆境中保持坚强，在顺境时保持清醒。时间告诉你什么叫衰老，回忆告诉你什么叫幼稚。只有在我们不需要外来 的赞许时，心灵才会真的自由。你没那么多观众，别那么累。温和对人对事。不要随意发脾气，谁都不欠你的。现在很痛苦，等过阵子回头看看，会发现其实那都不算事。和对自己有恶意的人绝交。人 有绝交，才有至交学会宽容伤害自己的人，因为他们很可怜，各人都有自己的难处，大家都不容易。学会放弃，拽的越紧，痛苦的是自己。低调，取舍间，必有得失。不要试图给自己找任何借口，错误 面前没人爱听那些借口。慎言，独立，学会妥协的同时，也要坚持自己最基本的原则。付出并不一定有结果。坚持可能会导致失去更多过去的事情可以不忘记，但一定要放下。活得轻松，任何事都作一 个最好的打算和最坏的打算。做一个简单的人，踏实而务实。不沉溺幻想。不庸人自扰。不说谎话，因为总有被拆穿的一天。别人光鲜的背后或者有着太多不为人知的痛苦尽量充实自己。不要停止学习。 不管学习什么，语言，厨艺，各种技能。注意自己的修养，你就是孩子的第一位老师。孝顺父母。不只是嘴上说说，即使多打几个电话也是很好的。爱父母，因为他们给了你生命，同时也是爱你爱的最 无私的人。