概率论第三讲
- 格式:doc
- 大小:464.50 KB
- 文档页数:8




第三讲§4 乘法公式,全概率公式,贝叶斯公式及其应用 1. 条件概率和事件的独立性在配对问题中,如何解决第二个问题?如果记事件k A 表示k 个人拿到自己的帽子,k B 表示其余n k -个人没有一个拿到自己的帽子,则所求事件即为k k A B ,问题即要计算Pr()k k A B 。
如果从古典概率角度来理解:#()##()Pr()###k k k k k k k kA B A A B A B S S A ==,前一项是事件k A 的概率,而后一项可以认为是把k A 作为样本空间,事件k k A B 的概率,这个概率也称为k A 发生的条件下,事件k B 发生的条件概率,记为Pr(|)k k B A 。
这个想法希望能在一般的概率问题中应用,所以引入条件概率这个概念。
定义 (条件概率)如果Pr()0A >,则称Pr()Pr()AB A 为事件B 关于事件A 的条件概率,记为Pr(|)B A 。
从概率空间出发来理解条件概率。
给定概率空间(,,)S P F ,对给定的事件A ,可定义样本空间和事件域:(,)A A F ,相应的条件概率空间(,,(|))A A P A ⋅F 可按如下方式定义:B A ∈F ,则Pr()Pr(|)Pr()AB B A A =。
容易证明,这是一个概率空间。
1)非负性:0)|(≥A B P ; 2)规范性:1)|(=A S P ;3)可列可加性:∑∞=∞==11)|()|(k k k k A B P A B P ,这里φ=j i B B ,j i ≠。
下面考虑一个简单的问题,来帮助理解条件概率。
例 1 抛掷硬币两次,已知事件A “正面至少出现一次”发生。
求两次得到同一面的事件B 概率。
解 从定义容易计算:3()4P A =,1()4P AB =,则31)|(=A B P 。
从另一角度看,所谓已知事件A ,即样本空间已缩小为)}1,0(),1,1(),0,1{(。

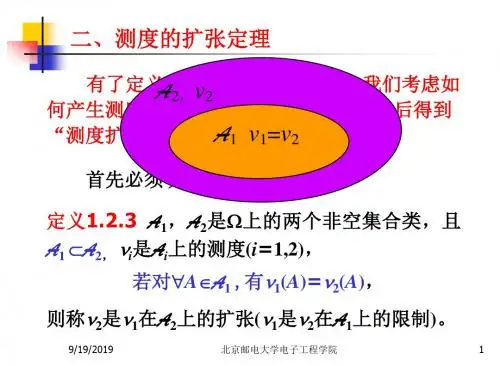
现代概率论03:测度空间(1)⽬录第三讲 测度空间(1)2.1 测度的定义及性质2.1.1 测度的公理化定义本节主要讨论测度的定义及性质,在此之前需要引⼊⼏个概念:⾮负集函数:给定空间 X 上的集合系 E ,将定义在 E 上,取值于 [0,∞] 上的函数称为⾮负集函数,常⽤希腊字母 µ,ν,τ,⋯ 来表⽰。
可列可加性:如果对任意可列个两两不交的集合 {A n ∈E,n ≥1} 满⾜ ∞⋃n =1A n ∈E ,均有µ∞⋃n =1An=∞∑n =1µ(An ),则称⾮负集函数 µ 具有可列可加性。
有限可加性:如果对任意有限个两两不交的集合 {A k ∈E,1≤k ≤n } 满⾜ n⋃k =1Ak∈E ,均有µn⋃k =1Ak=n∑k =1µ(Ak ),则称⾮负集函数 µ 具有有限可加性。
可减性:如果对 ∀A ,B ∈E ,满⾜ A ⊂B ,且有 B −A ∈E ,只要 µ(A )<∞ ,就有µ(B −A )=µ(B )−µ(A ),则称⾮负集函数 µ 具有可减性。
本节的核⼼是测度的公理化定义,具体如下:测度的公理化定义:指的是在抽象空间的集合上建⽴的测度。
设 E 是 X 上的集合系,且 ∅∈E 。
若 E 上的⾮负集函数 µ 满⾜:(1) µ(∅)=0 ;(2) 可列可加性,则称 µ 为 E 上的测度。
若 µ(A )<∞, ∀A ∈E ,则称测度 µ 为有限测度。
()()若 ∀A ∈E ,存在 {A n ∈E,n ≥1} ,使得 ∞⋃n =1An⊃A ,则称测度 µ 为 σ 有限测度。
命题 2.1.1:测度具有有限可加性和可减性。
命题 2.1.2:设 X ⊂R, E =Q R ,F 是 R 上⾮降右连续的实值函数。





第三讲§4 乘法公式,全概率公式,贝叶斯公式及其应用 1. 条件概率和事件的独立性在配对问题中,如何解决第二个问题?如果记事件k A 表示k 个人拿到自己的帽子,k B 表示其余n k -个人没有一个拿到自己的帽子,则所求事件即为k k A B ,问题即要计算Pr()k k A B 。
如果从古典概率角度来理解:#()##()Pr()###k k k k k k k kA B A A B A B S S A ==,前一项是事件k A 的概率,而后一项可以认为是把k A 作为样本空间,事件k k A B 的概率,这个概率也称为k A 发生的条件下,事件k B 发生的条件概率,记为Pr(|)k k B A 。
这个想法希望能在一般的概率问题中应用,所以引入条件概率这个概念。
定义 (条件概率)如果Pr()0A >,则称Pr()Pr()AB A 为事件B 关于事件A 的条件概率,记为Pr(|)B A 。
从概率空间出发来理解条件概率。
给定概率空间(,,)S P F ,对给定的事件A ,可定义样本空间和事件域:(,)A A F ,相应的条件概率空间(,,(|))A A P A ⋅F 可按如下方式定义:B A ∈F ,则Pr()Pr(|)Pr()AB B A A =。
容易证明,这是一个概率空间。
1)非负性:0)|(≥A B P ; 2)规范性:1)|(=A S P ;3)可列可加性:∑∞=∞==11)|()|(k k k k A B P A B P ,这里φ=j i B B ,j i ≠。
下面考虑一个简单的问题,来帮助理解条件概率。
例 1 抛掷硬币两次,已知事件A “正面至少出现一次”发生。
求两次得到同一面的事件B 概率。
解 从定义容易计算:3()4P A =,1()4P AB =,则31)|(=A B P 。
从另一角度看,所谓已知事件A ,即样本空间已缩小为)}1,0(),1,1(),0,1{(。
仍是古典概型问题,该空间中,事件|{(1,1)}B A =,因此,31)|(=A B P 。
在原概率空间中,事件B 的概率为21)(=B P 。
定义 (事件独立性)如果()()()P AB P A P B =,就称事件A 与B 独立。
定理 (独立的等价条件)下面三个条件是等价的。
(1)()()()P AB P A P B =; (2)(|)()P B A P B =; (3)(|)()P A B P A =。
定理 如果事件A 与B 独立,则A 所确定的事件与B 所确定的事件之间都独立。
2. 概率计算问题中的三个重要的公式 定理 (乘法公式))()|()|()|()(112211111A P A A P A A A P A A A P A A P n n n n n ---=。
定理 (全概率公式)设试验的样本空间为k nk B S 0== ,这里φ=j i B B ,j i ≠,且0)(>k B P ,那么∑==nk k k B P B A P A P 1)()|()(。
定理3(贝叶斯公式)在定理2条件下,再设0)(>A P ,那么∑==nk k ki i i B P BA PB P B A P A B P 1)()|()()|()|(。
这个公式的概率含义:我们可以认为对事件k B 的信息掌握得比较充分,即知道其发生的概率,和其它事件在该事件发生时的条件概率。
这些信息是先验的,即可由经验获得。
那么又经过新的试验,在该试验之下,过去的经验会有什么修正,即在试验事件发生条件下,原来的经验概率会有什么变化?这就是后验概率)|(A B P i 。
例 狼来了寓言的概率分析。
(p.47) 3. 应用本节将利用前面的结果来计算一些概率问题。
例 设袋中装有r 只红球,t 只白球,每次自袋中任取一只球,观察其颜色后放回,同时放入a 只同样颜色的球。
若在袋中连续取球四次,求第一,二次取到红球,且第三第四次取到白球的概率。
例 如果已知太阳连续升起了n 天,问(1)n +-th 天太阳仍升起的概率是多大? 解 记k A 为第k 天太阳升起。
要计算的是11(|)n n P A A A +。
因此,11111()(|)()n n n n n P A A A P A A A P A A ++=。
但这些概率的含义并不明确,因为在什么样的样本空间中考虑问题并不清楚。
对1n +天太阳升起的情况,可以作互不相容的分解:1n n S S S S +=,其中,k S 表示太阳升起的天数,0,1,,1k n =+。
现在面临选择:对()k P S 的概率作什么样的假设?数学上是无法解决该问题的,如果借助主观概率思想,对没有特别信息区分事件的发生可能性,就做出等可能假,即设这里的每一种可能性是相同的:011()()2n P S P S n +===+。
这时,讨论的问题就明确了。
利用全概率公式:1111101()(|)()(|)2n n n n k k n k k k P A A P A A S P S P A A S n ++====+∑∑如何计算1(|)n k P A A S ?在给定k S 时,所有的样本点可以视为k 个太阳升起的日子在1n +天中的分布情况,共1kn C +中情况。
如果k n <,显然有1(|)0n k P A A S =;而k n =时,有111(|)n n nn P A A S C +=; 而1k n =+,有11(|)1n n P A A S +=。
因此,11111()(1)21n n n P A A n C n +=+=++。
类似,k n ≤时,显然有11(|)0n k P A A S +=;而1k n =+,有111(|)1n n P A A S ++=。
即111101()(|)()2n n n k k k P A A P A A S P S n ++===+∑。
所以,111(|)2n n n P A A A n ++=+。
思考题 (无限Polya 罐模型)考虑更一般的模型。
一个罐中有黑白两种颜色的无限多个球,无放回抽取n 个球,观测到抽到n r -个白球,r 个黑球。
下一次抽到白球的概率是多少?答案是12n r n -++。
提示 思考方法类似。
如果记r B 为事件:前面n 次中,观测到抽到n r -个白球,r 个黑球。
而1n n B A +表示事件;观测到抽到n r -个白球,r 个黑球,而1n +次仍是白球。
当k n r <-或1k n r >-+时,(|)0n r k P B S -=;当k n r =-时,1(|)n r nr n r n r n C P B S C ---+=;当1k n r =-+时,111(|)n r nr n r n r n C P B S C --+-++=;所以,11111!()!(1)!(1)!!1()()22()!!(1)!1n r n rn n r n r n r n n C C n n r r n r r P B n C C n n r r n n ----+++-++-+=+==++-++。
类似,11111!(1)!!1()22()!!(1)!(2)(1)n rn r n n r n C n n r r n r P B A n C n n r r n n n -+-++-+-+===++-+++。
所以,11(|)2n r n r P A B n +-+=+。
例(是否改变选择问题)解首先也要明确我们考虑的问题。
要讨论的是改选后得奖(记为C)概率是多大?面临的样本空间:奖品被选中B,改选后得奖;奖品未被选中B,改选后得奖。
因此12 ()(|)()(|)()0133P C P C B P B P C B P B=+=⨯+⨯。
例三家厂同时生产某种产品,产品的不合格率和市场占有率分别为0.02,0.15;0.01,0.80;0.03,0.05市场上抽取一件此类产品,(1)求产品不合格的概率;(2)该产品是第二家厂生产的概率。
(如何划分样本空间)例对以往数据分析结果表明,设备调整良好时,产品合格率为98%,而当机器调整不好时,合格率为55%。
每天早上机器调试好的概率为95%。
求已知某天产品合格时,机器是调试好的概率。
(注意什么是先验的概率)例某种疾病在人群中的发病率为0.005。
此类病的确症率为0.95:即该人患此病时,通过检查能查出该病的概率;而误症率也为0.05:即该人不患此病时,检查却认为患该病的概率。
求检查认为该人患病时,此人确实患病的概率。
下面是独立性问题。
例串联,并联和串并联混合系统的可靠性(独立性直观理解或假设)。
例甲乙两人比赛乒乓球。
甲胜的概率为1/2p≥,问对甲而言,采用三局两胜有利还是五局三胜有利。
例轮流射击问题的获胜概率计算。
(p.52)习题课1. 分球入罐问题把n 个球放入r 个不同箱子。
记录每个箱子的球数,问得到的所有不同结果有多少种? 等价问题:1r n n n ++=的非负整数解有多少个?从装有标号为1~r 的球的罐中,有放回抽取n 个求,记录每个编号被抽到的次数,问有多少中可能结果?解 思考方法。
以三个球,有放回抽取5次为例。
上述图例表示:1号球抽到4次,2号求一次,3号球零次。
可见所有结果是5个√与2条|的位置的组合方式,共有:5531C +-或31531C -+-种方法。
注意:也是可能的结果之一。
一般结论:1n n r C +-或11r n r C -+-。
下面的2~3是类似的问题2. 做伯努利试验,直到成功r 次,才停止试验。
问需要n r +次的所有可能试验结果有多少?如果成功的概率是p ,该事件的概率是多少?3. 把n 个(无区别的)球放入r 个罐中,要求第i 个罐中,至少有i m 个球,问所有的放入方法有多少中?(假设1ri i n m =≥∑)习题4既用了加法,也用了乘法原理的思考方法。
4. 证明组合公式220()nnk nn k C C ==∑。
解 把等式改写为20nnk n knn n k C C C -==∑,结论对应着:把2n 个球等分成2组,则取出n 个球的过程可分解成从第一组取出k 个球,0k n ≤≤,即n 种方法,而每种方法又可分位两个步骤:第一组中取出k 个球,然后,第2组中取出n k -个球。
利用全概率公式推导递推关系从而解决问题的例子5~6。
5. 配对问题参加某聚会的n 个人都向房子中央扔出自己的帽子。
充分混合后,个人随机地抽取帽子。
问1) 没有一个人选到自己帽子的概率是多少? 2) 恰好有k 个人选到自己的帽子的概率是多少?解 1)方法1. 记事件“第i 个人选择自己的帽子”为i E ,则1111()(1)()nnj j i n j i j P E C P E E -===-∑。