第2章习题解

第二章原子结构和元素周期律习题解答1．指出下列各原子轨道相应的主量子数n及角量子数l的数值是多少？轨道数分别是多少？2p 3d 4s 4f 5s【解答】 2p 主量子数2，角量子数1，轨道数33d 主量子数3，角量子数2，轨道数54s 主量子数4，角量子数0，轨道数14f 主量子数4，角量子数3，轨道数75s 主量子数5，角量子数0，轨道数1 2．当主量子数n=4时，可能有多少条原子轨道？分别用Ψn,l,m 表示出来。

电子可能处于多少种运动状态？（考虑自旋在内）【解答】当n=4时，可能有n2=16条原子轨道。

n l M4 01230，±10，±1，±20，±1，±2，±3Ψ4,0,0，Ψ4,1,0，Ψ4,1,1，Ψ4,1,-1，Ψ4,2,0，Ψ4,2,1，Ψ4,2,-1，Ψ4,2,2，Ψ4,2,-2，Ψ4,3,0，Ψ4,3,1，Ψ4,3,-1，Ψ4,3,2，Ψ4,3,-2，Ψ4,3,3，Ψ4,3,-3 每条轨道上可以容纳两个自旋相反的电子，16条原子轨道，电子可能处于32种运动状态。

3．将下列轨道上的电子填上允许的量子数。

（1）n＝，l＝2，m=0，ms=±1/2（2）n=2，l= ，m=0，ms=±1/2（3）n=4，l=2，m= ，ms=－1/2（4）n=3，l=2，m=2，m=s=－1/2（5）n=2，l= ，m=－1，ms=＋1/2（6）n=5，l=0，m= ，ms【解答】（1） 3，4，5，……，正整数；（2） 0，1（3） 0，±1，±2（4） +1/2，-1/2（5） 1（6） 04．填上n、l、m、m s等相应的量子数：量子数确定多电子原子轨道能量E的大小；Ψ的函数式则是由量子数所确定；确定核外电子运动状态的量子数是；原子轨道或电子云的角度分布图的不同情况取决于量子数。

【解答】主量子数n和角量子数l；主量子数n、角量子数l和磁量子数m；主量子数n、角量子数l、磁量子数m和自旋量子数m；s 角量子数l和磁量子数m。

1. 2mol 298K ，5dm 3的He(g)，经过下列可逆变化：（1） 等温压缩到体积为原来的一半； （2） 再等容冷却到初始的压力。

求此过程的Q W U H S ∆∆∆、、、和。

已知=),(,g He C m p 20.8J •K -1•mol -1。

解：体系变化过程可表示为W=W 1+W 2=nRTln 12V V+0=2×8.314×298×ln0.5=-3435(J)Q=Q 1+Q 2=W 1+ΔU 2=-3435+n m v C ,ΔT=-3435+n m v C ,(298-298/2)=-3435+(-3716)=-7151(J)ΔU=ΔU 1+ΔU 2=ΔU 2=-3716(J)ΔS=ΔS 1+ΔS 2=nRln 12V V +⎰21,T T m v TdTnC =2×8.314×ln0.5+2×1.5×8.314ln0.5=-2818(1-∙K J )2. 10mol 理想气体从40℃冷却到20℃，同时体积从250dm 3 变化到50dm 3。

已知该气体的m p C ,=29.20J •K-1•mol-1，求S ∆。

解：假设体系发生如下两个可逆变化过程250dm 3 等温 50dm 3 等容 50dm 340℃ ΔS 1 40℃ ΔS 2 20℃ΔS=ΔS 1+ΔS 2=nRln 12V V +⎰21,T T m v TdTnC=10Rln25050+10×(29.20-8.314)×ln 4015.2732015.273++ =-147.6(1-∙K J )3. 2mol 某理想气体(m p C ,=29.36 J •K -1•mol -1)在绝热条件下由273.2K,1.0MPa 膨胀到203.6K ，0.1MPa 求该过程的Q W U H S ∆∆∆、、、和。

解：273.2K 绝热 203.6K1.0MPa 膨胀 0.1MPa等温压缩 等容冷却∵m p C ,=29.3611--∙∙mol K J∴ m v C ,=29.36-8.314=21.0461-∙K J且Q=0ΔU=⎰21,T T m v dT nC =2×21.046×(203.6-273.2)=-2930(J)W=-ΔU=2930(J)4. 有一带隔板的绝热恒容箱，在隔板两侧分别充以不同温度的H 2和O 2，且V 1=V 2(见图)，若将隔板抽去，试求算两种气体混合过程的S ∆（假设此两种气体均为理想气体）。

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ，位移)(t x 和电压)(t u r为输入量；位移)(t y 和电压)(t u c为输出量；k （弹性系数），μ（阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。

解：2-1(a) 取质量m 为受力对象，如图，取向下为力和位移的正方向。

作用在质量块m 上的力有外力f(t)，重力mg ，这两个力向下，为正。

有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ，这两个力向上，为负。

其中，0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。

根据牛顿第二定理F ma ∑=，有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中：0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式：22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成：22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。

2-1(b) 如图，取A 点为辅助质点，设该点位移为()Ax t ，方向如图。

再取B 点也为辅助质点，则该点位移即为输出量()y t ，方向如图A 点力平衡方程：1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程：2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得：21()()()Akx t x t y t k=-二边微分：21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②：221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式：1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成：()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。

2.有10 mol的气体（设为理想气体），压力为1000 kPa，温度为300K，分别求出等温时下列过程的功：
（1）在空气压力为100 kPa时，体积胀大1dm3；
（2）在空气压力为100 kPa时，膨胀到气体压力也是100 kPa；
（3）等温可逆膨胀到气体压力为100 kPa。
解（1）属于等外压膨胀过程
W1=-p环ΔV=-100kPa×1dm3=-100J
（2）也是等外压膨胀过程
W2=-p环（V2-V1）=-nRT(1-p2/p1)
=-10mol×8.314J·K-1·mol-1×300K(1-100/1000)
=-22448J
（3）等温可逆膨胀过程
W3=-nRTln(p1/p2)
=-10mol×8.314J·K-1·mol-1×300K×ln(1000/100)
=-57431J
4.在291K和pӨ压力下，1mol Zn(s)溶于足量稀盐酸中，置换出1mol H2并放热152kJ。若以Zn和盐酸为体系，求该反应所作的功及体系内能的变化。
解Zn(s)＋2HCl(aq) = ZnCl2(aq)＋H2(g)
W = -pΔV = -p(V2－V1)≈-pV(H2) = -nRT
= -(1mol)×(8.314J·K-1·mol-1)×(291K)
= -2.42kJ
ΔU= Q+W = (-152-2.42)kJ =-154.4kJ
5.在298K时，有2mol N2(g)，始态体积为15dm3，保持温度不变，经下列三个过程膨胀到终态体积为50 dm3，计算各过程的ΔU、ΔH、W和Q的值。设气体为理想气体。
=-5966J，
Q3=-W3=5966J。
7.理想气体等温可逆膨胀，体积从V1胀大到10V1，对外作了41.85kJ的功，体系的起始压力为202.65kPa。

习题 2.11．将下列命题符号化。

(1) 4不是奇数。

解：设A(x)：x是奇数。

a：4。

“4不是奇数。

”符号化为：¬A(a)(2) 2是偶数且是质数。

解：设A(x)：x是偶数。

B(x)：x是质数。

a：2。

“2是偶数且是质数。

”符号化为：A(a)∧B(a)(3) 老王是山东人或河北人。

解：设A(x)：x是山东人。

B(x)：x是河北人。

a：老王。

“老王是山东人或河北人。

”符号化为：A(a)∨B(a)(4) 2与3都是偶数。

解：设A(x)：x是偶数。

a：2，b：3。

“2与3都是偶数。

”符号化为：A(a)∧A(b)(5) 5大于3。

解：设G(x,y)：x大于y。

a：5。

b：3。

“5大于3。

”符号化为：G(a,b)(6) 若m是奇数，则2m不是奇数。

解：设A(x)：x是奇数。

a：m。

b：2m。

“若m是奇数，则2m不是奇数。

”符号化为：A(a)→A(b)(7) 直线A平行于直线B当且仅当直线A不相交于直线B。

解：设C(x,y)：直线x平行于直线y。

设D(x,y)：直线x相交于直线y。

a：直线A。

b：直线B。

“直线A平行于直线B当且仅当直线A不相交于直线B。

”符号化为：C(a,b)↔¬D(x,y)(8) 小王既聪明又用功，但身体不好。

解：设A(x)：x聪明。

B(x)：x用功。

C(x)：x身体好。

a：小王。

“小王既聪明又用功，但身体不好。

”符号化为：A(a)∧B(a)∧¬C(a)(9) 秦岭隔开了渭水和汉水。

解：设A(x,y,z)：x隔开了y和z。

a：秦岭。

b：渭水。

c：汉水。

“秦岭隔开了渭水和汉水。

”符号化为：A(a,b,c)(10) 除非小李是东北人，否则她一定怕冷。

解：设A(x)：x是东北人。

B(x)：x怕冷。

a：小李。

“除非小李是东北人，否则她一定怕冷。

”符号化为：B(a)→¬A(a)2．将下列命题符号化。

并讨论它们的真值。

(1) 有些实数是有理数。

解：设R(x)：x是实数。

第2章2-1 半径为a的无限薄带电圆盘上面电荷密度为ρ=r2，r为圆盘上任意点到圆心的距离，求圆盘上的总电量。

解：Q=∬ρ∙rdφdrS =∫r3∙dra∙∫dφ2π=πr42。

2-2 半径为a的球体内有均匀分布的电荷，其总电量为Q，若该球以角速度ω绕其自身的任意中轴旋转，求球体内的体电流密度。

解：J V⃗⃗⃗ =3qωrsinθ4πa3φ⃗⃗ 。

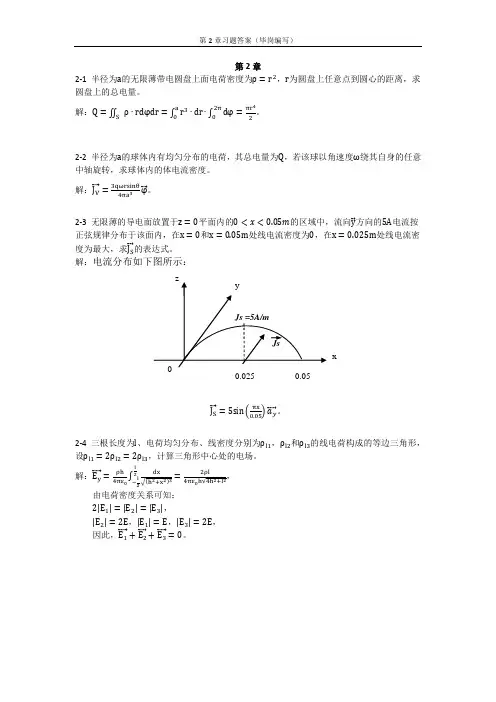
2-3 无限薄的导电面放置于z=0平面内的0<x<0.05m的区域中，流向y⃗方向的5A电流按正弦规律分布于该面内，在x=0和x=0.05m处线电流密度为0，在x=0.025m处线电流密度为最大，求J S⃗⃗ 的表达式。

解：电流分布如下图所示：x0.025 0.05J S⃗⃗ =5sin(πx0.05)a y⃗⃗⃗⃗ 。

2-4 三根长度为l、电荷均匀分布、线密度分别为ρl1，ρl2和ρl3的线电荷构成的等边三角形，设ρl1=2ρl2=2ρl3，计算三角形中心处的电场。

解：E y⃗⃗⃗⃗ =ρh4πε0∫√(h2+x2)3l2−l2=4πεh√4h2+l2，由电荷密度关系可知：2|E1|=|E2|=|E3|，|E2|=2E，|E1|=E，|E3|=2E，因此，E1⃗⃗⃗⃗ +E2⃗⃗⃗⃗ +E3⃗⃗⃗⃗ =0。

2-5 两无限长的同轴圆柱壳面，半径为a 和b ，内外导体上均匀分布电荷，密度分别为ρS1，ρS2，求r <a ，a <r <b ，r >b 时各点的电场及两导体间的电压。

解：用高斯定理求E 。

做高斯面（闭合面）， ∵轴对称∴高斯面为圆柱闭合面，为左图所示 ①E1（r ＜a ,内导体内） 设导体为理想导体，则E 1=0；②E2（a ＜r ＜b ，内导体与外导体之间圆柱空间）∵同轴无限长,∴圆柱侧面（高斯面）上E 2处处相等，且E只有ρ方向分量d 矢量为高斯封闭面的外法线n ds n s,=E 2·d s : 上下底面：E 2·d s =0（∵E 2⊥d s，cos90°=0） 侧面：E 2·d s =E 2·ds （∵E 2∥d s，cos 0°=1）10222222επρεπρalQlE dS E dS E S d E s S=====⋅∴⎰⎰⎰⎰⎰⎰侧侧∴ρρερˆ012aE s = ③3E( r ＞b ，外导体壳外)E 32πl ρ=212επρπρblal s s +∴3E =ρρερρˆ021ba s s + （2）两导体内电压ab Va ba d a d E d E l d E V sb a s b aba b a ab ln 10101ερρρερρρρρ===⋅=⋅=⎰⎰⎰⎰ 当r <a 时，E⃗ =0；当a <r <b 时，E ⃗ =ρS1a+ρS2brε0r ，U =∫E ⃗ ∙dr b a =(ρS1a +ρS2b )ε0ln ab 。

其中Δx为绝对误差；x为现有仪表的读数；A为 高精度仪表的读数
∆ x = x − A = ( 77 . 8 − 80 ) mA
= − 2 . 2 mA
C
= − ∆ x = 2 . 2 mA
∆x − 2.2 γ A = ×100% = ×100% = −2.75% A 80
∆x − 2.2 ×100% = −2.83% γ x = ×100% = x 77.8
实际相对误差为-2.75%;示值相对误差为-2.83%
∆x m 2 .2 γm = × 100% = × 100% = 2.2% 100 xm
在0.1、0.2、0.5、1.0、1.5、2.5、5.0七个等 级中只能是2.5级。 答：(1) –2.2mA，2.2mA，-2.83% (2) 2.5级 ■
U
Im
= 5 . 00 V
−3
I m = 1 × 10
A
5 . 00 U Im 3 = Ω = 5 × 10 Ω RI = −3 1 × 10 Im
测得值
Ux R′ = = RI + Rx x Ix
∆Rx = R′ − Rx = RI x
绝对误差 相对误差
∆Rx RI γ′ = = × 100 % R Rx Rx
± s2%
≤ 0 . 42 %
在0.1、0.2、0.5、1.0、1.5、2.5、5.0七个等 级中可以选0.2级，即
± s2%
= ± 0 .2 %
(3) 使用用量程为590V的电压表时
γ xm 3
xm 3 ∆x m 3 = × 100% = ± s3 % × x x
x
m 3
= 500
V
x = 250 |γ

=
(0.3 × 48.66 +
0.7 ×12) KJ·mol-1
=
23.0KJ·mol-1
B
∑ ∑ ∑ S
2-2 已知当 NaCl 溶液在 1kg 水中含物质的量为 n（单位为 mol）的 NaCl 时，体积 V 随 n 的变化关系为：
V/m3 = 1.00138×10-3 + 1.66253×10-5n/mol +1.7738×10-3(n/mol)3/2 + 1.194×10-7(n/mol)2
求当 n 为 2mol 时 H2O 和 NaCl 的偏摩尔体积为多少？ 解：设水用“A”表示，NaCl 用“B”表示,由题意得：
1
⎜⎜⎝⎛
∂V ∂n B
⎟⎟⎠⎞ = 1.66253 ×10−5
+ 1.7738 ×10−3
×
3 2
1
× (n / mol) 2
+ 1.194 × 10−7
× 2(n / mol)
那么当 n=2 时，NaCl 的偏摩尔体积
VB
= 1.66253 × 10−5
+ 1.7738 × 10−3
×
3
×
2
1 2
mol·dm3 = 0.547mol·dm-3
bB
=
nB mA
=
wB M (1 − wB )
=
0.095 0.18 × (1 − 0.095)
mol·kg-1 = 0.583mol·kg-1
2-4 若将 25℃、101.325KPa 纯理想气体的状态定为气体的标准状态，则氧气的标准
熵 S1O =205.03J·K-1·mol-1，现改为 25℃、100Kpa 的纯理想气体作为气体的标准态，氧气

第二章 习题一1.设函数210)(x x f =，试按定义求)1(/-f 。

解： 由于xx f x x f x f x ∆-∆+=→∆)()(lim)(0000/，故xx x f x f f x x ∆--∆+-=∆--∆+-=-→∆→∆2200/)1(10)1(10lim )1()1(lim )1(x x x x x x x ∆--∆+∆-+-=∆--∆+-=→∆→∆2220220)1()()1(2)1(lim 10)1()1(lim 10[]x xx x x x ∆+-=∆∆+∆-=→∆→∆2lim 10)(2lim 10020[]200210-=+-=。

2.设)(0/x f 存在，试利用导数的定义求下列极限： （1）x x f x x f x ∆-∆-→∆)()(lim000； （2）hh x f h x f h )()(lim 000--+→；解：（1）()()[]()x x f x x f xx f x x f x x ∆--∆-+-=∆-∆-→∆-→∆)(lim)()(lim000000， 将上式中的()x ∆-看成导数定义)()()(lim0/000x f xx f x x f x =∆-∆+→∆中的x ∆，便得()[])()(lim0/000x f xx f x x f x =∆--∆-+→∆-，故)()()(lim0/000x f xx f x x f x -=∆-∆-→∆；（2）[][]hx f h x f x f h x f h h x f h x f h h )()()()(lim )()(lim00000000----+=--+→→ [][]⎭⎬⎫⎩⎨⎧----+=→h x f h x f h x f h x f h )()()()(lim 00000 [][]hx f h x f hx f h x f h h )()(lim )()(lim000000----+=→→上式中的第一项即为导数的定义，结果为)(0/x f ； 第二项参见前一小题，结果为)(0/x f -， 故[])(2)()()()(lim0/0/0/000x f x f x f hh x f h x f h =--=--+→。

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ； （2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ； （4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ； （5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。

（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。

解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。

4
p0 LS ( p gh
得：
4 cos )( L h) d

d ( gh 2 ghl p0 h) 4 cos ( L h)
2—23 一根直径为 1mm 的玻璃管，竖直插入盛水银的容器里，管的下端在水银面以下 1cm 处，给出 20 -3 ℃时水银的α=465×10 N/m， 问： （1） 要在管的下端吹出一半球形气泡， 管中空气的计示压强是多少？ （2） 如果管内空气压强比一大气压低 3000Pa，水银在管内会升到多高？已知水银和玻璃的接触角为 140°。 （1）解：
2-15
有两根竖直毛细管，一根直径 d1=0.50 mm，另一根直径 d2=1.0 mm，将它们插入水银中，若接
触角 =138°，求两水银柱的高度差。
h
2 cos 1 1 ( ) 10.4mm g r1 r2
2
2-16 将内直径 d=5×10-4 m 的管子浅浅地插入酒精中，流入管中的酒精质量是多少?酒精的表面张力 系数 =22.9×10-3 N·m-1，与管接触角为 0。
h2
2 1 h1 31.4mm 1 2
长 L=110 mm，内径 d=20 μm 的玻璃毛细管竖直浸入水中，毛细管的上端密封，外界空气压强
为 p0＝1.013×105 Pa，问毛细管浸入水中的长度 X 应该是多长时，才能使毛细管内的水面与外部的水面相 平? 解：根据理想气体的状态方程

F 28.3 10 3 9.01 10 2 N / m 2 l 2 5 10
2-4 把一个框架竖直地放着，其上有一条可以移动的横杆以 ab，框架之间有肥皂液膜，如图所示。 今欲使横杆保持平衡，问横杆下面应挂多大重物?已知横杆质量为 0.05 g，长度 L 为 2.5 cm，肥皂膜的表面 张力系数为 45×10-3 N·m-1。 解：

R12 (Rab // 8 Rbc //12) //(Rac //10) 4
(b) R12 (10 // 14) //(6 // 12 8) 3.92 5. 对图 x2.5 所示电桥电路， 应用 Y 等效变换求： （1） 对角线电压 U ； （2） 电压 U ab 。
。
A 为 0。因为已经被短路掉，没有电流。
2. 电路如图 x2.2 所示，求电压 U 12 以及电流表 A1 和 A2 的读数。
解：如图 x2.2a 所示： R12 20 // 20 10 ， R13 4 // 6 2.4
i2
30 0.97 A ， i1 i2 0.5 0.48 A 31
解： R12 4 得到 R1
R13 6
R23 10
R2 R12 R23 2 R12 R23 R13
R13 R12 6 R12 R23 R13 5 R23 R13 3 R12 R23 R13
R3
3 2 U 5 3 5 2 5V 5 5
A. U S 40V 的理想电压源 B. I S 4A 的理想电流源 C. U S 0.4V 的理想电压源与 R 10 的电阻相并联的电路 D. U S 40V 的理想电压源与 R 10 的电阻相并联的电路 3.有 3 个电阻相并联，已知 R1 2，R2 3，R3 6 。在 3 个并联电阻的两端 外加电流 I S 18A 的电流源，则对应各电阻中的电流值分别为（ A. I R1 3A, I R 2 6A，I R 3 9A C. I R1 6A，I R 2 9A，I R 3 3A B ） 。
U ab (
24 6 24) 5 150V 5 5

2.7 总量为q 的电荷均匀分布于半径为a 的球体中，分别求球内、外的电场强度 解：由题意得，球体内的电荷体密度为3=4V 3q qa ρπ=由高斯定理：（1）当r>a 时，01svE d s dv ρε=⎰⎰外即：sin 222014=aE r r drd d πππρθθϕε⎰⎰⎰外r 2=4qE e r πε外 （2）当r<a 时，201svE d s dv ρε=⎰⎰即：224=E r πsin 2201r r drd d ππρθθϕε⎰⎰⎰2r 30=4qrE e a πε2.14 电场中有一半径为a 的介质球，已知1cos cos 300020-=-E +2r a E rεεθθεεΦ+（r a ≥）cos 02003=-E +2r εθεεΦ （r a ≤）验证球表面的边界条件，并计算球表面的极化电荷密度 解：（1）对于法向边界条件，cos 011003==-E +2n r εθεε∂Φ∂Φ∂∂cos 22003==-E +2n r εθεε∂Φ∂Φ∂∂ 由于 102==εεεε， 故：1212-+=n nεε∂Φ∂Φ∂∂cos cos )00000033--E +-E +2+2εεεθεθεεεε（）（=0 满足法向边界条件 对于切向边界条件： 在r=a 处，3cos cos 010020E E +2r a rεεθθεε-Φ=-+=cos 0003-E +2a εθεε2Φ=cos 003-E +2r εθεε= cos 0003-E +2a εθεε即：21Φ=Φ，满足切向边界条件（2）球表面的自由电荷密度 s ρ=0故极化电荷面密度： 2112()0ps n n n n D D E E ρε=-+- =(cos cos )00000033E -E +2+2εεεθθεεεε=()cos 00003E +2εεεθεε-2.19 有一半径为a ，带电量为q 的导体球，其球心位于两种介质的分界面上，两种介质的介电常数分别是1ε和2ε，分界面可视为无限大平面。

= 1 ⎛ ∂u ∂v ⎞ i ⎛ ∂v ∂u ⎞ ⎜ − ⎟ ⎜ + ⎟ ⎟ ⎟+ ⎜ 2⎜ ⎝ ∂x ∂y ⎠ 2 ⎝ ∂x ∂y ⎠
∂F =0 ∂z
可见 C-R 方程可表示为
则
f ( z) = u( x,− y) − i v( x,− y) .
若 f ( z) 解析，则 u, v 满足 C-R 条件：
∂u ∂v = ∂x ∂y
∂u ∂v =− ∂y ∂x
因此对于 Imz < 0 内的任一点 z = x + i y ,有
∂ ∂v( x,− y) ∂v( x,− y) ∂y ∂[−v( x,− y)] u( x,− y) = = = ∂x ∂( − y) ∂y ∂ (− y) ∂y
(
)
e2i z − 1 = − i (e2i z + 1)
e2i z =
1− i 1+ i
z=
1 1 ⎛ 1− i ⎞ 1 Ln⎜ (− i ) + 2kπ )] ⎟ = Ln(− i ) = [ln | − i | + i(arg 2 i ⎝ 1+ i ⎠ 2 i 2i
i ⎛ π 1⎞ ⎞ ⎛ ⎜ − + 2kπ ⎟ = ⎜ k − ⎟π , k = 0,±1,±2, L 2i ⎝ 2 4⎠ ⎠ ⎝
∂u ∂v ∂v ∂v =0 = = =0 解 得 ∂x ∂y 。 同 理 ， 可 解 得 ∂x vy 故 u, v 均 为 常 数 ， 分 别 记 为
u = C1 , v = C 2 ，则 f (z) = u + iv = C1 + iC2 = C 为一复常数。
4．如果 证
f (z) = u + i v 是一解析函数，试证： i f (z) 也是解析函数。

f(t) 1
f(3 t) 1
t
−2 −1 0
12
−1
⇒
t
− 2 −1 0
12
3
3
33
f(-3 t) 1
⇒
t
−2 3
−1 3
0 12 33
f(-3(t-2)) 1
⇒
0
45 33
t 78 33
图2-6 题 2-9（3）解答图
方法二：先翻转、再展缩、后平移。先翻转，再压缩 3 倍，后右移 2 个单位。
f (t) ⎯翻⎯⎯转→ f (−t) ⎯压⎯缩⎯3⎯倍→ f (−3t) ⎯右⎯移⎯2个单⎯⎯位→ f (−（3 t − 2）) = f (−3t + 6)
a
a
2
(2) 根据冲激信号的筛选特性 f (t)δ (t − t0 ) = f (t0 )δ (t − t0 ) ，可得 tδ (t) = 0δ (t) = 0
(3) 根据冲激信号的筛选特性可得 f (t) = sin t ⋅ δ (t − π ) = sin π ⋅δ (t − π ) = δ (t − π ) 。
(4) f (t) = δ (t − 1) − 2δ (t − 2) + δ (t − 3) (5) f (t) = r(t + 1) − r(t −1) − u(t −1) (6) f (t) = r(t + 2) − r(t + 1) − r(t −1) + r(t − 2)
【解】 题中各信号的波形如图 2-1所示。 f(t)
(1) f (3t)
(2) f (3t + 6)
(3) f (−3t + 6)
(4) f ( t ) 3

习 题 二1. 设)(1x F 与)(2x F 分别是随机变量X 与Y 的分布函数,为使)()(21x bF x aF -是某个随机变量的分布函数, 则b a ,的值可取为( A ).A . 52,53-==b a B . 32,32==b a C . 23,21=-=b a D . 23,21-==b a2. 一批产品20个, 其中有5个次品, 从这批产品中随意抽取4个, 求这4个产品中的次品数X 的分布律.解：因为随机变量X ＝{这4个产品中的次品数}X 的所有可能的取值为：0，1，2，3，4.且4015542091{0}0.2817323C C P X C ===≈； 31155420455{1}0.4696969C C P X C ===≈；2215542070{2}0.2167323C C P X C ===≈；1315542010{3}0.0310323C C P X C ===≈；041554201{4}0.0010969C C P X C ===≈.因此所求X 的分布律为：3． 如果服从0-1分布, 又知取1的概率为它取0的概率的两倍, 写出的分布律和分布函数.解：设{1}P x p ==，则{0}1P x p ==-. 由已知，2(1)p p =-，所以23p =X当0x <时，(){}0F x P X x =≤=；当01x ≤<时，1(){}{0}3F x P X x P X =≤===； 当1x ≥时，(){}{0}{1}1F x P X x P X P X =≤==+==.X 的分布函数为：⎪⎩⎪⎨⎧>=<≤<=11103/100)(x x x x F . 4. 一批零件中有7个合格品，3个不合格品，安装配件时，从这批零件中任取一个，若取出不合格品不再放回，而再取一个零件，直到取得合格品为止，求在取出合格品以前，已取出不合格品数的概率分布.解：设X ={在取出合格品以前，已取出不合格品数}. 则X 的所有可能的取值为0，1，2，3.7{0}10P x ==； 377{1}10930P x ==⋅=；3277{2}1098120P x ==⋅⋅=；32171{3}10987120P x ==⋅⋅⋅=.所以X5. 从一副扑克牌（52张）中发出5张，求其中黑桃张数的概率分布. 解：设X ＝{其中黑桃张数}.则X 的所有可能的取值为0，1，2，3，4，5.0513395522109{0}0.22159520C C P x C ===≈； 14133955227417{1}0.411466640C C P x C ===≈；23133955227417{2}0.274399960C C P x C ===≈； 32133955216302{3}0.0815199920C C P x C ===≈； 411339552429{4}0.010739984C C P x C ===≈； 50133955233{5}0.000566640C C P x C ===≈. 所以X 的概率分布为：6. 一家大型工厂聘用了100名新员工进行上岗培训，据以前的培训情况，估计大约有4%的培训者不能完成培训任务. 求： （1）恰有6个人不能完成培训的概率； （2）不多于4个的概率. 解：设X ＝{不能完成培训的人数}.则(100,0.04)X B ，（1）6694100{6}0.040.960.1052P X C ==⋅=;（2）4100100{4}0.040.960.629kk k k P X C-=≤=⋅=∑.7. 一批产品的接收者称为使用方，使用方风险是指以高于使用方能容许的次品率p 接受一批产品的概率. 假设你是使用方，允许次品率不超过05.0=p ，你方的验收标准为从这批产品中任取100个进行检验，若次品不超过3个则接受该批产品. 试求使用方风险是多少？（假设这批产品实际次品率为0. 06）.解：设X ＝{100个产品中的次品数}，则(100,0.06)X B ， 所求概率为1001003{3}(0.06)(0.94)0.1430K K K K P X C-≤≤==∑.8. 甲、乙两人各有赌本30元和20元，以投掷一枚均匀硬币进行赌博. 约定若出现正面，则甲赢10元，乙输10元；如果出现反面，则甲输10元，乙赢10元. 分别求投掷一次后甲、乙两人赌本的概率分布及相应的概率分布函数.解：设甲X ＝{投掷一次后甲的赌本}，乙X ＝{投掷一次后乙的赌本}.则甲X 的取值为40，20，且1{40}{20}2P X P X ====甲甲，1{10}{30}2P X P X ====乙乙， 所以甲X 与乙X 的分布律分别为：9. 设离散型随机变量X 的概率分布为：（1）{}2,1,2,,100kP X k a k === ； （2）{}2,1,2,kP X k a k -=== ，分别求（1）、（2）中常数a 的值.解：（1）因为{}1001001121,kk k P X k a =====∑∑即1002(12)112a -⋅=-，所以)12(21100-=a . （3）因为{}1121,kk k P X k a ∞∞-=====∑∑即121112a ⋅=-，所以1=a .10. 已知一电话交换台服从4=λ的泊松分布，求：（1）每分钟恰有8次传唤的概率；（2）每分钟传唤次数大于8次的概率.解：设X ＝{每分钟接到的传唤次数}，则()X P λ ，查泊松分布表得 （1）{8}{8}{9}0.05110.0214P X P X P X ==≥-≥=-； （2）{8}0.02136P X ≥=.11. 一口袋中有5个乒乓球，编号分别为1、2、3、4、5，从中任取3个，以示3个球中最小号码，写出X 的概率分布.解：X 的所有可能的取值为1，2，3.243563{1}105C P x C ====；23353{2}10C P x C ===；22351{3}10C P x C ===.所以X12. 设随机变量X 的密度函数为 ,010,⎩⎨⎧<<+=x b ax f(x)其它，且⎭⎬⎫⎩⎨⎧>=⎭⎬⎫⎩⎨⎧<3131X P X P ，试求常数a 和b .解：1301()3183a b P X ax b dx ⎧⎫<=+=+⎨⎬⎩⎭⎰；113142()393a b P X ax b dx ⎧⎫>=+=+⎨⎬⎩⎭⎰， 由421183932a b a b +=+=得，71.5,.4a b =-= 13. 已知随机变量X 的概率分布如下， X -1 0 1 2P 0. 2 0. 25 0. 30 0. 25求13+-=X Y 及12+=X Z 的概率分布.解：13+-=X Y 的所有可能的取值为4，1，-2，-5. 且{4}{1}0.2P Y P X ===-=；{1}{0}0.25P Y P X ====； {2}{1}0.3P Y P X =-===；{5}{2}0.25P Y P X =-===.所以13+-=X Y 的分布律为12+=X Z 的所有可能的取值为1，2，5且{1}{0}0.25P Z P X ====；{2}{1}{1}0.5P Z P X P X ===-+==； {5}{2}0.25P Z P X ====.所以12+=X Z 的分布律为14. 服从柯西分布的随机变量ξ的分布函数是F (x )=A +B x arctan , 求常数A , B ;{1}P X <以及概率密度f (x ).解：由()lim (arctan )02()lim (arctan )12x x F A B x A B F A B x A B ππ→-∞→+∞⎧-∞=+=-=⎪⎪⎨⎪+∞=+=+=⎪⎩得121A B π⎧=⎪⎪⎨⎪=⎪⎩.所以11()arctan 2F x x π=+； {1}{11}(1)(1)0.5P X P x F F <=-<<=--=；211()'()1f x F x x π==⋅+.15. 设连续型随机变量X 的分布函数为20,0(),011,1x F x Ax x x <⎧⎪=≤<⎨⎪≥⎩求：（1）常数A 的值；（2）X 的概率密度函数)(x f ；（3）{}2≤X P .解：（1）由()F x 的连续性得(10)(10)(1)1F F F -=+==即21lim 1x Ax -→=，所以1A =，20,0(),011,1x F x x x x <⎧⎪=≤<⎨⎪≥⎩；（2）2,01()'()0,x x f x F x <<⎧==⎨⎩其他；（3）{2}(2)1P X F ≤==.16. 设随机变量X 的分布密度函数为 , 01 , 1)(2⎪⎩⎪⎨⎧<-=其它当x xAx f 试求：（1）系数A ；（2）⎭⎬⎫⎩⎨⎧<<221X P ；（3）X 的分布函数)(x F . 解：（1）因为1111()arcsin f x dx A x A π+∞--∞-====⎰⎰所以1A π=，1() 0 ,x f x <=⎩其它； （2）12111221112()arcsin 23P X f x dx x π⎧⎫<<====⎨⎬⎩⎭⎰；（4）当1x <-时，(){}0f x P X x =≤=，当01x ≤<时，11(){}arcsin 2xf x P X x x π-=≤==+⎰， 当1x ≥时，1(){}1f x P X x -=≤==⎰，所以⎪⎪⎩⎪⎪⎨⎧≥<≤-+-<=1,111,arcsin 1211,0x x x x x F π）（ 17. 设随机变量)4,5(~N X ，求α使：（1）{}903.0=<αX P ；（2）{}01.05=>-αX P .解：由)4,5(~N X 得5~(0,1)2X N - （1）{}555()0.903222X P X P ααα---⎧⎫<=<=Φ=⎨⎬⎩⎭ 查标准正态分布表得：51.32α-=，所以6.7=α；（2）由{}01.05=>-αX P 得，{}50.99P X α-<=所以{}{}55PX P X ααα-<=-<-<5()()2()10.99222222X P ααααα-⎧⎫=-<<=Φ-Φ=Φ-=⎨⎬⎩⎭即()0.9952αΦ=，查标准正态分布表得2.582α=，所以16.5=α18. 设)2,10(~2N X ，求{}{}210 , 1310<-<<X P X P . 解：由)2,10(~2N X 得10~(0,1)2X N - {}101013=P 0 1.5(1.5)(0)0.99320.50.49322X P X -⎧⎫<<<<=Φ-Φ=-=⎨⎬⎩⎭；{}102{2102}P X P X -<=-<-<10{11}(1)(1)2(1)120.841310.68262X P -=-<<=Φ-Φ-=Φ-=⨯-=. 19. 某地8月份的降水量服从185mm,28mm μσ==的正态分布，求该地区8月份降水量超过250 m m 的概率.解：设随机变量X ＝{该地8月份的降水量}， 则2(185,28)X N ，从而185(0,1)28X N - 所求概率为185250185{250}{}1(2.32)10.98980.01022828X P X P --≥=>=-Φ=-= 20. 测量某一目标的距离时，产生的随机误差(cm)X 服从正态分布)400,0(N ，求在3次测量中至少有1次误差的绝对值不超过30 cm 的概率.解：由(0,400)X N 得(0,1)20XN 设Y ＝{在3次测量中误差的绝对值不超过30 cm 的次数}，则(3,)Y B p 其中{30}{3030}{ 1.5 1.5}20Xp P X P X P =<=-<<=-<< (1.5)( 1.5)2(1.5)120.933210.8664=Φ-Φ-=Φ-=⨯-=所以P {3次测量中至少有1次误差的绝对值不超过30 cm }={1}P Y ≥0331{0}10.86640.13360.9976P Y C =-==-⋅=21. 自动生产线在调整之后出现废品的概率为p , 当在生产过程中出现废品时立即重新进行调整, 求在两次调整之间生产的合格品数X 的概率函数.解：由已知，()X G p所以()(1),0,1,2i P X i p p i ==-= .22. 已知测量误差2~(7.5,10)X N ，X 的单位是mm ，问必须进行多少次测量，才能使至少有一次测量的绝对误差不超过10mm 的概率大于0. 9.解：设必须进行n 次测量才能使至少有一次测量的绝对误差不超过10mm 的概率大于0. 9.由已知2~(7.5,10)X N ，7.5~(0,1)10X N - 设Y ＝{n 次测量中，绝对误差不超过10mm 的次数}，则(,)Y B n p其中7.5{10}{0.25}(0.25)0.598710X p P X P -=≤=≤=Φ= 所求概率为{1}0.9P Y ≥>，即{0}0.1P Y =≤000.59870.40130.1n n C ⋅≤，解之得，3n ≥必须进行3次测量，才能使至少有一次测量的绝对误差不超过10mm 的概率大于0. 9. 23. 参加某项综合测试的380名学生均有机会获得该测试的满分500分. 设学生的得分)(~2σμ，N X ，某教授根据得分X 将学生分成五个等级：A 级：得分)(σμ+≥X ；B 级：)(σμμ+<≤X ；C 级：μσμ<≤-X )(；D 级：)()2(σμσμ-<≤-X ；F 级：)2(σμ-<X . 已知A 级和C 级的最低得分分别为448分和352分，则： （1）μ和σ是多少？（2）多少个学生得B 级？解：（1）由已知，448352μσμσ+=⎧⎨-=⎩，解之得40048μσ=⎧⎨=⎩（2）{}{01}X P X P μμμσσ-≤<+=≤<(1)(0)0.84130.50.3413=Φ-Φ=-=24. 一汽车沿一街道行驶，需要通过三个均设有红绿信号灯的路口，每个信号灯为红或绿是相互独立的，且红、绿两种信号显示时间相同. 以X 表示该汽车首次遇到红灯前已通过的路口数. 求X 的概率分布.解：X 的所有可能的取值为0，1，2，3.且1{0}2P X ==； 111{1}224P X ==⨯=；1111{2}2228P X ==⨯⨯=；1111{3}2228P X ==⨯⨯=；所以X 的概率分布为25. 设顾客在某银行窗口等待服务的时间X （min ）服从51=λ的指数分布. 某顾客在窗口等待服务，若超过10 min ，他就离开. 若他一个月到银行5次，求： (1) 一个月内他未等到服务而离开窗口的次数Y 的分布；(2) 求{}1≥Y P .解：（1）由已知，1(),(5,)5X E Y B p其中10{10}1{10}1()p P X P X f x dx -∞=>=-≤=-⎰110250115e dx e --=-=⎰所以Y 的分布为55{}(1)k kk P Y k C p p -==- 2255()(1),(0,1,2,3,4,5)k k k C e e k ---=-=；（2）{}02025511{0}1()(1)0.5167P Y P Y C e e --≥=-==--=.26. 设~()X E λ，求)0(>=a aX Y 的概率分布. 解：因为()(0)Y g X aX a ==>所以1'()0,(),'()y g x a h y h y a a =>==，而,0()0,x X e x f x x λλ-⎧≥=⎨<⎩，1()(())|'()|yy aa Y X f y f h y h y ee a aλλλλ--=⋅=⋅=，(0)y ≥ )0(>=a aX Y 的密度函数为,0()0,0y a Y e y f y a y λλ-⎧≥⎪=⎨⎪<⎩.27. 假设你要参加在11层召开的会议，在会议开始前5 min 你正好到达10层电梯口，已知在任意一层等待电梯的时间服从0到10 min 之间的均匀分布. 电梯运行一层的时间为10 s ，从11层电梯口到达会议室需要20 秒. 如果你不想走楼梯而执意等待电梯，则你能准时到达会场的概率是多少？解：设X ={在任意一层等待电梯的时间},则(0,10)X U ，由题意，若能准时到达会场，则在10等电梯的时间不能超过4.5 min ， 所求概率为 4.50{ 4.5}0.45100P X -≤==-.28. 已知每天去图书馆的人数服从参数为(0)λλ>的泊松分布. 若去图书馆的读者中每个人借书的概率为(01)p p <<，且读者是否借书是相互独立的. 求每天借书的人数X 的概率分布.解：设Y ={每天去图书馆的人数},则()Y P λ ，{},0,1,2,!iP Y i e i i λλ-===当{}Y i =时，(,)X B i p ，{}{}(1)k k i k i i kP X k P Y i C p p +∞-====⋅-∑!(1)(1)!!!()!iikk i kk i k ii k i ki e C p p e p p i i k i k λλλλ+∞+∞----===⋅-=-⋅-∑∑!(1)(1)!!()!!()!ik k i k k i ki k i ki k i p ep p e p i k i k k i k λλλλλ-+∞+∞----===-=-⋅--∑∑(1)()(1)e!()!!!k ki kk kk i kp pi kp p p ep e ek i k k k λλλλλλλλ-+∞-----==-=⋅=-∑ 即X 的概率分布为(){}e ,0,1,2,!k pp P X k k k λλ-=== . 29. 设某型号的电子元件寿命（h ）近似服从正态分布2(160,20)N ，随机选取4件，求4个电子元件的寿命都不小于180 h 的概率.解;设X ＝{某电子元件的寿命}，则2(160,20)X N ，从而160(0,1)20X N - ， 设Y ＝{4个电子元件中寿命不小于180 h 的件数}，则(4,)Y B p ， 其中160{180}{1}1(1)10.84130.158720X p P X P -=≥=≥=-Φ=-= 所以所求概率为444{4}0.15870.84130.0006P Y C ==⋅≈.。

1 ⎧ 2 1 ⎪ x sin , x ≠ 0 （2）∵ y = ⎨ ，而 lim y = lim x 2 sin = 0 = y x = 0 ，所以函数在 x = 0 处连续 x x →0 x →0 x ⎪ x=0 ⎩ 0,
1 x = 0 ，所以函数在 x = 0 点处可导. 而 lim x →0 x−0 x 2 sin
−2 sin cos (x + Δx) − cos x 3．解： ( cos x)′ = lim = lim Δx → 0 Δx →0 Δx Δx sin 2 x + Δx 2 = − sin x = - lim sin ⋅ lim Δx → 0 Δx → 0 Δx 2 2
4. 解：（1）不能，（1）与 f ( x ) 在 x0 的取值无关，当然也就与 f ( x ) 在 x0 是否连续无关， 故是 f ′( x0 ) 存在的必要条件而非充分条件. （2）可以，与导数的定义等价. （3）可以， 与导数的定义等价. 5. 解：（1） 5 x
9 −1 = 4 ，而 y′ = (x 2 )′ = 2 x ，令 2 x = 4 ， 3 −1
得： x = 2 ，所以该抛物线上过点 (2, 4) 的切线平行于此割线. 10.解：（1）连续，但因为
f (0+ h )− f (0 ) = h
因而 lim
h→0
3
h −0 1 = 2/ 3 h h
f (0 + h) − f (0) 1 = lim 2 / 3 = +∞ ，即导数为无穷大。 → h 0 h h
∴ f +′(0) ≠ f −′(0) = −1 ，所以 f ′(0) 不存在.
13. 解 ： 当 x > 0 时 ， f ( x) = x 是 初 等 函 数 ， 所 以 f ′( x) = 3 x ； 同 理 ， 当 x < 0 时