第2章习题解b
- 格式:doc
- 大小:154.50 KB
- 文档页数:4
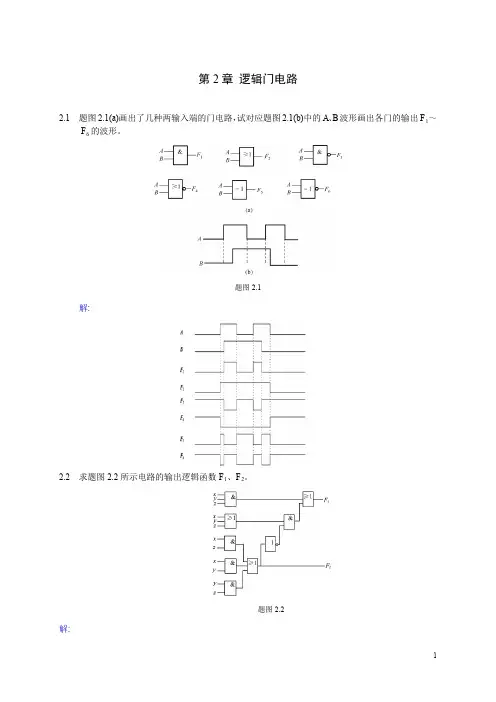
第2章逻辑门电路2.1 题图2.1(a)画出了几种两输入端的门电路,试对应题图2.1(b)中的A、B波形画出各门的输出F1~F6的波形。
题图2.1解:2.2 求题图2.2所示电路的输出逻辑函数F1、F2。
题图2.2解:2.3 题图2.3中的电路均为TTL门电路,试写出各电路输出Y1~Y8状态。
题图2.3解: Y1=0, Y2=0, Y3=Hi-Z, Y4=0, Y5=0, Y6=0, Y7=0, Y8=0.2.4 题图2.4中各门电路为CMOS电路,试求各电路输出端Y1、Y2和Y的值。
题图2.4解: Y1=1, Y2=0, Y3=0.2.5 6个门电路及A、B波形如题图2.5所示,试写出F1~F6的逻辑函数,并对应A、B波形画出F1~F6的波形。
题图2.5解:2.6 电路及输入波形分别如题图2.6(a)和2.6(b)所示,试对应A、B、C、x1、x2、x3波形画出F端波形。
题图2.6解:2.7 TTL与非门的扇出系数N是多少?它由拉电流负载个数决定还是由灌电流负载决定?解: N≤8 N由灌电流负载个数决定.2.8 题图2.8表示三态门用于总线传输的示意图,图中三个三态门的输出接到数据传输总线,D1D2、D3D4、…、D m D n为三态门的输入端,EN1、EN2、EN n分别为各三态门的片选输入端。
试问:EN信号应如何控制,以便输入数据D1D2、D3D4、…、D m D n顺序地通过数据总线传输(画出EN1~EN n 的对应波形)。
题图2.8解:用下表表示数据传输情况2.9 某工厂生产的双互补对称反相器(4007)引出端如题图2.9所示,试分别连接成:(1)反相器;(2)三输入与非门;(3)三输入或非门。
题图2.9解: (1) 反向器(2)与非门 (3)或非门2.10 按下列函数画出NMOS 电路图。
123()()()F AB CD E H G F A B CD AB CD F A B=+++=+++=⊕解:(1)(2) (3)2.11 将两个OC门如题图2.11连接,试写出各种组合下的输出电压u o及逻辑表达式。

第 2 章流体静力学大气压计的读数为100.66kPa(755mmHg),水面以下 7.6m 深处的绝对压力为多少?知: P a a水1000 kg / m3求:水下h 处绝对压力PP P a gh 解:1000175KP a烟囱高H=20m,烟气温度t s=300℃,压力为p s,确立惹起火炉中烟气自动流通的压力差。
烟气的密度可按下式计算: p=(1.25-0.0027t s)kg/m3,空气ρ3。
解:把 t s300 C 代入s s)kg / m3得s(1.25 0.0027t s) kg / m30.0027 300)kg / m30.44kg / m3压力差p=(a -s) gH ,把a 1.29kg / m3,s/ m3, g9.8N / kg ,H20m 分别代入上式可得p=( a -s)gH=(1.29-0.44)9.8 20Pa2已知大气压力为。
求以水柱高度表示时:(1)绝对压力为22时的相对压力;(2)绝对压力为时的真空值各为多少?解:p =p-p m2(1)相对压力:a大气以水柱高度来表示:a/g =19.62*1033)h= p/( 9.807*10(2)真空值:p v=p a68.5=29.6 KN / m 2以水柱高度来表示:h= a/g =29.6*103/ (9.807*103)p以下图的密封容器中盛有水和水银,若A 点的绝对压力为300kPa ,表面的空气压力为 180kPa ,则水高度为多少?压力表B 的读数是多少?解:水的密度1000 kg/m3,水银密度13600 kg/m3A 点的绝对压力为:p Ap 0h 2o ghHgg(0.8)300 10 3 =180103 +1000 9.8 h+13600求得: h=压力表 B 的读数p g p p a (300 101)KPa 199KPa以下图,在盛有油和水的圆柱形容器的盖上加载F=5788N 已知 h 1 =50cm ,h 2=30cm ,,油密度ρ 油=800kg/m 3 水银密度ρ Hg =13600kg/m 3,求 U 型管中水银柱的高度差 H 。

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ,位移)(t x 和电压)(t u r为输入量;位移)(t y 和电压)(t u c为输出量;k (弹性系数),μ(阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解:2-1(a) 取质量m 为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m 上的力有外力f(t),重力mg ,这两个力向下,为正。
有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ,这两个力向上,为负。
其中,0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。
根据牛顿第二定理F ma ∑=,有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中:0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式:22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成:22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。
2-1(b) 如图,取A 点为辅助质点,设该点位移为()Ax t ,方向如图。
再取B 点也为辅助质点,则该点位移即为输出量()y t ,方向如图A 点力平衡方程:1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程:2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得:21()()()Akx t x t y t k=-二边微分:21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②:221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式:1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成:()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。
第2章2-1 半径为a的无限薄带电圆盘上面电荷密度为ρ=r2,r为圆盘上任意点到圆心的距离,求圆盘上的总电量。
解:Q=∬ρ∙rdφdrS =∫r3∙dra∙∫dφ2π=πr42。
2-2 半径为a的球体内有均匀分布的电荷,其总电量为Q,若该球以角速度ω绕其自身的任意中轴旋转,求球体内的体电流密度。
解:J V⃗⃗⃗ =3qωrsinθ4πa3φ⃗⃗ 。
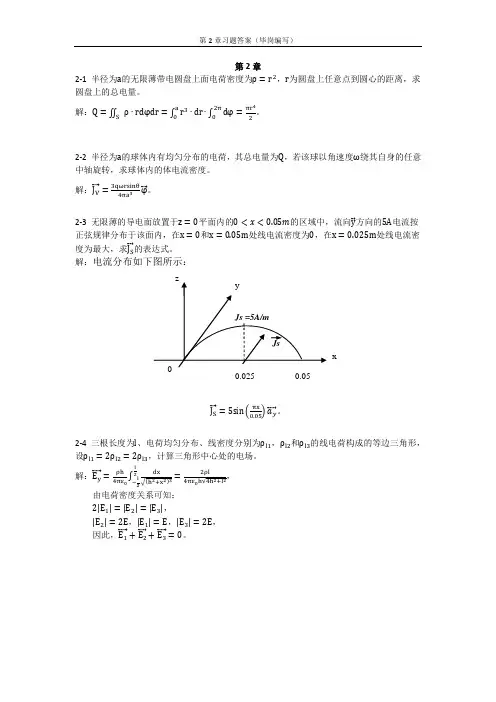
2-3 无限薄的导电面放置于z=0平面内的0<x<0.05m的区域中,流向y⃗方向的5A电流按正弦规律分布于该面内,在x=0和x=0.05m处线电流密度为0,在x=0.025m处线电流密度为最大,求J S⃗⃗ 的表达式。
解:电流分布如下图所示:x0.025 0.05J S⃗⃗ =5sin(πx0.05)a y⃗⃗⃗⃗ 。
2-4 三根长度为l、电荷均匀分布、线密度分别为ρl1,ρl2和ρl3的线电荷构成的等边三角形,设ρl1=2ρl2=2ρl3,计算三角形中心处的电场。
解:E y⃗⃗⃗⃗ =ρh4πε0∫√(h2+x2)3l2−l2=4πεh√4h2+l2,由电荷密度关系可知:2|E1|=|E2|=|E3|,|E2|=2E,|E1|=E,|E3|=2E,因此,E1⃗⃗⃗⃗ +E2⃗⃗⃗⃗ +E3⃗⃗⃗⃗ =0。
2-5 两无限长的同轴圆柱壳面,半径为a 和b ,内外导体上均匀分布电荷,密度分别为ρS1,ρS2,求r <a ,a <r <b ,r >b 时各点的电场及两导体间的电压。
解:用高斯定理求E 。
做高斯面(闭合面), ∵轴对称∴高斯面为圆柱闭合面,为左图所示 ①E1(r <a ,内导体内) 设导体为理想导体,则E 1=0;②E2(a <r <b ,内导体与外导体之间圆柱空间)∵同轴无限长,∴圆柱侧面(高斯面)上E 2处处相等,且E只有ρ方向分量d 矢量为高斯封闭面的外法线n ds n s,=E 2·d s : 上下底面:E 2·d s =0(∵E 2⊥d s,cos90°=0) 侧面:E 2·d s =E 2·ds (∵E 2∥d s,cos 0°=1)10222222επρεπρalQlE dS E dS E S d E s S=====⋅∴⎰⎰⎰⎰⎰⎰侧侧∴ρρερˆ012aE s = ③3E( r >b ,外导体壳外)E 32πl ρ=212επρπρblal s s +∴3E =ρρερρˆ021ba s s + (2)两导体内电压ab Va ba d a d E d E l d E V sb a s b aba b a ab ln 10101ερρρερρρρρ===⋅=⋅=⎰⎰⎰⎰ 当r <a 时,E⃗ =0;当a <r <b 时,E ⃗ =ρS1a+ρS2brε0r ,U =∫E ⃗ ∙dr b a =(ρS1a +ρS2b )ε0ln ab 。

第二章 动量守衡 质点动力学2-1 一个原来静止的原子核,经放射性衰变,放出一个动量为9.22×10-16g ⋅cm/s 的电子,同时该核在垂直方向上又放出一个动量为5.33×10-16g ⋅cm/s 的中微子,问蜕变后原子核的动量的大小和方向。
解: 衰变过程是: e v e B A ++→-,由动量守衡得 .0=++v e B P P P 大小:e B P P =--==s cm g s cm g /1065.10/1033.522.9161622⋅⨯=⋅⨯+=--.方向:3022.933.511===--tgtgθ;15030180=-=ϕ,1203090=+=φ.2-2 质量为M 的木块静止在光滑的水平桌面上。
质量为m ,速率为v 0的子弹水平地入射到木块内(见本题图)并与它一起运动。
求 (1)子弹相对于木块静止后,木块的速率和动量,以及子弹的动量;(2)在此过程中子弹施于木块的冲量。
解:(1)设木块的速率为v , 由动量守衡: v m M mv )(0+=;得0v mM m v +=, 木块的动量0v m M Mm mv p +==木,子弹的动量02v mM mmv p +==子.(2)子弹施予木块的冲量为 00v mM Mm P I +=-=木木.2-3 如本题图,已知绳的最大强度T 0 = 1.00 kg ,m = 500g , l = 30.0cm ,开始时m 静止。
水平冲量I 等于多大才能把绳子打断? 解: 要求向心力mg T evmF ->=02,即要求l mmg T v ->0,l mmg T mmv I ->-=00.故 l mg T m I )(0-=s m kg /86.0]100.30)8.9105008.91(10500[21233⋅=⨯⨯⨯⨯-⨯⨯=---2-4 一子弹水平地穿过两个前后并排在光滑水平桌面上的静止木块。
木块的质量分别为m 1和m 2;设子弹透过两木块的时间间隔为t 1和t 2,子弹在木块中所受阻力为恒力f ,求子弹穿过时两木块各以多大的速度运动.解: 当子弹穿出m 1时, m 1与 m 2一起运动, 故 1211)(v m m ft +=; 2111m m ft v +=.当子弹穿出m 2时, 12222v m v m ft -=,解得 222112212m ft m m ft m ft v v ++=+=.2-5 质量70kg 的渔人站在小船上,设船和渔人的总质量为200kg .若渔人在船上向船头走4.0m 后停止。



第二章需求与供给一、选择题1.随着公共汽车车票的价格上升,会出现公共汽车车票的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:B.本题考察需求量的含义,商品本身价格的变化导致的需求数量的变化被称为需求量的变化。
表示在不同的价格下消费者改变了消费数量。
2.随着公共汽车票的价格大幅下降,会出现私人汽车的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:D.本题考察需求的含义,商品本身价格以外的因素发生变化也就是非价格因素的变化导致的需求数量的变化被称为需求的变化。
表示在每一个与以前相同的价格下消费者改变了消费数量。
公共汽车和私人汽车互为替代品,替代品价格下降,被研究对象的需求会跟着下降,消费者在相同的价格下减少了对私人汽车的需求数量。
3.随着汽油价格大幅下降,会出现私人汽车的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:C.本题考察需求的含义,商品本身价格以外的因素发生变化也就是非价格因素的变化导致的需求数量的变化被称为需求的变化。
表示在每一个与以前相同的价格下消费者改变了消费数量。
汽油和私人汽车互为互补品,互补品价格下降,被研究对象的需求数量会增加,消费者在相同的价格下增加了对私人汽车的需求数量。
4. 随着养猪专业户的增加,会出现生猪的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:A. 本题考察需求量的含义,商品本身价格的变化导致的需求数量的变化被称需求量的变化。
表示在不同的价格下消费者改变了消费数量。
本题供给增加导致生猪价格下降,在较低的价格下消费者增加了生猪的需求数量,是需求量的变化。
5.随着商品房价格上升,商品房的()A.供给增加;B.供给量增加;C.供给减少;D.供给量减少。
解析:B.本题考察供给量的含义,商品本身价格的变化导致的供给数量的变化被称供给量的变化。
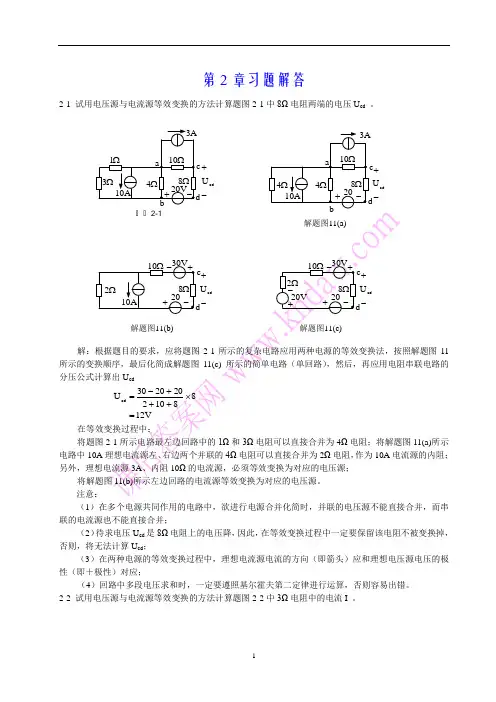
第2章习题解答2-1 试用电压源与电流源等效变换的方法计算题图2-1中8Ω电阻两端的电压U cd 。
解:根据题目的要求,应将题图2-111 将题图3Ω电阻可以直接合并为4Ω电阻;将解题图11(a)所示电路中10A 2Ω电阻,作为10A 电流源的内阻;注意:(1)在多个电源共同作用的电路中,欲进行电源合并化简时,并联的电压源不能直接合并,而串联的电流源也不能直接合并;(2)待求电压U cd 是8Ω电阻上的电压降,因此,在等效变换过程中一定要保留该电阻不被变换掉,否则,将无法计算U cd ;(3)在两种电源的等效变换过程中,理想电流源电流的方向(即箭头)应和理想电压源电压的极性(即+极性)对应;(4)回路中多段电压求和时,一定要遵照基尔霍夫第二定律进行运算,否则容易出错。
2-2 试用电压源与电流源等效变换的方法计算题图2-2中3Ω电阻中的电流I 。
题题2-1 -+cd U-+cd U 解题图11(a)-+cdU 解题图11(b) -+cd题题2-2解题图12(a)解题图12(i)解题图12(j)解:根据题目的要求,应用两种电源的等效变换法,将题图2-2所示电路按照解题图12所示的变换顺序,最后化简为解题图12(j)所示的电路,电流I 为A 2.0822I =+=注意:(1) 一般情况下,与理想电流源串联的电阻可视为短路、而与理想电压源并联的电阻可视为开路。
故题图2-2所示电路最左边支路中的2Ω电阻可视为0;(2)在变换过程中,一定要保留待求电流I 的支路不被变换掉;(3)根据电路的结构,应按照a-b 、c-d 、e-f 的顺序化简,比较合理。
2-3 计算题图2-3中1Ω电阻上的电压U ab 。
V题题2-3Ω解题图13(b)ΩΩ解题图13(e)13的顺序化简,将题图2-3所示U ab 为2-4 试用电压源与电流源等效变换的方法计算题图2-4中2Ω电阻中的电流I 。
36题题2-4解题图14(a)解: A 122228I =++-=2-5 应用支路电流法计算题图2-5所示电路中的各支路电流。
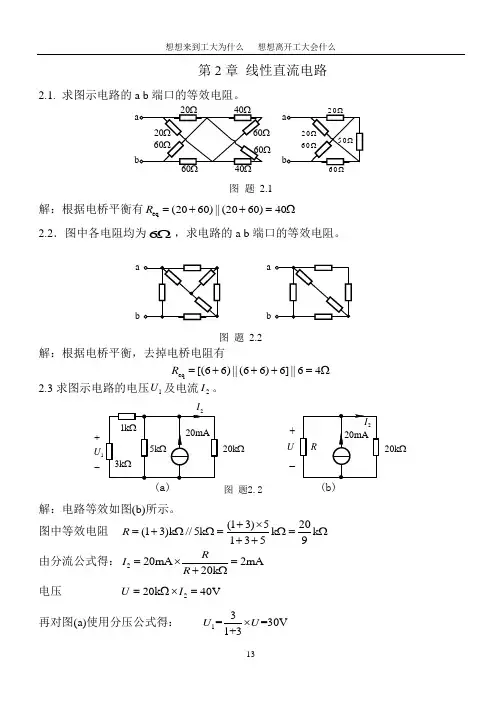
第2章 线性直流电路2.1. 求图示电路的a b 端口的等效电阻。
图 题 2.1解:根据电桥平衡有eq (2060)||(2060)40R =++=Ω2.2.图中各电阻均为6Ω,求电路的a b 端口的等效电阻。
abab图 题 2.2解:根据电桥平衡,去掉电桥电阻有eq [(66)||(66)6]||64R =+++=Ω2.3求图示电路的电压1U 及电流2I 。
20k Ω1U +-图 题2.220k Ω(b)+_U解:电路等效如图(b)所示。
图中等效电阻 (13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得:220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯=再对图(a)使用分压公式得:13==30V 1+3U U ⨯2.4 图示电路中要求21/0.05U U =,等效电阻eq 40k R =Ω。
求1R 和2R 的值。
2U +-1U 图 题2.3_1R U解:设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程:32113130.05(2) 40k (3)eqR U U R R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω再将3R 代入(1)式得 210k 3R =Ω 2.5求图示电路的电流I 。
图 题 2.5解:由并联电路分流公式,得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=- 2.6求图示电路的电压U 。
图 题2.5120Ω(a)(b)解:首先将电路化简成图(b)。
图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦由并联电路分流公式得211210A 6A R I R R =⨯=+及 21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得,3131200100400V U U U I I =-=-=- 2.7求图示电路的等效电阻x R 。
习题二2-1.两质量分别为m 和M (M m)≠的物体并排放在光滑的水平桌面上,现有一水平力F 作用在物体m 上,使两物体一起向右运动,如题图2-1所示,求两物体间的相互作用力? 若水平力F 作用在M 上,使两物体一起向左运动,则两物体间相互作用力的大小是否发生变化? 分析:用隔离体法,进行受力分析,运用牛顿第二定律列方程。
解:以m 、M 整体为研究对象,有:()F m M a =+…①以m 为研究对象,如图2-1(a ),有M m F F ma +=…② 由①、②,有相互作用力大小M m M F F m M =+若F 作用在M 上,以m 为研究对象,如图2-1(b )有M m F m a =…………③ 由①、③,有相互作用力大小M m m F F m M=+,发生变化。
2-2. 在一条跨过轻滑轮的细绳的两端各系一物体,两物体的质量分别为M 1和M 2 ,在M 2上再放一质量为m 的小物体,如图所示,若M 1=M 2=4m ,求m 和M 2之间的相互作用力,若M 1=5m ,M 2=3m ,则m 与M 2之间的作用力是否发生变化?分析:由于轻滑轮质量不计,因此滑轮两边绳中的张力相等,用隔离体法进行受力分析,运用牛顿第二定律列方程。
解:取向上为正,如图2-2,分别以M 1、M 2和m 为研究对象, 有: 111T M g M a -=222() ()M m g T M m a -++=-+2 M mmg ma F-=-又:T 1=T 2,则: 2M mF =1122M m g M M m++当M 1=M 2= 4m , 289M mm g F =当M 1=5m, M 2=3m, 2109M mm g F=,发生变化。
m(a )MFm(b )M F2-3.质量为M 的气球以加速度a 匀加速上升,突然一只质量为m 的小鸟飞到气球上,并停留在气球上。
若气球仍能匀加速向上,求气球的加速度减少了多少? 分析:用隔离体法受力分析,运用牛顿第二定律列方程。
第2章资金时间价值一、本章习题(一)单项选择题1.若希望在3年后取得500元,利率为10%,则单利情况下现在应存入银行()。
一定时期内每期期初等额收付的系列款项称为()。
A.永续年金B.预付年金C.普通年金D.递延年金3.某项永久性奖学金,每年计划颁发50 000元,若年利率为8%,采用复利方式计息,该奖学金的本金应为()元。
000 000 000 0004.某项存款年利率为6%,每半年复利一次,其实际年利率为()。
%某企业从银行取得50000元贷款,10年期,年利率12%,每年末等额偿还。
已知年金现值系数(P/A,12%,10)=,则每年应付金额为()元。
(6.在普通年金终值系数的基础上,期数加l、系数减1所得的结果,在数值上等于()。
A.普通年金现值系数B.即付年金现值系数C.普通年金终值系数D.即付年金终值系数7.以10%的利率借得50000元,投资于寿命期为5年的项目,为使该投资项目成为有利的项目,每年至少应收回的现金数额为()元。
8.下列各项中,代表即付年金现值系数的是()。
A.〔(P/A,i,n+1)-1〕B.〔(P/A,i,n+1)+1〕C.〔(P/A,i,n-1)-1〕D.〔(P/A,i,n-1)+1〕9.当银行利率为10%时,一项2年后付款800万元的购货,若按单利计息,相当于第一年初一次现金支付的购价为()万元。
"10.普通年金现值系数的倒数称为()。
A.复利现值系数B.普通年金终值系数C.偿债基金系数D.资本回收系数11.大华公司于2010年初向银行存入5万元资金,年利率为8%,每半年复利一次,则第10年末大华公司可得到本利和为()万元。
在下列各资金时间价值系数中,与偿债基金系数互为倒数关系的是()。
A.(P/F,i,n)B.(P/A,i,n)C.(F/P,i,n)D.(F/A,i,n)13.表示资金时间价值的利息率是()。
A.银行同期贷款利率B.银行同期存款利率C.没有风险和没有通货膨胀条件下社会资金平均利润率D.加权资本成本率14.为期2年的银行借款12000元,在单利率为14%,复利率为13%的条件下,其本利和分别为()。
第2章习题解答1.文法G[S]为:S->Ac|aBA->abB->bc写出L(G[S])的全部元素。
[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}==============================================2. 文法G[N]为:N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?[答案]G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D===============================================3.已知文法G[S]:S→dAB A→aA|a B→ε|bB问:相应的正规式是什么?G[S]能否改写成为等价的正规文法?[答案]正规式是daa*b*;相应的正规文法为(由自动机化简来):G[S]:S→dA A→a|aB B→aB|a|b|bC C→bC|b也可为(观察得来):G[S]:S→dA A→a|aA|aB B→bB|ε===================================================================== ==========4.已知文法G[Z]:Z->aZb|ab写出L(G[Z])的全部元素。
[答案]Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={a n b n|n>=1}===================================================================== =========5.给出语言{a n b n c m|n>=1,m>=0}的上下文无关文法。
2-12体。
设外壳脱离主体时相对于主体的速度为0,只有当下一级火箭发动后,才将上一级的外壳甩在后边。
求第三级火箭的最终速率;(2)若把48t 燃料放在12t 的外壳里组成一级火箭,问火箭最终速率是多少。
解: (1) p.50的 (2.10)式可写成⎰⎰=-⇒-=vv mm mm c v v mdm c dv 000ln对第一级火箭: 3ln 2500406060ln2500ln01=-==mm c v .对第二级火箭: 3ln 50003/201010ln250012=-+=v v .对第三级火箭:s m v v /6.82393ln 75003/211ln250023==-+=.(2 )s m v /6.40235ln 2500486060ln 2500==-=.2-13 一宇宙飞船以恒速v 在空间飞行,飞行过程中遇到一股微尘粒子流,后者以dm/dt 的速率沉积在飞船上。
尘粒在落到飞船之前的速度为u ,方向与v 相反,在时刻t 飞船的总质量为M (t ),试问:要保持飞船匀速飞行,需要多大的力? 解: 由动量定理得: ])([)]()([dm u v t M v d v dm t M P P+-++=-dt F dm u d v v d t M=-+≈)()( 两边求导得: F dtdmu v dt vd t M =-+)()(. ∵要求飞船匀速, 即 0=dt vd , u v 与的方向相反, 以v 为正向, 则dtdmu v F )( -=,即dtdm u v F )(+= 为向前的推力(此式的v 、u 为绝对值).2-14 一水平传送带将沙子从一处运送到另一处,沙子经一垂直的静止漏斗落到传送带上,传送带以恒定速率v 运动着(见本题图)。
忽略机件各部位的摩擦。
若沙子落到传送带上的速率是dm /dt ,试问:(1)要保持传送带以恒定速率v 运动,水平总推力F 多大?(2)若整个装置是:漏斗中的沙子落进以匀v 在平直光滑轨道上运动的货车里(见本题图b),以上问题的答案改变吗?解: (1) 在水平方向上, 由动量定理得:Fdt vdm mdv mv dv v dm m =+≈-++))((,两边求导得 dtdm vdtdv mF +=.即要求传送带以匀速运动时,水平总推力为 dtdm v F =(向前)(2) 光滑水平直轨道上,若没有沙子漏入,则只启动时用力,以后不用力,车子以匀速v 前进.现在沙子进来,也要保持匀速,便需用力了.因为车子越来越重, 用力公式同上; 即沙子持续进来,便要持续施力dtdm vF = ,问题的答案不改变.2-15 一质量为m 的质点在x-y 平面上运动,其位矢为 r = a cos ωt i +b sin ωt j ,求质点受力的情况。
解: t b y t a x si n , cos ωω== , 轨迹为12222=+by ax 的椭圆. 又jt b i t a j dtdy i dt dx vωωωωsin sin +-=+=,r j t b i t a dt v d a222sin cos ωωωωω-=--==.质点受力 r m a m f2ω-==,恒指向原点.2-16 如本题图所示,一质量为m A 的木块A 放在光滑的水平桌面上,A 上放置质量为m B 的另一木块B ,A 与B 之间的摩擦系数为μ,现施水平力推A ,问推力至少为多大时才能使A 、B 之间发生相对运动。
解: 对B : 0=-g m N B ,N a m f B B r μ==;得 g m a B B μ=. 对A : A A B r a m g m F f F =-=-μ ,得 AB A m gm F a μ-=.当B A a a > 时, A,B 之间发生相对运动, 即要求g m m F B A )(+>μ.2-17 如本题图所示,质量为m 2的三角形木块,放在光滑的水平面上,另一质量为m 1的立方木块放在斜面上。
如果接触面的摩擦可以忽略,两物体的加速度各若干? 解: 对m 1: ⎩⎨⎧-=-=g m N a m N a m y x 1211211cos si n θθ, 对m 2 : ⎪⎩⎪⎨⎧=--==0cos si n 222122222y y x a g m N N a m N a m θθ;又由运动学关系:211'a a a-=, xx y y x y a a a a a a 212111''tan --==θ, 解得 θtg a a a x x y )(211-=;代入运算最后得 θθθc o s s i n N ,s i n N 2122122212211m m g m m g m m m m m +=++=;⎪⎪⎩⎪⎪⎨⎧+++-=++-=++-=+-=θθθθθθθθθθctg m tg m m gtg m m m m g m m a ctg m tg m m g m m m g m a y x221212212211221221221)()(sin sin )()(sin cos sin ⎪⎩⎪⎨⎧=++=+=0)(sin cos sin 2221121212y x a ctg m tg m m g m m m g m a θθθθθ2-18 在桌上有一质量m 1的木板。
板上放一质量为m 2的物体。
设板与桌面间的摩擦系数为μ1,物体与板面间的摩擦系数为μ2,欲将木板从物体下抽出,至少要用多大的力? 解: ,111N f μ= g m m N )(211+=; ,222N f μ= g m N 22=.又 2121a m f f F =--, 222a m f =, 且要求 21a a >; 由此得 g m m F ))((2121++>μμ.2-19 设斜面的倾角θ是可以改变的,而底边不变。
求(1)若摩擦系数为μ,写出物体自斜面顶端从静止滑到底端的时间,与倾角θ 的关系,(2)若斜面倾角θ1= 60︒与θ2 = 45︒时,物体下滑的时间间隔相同,求摩擦系数μ.解: (1)摩擦力θμμcos mg N f ==,由运动方程ma f mg =-θsin ,得)cos (sin θμθ-=g a .此外由 221cos at d S ==θ, 可得 21])cos (sin cos 2[θμθθ-=g dt .(2) 又由 2121])45cos 45(sin 45cos 2[])60cos 60(sin 60cos 2[μμ-=-g dg d,可得 268.03221412121232145cos 60cos 45sin 45cos 60sin 60cos 22=-=--=--=μ2-20 本题图中各悬挂物体的质量分别为:m 1=3.0kg , m 2=2.0kg , m 3=1.0kg .求m 1下降的加速度。
忽略悬挂线和滑轮的质量、轴承摩擦和阻力,线不可伸长。
解: 各悬挂物体的运动方程分别为:1121112a m T g m T g m =-=-, 2222a m T g m =-, 3332a m g m T =-;运动学关系: 12'a a a -=, 13'a a a +=(其中a ’为m 2 , m 3相对于滑轮的加违度); 由此可得:232321323211/58.0124)12(3124)12(34)(4)(s m g g m m m m m m m m m m a =⨯⨯⨯++⋅⨯⨯-+⋅=++-+=.2-21 在本题图所示装置中,m 1与m 2及m 2与斜面之间的摩擦系数都为μ,设m 1>m 2,斜面的倾角θ 可以变动。
求θ 至少为多大时m 1、m 2才开始运动。
略去滑轮和线的质量及轴承的摩擦,线不可伸长。
解: m 2、m 2和斜面之间的摩擦力分别为θμμcos 111g m N f ==,θμμcos )(2122g m m N f +==; m 2、m 2的运动方程为 T f g m a m --=111s i n θ,f fg m T a m ---=122sin θ.由此可解出 g m m m m m m a 212121)3(s i n )(++--=μθ要求m 2、m 2开始运动,相当于要求0>a ; 由上式可得 μθ21213m m m m tg -+>.2-22 如本题图所示装置,已知质量m 1、m 2和m 3,设所有表面都是光滑的,略去绳和滑轮质量和轴承摩擦。
求施加多大水平力F 才能使m 3不升不降。
解: 运动方程为 a m m m F )(321++=, a m T 2=, 03=-T g m ;由此可得 g m m m m m F )(32123++=.。