带电粒子在电磁场中运动的科技应用

带电粒子在电磁场中运动的科技应用1.加速器带电粒子在电场中加速的科技应用主要是加速器。

加速加速器直线加速器、回旋加 速器、电子感应加速器有三种，在高考试题中，直线加速器往往不单独命题，常常与磁 偏转和回旋加速器结合起来，考查单一问题的多过程问题：回旋加速器有时单独命题， 也常常与直线加速器结合起来命题。

例1. 1930年劳伦斯制成了世界上第一台回旋加速器，英原 理如图1所示，这台加速器由两个铜质D 形盒Di 、 留有空隙，下列说法正确的是（ ）离子由加速器的中心附近进入加速器 离子由加速器的边缘进入加速器 离子从磁场中获得能疑 离子从电场中获得能量 A.B. C. D. 答案：AD解析：离子由加速器的中心附近进入加速器，在电场中加速获得能量，在磁场中偏 转时，洛伦兹力不做功，能量不变，由于进入磁场的速度越来越大，所以转动的半径也 越来越大，故选项AD 正确。

例2.电子感应加速器工作原理如图2所示（上 图为侧视图、下图为真空室的俯视图），它主要有上、 下电磁铁磁极和环形真空室组成。

当电磁铁绕组通以 交变电流时，产生交变磁场，穿过真空盒所包囤的区 域内的磁通量随时间变化，这时頁•空盒空间内就产生 感应涡旋电场。

电子将在涡旋电场作用下得到加速。

（1） 设被加速的电子被“约朿"在半径为r 的圆周 上运动，整个圆而区域内的平均磁感应强度为求 电子所在圆周上的感生电场场强的大小与&的变化率 满足什么关系。

（2） 给电磁铁通入交变电流，一个周期内电子能被加速几次？ （3）在（1）条件下，为了维持电子在恒泄的轨道上加速，电子轨道处的磁场从应 满足什么关系？解析：（1）设被加速的电子被“约朿"在半径为『的圆周上运动，在半径为「的圆而 上，通过的磁通量为0二"疗.&是整个圆而区域内的平均磁感应强度，电子所在圆周 上的感生电场场强为左‘°E 二 3 根据法拉第电磁感应龙律 Az 得,ec A5E 况2"二——帀 A/感生电场的大小 2 A/ 0（2）给电磁铁通入交变电流如图3所示，从而产生变化的磁场，变化规律如图4 所示（以图2中所标电流产生磁场的方向为正方向），要使电子能被逆时针（从上往下 看，以下同）加速，一方而感生电场应是顺时针方向，即在磁场的第一个或第四个1/4 周期内加速电子：而另一方面电子受到的洛仑兹力应指向圆心，只有磁场的第一或第二 个1/4周期才满足。

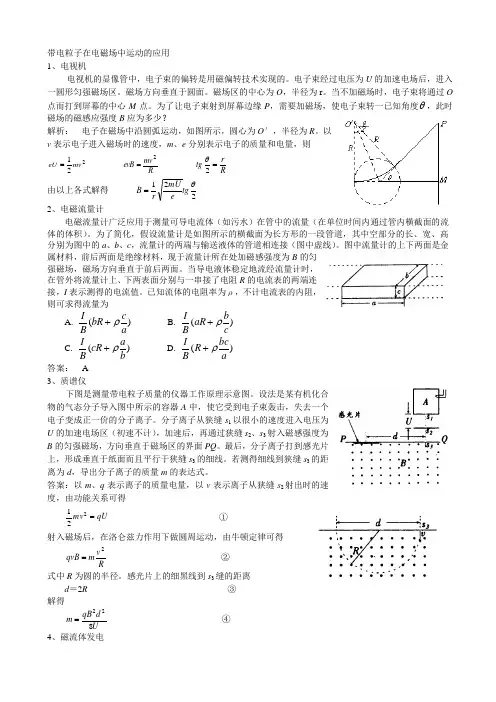
带电粒子在电磁场中运动的应用1、电视机电视机的显像管中，电子束的偏转是用磁偏转技术实现的。

电子束经过电压为U 的加速电场后，进入一圆形匀强磁场区。

磁场方向垂直于圆面。

磁场区的中心为O ，半径为r 。

当不加磁场时，电子束将通过O 点而打到屏幕的中心M 点。

为了让电子束射到屏幕边缘P ，需要加磁场，使电子束转一已知角度θ，此时磁场的磁感应强度B 应为多少？解析： 电子在磁场中沿圆弧运动，如图所示，圆心为O ′，半径为R 。

以v 表示电子进入磁场时的速度，m 、e 分别表示电子的质量和电量，则221mv eU = R mv evB 2= Rr tg =2θ 由以上各式解得 221θtg e mU r B = 2、电磁流量计电磁流量计广泛应用于测量可导电流体（如污水）在管中的流量（在单位时间内通过管内横截面的流体的体积）。

为了简化，假设流量计是如图所示的横截面为长方形的一段管道，其中空部分的长、宽、高分别为图中的a 、b 、c ，流量计的两端与输送液体的管道相连接（图中虚线）。

图中流量计的上下两面是金属材料，前后两面是绝缘材料，现于流量计所在处加磁感强度为B 的匀强磁场，磁场方向垂直于前后两面。

当导电液体稳定地流经流量计时，在管外将流量计上、下两表面分别与一串接了电阻R 的电流表的两端连接，I 表示测得的电流值。

已知流体的电阻率为ρ，不计电流表的内阻，则可求得流量为 A. )(ac bR B I ρ+ B. )(c b aR B I ρ+ C. )(b a cR B I ρ+ D. )(abc R B I ρ+ 答案： A3、质谱仪下图是测量带电粒子质量的仪器工作原理示意图。

设法是某有机化合物的气态分子导入图中所示的容器A 中，使它受到电子束轰击，失去一个电子变成正一价的分子离子。

分子离子从狭缝s 1以很小的速度进入电压为U 的加速电场区（初速不计），加速后，再通过狭缝s 2、s 3射入磁感强度为B 的匀强磁场，方向垂直于磁场区的界面PQ 。

带电粒子在电磁场中运动的相对论效应
等离子体理论研究中，电磁场是一种重要的物理场，它可以改变电荷粒子的运动轨迹。

质点在电磁场中的运动受到电磁力的影响，当质点带有电荷时，电磁力会改变它的运动方向和速度。

受电磁场影响而发生的运动称为电磁力学运动。

在电磁场中，电子和其他带电粒子的运动受到电磁力的影响。

质点在电磁场中的运动被称为电磁力学运动，其中最重要的物理过程是电磁力对质点运动的影响。

当带电粒子在电磁场中运动时，它们会受到电磁力的影响，使它们的运动方向发生变化，这一现象被称为相对论效应。

相对论效应是一种由物理学家阿尔伯特·爱因斯坦提出的重要概念，它描述了带电粒子在电磁场中运动时受到电磁力的影响。

这种效应可以用一个方程式来描述，这个方程式可以用来描述带电粒子在电磁场中运动时所受到的电磁力的大小和方向。

这个方程式可以描述电磁力对带电粒子运动的影响，让我们更好地理解电磁力在电磁场中的作用。

相对论效应在等离子体物理中发挥着重要作用，它是研究等离子体物理的基础，它可以帮助我们更好地理解带电粒子在电磁场中的运动。

相对论效应可以用来解释在电磁场中受到电磁力影响而发生的各种运动，如电子在电磁场中的运动，以及电磁场对电子的影响。

因此，相对论效应是等离子体物理研究不可或缺的一部分，它可以帮助我们理解电磁场如何影响电子和其他带电粒子的运动，以及如何影响等离子体的行为。

相对论效应也是现代物理学的一个重要概念，因为它可以帮助我们理解电磁场如何影响物质的运动，以及它如何影响宇宙中各种运动现象。

用Matlab仿真带电粒子在电磁场中的运动摘要：如果一个带电粒子在既有电场又有磁场的区域里运动，则其会受到相应的电磁力。

这里，运用MATLAB仿真带电粒子在电场中的运动，进一步讨论带电粒子在E≠0,B≠0;E=0,B≠O和E≠0,B=O并用该软件仿真出以上三种轨迹曲线。

关键字：Matlab；电磁学；仿真；电荷0 引言Matlab是美国MathWorks公司开发的一套高性能的数值计算和可视化软件。

它是一种以矩阵运算为基础的交互式程序语言，其应用范围涵盖了当今几乎所有的工业应用与科学研究领域，集数值分析、矩阵运算、信号处理和图形显示于一体。

其丰富的库函数和各种专用工具箱，将使用者从繁琐的底层编程中解放出来。

此外Matlab更强大的功能还表现在其有大量的工具箱(Toolbox)，如：控制系统、数值模拟、信号处理及偏微分方程等工具箱。

因此Matlab已成为大学科学研究中必不可少的工具。

Matlab具有丰富的计算功能和科学计算数据的可视化能力，特别是应用偏微分方程工具箱在大学物理电磁场的数值仿真中具有无比的优势。

下文是在利用Matlab 软件仿真带电粒子在不同电磁场中的运动轨迹。

1 带电粒子在均匀电磁场中的运动理论分析设带电粒子质量为m，带电量为q，电场强度E 沿y方向，磁感应强度B 沿z方向. 则带电粒子在均匀电磁场中的运动微分方程为则上面微分方程可化作：2 用Matlab仿真选择E 和B为参量，就可以分别研究E≠0，B=0和E=0，B≠0和E≠0，B≠0是粒子在电磁场中的运动轨迹。

首先编写微分方程函数文件ddlzfun.m，再编写解微分方程的主程序ddlz.m，运行结果如图所示。

研究时可以采用不同的初始条件和不同的参量观察不同的现象。

例如令E=0,B=2所得结果如图（1）所示；E=1,B=0所得结果如图（2）所示；E=1,B=2所得结果如图（3）所示。

（1）E=0,B=2参数运行结果图（1）所示是带电粒子在E=0,B=2的电磁场中运动时的轨迹，此时带电粒子只要受到洛仑兹力的作用,因此带电只改变方向不改变大小。

带电粒子在电磁场中的运动与辐射带电粒子在电磁场中的运动是一个经典物理学中的基本问题，也是电动力学研究的重要内容之一。

在电磁场的作用下，带电粒子受到洛伦兹力的作用，其轨迹和运动性质会发生变化，并且会辐射电磁波。

本文将探讨带电粒子在电磁场中的运动以及与之相关的辐射现象。

一、运动方程在电磁场中，带电粒子受到洛伦兹力的作用，其运动满足运动方程：m(d²r/dt²) = q(E + v × B)其中，m是带电粒子的质量，q是电荷量，r是位置矢量，t是时间，E是电场强度，B是磁感应强度，v是粒子的速度。

这个方程描述了带电粒子在电磁场中受力的情况，即电场和磁场对粒子的作用力。

通过求解这个运动方程，可以得到带电粒子的轨迹以及相应的运动性质。

二、洛伦兹力的效应带电粒子在电磁场中受到洛伦兹力的作用，这个力会改变粒子的运动状态。

具体来说，洛伦兹力可分为电场力和磁场力两个分量。

电场力与电场强度呈正比，其方向与电场强度的方向相同或相反，决定于带电粒子的电荷正负。

而磁场力与速度和磁感应强度的叉乘结果成正比，其方向垂直于速度和磁感应强度所决定的平面。

洛伦兹力的作用使得带电粒子的运动轨迹发生偏离，通常出现螺旋状的运动路径，称为洛伦兹运动。

带电粒子在电场和磁场的共同作用下，可以在特定的运动参数下呈现出稳定的轴向向前加速或向后减速运动。

三、带电粒子的辐射现象带电粒子在电磁场中的运动不仅仅影响其轨迹，还会产生辐射现象。

根据经典电动力学理论，加速运动的带电粒子会辐射出电磁波。

带电粒子辐射的功率与粒子的加速度成正比，具体表示为洛伦兹辐射公式：P = q²a²/6πε₀c³其中，P是辐射功率，q是电荷量，a是加速度，ε₀是真空介电常数，c是光速。

带电粒子的辐射包含两种成分：同步辐射和非同步辐射。

同步辐射主要发生在粒子的运动轨迹与电场方向相平行或完全垂直的情况下，其频率与粒子的圆周运动频率相等。

带电粒子自身电磁场对其运动的影响带电粒子是指带有电荷的微观粒子，其运动轨迹和性质都受到外部电场和磁场的影响。

然而，在运动过程中，带电粒子自身电荷的存在也会对其运动产生影响，这就是带电粒子自身电磁场的作用机制。

下面将从四个步骤分别阐述带电粒子自身电磁场对其运动的影响。

第一步：带电粒子的电场效应带电粒子自身电荷的存在使其周围形成一定的电场。

当带电粒子运动时，受到自身电场的影响，会受到一个自加速的作用，也就是说会受到向加速方向的力，从而使其运动轨迹发生改变，具体表现为曲线运动。

这种效应在粒子轨迹比较弯曲时尤为显著。

第二步：带电粒子的自身磁场在电磁学中，带电粒子的运动会产生磁场。

同样地，带电粒子自身电荷的存在也会产生磁场，这就是带电粒子的自身磁场。

由于自身磁场的影响是矢量叉积关系，所以带电粒子在自身磁场的作用下会受到一定的力矩，在运动中不断改变其自旋状态。

第三步：带电粒子的辐射效应当带电粒子加速运动时，会发出电磁辐射。

这种辐射会使带电粒子损失能量，由于能量守恒定律，为了保证能量的平衡，带电粒子的速度必须降低，也就是速度减慢。

这种效应在高速电子加速器等高能物理实验中尤为常见。

第四步：带电粒子的相互作用当两个带电粒子在运动过程中靠近时，它们之间的相互作用就会变得非常明显，其中一个带电粒子的自身磁场会对另一个带电粒子产生磁场作用，导致它的运动轨迹发生改变。

此外，如果两个带电粒子的运动速度很快，它们之间还会发生库仑相互作用，干扰彼此的运动状态。

综上所述，带电粒子自身电磁场对其运动的影响可以从带电粒子的电场效应、自身磁场、辐射效应和相互作用四个方面进行解释。

在某些高能物理实验或粒子加速器中，必须考虑这些效应的作用，以保证实验结果的准确性和稳定性。

带电粒子在电磁场中的运动一、教学目标：1. 让学生了解带电粒子在电磁场中的运动规律。

2. 让学生掌握带电粒子在电磁场中的动力学方程。

3. 培养学生运用物理知识解决实际问题的能力。

二、教学内容：1. 带电粒子在电场中的运动2. 带电粒子在磁场中的运动3. 带电粒子在电磁场中的运动方程4. 带电粒子在电磁场中的轨迹5. 带电粒子在电磁场中的加速和减速三、教学重点与难点：1. 教学重点：带电粒子在电磁场中的运动规律，动力学方程的运用。

2. 教学难点：带电粒子在电磁场中的轨迹计算，加速和减速过程的分析。

四、教学方法：1. 采用讲授法，讲解带电粒子在电磁场中的运动规律和动力学方程。

2. 采用案例分析法，分析带电粒子在电磁场中的轨迹和加速减速过程。

3. 采用讨论法，引导学生探讨带电粒子在电磁场中的运动特点。

五、教学过程：1. 导入：通过展示带电粒子在电磁场中的实验现象，引发学生对带电粒子在电磁场中运动规律的兴趣。

2. 新课：讲解带电粒子在电场中的运动规律，带电粒子在磁场中的运动规律，带电粒子在电磁场中的动力学方程。

3. 案例分析：分析带电粒子在电磁场中的轨迹，如圆周运动、螺旋运动等。

4. 课堂讨论：引导学生探讨带电粒子在电磁场中的加速减速过程，以及影响加速减速的因素。

6. 作业布置：布置相关练习题，巩固所学知识。

六、教学评估：1. 课堂问答：通过提问方式检查学生对带电粒子在电磁场中运动规律的理解程度。

2. 练习题：布置课后练习题，评估学生对动力学方程和轨迹计算的掌握情况。

3. 小组讨论：评估学生在讨论中的参与程度，以及对加速减速过程的理解。

七、教学拓展：1. 带电粒子在电磁场中的辐射：介绍带电粒子在电磁场中运动时产生的辐射现象，如电磁辐射、Cherenkov 辐射等。

2. 应用领域：探讨带电粒子在电磁场中运动在现实中的应用，如粒子加速器、电磁轨道等。

八、教学资源：1. 实验视频：展示带电粒子在电磁场中的实验现象，增强学生对运动规律的理解。

带电粒子在电磁场中的运动在物理学中，电磁场是一种具有电力和磁力效应的力场。

当带电粒子处于电磁场中时，它会受到电磁力的作用而发生运动。

本文将探讨带电粒子在电磁场中的运动规律及其相关特性。

一、洛伦兹力在电磁场中，带电粒子受到的力被称为洛伦兹力。

洛伦兹力由电场力和磁场力两部分组成，可以用如下公式表示：F = q(E + v × B)其中，F表示洛伦兹力，q为带电粒子的电荷量，E为电场强度，v 为带电粒子的速度，B为磁场强度。

根据洛伦兹力的方向，带电粒子会在电磁场中发生不同的运动。

如果电场力和磁场力方向相同或相反，带电粒子会受到一个向加速度的力，其运动轨迹将呈现弯曲的形状；如果电场力和磁场力方向垂直，带电粒子将受到一个向速度方向的力，其运动轨迹将变成圆形。

二、带电粒子在磁场中的运动当带电粒子以一定的速度进入磁场时，它会受到磁场力的作用，引起其运动轨迹的变化。

带电粒子在磁场中的运动可以通过以下几个特性进行描述：1. 弯曲半径带电粒子在磁场中做圆周运动，其弯曲半径由以下公式确定：r = mv / (qB)其中，r表示圆周运动的弯曲半径，m为带电粒子的质量，v为速度，q为电荷量，B为磁感应强度。

2. 周期带电粒子在磁场中做圆周运动的周期为：T = 2πm / (qB)其中，T表示周期，m为质量，q为电荷量，B为磁感应强度。

3. 轨道速度带电粒子在磁场中的轨道速度由以下公式确定：v = (qBr / m)其中，v表示轨道速度，q为电荷量，B为磁感应强度，r为弯曲半径，m为质量。

三、带电粒子在电场和磁场共存时的运动当带电粒子同时处于电场和磁场中时，其运动将会更为复杂。

在稳恒磁场的作用下，带电粒子将绕磁力线做螺旋线运动。

同时，在电场力的作用下，带电粒子的轨迹将受到偏转。

此时，带电粒子的运动方程可以通过以下公式描述：m(dv/dt) = q(E + v × B)其中，m为质量，v为速度，q为电荷量，E为电场强度，B为磁感应强度。

一、教学目标1. 让学生了解带电粒子在匀强磁场中的运动规律。

2. 让学生掌握洛伦兹力公式，并能够运用到实际问题中。

3. 培养学生的实验操作能力和观察能力，提高学生的科学思维能力。

二、教学内容1. 带电粒子在匀强磁场中的运动规律。

2. 洛伦兹力公式及其应用。

3. 实验操作步骤及数据分析。

三、教学重点与难点1. 教学重点：带电粒子在匀强磁场中的运动规律，洛伦兹力公式及其应用。

2. 教学难点：洛伦兹力公式的推导，实验数据的处理。

四、教学方法1. 采用实验演示法，让学生直观地观察带电粒子在匀强磁场中的运动。

2. 采用讲授法，讲解洛伦兹力公式及其应用。

3. 采用问题驱动法，引导学生思考和探讨问题。

五、教学过程1. 引入新课：通过回顾电流的磁效应，引导学生了解磁场对带电粒子的影响。

2. 实验演示：进行带电粒子在匀强磁场中的运动实验，让学生观察并记录实验现象。

3. 讲解洛伦兹力公式：结合实验现象，讲解洛伦兹力公式，并解释其物理意义。

4. 应用练习：给出实例，让学生运用洛伦兹力公式解决问题。

5. 实验数据分析：让学生分析实验数据，探讨带电粒子运动规律与磁场强度、粒子电荷量、粒子速度之间的关系。

6. 总结与拓展：总结本节课所学内容，提出拓展问题，引导学生课后思考。

7. 布置作业：布置相关练习题，巩固所学知识。

六、教学评价1. 通过课堂讲解、实验演示和练习题，评价学生对带电粒子在匀强磁场中运动规律的理解程度。

2. 通过学生实验操作和数据分析，评价学生的实验技能和观察能力。

3. 通过课后作业和拓展问题，评价学生对洛伦兹力公式的应用能力和科学思维能力。

七、教学资源1. 实验器材：带电粒子实验装置、电流表、电压表、磁铁、粒子源等。

2. 教学课件：带电粒子在匀强磁场中运动的动画演示、洛伦兹力公式的推导过程等。

3. 参考资料：相关学术论文、教学书籍、网络资源等。

八、教学进度安排1. 第一课时：引入新课，实验演示，讲解洛伦兹力公式。

第81讲 带电粒子在电磁场中运动的应用实例（多选）1．（2022•乙卷）一种可用于卫星上的带电粒子探测装置，由两个同轴的半圆柱形带电导体极板（半径分别为R 和R+d ）和探测器组成，其横截面如图（a ）所示，点O 为圆心。

在截面内，极板间各点的电场强度大小与其到O 点的距离成反比，方向指向O 点。

4个带正电的同种粒子从极板间通过，到达探测器。

不计重力。

粒子1、2做圆周运动，圆的圆心为O 、半径分别为r 1、r 2（R ＜r 1＜r 2＜R+d ）；粒子3从距O 点r 2的位置入射并从距O 点r 1的位置出射；粒子4从距O 点r 1的位置入射并从距O 点r 2的位置出射，轨迹如图（b ）中虚线所示。

则（ ）A ．粒子3入射时的动能比它出射时的大B ．粒子4入射时的动能比它出射时的大C ．粒子1入射时的动能小于粒子2入射时的动能D ．粒子1入射时的动能大于粒子3入射时的动能【解答】解：在截面内，极板间各点的电场强度大小与其到O 点的距离成反比，可设为 E =kr ，即Er ＝kA ．粒子3从距O 点r 2的位置入射并从距O 点r 1的位置出射，做向心运动，电场力做正功，则动能增大，粒子3入射时的动能比它出射时的小，故A 错误；B ．粒子4从距O 点r 1的位置入射并从距O 点r 2的位置出射，做离心运动，电场力做负功，则动能减小，粒子4入射时的动能比它出射时的大，故B 正确；C ．带正电的同种粒子1、2在均匀辐向电场中做匀速圆周运动，则有 qE 1＝m v 12r 1 qE 2＝mv 22r 2可得：12m v 12=qE 1r 12=qE 2r 22即粒子1入射时的动能等于粒子2入射时的动能，故C 错误； D ．粒子3做向心运动，则有 qE 2＞mv 32r 2可得：12m v 32＜qE 2r 22=12m v 12粒子1入射时的动能大于粒子3入射时的动能，故D 正确； 故选：BD 。

2．（2021•河北）如图，距离为d 的两平行金属板P 、Q 之间有一匀强磁场，磁感应强度大小为B 1，一束速度大小为v 的等离子体垂直于磁场喷入板间。

电磁场在科学技术中的应用命题趋势电磁场的问题历来是高考的热点：随着高中新课程计划的实施：高考改革的深化：这方面的问题依然是热门关注的焦点：往往以在科学技术中的应用的形式出现在问题的情景中：将其他信号转化成电信号的问题较多的会在选择题和填空题中出现：而用电磁场的作用力来控制运动的问题在各种题型中都可能出现：一般难度和分值也会大些：甚至作为压轴题。

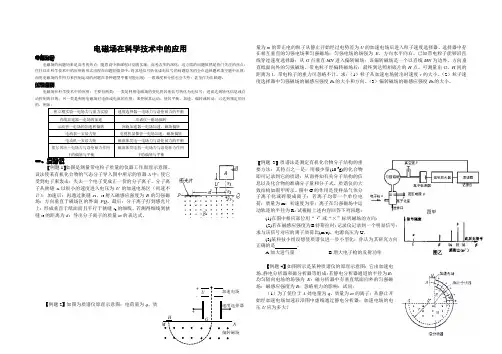
知识概要电磁场在科学技术中的应用：主要有两类：一类是利用电磁场的变化将其他信号转化为电信号：进而达到转化信息或自动控制的目的：另一类是利用电磁场对电荷或电流的作用：来控制其运动：使其平衡、加速、偏转或转动：已达到预定的目密立根实验—电场力与重力实验 速度选择器—电场力与洛伦兹力的平衡直线加速器—电场的加速 质谱仪—磁场偏转示波管—电场的加速和偏转回旋加速器—电场加速、磁场偏转 电流表—安培力矩 电视机显像管—电场加速、磁场偏转 电动机—安培力矩磁流体发电—电场力与洛伦兹力的平衡 霍尔效应—电场力与洛伦兹力作用下的偏转与平衡磁流体发电机—电场力与洛伦兹力作用下的偏转与平衡【例题1】如图是测量带电粒子质量的仪器工作原理示意图。

设法使某有机化合物的气态分子导入图中所示的容器A 中：使它受到电子束轰击：失去一个电子变成正一价的分子离子。

分子离子从狭缝s 1以很小的速度进入电压为U 的加速电场区（初速不计）：加速后：再通过狭缝s 2、s 3射入磁感应强度为B 的匀强磁场：方向垂直于磁场区的界面PQ 。

最后：分子离子打到感光片上：形成垂直于纸面而且平行于狭缝s 3的细线。

若测得细线到狭缝s 3的距离为d ：导出分子离子的质量m 的表达式。

【例题2】如图为质谱仪原理示意图：电荷量为q 、质量为m 的带正电的粒子从静止开始经过电势差为U 的加速电场后进入粒子速度选择器。

选择器中存在相互垂直的匀强电场和匀强磁场：匀强电场的场强为E 、方向水平向右。

已知带电粒子能够沿直线穿过速度选择器：从G 点垂直MN 进入偏转磁场：该偏转磁场是一个以直线MN 为边界、方向垂直纸面向外的匀强磁场。

回旋加速器原理及新进展1.引言1.1 概述回旋加速器是一种用于加速离子粒子的设备，其原理利用磁场和电场的力来加速带电粒子。

该设备的应用广泛，包括核物理研究、放射治疗、材料科学等领域。

本文将着重介绍回旋加速器的原理和最新进展。

在概述部分，我们将对回旋加速器进行简要概述，以帮助读者更好地理解后续内容。

回旋加速器是一种环形结构，由多个电极和磁铁构成。

当带电粒子进入回旋加速器后，它们会受到电场和磁场的作用力，从而始终保持在环形轨道上运动。

电场将粒子加速到一定速度，而磁场则被用来限制运动轨迹，使粒子保持在环形轨道上。

回旋加速器在粒子物理研究中起着重要作用。

通过加速高能离子粒子，科学家能够探索更深层次的物质结构和宇宙奥秘。

此外，回旋加速器还被应用于放射治疗，用于治疗癌症等疾病。

它也在材料科学中有重要的应用，可以用于表征材料的结构和性质。

近年来，回旋加速器领域取得了一些新的进展。

新型回旋加速器设计采用了更先进的技术和更高能量的粒子束。

这些新进展使得回旋加速器的加速效率大大提高，同时也提高了加速器的精度和可靠性。

在本文的后续部分，我们将详细介绍回旋加速器的原理和应用，并对最新的研究进展进行展望。

通过了解回旋加速器的原理和新进展，我们可以更好地了解其在科学研究和应用领域的重要性和潜力。

1.2 文章结构文章结构部分的内容如下：文章结构部分旨在介绍整篇文章的组织结构，让读者对即将阅读的内容有一个清晰的了解。

本文分为引言、正文和结论三个主要部分。

引言部分从概述、文章结构和目的三个方面入手，引导读者对回旋加速器原理及新进展的内容有一个整体的认识。

首先，在概述中，我们将简要介绍回旋加速器的背景和基本概念，包括其作为一种粒子加速器的重要性以及其在科学研究和应用领域中的广泛应用。

接下来，文章结构部分将详细说明本文的组织结构。

我们将分为引言、正文和结论三个部分，每个部分都有相应的子标题，以便读者能够快速定位和理解文中的内容。

最后，我们会阐明本文的目的。

电子在电磁场中运动规律的研究【实验目的】1．了解带电粒子在电磁场中的运动规律，电子束的电偏转、电聚焦、磁偏转、磁聚焦的原理；2．学习测量电子荷质比的一种方法。

【实验原理】1． 示波管的简单介绍： 示波管如图1所示示波管包括有：（1）一个电子枪，它发射电子，把电子加速到一定速度，并聚焦成电子束； （2）一个由两对金属板组成的偏转系统；（3）一个在管子末端的荧光屏，用来显示电子束的轰击点。

所有部件全都密封在一个抽成真空的玻璃外壳里，目的是为了避免电子与气体分子碰撞而引起电子束散射。

接通电源后，灯丝发热，阴极发射电子。

栅极加上相对于阴极的负电压，它有两个作用：①一方面调节栅极电压的大小控制阴极发射电子的强度，所以栅极也叫控制极；②另一方面栅极电压和第一阳极电压构成一定的空间电位分布，使得由阴极发射的电子束在栅极附近形成一个交叉点。

第一阳极和第二阳极的作用一方面构成聚焦电场，使得经过第一交叉点又发散了的电子在聚焦场作用下又会聚起来；另一方面使电子加速，电子以高速打在荧光屏上，屏上的荧光物质在高速电子轰击下发出荧光，荧光屏上的发光亮度取决于到达荧光屏的电子数目和速度，改变栅压及加速电压的大小都可控制光点的亮度。

水平偏转板和垂直偏转板是互相垂直的平行板，偏转板上加以不同的电压，用来控制荧光屏上亮点的位置。

2．电子的加速和电偏转：为了描述电子的运动，我们选用了一个直角坐标系，其z 轴沿示波管管轴，x 轴是示波管正面所在平面上的水平线，y 轴是示波管正面所在平面上的竖直线。

从阴极发射出来通过电子枪各个小孔的一个电子，它在从阳极2A 射出时在z 方向上具有速度Z v ；Z v 的值取决于K 和2A 之间的电位差C B 2V V V +=（图2）。

电子从K 移动到2A ，位能降低了2V e ∙；因此，如果电子逸出阴极时的初始动能可以忽略不计，那么它从2A 射出时的动能2z v m 21∙ 就由下式确定：22z V e v m 21∙=∙ （1） 此后，电子再通过偏转板之间的空间。

电磁场中的粒子运动与相互作用在自然界中，电磁场是广泛存在的一种现象。

在电磁场中，电子、质子和其他粒子的运动和相互作用受到电磁力的驱动和调控。

本文将探讨电磁场中的粒子运动和相互作用的一些基本原理和特点。

首先，让我们来看一下粒子在电磁场中的基本运动规律。

根据洛伦兹力的原理，当粒子带电荷并且处于电磁场中时，会受到电磁力的作用。

电磁力的大小和方向取决于粒子的电荷量、电磁场的强度和方向。

粒子受到的电磁力会改变其运动状态，使其加速或减速，甚至改变运动方向。

举个例子来说明。

假设有一个带正电荷的粒子，在存在磁场的情况下，其运动方向就会受到磁力的作用而改变。

磁力的大小与粒子的电荷量、速度和磁场的强度有关。

如果粒子的速度与磁场的方向垂直，那么粒子将受到一个垂直于其运动方向和磁场的力，从而沿着磁场曲线运动。

这被称为洛伦兹力定律，是电磁场中粒子运动的基本规律之一。

另一个重要的概念是磁场中的粒子可以具有一种称为“洛伦兹收缩”的现象。

洛伦兹收缩是指当粒子的运动速度接近光速时，其长度在运动方向上会发生压缩。

这是由于相对论效应造成的，称为洛伦兹收缩定律。

换句话说，当粒子的速度接近光速时，它在运动方向上的长度会缩短。

电磁场中的粒子还可以通过相互作用来产生其他的效应。

一个经典的例子是磁场中的电流。

根据法拉第电磁感应定律，当一个导体通过磁场移动时，会在导体两端产生电压。

这被称为感应电势。

这个现象被广泛应用在发电机和变压器等电力设备中。

粒子的运动和相互作用不仅受到电磁力的驱动，还受到其自身的电荷量和质量等性质的影响。

根据库仑定律，带相同电荷的粒子会相互排斥，而带相反电荷的粒子会相互吸引。

这导致了电荷分布在空间中的不均匀性，从而产生了电场。

电场中其他带电粒子会受到这个电场的作用力，从而产生相互作用。

此外，粒子的质量也对其运动和相互作用产生重要的影响。

根据牛顿第二定律，物体的加速度与作用力成正比，与物体的质量成反比。

因此，在电磁场中，粒子的质量越大，其对电磁力的响应越小，即加速度越小。

带电粒子在电磁场场中的运动云南省丽江市永胜县第三中学钟建荣1．掌握带电粒子在复合场中运动的基本分析；2．熟练复合场中的特殊物理模型的应用。

一、复合场的分类1．复合场：即电场与磁场有明显的界线，带电粒子分别在两个区域内做两种不同的运动，即分段运动，该类问题运动过程较为复杂，但对于每一段运动又较为清晰易辨，往往这类问题的关键在于分段运动的连接点时的速度，具有承上启下的作用。

2．叠加场：即在同一区域内同时有电场和磁场，此类问题看似简单，受力不复杂，但仔细分析其运动往往比较难以把握。

二、带电粒子在复合场中运动的基本分析1．带电粒子在电场中的运动（1）带电粒子在电场中的加速在匀强电场中的加速问题一般属于物体受恒力（重力一般不计）作用运动问题。

处理的方法有两种：①根据牛顿第二定律和运动学公式结合求解②根据动能定理与电场力做功，运动学公式结合求解。

基本方程：在非匀强电场中的加速问题一般属于物体受变力作用运动问题。

处理的方法只能根据动能定理与电场力做功，运动学公式结合求解。

基本方程：（2）带电粒子在电场中的偏转设极板间的电压为U，两极板间的距离为，极板长度为。

运动状态分析：带电粒子垂直于匀强电场的场强方向进入电场后，受到恒定的电场力作用，且与初速度方向垂直，因而做匀变速曲线运动──类似平抛运动如图。

运动特点分析：在垂直电场方向做匀速直线运：在平行电场方向，做初速度为零的匀加速直线运动：通过电场区的时间：粒子通过电场区的侧移距离：粒子通过电场区偏转角：带电粒子从极板的中线射入匀强电场，其出射时速度方向的反向延长线交于入射线的中点。

所以侧移距离也可表示为：2．带电粒子在磁场中的运动（1）带电粒子在磁场中运动时，若速度方向与磁感线平行，则粒子不受磁场力，做匀速直线运动；即：①为静止状态。

②则粒子做匀速直线运动。

（2）若速度方向与磁感线垂直，带电粒子在匀强磁场中做匀速圆周运动，洛伦兹力起向心力作用。

根据向心力公式：，得运动轨道半径公式：。

带电粒子在电磁场中的运动规律带电粒子是指在其内部带有电荷的基本粒子。

它们在电磁场中的运动规律是一项重要的物理研究领域。

本文将对带电粒子在电磁场中的运动规律进行探究，并解释其在实际应用中的重要性。

一、带电粒子在磁场中的运动规律在磁场中，带电粒子将受到磁力的作用力。

根据洛伦兹力公式F=q(v×B)，其中q是电荷，v是粒子的速度，B是磁场，F是磁力。

这个公式告诉我们，带电粒子在磁场中的运动规律是旋转。

也就是说，当一个带电粒子进入磁场时，它将被强制旋转。

这个现象被称为磁漩涡效应。

带电粒子绕磁场线运动的方向取决于粒子的电荷和速度的正负。

如果带电粒子具有正电荷，并且其速度是朝向磁场线的，那么它将绕着磁场线顺时针旋转；如果带电粒子具有负电荷，并且其速度是朝向磁场线的，那么它将绕着磁场线逆时针旋转。

二、带电粒子在电场中的运动规律在电场中，带电粒子同样将受到作用力。

这个力被称为电场力。

根据库仑定律F=k(q1q2)/r^2，其中k是库仑常数，q1和q2是两个电荷的大小，r是它们之间的距离，F是作用力。

这个公式告诉我们，带电粒子在电场中的运动规律是直线运动。

当一个带电粒子进入电场时，它将被电场力强制加速或减速。

如果带电粒子具有正电荷，并且是向着电场线行动的，它将会受到电场力的阻碍，经过一段时间后速度会变慢。

反之，如果带电粒子具有负电荷，并且是向着电场线行动的，它将会受到电场力的推动，经过一段时间后速度会变快。

三、带电粒子在交叉电磁场中的运动规律带电粒子在电场和磁场共存的环境中运动时，其运动规律将更为复杂。

如果磁场和电场的方向相互垂直，并且两者的强度相等，那么带电粒子将沿着垂直于磁场和电场的方向运动。

如果它们的强度不同，粒子将绕磁场线和电场线交汇的轨迹运动，也就是形成螺旋线。

四、带电粒子在实际应用中的重要性研究带电粒子在电磁场中的运动规律对于很多领域来说都具有重要意义。

在医学上，通过研究电磁场对人体内带电粒子的影响，可以设计出更安全、更有效的医疗仪器。

加速器的科学原理与应用加速器，是一种利用电磁场或者其他方法将带电粒子加速到高速度的设备。

它是现代粒子物理学中最重要的工具之一，可以用于研究基本粒子的物理性质、探索宇宙的起源和结构、开发新型材料等领域。

一、电磁加速器的原理在一个简单的电磁加速器中，加速器的核心部件是一个放置在真空管中的加速器管。

这个管子中有一个中空的金属环，叫做聚焦环（Focusing Ring），这个金属环里面有一个磁场，其方向平行于这个金属环的长度方向。

接下来，我们就来介绍这个加速器的原理。

首先需要将电子射流中的电子，以定向束流的方式输入聚焦环。

输入聚焦环时，射流中的电子会沿着环的轴线，在磁场的作用下产生一个绕轴运动的力。

这个力会将电子垂直于环面平面的方向推向管的中心。

当电子通过聚焦环，它们由于磁场的影响，会沿着轴线旋转。

这将产生一个向上的力，从而使得电子在管中运动。

管中同时存在一个与磁场垂直的电场E，它的作用是将这些电子加速。

由于这个加速器管是真空管，因此粒子之间会有一些碰撞。

碰撞会使得粒子损失能量，但在这个加速器中，聚焦环的作用可以把这个速度再次加速起来。

不同类型的加速器还有不同的原理。

例如，一些加速器通过将粒子放置在电场中进行加速。

这些加速器被称为线性加速器。

其他加速器利用非常强大的磁场来助推离子进行加速。

这种类型的加速器叫做磁聚焦器。

二、加速器的应用1.基本粒子研究：加速器被广泛用于研究基本粒子。

通过让这些粒子以接近光速的速度运动，物理学家可以获得更多的信息，从而更好的理解这些粒子的特性。

此外，利用加速器研究基本粒子还可以帮助科学家研究物质形成的基本原理，以及了解宇宙的形成和演化。

2.材料科学：加速器被用于研究材料。

通过研究材料的微观结构，科学家可以更好地了解它们的材料性质，以及如何改进它们的性能。

加速器可以提供很高的粒子能量，这使得科学家可以研究材料在极端环境下的行为，例如在极低温度的情况下，或在非常高压力和温度下。