当前位置：文档之家 › 典型环节与开环系统的频率特性

典型环节与开环系统的频率特性

  • 格式：ppt
  • 大小：2.93 MB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

自动控制原理 第5章 频率法_2-1

自动控制原理 第5章 频率法_2-1

1 2
)
(5-28)
M (w )
0.2 0.5
1
0.9
0
Mr
wr
wn w c
w
振荡环节的幅频特性
2 2
1 Tw 1 2 2 2 1 T w 2
这是一个标准圆方程，其圆心坐标是 1 ,0 ， 2 半径为 1 。且当ω 由 0 时， G( jw ) 由 0 90 ， 2 说明惯性环节的频率特性在 G( jw ) 平面上是实轴下 方半个圆周。
20
1 T
和
(w ) 45
0
的交点为
工程上常用简便的作图法来得到L(w曲线，方法如下：
w
1 T
L(w ) 20 lg
1 T w
2
2
0 (dB)
即当频率很低时， L(w可用零分贝线近似； 低频渐近线
w
1 T
L(w ) 20 lg
1 T w
2
2
20 lg wT (dB)
当 w 10 时，20 lg G( j10) 20 lg 10 20(dB)
。
8
设 w'
10w
'
，则有
(5-36)
dB L(w )
60
20 lg w 20 lg 10w 20 20 lg w
可见，积分环节的对数幅频特 性是一条在w=1（弧度/秒）处 穿过零分贝线（w轴），斜率为 -20dB/dec的直线。 几何 意义 积分环节的相频特性是
(1) 幅相曲线 振荡环节的传递函数为： ( s) G
1 T w j 2Tw 1
2 2

典型环节与开环系统的频率特性

典型环节与开环系统的频率特性

第五章 线性系统的频域分析法
6.一阶微分环节和二阶微分环节
dr (t ) G s ＝Ts +1 c(t ) T r (t ) dt
C(s) G s ＝ T 2 s 2 + 2 Ts 1 R(s)
2 d r (t ) dr (t ) 2 c(t ) T 2 T r (t ) 2 dt dt
传函典型环节表达式
第五章 线性系统的频域分析法
二 典型环节极坐标(Nyquist)图的绘制
1.放大环节（比例环节）
传递函数：G(s) K 频率特性： G( j) [G(s)]s j K Ke j 0 K j0
A( ) K ( ) 0
Im
放大环节的极坐标图是复 平面实轴上的一个点，它 到原点的距离为K。
第五章 线性系统的频域分析法
G(j0) 1 0
1 1 G j 45 2 T
G(j) 0 -90
不难看出，随着频率 ω=0→∞ 变化，惯性环节的幅值 逐步衰减，最终趋于 0 。相位的绝对值越来越大，但 最终不会大于90°，其极坐标图为一个半圆。
Im

s
实际微分环节实现电路
第五章 线性系统的频域分析法
4.积分环节
1 1 G s ＝ c t r t dt Ti s Ti 特点：输入消失后输出仍具有记忆功能。
dt
0
t
实例：电动机角速度与角度间的关系，物体行驶距离 与物体速度间的关系，模拟计算机中的积分器等。
特点：含一个储能元件，对突变的输入不能立即跟 随，输出无振荡。
0.63
第五章 线性系统的频域分析法
3.微分(超前)环节

自动控制原理 开环系统的频率特性—典型环节非最小相

自动控制原理 开环系统的频率特性—典型环节非最小相

频率特性
G
j
1
2 n2
j2
n
幅频特性
A G j
1
2 n2
2
2
n
2
不变！
相频特性
2
G
j
arctan
1
n 2
n2
A
1
2 n2
2
2
n
2
2
arctan
1
n 2
n2
2
arctan
1
n 2
n2
2
180 arctan
n
2 n2
1
0 A 1, 0
1 n
第四象限
不变！
0 ~ 90
Ts 1 频率特性 G j Tj 1
L 20 lg A 20 lg 1 T 22 180 arctanT
不变！
180 ~ 90
上页
L dB
40
20
3dB
0
0.1
12
180
0.5s 1
90 0 90
0.5s 1 0.5s 1
20
10
100
上页
7
11/22/2013
4，振荡环节
Gs
n2 s2 2ns n2
s2
1 n2 2
n s 1
频率特性
G
j
1
2 n2
1 j2
n
幅频特性
A G j
1
1
2 n2
2
2
n
2
不变！
相频特性
2
G
j
arctan
1
n 2Biblioteka n2A 11

5-2(2) 开环系统的频率特性

5-2(2) 开环系统的频率特性

分子分母同乘以 1
•
K [(an 1bm1 2 1) (bm1 an 1 )( j )] 2 [a n2 1 2 1] 2型系统， 2
K (an 1bm1 2 1) U ( ) 2 (an2 1 2 1)
1
2
1
3
2
所以，开环频率特性为：
G ( j ) A( ) e j ( ) G1 ( j ) G2 ( j ) G3 ( j )
A1 ( ) A2 ( ) A3 ( ) e j ( ) ( ) ( )
1 2 3
开环幅频特性 开环相频特性
第五章 线性系统的频域分析法
第二节 典型环节与开环系统的 频率特性
5-2-2 开环系统频率特性的绘制
项目 内 容
教 学 目 的 数坐标图的绘制方法。
掌握控制系统的概略极坐标图和渐近线形式的对
教 学 重 点 标图的绘制。
控制系统的概略极坐标图和渐近线形式的对数坐
教 学 难 点 渐近线形式的对数坐标图幅频特性的绘制。
i 1
n
对数幅频特性和相频特性都符合叠加原则。
K 例题2：设系统的开环传递函数 G( s) H ( s) sT1 s 1T2 s 1
（T1 ＞T2 ＞ 0，K ＞ 0），试绘制系统开环对数频率特性曲线。 解： 因为系统的开环频率特性为：G( j ) 1）对数幅频特性
K j ( jT1 1)( jT2 1)
0
lim G ( j ) K0

lim G ( j ) 0 180
曲线与坐标轴的交点
可由G（jω）=0分别求得曲线与实轴或虚轴的交点:（也可能不存在 交点，而有渐近线的情形，如本例和P201例5的情况）

自动控制原理 第五章(第一次课)

自动控制原理 第五章(第一次课)

autocumt@
18
中国矿业大学信电学院 常俊林
ω =1
1 12 + 2 2 e
(− tg
−1 1 2
)j
= 0 . 45 e
− 26 .6 o
c ss (t ) = 2 ⋅ 0 .45 sin t + 30 o − 26 .6 o = 0 .9 sin t + 3 .4 o
autocumt@ 13
(
)
(
)
中国矿业大学信电学院 常俊林
c(t ) = b1e
− s1t
+ ... + bn e
− sn t
+c1e
− jωt
+ c2e
jωt
css (t ) = c1e
− jωt
+ c2 e
jωt
其中: 其中
c1 = C ( s)( s + jω ) s = − jω
Aω = G ( s) ⋅ ( s + j ω ) s = − jω ( s + jω )( s − jω )
[ a (ω ) c (ω ) + b (ω ) d (ω )] + j[ b (ω ) c (ω ) − a (ω ) d (ω )] = c 2 (ω ) + d 2 (ω )
autocumt@ 9 中国矿业大学信电学院 常俊林
5-1 频率特性
b(ω )c(ω ) − a(ω )d (ω ) ϕ (ω ) = arctg a(ω )c(ω ) + b(ω )d (ω )
自ห้องสมุดไป่ตู้控制原理
r (t ) = 2 sin(t + 30 )

自动控制原理 第五章 第一讲 典型环节和开环频率特性

自动控制原理 第五章 第一讲 典型环节和开环频率特性

对数幅相曲线（又称尼柯尔斯曲线）：对数幅相图的横坐标表示对数相频 对数幅相曲线（又称尼柯尔斯曲线）：对数幅相图的横坐标表示对数相频 尼柯尔斯曲线）： 特性的相角，纵坐标表示对数幅频特性的幅值的分贝数。 特性的相角，纵坐标表示对数幅频特性的幅值的分贝数。
5.2 典型环节和开环频率特性
• 典型环节 • 典型环节的频率特性 • 最小相角系统和非最小相角系统
L(ω ) = −20 lg 1 + ω 2T 2
ω<<1/T, L(ω)≈-20lg1=0 ω>>1/T, L(ω)≈-20lgωT =-20(lgω-lg1/T)
(dB) 20 0 0.1 1/T -20 (o) 90 0 0.1 -90 1 10 ω 1 20dB/dec 10 ω -20dB/dec
幅频特性相同， 幅频特性相同，但相频特性符号相反 。 •最小相角系统的幅频特性和相频特性一一对应，只要根据其对 最小相角系统的幅频特性和相频特性一一对应， 数幅频曲线就能写出系统的传递函数 。 L(dB)
L(dB) 20 10 -20 ω L(dB) -20 100 50 -40 ω -40 -20 ω 2 ω1 ωc ω -40
典型环节
•比例环节：G（s）= K 比例环节： （ ） •惯性环节： G（s）= 1/(Ts+1)，式中T>0 惯性环节： （ ） ，式中 •一阶微分环节： G（s）= (Ts+1)，式中 一阶微分环节： （ ） ，式中T>0 •积分环节： G（s）= 1/s 积分环节： （ ） 微分环节： （ ） •微分环节： G（s）= s •振荡环节： G（s）= 1/[(s/ωn)2+2ζs/ωn+1]; 振荡环节： （ ） 式中ω ， 式中 n>0，0<ζ<1 二阶微分环节： （ ） •二阶微分环节： G（s）= (s/ωn)2+2ζs/ωn+1; 式中ω ， 式中 n>0，0<ζ<1

胡寿松《自动控制原理》(第7版)笔记和课后习题(含考研真题)详解(第5~6章)【圣才出品】

胡寿松《自动控制原理》(第7版)笔记和课后习题(含考研真题)详解(第5~6章)【圣才出品】

第5章线性系统的频域分析法5.1复习笔记本章考点：幅相特性曲线、伯德图的绘制，奈奎斯特稳定判据，稳定裕度计算。

一、频率特性1．定义幅频特性：稳态响应的幅值与输入信号的幅值之比A（ω）。

相频特性：稳态响应与正弦输入信号的相位差φ（ω）。

频率特性：幅频特性和相频特性在复平面上构成的一个完整向量G（jω）＝A（ω）e jφ（ω）。

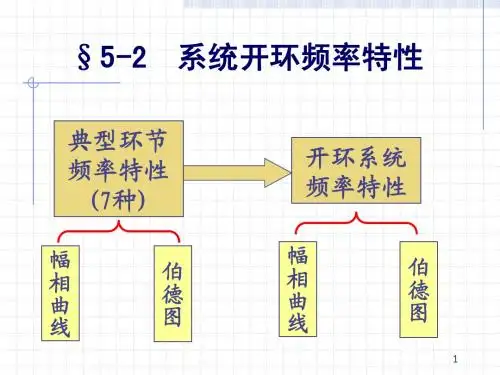
2．频率特性的几何表示法（重点）（1）幅相频率特性曲线（幅相曲线或极坐标图），横坐标为开环频率特性的实部，纵坐标为虚部， 为参变量。

（2）对数频率特性曲线（伯德图），由对数幅频特性曲线、对数幅相频特性曲线两幅图组成：①对数幅频特性曲线的纵坐标表示L（ω）＝20lgA（ω），单位是分贝，记作dB；②对数相频特性曲线的纵坐标为φ（ω），单位为度“°”。

（3）对数幅相曲线（尼科尔斯图），横坐标表示频率特性的相角φ（ω），纵坐标表示频率特性的幅值的分贝数L（ω）＝20lgA（ω）。

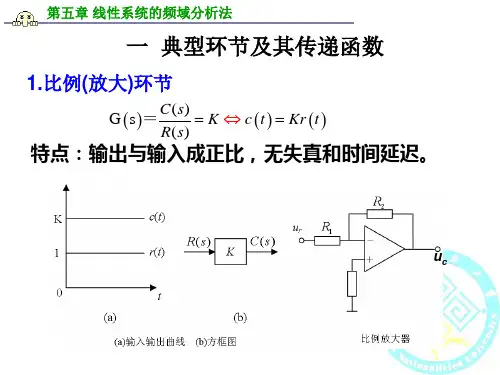
二、典型环节与开环系统的频率特性1．典型环节的频率特性一些主要典型环节的频率特性曲线总结如表5-1-1所示。

表5-1-1典型环节频率特性曲线总结2．开环幅相曲线绘制步骤（1）确定开环幅相曲线的起点（ω＝0＋）和终点（ω＝∞），确定幅值变化与相角变化。

（2）计算开环幅相曲线与实轴的交点。

令Im[G（jωx）H（jωx）]＝0或φ（ωx）＝∠G（jωx）H（jωx）＝kπ（k＝0，±1，…）称ωx为穿越频率，而开环频率特性曲线与实轴交点的坐标值为Re[G（jωx）H（jωx）]＝G（jωx）H（jωx）。

（3）分析开环幅相曲线的变化范围（象限、单调性）。

3．开环对数频率特性曲线绘制步骤（1）开环传递函数典型环节分解并确定一阶环节、二阶环节的交接频率；（2）绘制低频段渐近特性线：在ω＜ωmin频段内，直线斜率为－20vdB/dec；（3）作ω≥ωmin频段渐近特性线，交接频率点处斜率变化表如表5-1-2所示。

典型环节与系统频率特性

典型环节与系统频率特性

2．积分环节
<1>
G(s)= s1
A(ω )=ω1
G(ωj
)=
1 jω
φ (ω )=-90o
奈氏图
∞
Im 0
Re
<2> 伯德图 对数幅频特性：
ω=0 L(ω ) dB
20 -20dB/dec
L(ω )=20lgA(ω )=-20lgω
0 0.1 -20
1
10 ω
ω=1 L(ω )=-20lg1=0dB φ (ω )
节串联而成的：
幅频特性:
开积环分G(增环s)益节= sKυΠjΠ=ni=1υ-m1((τTjiss++11))系n时>统间m的常A阶数(ω次)=ωKυΠjΠi1=n=m-υ1
1+(ωτ i )2 1+(ω Tj )2
的个数
相频特性:
φ
(ω )=υ- 90o+
∑m tg-ω1 τ
i =1
i
∑nυ- tg-ω1
Im
1 0
L(ω ) dB
20 0
φ (ω )
0 -100 -200 -300
ω=0 Re
ω ω
第二节 典型环节与系统的频率特性
8．非最小相位环节
最小相位环节: 开环传递函数中没有s右半平面上
的极点和零点. 非最小相位环节:
开环传递函数中含有s右半平面上 的极点或零点.
最小相位环节对数幅频特性与对数相 频特性之间存在着唯一的对应关系.对非最 小相位环节来说,不存在这种关系.
第五章 频率特性法
第二节 典型环节与系统频率特性
频率特性法是一种图解分析法,它 是通过系统的频率特性来分析系统的性 能,因而可避免繁杂的求解运算.与其他 方法比较,它具有一些明显的优点.

实验四典型环节和系统频率特性的测量

实验四典型环节和系统频率特性的测量

实验四 典型环节和系统频率特性的测量一、实验目的1．了解典型环节和系统的频率特性曲线的测试方法；2．根据实验求得的频率特性曲线求取相应的传递函数。

二、实验设备同实验一三、实验内容1．惯性环节的频率特性测试；2．二阶系统频率特性测试；3．无源滞后—超前校正网络的频率特性测试；4．由实验测得的频率特性曲线，求取相应的传递函数；5．用软件仿真的方法，求取惯性环节和二阶系统的频率特性。

四、实验原理设G(S)为一最小相位系统（环节）的传递函数。

如在它的输入端施加一幅值为Xm 、频率为ω的正弦信号，则系统的稳态输出为 )sin()()sin(ϕωωϕω+=+=t j G Xm t Y y m ①由式①得出系统输出，输入信号的幅值比 )()(ωωj G Xmj G Xm Xm Ym == ② 显然，)(ωj G 是输入X(t)频率的函数，故称其为幅频特性。

如用db （分贝）表示幅频值的大小，则式②可改写为XmYm j G Lg L lg 20)(20)(==ωω ③ 在实验时，只需改变输入信号频率ω的大小（幅值不变），就能测得相应输出信号的幅值Ym ，代入上式，就可计算出该频率下的对数幅频值。

根据实验作出被测系统(环节)的对数幅频曲线，就能对该系统（环节）的数学模型作出估计。

关于被测环节和系统的模拟电路图，请参见附录。

五、实验步骤1.熟悉实验箱上的“低频信号发生器”，掌握改变正弦波信号幅值和频率的方法。

利用实验箱上的模拟电路单元，设计一个惯性环节（可参考本实验附录的图4-4）的模拟电路。

电路接线无误检查后,接通实验装置的总电源，将直流稳压电源接入实验箱。

2.惯性环节频率特性曲线的测试把“低频函数信号发生器”的输出端与惯性环节的输入端相连，当“低频函数信号发生器”输出一个幅值恒定的正弦信号时，用示波器观测该环节的输入与输出波形的幅值，随着正弦信号频率的不断改变，可测得不同频率时惯性环节输出的增益和相位（可用“李沙育”图形），从而画出环节的频率特性。

5-3典型环节开环频率特性

5-3典型环节开环频率特性
2 T arctan 1 T 2 2 G ( j ) 2 T 180 arctan 2 2 T 1 2 T arctan 1 T 2 2 GF ( j ) 2 T 180 arctan 2 2 T 1 1 T ； 1 T 1 T ； 1 T
ω 0 1/T |GF(jω)| 1 0.707 ∠GF(jω) -180o -135o jω 0 σ -1 0 1/T
2 2
∞ 0 -90o
∞
2.4 振荡环节G(s)和不稳定振荡环节GF(s)
G(s) 1 /(T s 2 Ts 1) ； GF (s) 1 /(T s 2 Ts 1) ； 1 1 G ( j ) ； G F ( j ) ； 2 2 2 2 1 T j 2 T 1 T j 2 T
Im ω= 0 0.6 0.5 0.4
ζ=0.8
1
2.5 一阶微分环节G(s)和不稳定一阶微分环节GF(s)
GF (s) Ts 1； G( s) Ts 1； G( j ) 1 j T ； GF ( j) 1 j T ； | G( j ) || GF ( j ) | (1 T 2 2 )1/ 2； G( j ) arctan T ； GF ( j) 180 arctan T ；
非最小相位环节 环节有零点或极点在S平 的面右半部。 ( K 0，T 0，0 1) 1.1 反向环节 K ； 1.2 惯性环节 1 /(Ts 1) ； 1.3 一阶微分环节 Ts 1； 1.4 振荡环节 1.5 二阶微分环节 2 2 2 2 T s 2 Ts 1； 1 /(T s 2 Ts 1) ； 2. 典型环节的频率特性及幅相曲线： 2.1 放大环节 G(s)=K 和反向环节 GF(s)=-K | G( j) || GF ( j) | K ； j G( j ) 0； -K K GF ( j) 180；

自动控制原理第五章PPT课件

自动控制原理第五章PPT课件

s (1 0 .1 s)
s1 0 .1 s
比例环节
一阶微分环节
积分环节
惯性环节
.
23
非最小相位环节 ：开环零点、极点位于S平面右 半部分
➢ 比例环节：-K
➢ 惯性环节：1/(-Ts+1)，式中. T>0
24
最小相位系统与非最小相位系统
除比例环节外，非最小相位环节和与之对应的最小相位环节的区别在于开环零极点的 位置，非最小相位环节对应于s右半平面开环零点或极点，而最小相位环节对应于s左半 平面开环零点或极点。
• 对于不稳定系统则不可以通过试验方法来确定，因 为输出响应稳态分量中含有由系统传递函数的不稳
定极点产生的发散或震荡分量。
.
8
线性定常系统的传递函数为零初始条件下，输出与输入的拉氏变换之比
其反变换为
G(s)= C(s) R(s)
g(t) 1 jG(s)estds
2 j j 式中位于G(s)的收敛域。若系统稳定，则可取零，如果r(t)的傅氏变换 存在，可令s=j,则有
d () 是 关 于 的 奇 函 数 。
.
5
.
6
因而
1
G (j) c b 2 2 ( () ) d a 2 2 ( () ) 2 ,
G (j) a r c ta n b ()c () a ()d () a ()c () d ()b ()
G ( j )c a (( )) jjd b ( ( ) )G (j )ej G (j)
Tddut0u0ui
TRC
uo t
取拉氏变换并带入初始条件uo0
1
1 A
U o ( s ) T s 1 [ U i( s ) T u o 0 ] T s 1 [ s 2 2 T u o 0 ]

自动控制原理-第5章2

自动控制原理-第5章2
2
时的情况。 讨论 0 ≤ ζ ≤ 1时的情况。当K=1时，频率特性为： 时 频率特性为：
1 G ( jω ) = (1 − T 2ω 2 ) + j 2ζωT
实频、虚频、幅频和相频特性分别为： 实频、虚频、幅频和相频特性分别为： 1 − T 2ω 2 − 2ζωT P(ω ) = , Q (ω ) = 2 2 2 2 2 2 (1 − T ω ) + 4ζ ω T (1 − T 2ω 2 ) 2 + 4ζ 2ω 2T 2
1
二、幅相曲线（极坐标图、奈奎斯特图） 幅相曲线（极坐标图、奈奎斯特图）
比例环节： ⒈ 比例环节： G ( s ) = K ;
G ( jω ) = K
P Q 虚频特性： 实频特性 ： (ω ) = K ；虚频特性： (ω ) = 0 ；
ϕ 幅频特性： (ω ) = K ；相频特性： (ω ) = 0 A 相频特性： 幅频特性：
ϕ (ω ) = −
− tg −1T1ω − tg −1T2ω
[分析 、当 ω = 0 时， (0) = −k (T1 + T2 ), Q(0) = −∞, ϕ (0) = − π 分析]1、 分析 P 2 G 显然， 显然，当 ω → 0 时， ( jω )的渐近线是一条通过实轴 − k (T1 + T2 ) 点， 且平行于虚轴的直线。 且平行于虚轴的直线。
A(ω ) = P (ω ) 2 + Q(ω ) 2 =
−1
1 (1 − T 2ω 2 ) 2 + (2ζωT ) 2
Q(ω ) −1 2ζωT ϕ (ω ) = tg = −tg P(ω ) 1 − T 2ω 2
6
振荡环节的奈氏图
1 − T 2ω 2 P (ω ) = (1 − T 2ω 2 ) 2 + 4ζ 2ω 2T 2 − 2ζω T Q (ω ) = (1 − T 2ω 2 ) 2 + 4ζ 2ω 2T 2

实验三 典型环节(或系统)的频率特性测量

实验三 典型环节(或系统)的频率特性测量

实验三 典型环节（或系统）的频率特性测量一．实验目的1．学习和掌握测量典型环节（或系统）频率特性曲线的方法和技能。

2．学习根据实验所得频率特性曲线求取传递函数的方法。

二．实验内容1．用实验方法完成一阶惯性环节的频率特性曲线测试。

2．用实验方法完成典型二阶系统开环频率特性曲线的测试。

3．用软件仿真方法求取一阶惯性环节频率特性和典型二阶系统开环频率特性，并与实验所得结果比较。

三、实验原理及说明1．实验用一阶惯性环节传递函数参数、电路设计及其幅相频率特性曲线：对于1)(+=Ts Ks G 的一阶惯性环节，其幅相频率特性曲线是一个半圆，见图3.1。

取ωj s =代入，得)()(1)(ωϕωωωj e r T j Kj G =+=(3-2-1)在实验所得特性曲线上，从半园的直径(0)r ，可得到环节的放大倍数K ，K ＝(0)r 。

在特性曲线上取一点k ω，可以确定环节的时间常数T ，kk tg T ωωϕ)(-=。

(3-2-2)实验用一阶惯性环节传递函数为12.01)(+=s s G ，其中参数为R 0=200K Ω，R 1＝200K Ω，C＝1uF ，参数根据实验要求可以自行搭配，其模拟电路设计参阅下图3.2。

在进行实验连线之前，先将U13单元输入端的100K 可调电阻顺时针旋转到底（即调至最大），使输入电阻R 0的总阻值为200K;其中，R1、C1在U13单元模块上。

U8单元为反相器单元，将U8单元输入端的10K 可调电阻逆时针旋转到底（即调至最小），使输入电阻R 的总值为10K;注明：所有运放单元的+端所接的100K 、10K 电阻均已经内部接好，实验时不需外接。

图3.22．实验用典型二阶系统开环传递函数参数、电路设计及其幅相频率特性曲线：对于由两个惯性环节组成的二阶系统，其开环传递函数为12)1)(1()(2221++=++=Ts s T Ks T s T K s G ξ )1(≥ξ 令上式中 s j ω=，可以得到对应的频率特性 )(22)(12)(ωϕωωξωωj e r T j T Kj G =++-=二阶系统开环传递函数的幅相频率特性曲线，如图所示。

自动控制原理 第5章

自动控制原理 第5章
2 2
⇒
X 2 − X +Y 2 = 0
（下半圆） 下半圆）
Y = −ω T X
§5.2 典型环节与开环系统的频率特性
1 G( s) = 不稳定惯性环节 Ts − 1 1 G ( jω ) = − 1 + jω T 1 G = 1 + ω 2T 2 ωT ∠ G = − arctan = − ( 180° − arctan ω T ) = −180° + arctan ω T -1
ω ω ⑹ G ( jω ) = 1 1 − 2 + j 2ξ ωn 2 ωn ω ω ⑺ G ( jω ) = 1 − 2 + j 2ξ ωn ωn ω2 ω 1 − 2 − j 2ξ ωn ωn ⑻ G ( jω ) = e − jτ ω
2
jω
ω ω2 1 − 2 + j 2ξ ωn ωn
建 模
§5.1
频率特性
cs (t ) = A
2
r ( t ) = A sin ω t
1+ω T
2
§5.1.2 频率特性 G(jω) 的定义 ω 定义一： 定义一： G ( jω ) = G ( jω ) ∠G ( jω )
G ( jω ) = cs (t ) 1 = r (t ) 1 + ω 2T 2
∠ c s (t ) = − 63.4° + 30° = − 33.4°
ω =2
cs (t ) =
3 sin( 2t − 33.4° ) 5
s Φ e ( s) = s+1
ω =2 2 es (t ) ω jω Φ e ( jω ) = = = = 2 1 + jω 3 5 1+ω

5-2(1) 典型环节的频率特性

5-2(1) 典型环节的频率特性
∵ 幅频特性
A( )
1
2 2 2 2 (1 2 ) 4 2 n n
相频特性
n ( ) arctg 2 1 2 n
2
其中，对于相频特性
2 n 当： n 时， ( ) arctg 2 1 2 n
当： n 时， ( ) 180 arctg
L（ω ）
j
ω =∞ ω ωn 0
20 0 φ（ω ） 1 ω =0 180° 0 (b)
[40] ωn ω
ω
（ a）
二阶微分环节的频率特性曲线图
8. 延迟环节 （教材P204）
传递函数 G(s)
频率特性
G( j) e j A() e j ( )
e
s
(1) 幅相曲线: （教材P204图5-25） 幅频特性 A（ω）= 1 相频特性 φ（ω） = -ωτ（rad）= - 57.3ωτ (°) (2) 对数频率特性曲线(Bode图): 1） 对数幅频特性 L(ω)=20lgA(ω)= 0 2） 对数相频特性：φ（ω） = -ωτ（rad）=-57.3ωτ(°)
ω →0
0
(a) 微分环节的幅相曲线
(2) 对数频率特性曲线(Bode图):
∵ 对数幅频特性 L(ω)=20lg∣G（jω）∣ = 20lgω 对数相频特性 φ（ω） = 90° ∴ 微分环节的Bode图如图(b)所示。
L（ω）
20
0
20dB/dec 1 10
φ（ ω ） 90° 0
ω
ω
(b) 微分环节的Bode图
r n 1 2 2
1 M r A(r ) 2 1 2 2 0 2
显然
对于不同的系统阻尼,振荡环节的谐振峰值Mr，谐振频率ωr不同， 参见教材P195-196分析。

5-2频率特性曲线的绘制

5-2频率特性曲线的绘制

由图可见无论是欠 阻尼还是过阻尼系 统，其图形的基本 形状是相同的。 当过阻尼时，阻尼 系数越大其图形越 接近圆。
-2
0.2
04:54 16
（2）Bode图（对数频率特性）：
幅频特性为：
A( )
1 (1 T 2 2 )2 (2T )2
相频特性为：
( ) tg 1
04:54
1 称为转折频率。斜率为-40dB/Dec。 T
17
1 相频特性： ( ) tg
2 T 1 T 2 2
1 , ( ) ; , ( ) 。 T 2
几个特征点： 0, ( ) 0;
下图是当T=1时的图
G ( j ) jT 1
j 0
（1）Nyquist图（幅相频率特性）：
ω
1
A( ) 1 T 2 2 , ( ) tg 1T
（2）Bode图（对数频率特性）：
L( ) 20lg 1 T 2 2
对数幅频特性（用渐近线近似）：
L( ) 0 20lg A( ) 0 L( ) 20lg A( ) 20lgT
20
16 12

0.1 0.2 0.3 0.5 0.7 1 .0
10
8 4 0 -4 -8
1 10T 1 5T 1 2T 1 T 2 T
0
渐近线

0.1 0.2 0.3 0.4 0.5 0.6
-10
0 .7 0 .8 1 .0
04:54
低频段渐进线 高频段渐进线
12
这是斜率为+20dB/Dec的直线。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

起点终点和交点
起点G(s) 10
终 点G(s)
60 s2
交点：G(j 6)
0 j4.9
起点
180
终点
: :
分子分母保留最低次方 分子分母保留最高次方
60 G(j) (6 2 ) j5
若 Re[GH] 0有解,则与虚轴相交
若 Im[GH] 0有解,则与实轴相交
开环幅相曲线的绘制例2 (P198)
非最小相角环节相角小结(P193)
G(s)
名 称 ＝0 ＝
G(s)=k (k<0)
不稳定的 比例环节
恒定-180o
G(s)= -Ts+1
不稳定的 一阶微分
0o ~ -90o
1 G(s)= -Ts+1
不稳定的 惯性环节
G(s) T2s2 2Ts 1
不稳定的 二阶微分
0o ~ +90o 0o ~ -180o
jIm[G(jω)]
G(s)=s
4
3
G(j) j
2
1
这是一个正的纯虚矢量
0
Re[G(jω)]
从0 ~ 变化时，各矢量的角度均为 90o
矢量的模随着ω的增大而增大
积分环节的幅相曲线(P192)
jIm[G(jω)]
G(s)=
1
s
0
G(j) 1 ＝ j 1
j
Re[G(jω)]
这是一个负的纯虚矢量
从0＋ ~ 变化时，各矢量的角度均为－90o
Tω>1时，实部为负，矢量在第二象限
从0 ~ 时，矢量的角度从0o ~ 90o ~ 180o
振荡环节G(jω)分析(P194)0 1
G(s)
s2
n2 2ns n2
T2s2
1 2Ts
1
1
2T
G(j) (1 T22 )2 42T22 arctg 1 T22
G(j0) 10o G(j) 0 180o
10(s 1) GH
s2 (2s 1)
起 点GH
10 s2
,
180
终 点GH 5 ,0 180 s2
10(j 1) G(j)H(j) 2(j2 1)
1时GH 20 2(3 j) 3 j
jIm[GH]
0 Re[GH]
10(2 1) G(j)H(j) 2[(22 11
G(j) 1 j0.5 1
A() 0.252 1
() tg10.5
0 0.5 1 2 4 5 8 20
A() 1 0.97 0.89 0.71 0.45 0.37 0.24 0.1
() 0° -14.5 ° -26.6 ° -45 ° -63.4 ° -68.2 ° -76 ° -84 °
令 dA() 0, 得 d
G( jn )
G(j 1 ) T
1 2
90o
r n 1 22
A(r ) Am 2
1 1 2
(0 0.707)
振荡环节G(jω)曲线(P194) （Nyquist曲线）
j
1 0
r n 1 22
A(r ) 2
1 1 2
1 A(n ) 2
典型环节相角小结(补充) ＝0 ＝
G(s)=k G(s)=s
比例环节 微分环节
sj d
dt
G(s) 1 积分环节
s
G((ss))=TTs+s 1 1 一阶微分
0
GG((ss))
11 TTss1
惯性环节
不稳定的…
G(s) T22s22 2TTss11 二阶微分
1 G(s) T2s2 2Ts 1
振荡环节
微分环节的幅相曲线(P192)
G(s)=s
微分环节
恒定正90o
G(s)=
1
s
积分环节
恒定负90o
G(s)=Ts+1 一阶微分 0o ~ +90o
G(s)=
1 Ts+1
惯性环节
0o ~ -90o
G(s) T2s2 2Ts 1二阶微分 0o ~ 90o ~ 180o
Gs)
T2s2
1 2Ts
振荡环节
1
0o ~ -90o ~ -180o
开环幅相曲线的绘制例3 (P198)
GH
2(s2
5s s3
4)
起 点GH
8 s3
270
起点终点和交点
jIm[GH]
终 点GH 2 s
0 90
2.5 0
Re[GH]
交 点G(j)H(j) 2[(4 2 ) j5] j3
G(j2)H(j2) 2.5
开环幅相曲线的绘制例4 (P198)
j Im[G(jω)] 0
Re[G(jω)] 1
二阶微分的幅相曲线(P194)
G(s) T2s2 2Ts 1
jIm[G(jω)]
G(j 1 ) j2 T
0
G(j) (1 T22 ) j2T
1 Re[G(jω)]
矢量的虚部始终为正
Tω<1时，实部为正，矢量在第一象限 Tω＝1时，实部为零，矢量在正虚轴上
矢量的模随着ω的增大而减小
一阶微分的幅相曲线(P192)
jIm[G(jω)]
G(s)= Ts+1
4
3
G(j) jT＋1
2
1
这是一个实部衡为1
01
虚部随ω增大而增大的矢量
Re[G(jω)]
矢量的角度从0o ~ 90o 变化
矢量的模随着ω的增大从1变化到无穷
惯性环节G(jω)
(P192)
G(s)
=
封面
制作人南京航空航天大学王凤如 xwfr01@
5-2目录
1、典型环节 2、典型环节的频率特性 3、开环幅相曲线 4、开环对数频率特性曲线 5、延迟环节和延迟系统 6、传递函数的频域实验确定（实验课讲）
典型环节(192页)
G(s)=k G(s)=s
比例环节 微分环节
sd
(s)
1
Ts d1t
s G(s) 1 s G(s)=Ts+1
积分环节 一阶微分
一1阶系统 dt
1 (s) T2s2 2Ts 1
G(s) 1 惯性环节 Ts 1
欠阻尼二阶系统
G(s) T2s2 2Ts 1 二阶微分
1 Gs) T2s2 2Ts 1
振荡环节
典型环节零极点分布图(补充)
GH 10 s(s 5)
起点终点和交点
起 点G(s)
2 s
90起点 : 分子分母保留最低次方
终 点G(s)
10 s2
0 180
终点: 分子分母保留最高次方
交点：无jI交m[G点(j)] 若 Re[GH] 0有解, 则与虚轴相交
10
G(j) 02 Rje5[G(j)] 若 Im[ GH] 0有解, 则与实轴相交
1
不稳定的
G(s) T2s2 2Ts 1 振荡环节
0o ~ +180o
延迟环节(P204)
G(s) eTs
G(j) e jT
-1
A() 1
() T
j I m[G( j)]
0
1 Re[G(j)]
与其它环节串联时只影 响角度不影响模
开环幅相曲线的绘制例1 (P198)
G(s)
60
(s 2)(s 3)