反射棱镜物像坐标变化判断方法的比较研究

第三章 棱镜和棱镜和反射镜反射镜棱镜是光学系统中最常用的光学元件之一，它是由平面围成的光学单元，如图 3.1.1 (a)和 (b) 所示。

按照它们的应用领域可分为两大类。

1) 在光谱仪器类中，棱镜的作用是使光发生色散，也就是说把不同波长的光分散开。

这类棱镜通常称为光谱棱镜；2) 在绝大多数光学仪器中，特别是在成像仪器中所使用的棱镜主要利用光的反射来使光束平移、偏折或改变方向，或者使像的正倒发生改变，如图3.1.1 (b) 所示。

很显然，成像仪器中的棱镜和光谱仪器中的棱镜作用是不同的，前者需要尽量减少或消除光的色散而后者则充分利用棱镜的色散特性。

表面为平面的反射镜除了不具备使光色散的能力之外，它和棱镜的作用基本相同，用作使光束位移、偏折和改变方向，以及改变图像的正倒关系。

为了使入射到反射镜的光尽可能多地反射，必须在其基底材料 (抛光的玻璃或金属表面) 上镀以铝膜或银膜，反射率可达到90％或更高。

然而随着时间的推移，铝层和银层将会逐渐老化，反射率也要随之降低。

而反射棱镜则不同，大多数棱镜的反射面将使光发生全反射，理论上的反射率为100％。

这就不存在反射面的老化问题。

有的棱镜的反射面不符合全反射的条件，同样也需要镀反射膜，这样的膜层也会存在老化问题。

当然，棱镜也有缺点，由于光束在棱镜中要传播一定的长度，对棱镜材料的均匀性和光吸收要求很严格．否则会引起光程差，降低以像质量，引起光能损失等。

另外，与反射镜相比，棱镜的体积较大，重量较重，相应地，成本也会增加。

因此在应用时，要根据实际情况，权衡利弊，合理地选择棱镜和反射镜。

通常，当要求反射的光束口径较大时，最好选择反射镜。

反射光束的口径较小时，最好选择棱镜，因为大尺寸、高质量的棱镜材料很难挑选，即使找到了，成本也很高。

当然，这只是一般的情况，在进行光学设计时，要根据具体情况具体分析。

比如有时出于调控和稳定性考虑，虽然体积大些，也要选择棱镜。

3.1 色散棱镜图3.1.l (a) 是一个典型的色散棱镜。

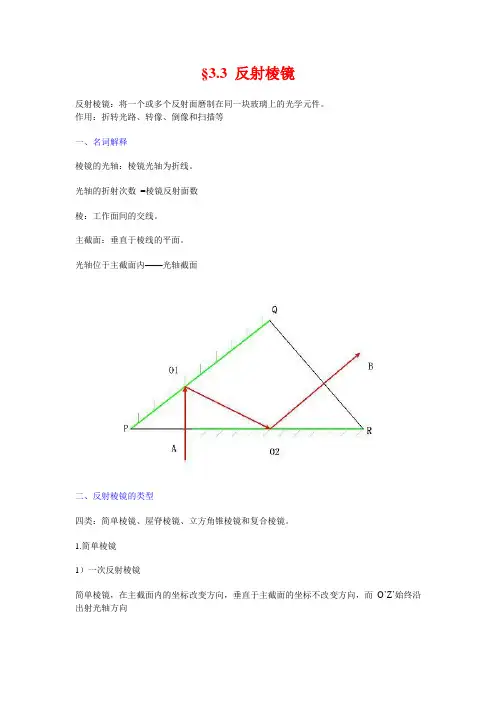
§3.3 反射棱镜反射棱镜：将一个或多个反射面磨制在同一块玻璃上的光学元件。

作用：折转光路、转像、倒像和扫描等一、名词解释棱镜的光轴：棱镜光轴为折线。

光轴的折射次数=棱镜反射面数棱：工作面间的交线。

主截面：垂直于棱线的平面。

光轴位于主截面内——光轴截面二、反射棱镜的类型四类：简单棱镜、屋脊棱镜、立方角锥棱镜和复合棱镜。

1.简单棱镜1）一次反射棱镜简单棱镜，在主截面内的坐标改变方向，垂直于主截面的坐标不改变方向，而O’Z’始终沿出射光轴方向2).二次反射棱镜（相当于一个双面镜）其出射光线与入射光线的夹角取决于两反射面的夹角，像与物一致，不存在镜像。

2．屋脊棱镜3．立方角锥棱镜重要特性：光线以任意方向从底面入射，出射光线始终平行于入射光线。

当棱镜绕其顶点旋转时，出射光线方向不变，仅产生一个位移。

4．棱镜的组合一复合棱镜1）分光棱镜2) 分色棱镜：主要用于彩色电视摄影机中。

3）转像棱镜主要特点：出射光轴与入射光轴平行，实现完全倒像，并能折叠很长的光路在棱镜中，可用于望远镜系统中实现倒像。

4）双像棱镜三、棱镜系统的成像方向判断判断原则：1．O’Z’坐标轴和光轴的出射方向一致。

2．垂直于主截面的坐标轴o’y’视屋脊面的个数而定，如果有奇数个屋脊面，则其像坐标轴方向与物坐标轴oy方向相反；没有屋脊面或屋脊面个数为偶数，则像坐标轴方向与物坐标轴方向一致。

3．平行于主截面的坐标轴o’x’的方向视反射面个数（屋脊面算二个反射面）而定。

如果物坐标系为右手坐标系，当反射面个数为偶数时，O’X’坐标轴按右手坐标系确定；而当反射面个数为奇数时，O’X’坐标轴依左手坐标系确定。

四、反射棱镜的等效作用与展开1、等效作用与展开方法：棱镜的等效作用：平面镜+平行平板棱镜展开方法：在棱镜上截面内，按反射面的顺序，以反射面与主截面的交线为轴，依次使上截面翻转180°，便可得到棱镜的等效平行平板。

2、棱镜等效平板厚度L的计算：L＝KD1）直角棱镜对于一次反射的直角棱镜，其光轴长度和结构参数KL＝D，K＝1对于二次反射直角棱镜（如图3-21a所示）L＝2D，K＝22)道威棱镜等效平行平板的厚度为（光轴不垂直于入射面和折射面）3)五角棱镜由可知，其光轴长度和结构参数分别为4）等腰棱镜设棱镜的顶角为β，L=D tgα=D ctg（β/2），K＝ctg(β／2）。

摘要：利用光线在三棱镜中折射时所产生的最小偏向角是测量棱镜玻璃折射率的一种经典实验方法,这种方法简单、明了,物理现象明显。

本文对测量棱镜的折射率的实验进行了详细的讨论，分步测量了棱镜角，最小偏向角和折射率，并分别进行了实验过程和数据分析。

就可以对测量棱镜角的折射率的实验方法有更好的掌握，并进一步学习分光计的使用方法。

最后，简单介绍了本文内容在普罗望远镜中的应用。

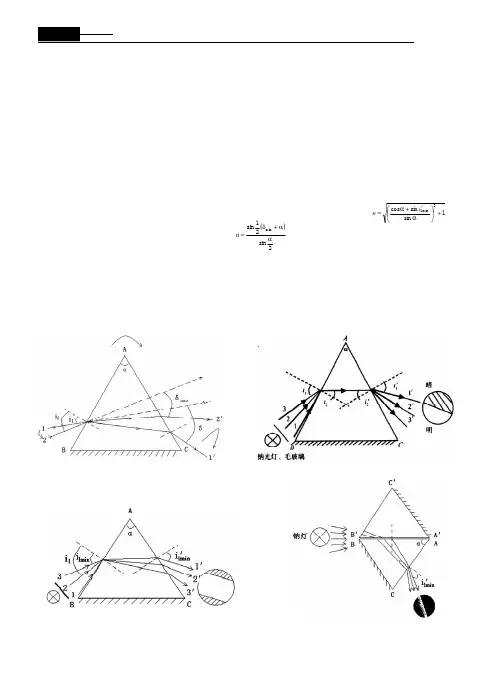
关键词：棱镜、折射率、最小偏向角目录一引言 (1)二棱镜角的测量 (2)2.1实验内容 (2)2.2 实验数据 (3)2.3 误差计算 (4)三最小偏向角 (5)3.1 实验内容 (5)3.2 实验数据 (6)3.3 误差计算 (7)四折射率的计算 (8)4.1 计算结果 (8)4.2 误差计算 (8)五实验结论 (9)六棱镜折射率在光学中的应用 (9)一引言如果一条光线对称地通过棱镜，也就是说，当它射到棱镜第一个面上的入射角等于第二个面上射出的出射角时（见图1），那么它所受到的偏转为最小（最小偏向角）。

在这种情况下，下面的等式成立：)2/ s i n(]2/)s i n[(γγδ+=n（1）其中n为冷静的折射率，γ为其棱镜角，δ为光线的最小偏向角。

因此，如果δ和γ为已知，则n就可计算。

γδ图一本实验的目的，是利用一架构造比较简单的分光计测量棱镜对钠黄光（D线）的折射率。

分光计的平行光管是固定的，望远镜只能绕分光计的垂直轴左右旋转，而且只有一个装有十字丝的普通目镜。

分光计上放置棱镜的载物平台也不能调节。

如果所有通过棱镜的光线都要满足最小偏向的条件，则这些光线必须互相平行的射入棱镜。

应用平行光管的目的就在于此；它是一个圆筒，在光进入的一端有一铅直狭缝，另一端装一会聚透镜。

如果狭缝的位置恰在透镜的焦平面上，则来自缝上各点的光线，在通过透镜后射出时，都将相互平行前进，如果把望远镜调节到无穷远，而且——不问中间是否有棱镜——把它放在平行光的光路中，那么当狭缝为单色光所照亮时，望远镜中就会清楚看到狭缝的象。

识别棱镜模型的方法一、引言棱镜模型是一种在光学实验中广泛应用的工具，它可以将光线分离成不同的波长，用于分析和研究光的性质。

本文将介绍几种常用的方法来识别棱镜模型，包括外观特征、光线折射和色散效应等方面。

二、外观特征识别棱镜模型通常由透明的玻璃或塑料制成，外形呈三棱柱状。

我们可以通过观察它的形状、透明度和表面质量等特征来判断是否为棱镜模型。

正规的棱镜模型应具有清晰的边缘、平整的表面和均匀的透明度。

此外，还可以通过观察它的标志或商标来确认是否为正品。

三、光线折射识别棱镜模型的主要功能是分离光线并使其发生折射。

我们可以利用这一特性来识别棱镜模型。

首先，将棱镜模型放置在光源附近，如太阳光或白炽灯光。

然后观察光线经过棱镜模型后的路径变化。

正常的棱镜模型会使光线发生折射并分散成不同的颜色，形成彩虹色的光谱。

如果光线经过棱镜模型后没有发生明显的折射或颜色分散现象，那么可能不是真正的棱镜模型。

四、色散效应识别色散是指光在不同介质中传播时由于折射率的差异而导致的波长分离现象。

棱镜模型可以利用色散效应将光分散成不同的颜色。

我们可以通过观察棱镜模型分散光线的效果来判断其是否为真正的棱镜模型。

将棱镜模型放置在光源附近，使光线通过棱镜模型后在墙壁或屏幕上形成光谱。

正规的棱镜模型会产生连续的光谱，从红色到紫色变化连续而不间断。

如果光谱不连续或存在缺失颜色，那么可能是假冒的棱镜模型。

五、使用光谱仪识别光谱仪是一种专门用于分析光谱的仪器，可以精确测量光线的波长和强度。

使用光谱仪可以更加准确地识别棱镜模型。

将棱镜模型放置在光谱仪的入射光束中，然后观察光谱仪的显示结果。

正规的棱镜模型应该能够产生明确的、连续的光谱，并且波长和强度的测量结果应该与理论值相符合。

如果测量结果与理论值有明显差异，那么可能是次品或假冒的棱镜模型。

六、结论通过外观特征识别、光线折射和色散效应观察以及使用光谱仪等方法，我们可以准确地识别棱镜模型。

在实际应用中，我们需要注意选择正规的棱镜模型，并且可以结合多种方法进行判断，以确保获得准确的实验结果和分析数据。