第4章:平面反射镜与棱镜
- 格式:pdf
- 大小:494.39 KB
- 文档页数:11



<<光学工程基础>>参考文献和习题1 光波、光线和成像参考文献:1. Walker Bruce H. Optical Engineering Fundamentals. Bellingham, Washington: SPIE,19982. 袁旭滄. 应用光学. 北京:国防工业出版社,19883. Ditteon Richard 著,詹涵菁译. 现代几何光学. 长沙:湖南大学出版社,20044. Smith W J. Modern Optical Engineering. Boston: The McGreaw-Hill Companies, Inc, 20015. 陈熙谋. 光学•近代物理. 北京:北京大学出版社,20026. 钟钖华. 现代光学基础. 北京:北京大学出版社,20037. Ghatak A K, Thyagarajan K. Contemporary Optics. New Y ork: Plenum Publishing Corporation, 19788. 彭旭麟,罗汝梅. 变分法及其应用. 武汉:华中工学院出版社,19839. Kidger Michael J. Fundamental Optical Design. Bellingham, Washington: SPIE,200210. Jenkins F , White H. Fundamentals of Optics. New Y ork: The McGreaw -Hill Companies, Inc, 197611. Hecht E. Optics. Reading, Massachusetts: Addison-Wesley, 1987习题:1. 简述几何光学的几个基本定律。
2. 简述成像的基本概念。
3. 光在真空中的速度是多少?在水中呢?在钻石中呢?4. 画出折射角i '随入射角i 变化的函数曲线,条件是1=n ,n '是下列值:(a) 1.333;(b)1.5163;(c) 1.78831。


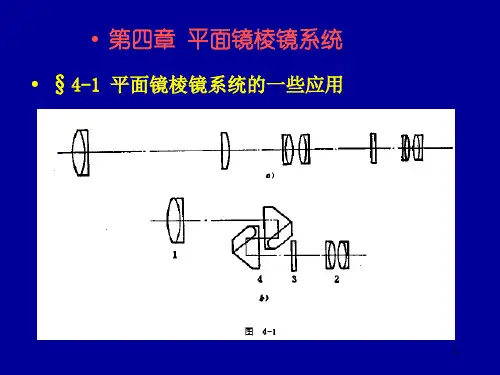



棱镜的原理、分类及⽤途推荐访问: 棱镜的⼀个显着特点是能够模仿作为⼀个平⾯镜系统,来模拟棱镜媒介中的光反射。
更换反射镜组件可能是最有⽤的棱镜应⽤,因为它们都折射或折叠光线和改变图像同位。
要实现类似单个棱镜的效果,通常需要使⽤多个反射镜。
因此,⽤⼀个棱镜来代替⼏个反射镜可减少潜在的校准错误,提⾼准确性和减少系统的规模和复杂性。
棱镜的发现 ⽜顿在1666年发现光的⾊散现象,⽽中国⼈在这⼀⽅⾯⼜领先于外国⼈。
中国⼈在公元10世纪,把经⽇光照射以后的天然透明晶体叫做“五光⽯”或“放光⽯”,认识到“就⽇照之,成五⾊如虹霓”。
这是世界上对光的⾊散现象的最早认识。
它表明⼈们已经对光的⾊散现象从神秘中解放出来,知道它是⼀种⾃然现象,这是对光的认识的⼀⼤进步。
⽐⽜顿通过三棱镜把⽇光分成七⾊,说明⽩光是由这七⾊光复合⽽成的认识早了七百年。
棱镜是透明材料制成的多⾯体,是重要的光学元件。
光线⼊射出射的平⾯叫侧⾯,与侧⾯垂直的平⾯叫主截⾯。
根据主截⾯的形状可分成三棱镜、直⾓棱镜、五⾓棱镜等。
三棱镜的主截⾯是三⾓形,有两个折射⾯,它们的夹⾓叫顶⾓,顶⾓所对的平⾯为底⾯。
根据折射定律光线经过三棱镜,将两次向底⾯偏折,出射光线与⼊射光线的夹⾓q叫做偏折⾓。
其⼤⼩由棱镜介质的折射率n和⼊射⾓i决定。
当i固定时,不同波长的光有不同的偏折⾓,在可见光中偏折⾓最⼤的是紫光,最⼩的是红光。
棱镜的作⽤ 1、常⽤数码设备:照相机、闭路电视、投影机、数码相机、数码摄录机、CCD镜头及各类光学设备。
2、科学技术:望远镜、显微镜、⽔准仪、指纹仪、枪械瞄准镜、太阳能转换器及各类测量仪器。
3、医疗仪器:膀胱镜、胃镜及各类激光治疗设备。
现代⽣活中,棱镜被⼴泛应⽤于数码设备、科学技术、医学仪器等领域。
⼀些光学实验也离不开棱镜。
消费者可以去当地光学仪器销售点进⾏购买。
当然,在互联⽹经济飞速发展的今天,我们也可以通过⽹络购物来买到所需要的东...查看全⽂与棱镜的发现|作⽤|制备相关⽂章棱镜的发现|作⽤|制备棱镜的分类棱镜的分类推荐访问: 棱镜共有四种主要类型:⾊散棱镜、偏转或反射棱镜、旋转棱镜和偏移棱镜。

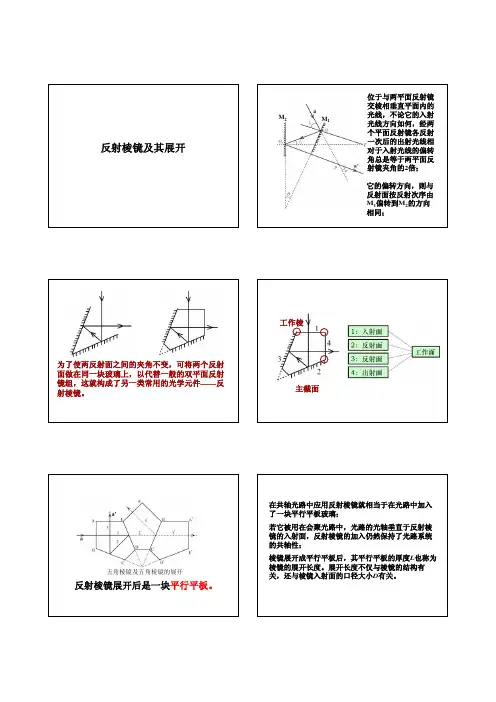
M 1
M 2
位于与两平面反射镜交棱相垂直平面内的光线,不论它的入射光线方向如何,经两个平面反射镜各反射一次后的出射光线相对于入射光线的偏转角总是等于两平面反射镜夹角的它的偏转方向,则与反射面按反射次序由M 相同;
为了使两反射面之间的夹角不变,可将两个反射面做在同一块玻璃上,以代替一般的双平面反射镜组,这就构成了另一类常用的光学元件——反主截面
工作棱
五角棱镜及五角棱镜的展开
反射棱镜展开后是一块平行平板。
1
αβγ===121'
AC h h du =−=ACD :111/'/CD AC u du u ==。
基本的光学结构光学是研究光的传播和性质的科学领域,而光学结构则是指用于控制光的传播和处理光的器件或系统。
本文将介绍几种基本的光学结构,包括透镜、棱镜、反射镜和光纤。
一、透镜透镜是一种光学元件,可以将光线聚焦或发散。
透镜的基本结构是两个曲面,其中一个或两个曲面是球面。
透镜根据其形状可分为凸透镜和凹透镜。
凸透镜能够将平行光线聚焦到焦点上,而凹透镜则能够使入射光线发散。
透镜的焦距决定了它的聚焦能力。
焦距较短的透镜能够使光线更快地聚焦,而焦距较长的透镜则使光线聚焦的位置更远。
透镜在光学领域有广泛的应用,如在相机、望远镜和显微镜中用于调节图像的清晰度和放大倍数。
二、棱镜棱镜是一种光学元件,具有三角形的截面。
它能够改变光线的传播方向和折射角度。
棱镜的基本结构是由两个平面和一个或多个折射面组成。
当光线从一种介质进入另一种介质时,会发生折射现象,棱镜利用这一现象来分离白光成各种颜色的光谱。
棱镜的折射角度取决于入射光线的入射角度和两种介质的折射率。
不同形状和材料的棱镜对光的分离效果也有所不同。
棱镜在光谱分析、光通信和光学仪器中起着重要的作用。
三、反射镜反射镜是一种光学元件,能够反射光线。
根据其反射面的形状,反射镜可分为平面镜、球面镜和非球面镜。
平面镜的反射面是一个平面,能够将入射光线反射为相同角度的出射光线。
球面镜和非球面镜的反射面是曲面,能够使光线聚焦或发散。
反射镜的反射效果取决于其表面的光学质量和反射涂层的特性。
高质量的反射镜具有高反射率和低散射率,能够产生清晰的反射图像。
反射镜在激光器、望远镜和光学测量中被广泛使用。
四、光纤光纤是一种能够传输光信号的细长结构,由光纤芯和包覆层组成。
光纤的核心是一个具有较高折射率的介质,而包覆层则是一个折射率较低的介质。
光线通过光纤时会发生全反射现象,从而沿着光纤传播。
光纤的基本结构使其具有很多优点,如高带宽、低损耗和抗干扰能力强。
光纤广泛应用于通信领域,用于传输电话、互联网和电视信号。
第四章 光学材料光学材料包含光学玻璃、工程塑料、天然晶体、人工晶体,以及若干种金属,如锆、银、金、镍、锗、铍及其若干金属和非金属氧化物。
作为光学材料,必须满足一些基本要求,如要具有良好的机械性能和化学稳定性,可加工性,具有均匀的折射率分布等。
用作镜头的光学材料,最重要的性能是折射率和透过率,这两个物理量都随波长变化,是波长的函数。
折射率随波长的变化称为色散。
影响光学材料透过率的主要因素有界面的反射损失和材料的吸收损失。
对反射用的光学材料而言,反射率是最重要的指标。
光学镀膜是在光学元件(透镜、棱镜、反射镜等)表面镀上单层或多层金属或非金属薄膜以改善光学性能,例如:增透膜,反射膜,半反半透膜,以及其它特殊用途的膜层。
§1.透射光学材料的特性一.光能的反射和吸收损失根据菲涅尔公式,光由普通介质材料表面反射的系数为:⎥⎦⎤⎢⎣⎡+-++-=)(tan )(tan )(sin )(sin 21/2/2/2/2I I I I I I I I R 式中I 和/I 是入射角和折射角。
当光垂直入射时:2/2/)()(n n n n R +-=式中:n 和/n 透镜表面前后介质的折射率。
对于透镜来说,表面的反射是一种光能损失。
对于由k 个表面组成的光学系统,不计材料的吸收损失时,其透过率为:kkt R T 11)1(=-=在光学系统中,胶合面两边介质的折射率差通常小于0.3,因此,反射损失通常小于%5.0,可以忽略不计。
光经过光学材料时,光能量难免不被吸收,光经过厚度为x mm 的光学材料,如果只计吸收,其透过率为axxet K -==2式中:a 为材料的吸收系数如果把光学材料表面的反射损失和材料内部的吸收损失均考虑在内,则光学系统的透过率是其表面透过率和材料内部透过率的乘积:axk xket t t K T T -⋅=⋅==1211上面只是适用于各反射面的反射率相同的情况。
对于空气中的单透镜来说,两个反射面(折射面)的反射率以及透过率不同,则透过率为212211R R K K T T T -=如果忽略材料的内部吸收(1=K ),则单透镜: 21211R R T T T -=二. 折射率光学材料的折射率是光学材料的另一个重要的指标参数,它是波长的函数,如图4-1所示。
M 1
M 2
位于与两平面反射镜交棱相垂直平面内的光线,不论它的入射光线方向如何,经两个平面反射镜各反射一次后的出射光线相对于入射光线的偏转角总是等于两平面反射镜夹角的它的偏转方向,则与反射面按反射次序由M 相同;
为了使两反射面之间的夹角不变,可将两个反射面做在同一块玻璃上,以代替一般的双平面反射镜组,这就构成了另一类常用的光学元件——反主截面
工作棱
五角棱镜及五角棱镜的展开
反射棱镜展开后是一块平行平板。
1
αβγ===121'
AC h h du =−=ACD :111/'/CD AC u du u ==。
图4-2 虚物经平面反射镜成实像图4-1 平面反射镜成像
左手系
右手系
图4-3 平面反射的物像空间对应关系
AFM 探针
卡文迪许测量万有引力常数
图4-5 双平面反射镜系统
M 1
M 2
图4-6 能将光路转折的双平面反射镜和反射棱镜
(a)双平面反射镜
为了使两反射面之间的夹角不变,可将两个反射(b)反射棱镜
主截面
工作棱
图4-7 五角棱镜及五角棱镜的展开
棱镜展开
若它被用在会聚光路中,光路的光轴垂直于反射棱镜的入射面,反射棱镜的加入仍然保持了光路系统靴形棱镜
图4-8 平行平板的成像
1
αβγ===(4-6)
图4-9 平行平板的延伸量
121'
AC h h du
=−=
/
CD AC u du
==
4.2.3 反射棱镜的正像作用
图4-10 反射棱镜的物方坐标系和像方坐标系
图4-11 一次反射的直角棱镜图4-12 确定y轴成像方向的另一
种方法、二次反射直角棱镜的成像分析
图4-13 二次反射的直角棱镜
互垂直的反射面依次反射而改变方向,从而得到
物体的相似像。
相互垂直
屋
,带有屋脊
屋脊
图4-15 直角屋脊棱镜的成像方向确定
图4-14 屋脊棱镜
图4-16 列曼屋脊棱镜的成像(a)
图4-16 列曼棱镜的成像(b)
图4-17 普罗棱镜
图4-18 转轴P与它经棱镜所成的像P'
其中N为棱镜的反射次数。
图4-19 立方体xyz与立方体经平面反射镜所成的像x'y'z'
4-20 向量g绕轴P旋转角Δθ后成向量i i
'b b
⎡⎤⎡⎤⎡⎤
图4-21 一次反射直角棱镜的成像
1)cos θαθ−Δ−Δ4-22棱镜转动引起的光轴偏
图4-23棱镜转动引起的像倾斜
图4-24 列曼屋脊棱镜成像
图4-25 K II-80°-90°空间棱镜
(a)轴测图
(c)顺x 方向
投影图
(b)顺z 方向
投影图
o 'cos100'==
i j
K 冕牌玻璃n 小V大F 火石玻璃n 大V小
、判断如图所示的光学系统的成像方向。
y
×x z。