8.1单一参数元件电路
- 格式:doc
- 大小:271.50 KB
- 文档页数:7


第8章 正弦交流电路学习目标掌握电阻、电感、电容元件电流、电压关系及功率关系掌握R —L —C 串联电路电压、电流关系,理解复阻抗概念。
学会分析方法。
掌握R-L-C 并联电路的电流、电压关系及计算。
掌握正弦交流电路的功率和功率因素。
了解提高功率因素的意义,并掌握提高功率因素方法及并联电容器的计算。
学法指导首先从单一元件的电压-电流的大小和相位关系介绍基础上引入相量式欧姆定律;抓住参考相量和单一元件的相量式欧姆定律,有相量图和相量式两种分析方法;结合阻抗的连接和相量式基尔霍夫定律以及直流电路的分析方法,可以学会分析RLC 串联和RLC 并联电路及一般交流电路的分析;从能量角度谈功率因数及其提高方法。
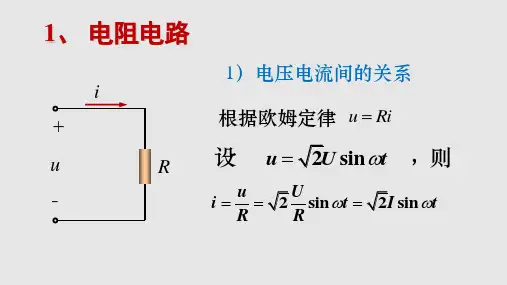
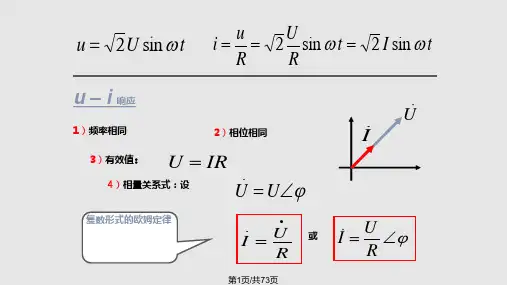
学习过程第一节 单一参数元件电路一、基础知识梳理1、纯电阻电路电压、电流的关系如果电压u =U m sin (ωt+ψu ),根据欧姆定律,通过电阻的电流瞬时值为i = =I m sin (ωt+ψi ) 数值关系:I m =U m /R 即: 欧姆定律相位关系:ψu =ψi 即:同相位即:两个复数比是一个实数。
这说明电阻元件上,瞬时值、最大值、有效值均符合欧姆定律。
2纯电感电路电压、电流的关系R u Rψt ωsin(U m m )+R IU I U m m ==R 0R I U o mm ==&&设:i=I m sin ωt ,ψi =0则由数学推导可知,u=I m ωLsin (ωt+90°)即电压的最大值为:U Lm =ωLI m 数值上: 欧姆定律式中X L =ωL =2πfL X L 称为电感抗,简称感抗,它的单位是欧姆。
相位关系:电压超前电流90°相量关系:则:其中:J 为旋转因子结论: ⑴瞬时值不符合欧姆定律; ⑵最大值、有效值之间具有欧姆定律;⑶JX L =JWL 是感抗的复数形式;⑷相位上电压相量超前电流相量90°。
3、纯电容电路电压、电流的关系在前面我们已经学过,稳压直流电不能通过电容器,但在电容器充放电过程中,却会引起电流。






8.1 单一参数的交流电路考纲要求:1、熟练掌握纯电阻电路、纯电感电路和纯电容电路中电流和电压的关系及功率。
2、理解电阻、电感和电容在直流电路和交流电路中的作用。
3、理解正弦交流电路中感抗、容抗、有功功率、无功功率、视在功率、功率因数、阻抗、复数阻抗、电压三角形、电流三角形、阻抗三角形、功率三角形的概念。
教学目的要求:1、掌握单一参数电路中电压与电流的大小关系、相位关系和功率关系2、掌握单一参数的复数形式教学重点:掌握单一参数电路中电压与电流的大小关系、相位关系和功率关系教学难点:单一参数电路的复数形式课时安排:3节 课型:复习教学过程:【知识点回顾】一、纯电阻电路1、定义: 。
2、纯电阻电路中电压与电流的关系(1)大小关系:I= (2)相位关系:电压与电流 电压与电流的波形图和相量图:(3)纯电阻电路的复阻抗Z R =∙∙I U R =3、纯电阻电路中的功率(1)有功功率: 电阻消耗的功率P=(2)无功功率: (3)视在功率:二、纯电感电路1、定义: 。
2、纯电感电路中,电感对交流电的阻碍作用来源:感抗: 即X L = = (Ω)2、纯电感电路中电压与电流的关系(1)大小关系:I= (2)相位关系: 超前 900 电压与电流的波形图和相量图(3)纯电感电路的复阻抗Z L =∙∙I U L = 3、纯电感电路中的功率(1)有功功率: P= = (2)无功功率: Q= =(3)视在功率:S= =三、纯电容电路1、定义: 。
2、纯电容电路中,电容对交流电的阻碍作用来源: 。
容抗: 。
即X C = = (Ω)2、纯电容电路中电压与电流的关系(1)大小关系:I= (2)相位关系: 超前 900 电压与电流的波形图和相量图(3)纯电容电路的复阻抗Z L =∙∙I U C =3、纯电容电路中的功率(1)有功功率: P= = (2)无功功率: Q= =(3)视在功率: S= =【课前练习】一、判断题:1、在纯电阻电路中电阻值与频率反正比。

1.通过课后练习复习正弦量的旋转矢量表示。
2.通过提问复习电路基本定律、功率计算。
【新课讲授】:一 单一理想元件的交流电路纯电阻电路一、电流、电压间的数量及相位关系演示实验一:如图1所示连接好电路,改变信号发生器的输出电压和频率,观察、记录电流表和电压表的读数情况,研究电流、电压间的数量关系。
注意分析电流、电压关系是否受电源频率变化影响。
现象:从电流表,电压表的读数看出,电压有效值与电流有效值之间成正比(与电源频率变化无关),比值等于电阻的阻值。
分析:实验表明电压有效值与电流有效值服从欧姆定律,即R U I R =其电压、电流最大值也同样服从欧姆定律,即R U I R m m =演示实验二:将超低频信号发生器的频率选择在6Hz 左右,当开关S 闭合以后,仔细观察直流电流表、直流电压表的指针变化情况,及其之间的时间关系。
现象:电流表和电压表的指针同时到达左边最大值,同时归零,又同时到达右边最大值,即电流表与电压表同步摆动。
分析:实验表明纯电阻电路中,电流与电压相位相同,相位差为零,即0=-=i u ϕϕϕ小结:纯电阻电路中,电压与电流同相,电压瞬时值与电流瞬时值之间服从欧姆定律,即图1 纯电阻电路R u i R =注意:在交流电路中,上式是纯电阻电路所特有的公式,只有在纯电阻电路中,任一时刻的电压、电流瞬时值服从欧姆定律。
教师总结:根据我们刚才所作的演示实验结果表明,在纯电阻电路中电流、电压的瞬时值、最大值、有效值之间均服从欧姆定律,且同相。
我们可以用如下图2波形图、图3旋转矢量图来形象地表述这种关系。
二、纯电阻电路的功率1、瞬时功率某一时刻的功率叫做瞬时功率,它等于电压瞬时值与电流瞬时值的乘积。
瞬时功率用小写字母p 表示ui p = (式5-9)以电流为参考正弦量)sin(t I i m ω=,则电阻R 两端的电压为t U u m R ωsin =,将i ,u R 带入(式5-9)中t UI UI t I t U uip m m ωωω2cos )sin()sin(-=⋅== (式5-10)分析:瞬时功率的大小随时间作周期性变化,变化的频率是电流或电压的2倍,它表图2 纯电阻电路波形图图3 纯电阻电路旋转矢量图图4 纯电阻电路功率曲线示出任一时刻电路中能量转换的快慢速度。
单一参数的交流电路一、电阻电路电阻元件的电压和电流关系如图1-2-7所示。
图1-2-7 电阻1.伏安关系设电阻元件中电流为根据欧姆定律:则图1-2-8 电阻伏安波形图图1-2-9 电阻相量图2.相量关系结论:(1)电阻元件两端的电压和电流的相量值、瞬时值、最大值、有效值均服从欧姆定律。
(2)电阻两端的电压与电流同相(电压电流的复数比值为一实数)。
二、电阻元件的功率1.瞬时功率(instantaneous power)该电阻元件的电流:设则:其波形如图1-2-10所示。
由图1-2-10可见,电阻元件的瞬时功率大于(等于)零。
图1-2-10 电阻瞬时功率波形图2.平均功率(有功功率)瞬时功率在一个周期内的平均值(见图1-2-11):图1-2-11 电阻平均功率波形图注意:通常铭牌数据或测量的功率均指有功功率。
【例2.9】电阻元件电压、电流的参考方向关联。
=1.414sin(ωt+30)A 已知:电阻R=100 Ω,通过电阻的电流iR求:(1)电阻元件的电压和u ;RP ;(2)电阻消耗的功率R(3)画相量图。
解:(1)(2)(3)相量图如图1-2-12所示。
三电感电路(一)电磁感应定律1831 年,法拉第从一系列实验中总结出:当穿过某一导电回路所围面积的磁通发生变化时,回路中即产生感应电动势及感应电流,感应电动势的大小与磁通对时间的变化率成正比。
这一结论称为法拉第定律。
这种由于磁通的变化而产生感应电动势的现象称为电磁感应现象。
1834 年,楞次进一步发现:闭合导体回路中的感应电流,其流向总是企图使感应电流自己激发的穿过回路面积的磁通量能够抵消或补偿引起感应电流的磁通量的增加或减少。
这一结论即是楞次定律。
法拉第定律经楞次补充后,完整地反映了电磁感应的规律。
电磁感应定律指出:如果选择磁通Φ的参考方向与感应电动势e 的参考方向符合右手螺旋关系,如右图所示。
对一匝线圈来说,其感应电动势可以描述为式中,磁通的单位为韦伯(Wb),时间的单位为秒(s),电动势的单位为伏特(V)。
第8章 正弦交流电路
学习目标
掌握电阻、电感、电容元件电流、电压关系及功率关系
掌握R —L —C 串联电路电压、电流关系,理解复阻抗概念。
学会分析方法。
掌握R-L-C 并联电路的电流、电压关系及计算。
掌握正弦交流电路的功率和功率因素。
了解提高功率因素的意义,并掌握提高功率因素方法及并联电容器的计算。
学法指导
首先从单一元件的电压-电流的大小和相位关系介绍基础上引入相量式欧姆定律;抓住参考相量和单一元件的相量式欧姆定律,有相量图和相量式两种分析方法;结合阻抗的连接和相量式基尔霍夫定律以及直流电路的分析方法,可以学会分析RLC 串联和RLC 并联电路及一般交流电路的分析;从能量角度谈功率因数及其提高方法。
学习过程
第一节 单一参数元件电路
一、基础知识梳理
1、纯电阻电路电压、电流的关系
如果电压u =U m sin (ωt+ψu ),根据欧姆定律,通过电阻的电流瞬时值为
i = = =I m sin (ωt+ψi ) 数值关系:I m =U m /R 即:
相位关系:ψu =ψi 即:同相位
即:两个复数比是一个实数。
这说明电阻元件上,瞬时值、最大值、有效值均符合欧姆定律。
2纯电感电路电压、电流的关系
R u R
ψt ωsin(U m m )+R I U I U m m ==R 0R I U o m
m ==&&
设:i=I m sin ωt ,ψi =0则由数学推导可知,
u=I m ωLsin (ωt+90°)
即电压的最大值为:
U Lm =ωLI m 数值上: 欧姆定律
式中X L =ωL =2πfL X L 称为电感抗,简称感抗,它的单位是欧姆。
相位关系:电压超前电流90°
相量关系:
则:
其中:J 为旋转因子
结论:
⑴瞬时值不符合欧姆定律;
⑵最大值、有效值之间具有欧姆定律;
⑶JX L =JWL 是感抗的复数形式;
⑷相位上电压相量超前电流相量90°。
3、纯电容电路电压、电流的关系
在前面我们已经学过,稳压直流电不能通过电容器,但在电容器充放电过程中,却会
引起电流。
当电容器接到交流电路中时,由于外加电压不断变化,电容器就不断充放电,电路中就不断有电流流过。
这就称为交流电通过电容器。
若u=U m sin ωt 则由数学推导可知,
i=CU Cm ωcos ωt
电流的最大值为:
I m =ωCU cm
数值上:
t
Δi ΔL dt di L u ==L m
m X L ωI U I U ===οο&&90U U ,0I I
==L L jX 90X 90I U 0I 90U I U ====οοοο&&&&I
&C
m m X C ω1I U I U ===
式中X C 称为电容抗,简称容抗。
上式表明:在纯电容电路中,电流的有效值等于它两端电压的有效值除以它的容抗。
容抗是用来表示电容器对电流阻碍作用大小的一个物理量。
它的大小可用公式计算,单位是欧姆。
容抗的大小与频率及电容量成正比。
当电容器的容量一定时,频率f 愈高则容抗X C 愈小。
在直流电路中,因频率f=0,故电容器的容抗等于无限大。
这表明,电容器接入直流电路时,在稳态下是处于断路状态。
相位上:ψ当ψu =0时,ψi =90°。
也就是说电容元件的电流要比它两端的电压超前
90°,或者说,电压总是滞后电流90°。
即ψi =ψu +90°。
这就是电流与电压的相位关系。
相量关系:
结论: ⑴电流和电压瞬时值的关系是微分或积分关系;
⑵引入容抗(X c )、正弦交流电流、电压的最大值、有效值符合欧姆定律;
⑶-jX c 复容抗;
⑷相位上电流相量超前电压相量90°。
二、应用举例
应用一:有一个220V 、100W 的电烙铁,接在220V 、50Hz 的电源上。
要求:
(1)绘出电路图,并计算电流的有效值。
(2)计算电烙铁消耗的电功率。
(3)画出电压、电流相量图。
应用分析:
解:(1)电路如图,
484100
2202
2===P U R (Ω) ΩfC π21C ω1X C ==c c jX 90X 90
I 0U I U -=-==οοο&&I &U
&οο&&90I I ,0U U ==
45.0484220===R U I (A) (2)10045.0220=⨯==UI P (W) (3)相量图如图所示。
例1:把L =51mH 的线圈(线圈电阻极小,可忽略不计),接在u =2202sin(314t +60o) V 的交流电源上,试计算:
(1)X L 。
(2)电路中的电流i 。
(3)画出电压、电流相量图。
解:(1)16105131423=⨯⨯==-fL X L π(Ω)
(2)︒-=︒
︒==30/75.1390/1660/220L jX U I &&(A ) )30314sin(275.13︒-=t i (A )
(3)相量图如图所示。
举一反三:把C =140μF 的电容器,接在u =102sin314t V 的交流电路中,试计算:
(1)X C 。
(2)电路中的电流i 。
(3)画出电压、电流相量图。
巩固训练
1、在纯电阻正弦交流电路中,已知路端电压u=102sin(ωt-6
π)伏,电阻R=10欧,那么电流i= ,电压与电流的相位差φ= 电阻上消耗的功率P= 瓦。
2、 在纯电阻电路中,下列各式正确的是: ( )
A 、i=R U ;
B 、I= R U ;
C 、.I =R
u ; D 、i=R U m 3、如图所示电路中,电阻R=2K ,接到正弦电压上,若最大值为537V ,则电流表的读数为 ,电压表的读数为 。
4.在纯电感电路中,电流与电压的频率 ,电压 电流90°。
5.把一个的电感元件接到频率为50HZ ,电压有效值为10V 的正弦交流电上,问电流是多少如果保持电压不变,而电源频率变为5KHZ ,这时电流将为多少
6.纯电阻元件的复阻抗Z= ,纯电感元件的复阻抗Z= ,纯电容元件的复阻抗Z= 。
7.纯电阻电路复数形式的欧姆定律为 ,纯电感电路复数形式的欧姆定律为 纯电容电路复数形式的欧姆定律为 。
8.正弦交流电压V t u )3100sin(220ππ+
=,将它加在100Ω的电阻两端,每分钟放出的
热量为 ;将它加在F C μπ1
=的电容器两端,通过该电容器的电流瞬时值表达式为 ;将它加在H L π1=
的电感两端,通过该电感的电流瞬时值表达式
为 。
三、课后巩固 1、如图所示,已知R 1= R 2=2k Ω,u = 220√2sin(314t + 90) V ,求电流表、电压表的读数。
2、一个电阻为10 k Ω的负载,接到u = 220√2sin(314t + 45) V 的交流电源上,求(1)流过负载的电流为多大(2)写出电流的瞬时值的表达式,并画出它们的波形图。
(3)电阻消耗的功率P 为多少
3.已知某电感线圈感抗X L =20欧,若加在该线圈两端正弦交流电压为u = 50sin(314t -60) ,则流过该线圈的电流为i= 。
4.已知在某纯电感电路中加上220V 的市电,设电压的初相为45,感抗为5欧,写出电流的瞬时值表达式和相量式,画出相量图。
5.已知C=10PF ,当f1=106HZ ,则X C = Ω,当f2=103HZ ,则X C = Ω。
6.在64μF 电容器两端加。
设电压u 和电流i 的方向一致,则在t=T/4时电流的瞬时值为i= A ,电压的瞬时值u= V 。
7.对于直流来讲,即f=0时,此时,X L = ,X C = ;对于交流来讲,即f ≠0时,若f 增加时,此时,X L = ,X C = 。
举一反三:
解:(1)7.22101403141216
=⨯⨯==-fC X C π(Ω) (2)︒=︒
-︒=-=90/44.090/7.220/10C jX U I &&(A ) )90314sin(244.0︒+=t i (A )
(3)相量图如图所示。
巩固训练
1、2sin(ωt-/6) 0 100W
2、 B
3、 380V
4、 相同 超前
5、
6、 R j ωL 1/j ωC
7、 R U I /..= jXL U I /..= jXC U I -=/.
.
8、 14520J *10-2sin(100t+5/6)A (100t-1/6)A
课后巩固
1、55mA 110V
2、I=22 mA i=222sin(314t+45o ) mA P= mW
3、i=(314t-150o )A
4、i=442sin(314t-45o )A .
I=44∠-/4
5、Ω15900KΩ
6、0 220
7、0 2fL 增大1/2fC 减小。