第六章 正弦交流电剖析

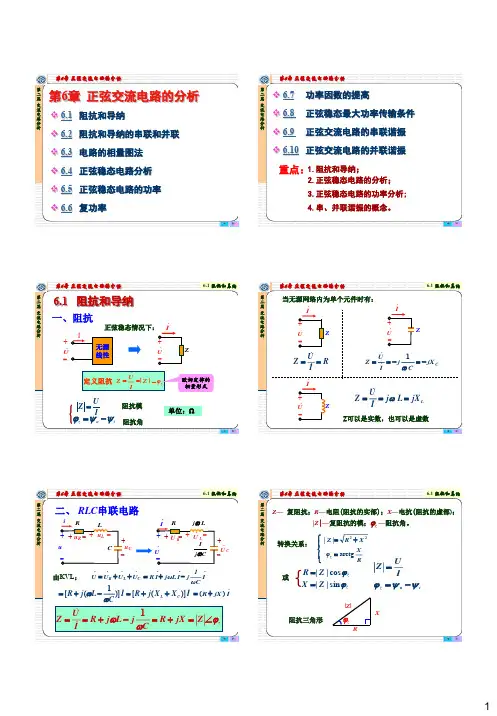
相量法复数的表达式一个复数Z 有以下四种表达式。

1．直角坐标式(代数式)Z = a + j b式中，a 叫做复数Z 的实部，b 叫做复数Z 的虚部。

在直角坐标系中，以横坐标为实数轴，纵坐标为虚数轴，这样构成的平面叫做复平面。

任意一个复数都可以在复平面上表示出来。

例如复数A = 3 + j2在复平面上的表示如图9-1所示。

2．三角函数式在图9-1中，复数Z 与x 轴的夹角为 θ，因此可以写成Z = a + j b = |Z |(cos θ + jsin θ)式中|Z |叫做复数Z 的模，又称为Z 的绝对值，也可用r 表示，即22|Z | b a r +==θ 叫作复数Z 的辐角，从图9-1中可以看出⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧<<+π-><-π>=)0 0( arctan )0 0( arctan )0( arctan b a a b b a a b a a b ，，θ 复数Z 的实部a 、虚部b 与模|Z |构成一个直角三角形。

3．指数式利用欧拉公式，可以把三角函数式的复数改写成指数式，即Z =|Z |(cos θ + jsin θ) =|Z |e j θ4．极坐标式(相量式)复数的指数式还可以改写成极坐标式，即Z =|Z |/θ以上这四种表达式是可以相互转换的，即可以从任一个式子导出其它三种式子。

复数的四则运算设Z 1= a + j b =|Z 1|/α ，Z 2 = c + j d = |Z 2|/β ，复数的运算规则为1．加减法 Z 1 ± Z 2 = (a ± c ) + j(b ± d )2．乘法 Z 1 · Z 2 = |Z 1| · |Z 2|/α + β3．除法21Z Z =4．乘方 nn Z Z 11=/n α正弦量的复数表示法正弦量可以用复数表示，即可用振幅相量或有效值相量表示，但通常用有效值相量表示。

单相正弦交流电路的基本知识本章的学习重点：● 正弦交流电路的基本概念；● 正弦量有效值的概念和定义，有效值与最大值之间的数量关系；● 三大基本电路元件在正弦交流电路中的伏安关系及功率和能量问题。

3．1 正弦交流电路的基本概念1、学习指导（1）正弦量的三要素正弦量随时间变化、对应每一时刻的数值称为瞬时值，正弦量的瞬时值表示形式一般为解析式或波形图。

正弦量的最大值反映了正弦量振荡的正向最高点，也称为振幅。

正弦量的最大值和瞬时值都不能正确反映它的作功能力，因此引入有效值的概念：与一个交流电热效应相同的直流电的数值定义为这个交流电的有效值。

正弦交流电的有效值与它的最大值之间具有确定的数量关系，即I I 2m 。

周期是指正弦量变化一个循环所需要的时间；频率指正弦量一秒钟内所变化的周数；角频率则指正弦量一秒钟经历的弧度数，周期、频率和角频率从不同的角度反映了同一个问题：正弦量随时间变化的快慢程度。

相位是正弦量随时间变化的电角度，是时间的函数；初相则是对应t=0时刻的相位，初相确定了正弦计时始的位置。

正弦量的最大值（或有效值）称为它的第一要素，第一要素反映了正弦量的作功能力；角频率（或频率、周期）为正弦量的第二要素，第二要素指出了正弦量随时间变化的快慢程度；初相是正弦量的第三要素，瞎经确定了正弦量计时始的位置。

一个正弦量，只要明确了它的三要素，则这个正弦量就是唯一地、确定的。

因此，表达一个正弦量时，也只须表达出其三要素即可。

解析式和波形图都能很好地表达正弦量的三要素，因此它们是正弦量的表示方法。

（2）相位差相位差指的是两个同频率正弦量之间的相位之差，由于同频率正弦量之间的相位之差实际上就等于它们的初相之差，因此相位差就是两个同频率正弦量的初相之差。

注意：不同频率的正弦量之间是没有相位差的概念而言的。

相位差的概念中牵扯到超前、滞后、同相、反相、正交等术语，要求能够正确理解，要注意超前、滞后的概念中相位差不得超过±180°；同相即两个同频率的正弦量初相相同；反相表示两个同频率正弦量相位相差180°，注意180°在解析式中相当于等号后面的负号；正交表示两个同频率正弦量之间的相位差是90°。

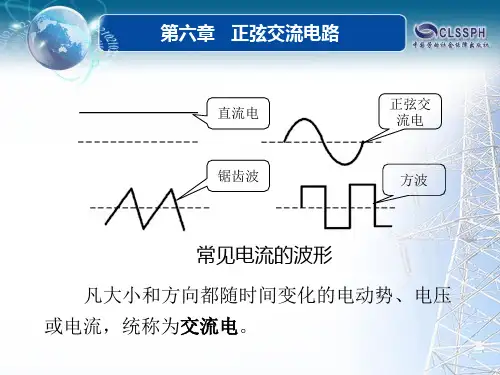
正弦交流电路分析_正弦量的三要素正弦沟通电路简称沟通电路，是实际应用中最常用的一种电路。

正弦沟通电是最常见的一种电源。

其特点是大小和方向均按正弦规律变化。

正弦沟通电动势、电压、电流统称为正弦量。

争论正弦沟通电路的重要性:1.应用广泛. 在强电方面，电能的产生、输送和安排几乎采纳的都是正弦沟通电。

在弱电方面也常用正弦信号作为信号源。

2.正弦沟通电的优点利用变压器可以将正弦沟通电压便利地进行上升和降低，既简洁敏捷又经济。

正弦量变化平滑，在正常状况下不会引起过电压而破坏电气设备的绝缘。

电子技术中大量存在的非正弦周期信号，可通过傅里叶级数分解成一系列不同频率的正弦重量。

这类问题可通过叠加定理按正弦电路的方式处理…。

弦正量有以下多种表示法:1、三角函数表示2、波形表示3、旋转有向线段表示4、向量表示（1）向量图（2）向量式（代数式、指数式、极坐标式）正弦量的参考方向:正弦量的参考方向是指正半周时的方向。

1、正弦量的三要素角频率（弧度/秒）ω,幅值（最大值）Im,初相角φ1.角频率、频率和周期周期（Period）：T 变化一周所需的时间单位：秒( s )，毫秒( ms )...2. 幅值、有效值(Amplitude and Virtual Value)反映正弦量变化的幅度用Im 表示。

在工程应用中常用有效值表示正弦量的大小。

沟通仪表指示的读数、电器设备的额定电压、额定电流都是指有效值。

民用电220 V、380 V指的也是供电电压的有效值。

有效值定义：让正弦沟通电和直流电分别通过两个阻值相等的电阻，假如在相同的时间T 内，两个电阻消耗的能量相等，那么，就称该直流电的值为正弦沟通电的有效值。

取一个周期（T ）的信号来考虑:有效值定义3.相位和相位差(Phase and Phase difference)说明：φ反映正弦量变化的起始位置两个同频率正弦量之间的相位差= 初相位之差计时起点不同，正弦量的初相位不同，但同频率正弦量之间的相位差不会转变，总是等于初相位之差。