第四章 斜齿行星齿轮传动系统动力学分析精选

机械齿轮传动系统的动力学分析与优化齿轮传动是一种常见的动力传递机构，具有传递力矩大、传动效率高等优点，在工业生产中得到广泛应用。

但是，由于齿轮传动系统存在着一些固有的问题，如齿轮啮合时的振动和噪音、齿面磨损等，因此对其进行动力学分析和优化是非常重要的。

1. 动力学分析1.1 齿轮啮合的动力学模型齿轮啮合过程中，齿轮之间存在着瞬时的压力、速度和加速度变化。

可以通过建立齿轮啮合的动力学模型来分析其动态特性。

常用的方法包括等效单齿转动法和有限元法。

通过分析齿轮齿面接触应力和应力分布，可以预测系统的振动和噪音水平，为后续的优化提供依据。

1.2 动力学参数的测量和计算为了进行动力学分析，需要测量和计算一些关键参数，如齿轮的啮合刚度、传递误差、滚子轴承的刚度等。

其中，传递误差是影响齿轮传动系统性能的重要因素之一，其大小与齿轮加工质量、啮合配合、齿轮轴向和径向跳动等因素有关。

通过合理的测量方法和计算模型，可以准确地获取这些参数，并对系统进行分析。

2. 动力学优化2.1 齿轮传动系统的振动和噪音控制由于齿轮啮合时的动态特性，齿轮传动系统常常会产生振动和噪音。

为了减小振动和噪音的水平，可以从多个方面进行优化，如合理设计齿形、减小啮合间隙、提高齿轮加工精度等。

此外，也可以采用减振装置，如弹性联轴器、减震器等，来降低系统的振动能量传递。

2.2 传动效率的提高传动效率是衡量齿轮传动系统性能的重要指标之一。

为了提高传动效率，可以从减小传动误差、改善齿轮表面质量、减小传动间隙等方面入手。

此外，合理选择润滑方式和润滑油，也可以有效地降低系统的摩擦和磨损，提高传动效率。

2.3 齿轮传动系统的寿命预测齿轮传动系统的寿命是评估其使用寿命和可靠性的重要指标。

通过综合考虑齿轮的强度、疲劳寿命和磨损等影响因素，可以建立寿命预测模型，对系统进行寿命预测和优化设计。

此外，还可以通过监测齿轮的工作状态和健康状况，进行实时的故障诊断和维护。

3. 总结齿轮传动系统的动力学分析和优化是提高其性能和可靠性的重要手段。

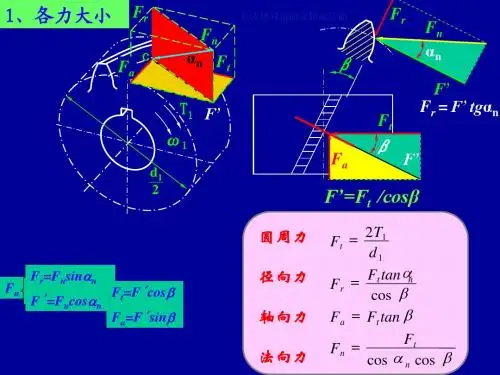
图１　单对啮合齿轮三维模型 图２　直齿圆柱齿轮轮齿受力图根据力平衡条件和各力之间的几何关系计算齿轮所受力，即：圆周力：1122100010020tT F N N d ×=== （1）图３　圆周动态啮合力仿真曲线图４　径向动态啮合力仿真曲线图５　法向动态啮合力仿真曲线通过图6可得出主动轮2所受力矩，而齿轮1负载力矩为1000N·mm。

齿轮2所受力矩根据力的大小围绕1000N·mm波动，所以齿轮在传动过程中所输出力矩并不是一个恒定值，而是会随齿轮动态啮合力大小不断变化。

图６　齿轮２所受力矩仿真曲线图７　齿轮１角速度仿真曲线４　结语首先，根据齿轮传动过程中所受力的大小，由公式计算齿轮的静态啮合力。

其次，利用仿真软件对齿轮实际运动过程中的工况进行动力学仿真，得到实际工况下的动态啮合力和速度图像。

最后，通过得到的动力学图像与静力学条件下计算得到的静态力进行对比验证，并分析了齿轮运动过程中的工况。

参考文献[1]夏永.基于ADAMS的风电齿轮箱动力学仿真分析[D].大连：大连理工大学，2014.[2]江志祥，朱增宝，季军.基于UG与ADAMS的行星齿轮减速器动力学仿真分析[J].煤矿机械，2013，（6）：43-44.[3]张白鸽，岑海堂.基于ADAMS的椭圆齿轮动力学仿真分析[J].机械工程与自动化，2016，（2）：98-100.[4]陈涛.风力发电机组齿轮箱传动系统动力学仿真与分析[D].北京：华北电力大学，2015.[5]钱直睿，黄晓燕，李明哲，李东平.多轴齿轮传动系统的动力学仿真分析[J].中国机械工程，2006，（3）：241-244.Dynamic Analysis of Gear TransmissionＭＡ　Ｍｉｎｂｏ，　ＣＵＩ　Ｈｕａｎｙｏｎｇ，　ＷＡＮＧ　Ｃｈｅｎｇ，　ＳＵＮ　Ｈａｏ（Ｓｃｈｏｏｌ　ｏｆ　Ｍｅｃｈａｎｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，　Ｕｎｉｖｅｒｓｉｔｙ　ｏｆ　Ｊｉｎａｎ，　Ｊｉｎａｎ　２５００２２）Abstract:　Ｉｎ　ｔｈｉｓ　ｐａｐｅｒ，　ａ　ｐａｉｒ　ｏｆ　ｍｅｓｈｉｎｇ　ｔｅｅｔｈ，　ｆｏｒ　ｅｘａｍｐｌｅ，　ｔｈｒｏｕｇｈ　ｔｈｅ　ｆｏｒｍｕｌａ　ｔｏ　ｃａｌｃｕｌａｔｅ　ｔｈｅ　ｓｔａｔｉｃ　ｆｏｒｃｅ　ｂｅｔｗｅｅｎ　ｔｈｅ　ｔｅｅｔｈ，　ａｎｄ　ｔｈｅ　ｅｓｔａｂｌｉｓｈｍｅｎｔ　ｏｆ　ｉｔｓ　ｔｈｒｅｅ－ｄｉｍｅｎｓｉｏｎａｌ　ｍｏｄｅｌ，　ｉｎ　ｔｈｅ　ｓｉｍｕｌａｔｉｏｎ　ｓｏｆｔｗａｒｅ　ｆｏｒ　ｉｔｓ　ｄｙｎａｍｉｃ　ｓｉｍｕｌａｔｉｏｎ．　Ｔｈｅ　ｒｅｓｕｌｔｓ　ｏｆ　ｓｉｍｕｌａｔｉｏｎ　ａｒｅ　ｃｏｍｐａｒｅｄ　ｗｉｔｈ　ｔｈｏｓｅ　ｏｂｔａｉｎｅｄ　ｂｙ　ｓｔａｔｉｃｓ，　ａｎｄ　ｔｈｅ　ｌａｗｓ　ｏｆ　ｍｏｔｉｏｎ　ａｒｅ　ｆｏｕｎｄ．Key words：ｇｅａｒ　ｆｏｒｃｅ，　ｄｙｎａｍｉｃ　ｍｅｓｈｉｎｇ　ｆｏｒｃｅ，　ｄｙｎａｍｉｃ　ｓｉｍｕｌａｔｉｏｎ。

基于多体动力学的行星齿轮传动系统研究行星齿轮传动系统是一种高效率、高精度的传动装置，广泛应用于机械工程和自动化领域。

在过去的几十年里，随着计算机技术的飞速发展，研究人员开始更深入地研究行星齿轮传动系统的动力学行为。

多体动力学是一种用于描述和分析系统中多个物体之间相互作用的数学模型。

本文将探讨如何利用多体动力学方法研究行星齿轮传动系统。

首先，行星齿轮传动系统由太阳齿轮、行星齿轮和内齿轮组成。

太阳齿轮位于行星轴的中心，内齿轮围绕太阳齿轮旋转，行星齿轮与太阳齿轮和内齿轮相连接。

传动比由齿轮的尺寸和齿数决定，控制了输出轴的旋转速度和力矩。

在多体动力学模型中，每个齿轮被建模为一个刚体，其运动由牛顿力学定律描述。

通过建立各个齿轮的运动方程，并考虑他们之间的接触和相互作用力，可以分析传动系统的动力学行为。

其中的关键问题是确定行星轮和内齿轮的轨迹和接触点，以及计算系统中的力和力矩。

在传动系统中，齿轮的接触问题是一个重要的研究方向。

行星齿轮传动系统的齿轮接触分析包括接触点位置确定和接触力计算两个方面。

接触点位置的确定需要考虑到齿轮的几何参数和初始位置，可以通过数值求解等方法得到。

接触力的计算涉及到齿轮之间的接触力和支撑力，并且需要考虑到张力、撞击和摩擦等因素。

此外，传动系统的动力学分析还需要考虑到诸如振动、噪声和寿命等方面的问题。

通过对行星齿轮传动系统的多体动力学模型进行仿真和分析，可以评估系统的性能和可靠性，并优化设计和参数选择。

例如，在避免共振、降低振动和噪声水平以及提高传动效率方面，多体动力学分析可以发挥重要作用。

综上所述，基于多体动力学的行星齿轮传动系统研究为我们深入理解传动机构的运行原理和行为提供了一个有效的方法。

通过对齿轮接触、力学行为和系统性能进行建模和仿真，我们可以更好地优化传动系统的设计和运行。

尽管研究中还存在许多问题和挑战，但多体动力学方法无疑将持续为行星齿轮传动系统的研究和应用提供重要支持。

基于有限元法的行星齿轮传动系统的动力学分析一、引言行星齿轮传动作为一种重要的传动装置，在工程应用中具有广泛的应用。

其具有结构紧凑、承载能力高、传动效率高等优点，因此在航空航天、机械制造等领域被广泛使用。

然而，在实际应用过程中，行星齿轮传动系统常常面临着各种挑战，如振动、噪声、疲劳等问题。

因此，对于行星齿轮传动系统的动力学行为进行深入研究，对于提高其工作性能具有重要意义。

二、有限元法简介有限元法是一种常用的工程分析方法，可以用来研究结构的应力、变形、振动等问题。

其基本原理是将复杂的结构分割为有限的单元，通过求解各单元内的位移和应力，最终得到整个结构的行为。

有限元法能够较为准确地模拟和分析实际结构的动态响应，因此被广泛应用于行星齿轮传动系统的研究。

三、行星齿轮传动系统的结构及工作原理行星齿轮传动系统由太阳轮、行星轮、内齿轮和行星架等组成。

其中，太阳轮是输入轴，内齿轮为输出轴，行星轮通过行星架与太阳轮和内齿轮相连。

在行星齿轮传动系统中，太阳轮提供动力输入，通过行星轮的转动将动力传递给内齿轮，实现输出轴的运动。

四、行星齿轮传动系统的动力学模型建立1.建立行星齿轮传动系统的有限元模型为了研究行星齿轮传动系统的动力学行为，首先需要建立其准确的有限元模型。

通过考虑行星轮、齿轮、轴承等各个部件的刚度和质量等参数，可以建立行星齿轮传动系统的有限元模型。

2.确定边界条件和加载条件在进行有限元分析之前，需要确定边界条件和加载条件。

边界条件是指限定结构的位移和转角，在行星齿轮传动系统中，常常将太阳轮固定，将内齿轮的运动约束为指定的转速。

加载条件则是指施加在结构上的外部载荷，在行星齿轮传动系统中，可以考虑太阳轮的输入力作用于行星轮上。

五、行星齿轮传动系统的动力学分析1.求解结构的模态特性通过有限元方法可以求解行星齿轮传动系统的模态特性，即结构的固有频率和模态形态。

模态分析可以帮助工程师了解结构的振动特性，以及确定可能的共振问题。

行星齿轮传动系统的动力学建模与分析齿轮传动系统是一种常见的机械传动形式，由多个齿轮通过啮合传递动力。

在齿轮传动系统中，行星齿轮传动系统是一种常见的结构。

它由中央太阳齿轮、外圈行星齿轮和内圈行星齿轮组成。

行星齿轮传动系统具有紧凑结构、传动比变化范围广和承载能力强的特点，所以在很多机械传动系统中得到广泛应用。

了解行星齿轮传动系统的动力学特性对于设计和优化机械传动系统具有重要意义。

行星齿轮传动系统的动力学建模是研究其特性的基础。

一般而言，行星齿轮传动系统的动力学研究可以分为两个方面：传动系统的静态行为和传动系统的动态行为。

首先，我们来讨论行星齿轮传动系统的静态行为。

行星齿轮传动系统的静态行为主要包括传动比和齿轮位置分析。

传动比决定了输入轴和输出轴的转速比，对于不同的工况要求，传动比的变化范围也是需要考虑的因素。

齿轮位置分析是指确定各个齿轮之间的相对位置，这对于齿轮的啮合是否合理具有重要影响。

在行星齿轮传动系统的静态行为分析中，可以采用几何法和力学法相结合的方法，来求解传动比和齿轮位置。

几何法主要通过几何关系求解，力学法则涉及到力矩平衡和力平衡，求解过程需要考虑到齿轮的几何关系和曲柄等部件的力学特性。

其次，我们来讨论行星齿轮传动系统的动态行为。

行星齿轮传动系统的动态行为主要包括齿轮振动、齿轮动力学和齿轮传动系统的自激振动分析。

齿轮振动是指齿轮在运动过程中由于齿轮的不平衡、啮合刚度等因素引起的振动。

齿轮动力学是指齿轮在运动过程中由于齿轮的载荷和齿轮啮合行为引起的力学现象。

自激振动是指齿轮传动系统由于齿轮的不均匀磨损、齿轮啮合误差等因素引起的自激振动。

行星齿轮传动系统的动态行为分析需要采用系统动力学和振动理论等方法，通过建立数学模型来求解相应的动力学方程。

对于行星齿轮传动系统的动态行为分析，可以分为线性动力学分析和非线性动力学分析。

线性动力学分析是指在小扰动情况下对齿轮传动系统进行的分析，一般求解线性化的动力学方程来得到系统的频率响应和稳定性。

第四章斜齿行星齿轮传动系统动力学分析4.1 引言行星齿轮传动由于具有重量轻、结构紧凑、传动比大、效率高等优点，在民用、国防领域中都得到了广泛的应用，行星齿轮传动的振动和噪声是影响传动系统寿命和可靠性的重要因素。

近年来，国内外学者对行星齿轮传动的动态特性进行了大量研究：J.Lin、R.G.Parker、宋轶民等分析了行星齿轮传动的固有特性[42-49]；A.Kahraman等研究了行星齿轮传动的均载特性 [50-52]，并分析了加工误差对动态响应的影响[53-54]；R.G.Parker等还提出了通过控制啮合相位差抑制系统振动的方法[55-57]；潜波、罗玉涛、D.R.Kiracofe等探讨了复杂行星齿轮传动的动力学建模与分析[59-65]；沈允文、孙涛、孙智民等对星型齿轮传动和行星齿轮传动的非线性动力学特性进行了深入研究[66-70]。

目前，关于行星齿轮传动的研究多针对直齿行星轮系，而对斜齿行星传动的研究还很少，所建立的模型也有待进一步完善。

建立精确的动力学模型，是研究动态特性的首要工作，本章针对斜齿行星齿轮传动，以变形协调分析为基础，建立了其耦合非线性动力学模型，推导了其运动微分方程，最后分析了斜齿行星轮系的自由振动特性，对固有频率和固有振型的特点进行了总结。

4.2 系统的动力学模型及方程4.2.1 传动系统的动力学模型行星齿轮传动平移-扭转耦合动力学模型考虑的自由度非常多，因此其动力学方程也非常复杂。

为方便动力学方程的推导，建立各个集中质量的坐标系如下：OXY为静坐标系，其原点在行星轮系的几何中心，坐标系不随行星轮系运动；Oxy 为行星架随动坐标系，其原点在行星架回转中心，固连在行星架上随行星架的运O x y为行动而等速运动，其x轴正向通过第一个行星轮中心平衡位置；坐标系n n n星轮坐标系，也固连在行星架上随之等速旋转，其原点位于行星轮的中心平衡位置，x轴通过太阳轮中心与行星轮中心的连线指向内齿圈，y轴与行星架相切指向行星轮中心运动速度方向。

（一） 直齿圆柱齿轮传动的扭转振动模型若忽略传动轴的扭转变形，只考虑齿轮副处的变形，则得到最简单的扭转振动模型，如图1所示。

其中r b1、r b2为主从动齿轮的基圆直径，k v 为齿轮副的综合啮合刚度，并且考虑齿轮副的啮合阻尼系数c v 以及齿廓误差e 的作用，主动轮上作用与转动方向相同的驱动力矩T 1，从动轮上作用与转动方向相反的阻力矩T 2图1 齿轮副的扭转振动模型啮合线上的综合变形δi 可写为：1122i b b i r r e δθθ=--(1)设重合度小于2，啮合齿对为i ，法向啮合力可以表示为：()()()11221122i vi i vi i vi b b i vi b b i i i iF F k c k r r e c r r e δδθθθθ⎡⎤==+=--+--⎣⎦∑∑∑ (2) 式中：i 为参与啮合的齿对序号，i =1,2；k vi 、c vi 为齿对i 在啮合点位置的综合啮合刚度和阻尼系数。

主、从动齿轮的力矩平衡方程为：12111222b b J T r F J T r F θθ=-=- (3)将(2)带入(1)中得到：()()()()111112211221222112211222b vi b b i vi b b i i b vi b b i vi b b i iJ r k r r e c r r e T J r k r r e c r r e T θθθθθθθθθθ⎡⎤+--+--=⎣⎦⎡⎤---+--=-⎣⎦∑∑ (4)由此式可看出，即使主动齿轮转速以及传动载荷恒定，由于时变综合刚度k v 的变化，也会使从动轮的转动出现波动，即造成齿轮的圆周振动。

为了方便讨论时变综合刚度k v 对振动方程(4)的影响，定义啮合线上两齿轮的相对位移x 为：1122b b x r r θθ=- (5)不考虑齿轮传动的效率，齿轮的静态啮合力为：12012b b T T F r r ==(6)将式(5)、(6)带入方程(4)中，则可将其简化为一元微分方程：e v v d m x c x k x F ++= (7)式中，m e 称为系统的当量质量：12222112e b b J J m J r J r =+ (8)激振力为：0d vi i vi i iiF F c ek e =++∑∑ (9)根据方程(9)可以将一对齿轮的振动视为单自由度系统的振动，如图2所示。

第３０卷第９期２０１５年９月航空动力学报Ｊｏｕｒｎａｌ　ｏｆ　Ａｅｒｏｓｐａｃｅ　ＰｏｗｅｒＶｏｌ．３０Ｎｏ．９Ｓｅｐ．２０１５文章编号：１０００－８０５５（２０１５）０９－２２９８－０７ ｄｏｉ：１０．１３２２４／ｊ．ｃｎｋｉ．ｊａｓｐ．２０１５．０９．０３２斜齿行星齿轮传动系统振动模式与动载特性林　何，王三民，董金城（西北工业大学机电学院，西安７１００７２）摘 要：斜齿行星传动在高速重载场合中应用越来越广泛，其振动模式和动载特性研究对减振降噪设计具有重要意义．针对斜齿行星齿轮传动系统，建立了随动坐标系，推导了含陀螺效应的多自由度间隙非线性动力学方程，求解了系统的固有特性．结果表明：斜齿行星齿轮系统存在３种典型振动模式，即轴向平移－扭转耦合振动模式（重根数ｒ＝１），径向平移振动模式（重根数ｒ＝２）和行星轮振动模式（重根数ｒ＝Ｎ－３，Ｎ＞３）；综合考虑啮合刚度、齿侧间隙、综合误差和外载荷等激励作用，研究了啮合相位差和激励方式对动载系数的影响规律，结果表明计入啮合相位差时动载系数有所增大，当刚度波动系数ζ＝１．７２３时，系统分岔为２周期次谐响应，随着激励参数的变化，内啮合较外啮合更快的进入混沌状态．关　键　词：随动坐标系；陀螺效应；动载系数；啮合相位差；外激励中图分类号：Ｖ２３３．１；ＴＨ１１３．１ 文献标志码：Ａ收稿日期：２０１４－０２－２７基金项目：国家高技术研究发展计划（２００９ＡＡ０４Ｚ４０４）作者简介：林何（１９８５－），男，湖北襄阳人，博士生，主要从事齿轮系统动力学研究．Ｖｉｂｒａｔｉｏｎ　ｍｏｄｅ　ａｎｄ　ｄｙｎａｍｉｃａｌ　ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ　ｏｆ　ｈｅｌｉｃａｌｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｔｒａｉｎＬＩＮ　Ｈｅ，ＷＡＮＧ　Ｓａｎ－ｍｉｎ，ＤＯＮＧ　Ｊｉｎ－ｃｈｅｎｇ（Ｓｃｈｏｏｌ　ｏｆ　Ｍｅｃｈａｎｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，Ｎｏｒｔｈｗｅｓｔｅｒｎ　Ｐｏｌｙｔｅｃｈｎｉｃａｌ　Ｕｎｉｖｅｒｓｉｔｙ，Ｘｉ’ａｎ　７１００７２，Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｔｒａｎｓｍｉｓｓｉｏｎ　ｗａｓ　ａｐｐｌｉｅｄ　ｍｏｒｅ　ｅｘｔｅｎｓｉｖｅｌｙ　ｉｎ　ｈｉｇｈ－ｓｐｅｅｄ　ａｎｄ　ｈｅａｖｙ　ｌｏａｄ　ｓｉｔｕａｔｉｏｎｓ，ａｓ　ｔｈｅ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅ　ａｎｄ　ｄｙｎａｍｉｃ　ｃｈａｒａｃｔｅｒｉｓｔｉｃ　ｈａｄ　ｓｉｇｎｉｆｉ－ｃａｎｔ　ｉｎｆｌｕｅｎｃｅ　ｏｎ　ｖｉｂｒａｔｉｏｎ　ａｎｄ　ｎｏｉｓｅ　ｒｅｄｕｃｔｉｏｎ．Ｔａｒｇｅｔｉｎｇ　ｔｈｅ　ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｔｒａｎｓ－ｍｉｓｓｉｏｎ　ｓｙｓｔｅｍ，ｃｏ－ｍｏｖｉｎｇ　ｃｏｏｒｄｉｎａｔｅ　ｓｙｓｔｅｍ　ｗａｓ　ｃｏｎｄｕｃｔｅｄ，ｔｈｅ　ｍｕｌｔｉ－ｄｅｇｒｅｅ　ｏｆ　ｆｒｅｅｄｏｍｎｏｎｌｉｎｅａｒ　ｄｙｎａｍｉｃａｌ　ｅｑｕａｔｉｏｎｓ　ｉｎｃｌｕｄｉｎｇ　ｇｙｒｏｓｃｏｐｉｃ　ｅｆｆｅｃｔ　ａｎｄ　ｂａｃｋｌａｓｈ　ｗａｓ　ｄｅｒｉｖｅｄ，ａｎｄ　ｔｈｅｎａｔｕｒａｌ　ｃｈａｒａｃｔｅｒｉｓｔｉｃ　ｏｆ　ｔｈｅ　ｓｙｓｔｅｍ　ｗａｓ　ｓｏｌｖｅｄ．Ｔｈｅ　ｒｅｓｕｌｔｓ　ｓｈｏｗ　ｔｈａｔ　ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒｔｒａｉｎ　ｈａｓ　ｔｈｒｅｅ　ｔｙｐｉｃａｌ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅｓ：ａｘｉａｌ　ｔｒａｎｓｌａｔｉｏｎａｌ－ｒｏｔａｔｉｏｎａｌ　ｃｏｕｐｌｅｄ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅ（ｍｕｌｔｉｐｌｉｃｉｔｙ　ｒ＝１），ｔｒａｎｓｌａｔｉｏｎａｌ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅ（ｍｕｌｔｉｐｌｉｃｉｔｙ　ｒ＝２）ａｎｄ　ｐｌａｎｅｔ　ｖｉｂｒａｔｉｏｎｍｏｄｅ（ｍｕｌｔｉｐｌｉｃｉｔｙ　ｒ＝Ｎ－３，Ｎ＞３）；ｉｎ　ｃｏｎｓｉｄｅｒａｔｉｏｎ　ｏｆ　ｍｅｓｈ　ｓｔｉｆｆｎｅｓｓ，ｂａｃｋｌａｓｈ，ｇｅｎｅｒａｌｅｒｒｏｒｓ　ａｎｄ　ｅｘｔｅｒｎａｌ　ｌｏａｄ，ｉｎｆｌｕｅｎｃｅ　ｌａｗｓ　ｏｆ　ｍｅｓｈ　ｐｈａｓｅ　ｄｉｆｆｅｒｅｎｃｅ　ａｎｄ　ｅｘｃｉｔａｔｉｏｎ　ｗａｙｓ　ｔｏ　ｄｙ－ｎａｍｉｃａｌ　ｃｏｅｆｆｉｃｉｅｎｔ　ｈａｖｅ　ｂｅｅｎ　ｓｔｕｄｉｅｄ，ｓｈｏｗｉｎｇ　ｔｈａｔ　ｍｅｓｈ　ｐｈａｓｅ　ｄｉｆｆｅｒｅｎｃｅ　ｍａｋｅｓ　ｔｈｅ　ｄｙｎａｍｉ－ｃａｌ　ｃｏｅｆｆｉｃｉｅｎｔ　ｉｎｃｒｅａｓｅ；ｗｈｅｎ　ｓｔｉｆｆｎｅｓｓ　ｆｌｕｃｔｕａｔｉｏｎ　ｃｏｅｆｆｉｃｉｅｎｔζ＝１．７２３，ｔｈｅ　ｓｙｓｔｅｍ　ｉｓ　ｂｉｆｕｒ－ｃａｔｅｄ　ｉｎｔｏ　２－ｐｅｒｉｏｄ　ｓｕｂ－ｈａｒｍｏｎｉｃ　ｒｅｓｐｏｎｓｅ，ｗｉｔｈ　ｔｈｅ　ｃｈａｎｇｅｓ　ｏｆ　ｅｘｃｉｔａｔｉｏｎ　ｐａｒａｍｅｔｅｒｓ，ｉｎｔｅｒ－ｎａｌ　ｅｎｇａｇｅｍｅｎｔ　ｔｕｒｎｉｎｇ　ｉｎｔｏ　ｔｈｅ　ｃｈａｏｔｉｃ　ｓｔａｔｅ　ｉｓ　ｅａｒｌｉｅｒ　ｔｈａｎ　ｅｘｔｅｒｎａｌ　ｅｎｇａｇｅｍｅｎｔ．Ｋｅｙ　ｗｏｒｄｓ：ｃｏ－ｍｏｖｉｎｇ　ｃｏｏｒｄｉｎａｔｅ　ｓｙｓｔｅｍ；ｇｙｒｏｓｃｏｐｉｃ　ｅｆｆｅｃｔ；ｄｙｎａｍｉｃａｌ　ｃｏｅｆｆｉｃｉｅｎｔ；ｍｅｓｈ　ｐｈａｓｅ　ｄｉｆｆｅｒｅｎｃｅ；ｅｘｔｅｒｎａｌ　ｅｘｃｉｔａｔｉｏｎｓ　第９期林　何等：斜齿行星齿轮传动系统振动模式与动载特性 斜齿行星齿轮系统具有传动比大、平稳性好、结构紧凑、承载能力高等优点，在航空航天、汽车、船舶等领域中得到了广泛应用［１］．为了改善其均载特性，提高其承载能力，国内外学者对行星齿轮系统的动力学特性都开展了许多有益的研究：杨通强、Ｐａｒｋｅｒ和Ｅｒｉｔｅｎｅｌ等［２－４］分析了行星齿轮系统的固有特性；Ａｍｂａｒｉｓｈａ等［５］提出了通过控制啮合相位差来抑制系统的振动．相比直齿行星齿轮传动斜齿行星传动由于受力和结构复杂而考虑的自由度较多，且由于轴向分力引起激励，振动模式较为复杂，而传统的研究大多只对其固有特性进行了分析而对动载特性研究较少．为准确全面的分析斜齿行星齿轮系统的动力学特性，建立了行星架随动坐标系，并基于随动坐标系构建了平移－扭转耦合动力学模型，推导了含陀螺效应的多自由度运动微分方程，采用Ｒｕｎｇｅ－Ｋｕｔｔａ法求解了斜齿行星齿轮传动系统的固有特性和动载特性．１　动力学模型斜齿行星齿轮传动系统由太阳轮、行星架、内齿圈和Ｎ个行星轮组成．图１所示为含３个行星轮的斜齿行星齿轮系统动力学模型，各啮合齿轮副和弹性支撑处均含有阻尼，为保持模型简洁阻尼符号图中未标出．图中ＯＸＹ为固定坐标系，原点在行星轮系的对称中心；Ｏｘｙ为行星架随动坐标系，固连在行星架上随行星架的转动而运转；Ｏｎｘｎｙｎ（ｎ＝１，２，３）为行星轮坐标系，随着行星架做等速旋转，其原点位于行星轮的几何中心位置．图１　斜齿行星齿轮系统平移－扭转耦合动力学模型Ｆｉｇ．１　Ｔｒａｎｓｌａｔｉｏｎａｌ－ｔｏｒｓｉｏｎａｌ　ｃｏｕｐｌｅｄ　ｄｙｎａｍｉｃａｌ　ｍｏｄｅｌｏｆ　ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｔｒａｉｎ行星轮系传动中，行星轮在自转的同时围绕着太阳轮做圆周运动，为分析陀螺效应对系统振动的影响建立图２所示行星轮系随动坐标系，其中ＯＸＹ为绝对参考坐标系，Ｏｘｙ为随动坐标系，Ｏ为行星传动理论安装中心，ωｃ为随动角速度．图２　行星轮系随动坐标系Ｆｉｇ．２　Ｃｏ－ｍｏｖｉｎｇ　ｃｏｏｒｄｉｎａｔｅ　ｓｙｓｔｅｍ　ｏｆ　ｐｌａｎｅｔａｒｙｇｅａｒ　ｔｒａｉｎ根据坐标变换理论知ＸＹ熿燀燄燅Ｚ＝ｃｏｓωｃｔ－ｓｉｎωｃｔ　０ｓｉｎωｃｔ　ｃｏｓωｃｔ　００　０　熿燀燄燅１熿燀燄燅ｘｙｚ（１） 随动坐标系下各矢量方向的加速度为¨ｘ¨ｙ¨熿燀燄燅ｚ＝ｃｏｓωｃｔ　ｓｉｎωｃｔ　０－ｓｉｎωｃｔ　ｃｏｓωｃｔ　００　０　熿燀燄燅１Ｘ··Ｙ··Ｚ熿燀燄燅··（２）式中｛Ｘ··，Ｙ··，Ｚ··｝Ｔ为绝对加速度矢量在固定坐标系中的分量．由式（１）、式（２）可得各行星轮ｉｎ（ｎ＝１，２，３）在动坐标系中的质心运动加速度ａｉｘ＝¨ｘｉ－２ωｃ ｙｉ－ω２ｃｘｉａｉｙ＝¨ｙｉ＋２ωｃ ｘｉ－ω２ｃｙ烅烄烆ｉ（３） 图３为内、外啮合齿轮副集中质量动力学模型．斜齿行星齿轮传动系统的广义坐标取为：太阳轮、行星轮、内齿圈及行星架的扭转线位移珘ｕｉ＝ｒｉφｉ，其中ｒｉ，φｉ分别为构件ｉ的基圆半径和扭转角位移；以及在端面和轴向的平移线位移珘λｉ＝｛ｘｉ，ｙｉ，ｚｉ｝Ｔ（ｉ＝ｓ，ｐ，ｒ，ｃ），则系统动力学模型共含有１２＋４ｎ个自由度，系统的广义坐标矢量为ｑ＝｛ｘｓ，ｙｓ，ｚｓ，ｕｓ，ｘｒ，ｙｒ，ｚｒ，ｕｒ，ｘｃ，ｙｃ，ｚｃ，ｕｃ，ｘ１，ｙ１，ｚ１，ｕ１，…，ｘｎ，ｙｎ，ｚｎ，ｕｎ｝Ｔ 假设由太阳轮指向行星轮方向、行星轮指向内齿圈方向为啮合线正方向，考虑啮合线上的相对位移以及各广义坐标方向的叠加性，可得随动坐标系下含啮合误差的构件间相对位移如下：９９２２航　空　动　力　学　报第３０卷图３　构件间的动力学模型Ｆｉｇ．３　Ｄｙｎａｍｉｃａｌ　ｍｏｄｅｌ　ｂｅｔｗｅｅｎ　ｔｈｅ　ｃｏｍｐｏｎｅｎｔｓδｓｎ＝（ｕｓ＋ｕｎ－ｘｎｓｉｎα－ｘｓｓｉｎψｓｎ－ｙｎｃｏｓα＋　ｙｓｃｏｓψｓｎ）ｃｏｓβ＋（ｚｓ－ｚｎ）ｓｉｎβ－ｅｓｎ（ｔ）δｒｎ＝（ｕｒ－ｕｎ＋ｘｎｓｉｎα－ｘｒｓｉｎψｒｎ－ｙｎｃｏｓα＋　ｙｒｃｏｓψｒｎ）ｃｏｓβ＋（ｚｎ－ｚｒ）ｓｉｎβ－ｅｒｎ（ｔ）δｃｎｘ＝ｘｃ－ｕｃｓｉｎψｎ－ｘｎｃｏｓψｎ＋ｙｎｓｉｎψｎδｃｎｙ＝ｙｃ＋ｕｃｃｏｓψｎ－ｘｎｓｉｎψｎ－ｙｎｃｏｓψｎδｃｎｚ＝ｚｃ－ｚｎδｃｎｕ＝ｕｃ－ｙｎ－ｘｃｓｉｎψｎ＋ｙｃｃｏｓψｎδｐｎｘ＝ｘｎ－ｘｃｃｏｓψｎ－ｙｃｓｉｎψｎδｐｎｙ＝ｙｎ－ｕｃ＋ｘｃｓｉｎψｎ－ｙｃｃｏｓψ烅烄烆ｎ（４）式中δｃｎｘ，δｃｎｙ，δｃｎｚ，δｃｎｕ分别为行星轮与行星架在ｘｃ，ｙｃ，ｚｃ，ｕｃ方向的相对位移；δｐｎｘ，δｐｎｙ分别为行星轮与行星架在ｘｎ，ｙｎ方向的相对位移；ｅｓｎ（ｔ），ｅｒｎ（ｔ）分别为行星轮与太阳轮、内齿圈间的综合传动误差，且ｅｉｊ（ｔ）＝Ｅｉｊｓｉｎ（ωｉｊｔ＋φｉｊ）．ωｉｊ为齿轮ｉ与ｊ的啮合齿频（ｉ＝ｓ，ｒ；ｊ＝ｎ）；ψｓｎ，ψｒｎ分别为行星轮与太阳轮、内齿圈在ｘｃ方向的夹角，其值为ψｓｎ＝２π（ｎ－１）／Ｎ－α，ψｒｎ＝２π（ｎ－１）／Ｎ＋α．设齿轮副的侧隙为２ｂ，则行星轮与太阳轮、内齿圈之间的法向啮合力为Ｆｓｎ＝ｋｉｊ（ｔ）ｆ（δｓｎ，ｂ）＋ｃｓｎ δｓｎＦｒｎ＝ｋｉｊ（ｔ）ｆ（δｒｎ，ｂ）＋ｃｒｎ δｒ烅烄烆ｎ（５）式中ｋｉｊ（ｔ）＝珔ｋａ［１＋ζｓｉｎ（ωｉｊｔ＋φｉｊ）］．其中珔ｋａ，ζ分别为刚度均值和刚度波动系数；ｆ（δｓｎ，ｂ），ｆ（δｒｎ，ｂ）分别为行星轮与太阳轮、内齿圈间的间隙非线性函数．设构件ｊ的质量为ｍｊ，转动惯量为Ｉｊ，阻尼为ｃｊ，刚度为ｋｊ，构件所受外力矩为Ｔｊ，行星轮个数为Ｎ．根据牛顿第二定律和质点系相对质心动量矩定理，采用集中参数法可建立系统各构件在广义坐标下的平衡方程．太阳轮的运动微分方程ｍｓ（¨ｘｓ－２ωｃ ｙｓ－ω２ｃｘｓ）－∑Ｎｎ＝１Ｆｓｎｃｏｓβｓｉｎψｓｎ＋ｃｓ ｘｓ＋ｋｓｘｓ＝０ｍｓ（¨ｙｓ＋２ωｃ ｘｓ－ω２ｃｙｓ）＋∑Ｎｎ＝１Ｆｓｎｃｏｓβｃｏｓψｓｎ＋ｃｓ ｙｓ＋ｋｓｙｓ＝０ｍｓ¨ｚｓ＋∑Ｎｎ＝１Ｆｓｎｓｉｎβ＋ｃｓｚ ｚｓ＋ｋｓｚｚｓ＝０Ｉｓｒ２ｓ¨ｕｓ＋∑Ｎｎ＝１Ｆｓｎｃｏｓβ＋ｋｓｕｕｓ＋ｃｓｕ ｕｓ＝Ｔｓｒ烅烄烆ｓ（６） 行星架的运动微分方程ｍｃ（¨ｘｃ－２ωｃ ｙｃ－ω２ｃｘｃ）＋∑Ｎｎ＝１ｃｐ δｃｎｘ＋∑Ｎｎ＝１ｋｐδｃｎｘ＋ｃｃ ｘｃ＋ｋｃｘｃ＝０ｍｃ（¨ｙｃ＋２ωｃ ｘｃ－ω２ｃｙｃ）＋∑Ｎｎ＝１ｃｐ δｃｎｙ＋∑Ｎｎ＝１ｋｐδｃｎｙ＋ｃｃ ｙｃ＋ｋｃｙｃ＝０ｍｃ¨ｚｃ＋∑Ｎｎ＝１ｃｐｚ δｃｎｚ＋∑Ｎｎ＝１ｋｐｚδｃｎｚ＋ｃｃｚ ｚｃ＋ｋｃｚｚｃ＝０Ｉｃｒ２ｃ¨ｕｃ＋∑Ｎｎ＝１ｃｐ δｃｎｕ＋∑Ｎｎ＝１ｋｐδｃｎｕ＋ｃｃｕ ｕｃ＋ｋｃｕｕｃ＝－Ｔｃｒ烅烄烆ｃ（７） 行星轮的运动微分方程００３２　第９期林　何等：斜齿行星齿轮传动系统振动模式与动载特性ｍｎ（¨ｘｎ－２ωｃ ｙｎ－ω２ｃｘｎ）－Ｆｓｎｃｏｓβｓｉｎα＋Ｆｒｎｃｏｓβｓｉｎα＋ｃｐ δｐｎｘ＋ｋｐδｐｎｘ＝０ｍｎ（¨ｙｎ＋２ωｃ ｘｎ－ω２ｃｙｎ）－Ｆｓｎｃｏｓβｃｏｓα－Ｆｒｎｃｏｓβｃｏｓα＋ｃｐ δｐｎｙ＋ｋｐδｐｎｙ＝０ｍｎ¨ｚｎ－Ｆｓｎｓｉｎβ＋Ｆｒｎｓｉｎβ－ｃｐｚ δｃｎｚ－ｋｐｚδｃｎｚ＝０（Ｉｎ／ｒ２ｎ）¨ｕｎ＋Ｆｓｎｃｏｓβ－Ｆｒｎｃｏｓβ＝烅烄烆０（８） 内齿圈的运动微分方程ｍｒ（¨ｘｒ－２ωｃ ｙｒ－ω２ｃｘｒ）－∑Ｎｎ＝１Ｆｒｎｃｏｓβｓｉｎψｒｎ＋ｃｒ ｘｒ＋ｋｒｘｒ＝０ｍｒ（¨ｙｒ＋２ωｃ ｘｒ－ω２ｃｙｒ）＋∑Ｎｎ＝１Ｆｒｎｃｏｓβｃｏｓψｒｎ＋ｃｒ ｙｒ＋ｋｒｙｒ＝０ｍｒ¨ｚｒ－∑Ｎｎ＝１Ｆｒｎｓｉｎβ＋ｃｒｚ ｚｒ＋ｋｒｚｚｒ＝０Ｉｒｒ２ｒ¨ｕｒ＋∑Ｎｎ＝１Ｆｒｎｃｏｓβ＋ｃｒｕ ｕｒ＋ｋｒｕｕｒ＝Ｔｒｒ烅烄烆ｒ（９）式（６）～式（９）为含陀螺效应随动坐标系下构件的运动微分方程，可以看出，陀螺效应对系统影响的大小主要取决于行星架的转速ωｃ．上述方程组可统一表述为Ｍ¨ｑ＋（Ｃｂ＋Ｃｍ＋ωｃＧ） ｑ＋（Ｋｂ＋Ｋｍ－ω２ｃＫω）ｑ＝Ｔ（１０）式中Ｍ为构件质量矩阵，Ｔ为外载荷向量，ｑ＝［ｘｉ，ｙｉ，ｚｉ，ｕｉ］Ｔ，（ｉ＝ｓ，ｎ，ｒ，ｃ）；Ｃｂ，Ｃｍ，Ｇ分别为支承阻尼矩阵、啮合阻尼矩阵、陀螺矩阵；Ｋｂ，Ｋｍ，Ｋω分别为支承刚度矩阵、啮合刚度矩阵、向心刚度矩阵．为降低动力学方程的维数，引入一组相对位移矢量Ｘ＝｛δｓｎ，δｒｎ，δｃｎ｝Ｔ作为新的广义坐标，合并消除式（６）～式（９）中扭转振动方程的刚体位移．为提高数值计算的质量和精度定义量纲一化时间τ和位移标称尺度ｂｃ，对降维后的系统方程进行量纲一化处理，所需变量如下［６－９］：τ＝ｔ／ωｎ，　ωｎ＝ｋｓ１（１／Ｍｓ＋１／Ｍ１槡）珡Ｘ（τ）＝ｘ（ｔ）／ｂｃ，　珋ｅ¨（τ）＝¨ｅ（ｔ）／ω２ｎｂｃＭｓ＝Ｉｓ／ｒ２ｂｓ，　Ｍ１＝Ｉ１／ｒ２ｂ１式中Ｍｓ，Ｍ１为太阳轮、行星轮１的等效质量；ｒｂｓ，ｒｂ１为太阳轮、行星轮１的基圆半径．量纲一化后的系统振动方程可整理成如下２阶微分方程的矩阵形式：珨Ｍ珚Ｘ··＋珚Ｃ珚Ｘ·＋珚Ｋｆ（珚Ｘ）＝珚Ｔ（１１）式中珨Ｍ，珚Ｃ，珚Ｋ，ｆ（珚Ｘ），珚Ｔ分别为量纲归一化后的系统质量矩阵、阻尼矩阵、刚度矩阵、间隙函数列矢量和载荷矢量．齿轮副间因啮合刚度的时变性和内外部载荷的激励而产生振动，对于非变位的渐开线齿轮，为准确衡量其动载特性定义如下关系式［１０］：Ｋｖ＝珔ｋａｘ（ｔ）＋ｃ ｘ（ｔ）ｆｎ（１２）其中ｆｎ＝Ｔ／（Ｎｒｂｓｃｏｓβ）为啮合副接触线上的法向静载荷，Ｋｖ为量纲一化动载系数．２　动力学特性２．１　固有特性分析表１为斜齿行星齿轮传动系统的动力学参数，其中齿轮模数ｍ＝４，压力角α＝２０°，螺旋角β＝１２°，扭转阻尼比ξ＝０．００５，啮合阻尼比ζ＝０．０３．表１　斜齿行星齿轮系统动力学参数Ｔａｂｌｅ　１　Ｄｙｎａｍｉｃ　ｐａｒａｍｅｔｅｒｓ　ｏｆ　ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｔｒａｉｎ参数太阳轮行星轮内齿圈行星架齿数２３　４３　１０９转动惯量／（ｋｇ·ｍ２）０．００１　２７　０．００１　６６　０．０４１　４　０．０２３　７支承刚度／（Ｎ／ｍ）ｋｘ＝ｋｙ＝１．０８×１０８　ｋｚ＝１．３３×１０８扭转刚度／（Ｎ／ｍ）ｋｓ＝ｋｐ＝ｋｃ＝０　ｋｒ＝１０９啮合刚度／（Ｎ／ｍ）ｋｓｎ＝１．２６×１０８　ｋｒｎ＝１．５３×１０８当不考虑系统阻尼和外部激励项时，系统动力学模型简化为［ｋｉ（ｔ）－ω２ｉｍｉ］ηｉ＝０　（ｉ＝ｓ，ｎ，ｒ，ｃ）（１３）ｍｉ＝ｄｉａｇ｛ｍｉ，ｍｉ，ｍｉ，Ｍｉ｝式中ｍｉ为构件ｉ的质量，Ｍｉ为构件ｉ的等效质量，ηｉ＝｛ｘｉ，ｙｉ，ｚｉ，ｕｉ｝Ｔ为ｎ阶模态振型矢量．取行星轮数目Ｎ＝３，４，５时，解得系统固有频率含３类重根，其重根数和固有频率如表２所１０３２航　空　动　力　学　报第３０卷示，３类重根分别对应着３种振动模式，即中心构件轴向平移－扭转耦合振动、中心构件径向平移振动、以及行星轮振动模式．设系统固有频率为ωｉ（ｉ＝１，２，３，…，４　Ｎ＋１２），则单重根（１０个）对应中心构件轴向平移扭转振动模式，双重根（７对）对应中心构件径向平移振动模式，行星轮振动模式时的重根数ｒ（ｒ＝Ｎ－３，Ｎ＞３）与行星轮数目Ｎ相关．系统第ｊ阶固有频率ωｊ，其对应的振型矢量为ηｊ＝｛ζｊｉ｝Ｔ，其中ζ＝ｘ，ｙ，ｚ，ｕ；ｉ＝ｓ，ｎ，ｒ，ｃ；ｊ＝１，２，３，…，４　Ｎ＋１２）．以行星轮数目Ｎ＝４为例，系统共有２８个特征值，其３种振动模式的振型如图４所示，任一模式下构件均存在某些振型矢量元素为０，即未引起振动．图５为对应的３种模式的振动示意图，其中图５（ａ）为中心构件轴向平移－扭转耦合振动模式（ｚ，ｕ方向振动），对应１０阶固有频率，重根数为１；图５（ｂ）为中心构件径向平移振动模式（ｘ，ｙ方向振动），共有１４阶固有频率，重根数为２；图５（ｃ）为行星轮振动模式（ｘ，ｙ，ｚ，ｕ方向均振动），含有４阶固有频率，此时中心构件未振动，重根数为１．表２　系统固有频率的重根数与固有频率Ｔａｂｌｅ　２　Ｍｕｌｔｉｐｌｉｃｉｔｙ　ａｎｄ　ｎａｔｕｒａｌ　ｆｒｅｑｕｅｎｃｙ　ｏｆ　ｔｈｅ　ｓｙｓｔｅｍ行星轮数固有频率ω／Ｈｚ中心构件轴向平移扭转模式（重根数ｒ＝１）中心构件径向平移模式（重根数ｒ＝２）行星轮模式（重根数ｒ＝Ｎ－３）３０，７５７，１　０４１，１　９６４，２　４５５，２　８８４，３　０１９，３　７１０，６　１９３，６　３５４９４８，１　２５５，２　１５６，２　５３８，２　８７０，４　８２８，５　９４２４０，７２１，９６９，２　０４９，２　５３３，２　９０３，３　１５０，３　７３１，６　４９８，６　９６２９２３，１　２３９，２　１４１，２　５２９，２　９８１，４　９２８，６　３７８２　１４１，２　４８５，４　０９７，４　５５６５０，６８９，８９３，２　０８４，２　５８７，２　９０２，３　２９３，３　８０７，６　７７６，７　５２６８９９，１　２１４，２　１８８，２　５２２，３　１０１，５　０２１，６　７８０２　１４１，２　４８５，４　０９７，４　５５６图４　Ｎ＝４时系统３种振动模式的振型图Ｆｉｇ．４　Ｔｈｒｅｅ　ｔｙｐｅｓ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅ　ｄｉａｇｒａｍｓ　ｏｆｓｙｓｔｅｍ　ｗｈｅｎ　Ｎ＝４２．２　啮合相位差对动载特性的影响行星齿轮啮合传动中，前后齿面均承受载荷，啮合相位差的存在使内外啮合之间产生异步啮图５　３种振动模式的振动示意图Ｆｉｇ．５　Ｔｈｒｅｅ　ｔｙｐｅｓ　ｖｉｂｒａｔｉｏｎ　ｓｃｈｅｍａｔｉｃ　ｄｉａｇｒａｍｓ合，其相位关系主要由齿轮齿数和行星轮个数决定．假定以图１中行星轮１的位置为基准，当行星架转动２π角时，从行星轮１到达行星轮ｉ需完成ψｉｚｓ／２π次啮合次数，从而可得行星轮的啮合相位关系为［１１－１２］ψｓｉ＝±ｉｚｓ２π ψｒｉ＝ｉｚｒ２π（１４）式中“＋”表示行星架逆时针转动，“－”表示行星架顺时针转动， ｉ为第ｉ个行星轮与基准行星轮圆周方向的夹角．以４个行星轮为例，各行星轮之间的周向夹角为π／２，行星架逆时针转动时，其啮合相位关系２０３２　第９期林　何等：斜齿行星齿轮传动系统振动模式与动载特性分别为０，ｚｒ／４，ｚｒ／２，３ｚｒ／４．图６为相位差与动载特性的关系，由图６知未考虑啮合相位差时外、内啮合的动载系数分别为１．２８和１．３５，计入啮合相位差时动载系数分别为１．４１和１．４３，两者均有所增大，此时内啮合的振动强于外啮合．图６　动载系数Ｋｖ时间历程Ｆｉｇ．６　Ｔｉｍｅ　ｈｉｓｔｏｒｉｅｓ　ｏｆ　ｄｙｎａｍｉｃａｌ　ｃｏｅｆｆｉｃｉｅｎｔ　Ｋｖ２．３　多激励对动载特性的影响图７为系统在多种激励下的动载系数时间历程（图中ｓ－ｐ，ｒ－ｐ分别表示行星轮与太阳轮、内齿圈间的啮合．图７（ａ）刚度波动系数ζ＝１．７１５；图７（ｂ）齿侧间隙ｂ＝１００μｍ；图７（ｃ）综合误差ｅ＝１５μｍ；图７（ｄ）外载荷ｌ＝３　５６４Ｎ·ｍ）．外部载荷的波动以行星架负载所受载荷的谐波函数形式给出即ｌ＝Ｔｓｉ［１＋λｓｉｎ（ωｃｔ＋ ）］．４种激励下的Ｋｖ均为单周期简谐响应，都在１附近波动，振幅不同，均为正面冲击，综合误差激励时动载系数最大，且太阳轮、行星轮间的动载系数均大于行星轮、内齿圈间的动载系数［１３－１５］．由图８（图中横坐标、纵坐标的数值进行了量纲一化的处理）系统对时变刚度的响应知，ζ＝１．７２３时内啮合动载系数的时间历程为简谐函数，外啮合则为多频响应，显示出非线性特征，根据Ｐｏｉｎｃａｒé映射（图８（ｃ））和ＦＦＴ（快速傅里叶变换）频谱分析（图８（ｄ））知内、外啮合均为２周期次谐响应，系统周期在此处分岔为２Ｔ．改变激励参数，当ｂ＝１５０μｍ，ｅ＝２０μｍ时，图９（ａ）所示内啮合相图开始出现非重叠，此时Ｋｖ为多周期谐响应；图９（ｂ）中ｌ＝３　２０８Ｎ·ｍ时，相图７　不同激励下的动载系数时间历程Ｆｉｇ．７　Ｔｉｍｅ　ｈｉｓｔｏｒｉｅｓ　ｏｆ　ｄｙｎａｍｉｃａｌ　ｃｏｅｆｆｉｃｉｅｎｔ　ｕｎｄｅｒ　ｖａｒｉｏｕｓ　ｅｘｃｉｔａｔｉｏｎｓ图８　ζ＝１．７２３时系统动态响应Ｆｉｇ．８　Ｄｙｎａｍｉｃ　ｒｅｓｐｏｎｓｅｓ　ｏｆ　ｓｙｓｔｅｍ　ｗｈｅｎζ＝１．７２３图９　不同激励下的系统动态响应Ｆｉｇ．９　Ｄｙｎａｍｉｃ　ｒｅｓｐｏｎｓｅｓ　ｏｆ　ｓｙｓｔｅｍ　ｕｎｄｅｒ　ｖａｒｉｏｕｓ　ｅｘｃｉｔａｔｉｏｎｓ３０３２航　空　动　力　学　报第３０卷平面为一定区域相互层叠的椭圆，内、外啮合均表现出强非线性，系统进入混沌状态［１６－１８］，上述亦表明内啮合较外啮合更快的进入混沌状态．３　结　论１）斜齿行星齿轮系统含有３种典型振动模式：即轴向平移－扭转耦合振动模式（重根数ｒ＝１），径向平移振动模式（重根数ｒ＝２），行星轮振动模式（重根数ｒ＝Ｎ－３，Ｎ＞３）．２）啮合相位差的存在使内、外啮合的动载系数有所增大，动力学设计时应考虑啮合相位差的影响．３）在多种激励分别作用下系统为单周期简谐响应，当刚度波动系数ζ＝１．７２３时，系统分岔为２周期次谐波响应，改变激励参数时，内啮合较外啮合更快的进入混沌状态．参考文献：［１］　屈文涛．直升机动力旋翼系统及航空齿轮系统的振动研究［Ｄ］．西安：西北工业大学，１９９５．ＱＵ　Ｗｅｎｔａｏ．Ｓｔｕｄｙ　ｏｎ　ｈｅｌｉｃｏｐｔｅｒ　ｒｏｔｏｒ　ｄｙｎａｍｉｃ　ｓｙｓｔｅｍ　ａｎｄｔｈｅ　ｖｉｂｒａｔｉｏｎ　ｏｆ　ｔｈｅ　ｇｅａｒ　ｓｙｓｔｅｍ［Ｄ］．Ｘｉ’ａｎ：ＮｏｒｔｈｗｅｓｔｅｒｎＰｏｌｙｔｅｃｈｎｉｃａｌ　Ｕｎｉｖｅｒｓｉｔｙ，１９９５．（ｉｎ　Ｃｈｉｎｅｓｅ）［２］　杨通强，宋轶民，张策，等．斜齿行星齿轮系统自由振动特性分析［Ｊ］．机械工程学报，２００５，４１（７）：５０－５５．ＹＡＮＧ　Ｔｏｎｇｑｉａｎｇ，ＳＯＮＧ　Ｙｉｍｉｎ，ＺＨＡＮＧ　Ｃｅ，ｅｔ　ａｌ．Ｐｒｏｐ－ｅｒｔｙ　ａｎａｌｙｓｉｓ　ｏｆ　ｆｒｅｅ　ｖｉｂｒａｔｉｏｎ　ｏｆ　ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒｔｒａｉｎｓ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｍｅｃｈａｎｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，２００５，４１（７）：５０－５５．（ｉｎ　Ｃｈｉｎｅｓｅ）［３］　Ｐａｒｋｅｒ　Ｒ　Ｇ，Ｌｉｎ　Ｊ．Ｍｅｓｈ　ｐｈａｓｉｎｇ　ｒｅｌａｔｉｏｎｓｈｉｐｓ　ｉｎ　ｐｌａｎｅｔａｒｙａｎｄ　ｅｐｉｃｙｃｌｉｃ　ｇｅａｒｓ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｍｅｃｈａｎｉｃａｌ　Ｄｅｓｉｇｎ，２００４，１２６（２）：３６５－３７０．［４］　Ｅｒｉｔｅｎｅｌ　Ｔ，Ｐａｒｋｅｒ　Ｒ　Ｇ．Ｍｏｄａｌ　ｐｒｏｐｅｒｔｉｅｓ　ｏｆ　ｔｈｒｅｅ－ｄｉｍｅｎ－ｓｉｏｎａｌ　ｈｅｌｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒｓ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｓｏｕｎｄ　ａｎｄ　Ｖｉ－ｂｒａｔｉｏｎ，２００９，３２５（１）：３９７－４２０．［５］　Ａｍｂａｒｉｓｈａ　Ｖ　Ｋ，Ｐａｒｋｅｒ　Ｒ　Ｇ．Ｓｕｐｐｒｅｓｓｉｏｎ　ｏｆ　ｐｌａｎｅｔ　ｍｏｄｅｒｅｓｐｏｎｓｅ　ｉｎ　ｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｄｙｎａｍｉｃｓ　ｔｈｒｏｕｇｈ　ｍｅｓｈ　ｐｈａｓｉｎｇ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｖｉｂｒａｔｉｏｎ　ａｎｄ　Ａｃｏｕｓｔｉｃｓ，２００６，１２８（２）：１３３－１４２．［６］　Ｍａｒｋ　Ｖ　Ｄ，Ｈｉｎｅｓ　Ｊ　Ａ．Ｓｔａｔｉｏｎａｒｙ　ｔｒａｎｓｄｕｃｅｒ　ｒｅｓｐｏｎｓｅ　ｔｏｐｌａｎｅｔａｒｙ－ｇｅａｒ　ｖｉｂｒａｔｉｏｎ　ｅｘｃｉｔａｔｉｏｎ　ｗｉｔｈ　ｎｏｎ－ｕｎｉｆｏｒｍ　ｐｌａｎ－ｅｔ　ｌｏａｄｉｎｇ［Ｊ］．Ｍｅｃｈａｎｉｃａｌ　Ｓｙｓｔｅｍｓ　ａｎｄ　Ｓｉｇｎａｌ　Ｐｒｏｃｅｓｓｉｎｇ，２００９，２３（４）：１３６６－１３８１．［７］　孙智明，沈允文，李素有．封闭行星齿轮传动系统的扭振特性研究［Ｊ］．航空动力学报，２００１，１６（２）：１６３－１６６．ＳＵＮ　Ｚｈｉｍｉｎ，ＳＨＥＮ　Ｙｕｎｗｅｎ，ＬＩ　Ｓｕｙｏｕ．Ａ　ｓｔｕｄｙ　ｏｎ　ｔｏｒｓｉｏｎａｌｖｉｂｒａｔｉｏｎ　ｉｎ　ａｎ　ｅｎｃａｓｅｄ　ｄｉｆｆｅｒｅｎｔｉａｌ　ｇｅａｒ　ｔｒａｉｎ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆＡｅｒｏｓｐａｃｅ　Ｐｏｗｅｒ，２００１，１６（２）：１６３－１６６．（ｉｎ　Ｃｈｉｎｅｓｅ）［８］　李润方，王建军．齿轮系统动力学：振动、冲击、噪声［Ｍ］．北京：科学出版社，１９９７．［９］　Ｓｏｎｄｋａｒ　Ｐ，Ｋａｈｒａｍａｎ　Ａ．Ａ　ｄｙｎａｍｉｃ　ｍｏｄｅｌ　ｏｆ　ａ　ｄｏｕｂｌｅ－ｈｅｌ－ｉｃａｌ　ｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｓｅｔ［Ｊ］．Ｍｅｃｈａｎｉｓｍ　ａｎｄ　Ｍａｃｈｉｎｅ　Ｔｈｅｏ－ｒｙ，２０１３，７０（７）：１５７－１７４．［１０］　郭家舜，王三民，刘海霞．某新型直升机传动系统弯－扭耦合振动特性研究［Ｊ］．振动与冲击，２００９，２８（１０）：１３２－１４０．ＧＵＯ　Ｊｉａｓｈｕｎ，ＷＡＮＧ　Ｓａｎｍｉｎ，ＬＩＵ　Ｈａｉｘｉａ．Ｌａｔｅｒａｌ－ｔｏｒ－ｓｉｏｎａｌ　ｃｏｕｐｌｅｄ　ｖｉｂｒａｔｉｏｎ　ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ　ｏｆ　ｔｒａｎｓｍｉｓｓｉｏｎ　ｏｆ　ａｎｅｗ　ｔｙｐｅ　ｈｅｌｉｃｏｐｔｅｒ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｖｉｂｒａｔｉｏｎ　ａｎｄ　Ｓｈｏｃｋ，２００９，２８（１０）：１３２－１４０．（ｉｎ　Ｃｈｉｎｅｓｅ）［１１］　秦大同，肖正明，王建宏．基于啮合相位分析的盾构机减速器多级行星齿轮传动动力学特性［Ｊ］．机械工程学报，２０１１，４７（２３）：２０－２９．ＱＩＮ　Ｄａｔｏｎｇ，ＸＩＡＯ　Ｚｈｅｎｇｍｉｎｇ，ＷＡＮＧ　Ｊｉａｎｈｏｎｇ．Ｄｙｎａｍ－ｉｃ　ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ　ｏｆ　ｍｕｌｔｉ－ｓｔａｇｅ　ｐｌａｎｅｔａｒｙ　ｇｅａｒｓ　ｏｆ　ｓｈｉｅｌｄｔｕｎｎｅｌｉｎｇ　ｍａｃｈｉｎｅ　ｂａｓｅｄ　ｏｎ　ｐｌａｎｅｔ　ｍｅｓｈ　ｐｈａｓｉｎｇ　ａｎａｌｙｓｉｓ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｍｅｃｈａｎｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，２０１１，４７（２３）：２０－２９．（ｉｎ　Ｃｈｉｎｅｓｅ）［１２］　史志伟．行星传动啮合相位计算方法研究［Ｊ］．科学计算与工程，２０１１，１１（２２）：５２８６－５２８９．ＳＨＩ　Ｚｈｉｗｅｉ．Ａ　ｍｅｔｈｏｄ　ｔｏ　ｄｅｔｅｒｍｉｎｅ　ｔｈｅ　ｍｅｓｈ　ｐｈａｓｉｎｇ　ｉｎｐｌａｎｅｔａｒｙ　ｇｅａｒ　ｔｒａｉｎ［Ｊ］．Ｓｃｉｅｎｃｅ　Ｔｅｃｈｎｏｌｏｇｙ　ａｎｄ　Ｅｎｇｉｎｅｅｒ－ｉｎｇ，２０１１，１１（２２）：５２８６－５２８９４．（ｉｎ　Ｃｈｉｎｅｓｅ）［１３］　Ｔａｍｍｉｎａｎａ　Ｖ　Ｋ，Ｋａｈｒａｍａｎ　Ａ，Ｖｉｊａｙａｋａｒ　Ｓ．Ａ　ｓｔｕｄｙ　ｏｆｔｈｅ　ｒｅｌａｔｉｏｎｓｈｉｐ　ｂｅｔｗｅｅｎ　ｔｈｅ　ｄｙｎａｍｉｃ　ｆａｃｔｏｒｓ　ａｎｄ　ｔｈｅ　ｄｙ－ｎａｍｉｃ　ｔｒａｎｓｍｉｓｓｉｏｎ　ｅｒｒｏｒ　ｏｆ　ｓｐｕｒ　ｇｅａｒ　ｐａｉｒｓ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆＭｅｃｈａｎｉｃａｌ　Ｄｅｓｉｇｎ，２００７，１２９（１）：７５－８４．［１４］　Ｓｗｅｅｎｅｙ　Ｐ　Ｊ，Ｒａｎｄａｌｌ　Ｒ　Ｂ．Ｇｅａｒ　ｔｒａｎｓｍｉｓｓｉｏｎ　ｅｒｒｏｒ　ｍｅａｓ－ｕｒｅｍｅｎｔ　ｕｓｉｎｇ　ｐｈａｓｅ　ｄｅｍｏｄｕｌａｔｉｏｎ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　Ｍｅｃｈａｎｉ－ｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ　Ｓｃｉｅｎｃｅ，１９９６，２１０（３）：２０１－２１３．［１５］　Ｖｅｌｅｘ　Ｐ，Ａｊｍｉ　Ｍ．Ｄｙｎａｍｉｃ　ｔｏｏｔｈ　ｌｏａｄｓ　ａｎｄ　ｑｕａｓｉ－ｓｔａｔｉｃｔｒａｎｓｍｉｓｓｉｏｎ　ｅｒｒｏｒｓ　ｉｎ　ｈｅｌｉｃａｌ　ｇｅａｒｓ：ａｐｐｒｏｘｉｍａｔｅ　ｄｙｎａｍｉｃｆａｃｔｏｒ　ｆｏｒｍｕｌａｅ［Ｊ］．Ｍｅｃｈａｎｉｓｍ　ａｎｄ　Ｍａｃｈｉｎｅ　Ｔｈｅｏｒｙ，２００７，４２（１１）：１５１２－１５２６．［１６］　张锁怀，沈允文，董海军，等．转速和不平衡质量对齿轮拍击振动的影响［Ｊ］．航空动力学报，２００３，１８（１）：１９７－２０３．ＺＨＡＮＧ　Ｓｕｏｈｕａｉ，ＳＨＥＮ　Ｙｕｎｗｅｎ，ＤＯＮＧ　Ｈａｉｊｕｎ，ｅｔ　ａｌ．Ｔｈｅ　ｉｎｆｌｕｅｎｃｅ　ｏｆ　ｓｐｅｅｄ　ａｎｄ　ｍａｓｓ　ｕｎｂａｌａｎｃｅ　ｏｎ　ｄｙｎａｍｉｃｃｈａｒａｃｔｅｒｉｓｔｉｃｓ　ｏｆ　ａ　ｇｅａｒ－ｒａｔｔｌｉｎｇ　ｓｙｓｔｅｍ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆＡｅｒｏｓｐａｃｅ　Ｐｏｗｅｒ，２００３，１８（１）：１９７－２０３．（ｉｎ　Ｃｈｉｎｅｓｅ）［１７］　朱自冰，朱如鹏，鲍和云．两级星型齿轮传动系统非线性动力学研究［Ｊ］．航空动力学报，２００７，２２（１１）：１９６３－１９７０．ＺＨＵ　Ｚｉｂｉｎｇ，ＺＨＵ　Ｒｕｐｅｎｇ，ＢＡＯ　Ｈｅｙｕｎ．Ｎｏｎ－ｌｉｎｅａｒ　ｄｙ－ｎａｍｉｃ　ｓｔｕｄｙ　ｏｆ　２－ｓｔａｇｅ　ｇｅａｒ　ｔｒａｉｎ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆ　ＡｅｒｏｓｐａｃｅＰｏｗｅｒ，２００７，２２（１１）：１９６３－１９７０．（ｉｎ　Ｃｈｉｎｅｓｅ）［１８］　崔亚辉，刘占生，叶建槐，等．内外激励作用下含侧隙的齿轮传动系统的分岔和混沌［Ｊ］．机械工程学报，２０１０，４６（１１）：１２９－１３６．ＣＵＩ　Ｙａｈｕｉ，ＬＩＵ　Ｚｈａｎｓｈｅｎｇ，ＹＥ　Ｊｉａｎｈｕａｉ，ｅｔ　ａｌ．Ｂｉｆｕｒｃａｔｉｏｎａｎｄ　ｃｈａｏｓ　ｏｆ　ｇｅａｒ　ｔｒａｎｓｍｉｓｓｉｏｎ　ｓｙｓｔｅｍ　ｗｉｔｈ　ｃｌｅａｒａｎｃｅ　ｓｕｂ－ｊｅｃｔｅｄ　ｔｏ　ｉｎｔｅｒｎａｌ　ａｎｄ　ｅｘｔｅｒｎａｌ　ｅｘｃｉｔａｔｉｏｎ［Ｊ］．Ｊｏｕｒｎａｌ　ｏｆＭｅｃｈａｎｉｃａｌ　Ｅｎｇｉｎｅｅｒｉｎｇ，２０１０，４６（１１）：１２９－１３６．（ｉｎ　Ｃｈｉｎｅｓｅ）（编辑：秦理曼、叶　青）４０３２。