第九讲节约里程法案例详解
- 格式：ppt
- 大小：1.20 MB
- 文档页数：61
下载文档原格式
合集下载
物流工程——节约里程法
物流配送——节约里程法(Saving Algorithm)
• 车辆调度程序法(Vehicle Scheduling Program:VSP) • 又称节约算法，是指用来解决运输车辆数目不确定的问题 的最有名的启发式算法。 核心思想: • 节约里程法核心思想是依次将运输问题中的两个回路合并 为一个回路，每次使合并后的总运输距离减小的幅度最大， 直到达到一辆车的装载限制时，再进行下一辆车的优化。 优化过程分为并行方式和串行方式两种。
（0.9）
P3
4
P2
以此类推，如果前面涉及了某些 路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
（1.7）
5
6 8
（1.4）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
5
（0.9）
P3
4
P2
（1.7）
配送线路1
（1.4）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
案例： • 宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见 下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优 化方法。公司客户分布在全国各地,这里主要以广东省内7家客户 及省外一家特殊客户的一次配送为例。
客户(i) 货运量 (qi) 东莞 江门 4.3 1.8 惠州 0.7 阳江 2.2 汕尾 3.6 揭阳 3.6 汕头 1.6 漳州 2
（2.4）
节约里程法
（0.9）
P3
（1.7）
P2
6 8
（1.4）
• 车辆调度程序法(Vehicle Scheduling Program:VSP) • 又称节约算法，是指用来解决运输车辆数目不确定的问题 的最有名的启发式算法。 核心思想: • 节约里程法核心思想是依次将运输问题中的两个回路合并 为一个回路，每次使合并后的总运输距离减小的幅度最大， 直到达到一辆车的装载限制时，再进行下一辆车的优化。 优化过程分为并行方式和串行方式两种。
（0.9）
P3
4
P2
以此类推，如果前面涉及了某些 路线，往后就考虑未涉及的路线 P2P3----P3P4-----P1P5
（1.7）
5
6 8
（1.4）
P4
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
5
（0.9）
P3
4
P2
（1.7）
配送线路1
（1.4）
P4
8
7
P0
10
8
P5
P1
(1.5)
（2.4）
节约里程法
案例： • 宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见 下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优 化方法。公司客户分布在全国各地,这里主要以广东省内7家客户 及省外一家特殊客户的一次配送为例。
客户(i) 货运量 (qi) 东莞 江门 4.3 1.8 惠州 0.7 阳江 2.2 汕尾 3.6 揭阳 3.6 汕头 1.6 漳州 2
（2.4）
节约里程法
（0.9）
P3
（1.7）
P2
6 8
（1.4）
节约里程法PPT课件
的使用率和周转率。
实施效果
通过节约里程法的应用，共享单 车的调度系统得到了优化，高峰 时段的供不应求问题得到了缓解， 提高了共享单车的服务质量和用
户体验。
06
总结与展望
总结节约里程法的原理与应用
要点一
总结
要点二
应用
节约里程法的原理是基于车辆运输路径优化，通过合理安 排车辆行驶路线，减少车辆空驶和重复行驶的距离，达到 降低运输成本和提高运输效率的目的。在实际应用中，该 方法广泛应用于物流配送、公共交通和共享出行等领域。
节约里程法的应用场景
物流配送路线规划
总结词
节约里程法在物流配送路线规划中，能够优化车辆行驶路径，减少运输成本和 时间。
详细描述
通过计算各需求点之间的距离节约量，选择最佳的配送路线，使得车辆在满足 客户需求的同时，总行驶距离最短，从而达到节约成本和时间的目的。
公共交通路线规划
总结词
节约里程法在公共交通路线规划中， 能够提高线路效率和乘客出行体验。
里程法更注重求解的稳定性。
05
节约里程法的实际案例分 析
某快递公司的配送路线优化
01
02
03
背景介绍
某快递公司面临配送路线 不优化、成本高昂的问题， 需要采用节约里程法进行 配送路线的优化。
解决方案
利用节约里程法，对快递 公司的配送路线进行重新 规划，减少重复行驶和空 驶，提高车辆装载率。
实施效果
低运输成本。
它主要应用于多个发货点之间， 通过合并多个货物装载在同一辆
车上，实现运输效率最大化。
节约里程法的基本思想是通过优 化运输路线，减少车辆空驶和重 复行驶，提高运输效率，降低运
输成本。
适用范围与条件
实施效果
通过节约里程法的应用，共享单 车的调度系统得到了优化，高峰 时段的供不应求问题得到了缓解， 提高了共享单车的服务质量和用
户体验。
06
总结与展望
总结节约里程法的原理与应用
要点一
总结
要点二
应用
节约里程法的原理是基于车辆运输路径优化，通过合理安 排车辆行驶路线，减少车辆空驶和重复行驶的距离，达到 降低运输成本和提高运输效率的目的。在实际应用中，该 方法广泛应用于物流配送、公共交通和共享出行等领域。
节约里程法的应用场景
物流配送路线规划
总结词
节约里程法在物流配送路线规划中，能够优化车辆行驶路径，减少运输成本和 时间。
详细描述
通过计算各需求点之间的距离节约量，选择最佳的配送路线，使得车辆在满足 客户需求的同时，总行驶距离最短，从而达到节约成本和时间的目的。
公共交通路线规划
总结词
节约里程法在公共交通路线规划中， 能够提高线路效率和乘客出行体验。
里程法更注重求解的稳定性。
05
节约里程法的实际案例分 析
某快递公司的配送路线优化
01
02
03
背景介绍
某快递公司面临配送路线 不优化、成本高昂的问题， 需要采用节约里程法进行 配送路线的优化。
解决方案
利用节约里程法，对快递 公司的配送路线进行重新 规划，减少重复行驶和空 驶，提高车辆装载率。
实施效果
低运输成本。
它主要应用于多个发货点之间， 通过合并多个货物装载在同一辆
车上，实现运输效率最大化。
节约里程法的基本思想是通过优 化运输路线，减少车辆空驶和重 复行驶，提高运输效率，降低运
输成本。
适用范围与条件
6.节约里程法用
节约里程表
ABCDEFGHI
A
16 10 3 0 0 0 6 12
B
14 7 2 0 0 0 6
C
11 6 0 0 0 0
D
71 00 0
E
8 00 0
F
60 0
G
60
H
8
I
根据节约里程表中节约里程多少的顺 序，由大到小排列，编制节约里程顺 序表，以便尽量使节约里程最多的点 组合装车配送。
顺位 里程 节约里 顺位 里程 节约里 顺位 里程 节约里
总共节约里程为：362－170=192 或（33+34+16）+（28+21）+（22+18+18）+2=192
例：由配送中心P向A—I等9个用户配送货物。图中 连线上的数字表示公路里程（km）。靠近各用户 括号内的数字，表示各用户对货物的需求量（t）。 配送中心备有2t和4t载重量的汽车，且汽车一次 巡回走行里程不能超过35km，设送到时间均符合 用户要求，求该配送中心的最优送货方案。
根据节约里程排序表和配车（车辆的载重和容积因素）、 车辆行驶里程等约束条件，渐进绘出配送路径：
(0.9)
C
5
(1.2)
4
D
6
B (0.5)
5
(1.6)
E
6
路径A A (1.7)
(1.1)
9 路径B
P
10
F
10
路径C
G
(0.9)
12
7
8
H
6
I (0.6)
(0.9)
• 路径A：4t车，走行32km，载重量3.7t； • 路径B：4t车，走行31km，载重量3.9t； • 路径C：2t车，走行30km，载重量1.8t。
节约里程法PPT课件
授课：XXX
35
配送线路的优化
（一）直送式配送：位势法 （二）分送式配送：节约里程法 1、节约里程的基本原理
用一辆车将所有客户的货物装在一起，沿着一条精心 选择的最佳路线，将货物送到客户手中。 目标：节约车辆、节约费用、缓解交通压力、减少环 境污染。
△S = S1 + S2 - S3
授课：XXX
36
送货，需要2t货车10辆，走行授总课里：X程XX148km。
14
案例分析
• 例 ： 某 一 配 送 中 心 p0 向 10 个 客 户 pj(j=1,2,…,10) 配 送 货 物 ， 其 配 送 网 络 如 图 11-9所示。图中括号内的数字表示客户的需 求量（T），线路上的数字表示两节点之间 的距离。配送中心有2t和4t两种车辆可供使 用，试制定最优的配送方案。
节约里程
顺序排位
15
13
13
13
11
13
10
16
10
16
9
16
9
19
9
19
8
21
8
22
7
22
6
22
授课：XXX
连接线
F－ G G－ H H－ I B－ I A－ D F－ H B－ E D－ F G－ I C－ J E－ G F－ I
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
13
第四步：根据节约里程排序表和配送车辆载重及行驶里程等约束条件，
第四步：确定配送线路。从分类表中，按节约里程大小顺序，组成线路图
授课：XXX
19
• （1）初始方案：对每一客户分别单独派车 送货，结果如图11-10。
《节约里程法》详解
"节约里程法"英文翻译：节约里程法(Saving Algorithm)内容摘要：节约里程法又称节约算法，是指用来解决运输车辆数目不确定的VRP问题的最有名的启发式算法。
什么是节约里程法节约里程法又称节约算法，是指用来解决运输车辆数目不确定的VRP问题的最有名的启发式算法。
节约里程法的基本原理节约里程法的基本思路如下图,已知O点为配送中心,它分别向用户A和B送货。
设O点到用户A和用户B的距离分别为a和b。
用户A和用户B之间的距离为c,现有两种送货方案,如图下(a)和(b)所示。
在上图(a)中配送距离为2(a+b)；图上(b)中,配送距离为a+b+c。
对比这两个方案,哪个更合理呢？这就要看哪个配送距离最小,配送距离越小,则说明方案越合理。
由上图(a)中的配送距离,减去图1(b)中的配送距离可得出:2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c(1)如果把上图(b)看成一个三角形,那么a、b、c则是这个三角形三条边的长度。
由三角形的几何性质可知,三角形中任意两条边的边长之和,大于第三边的边长。
因此,可以认定(1)式中结果是大于零的。
即:a+b－c＞0(2)由(2)式可知,(b)方案优于(a)方案,节约了(a+b-c)的里程,这种分析方案的优劣式的思想,就是节约里程法的基本思想。
、拓展资料：一、节约里程法核心思想节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
二、节约里程法示例例:有一配送P具有如图所示的配送网络,其中A-J表示收货站,()内数字表示发送量(吨),路线上的数字表示道路距离(公里)。
问为使行走距离尽量小,应该如何去求配送线路?假设能够利用的车是2吨车(即最大载重量是2吨)和4吨车两种,并限制车辆一次运行的初步距离是30公里。
节约里程法典型实例
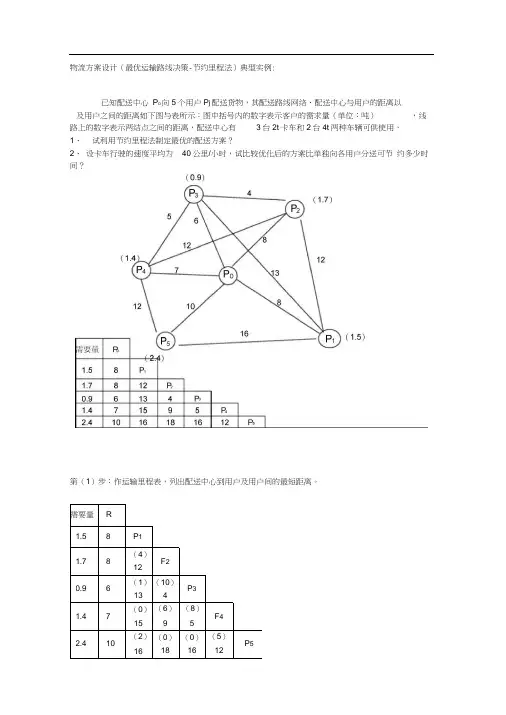
物流方案设计（最优运输路线决策-节约里程法）典型实例:已知配送中心P O向5个用户P j配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图与表所示：图中括号内的数字表示客户的需求量（单位：吨），线路上的数字表示两结点之间的距离，配送中心有3台2t卡车和2台4t两种车辆可供使用，1、试利用节约里程法制定最优的配送方案？2、设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间？第（1）步：作运输里程表，列出配送中心到用户及用户间的最短距离。
得初始方案配送距离=39X 2=78KM第（5）步：根据载重量约束与节约里程大小，将各客户结点连接起来，形成二个配送路线。
即A B 两配送方案。
序号 路线 节约里程 序号 路线 节约里程1 P 2P 3 10 6 P i F 52 2 P 3P 4 8 7 P i P3 1 3 P 2P4 6 8 F 2F5 0 4 P 4P 5 5 9 F 3F 5 0 5P l P 2410P i F 4第（2）步：由运输里程表、按节约里程公式，求得相应的节约里程数，如上表（ 第（3）步：将节约里程 sij 进行分类，按从大到小顺序排列第（4）步：确定单独送货的配送线路）内。
(1.5)①配送线路A：P0-P2-P3-P4- P 0 运量q A= q 2+q3+q4 = 1.7+0.9+1.4 = 4t 用一辆4t 车运送节约距离S A =10 +8 = 18km②配送线路B: P 0-P5 -P 1-P0 运量q B =q 5+q1=2.4+1.5=3.9t<4t 车用一辆4t 车运送节约距离S B=2km第（6）步：与初始单独送货方案相比，计算总节约里程与节约时间总节约里程：△ S= S A+S B= 20 km与初始单独送货方案相比，可节约时间：△T = △ S/V=20/40=0.5小时。
第九讲节约里程法案例详解
3. 配送物的数量和重量 数量和重量的增加虽说会使配送作业量增大，但大批 量的作业往往使配送效率提高，配送的数量和重量是委托 人获得价格折扣的理由 4. 货物种类及作业过程 不同种类的货物配送难度不同，对配送作业要求不 同，承担的责任也不一样，因而对成本会产生较大幅度的 影响。采用原包装配送的成本支出显然要比配装配送要低， 因而不同的配送作业过程，直接影响配送成本
按功能计算物流配送成本
是指分别按备货、搬运、储存、分拣、加工、 是指分别按备货、搬运、储存、分拣、加工、 配装、配送等功能来计算成本。 配装、配送等功能来计算成本。
例：某配送中心配送成本的计算
配送成本=分拣成本+配装成本+ 配送成本=分拣成本+配装成本+流通加工成 本+配送运输成本
分拣成本的计算 分拣成本是指分拣机械及人工在完成货物分 拣过程中所发生的各项费用之和。 （1）折旧费：分拣设备按规定进行计提的折旧 费，根据“固定资产折旧计算表”中按照分拣设 备提取的折旧金额计入成本。 （2）修理费：分拣设备进行保养和修理所发生 的工料费用，辅助生产部门对分拣设备进行保养 和维修的费用，根据“辅助生产费用计入分拣成 本表”中分配的分拣成本金额既然成本。
根据节约里程表中节约里程多少的顺序，由大 到小排列，编制节约里程顺序表，以便尽量使节约 里程最多的点组合装车配送。
顺位 号
里程
节约里程
顺位 号
里程
节约里 程
顺位 号
里程
节约里程
1 2 3 4 5 6
A-B B-C A-I C-D A-C E-F
16 14 12 11 10 8
6 8 8 10 10 10
5. 外部成本 配送经营时或需要使用到配送企业以外的资 源，比如当地的起吊设备租赁市场具有垄断性， 则配送企业就需要租用起吊设备从而增加成本支 出。如当地的陆桥普遍收费且无管制，则必然使 配送成本居高不下 。
节约里程法应用案例
节约里程法应用案例在当今竞争激烈的商业环境中，物流成本的有效控制对于企业的生存和发展至关重要。
节约里程法作为一种优化配送路线的有效方法，能够显著降低运输成本，提高物流效率。
接下来，让我们通过一个具体的案例来深入了解节约里程法的实际应用。
假设我们有一家位于城市中心的配送中心，需要向位于城市不同区域的五个客户（A、B、C、D、E）配送货物。
每个客户的需求量以及他们之间的距离如下表所示：｜客户|需求量（吨）｜与配送中心距离（公里）｜｜｜｜｜｜A|5|10|｜B|8|12|｜C|3|8|｜D|6|15|｜E|4|11|｜客户|A|B|C|D|E|｜｜｜｜｜｜｜｜A| ｜ 18 ｜ 22 ｜ 25 ｜ 16 ｜｜B| 18 ｜｜ 10 ｜ 18 ｜ 12 ｜｜C| 22 ｜ 10 ｜｜ 14 ｜ 9 ｜｜D| 25 ｜ 18 ｜ 14 ｜｜ 20 ｜｜E| 16 ｜ 12 ｜ 9 ｜ 20 ｜｜首先，我们按照传统的方法，即每个客户单独配送，计算出总运输里程。
配送中心到客户 A 的往返里程为 2×10 ＝ 20 公里。
配送中心到客户 B 的往返里程为 2×12 ＝ 24 公里。
配送中心到客户 C 的往返里程为 2×8 ＝ 16 公里。
配送中心到客户 D 的往返里程为 2×15 ＝ 30 公里。
配送中心到客户 E 的往返里程为 2×11 ＝ 22 公里。
总运输里程为 20 ＋ 24 ＋ 16 ＋ 30 ＋ 22 ＝ 112 公里。
接下来，我们应用节约里程法来优化配送路线。
第一步，计算两两客户之间的节约里程数。
例如，客户 A 和客户 B 之间的节约里程数为：（配送中心到 A 的距离＋配送中心到 B 的距离 A 到 B 的距离）× 2 ＝（10 ＋ 12 18）× 2 ＝ 8 公里。
按照同样的方法，计算出所有两两客户之间的节约里程数，如下表所示：｜客户|A|B|C|D|E|｜｜｜｜｜｜｜｜A| ｜ 8 ｜ 6 ｜ 5 ｜ 2 ｜｜B| 8 ｜｜ 4 ｜ 3 ｜ 4 ｜｜C| 6 ｜ 4 ｜｜ 2 ｜ 3 ｜｜D| 5 ｜ 3 ｜ 2 ｜｜ 5 ｜｜E| 2 ｜ 4 ｜ 3 ｜ 5 ｜｜第二步，根据节约里程数的大小对路线进行合并和优化。
[管理学]第九讲节约里程法案例详解
![[管理学]第九讲节约里程法案例详解](https://img.taocdn.com/s1/m/8bcf0bf476a20029bd642d71.png)
某配送中心配送网络图
(0.9)
C
4
5
(1.2)
D
4
B (0.5)
7
5
6
(1.6) E
6 5
8
5
A (1.7)
7
11
9
P
6
(1.1) F
10 10
3
4
I (0.6)
14
5
G
(0.9)
7 12
H
(0.9)
计算配送中心至各用户以及各用户之间的最 短距离，列表得最短距离表：
PABCDEFGHI
P
11 10 9 6 7 10 10 8 7
A
5 10 14 18 21 21 13 6
B
5 9 15 20 20 18 11
C
4 10 19 19 17 16
D
6 15 16 14 13
E
9 17 15 14
F
14 18 17
G
12 17
H
7
I
由最短距离矩阵，利用节约法计算出各用户 之间的节约里程，编制节约里程表：
ABCDEFGHI
A
16 10 3 0 0 0 6 12
2.分拣费用
（1）分拣人工费用。这是指从事分拣工作的作业人员 及有关人员工资、奖金、补贴等费用的总和。
（2）分拣设备费用。这是指分拣机械设备的折旧费用 及修理费用。
3.配装费用
（1）配装材料费用。常见的配装材料有木材、纸、自然纤 维和合成纤维、塑料等。这些包装材料功能不同，成本相 差很大。
（2）配装辅助费用。除上述费用外，还有一些辅助性费用， 如包装标记、标志的印刷，拴挂物费用等的支出。
节约里程法
节约里程法1.原理设P 为配送中心，A 和B 为收货点，相互之间的道路距离为a , b , c 。
若分别使用两辆货车分别向A 、B 两地往返送货，其行驶里程为:2a+2b 。
但若使一辆货车（货车可以满载两地送货）由P → A →B →P ，单线巡回送货，其行驶总里程为a+c+b 。
两者相比，后一种方案比前一种送货方案可节省的运输距离是： （2a+2b ）-（a+c+b ）= a + b - c > 0这一节约距离称为节约里程，所以我们称这种方法为“节约里程法”。
2 .实例由于案例所给内容有限，所以我们自行上网查找了一些资料。
下图是我们找到的位于郑明现代物流有限公司上海总部周边的一些大型商超，下面我们就假设这些超市为郑明现代物流有限公司的配送点，利用节约里程法来设计末端配送网络的合理运输。
上海郑明现代物流有限公司周边的商超配送点PABacb图X-X备注：1 . 红色五角星所在位置即为郑明现代物流有限公司的所在地(P)2 . 紫色圆圈即为超市配送点的位置及其名称（从左至右依次为：城市超市(A)、沃尔玛超市(B)、世纪华联超市(C)、联华超市(F)、家乐福超市(D)、大润发超市(E)）为直观清晰的了解郑明现代物流有限公司与给超市配送点之间的关系，我们将上图简化为下图（图X-X）的简易图形。
线段旁的数字为两者之间的距离，单位：km.图X-X节约里程法的求解过程如下：1.计算配送中心P 到各个配送点及各配送点之间的最短路距离，如下表最短距离表P ABCDEFP A 4.7B 2.8 6.8C 0.6 4.2 2.9D 8 12.7 6.1 8.6E 7.4 12.1 9.2 8 3.1F1.83.24.62.49.89.14.26.12.96.80.62.883.17.49.11.83.2BDFA C EP2.计算各个配送点之间的节约里程，如下表节约里程表A B C D E FAB 0.7C 1.1 0.5D 0 4.7 0E 0 1 0 12.3F 3.3 0 0 0 0.13.进行排序：节约里程排序表序号连接节约序号连接节约1 DE 12.3 8 AD 02 BD 4.7 9 AE 03 AF 3.3 10 BF 04 AC 1.1 11 CD 05 AB 0.7 12 CE 06 BC 0.5 13 CF 07 EF 0.1 14 DF 04.得出线路安排线路一：P →E →D →B →P 节约里程为：12.3+4.7= 17 km 线路二：P →F →A →C →P 节约里程为：3.3+1.1= 4.4 km如果没有使用节约里程法来进行商超的配送，那么结果是怎样的呢？假定初始配送方案是由中心点P 按最短路径向其余各个点分别进行送货，则总配送里程为：2x(0.6+4.2+1.8+7.4+8+2.8)=49.6 km 。
节约里程法ppt课件
G
H
I
J
表2 最短距离表
第二步：由最短距离表，利用“节约里程”法计算出各连锁分店之间 的节约里程，做出节约里程表（见表3），计算结果有正有负，节约里 程为负数时，无实际意义，在表内写0。
表3 节约里程表
A A B C D E F G H I J
B
C
D
E
F
G
H
I
J
第三步：将节约里程由大到小顺序排列，列出节约里程排序表（见表 4），以便尽量使节约里程最多的点组合装车配送。
配送线路的优化
一、配送线路的优化方法 ㈡一对多配送的最短路线问题
节约里程法
原理：三角形一边之长必定小于另外两边之和。
A
L1 配 送 中 心 用 户 L1 配 送 中 心 L3
A
用 户
P
L2 往 返 发 货
P
L2 巡 回 发 货
B
用 户
B
用 户
在汽车载重量允许的情况下，采用巡回发货比采用往返发货可节约汽车走行 里程为：∆L=[2(L1+L2)]-(L1+L2+L3)=L1+L2-L3
• （1）初始方案：对每一客户分别单独派车 送货，结果如图11-10。
• 修正方案4
第四节
配送路线设计
一、配送路线选择问题
物流中心在组织货物配送时，有n个客户，处在同一城市不同地区，如 何取定最佳的配送路线？
例题：如图8-1所示的运输网络，试求出最优路线。
V1 10 V
3
10
V
6
V1
10
V310来自第一步：计算最短距离。根据配送网络中的已知条件， 计算配送中心与客户及客户之间的最短距离，结果见表 11-11。 第二步：计算节约里程sij,结果见表11-12。
物流线路规划节约里程法案例详解
节约里程法案例详解假如由一家配送中心P向两个用户A、B送货，配送中心到两客户的最短距离分别是L1和L2，A和B间的最短距离为L3，AB的货物需求量分别是Q1和Q2，且Q1+Q2小于车辆装载量Q【如果Q1+Q2大于车辆装载量Q，那一辆车就无法装完两位客户的货物】。
如下图所示：如果配送中心用两辆汽车分别对A、B两个用户各自往返送货时，汽车行驶的总里程L是L=2（L1+ L2）如果用一辆汽车向A、B两个用户巡回送货，则汽车行驶总里程L′为L′= L1+ L2+L3根据三角形的一边之长必定小于另外两边之和的原理，后一种配送方案比前一种方案节约里程△L为△L=2（L1+ L2）-（L1+ L2+L3）= L1+ L2-L3【这就是节约里程法产生的初衷，以最短距离最优配载完成送货作业】案例：位于市内的百家姓配送中心（P0）向它旗下的10家连锁商店p i(i=1,2,…,10)配送商品，其配送网络如下图所示。
图中括号内的数字表示每一家连锁店的需求量（t），线路上的数字表示两节点之间的距离（km）。
配送中心现有2t和4t车辆可供使用（无数量限制），并且每辆车配送距离不得超过30km。
请为百家姓配送中心制定最优的配送方案。
分析：初始方案：如果从P点向各点分别派车送货。
1、从百家姓配送中心出发，需要设计10条配送线路，分别向10家连锁店配送商品；2、需要10辆2t的配送车辆（每家连锁店的需要量都低于2t），总配送距离为148km。
第二种：节约里程法解题思路：相互间的节约里程计算根据△L== L1+ L2-L3 原理，例如以“百家姓配送中心交通图”中的P0（配送中心）到客户d、客户c的节约里程为例：dc△L==P0d(L1)+P0c (L2)-dc(L3 )==8 + 7 - 5=10如此计算出客户d和客户c间的节约里程数为10，以此方法计算出各个节点的节约里程数。
方案修正过程（优化到最终线路）1、方案修正过程实际上是线路规划过程，根据节约里程法原理从节约里程数最大的节点开始选择（这是先要排序的原因）；2、所有规划线路的起点和终点都是配送中心，这里是P0；3、最大节约里程是a和b间的节约里程数15，那么路线的走向可以是P0-A或P0-B。
节约里程法案例
由配送中心A 向两个用户M 、N 送货，A 至M 、N 的最短距离分别为l1和l2，M 、N 之间的距离为l3，用户M 、N 对货物的需求量分别为q1和q2。
如图：若用两辆汽车分别对A 、B 两个用户所需货物，各自往返送货时，汽车直行总里程为：l=2（l1+l2）如果改为有一辆汽车向M 、N 两个用户巡回送货（设q1+q2<汽车标重载重量），则汽车走行里程为： l=l1+l2+l3后一种送货方案比前一种送货方案节约的汽车走行里程为： △l=[2（l1+l2）]-（l1+l2+l3）=l1+l2-l34 案例分析如图所示：由配送中心P 向A-H8个用户配送货物。
图中连线上的数字表示两点间的里程（km ），图中靠近个用户括号内的数字，表示各用户对货物的需求量（t ）。
配送中心备有2t 和3t 载重量的汽车，且汽车一次巡回里程不超过35km 。
色送到时间均符合客户要求。
求改配送中心的最优送货方案。
﹙q1﹚（q2）节约里程表A B C D E F G HA 9 2 0 0 0 0 7B 8 5 0 0 0 6C 11 3 0 0 0D 10 5 0 0E 9 2 0F 13 3G 6H根据节约里程表中节约里程的顺序，由大到小排列，编制节约里程顺序表。
节约里程顺序表根据节约里程顺序表和配车（车辆的载重），车辆行驶里程等约束条件，渐进绘出如图所示配送路径.路径A：2t车，走行24km，载重量1.8t。
路径B：3t车，走行33km，载重量3.0t。
路径C：3t车，走行23km，载重量2.8t。
总共行走80km，节约里程60km。
从图中可看：一次确定的A、B、C三条路径均符合配送中心的约束条件。
需要2t汽车1辆，3t汽车2辆，总走行里程为80km，若简单的每个用户派一辆汽车配送，需要2t汽车8辆，走行总里程为140km。
通过比较可以看出，利用节约里程法制定配送方案确定送货路径，具有明显效果。
配送路线优化(里程节约法)
5
P4
P5 2.4 10 16 18 16 12 P5
节约里程法
第2步：按节约里程公式求得相应的节约里程数
需求量 P0
1.5 8
P1
12 1.7 8
4
13 0.9 6
1
15 1.4 7
0
16 2.4 10
2
P2
4
10
P3
9
5
6
8
P4
18
16
12
0
0
5
P5
节约里程法
第 3 步：将节约里程按从大到小顺序排列
（0.9）
P3
4
（1.7）
P2
5
6
8
（1.4）
P4
7
P0
10
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
P1 (1.5)
节约里程法 （0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
P1 (1.5)
请为百家姓配送中心制定最优的配送方案。
第一步：计算最短距离。根据配送网络中的已知条件， 计算配送中心与客户及客户之间的最短距离，结果见表 11-11。 第二步：计算节约里程sij,结果见表11-12。
第三步：将节约sij,进行分类，按从大到小的顺序排 列，得表11-13
节约里程法典型实例
物流方案设计（最优运输路线决策－节约里程法）典型实例：已知配送中心P O向5个用户P j配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图与表所示：图中括号内的数字表示客户的需求量（单位：吨），线路上的数字表示两结点之间的距离，配送中心有3台2t卡车和2台4t两种车辆可供使用，1、试利用节约里程法制定最优的配送方案？2、设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间？（0.9）第（1）步：作运输里程表，列出配送中心到用户及用户间的最短距离。
-第（2）步：由运输里程表、按节约里程公式，求得相应的节约里程数，如上表（ ）内。
第（3）步：将节约里程sij 进行分类，按从大到小顺序排列得初始方案配送距离=39×2=78KM第（5）步：根据载重量约束与节约里程大小，将各客户结点连接起来，形成二个配送路线。
即A 、B 两配送方案。
（（2.4）1.5）（（0.9））①配送线路A：P0-P2-P3-P4- P0运量q A= q2+q3+q4= 1.7+0.9+1.4= 4t用一辆4t车运送节约距离S A =10 +8 = 18km②配送线路B: P0-P5-P1-P0运量q B =q5+q1=2.4+1.5=3.9t<4t车用一辆4t车运送节约距离S B=2km第（6）步：与初始单独送货方案相比，计算总节约里程与节约时间总节约里程：△S= S A+ S B= 20 km与初始单独送货方案相比，可节约时间：△T =△S/V=20/40=0.5小时欢迎下载，谢谢观看！资料仅供参考学习-。
物流工程——节约里程法ppt课件
P2
8
8
P5
P1 (1.5)
配送线路1：
（2.4）
运量 = 1.7+0.9+1.4= 4t
运行距离＝8＋4＋5＋7＝24km
用一辆 4t车运送
节约距离 =18km（即2*21-24）
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 节约距离=2km（即2*18-34）
P2P3----P3P4-----P1P5
（1.7）
P2
5
6
8
（1.4）
P4
7
P0
10
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
练习题
某连锁零售店，下设有一个配送中心P和10个连 锁分店A～J，配送中心和各连锁分店及各连锁分店之 间的位置关系如下图1所示，两点间连线上的数字为 两点间的路线长度（单位：公里）。各连锁分店对某 种商品的需求量见表1，该商品由配送中心统一采购 并进行配送。配送中心备用2t和4t的货车，限定送货 车辆一次巡回距离不超过35公里，设送到时间均符合 用户要求，求配送中心的最优送货方案。
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
8
8
P5
P1 (1.5)
配送线路1：
（2.4）
运量 = 1.7+0.9+1.4= 4t
运行距离＝8＋4＋5＋7＝24km
用一辆 4t车运送
节约距离 =18km（即2*21-24）
配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离＝8＋10＋16＝34km 用一辆 4t车运送 节约距离=2km（即2*18-34）
P2P3----P3P4-----P1P5
（1.7）
P2
5
6
8
（1.4）
P4
7
P0
10
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
P2
8
8
P5
（2.4）
P1 (1.5)
节约里程法
（0.9）
P3
4
5
（1.4）
P4
配送线路1
7
P0
10
（1.7）
练习题
某连锁零售店，下设有一个配送中心P和10个连 锁分店A～J，配送中心和各连锁分店及各连锁分店之 间的位置关系如下图1所示，两点间连线上的数字为 两点间的路线长度（单位：公里）。各连锁分店对某 种商品的需求量见表1，该商品由配送中心统一采购 并进行配送。配送中心备用2t和4t的货车，限定送货 车辆一次巡回距离不超过35公里，设送到时间均符合 用户要求，求配送中心的最优送货方案。
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法
A2、A3、A4共同配送 需求总量：1.5+2.2+1.0=4.7（t） 选一辆载重5吨的汽车 A1、A5共同配送 需求总量：0.8+2.1=2.9（t） 选一辆载重3吨的汽车
共节约的里程数为4+3+2=9（公里）
配送路径如下
A1
0.8
2.1
A5
5
4 3
A0
3
A2
1.5
2
4
1.0
A4
4A3Biblioteka 2.2• 案例：某货物配送中心A0
每两地之间的最短路径
A0 3 3 5 2 4 A1 4 8 5 5 A2 4 5 7 A3 4 8 A4 4 A5
L12=3+3-4=2 L13=0 L14=0 L15=7-5=2 L23=8-4=4 L24=0 L25=0
L34=3 L35=1 L45=2
按节约里程数排序
节约里程法
目录
基本原理 案例分析 优缺点分析 改进建议
2
A
B
1 P
1
如果P（配送中心）分别向A、B客户送货，有两种送货方案 第一种：P—A—P—B—P 总距离为：L1=2（PA+PB） 第二种：P—A—B—P 总距离为：L2=PA+AB+PB
• • • •
PAB可以看作三角形，PA+PB>=AB L1 >=L2 可以看出方案二优于方案一 二都比较方案二比方案一节约了里程 L=PA+PB-AB
宝洁案例
110
• 还可以用两个8T、一个5T的车，但费用就 要高一点
缺点： 第一：利用节约法选择配送路线过于强调节 约路程，而没有考虑行程中的时间因素。 第二：利用节约法选择配送路线不能对客户 的需求的需求进行灵活多变的处理。节约 法更适合需求稳定或需求的时间不紧迫， 这显然不满足现代多变的市场环境。
两个例子-节约里程法
ቤተ መጻሕፍቲ ባይዱ原理
该方法基于节约思想，即在一辆运输车辆上装载多个客户的货物，通过合理规 划运输路线，使得车辆可以依次经过这些客户的所在地，并在满足车辆载重和 容量限制的前提下，实现运输里程的最小化。
发展历程及应用领域
发展历程
节约里程法最初由国外学者提出，后来经过不断改进和完善 ，逐渐形成了较为成熟的理论体系。目前，该方法已经在国 内外得到了广泛应用。
空间。
挑战
新技术的发展和应用需要大量的投入和研发，同时也需要面对技术更新换代快、数据安 全等问题。此外，新技术在节约里程法中的应用还需要与实际业务场景相结合，需要进
行不断的实践和调整。
行业应用拓展方向预测
物流行业
节约里程法在物流行业的应用已经比较成熟，未来可以进 一步拓展到智能物流、绿色物流等领域，实现更加高效、 环保的物流运输。
局限性
虽然节约里程法在优化运输路径方面具有一定的优势，但也存在一些局限性。例如，该方法只考虑了运输里程的 节约，而忽略了其他因素（如时间、服务质量等）对运输成本的影响。此外，在实际应用中，还需要考虑车辆的 载重和容量限制、道路状况、客户需求等多种因素，这也会增加该方法的复杂性和难度。
02 节约里程法实例一：物流 配送优化
01
节约里程法的时间复杂度主要取决于需求点的数量和合并运输的次数。
02
在需求点数量较多的情况下，算法可能需要较长的时间来寻找最优解。
03
为了优化算法，可以考虑采用启发式搜索策略，如贪婪算法、遗传算 法等，来加快搜索速度并提高解的质量。
04
此外，还可以考虑对需求点进行聚类处理，以减少合并运输的次数和 降低算法复杂度。
节约里程法在路线规划中应用
景点间距离与交通方式选择
该方法基于节约思想，即在一辆运输车辆上装载多个客户的货物，通过合理规 划运输路线，使得车辆可以依次经过这些客户的所在地，并在满足车辆载重和 容量限制的前提下，实现运输里程的最小化。
发展历程及应用领域
发展历程
节约里程法最初由国外学者提出，后来经过不断改进和完善 ，逐渐形成了较为成熟的理论体系。目前，该方法已经在国 内外得到了广泛应用。
空间。
挑战
新技术的发展和应用需要大量的投入和研发，同时也需要面对技术更新换代快、数据安 全等问题。此外，新技术在节约里程法中的应用还需要与实际业务场景相结合，需要进
行不断的实践和调整。
行业应用拓展方向预测
物流行业
节约里程法在物流行业的应用已经比较成熟，未来可以进 一步拓展到智能物流、绿色物流等领域，实现更加高效、 环保的物流运输。
局限性
虽然节约里程法在优化运输路径方面具有一定的优势，但也存在一些局限性。例如，该方法只考虑了运输里程的 节约，而忽略了其他因素（如时间、服务质量等）对运输成本的影响。此外，在实际应用中，还需要考虑车辆的 载重和容量限制、道路状况、客户需求等多种因素，这也会增加该方法的复杂性和难度。
02 节约里程法实例一：物流 配送优化
01
节约里程法的时间复杂度主要取决于需求点的数量和合并运输的次数。
02
在需求点数量较多的情况下，算法可能需要较长的时间来寻找最优解。
03
为了优化算法，可以考虑采用启发式搜索策略，如贪婪算法、遗传算 法等，来加快搜索速度并提高解的质量。
04
此外，还可以考虑对需求点进行聚类处理，以减少合并运输的次数和 降低算法复杂度。
节约里程法在路线规划中应用
景点间距离与交通方式选择
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、短期成本 (一)短期成本的分类 (二)各种短期成本的变动及其关系
（一）短期成本的分类 1.短期总成本 1.短期总成本 2.短期平均成本 2.短期平均成本 3.短期边际成本 3.短期边际成本
1.短期总成本 总成本：是企业生产某一产量的各项成本之和。 总成本：是企业生产某一产量的各项成本之和。 是企业生产某一产量的各项成本之和 STC=TFC+STVC
4.流通加工费用 （1）流通加工设备费用。流通加工设备因流通加工形式不 同而不同，购置这些设备所支出的费用，以流通加工费用 的形式转移到被加工产品中去。 （2）流通加工材料费用。这是指在流通加工过程中，投人 到加工过程中的一些材料消耗所需要的费用，即流通加工 材料费用。 （3）在流通加工过程中从事加工活动的管理人员、工人及 有关人员工资、奖金等费用的总和。
根据节约里程表中节约里程多少的顺序，由大 到小排列，编制节约里程顺序表，以便尽量使节约 里程最多的点组合装车配送。
顺位 号
里程
节约里程
顺位 号
里程
节约里 程
顺位 号
里程
节约里程
1 2 3 4 5 6
A-B B-C A-I C-D A-C E-F
16 14 12 11 10 8
6 8 8 10 10 10
3. 配送物的数量和重量 数量和重量的增加虽说会使配送作业量增大，但大批 量的作业往往使配送效率提高，配送的数量和重量是委托 人获得价格折扣的理由 4. 货物种类及作业过程 不同种类的货物配送难度不同，对配送作业要求不 同，承担的责任也不一样，因而对成本会产生较大幅度的 影响。采用原包装配送的成本支出显然要比配装配送要低， 因而不同的配送作业过程，直接影响配送成本
（二）配送成本的影响因素 配送成本是各种作业活动的费用，它的大小与下面的因素 有关： 1. 时间 配送时间持续的后果是占用了配送中心，耗用了配送 中心的固定成本。而这种成本往往表现为机会成本，使得 配送中心不能提供其他配送服务获得收入或者在其他配送 服务上增加成本 2. 距离 距离是构成配送运输成本的主要内容。距离越远，也 就意味着运输成本增高，同时造成运输设备增加，送货员 增加等。
二、短期成本理论
短期成本的分类、 短期成本的分类、曲线图以及短期产量曲线 与短期成本曲线之间的关系
节约里程法应用案例3
由配送中心P向A~I等9个用户配送货物。图中连 线上的数字表示公路里程（km）。靠近各用户括号内 的数字，表示各用户对货物的需求量（t）。配送中心 备有2t和4t载重量的汽车，且汽车一次巡回走行里程 不能超过35km，设送到时间均符合用户要求，求该配 送中心的最优送货方案。
6 (1.6) 6
E
路径A
P
7
10 8
A
(1.7)
9
路径B
10
6
(1.1)
F
I
(0.6)
路径C
G
(0.9) 12
H
(0.9)
路径A： 车 走行32km，载重量 路径 ：4t车，走行 ，载重量3.7t； ； 路径B： 车 走行31km，载重量 路径 ：4t车，走行 ，载重量3.9t； ； 路径C： 车 走行30km，载重量 路径 ：2t车，走行 ，载重量1.8t。 。 总共走行里程93km，共节约里程 总共走行里程 ，共节约里程63km。 。
总的来说，配送成本包括以下费用支出： 资本成本分摊、支付利息、员工工资福利、行 政办公费用、商务交易费用、自有车辆设备运行 费、保险费或者残损风险、工具以及耗损材料费、 分拣装卸搬运作业费、车辆租赁费等。
配送成本费用的核算是多环节的核算，是各个配送 环节或活动的集成。配送各个环节的成本费用核算都具有 各自的特点，如流通加工的费用核算与配送运输费用的核 算具有明显的区别，其成本计算的对象及计算单位都不同。
某配送中心配送网络图
计算配送中心至各用户以及各用户之间的最 短距离，列表得最短距离表：
P P A B C D E F G H I
A 11
B 10 5
C 9 10 5
D 6 14 9 4
E 7 18 15 10 6
F 10 21 20 19 15 9
G 10 21 20 19 16 17 14
H 8 13 18 17 14 15 18 12
（5）分拣间接费用 分拣间接费用是指配送分拣管理部门为管理和组 织分拣作业，需要由分拣成本分担的各项管理费 用和业务费用。 分拣直接费用与间接费用就构成了配送环节的分 拣成本，即： 分拣成本=分拣直接费用+分拣间接费用
配装成本的计算 配装成本是指在完成配装货物过程中所发生 的各种费用之和。 （1）材料费：配装过程中消耗的各种材料，如 木材、包装纸、金属、塑料等。根据“材料发出 凭证汇总表”、“领料单”及“领料登记表”等 初始凭证，配装成本好用的金额计入成本。 （2）工资及职工福利费：工资是按规定支付给 装配作业职工的标准工资、奖金和津贴等。职工 福利费是按标准的工资总额和提取标准计提的职 工福利费。根据“工资分配汇总表”和“职工福 利费”中分配的配装成本的金额计入成本。
某配送中心配送网络图
计算配送中心至各用户以及各用户之间的最 短距离，列表得最短距离表：
P P A B C D E F G H I
A 11
B 10 5
C 9 10 5
D 6 14 9 4
E 7 18 15 10 6
F 10 21 20 19 15 9
G 10 21 20 19 16 17 14
H 8 13 18 17 14 15 18 12
按功能计算物流配送成本
是指分别按备货、搬运、储存、分拣、加工、 是指分别按备货、搬运、储存、分拣、加工、 配装、配送等功能来计算成本。 配装、配送等功能来计算成本。
例：某配送中心配送成本的计算
配送成本=分拣成本+配装成本+ 配送成本=分拣成本+配装成本+流通加工成 本+配送运输成本
分拣成本的计算 分拣成本是指分拣机械及人工在完成货物分 拣过程中所发生的各项费用之和。 （1）折旧费：分拣设备按规定进行计提的折旧 费，根据“固定资产折旧计算表”中按照分拣设 备提取的折旧金额计入成本。 （2）修理费：分拣设备进行保养和修理所发生 的工料费用，辅助生产部门对分拣设备进行保养 和维修的费用，根据“辅助生产费用计入分拣成 本表”中分配的分拣成本金额既然成本。
短期边际成本
TVC B ● STVC C● A ●
O C SAVC1=SAVC3 SAVC2 O
Q1
Q2 Q3
Q SMC SAVC
● ● ●
●
Q1
Q2 Q3
Q
二、各种短期成本的变动及其关系
三、配送成本
（一）定义
配送成本(Distribution Cost)是配送过程中所支付的费 用总和。 配送成本主要由备货、存储、送货三个环节所发生的 费用组成。
根据节约里程表中节约里程多少的顺序，大 到小排列，编制节约里程顺序表，以便尽量使节约 里程最多的点组合装车配送。
顺位 号
里程
节约里程
顺位 号
里程
节约里 程
顺位 号
里程
节约里程
1 2 3 4 5 6
A-B B-C A-I C-D A-C E-F
16 14 12 11 10 8
6 8 8 10 10 10
H-I B-D D-E A-H B-I C-E
8 7 7 6 6 6
10 10 15 16 17
F-G G- H A-D B-E D-F
6 6 3 2 1
根据节约里程排序表和配车（车辆的载重和容积因素）、车辆行驶里程 等约束条件，渐进绘出配送路径： (0.9)
C
5 (1.2)
9
B
(0.5) 5
D
6 (1.6) 6
5. 外部成本 配送经营时或需要使用到配送企业以外的资 源，比如当地的起吊设备租赁市场具有垄断性， 则配送企业就需要租用起吊设备从而增加成本支 出。如当地的陆桥普遍收费且无管制，则必然使 配送成本居高不下 。
（三）配送成本的计算
按支付形态计算物流配送成本
按运输成本、保管费、 按运输成本、保管费、包装材料费等支付形 态计算的配送成本。 态计算的配送成本。
I 7 6 11 16 13 14 17 17 7
由最短距离矩阵，利用节约法计算出各用户 之间的节约里程，编制节约里程表：
A A B C D E F G H I
B 16
C 10 14
D 3 7 11
E 0 2 6 7
F 0 0 0 1 8
G 0 0 0 0 0 6
H 6 0 0 0 0 0 6
I 12 6 0 0 0 0 0 8
I 7 6 11 16 13 14 17 17 7
由最短距离矩阵，利用节约法计算出各用户 之间的节约里程，编制节约里程表：
A A B C D E F G H I
B 16
C 10 14
D 3 7 11
E 0 2 6 7
F 0 0 0 1 8
G 0 0 0 0 0 6
H 6 0 0 0 0 0 6
I 12 6 0 0 0 0 0 8
E
路径A
P
7
10 8
A
(1.7)
9
路径B
10
6
(1.1)
F
I
(0.6)
路径C
G
(0.9) 12
H
(0.9)
路径A： 车 走行32km，载重量 路径 ：4t车，走行 ，载重量3.7t； ； 路径B： 车 走行31km，载重量 路径 ：4t车，走行 ，载重量3.9t； ； 路径C： 车 走行30km，载重量 路径 ：2t车，走行 ，载重量1.8t。 。 总共走行里程93km，共节约里程 总共走行里程 ，共节约里程63km。 。