数控车床椭圆加工实例精讲1

数控车床加工椭圆的宏程序随着数控技术不断进步, 数控车床加工中各种复杂形面也日渐增多, 如椭圆、抛物线、正弦曲线、余弦曲线、双曲线等各种非圆曲面。

对于上述各种复杂成形面, 利用CAM 软件进行自动编程相对简单, 但由于种种原因, 在绝大多数情况下数控车床主要还是依靠手工编程。

椭圆轴线与数控车床Z 轴重合的情形相对比较简单, 其解决方案也多见于各类文献, 但在本例中椭圆轴线与数控车床Z 轴呈一定夹角, 编程和加工难度陡增,主要原因如下: ①机床数控系统本身既不存在加工椭圆等非圆曲线的G 指令, 更没有类似G68 这样的旋转指令, 使编程难度大大增加。

②加工中变量的参数直接影响着加工的效率以及质量, 很容易产生过切报警, 即使程序正确无误, 实际加工时的参数调整也非常困难, 直接影响着加工能否顺利进行, 以及加工精度能否保证。

总而言之, 目前尚未见有表述类似实例的文章。

本实例进行了有益的尝试和探索, 给出了切实可行的解决方案, 为类似问题提供了难得的参考及借鉴。

椭圆宏程序的编制如下。

1. 椭圆方程宏程序主要利用各种数学公式进行运算加工, 因此编制旋转椭圆程序操作者必须要掌握椭圆方程和旋转公式等各种数学公式的计算方法并加以灵活运用。

椭圆方程有两种形式, 分别是椭圆的标准方程和参数方程。

椭圆标准方程:椭圆参数方程:其中a 、b 分别为X、Z 所对应的椭圆半轴。

2. 旋转公式由于数控车床并不像加工中心那样存在着旋转指令, 所以要利用旋转公式来进行椭圆的旋转。

旋转公式的定义:如图1 所示, 平面上绕点O 旋转, 使平面上任意一对对应点P 和P′与一个定点O 连接的线段都相等, 即OP = OP′, 且角∠POP′等于角θ, 点O称为旋转中心, 角θ称为旋转角。

旋转公式: 如图1 所示, 取直角坐标系, 以原点O为旋转中心, 旋转角为θ, 平面上任意一点P ( x, z) 旋转到P′( x′, z′) , 令∠XOP= α, 则∠XOP′= α+ θ, 且OP = OP ′。

数控车床加工对象为各种类型的回转面，其中对于圆柱面、锥面、圆弧面、球面等的加工，可以利用直线插补和圆弧插补指令完成，而对于椭圆等一些非圆曲线构成的回转体，加工起来具有一定的难度。

这是因为大多数的数控系统只提供直线插补和圆弧插补两种插补功能，更高档的数控系统提供双曲线、正弦曲线和样条曲线插补功能，但是一般都没有椭圆插补功能。

因此，在数控机床上对椭圆的加工大多采用小段直线或者小段圆弧逼近的方法来编制椭圆加工程序。

在这里结合工作实践对车削椭圆轮廓的宏程序的编制方法进行探讨。

一、椭圆宏程序的编制原理数控系统的控制软件，一般由初始化模块、输入数据处理模块、插补运算处理模块、速度控制模块、系统管理模块和诊断模块组成。

其中插补运算处理模块的作用是依据程序中给定的轮廓的起点、终点等数值对起点终点之间的坐标点进行数据密化，然后由控制软件，依据数据密化得到的坐标点值驱动刀具依次逼近理想轨迹线的方式来移动，从而完成整个零件的加工。

依据数据密化的原理，我们可以根据曲线方程，利用数控系统具备的宏程序功能，密集的算出曲线上的坐标点值，然后驱动刀具沿着这些坐标点一步步移动就能加工出具有椭圆、抛物线等非圆曲线轮廓的工件。

二、椭圆宏程序的编制步骤宏编程一般步骤：1.首先要有标准方程（或参数方程）一般图中会给出。

2.对标准方程进行转化，将数学坐标转化成工件坐标标准方程中的坐标是数学坐标，要应用到数控车床上，必须要转化到工件坐标系中。

3.求值公式推导利用转化后的公式推导出坐标计算公式4.求值公式选择根据实际选择计算公式5.编程公式选择好后就可以开始编程了三、加工实例下面分别就工件坐标原点与椭圆中心重合，偏离等2种情况进行编程说明。

（1）工件坐标原点与椭圆中心重合椭圆标准方程为①转化到工件坐标系中为②根据以上公式我们可以推导出以下计算公式③④在这里我们取公式③。

凸椭圆取+号，凹椭圆取-号。

即X值根据Z值的变化而变化，公式④不能加工过象限椭圆，所以舍弃。

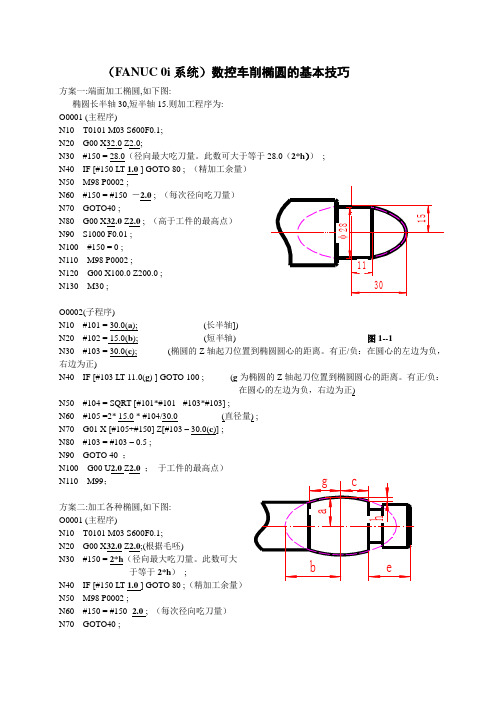
（FANUC 0i 系统）数控车削椭圆的基本技巧方案一:端面加工椭圆,如下图:椭圆长半轴30,短半轴15.则加工程序为: O0001 (主程序)N10 T0101 M03 S600F0.1; N20 G00 X32.0 Z2.0;N30 #150 = 28.0（径向最大吃刀量。

此数可大于等于28.0（2*h ）） ; N40 IF [#150 LT 1.0 ] GOTO 80 ; （精加工余量） N50 M98 P0002 ;N60 #150 = #150 －2.0 ; （每次径向吃刀量） N70 GOTO40 ;N80 G00 X 32.0 Z 2.0 ; （高于工件的最高点） N90 S1000 F0.01 ; N100 #150 = 0 ; N110 M98 P0002 ;N120 G00 X100.0 Z200.0 ;N130 M30 ;O0002(子程序)N10 #101 = 30.0(a ); (长半轴])N20 #102 = 15.0(b ); (短半轴) 图1--1N30 #103 = 30.0(c ); (椭圆的Z 轴起刀位置到椭圆圆心的距离。

有正/负：在圆心的左边为负，右边为正)N40 IF [#103 LT 11.0(g ) ] GOTO 100 ; (g 为椭圆的Z 轴起刀位置到椭圆圆心的距离。

有正/负：在圆心的左边为负，右边为正)N50 #104 = SQRT [#101*#101 - #103*#103] ;N60 #105 =2* 15.0 * #104/30.0 (直径量) ; N70 G01 X [#105+#150] Z[#103 – 30.0(c )] ; N80 #103 = #103 – 0.5 ; N90 GOTO 40 ；N100 G00 U 2.0 Z 2.0 ； 于工件的最高点） N110 M99；方案二:加工各种椭圆,如下图: O0001 (主程序)N10 T0101 M03 S600F0.1;N20 G00 X 32.0 Z 2.0;(根据毛呸)N30 #150 = 2*h （径向最大吃刀量。

椭圆形加工宏程序的编程实例数控宏程序编程实例
实际应用中，还经常会遇到各种各样的椭圆形加工特征。

在现今的数控系统中，无论硬件数控系统，还是软件数控系统，其插补的基本原理是相同的，只是实现插补运算的方法有所区别。

常见的是直线插补和圆弧擂补，没有椭圆插补，手工常规编程无法编制出椭圆加工程序，常需要用电脑逐一编程，但这有时受设备和条件的限制。

这时可以采用拟合计算，用宏程序方式，手工编程即可实现，简捷高效，并且不受条件的限制。

加工如下图所示的椭圆形的半球曲面，刀具为R8的球铣刀。

利用椭圆的参数方程和圆的参数方程来编写宏程序。

椭圆的参数方程为：X=A*COS&；
Y=B*COS&；
其中，A为椭圆的长轴，B为椭圆的短轴。

编制参考宏程序如下：
%0012
#1=0
#2=20 (短半轴)
#3=30（长半轴）
#4=1（角度增量值）
#5=90（球面角度终止值）WHILE #5 GE #1 DO1
#6=#3*COS[#5*PI/180]+4 #7=#2*SIN[#5*PI/180]
G01X[#6]F800
Z[#7]
#8=360
#9=0
WHILE #9 LE #8 DO2
#10=#6*COS[#9*PI/180]
#11=#6*SIN[#9*pi/180]*2/3 G01X[#10]Y[#11]F800
#9=#9+1(计数器)
END1
#5=#5-#4(计数器)
END2
M99
在上例中可看出，角度每次增加的大小和最后工件的加工表面质量有较大关系，即记数器的每次变化量与加工的表面质量和效率有直接关系。

A PPLICATION技术与应用168ＯＣＣＵＰＡＴＩＯＮ2014 06摘 要：目前，在机械加工中，非圆曲线越来越被广泛地应用，依靠传统的靠模加工已经不能满足现实的精度要求，取而代之的是在数控机床上进行加工。

本文对常见的椭圆加工的几种常用方法进行编程示例。

关键词：数控编程 椭圆 方法简析数控车床上椭圆加工的编程方法文/史先伟目前，随着数控机床的广泛应用，机械生产加工技术不断进步，对各种各样工件加工精度要求进一步提高，非圆曲线的加工情况也越来越多，精度要求也越来越高。

但依靠传统的普通机床上进行靠模加工，已经不能满足现实的加工精度要求。

笔者以下图所示椭圆加工为例，采用FANUC数控系统，总结以下编程方法，供大家参考。

图一、G73仿形法1.利用直角坐标方程进行加工这个方法需要首先设定某一个坐标为自变量，然后用该坐标把另外一个坐标表示出来。

在此，把Z 轴方向的坐标设为变量#1，则X 轴方向的坐标#2可以用#1表示为：/3（即：#2=1/3*SQRT[900-#1*#1]）。

加工程序如下：O 1; N 2 #2=1/3*SQRT[900-#1*#1];G 99 T 0101; G 01 X[2*#2] Z[#1-30.];M 03 S 500; #1=#1-0.1;G 00 X 21.Z 5.; IF[#1GT 0] GOTO 2;G 73 U 11. W 0 R 5; N 3 X 21.;G 73 P 1 Q 3 U 1. W 0 F 0.2; G 70 P 1 Q 3;N 1 G 00 X 0; G 00 X 100. Z 100.;G 1 Z 0 F 0.06; M 05;#1=30.; M 30;2.利用参数方程进行加工该椭圆参数方程为：，设自变量为#1；则可得Z 为#2=30*COS[#1],X 为#3=10*SIN[#1]。

加工程序 如下：O 2; #3=10.*SIN[#1];G 99 T 0101; G 01 X[2*#3] Z[#2-30.];M 03 S 500; #1=#1+1.;G 00 X 21.Z 5.; IF[#1LT 90] GOTO 2;G 73 U 11. W 0 R 5; N 3 X 21.;G 73 P 1 Q 3 U 1. W 0 F 0.2; G 70 P 1 Q 3;N 1 G 00 X 0; G 00 X 100. Z 100.;G 1 Z 0 F 0.06; M 05;#1=0; M 30;N 2 #2=30.*COS[#1];二、G90车削椭圆采用G 90车削椭圆时，我们一般只是利用直角坐标方程来进行，这样在车削时的切削深度比较容易控制，而参数方程就不太容易控制。

数控车床椭圆加工实例精讲The Standardization Office was revised on the afternoon of December 13, 2020数控车床椭圆加工实例精讲原创作者：曾经自然联系QQ：919000323【摘要】在数控车床上加工非圆曲线是数控教学中的一个难点，而且非圆曲线的加工在数控大赛中也屡见不鲜。

而椭圆的加工是非圆曲线加工中最常见的，本文将针对华中数控车椭圆的宏程序加工，详细解释思路和程序含义，并用斯沃仿真软件进行加工模拟，让初学者能够真正理解椭圆加工的精髓，做到举一反三。

【关键字】椭圆加工宏程序精髓仿真一知识引入1 椭圆的标准方程：12222=+aZbX其中a为椭圆的长半轴，b为椭圆的短半轴2 椭圆宏程序结构流程：①开始----②给自变量赋初始值----③循环条件----④因变量表达式赋值----⑤椭圆插补----⑥步距变化----⑦结束二加工图纸三椭圆加工宏程序思路1 首先确定图纸中的椭圆为凹椭圆，宏程序中要体现出区别。

2 图纸中椭圆中心的坐标跟工件原点不重合，所以这个可以称为偏心椭圆。

3 必须了解一点，我们计算椭圆上的所有坐标都是依据椭圆中心来计算的，而我们编程的时候所有的坐标是相对工件原点来计算的。

4 自变量赋初始值，由于只有X和Z两个方向的变量，所以我们只要对其中的一个坐标进行赋值就可以，然后确定加工的区间，计算另外一个变量。

5 椭圆精加工宏程序的编写。

（按照椭圆宏程序结构流程)6 由于我们写的宏程序只是椭圆精加工，所以还要考虑粗加工，而华中21世纪星系统的数控车床G71指令可以嵌套宏程序，所以我们可以用这个指令来进行粗加工。

四加工程序详解O0001G95G97M03S500T0101F0.3 程序初始化G0X72Z2 快速点定位（循环起刀点）G71U2R1P10Q20X0.6Z0 粗车循环M03S1200F0.1 设置精加工参数N10G0X0G1Z0#1=0 ; 椭圆Z向加工起点相对于椭圆中心的坐标WHILE#1LE[40] ; 判断椭圆孤是否走到Z向终点(相对圆心中点数值) #2=-25/40*SQRT[40*40-#1*#1] 计算椭圆方程中的X坐标（凹圆弧取负）G1X[#2*2+50]Z[- #1] 椭圆插补，实际上椭圆加工的X和Z值(此处要考虑中心点的偏移和Z方向实际加工的距离)#1=#1+0.2 步距0.2，既Z值递增量为0.2，(此值过大影响精度，过小加工速度过慢，应在满足精度的前提下尽可能取大值)ENDWG1Z-60X70N20Z-70G0X100Z100M30五斯沃仿真模拟加工1 回参考点2 毛坯设置选择图标，点设置毛坯，把直径改为70。

数控车床加工椭圆的方法摘要本文讲述在数控车床上利用椭圆直角坐标和极坐标方程，通过对宏程序进行编程来加工椭圆，同时总结了针对不同尺寸规格椭圆的编程方法。

关键词数控车床；加工椭圆；方法1概述二维轮廓的椭圆形零件在日常生活中使用得非常多，尤其是在机械制造业中更是应用广泛，但是，该零件加工起来的难度是非常大的。

椭圆形零件的加工方法有很多种，比较常见的有以下几种：在普通车床上进行近似加工[1]；根据椭圆的形成原理，设计专用的加工装置进行加工[2]；在数控车床上利用“虚拟轴”原理实现椭圆曲线的数控加工[3]；利用圆弧逼近法[4]、直线逼近法加工等。

本文仅讨论利用直线逼近法（宏程序）加工椭圆。

2直线逼近法现今，计算机和自动化技术发展迅速，数控车床相关技术也随之不断进步，给椭圆形截面零件的加工创造了很好的条件。

从目前的技术来说，各种数控车床进行椭圆加工的插补原理基本相同，不同的是实现插补运算的方法。

圆弧插补与直线插补是两种常用的实现插补运算的方法，但是目前还没有椭圆插补。

因为受到各方面的限制，尤其在设备和条件方面，通常我们无法手工来编制程序，必须借助于电脑来实现。

一般来说，通过拟合运算及直线逼近法编写宏程序来加工椭圆。

宏程序指令适用于抛物线、双曲线、椭圆等没有插补指令的非圆曲线编程；还适用于图形相同，只是尺寸不同的一系列零件编程，同样还适用于工艺路线一样，只是位置数据不同的系列零件的编程。

相比于其他编程方法，宏程序实现椭圆形截面零件的加工的优点在于，其能有效的简化程序，提高程序的运行速度，并且能扩展数控机床的使用范围。

3用户宏程序法数控车床通过程序来实现某项功能，将编写的程序存储在数控车床中，并将这些实现某项功能的程序用某个简单命令代表，利用数控车床进行加工时，只需要写入代表命令就可以执行相应的功能，极大的减少了操作流程，提高了工作效率。

其中，把存入数控机床的一组程序称作用户宏程序主体，简称为宏程序；把代表命令称作用户宏程序命令，简称为宏命令。