下载文档原格式
剪应力计算公式材料力学
材料力学中的剪应力是指材料在受到剪切作用时所产生的内部应力。
剪应力的计算公式可以根据不同的情况采用不同的方法进行推导和求解。
一、简单剪切
在材料力学中，对于简单剪切情况，剪应力计算公式可以通过横截面上的剪切力和截面积的比值得到。
假设剪切力为F，截面积为A，则公式可以表示为：
τ=F/A
其中，τ表示剪应力。
二、剪切应力分布
在一些情况下，剪切力在横截面上并不是均匀分布的，呈现出剪切力随位置的变化。
此时，可以通过剪切力的微元来表示剪应力。
假设在横截面上的一些位置处x，剪切力的微元为dF，则剪应力的计算公式可以表示为：
τ=dF/dA
其中，dA表示横截面上剪切力微元的大小。
三、剪应力与剪切应变
在材料力学中，剪应力和剪切应变之间存在一定的关系。
剪应力与剪切应变的计算公式可以通过剪切模量（用G表示）得到。
假设剪切应变为γ，则剪应力的计算公式可以表示为：
τ=Gγ
四、剪应力对于材料的破坏
在材料力学中，剪应力对于材料的破坏具有重要的影响。
当剪应力达到材料的抗剪强度时，材料就会发生破坏。
剪应力与抗剪强度的关系通常可以通过拉伸试验或剪切试验得到。
总结：
剪应力的计算公式可以根据不同的情况采用不同的方法进行推导和求解。
一般情况下，可以通过剪切力和截面积的比值来计算剪应力。
在剪切力分布不均匀的情况下，需要使用剪切力微元来表示剪应力。
剪应力与剪切应变之间存在一定的关系，可以通过剪切模量来计算。
剪应力对于材料的破坏具有重要的影响，当剪应力达到材料的抗剪强度时，材料就会发生破坏。
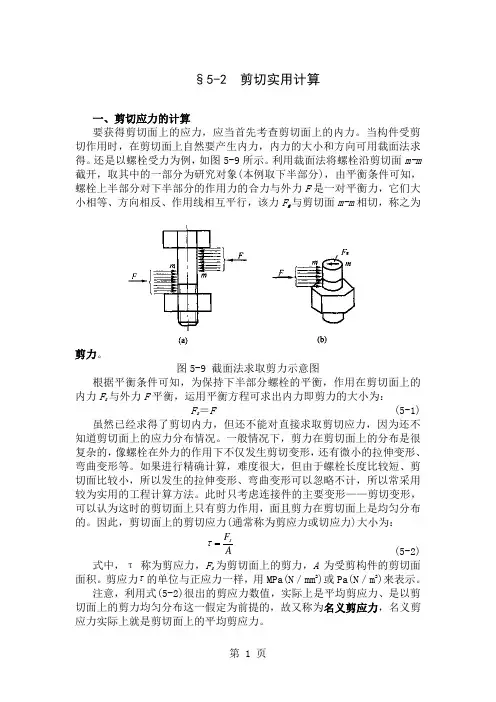
§5-2 剪切实用计算一、剪切应力的计算要获得剪切面上的应力，应当首先考查剪切面上的内力。
当构件受剪切作用时，在剪切面上自然要产生内力，内力的大小和方向可用裁面法求得。
还是以螺栓受力为例，如图5-9所示。
利用裁面法将螺栓沿剪切面m-m 截开，取其中的一部分为研究对象(本例取下半部分)，由平衡条件可知，螺栓上半部分对下半部分的作用力的合力与外力F 是一对平衡力，它们大小相等、方向相反、作用线相互平行，该力F s 与剪切面m-m 相切，称之为剪力。
图5-9 截面法求取剪力示意图根据平衡条件可知，为保持下半部分螺栓的平衡，作用在剪切面上的内力F s 与外力F 平衡，运用平衡方程可求出内力即剪力的大小为：F s ＝F (5-1)虽然已经求得了剪切内力，但还不能对直接求取剪切应力，因为还不知道剪切面上的应力分布情况。
一般情况下，剪力在剪切面上的分布是很复杂的，像螺栓在外力的作用下不仅发生剪切变形，还有微小的拉伸变形、弯曲变形等。
如果进行精确计算，难度很大，但由于螺栓长度比较短、剪切面比较小，所以发生的拉伸变形、弯曲变形可以忽略不计，所以常采用较为实用的工程计算方法。
此时只考虑连接件的主要变形——剪切变形，可以认为这时的剪切面上只有剪力作用，面且剪力在剪切面上是均匀分布的。
因此，剪切面上的剪切应力(通常称为剪应力或切应力)大小为： sF A τ=(5-2)式中，τ称为剪应力，F s 为剪切面上的剪力，A 为受剪构件的剪切面面积。
剪应力τ的单位与正应力一样，用MPa(N ／mm 2)或Pa(N ／m 2)来表示。
注意，利用式(5-2)很出的剪应力数值，实际上是平均剪应力、是以剪切面上的剪力均匀分布这一假定为前提的，故又称为名义剪应力，名义剪应力实际上就是剪切面上的平均剪应力。
二、剪切应变的计算为分析物体受剪力作用后的变形情况，从剪切面上取一直角六面体分析。
如图5-10所示，在剪力作用下，相互垂直的两平面夹角发生了变化，即不再保持直角，则此角度的改变量γ称为剪应变、又称切应变。
剪切力的计算方法精编版首先，我们先来了解一下剪切力的概念和背景知识。
剪切力是指物体在受到垂直于其截面的剪切应力时，所受到的力的大小。
剪切应力是指物体内部由于受到力的作用而产生的应力，其沿截面施加的作用力垂直于截面。
1.应力-应变关系法应力-应变关系法是计算剪切力最常用的方法之一、根据钢材等材料的线性弹性特性，剪切应力和应变之间存在线性关系，可以通过杨氏模量来计算剪切力。
公式如下所示：剪切力=剪切应力×截面积其中，剪切应力可以通过应力-应变关系得出，应变根据物体的受力情况和形状可以进行计算。
2.扭矩法扭矩法是一种通过扭转杆件来计算剪切力的方法。
当杆件受到扭矩作用时，杆件会在截面上产生剪切应力，从而产生剪切力。
根据弹性力学理论，扭矩和剪切力之间存在线性关系，公式如下所示：剪切力=扭矩×距离/截面极性矩其中，截面极性矩可以通过截面形状进行计算。
3.力矩法力矩法是一种通过受力物体的力矩平衡条件来计算剪切力的方法。
根据力矩平衡定律，物体受到的剪切力和力矩之间存在平衡关系，公式如下所示：剪切力=ΣM/距离其中，ΣM表示所有受力物体的力矩的代数和，距离表示力矩的作用距离。
4.梁的转角法梁的转角法是一种通过梁的转角来计算剪切力的方法。
当梁受到外力作用时，会产生转角，根据梁的弹性力学公式可以计算出剪切力。
公式如下所示：剪切力=F×L/θ其中，F表示梁所受外力的大小，L表示梁的长度，θ表示梁的转角。
这些方法可以根据具体情况和需求来选择使用。
在进行剪切力的计算时，需要明确剪切应力、截面积、扭矩、距离、力矩和转角等参数的具体值，并进行合理的单位换算以确保计算结果的准确性。
需要注意的是，剪切力的计算方法可能会受到材料的非线性特性、几何形状的复杂性等多种因素的影响，因此在实际应用中需要进行合理的简化和适当的修正。
综上所述，剪切力的计算方法包括应力-应变关系法、扭矩法、力矩法和梁的转角法等。
选择适当的计算方法需要根据具体情况和实际需求来决定，同时需要注意考虑材料的特性以及几何形状的复杂性等因素。
剪切及挤压应力计算剪切应力是物体内部的应力状态之一，指物体内部各部分相对于其它部分的平动趋势。
挤压应力则是指物体受到外部挤压力作用后内部产生的应力。
剪切及挤压应力计算需要考虑物体的形状、尺寸以及施加力的方向和大小。
对于剪切应力的计算，可以通过剪切力与剪切面积之比来求得。
假设一个物体受到平行于其中一平面的剪切力作用，剪切力的大小为F，剪切面的积为A。
剪切应力可以表示为τ=F/A。
其中τ表示剪切应力。
如果物体的形状不规则，可以将其划分为多个小面元，然后求和计算得到总的剪切应力。
对于挤压应力的计算，可以通过挤压力与挤压面积之比来求得。
假设一个物体受到垂直于其中一平面的挤压力作用，挤压力的大小为P，挤压面的积为A。
挤压应力可以表示为σ=P/A。
其中σ表示挤压应力。
如果物体的形状不规则，可以将其划分为多个小面元，然后求和计算得到总的挤压应力。
剪切应力和挤压应力的计算都需要明确给定施加力的方向和大小，以及物体的面积。
对于规则形状的物体，可以通过几何方法直接计算得到。
对于不规则形状的物体，需要采用数值方法进行近似计算。
除了这种简单情况外，对于复杂的物体形状和受力情况，需要运用工程力学的知识，通过应力分析、协调方程等方法来进行计算。
在这种情况下，需要考虑物体的几何形状、材料的性质、受力的位置和大小等因素，以得到更精确的剪切应力和挤压应力的计算结果。
最后，需要注意的是，剪切应力和挤压应力是物体内部的应力状态，其大小与物体的尺寸和形状有关。
在工程设计中，需要根据所需的应力状态来选择合适的材料和设计结构，以保证物体在受力情况下不会发生破坏或变形。
总之，剪切应力和挤压应力的计算是工程力学中重要的内容之一，需要综合运用几何学、力学、材料学等知识，通过适当的数值计算或工程分析方法来进行。
这样可以为工程设计提供可靠的理论基础，以保证物体的强度和稳定性。
§5-2 剪切实用计算一、剪切应力的计算要获得剪切面上的应力，应当首先考查剪切面上的内力。
当构件受剪切作用时，在剪切面上自然要产生内力，内力的大小和方向可用裁面法求得。
还是以螺栓受力为例，如图5-9所示。
利用裁面法将螺栓沿剪切面m-m 截开，取其中的一部分为研究对象(本例取下半部分)，由平衡条件可知，螺栓上半部分对下半部分的作用力的合力与外力F 是一对平衡力，它们大小相等、方向相反、作用线相互平行，该力F s 与剪切面m-m 相切，称之为剪力。
图5-9 截面法求取剪力示意图根据平衡条件可知，为保持下半部分螺栓的平衡，作用在剪切面上的内力F s 与外力F 平衡，运用平衡方程可求出内力即剪力的大小为：F s ＝F (5-1)虽然已经求得了剪切内力，但还不能对直接求取剪切应力，因为还不知道剪切面上的应力分布情况。
一般情况下，剪力在剪切面上的分布是很复杂的，像螺栓在外力的作用下不仅发生剪切变形，还有微小的拉伸变形、弯曲变形等。
如果进行精确计算，难度很大，但由于螺栓长度比较短、剪切面比较小，所以发生的拉伸变形、弯曲变形可以忽略不计，所以常采用较为实用的工程计算方法。
此时只考虑连接件的主要变形——剪切变形，可以认为这时的剪切面上只有剪力作用，面且剪力在剪切面上是均匀分布的。
因此，剪切面上的剪切应力(通常称为剪应力或切应力)大小为：sF A τ=(5-2)式中，τ称为剪应力，F s 为剪切面上的剪力，A 为受剪构件的剪切面面积。
剪应力τ的单位与正应力一样，用MPa(N ／mm 2)或Pa(N ／m 2)来表示。
注意，利用式(5-2)很出的剪应力数值，实际上是平均剪应力、是以剪切面上的剪力均匀分布这一假定为前提的，故又称为名义剪应力，名义剪应力实际上就是剪切面上的平均剪应力。
二、剪切应变的计算为分析物体受剪力作用后的变形情况，从剪切面上取一直角六面体分析。
如图5-10所示，在剪力作用下，相互垂直的两平面夹角发生了变化，即不再保持直角，则此角度的改变量γ称为剪应变、又称切应变。
剪切应力计算精编 Document number：WTT-LKK-GBB-08921-EIGG-22986拉伸、压缩与剪切1 基本概念及知识要点1.1 基本概念轴力、拉（压）应力、力学性能、强度失效、拉压变形、胡克定律、应变、变形能、静不定问题、剪切、挤压。
以上概念是进行轴向拉压及剪切变形分析的基础，应准确掌握和理解这些基本概念。
1.2 轴向拉压 的内力、应力及变形1．横截面上的内力：由截面法求得横截面上内力的合力沿杆的轴线方向，故定义为轴力F N ，符号规定：拉力为正，压力为负。
工程上常以轴力图表示杆件轴力沿杆长的变化。
2．轴力在横截面上均匀分布，引起了正应力，其值为 F Aσ=N 正应力的符号规定：拉应力为正，压应力为负。
常用的单位为MPa 、Pa 。
3．强度条件强度计算是材料力学研究的主要问题之一。
轴向拉压时，构件的强度条件是[]F Aσσ=≤N可解决三个方面的工程问题，即强度校核、设计截面尺寸及确定许用载荷。
4．胡克定律线弹性范围内，杆的变形量与杆截面上的轴力F N 、杆的长度l 成正比，与截面尺寸A 成反比；或描述为线弹性范围内，应力应变成正比，即F ll E EA σε∆==N式中的E 称为材料的弹性模量，EA 称为抗拉压刚度。
胡克定律揭示在比例极限内，应力和应变成正比，是材料力学最基本的定律之一，一定要熟练掌握。
1.3 材料在拉压时的力学性能材料的力学性能的研究是解决强度和刚度问题的一个重要方面。
材料力学性能的研究一般是通过实验方法实现的，其中拉压试验是最主要、最基本的一种试验，由它所测定的材料性能指标有：E —材料抵抗弹性变形能力的指标；b s σσ,—材料的强度指标；ψδ, —材料的塑性指标。
低碳钢的拉伸试验是一个典型的试验。
详见教材，应理解本部分知识。
1.4 简单拉压静不定问题1． 未知力的个数超过静力平衡方程个数的问题为静不定问题，其中未知力可以是结构的约束反力或构件的内力。
截面剪切应力计算公式在我们学习力学的过程中，截面剪切应力计算公式可是个相当重要的家伙！这玩意儿就像一把神奇的钥匙，能帮我们打开理解物体内部受力情况的大门。
咱先来说说啥是截面剪切应力。
想象一下，你拿着一把剪刀去剪一张纸，纸被剪断的那个地方，受到的就是剪切力。
而截面剪切应力呢，就是在某个横截面上面，单位面积所受到的这种剪切力。
那截面剪切应力计算公式到底是啥呢？它通常可以表示为τ = VQ /Ib 。
这里面，V 表示的是剪力，Q 是所求应力点到截面形心的距离与该点所在截面一侧部分的面积对形心的静矩的乘积，I 是整个截面对于中性轴的惯性矩，b 则是所求应力点处截面的宽度。
就拿我们生活中的一个例子来说吧，有一次我去工地，看到工人师傅们在搭建钢梁。
那钢梁长长的，承受着各种力。
我就好奇地问师傅，这钢梁会不会被剪断啊？师傅笑着说，这就得看截面剪切应力啦。
他们在设计的时候，就得用这个公式来算一算，确保钢梁能稳稳地支撑起整个建筑。
比如说这钢梁是个矩形截面的，宽是 b ，高是 h 。
那它对中性轴的惯性矩 I 就等于 bh³ / 12 。
要是剪力 V 已经知道了，再根据具体受力点的位置算出 Q ，就能算出截面剪切应力τ 了。
如果算出来的应力超过了材料能承受的极限，那可就危险啦，钢梁可能就会出问题。
在实际工程中，比如桥梁的建造，要是没算好截面剪切应力，那后果不堪设想。
桥可能在使用过程中突然断裂，这得多吓人啊！所以这个公式对于工程师们来说，那可真是宝贝，得精确计算，一点儿都不能马虎。
咱们再回到学习中来，同学们在学习这个公式的时候，可别被那些字母和符号给吓住了。
其实啊，只要多做几道题，多结合实际想一想，就会发现它也没那么难。
比如说，给你一道题，告诉你一个钢梁的尺寸和所受的剪力，让你算截面剪切应力。
这时候，别慌，先把公式写出来，把已知的数值代入进去，一步一步来。
算的时候要仔细，单位可别弄错了。
而且啊，这个公式还和其他的力学知识有关系呢。
式中：T —横截面上的扭矩，由截面法通过外力偶矩求得。
ρ —该点到圆心的距离。
Ip —极惯性矩，纯几何量，无物理意义。
剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三个常数。
钢材的G 值约为80GPa
其中：P — 功率，千瓦（kW ）
n — 转速，转/分（rpm ）
其中：P — 功率，马力（PS ）
n — 转速，转/分（rpm ）
1kW = 1000N·m/s = 1.36PS
圆轴扭转时的强度计算
强度计算三方面： ① 校核强度： ② 设计截面尺寸：
③ 计算许可载荷：
圆轴扭转时的变形 · 刚度计算
刚度条件
[q ]称为许用单位扭转角。
精密机器轴： [q] = （ 0.15 ~ 0.30 ）º/m
一般传动轴： [q] = （ 0.30 ~ １.0 ）º/m
精度不高的轴： [q] = （ １.0 ~ ２.５ ）º/m
p
I T ρτρ⋅=)
1(2μ+=E G m)(kN 55.9⋅=n P m m)(kN 024.7⋅=n P m ][max max ττ≤=t W T ][max τT W t ≥⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-）（空：实：433116 16 αππD D W t ]
[max τt W T ≤[]/m)( '180 max ︒≤⋅=ϕπ
θp GI T。
拉伸、压缩与剪切1基本概念及知识要点1.1 基本概念轴力、拉（压）应力、力学性能、强度失效、拉压变形、胡克定律、应变、变形能、静不定问题、剪切、挤压。
以上概念是进行轴向拉压及剪切变形分析的基础，应准确掌握和理解这些基本概念。
1.2 轴向拉压 的内力、应力及变形1．横截面上的内力：由截面法求得横截面上内力的合力沿杆的轴线方向，故定义为轴力F N ，符号规定：拉力为正，压力为负。
工程上常以轴力图表示杆件轴力沿杆长的变化。
2．轴力在横截面上均匀分布，引起了正应力，其值为F Aσ=N正应力的符号规定：拉应力为正，压应力为负。
常用的单位为MPa 、Pa 。
3．强度条件强度计算是材料力学研究的主要问题之一。
轴向拉压时，构件的强度条件是[]F Aσσ=≤N可解决三个方面的工程问题，即强度校核、设计截面尺寸及确定许用载荷。
4．胡克定律线弹性范围内，杆的变形量与杆截面上的轴力F N 、杆的长度l 成正比，与截面尺寸A成反比；或描述为线弹性范围内，应力应变成正比，即F l l E EAσε∆==N式中的E 称为材料的弹性模量，EA 称为抗拉压刚度。
胡克定律揭示在比例极限内，应力和应变成正比，是材料力学最基本的定律之一，一定要熟练掌握。
1.3 材料在拉压时的力学性能材料的力学性能的研究是解决强度和刚度问题的一个重要方面。
材料力学性能的研究一般是通过实验方法实现的，其中拉压试验是最主要、最基本的一种试验，由它所测定的材料性能指标有：E —材料抵抗弹性变形能力的指标；b s σσ,—材料的强度指标；ψδ, —材料的塑性指标。
低碳钢的拉伸试验是一个典型的试验。
详见教材，应理解本部分知识。
1.4 简单拉压静不定问题1． 未知力的个数超过静力平衡方程个数的问题为静不定问题，其中未知力可以是结构的约束反力或构件的内力。
2． 解决静不定问题，除列出静力平衡方程外，还需列出一定数量的补充方程，这些补充方程可由结构各部分变形之间的几何关系以及变形和力之间的物理关系求得，将补充方程和静力平衡方程联立求解，即可得出全部未知力。
3． 静不定结构还有一个特性，即由于杆件在制造中的误差，将引起装配应力；由于温度变化会引起温度应力。
1.5 应力集中的概念工程实际中，由于结构上和使用上的需要，有些零件必须有切口、切槽和螺纹等。
在构件尺寸的突变处，发生局部应力急剧增加的现象，称为应力集中现象。
1.6 剪切和挤压的实用计算1． 工程中经常使用到联接件，如铆钉、销钉、键或螺栓等。
联接件一般受剪切作用，并伴随有挤压作用，因而联接件应同时满足剪切强度和挤压强度。
有时还要考虑被联接部分的拉伸强度问题。
2． 两作用外力之间发生相互错动的面称为剪切面。
剪切面上的切应力为F Aτ=s，其中F s 为剪力，A 为剪切面的面积，即假设切应力在剪切面上均匀分布。
剪切强度条件[]F Aττ=≤s3． 产生相互挤压的表面称为挤压面。
挤压面上的挤压应力为bs bsF A σ=，式中F 为挤压力，A bs 为挤压面积，即假设挤压应力在挤压面上均匀分布。
挤压强度条件为[]b s b s bsFA σσ=≤2 重点与难点及解析方法2.1 轴向拉压的应力、强度计算及变形计算强度计算是本章的重点内容，它能够解决三类工程问题。
而胡克定律是联系力与变形的基本定律，应重点掌握。
解析方法：1 对等截面直杆，横截面上的正应力最大，强度计算时必须明确在哪个截面进行强度计算；而纵向截面上的应力等于零。
2应用胡克定律计算变形时，内力应以代数值代入。
求解结构上节点的位移时，设想交于该节点的各杆，沿各自的轴线自由伸缩，从变形后各杆的终点作各杆轴线的垂线，这些垂线的交点即为节点新的位置。
2.2 简单拉压静不定问题解静不定问题的关键是列出正确的变形几何关系。
在列几何关系时，注意假设的变形应是杆件可能的变形。
解析方法：1列静力平衡方程；2根据变形协调关系列出变形的几何关系；3 列出力与变形之间的物理关系；4 联立解方程组求出未知力。
2.3材料在拉压时的力学性能力学性能是材料在外力作用下表现出的变形、破坏等方面的特性。
是通过实验研究的方法来实现的，这种方法对我们以后的工程设计有一定的指导作用。
应理解力学性质中涉及到的几个强度指标及塑性指标。
2.4 剪切和挤压的强度计算联接件的强度计算，关键在于正确判断剪切面和挤压面。
剪切面积为受剪面的实际面积，当挤压面为半圆柱面时，一般取圆柱的直径平面面积为挤压面面积，以简化运算。
3 典型问题解析3.1 轴向拉压的强度、变形计算例题2.1：已知AC杆为直径d＝25mm的A3圆钢，材料的许用应力[σ]＝141MPa，AC、AB杆夹角α＝30°，如图2－1（a）所示，A处作用力F＝20kN，求：1校核AC杆的强度；2选择最经济的直径d；3若用等边角钢，选择角钢型号。
解：图2－1（a）（b）1校核AC 杆的强度用一截面将AC 、AB 杆截开，取A 节点作为研究对象，如图2－1（b ）所示，利用平衡方程计算1F N 。
110sin 30040kNyF FF F =∑N N ＝－＝代入强度条件，校核AC 杆的强度[]1326401081.5MPa 25104AC F A σσπ⨯<⨯⨯N －＝＝＝满足强度要求,安全。
2 选择最佳截面尺寸，根据强度条件[]321624010284mm 14110419.02mmF A A d d σπ⨯≥==⨯=≥==NAC 杆的直径取为20mm ，即可满足强度要求。
3选择等边角钢型号A ≥284mm 2 ，查表可选50×3号等边角钢。
解题指导：杆件轴力方向未知时，可使用设正法，即假设轴力为正，由平衡方程求解出的结果为正，说明是拉力；结果为负，说明是压力。
例题2.2：零件受力如图2－2所示，其中F P ＝50 kN 。
求零件横截面的最大正应力，并指出发生在哪一横截面上。
图2－2解：用截面法分析零件各横截面上的轴力，得轴力都是相同的，即N P F F =又因为开孔使截面积减小，所以最大正应力可能发生在孔径比较小的两个横截面上I 一I 或II －II 上。
对于I 一I 截面，其横截面积()24215022mm 20mm 560mm =56010m .A -=-⨯=⨯对于II 一II 截面，其横截面积()24225022mm 15mm 2840mm =84010m .A -=-⨯⨯=⨯则最大正应力发生在I 一I 截面,，其上之正应力3N P max42115010N8929MPa 5.6010mF F A A .σ⨯====⨯－ 解题指导：由于开孔，在孔边形成应力集中，因而横截面上的正应力并不是均匀分布的。
严格地讲，不能采用上述方法计算应力。
上述方法只是不考虑应力集中时的应力，称为“名义应力”。
如果将名义应力乘上一个应力集中系数，就可得到开孔附近的最大应力。
应力集中系数可从有关手册中查得。
例题2.3图2－3（a ）所示铰接正方形结构，各杆的横截面面积均为30cm 2，材料为铸铁，其许用拉应力[]30MPa σ=t ，许用压应力[]c 120MPa σ=，试求结构的许可载荷。
解：1 求各杆轴力取B 节点作为研究对象，如图2－3（b ）所示，代平衡方程2cos 450F F -=N 1，F =N 1（拉） 即AB 、BC取A 节点作为研究对象，如图2－3（c ）所示，代平衡方程2cos 450F F -=N2N 1， F F =-N2（压）即AD 、DC，AC 杆轴力为F -。
2 求许可载荷由斜杆的拉伸强度条件[]F A σσ==≤N t t 1[]()()4630103310127.3kN F σ-≤=⨯⨯⨯=t由AC 杆的压缩强度条件[]F FA Aσσ==≤N2c c []()()46301012010360kN F A σ-≤=⨯⨯⨯=c故结构的许可载荷为[]127.3kN F =解题指导：尽管拉力F N1要比压力F N2小约40%，但结构的许可载荷还是受拉伸强度所限制,这是因为铸铁的抗拉强度要比其抗压强度低得多。
在图2－3工程实际中，受压构件通常选用铸铁等脆性材料，而受拉构件一般选用低碳钢等塑性材料，以合理地利用各种材料的力学性能。
例题2.4：图2－4（a ）所示之结构中，AB 和AC 均为Q235钢制成的圆截面杆，直径相同d ＝20mm ，许用应力[]σ＝160 MPa 。
试确定该结构的许用载荷。
解：1 由平衡条件计算各杆轴力，设AB 杆轴力为N1F ，AC 杆轴力为N2F ，如图2－4（b ）所示。
对于节点A ，由0x F ∑=得sin 30sin 45F F =N1N2 （1）由0y F ∑=得cos30cos 45F F F +=N1N2 （2）将（1）、（2）式联解N 0.732F F ==1N20.518F F ==可见AB 杆比AC 杆受力大，而两者的材料及横截面尺寸都是相同的。
因此，两根杆的危险程度不同。
如果AB 杆的强度得到满足，AC 杆的强度也一定安全。
2 根据强度条件计算许用载荷[]N1AB F Aσσ=≤ 有[]240732πFd.σ⨯⨯≤ 据此解得[]()26-3216010π2010π6867kN 4073240732dF ...σ⨯⨯⨯⨯≤==⨯⨯图2－4因而得[]68.67F =kN若改为，由强度条件计算许用轴力 [][]246N112101601050.3kN 4F A πσ-⨯⨯≤=⨯⨯=[][]24622101601050.3kN 4F A πσ-⨯⨯≤=⨯⨯=N2由于AB 、AC 杆不能同时达到最大许用容许轴力，则将[]N1F ，[]N2F 代入（2）式，解得[]79.1kN F =这个解显然是错误的。
解题指导：上述错误解法，实际上认为两根杆同时达到了危险状态。
但实际上，两根杆的材料、截面尺寸相同，而受力不同，因而应力不同，其中受力较大的杆中应力达到许用应力时，另一根的应力必然小于许用应力。
因而二者不可能同时到达危险状态。
例题2.5：1、2杆均为圆截面钢杆，杆端为铰接。
两杆长度L 、直径d 、材料E 均相等，A 处作用力F ，如图2－5所示，试求节点A 在力F 作用下的位移。
解：在力F 作用下，杆1、2为轴向拉伸，由静力平衡关系得：图2－50sin sin 2cos 2cos y FF 0 xF F F F F F F F F αααα=======∑∑N1N2N1N2N1N1N2代入胡克定律解得1、2杆的变形量N 1222cos 4F L FLL L EA E d πα∆=∆=＝但两杆铰接在一起，不能自由伸长，可判断出变形后节点A 位移向下。
分别以B 、C 为圆心，1L L +∆、2L L +∆为半径作圆弧，所作圆弧的交点A 1就是杆件变形后节点A 的位置。
