当前位置：文档之家 › 高等量子力学 算符

高等量子力学 算符

  • 格式：ppt
  • 大小：1.66 MB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

高等量子力学5-1--5-2

高等量子力学5-1--5-2

{
m
2
}
（n1 +n2）个基矢
α ⊕ ψ = ∑ ν i αi ⊕ ∑ ε m ψ m
i m
(+) (+)
= ∑ ν i αi ⊕ φ i
( 2)
2)
( ×)
( =∑( ν
i i
= ∑ ν i αi ⊕ φ (
i
⊕ φ(
2)
( )α + ∑ ( φ
m i m
)
(1) + φ ⊕ ∑ εm ψ m m + ∑ φ( ) + εm ψ m
Pr oof ( ∆′ ) : ( A ⊗ L )( B ⊗ M ) ( α ⊗ ψ
（□）
= ( A ⊗ L)( B α ⊗ M ψ = A( B α ) ⊗ L ( M ψ = AB α ⊗ LM ψ
（□） 算符乘积定义
)
)
)
（□）
= ( AB ⊗ LM ) ( α ⊗ ψ
A指A ⊗ I (
1 2)
基矢
Eim = ν i ⊗ ε m = ν i ε m 共n1 × n2个，是R1 ⊗ R2的维数
∴以 Eim 为基矢的表象是K ⊗ P( KP)表象
讨论R1 ⊗ R2中，矢量 α ⊗ ψ 和算符A ⊗ L的矩阵表示 例：n1 = 2, n2 = 3
α1ψ 1 K ⊗ P表象中 α ⊗ ψ α1ψ 2 ψ 1 α1 α1ψ 3 α ⊗ ψ = ⊗ ψ 2 = α 2 ψ α 2ψ 1 3 α 2ψ 2 α ψ 2 3
R1 R2
K 表象
KP表象
P表象

量子力学中的运动学算符

量子力学中的运动学算符

量子力学中的运动学算符量子力学作为现代物理学的重要分支，研究物质和能量在微观尺度上的行为。

运动学是量子力学的一个基础概念，它描述了粒子在空间中的运动轨迹以及位置与时间的关系。

在量子力学中，运动学算符是描述粒子运动状态的数学工具。

本文将介绍量子力学中的运动学算符及其基本性质。

一、位置算符在经典力学中，位置是描述物体在空间中所处位置的物理量。

在量子力学中，位置算符表示对粒子位置的测量。

位置算符通常用符号̂表示，其本征态表示为|r⟩。

位置算符的本征值就是粒子的位置坐标，即|r⟩与对应的本征值r。

位置算符的表示形式为：r = r其中r是一个三维矢量，包含粒子在三个坐标轴上的位置。

二、动量算符在经典力学中，动量是物体的质量和速度的乘积。

在量子力学中，动量算符表示对粒子动量的测量。

动量算符通常用符号̂表示，其本征态表示为|r⟩。

根据量子力学理论，动量算符与位置算符是互补的，即它们不能同时被精确测量到。

动量算符的表示形式为：r= −rℏ∇其中r是虚数单位，ℏ是普朗克常数，∇是梯度算子。

动量算符与位置算符的本征值存在对应关系，即动量本征值为粒子的动量。

三、角动量算符在量子力学中，角动量算符描述了粒子的自旋和轨道角动量。

角动量算符与位置算符和动量算符类似，也是量子力学中的重要概念。

角动量算符通常用符号̂表示，其本征态表示为|r, r⟩，其中r为角动量大小，r为角动量在某个方向上的投影。

角动量算符有三个分量：rr，rr和rr。

三个分量满足角动量的对易关系，即：[rr, rr] = rℏrr[rr, rr] = rℏrr[rr, rr] = rℏrr其中[r, r]表示算符r和r的对易子。

这些对易关系表明了角动量算符的非对易性，与经典力学中角动量的对易性质不同。

四、能量算符在量子力学中，能量是一个系统的基本物理量，描述了物体的能级和储备能量。

能量算符表示对系统能量的测量。

能量算符通常用符号̂表示，其本征态表示为|r⟩。

高等量子力学31产生算符和消灭算符

高等量子力学31产生算符和消灭算符
2; bα b β 2; bα b β 2; ab
2; bb
)
bα b β
∑
= 2; ab 2; ab 2; ab + 2; ba 2; ba 2; ab 2; ab 2; ab 2; ab = 2; ab 2; ab 2; ab + ε 2 2; ba 2; ba 2; ab = 2 2; ab 2; ab 2; ab = 2; ab
分析:① 分析 ① a( b) 把n粒子基矢 → (n-1)粒子基矢⇒ a ( b ) ——消灭算符 粒子基矢 粒子基矢 消灭算符
中有一个离子处于b态则 ②如在 n; bα b β bγ Lbν 中有一个离子处于 态则 a( b) 的作用正 是去掉该粒子,得出其余 个粒子的态,若没有粒子处于 是去掉该粒子 得出其余(n-1)个粒子的态 若没有粒子处于 得出其余 个粒子的态 若没有粒子处于b 才有)， 的作用是将处于b态 ③若 n; bα bbb L bν (Bose才有 ，则 a( b) 的作用是将处于 态 才有 的粒子对称去掉一个，仍得出(n-1)粒子的态 的粒子对称去掉一个，仍得出(n-1)粒子的态 对此态的作用结果为0 态,则 a( b) 对此态的作用结果为 则
0
n; b α ′b β ′ L bν ′ = 1
离散形式
验证： 验证：
b b L bν ′
α′ β′
∑
n; b α ′b β ′ L bν ′
n; b α ′b β ′ L bν ′ n; b α b β L bν 1 ε p Pδ bα ′bα δ b β ′b β L δ bν ′bν ∑ n! P
§31
产生算符和消灭算符
Rn n ; b α b β L bν
没有 明显联系

高等量子力学_第二章_算符

高等量子力学_第二章_算符

条件（1） ：在值域中取一任意 ，证明在定义域有 存在：
1 AB AB

可见对于任意 ，确有 存在，这个 就是 B 。
条件（2） ：若 A 1 A 2 ，用 C 作用在此式两边：
CA 1 CA 2
但此式就是 1 2 ，条件(2)也得到满足，因此 A1 存在。
§2-2 算符的代数运算
在量子力学中，经常出现不可对易线性算符的代数运算， 在这一小节里，我们举几个较复杂的运算例子；并且用代数方 法证明两个常用的算符等式（2.9）和（2.14）两式。
设 A 和 B 为两个线性算符，互不对易。首先我们定义多重对 易式 [ Ai , B]和[ B, Ai ] ：
A A A A a A a
(2.1)
满足下列二条件的，称为反线性算符：
A A A A a A a
*
(2.2)
其中a是任意常数。在量子力学中出现的算符，绝大多数都是线 性算符，下面我们只讨论线性算符。 算符对其定义域中每一个右矢作用，都应有确定的结果。 定义一个具体的算符应当规定其定义域，并指出它对其定义域 中每一个矢量作用的结果。而确定一个具体的线性算符，只须 规定它对其定义域中的一组线性无关的右矢（例如一组基矢） 中每个右矢的作用结果即可。
A B
若两个算符 A和B 满足
[ A, B] AB BA
AB BA
则说这两个算符是可对易的，或称为两个算符对易。 定义： (2.2)
经常使用的几个对易关系：
ˆ ˆ ˆ ˆ [ F , G ] [G , F ]
ˆ ˆ ˆ ˆ ˆ ˆ ˆ [F , G M ] [F , G ] [F , M ]

量子力学之算符

量子力学之算符

i
但是坐标算符与其非共轭动量 对易，各动量之间相互对易。
x pˆ pˆ x i
pˆ pˆ pˆ pˆ 0
, x, y, z
量子力学中最基本的 对易关系。
xpˆ y pˆ y x 0
xpˆ z
pˆ z
x
0
pˆ x pˆ y pˆ y pˆ x 0
ypˆ x pˆ x y 0 zpˆ x pˆ xz 0
~ x
x
)
0
由于ψ、φ是 任意波函数,
( ~ x
x
)
0
~ x
x
所以
同理可证:
~ pˆ x pˆ x
可以证明： ( Aˆ Bˆ ) B~ˆ A~ˆ
(11)厄密共轭算符
算符 Ô 之厄密共轭算符 Ô + 定义:
由此可得：:
d *Oˆ d (Oˆ )*
d *Oˆ d (Oˆ )*
pˆ* (i)* i pˆ
（10）转置算符
算 符Uˆ 的 转 置 算 符U~ˆ 定 义 为 ：
d *U~ˆ dUˆ *
式中 和 是两个任意函数。
例1：
~ x
x
证：
dx
*
~ x
利用波函数标准条件: 当|x|→∞ 时ψ,→ 0。
dx
x
*
* |
dx
*
x
dx
*
x
dx
*
(
（2）算符相等
若两个算符 Ô 、Û 对体系的任何波函数 ψ的运算结果都相 同，即Ô ψ= Û ψ，则算符Ô 和算符Û 相等记为Ô = Û 。
（3）算符之和
Hˆ Tˆ Vˆ
表明
Ham ilton算 符Hˆ 等 于

高等量子力学 角动量算符和角动量表象 自旋表象PPT课件

高等量子力学 角动量算符和角动量表象 自旋表象PPT课件

另一幺正性关系是
l
'' '' lm lm l0 ml
l
Ylm* , Ylm ','
1
sin
'
'
l0 ml
(8.70)
这也是函数形式的球谐函数的完全性关系.
第18页/共30页
任何函数 r,, 都可以展开成为
l
r, , clmRlmrYlm , l 0 ml
Ylm* 1,1 Ylm 2,2
ml
2l
4
1
Pl
cos
(8.72)
式中 1,1 和 2 ,2 代表两个单位矢量的方向,而 是二矢量间
的夹角.
另一个有用公式为
eikr 4
l
il jl
kr Ylm*
ek
Ylm
er
l0 ml
2l 1il jl krPl cos
(8.73)
式中
mm！ ！eim
sinm
d
d
cos
lm sin 2l
(8.64)
Ylm* , 1mYl,m,
全部球谐函数构成完全函数组 。
第13页/共30页
§8-5 lm 表象和 表象
在以单粒子的位置 x, y, z 或 r,, 为自变量的函数空间中,
我们建立了与抽象的希尔伯特空间一一对应的态矢量和算符,而且 把这一函数空间分解为两个较小的函数空间的直积空间:一个是以 r 为自变量的函数所组成的空间,以算符 Rˆ 的本征矢量为基矢;另一
jm jm jj mm
（8.16）
此式对轨道角动量、自旋角动量或其它角动量的本征矢量均成立。
第10页/共30页

量子力学——算符（精品pdf）

量子力学——算符（精品pdf）
量子力学
算符
目录
一、位置算符
1.1 厄米算符 1.2 （位置算符）本征值与本征函数
1.3 正则对易关系
二、动量算符
2.1 动量算符导引 2.2 （动量算符）本征值与本征函数
七、自旋算符
7.1 概论 7.2 发展史 7.3 自旋量子数
7.3.1 基本粒子的自旋 7.3.2 亚原子粒子的自旋 7.3.3 原子和分子的自旋
中心的角色。角动量，动量，与能量是物体运动的三个基
本特性
目录 3.1 简介 3.2 数学定义 3.3 角动量是厄米算符 3.4 对易关系
3.4.1 角动量算符算符与自己的对易关系 3.4.2 角动量平方算符与角动量算符之间的对易关系 3.4.3 哈密顿算符与角动量算符之间的对易关系 3.4.4 在经典力学里的对易关系 3.5 (角动量)本征值与本征函数
目录 1.1 厄米算符 1.2 本征值与本征函数 1.3 正则对易关系
返回目录 3/52
1.1厄米算符
由于每一种经过测量而得到的物理量都是实值的。所以，可观察量 O 的期望值是 实值的：
对于任意量子态 ，这关系都成立：
根据伴随算符的定义，假设 是 的伴随算符，则
因此，
这正是厄米算符的定义。所以，表示可观察量的算符 ，都是厄米算符。
2.3 厄米算符 2.4 正则对易关系
7.3.4 自旋与统计
7.4 自旋的方向
三、角动量算符
3.1 简介 3.2 数学定义 3.3 角动量是厄米算符 3.4 对易关系
3.4.1 角动量算符算符与自己的对易关系 3.4.2 角动量平方算符与角动量算符之间的对易关系 3.4.3 哈密顿算符与角动量算符之间的对易关系
经过一番繁杂的运算，终于得到想要的方程

量子力学 算符

量子力学 算符

ˆx ˆ 1 0 ˆx ˆD D
注：对于单纯是作常数乘法的算符，常省略抑扬符。
（5）算符服从乘法结合律
ˆ (B ˆ) (A ˆB ˆ ˆC ˆ )C A
d ˆ ˆ ˆ 3 ˆ ˆ, C , Bx 例如： A dx
ˆ 3x ˆ (B ˆ )] f D ˆC ˆC ˆ (3xf ) 3 f 3xf ˆ, [ A B
量子力学的哈密顿算符：
2 2
px V ( x) 2m
其本征值为体系 能量的可能值
2
d ˆ H V ( x) 2 2m dx
这种经典力学的物理量（如能量，坐标和动量等等） 与量子力学算符之间的对应性是普遍的。这是量子力 学的一个基本假定。即：每一物理量都有一个对应的 量子力学算符。 问题：如何得到物理量F所对应的量子力学算符呢？
第一步：写出F作为笛卡儿坐标和对应动量的函数的经 典力学表示。 第二步：做以下变换：
笛卡儿坐标q代之以该坐标去乘的算符，即：q ˆ q 线动量的每个笛卡儿分量pq代之以算符：
i ˆq p 2 i i q i q q
例:
对应于坐标的算符是乘以坐标：
2 2 d ˆ T ˆ V ˆ H V ( x) 2 2m dx
这与不含时间的薛定谔方程一致。
d [ V ( x)] ( x) E ( x) 2 2m dx
2
2
量子力学算符与体系对应的性质的关系
ˆ 的具有本征值 若i 是 F
a i 的本征函数，则有：
ˆ a F i i i
由此可见，算符的假设和薛定谔方程实际上是一致的。
2
2
量子力学体系的态用包含我们可能了解的关于体系的全 部知识的态函数Ψ(x，t)来描述。Ψ如何给出关于性质F 的知识呢？

喀兴林高等量子力学习题EX2.算符

喀兴林高等量子力学习题EX2.算符

EX2.算符2.1证明下列常用公式 （陈玉辉解答 项鹏核对 ） （1）C B A C A B BC A ],[],[],[+= 证明： CB AC A B C BA AB CA AC B BAC ABC BCA BAC BCAABC BC A ],[],[][][],[+=-+-=-+-=-= （2）B C A C B A C AB ],[],[],[+= 证明：BC A C B A B CA AC CB BC A CAB ACB ACB ABC CABABC C AB ],[],[][][],[+=-+-=-+-=-=2.2 若算符B 与],[B A 对易，证明： （陈玉辉解答 项鹏核对 ）],[],[1B A nB B A n n -=证明：],[],[],[],[111---+=⋅=n n n n B A B B B A B B A B A 将n 换成（n-1）,就有],[],[],[221---+=n n n B A B B B A B A],[],[2],[],[],[],[2212211-----+=++=⇒n n n n n n B A B B B A B A B B B A B B A B A重复这种递推过程（n-1）次，即得],[],[],)[1(],[],)[1(],[111)1(11B A nB B A B B B A n B A B B B A n B A n n n n n n n n -------=+-=+-=#练习2.3 证明： （输入人：杜花伟 核对人：王俊美）（1）若A 有逆，a ≠0，则aA 也有逆，且111)(--=A a aA ；（2）若A,B 都有逆，则AB 也有逆，且111)(---=A B AB ； （3）})(1{)(111---+-=+B A B A B A ；（4）⋅⋅⋅+++=--------11121111)(BA BA A BA A A B A λλλ.(λ为复数); 证明：（1）若A 有逆，a ≠0，满足1,111==--aa AA ，则 11111==----AA aa A aAa 所以aA 有逆,且111)(--=A aaA . (2) 若A,B 都有逆,满足1,111==--BB AA ,则 1111==---AA A ABB 所以AB 有逆,且111)(---=A B AB . (3)})(1{})())({(}))({(})({)()(111111111111------------+-=+-++=+-+=+=+=+B A B A B A B B A B A A B A B B A A B A A A B A A A B A(4) 由于1)1(--χ（x 极小,即x →0时）展为级数: ⋅⋅⋅++++=--3211)1(χχχχ故(⋅⋅⋅+++=⋅⋅⋅+++=-=-=----------------111211*********11)1()1()]1([)(BA BA A BA A A BA BA BA A BA A BA A B A λλλλλλλ#2.4 若线性算符A 有逆，{|μ>}（i=1,2,3,…，n ）是A 的有限维的定义域的中的一组完全集。

高等量子力学2-4——3-3

高等量子力学2-4——3-3
幺正算符联系
Proof： 利用Parseval等式证明。
幺正变换
幺正算符U 作用 矢量空间的全部矢量 U (**)
不改变： 矢量的模 内积 正交性
U
（2.29）——矢量的幺正变换
(*)
| U | U | | U | U | i | j U i | U j i | j
2 P123 i i i 1 3

j 1
3
j
j i ij i i i P
i , j 1 i 1
3
3
123
讨论整个空间的投影，这时投影算符 P i i P i i 完全性定理(2)
i i
A(C )=aC ( )
A 1 =a 1 若 （ a A 1 2 ） （ 1 2 ） A 2 =a 2 满足, 则算符A的属同一本征值a的本征矢量全体 本征子空间的维数S —称所属本征值的简并度， 这个本征值或这组本征矢称是S 重简并的。S 1，称无简并。 指出S维本征子空间，只需给其中一组S 个线性无关的本征矢。 有时说，某本征值有S 个 本征矢。
RA( R
i 1, 2, ...
1
R
R ) i =ai R i
即 B ( R i ) ai ( R i ) 0,因为R有逆
( )
1
所有的ai也都是B的本征值（或许B还有别的本征值，本征矢？）
反过来，设已知B的全部本征值和相应的本征矢满足： B i =bi i
物理上称矢量的幺正变换为矢量在多维空间中的转动。
对算符也可以做幺正变换

量子力学常用计算公式

量子力学常用计算公式

量子力学常用计算公式1. 哈密顿算符（Hamiltonian Operator）哈密顿算符在量子力学中用于描述系统的总能量。

它的一般形式为：H = K + V其中，K表示动能算符，V表示势能算符。

2. 薛定谔方程（Schrödinger Equation）薛定谔方程是量子力学的基本方程，描述了量子系统的时间演化。

其一维形式为：iℏ∂ψ/∂t = -ℏ^2/(2m) ∂^2ψ/∂x^2 + Vψ其中，i表示虚数单位，ℏ为约化普朗克常数，m为粒子的质量，ψ为波函数，V为势能。

3. 波函数归一化（Normalization of Wavefunction)波函数必须满足归一化条件，即在整个空间积分后等于1。

对一维情况而言，归一化条件表示为：∫|ψ|^2 dx = 14. 物理量期望值（Expectation Value of Physical Quantity)物理量的期望值表示在量子态中对该物理量进行测量得到的平均值。

对一个可观测量A而言，其期望值定义为：<E[A]> = ∫ψ*Aψ dx其中，A表示物理量算符，ψ为波函数，*表示复共轭。

5. 不确定度原理（Uncertainty Principle)不确定度原理描述了同时测量一对共轭物理量（如位置和动量）的限制。

其数学表达为：ΔxΔp >= ℏ/2其中，Δx表示位置测量精度，Δp表示动量测量精度，ℏ为约化普朗克常数。

6. 一维势阱（One-dimensional Potential Well)一维势阱是一个常见的量子力学模型，用于探讨粒子在势能为零或有限的区域内的行为。

在无穷深势阱中，粒子的波函数为定态波函数，表示为：ψ_n(x) = sqrt(2/L) * sin(nπx/L)其中，L表示势阱的长度，n为正整数。

7. 自旋（Spin)自旋是粒子的固有属性，在量子力学中用于描述粒子的角动量。

自旋算符的本征态表示自旋的量子态，常用的自旋算符包括Sx、Sy和Sz。

高等量子力学角动量算符和角动量表象自旋表象

高等量子力学角动量算符和角动量表象自旋表象

在量子力学中，波函数可以在不同的表 象之间进行转换。对于角动量表象和坐 标表象之间的转换，可以通过傅里叶变
换或拉普拉斯变换实现。
在进行表象转换时，需要注意不同表象 之间基函数的正交性和完备性，以及转 换过程中可能出现的数学困难和物理意
义的变化。
在实际应用中，可以根据具体问题的需 要选择合适的表象进行描述和计算，以
未来发展趋势预测
要点一
发展新的理论和方法
随着科学技术的不断进步和计算能力 的不断提高，未来有望发展出更为精 确和高效的理论和方法来处理角动量 和自旋相关的问题。例如，基于量子 计算机的新型算法和模拟方法有望在 解决复杂多体问题方面取得突破。
要点二
拓展应用领域
角动量和自旋作为量子力学中的基本 概念和工具，在各个领域都有着广泛 的应用前景。未来有望将角动量和自 旋的理论和方法拓展到更多的领域， 如量子信息、量子计算、量子模拟等 前沿领域。
自旋算符定义及性质描述
自旋算符定义
自旋算符是用于描述粒子自旋状态的算符，包括自旋角动量算符和其分量算符。
自旋算符性质
自旋算符满足角动量算符的一般性质，如对易关系、本征值问题等。此外，自旋 算符还具有一些特殊性质，如自旋量子数的取值只能是整数或半整数。
自旋算符在量子力学中地位和作用
描述粒子内禀属性
角动量性质
角动量是守恒的，即在没有外力矩作 用的情况下，物体的角动量保持不变 。此外，角动量具有叠加性，多个物 体的角动量可以相加。
量子力学中角动量重要性
描述微观粒子状态
在量子力学中，角动量是描述微观粒子状态的重要物理量之一，它与粒子的自 旋、轨道运动等密切相关。
解释原子光谱
角动量的量子化假设成功解释了原子光谱的规律性，为量子力学的发展奠定了 基础。

高等量子力学 密度算符和密度矩阵

高等量子力学 密度算符和密度矩阵
1、 trρ = 1 (14.20)
n
证明： 证明：取一组基 { n } , 利用完全性关系 ∑ n n = 1 , 有
trρ = ∑∑ n ψ i pi ψ i n = ∑∑ ψ i n n ψ i pi
n i n i
= ∑ ψ i ψ i pi = ∑ pi = 1
i i
2、
= 1, trρ < 1.
例如一个系统处于 ψ 1 态的概率为 p1 , 处于 ψ 2 态的概 率为 p 2 ( p1 + p 2 = 1) , 系统的这个态目前还无法作简单的描 我们只能用下面的写法表示这个态： 写, 我们只能用下面的写法表示这个态：
ψ 1 : p1 ψ 2 : p2
(14.2)
纯态和混合态是完全不同的两种状态, 即使在(14.1)式 纯态和混合态是完全不同的两种状态 即使在 式 和 (14.2)式中有 c1 = p1 , c 2 式中有
这个状态也是纯态. 这个状态也是纯态.
(14.1)
有时由于统计物理的原因或量子力学本身的原因系统的状 有时 由于统计物理的原因或量子力学本身的原因系统的状 由于统计物理的原因或量子力学本身的原因 在一个确定的态中, 态无法用一个态矢量来描写. 系统并不处在一个确定的态中 而 无法用一个态矢量来描写 系统并不处在一个确定的态中 等各态中, 是有可能处于 ψ 1 , ψ 2 , L ,等各态中 分别有概率 p1, p 2 , L . 这 等各态中 种状态无法用一个态矢量表示, 称为混合态 种状态无法用一个态矢量表示 称为混合态. 混合态
下面看混合态. 取一个比(14.2)式更一般的混合态如下： 式更一般的混合态如下： 下面看混合态 取一个比 式更一般的混合态如下
ψ 1 : p1 , ψ 2 : p2 , LLL

高等量子力学 张量算符

高等量子力学 张量算符

§4.2 分离对称性，宇称或空间反演
上面讨论的是连续性对称操作，即对称操作可由相继 无穷小对称算符所得。量子力学中有用的对称操作并 不限于此种形式，可有分立而非连续的对称操作，如 宇称，晶格平移和时间反演。
宇称或空间反演操作将r变为-r，右手坐标系变为左手 坐标系。量子力学中我们讨论的常是作用于态矢而不 是坐标系的变换。
该态在|R>和|L>间震荡，震荡角频率为
该震荡可看成量子力学的隧道贯穿，粒子在经典 物理禁止的区域隧穿而震荡于两态间。如势垒无 穷高，则EA=ES，从而ω=0，不再震荡。
注：对无穷高势垒， |R>和|L>均是H的本征态， 但|R>和|L>均非π的本征态。即H所具有的宇称不 一定反映在其本征态上，这是简并与对称破缺的 一个简单例子。这种现象在自然界相当普遍，如 铁磁现象，糖与氨基酸的手性等。
注意:非简并性对得出|n>是π的本征态是非常 重要的。若有简并，如氢原子体系， Cp|2p>+Cs|2s>是H本征态，但并非π的本征态。 又如动量本征态也是H本征态，但|p’> 和 |-p’> 简并, |p’>并非π的本征态.
当然，我们可以通过组合H的简并本征态而得 到π的本征态，如|α>=[|p’>±|-p’>]便是π和H的 共同本征态
如对转动，[D(R), H ] 0,则
v [J , H ] 0,
[J 2, H ] 0,
可构造H,J2,Jz的共同本征态|n;j,m>。由上所知，
所有D(R) |n;j,m>态能量简并。
由于 D(R) njm
njm
D( j) mm
(
R)
,
改变表征D(R)

量子力学6-力学量算符

量子力学6-力学量算符

一维情况： x = < x >= ∫
∞
−∞
Ψ ∗ ( x ) xΨ ( x )dx
∞ −∞
F 是任一 学量算符
力
px = < px > = ∫ F = < F >= ∫
∞
ˆ x Ψ ( x )dx Ψ∗ ( x) p
−∞
ˆ Ψ ( x )dx Ψ ∗ ( x )F
若波函数未归一化，则 ∗ ˆ Ψ(r ( ) )dr Ψ r F ∫∫∫ F = < F >= ∗ Ψ ( r ) Ψ ( r )dr ∫∫∫
∫τ
2 3 ψ ( r ) d r = 有限值
0
(39)
如果取波函数的孤立奇点r0=0，当r→0时，上式的积分应该趋于0， 即要求
2 r ψ (r ) → 0
3
若当
r → 0,ψ ~ 1 / r s
，则要求
s < 3/ 2
(b) 一个真实的波函数应该满足归一化条件
∫
全
2 3 ψ (r ) d r = 1
p = ∫ p φ ( p ) dp = 0
2 −∞
+∞
粒子动量平方的平均值
p = ∫ p φ ( p ) dp = λ2 2
2 2 2 −∞
+∞
i px x 1 ∗ dx Ψ ( x )e ∫ 2π
=∫
p x c( p x )dp x
1 = ∫ 2π 1 = ∫ 2π
∗
∗ Ψ ∫ ( x )e
i px x
p x c( p x )dxdp x
i px x d ∗ ∫ Ψ ( x )(− i dx )e c( p x )dxdp x

量子力学中的算符和Dirac符号

量子力学中的算符和Dirac符号

二、Dirac符号的引入
• 量子力学的语言是Dirac符号法，它有两个优点： 一是无需采用具体表象来讨论问题； 二是运算简洁。
• Dirac符号法，也称为q数理论，而q数理论核心 内容之一就是表象可以用以坐标为变量的波函数 Ψ (x ,t )来描写， 力学量则以作用在这种波函数上的算符来表示，这是 量子力学中态和力学量的一种具体表述方式。态还可 以用其他变量的函数作为波函数来描写体系的状态。 • 微观粒子体系的状态（量子态）和力学量的具体表示 形式称为表象。
• 线性算符的充分条件：
ˆ [ f ( x) g ( x)] A ˆ f ( x) A ˆ g ( x) A ˆ [cf ( x)] cA ˆ f ( x) A
量子力学的一个基本假设：力学量用线性厄米算符表 示，即，量子力学中表示力学量的算符一定是线性厄 米算符。 利用力学量的算符可以预言在给定状态里测量这一力 学量所得结果的期望值——平均值。 可得到给定状态里该力学量的表象
• 算符的加法满足通常的代数法则； • 算符的乘法满足通常的结合律和分配率，但一般 不满足交换律。 ˆ和B ˆB ˆ ，则称算符 A ˆ =B ˆA ˆ 是可对易的。 如果A
算符的对易
定义算符的对易关系：
ˆ与 B ˆ 满足交换律，那么就称算符可对 • 如果算符 A ˆ ,B ˆ ]= 0 易，即 [A ˆ 和B ˆ 有共同的本征函 ˆ 、 ˆ 相互对易，则 A 若A B 数系； ˆ 和B ˆ 有共同的本征函数系，则A ˆ 相互对 ˆ 和B 若A 易。 如果两个算符之间不对易，则它们不能同时有确 ˆ p和 r 定值。 如 ˆ
a , a , , a ,
* 1 * 2 * n
• 力学量 O的狄拉克符号表示：

量子力学量子力学中的哈密顿算符和薛定谔方程

量子力学量子力学中的哈密顿算符和薛定谔方程

量子力学量子力学中的哈密顿算符和薛定谔方程量子力学是研究微观粒子行为的物理学分支，它描述了物质的非经典性质。

其中，哈密顿算符和薛定谔方程是量子力学的两个核心概念。

本文将详细介绍哈密顿算符和薛定谔方程，并探讨它们在量子力学中的重要性和应用。

一、哈密顿算符哈密顿算符是量子力学中的一个重要数学运算符，它用于描述物理系统的总能量。

哈密顿算符通常用符号H表示，是根据系统的动力学性质和相互作用而确定的。

在经典力学中，哈密顿函数用于描述质点的动力学性质，而在量子力学中，哈密顿算符承担了相同的作用。

它是一个厄米算符，即满足H† = H，其中†表示厄米共轭。

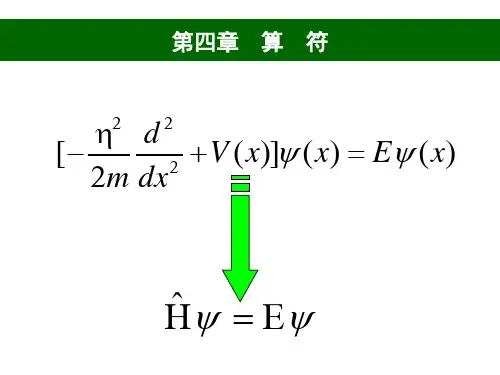
在一维情况下，哈密顿算符可以表示为：H = -(h²/2m) * (∂²/∂x²) + V(x)其中，h是普朗克常量的约化值，m是粒子的质量，∂²/∂x²是对位置x求二阶偏导数的操作，V(x)是势能函数。

二、薛定谔方程薛定谔方程是描述量子力学体系的基本方程，它通过一个波函数Ψ(x, t)来描述粒子的状态演化。

在定态情况下，薛定谔方程可以写为：HΨ(x) = EΨ(x)其中，H是哈密顿算符，Ψ(x)是粒子的波函数，E是粒子的能量。

薛定谔方程是一个偏微分方程，通过求解它，我们可以得到系统的能级和波函数。

薛定谔方程显示了量子尺度下粒子的特殊性质。

与经典力学不同，量子力学中的物体不再具有确定的轨道和位置，而是展现出粒子和波的二重性。

三、哈密顿算符和薛定谔方程的应用哈密顿算符和薛定谔方程在量子力学中有广泛的应用。

它们不仅被用于处理简单的量子体系，如一维无限深势阱和谐振子等，还可以描述复杂的原子、分子和固体体系。

通过求解薛定谔方程，我们可以得到体系的能级和波函数分布，从而揭示了量子系统的结构和性质。

例如，在原子物理中，通过求解薛定谔方程，我们可以得到氢原子的精确能级和波函数，解释氢光谱的谱线。

此外，哈密顿算符和薛定谔方程还导致了其他量子力学的重要概念，如驰豫过程、量子隧穿和量子纠缠等。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
为交）；至于 BA的定义域，若 A 的值域在 B 的定义域之内，则 BA 的定义域就是 A 的定义域，若 A 的值域只有一部分在 B 的定义 域内，则 BA的定义域要比 A 的定义域小。
两个算符相等的定义是： A与B 有相同的定义域并且对域内
任意矢量 有
这时我们记作
2020/4/1
A B AB
若两个算符 A和B 满足 ABBA
线性算符的定义域，可以是整个右矢空间本身，也可以是 它的一个子空间。
可以证明，线性算符具有下列性质：
（1）线性算符的值域也是右矢空间（大空间本身或其子空间）。 （2）若定义域是有限维的空间，则值域空间的维数等于或小于
定义域空间的维数。 （3）在定义域中，那些受A的作用得到零矢量的右矢全体，也
构成一个右矢空间（定义域的子空间）。 复数对右矢的数乘，可以看成算符对右矢的作用，每一个
A [A （ i） ， B ] [A （ i） ， B ]A [A （ i 1 ） ， B ]
n A i,B A n i i n 0n n ! i!i!A i,B A n 1 i i n 0n n ! i!i!A i 1 ,B A n i
在上式右边第二个取和式中，取j=i+1，得
§2-2 算符的代数运算
在量子力学中，经常出现不可对易线性算符的代数运算， 在这一小节里，我们举几个较复杂的运算例子；并且用代数方 法证明两个常用的算符等式（2.9）和（2.14）两式。
设 A 和 B 为两个线性算符，互不对易。首先我们定义多重对
易式[ Ai , B]和[B, Ai ] ：
A 0,BB
2020/4/1
由上述定义可知，除交换律不一定成立外，算符之间服从 一般的加、减、乘和幂次的代数运算法则：
ABC ABAC ABC ABC
等等。
A3 AAA
可以用算符和复数构成一个多项式作为算符的函数：
F A a 0 a 1 A a 2 A 2 a n A n
甚至可以构成无穷级数（我们不去仔细考察由此引起的数学问 题），例如可以写
2020/4/1 A [A （ i） ， B ] [A （ i） ， B ]A [A （ i 1 ） ， B ]
（ 2 .6 ） （ 2 .7 ）
例1：证明：
A n B i n 0 n i A i,B A n i i n 0n n ! i! i!A i,B A n i （2.8）
复数都可以看成一个算符；其定义域和值域均为全空间：
a a
其中两个特殊的算符： ， 1 ， 1
对一切 成立；前者称为零算符，后者称为单位算符。 2020/4/1
两个算符 A与B 的和 A B 及乘积 BA的定义是：
AB AB
BA BA
A B 的定义域是 A与B 两算符的定义域的共同部分（数学上称
dddd22F2F2 eeAA AA,, AA,,BB eeAA eA[A(2),B]eA
[ A ,[ A ,B ] ] A [ A ,B ] [ A ,B ] A
将 F () 作 Taylar 展开：
e A B A e F i 01 i! d d iF i 0i i 01 i!A i,Bi
A () f e A e B A (e A B )
A () fe A e B A B e e B e (A B )
A () e B A B e 1 [B ()(ຫໍສະໝຸດ ),A ] 1i[B (i),A ]
i 0 i!
i 0 i!
2020/4/1
A () e B A B e 1 [B ()(i),A ] 1i[B (i),A ]
1 a A 2 1 !a 2 A 2 3 1 ！ a 3 A 3 n 0n 1 !a n A n e aA (2.3)
2020/4/1
注意上式是算符的指数函数的定义式。在此定义下，关系式
eAeBeAB (当[A,B]=0 时成立)
而当[A, B] 0 时是不成立的（参见本节§2-2）。 逆算符 设在一个右矢空间中，算符 A 把定义域中的一个右矢
A ( ) e f A A B e ( A e B ) e A [ B , A ] e B e ( A B )
A () f A A e e B e (A B )[B ,A ]e A e B e (A B )
i 0 i!
i 0 i!
A [ B ,A ] 2 [ B ( 2 ),A ]
A[B,A]
[B (2),A ][B ,[B ,A ] ]0
d(f ) A () f e A e B A B e e B e (A B ) d
f()eA eBe(A B )
A () fe A ( A [ B ,A ]e B ) e ( A B )
B ,A 0 B
A 1,BA ,B B ,A 1 B ,A
A 2,BA ,A ,B B ,A 2 B ,A ,A
（2.5）
……………….. ………………….
显然，对于[ Ai, B] 型的多重对易式有 [A ， [A （ i） ， B ] ][A （ i 1 ） ， B ]
则说这两个算符是可对易的，或称为两个算符对易。
定义：
[A,B]AB BA
(2.2)
经常使用的几个对易关系：
[F ˆ,G ˆ][G ˆ,F ˆ]
[F ˆ,G ˆ M ˆ] [F ˆ,G ˆ] [F ˆ,M ˆ] [F ˆ,G ˆM ˆ] G ˆ[F ˆ,M ˆ] [F ˆ,G ˆ]M ˆ
[F ˆG ˆ,M ˆ] F ˆ[ G ˆ,M ˆ] [F ˆ,M ˆ] G ˆ [A ˆ,[B ˆ,C ˆ] ][B ˆ,[C ˆ,A ˆ] ][C ˆ,[A ˆ,B ˆ] ]0(Ja恒 co等 b
一个算符A，其定义域是一个矢量空间，而又满足下列条件的， 称为线性算符：
AAA
AaAa
(2.1)
满足下列二条件的，称为反线性算符：
AAA
AaAa*
(2.2)
其中a是任意常数。在量子力学中出现的算符，绝大多数都是线 性算符，下面我们只讨论线性算符。
算符对其定义域中每一个右矢作用，都应有确定的结果。
定义一个具体的算符应当规定其定义域，并指出它对其定义域 中每一个矢量作用的结果。而确定一个具体的线性算符，只须 规定它对其定义域中的一组线性无关的右矢（例如一组基矢） 中2每020/个4/1 右矢的作用结果即可。
n 1
n !
A j,BA (n n 11 )i j
j 1nj1!j 1!
将此式的求和傀标j再改成i，即可与第一和式相加，于是得
A n 1 B n i 0 1n n 1 1 ! i!i!A i,B A n 1 i
这是与原式完全相同的形式，只是原来的n成为n+1，这说明原 式若对n成立，对n+1亦成立。由于我们已经证明原式对n=1成 立，20因20/4此/1 ，原式对任何整数n都成立。证毕。
2020/4/1
A 0,BB A 1,BA ,B A 2,BA ,A ,B B
A n B i n 0 n i A i,B A n i i n 0n n ! i! i!A i,B A n i
B An1Bi n0n iA[A （ i） ， B]Ani
2020/4/1
(2.9)式这一类算符等式，还有一种证明方法是引入一个实变
量 ，构造一个含 和一些算符的式子，把它看成 的函数 F ()
而对它进行求导或积分，最后在所得等式中令 =1。
为证明（2.9）式可取
F eABe A
eAB eA
1Ai,B
i0i!
这时
ddddFFeeAAAABBBBAeAA eeAA[AA ,,BB e]e AAA
上式右端可把取和上限推至无穷，由于 m!当m 0 时定义为 ，
i 的上限实际上仍是 n。
证明： 用数学归纳法证明，当n=1时上式为
A B B A [A ,B ]
原式成立。下面我们从原式出发，推出用n+1代替n的同样形 式的式子。
将原式从左方用A作用，得
An1Bi n0n iA[A （ i） ， B]Ani
§2 算符
主要内容： §2-1 定义 §2-2 算符的代数运算 §2-3 作用于左矢的算符 §2-4 厄米算符和幺正算符 §2-5 投影算符
2020/4/1
算符是矢量空间中又一重要概念。在这一节里，我们在右 矢空间中引入算符，并从左右矢空间的对应关系去讨论算符及 其性质。这些性质很容易回到单一空间的表示方法中去。
§2-1 定义
规定一个具体的对应关系，用 A 来表示。使右矢空间中的某
些右矢与其中一些右矢相对应，例如使 与 相对应，记为
A
这样的对应关系 A 称为算符。我们说算符 A 作用于右矢 ，
得到右矢 。
在算符的定义中，被算符A作用的右矢全体，称为A的定义 域；得出的右矢全体称为值域。二者可以不同，也可以部分或 完全2020重/4/1合。通常算符的定义域与值域都是整个空间。
AB=1, CA=1
(2.4)
则算符A有逆，而且
A1BC
证明: 我们证明这样的A满足有逆条件(1)和(2)。
条件（1）：在值域中取一任意 ，证明在定义域有 存在：
1 A B A B
可见对于任意 ，确有 存在，这个 就是 B 。
2020/4/1
条件（2）：若 A1 A 2 ，用 C 作用在此式两边：
n 1 !A A B e Ae ABeA[n 0n 1!AnB]eA n 0n 1 !i 0n n ! i!i!A i,B A n i e A i
!i!A i,B A n i e A i 01 i!A i,B n 0n1 i!A n i e Ai 01 i!A i,B
当于算符的除法，有时也写成 A1 1 A
不是所有的算符都有逆。一个算符A有逆的条件如下：