(整理)轴心受力构件五
- 格式:doc
- 大小:723.50 KB
- 文档页数:32

轴心受力构件习题及答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(轴心受力构件习题及答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为轴心受力构件习题及答案的全部内容。
轴心受力构件习题及答案一、选择题1。
一根截面面积为A,净截面面积为A n的构件,在拉力N作用下的强度计算公式为______。
2。
轴心受拉构件按强度极限状态是______.净截面的平均应力达到钢材的抗拉强度毛截面的平均应力达到钢材的抗拉强度净截面的平均应力达到钢材的屈服强度毛截面的平均应力达到钢材的屈服强度3。
实腹式轴心受拉构件计算的内容有______。
强度强度和整体稳定性强度、局部稳定和整体稳定强度、刚度(长细比)4. 轴心受力构件的强度计算,一般采用轴力除以净截面面积,这种计算方法对下列哪种连接方式是偏于保守的?摩擦型高强度螺栓连接承压型高强度螺栓连接普通螺栓连接铆钉连接5. 工字型组合截面轴压杆局部稳定验算时,翼缘与腹板宽厚比限值是根据______导出的。
6。
图示单轴对称的理想轴心压杆,弹性失稳形式可能为______。
X轴弯曲及扭转失稳Y轴弯曲及扭转失稳扭转失稳绕Y轴弯曲失稳7。
用Q235号钢和16锰钢分别建造一轴心受压柱,其长细比相同,在弹性范围内屈曲时,前者的临界力______后者的临界力。
大于小于等于或接近无法比较8。
轴心受压格构式构件在验算其绕虚轴的整体稳定时采用换算长细比,是因为______。
格构构件的整体稳定承载力高于同截面的实腹构件考虑强度降低的影响考虑剪切变形的影响考虑单支失稳对构件承载力的影响9. 为防止钢构件中的板件失稳采取加劲措施,这一做法是为了______。

第四章轴心受力构件一、轴心受力构件的特点和截面形式轴心受力构件包括轴心受压杆和轴心受拉杆。
轴心受力构件广泛应用于各种钢结构之中,如网架与桁架的杆件、钢塔的主体结构构件、双跨轻钢厂房的铰接中柱、带支撑体系的钢平台柱等等。
实际上,纯粹的轴心受力构件是很少的,大部分轴心受力构件在不同程度上也受偏心力的作用,如网架弦杆受自重作用、塔架杆件受局部风力作用等。
但只要这些偏心力作用非常小(一般认为偏心力作用产生的应力仅占总体应力的3%以下。
)就可以将其作为轴心受力构件。
轴心受力的构件可采用图中的各种形式。
其中a)类为单个型钢实腹型截面,一般用于受力较小的杆件。
其中圆钢回转半径最小,多用作拉杆,作压杆时用于格构式压杆的弦杆。
钢管的回转半径较大、对称性好、材料利用率高,拉、压均可。
大口径钢管一般用作压杆。
型钢的回转半径存在各向异性,作压杆时有强轴和弱轴之分,材料利用率不高,但连接较为方便,单价低。
b) 类为多型钢实腹型截面,改善了单型钢截面的稳定各向异性特征,受力较好,连接也较方便。
c) 类为格构式截面,其回转半径大且各向均匀,用于较长、受力较大的轴心受力构件,特别是压杆。
但其制作复杂,辅助材料用量多。
二、轴心受拉杆件轴心受拉杆件应满足强度和刚度要求。
并从经济出发,选择适当的截面形式,处理好构造与连接。
1、强度计算轴心拉杆的强度计算公式为:(6-1)式中:N——轴心拉力;A n——拉杆的净截面面积;f ——钢材抗拉强度设计值。
当轴心拉杆与其它构件采用螺栓或高强螺栓连接时,连接处的净截面强度计算如连接这一章所述。
公式(6-1)适用于截面上应力均匀分布的拉杆。
当拉杆的截面有局部削弱时,截面上的应力分布就不均匀,在孔边或削弱处边缘就会出现应力集中。
但当应力集中部分进入塑性后,内部的应力重分布会使最终拉应力分布趋于均匀。
因而须保证两点:(1)选用的钢材要达到规定的塑性(延伸率)。
(2)截面开孔和消弱应有圆滑和缓的过渡,改变截面、厚度时坡度不得大于1:4。








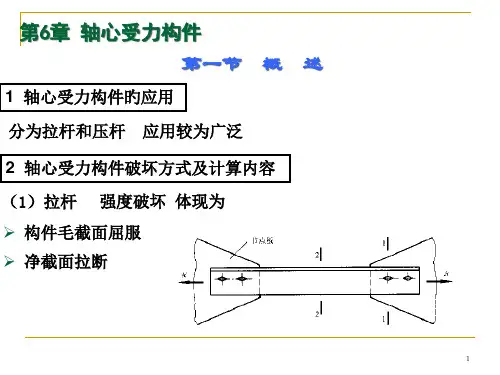
轴心受力构件设计轴心受拉构件时需进行强度和刚度的验算,设计轴心受压构件时需进行强度、整体稳定、局部稳定和刚度的验算。
一、轴心受力构件的强度和刚度1.轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服点为承载力极限状态f A N n ≤=σ (1) 式中 N ——构件的轴心拉力或压力设计值;n A ——构件的净截面面积;f ——钢材的抗拉强度设计值。
采用高强度螺栓摩擦型连接的构件,验算最外列螺栓处危险截面的强度时,按下式计算:f A N n≤='σ (2) 'N =)5.01(1n n N - (3)式中 n ——连接一侧的高强度螺栓总数;1n ——计算截面(最外列螺栓处)上的高强度螺栓数;0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆,除按式(2)验算净截面强度外,还应按下式验算毛截面强度f A N ≤=σ (4)2.轴心受力构件的刚度计算轴心受力构件的刚度是以限制其长细比保证][λλ≤ (5) 式中 λ——构件的最大长细比;[λ]——构件的容许长细比。
二、 轴心受压构件的整体稳定1.理想轴心受压构件的屈曲形式理想轴心受压构件可能以三种屈曲形式丧失稳定:①弯曲屈曲 双轴对称截面构件最常见的屈曲形式。
②扭转屈曲 长度较小的十字形截面构件可能发生的扭转屈曲。
③弯扭屈曲 单轴对称截面杆件绕对称轴屈曲时发生弯扭屈曲。
2.理想轴心受压构件的弯曲屈曲临界力若只考虑弯曲变形,临界力公式即为著名的欧拉临界力公式,表达式为N E =22l EI π=22λπEA (6) 3.初始缺陷对轴心受压构件承载力的影响实际工程中的构件不可避免地存在初弯曲、荷载初偏心和残余应力等初始缺陷,这些缺陷会降低轴心受压构件的稳定承载力。
1)残余应力的影响当轴心受压构件截面的平均应力p f >σ时,杆件截面内将出现部分塑性区和部分弹性区。
由于截面塑性区应力不可能再增加,能够产生抵抗力矩的只是截面的弹性区,此时的临界力和临界应力应为:N cr =22l EI e π=22lEI π·I I e (7) cr σ=22λπE ·I I e (8) 式中 I e ——弹性区的截面惯性矩(或有效惯性矩);I ——全截面的惯性矩。
第四章轴心受力构件公式整理1.应变公式:轴心受力构件的应变公式描述了受力构件在轴向受力作用下的变形情况。
应变公式主要有以下两种形式:(1)需要计算伸长形变的情况下:在受力过程中,轴心受力构件发生的伸长形变与受力大小和材料的弹性模量有关。
应变公式可表示为:ε=ΔL/L其中,ε表示轴向应变;ΔL表示受力构件发生的伸长形变;L表示受力构件的初始长度。
(2)不需要考虑伸长形变的情况下:在一些情况下,受力构件的长度相对较短,可以忽略伸长形变的影响。
此时,应变公式可以表示为:ε=δ/h其中,ε表示轴向应变;δ表示构件上其中一截面上的位移;h表示受力构件的高度。
2.应力公式:轴心受力构件的应力公式描述了受力构件在轴向受力作用下的应力分布情况。
应力公式主要有以下两种形式:(1)线性弹性应力公式:在弹性阶段,应力与应变成正比,最常用的应力公式是线性弹性应力公式:σ=E*ε其中,σ表示轴向应力;E表示受力构件材料的弹性模量;ε表示轴向应变。
(2)线性弹塑性应力公式:在考虑弹塑性情况下,应力与应变的关系不再是线性的。
此时,应力公式可以表示为:σ=σe+σp其中,σ表示轴向应力;σe表示弹性应力;σp表示塑性应力。
3.弯矩公式:轴心受力构件在受到弯矩作用时,会引起构件的弯曲变形。
弯矩公式描述了轴心受力构件在弯矩作用下的变形情况。
弯矩公式主要有以下几种形式:(1)切线法公式:根据切线法,弯曲截面上的任意一点都受到一个弯矩的作用。
弯矩公式可以表示为:M=σ*S其中,M表示弯矩;σ表示轴向应力;S表示截面的静矩。
(2)一阶弹性理论公式:在一阶弹性理论中,构件的截面仍然平面,但允许在截面平面上有变形。
弯矩公式可以表示为:M=σ*I/y其中,M表示弯矩;σ表示轴向应力;I表示截面的惯性矩;y表示截面上任一点到中性轴的距离。
(3)符合木尔斯定理的公式:木尔斯定理适用于构件截面受平面弯矩时产生的应力。
弯矩公式可以表示为:M=W*y/I其中,M表示弯矩;W表示截面上的轴向力;y表示截面上任一点到中性轴的距离;I表示截面的惯性矩。
第四章轴心受力构件一、轴心受力构件的特点和截面形式轴心受力构件包括轴心受压杆和轴心受拉杆。
轴心受力构件广泛应用于各种钢结构之中,如网架与桁架的杆件、钢塔的主体结构构件、双跨轻钢厂房的铰接中柱、带支撑体系的钢平台柱等等。
实际上,纯粹的轴心受力构件是很少的,大部分轴心受力构件在不同程度上也受偏心力的作用,如网架弦杆受自重作用、塔架杆件受局部风力作用等。
但只要这些偏心力作用非常小(一般认为偏心力作用产生的应力仅占总体应力的3%以下。
)就可以将其作为轴心受力构件。
轴心受力的构件可采用图中的各种形式。
其中a)类为单个型钢实腹型截面,一般用于受力较小的杆件。
其中圆钢回转半径最小,多用作拉杆,作压杆时用于格构式压杆的弦杆。
钢管的回转半径较大、对称性好、材料利用率高,拉、压均可。
大口径钢管一般用作压杆。
型钢的回转半径存在各向异性,作压杆时有强轴和弱轴之分,材料利用率不高,但连接较为方便,单价低。
b) 类为多型钢实腹型截面,改善了单型钢截面的稳定各向异性特征,受力较好,连接也较方便。
c) 类为格构式截面,其回转半径大且各向均匀,用于较长、受力较大的轴心受力构件,特别是压杆。
但其制作复杂,辅助材料用量多。
二、轴心受拉杆件轴心受拉杆件应满足强度和刚度要求。
并从经济出发,选择适当的截面形式,处理好构造与连接。
1、强度计算轴心拉杆的强度计算公式为:(6-1)式中:N——轴心拉力;A n——拉杆的净截面面积;f ——钢材抗拉强度设计值。
当轴心拉杆与其它构件采用螺栓或高强螺栓连接时,连接处的净截面强度计算如连接这一章所述。
公式(6-1)适用于截面上应力均匀分布的拉杆。
当拉杆的截面有局部削弱时,截面上的应力分布就不均匀,在孔边或削弱处边缘就会出现应力集中。
但当应力集中部分进入塑性后,内部的应力重分布会使最终拉应力分布趋于均匀。
因而须保证两点:(1)选用的钢材要达到规定的塑性(延伸率)。
(2)截面开孔和消弱应有圆滑和缓的过渡,改变截面、厚度时坡度不得大于1:4。
2、刚度计算为了避免拉杆在使用条件下出现刚度不足、横向振动以造成过大的附加应力,拉杆设计时应保证具有一定的刚度。
普通拉杆的刚度按下式用长细比来控制。
(6-2)式中:——拉杆按各方向计算得的最大长细比;l0——计算拉杆长细比时的计算长度;i ——截面的回转半径(与l0相对应);——容许长细比。
按规范采用。
对于施加预拉力的拉杆,其容许长细比可放宽到1000。
三、轴心受压杆件轴心压杆的破坏形式有强度破坏、整体失稳破坏和局部失稳破坏三种。
(一)强度破坏轴心压杆的截面若无削弱,就不会发生强度破坏。
截面削弱的程度较整体失稳对承载力的影响小,也不会发生强度破坏。
如截面削弱的程度较整体失稳对承载力的影响大,则会发生强度破坏。
轴心压杆的强度计算方法同轴心拉杆。
(二)整体失稳破坏●轴心受压杆的整体稳定概述●轴心压杆的弹性微分方程●弯曲失稳的极限承载力●实腹式轴心压杆整体稳定的实用计算公式●格构式轴心压杆整体稳定的实用计算公式1、轴心受压杆的整体稳定概述整体失稳破坏是轴心受压构件的主要破坏形式。
有关轴心压杆的整体稳定问题的理论经历了由理想状态杆件的单曲线函数关系到实际状态杆件多曲线函数关系的沿革。
传统的理想状态压杆的单曲线稳定理论认为轴压杆是理想状态的,它在达到临界压力之前没有横向位移,达到临界压力之后曲线出现分枝。
此理论先由欧拉(Euler)提出,后由香莱(Shanley)用切线模量理论完善了分枝后的曲线。
其图如图。
由传统的理论得出的杆件长细比与临界压应力之关系图为单曲线,如图。
这种理论在世界各国一直被沿用到20世纪60年代。
20世纪60年代以后,新的压杆整体稳定理论在大量的试验基础上提出。
实际情况说明压杆不可能完全处于理想状态,有初弯曲、初偏心、残余应力等多种不利因素的影响。
试验曲线表明,压杆在承受轴压力的整个过程中都有侧向位移,只是开始侧向位移较小而接近极限承载力时侧向位移较大,到最后甚至不能收敛。
如图。
大量试验结果还表明:压杆的—关系并非象传统理论那样可以用一根曲线概括,试验点有相当大的分布范围,如图。
经分析,轴压构件的稳定极限承载力受到以下多方面因素的影响:∙构件不同方向的长细比.∙截面的形状和尺寸∙材料的力学性能∙残余应力的分布和大小∙构件的初弯曲和初扭曲∙荷载作用点的初偏心∙支座并非理想状态的弹性约束力∙构件失稳的方向等等由此提出以具有初始缺陷的实际轴心压杆作为力学模型,用开口薄壁轴心压杆的弹性微分方程来研究轴压杆的稳定问题。
2、轴心压杆的弹性微分方程轴压杆件的弹性微分方程为:(6-3a)(6-3b)(6-3c)式中:N ——轴心压力;I x、I y——对主轴x-x和y-y的惯性矩;——扇性惯性矩;,其中为以扭转中心为极的扇性坐标;u、v、——构件剪力中心轴的三个初始位移分量,即考虑初弯曲和初扭曲等初始缺陷;x0、y0——剪力中心坐标;(6-4)(6-5)——截面上的残余应力,以拉应力为正。
对于杆件的对称与否可分为:∙双轴对称截面的弯曲失稳和扭转失稳∙单轴对称截面的弯曲失稳和扭转失稳∙不对称截面的弯曲失稳和扭转失稳∙轴压杆整体失稳的三种形式3、弯曲失稳的极限承载力1)弯曲失稳极限承载力的准则按弹性微分方程求解轴压杆的弯曲失稳极限承载力,目前常用的准则有二种。
一种采用边缘纤维屈服准则,即当截面边缘纤维的应力达到屈服点时就认为轴心受压构件达到弯曲失稳极限承载力。
另一种则采用稳定极限承载力理论,即当轴心受压构件的压力达到图6.4所示极值型失稳的顶点时,才达到了弯曲失稳极限承载力。
2)界应力σcr按边缘纤维屈服准则的计算方法弯曲变形的微分方程为(6-6a),即(a)假定压杆为两端简支,杆轴具有正弦曲线的初弯曲,即,式中为压杆中点的最大初挠度。
由上式可解得压杆中点的最大挠度为(6-14)——绕轴x-x的欧拉临界力。
式中:NEx由边缘纤维屈服准则可得(6-15)将式(6-14)代入上式,并解出平均应力后,即得佩利(perry)公式(6-16)式中:——初始偏心率;(6-17)即可由式求得关系。
我国冷弯薄壁型钢结构技术规范采用了这个方法,并给定,称为轴心压杆稳定系数。
用下式计算(6-18)式中:——轴心压杆稳定系数;—— 相对长细比;(6-19)—— 按表6-2取用。
(相关知识2)初 偏 心 率表6-23) 界应力σcr 按稳定极限承载力理论的计算方法轴心受压构件考虑初始缺陷后的受力属于压弯状态,用数值积分法求解微分方程,可以考虑影响轴心压杆稳定极限承载力的许多因素,如截面的形状和尺寸、材料的力学性能、残余应力的分布和大小、构件的初弯曲和初扭曲、荷载作用点的初偏心、构件的失稳方向等等,因此是比较精确的方法。
我国钢结构设计规范采用了这个方法。
图是12种不同截面尺寸,不同残余应力值和分布以及不同钢材牌号的轴心受压构件用上述方法计算得到的曲线。
从图中可以看出,由于截面形式以及初始缺陷等因素的影响,轴心受压构件的柱子曲线分布在一个相当宽的带状范围内。
轴心受压构件的试验结果也说明了这一点,见图。
)来反映显然是不够合理的。
现在因此,用单一柱子曲线,即用一个变量(长细比已有不少国家包括我国在内已经采用多条柱子曲线。
我国钢结构设计规范采用的方法为:考虑l/1000 的初弯曲,选用不同的截面形式、不同的残余应力模式计算出近200条柱子曲线,这些曲线呈相当宽的带状分布。
然后根据数理统计原理,将这些柱子曲线分成a、b、c三组。
这三条平均曲线以其95%的信赖度全部覆盖了这些曲线所组成的分布带。
具体见柱子曲线。
(相关知识如下)轴压构件柱子曲线和截面分类钢结构设计规定采用将各种截面分成a、b、c三组,各柱子曲线为:当时(6-20)当时式中:、、——系数,根据不同曲线类别按6-3取用。
、、表6-3这一方法及以上参数可用于计算机编程计算,而实际计算则是用更简便的查表法。
对于弯扭失稳的稳定极限承载力,经过大量的计算和比较,规范认定可以按c曲线计算。
这是轴压杆弯扭失稳的简化计算方法。
轴心受压构件的截面分类(板厚t f40mm)表6-4(a)<4、实腹式轴心压杆整体稳定的实用计算公式根据上面所述并考虑安全度后,实腹式轴心压杆可按下式计算其整体稳定性(6-22)式中: ――压杆的毛截面面积;――轴心压杆稳定系数,根据压杆的长细比和截面分类查表确定。
5、格构式轴心压杆整体稳定的实用计算公式图所示为两种不同的格构式构件。
左侧两个为缀条构件,构件的两个肢用缀条连系;右侧为缀板构件,构件的两个肢用缀板连系。
双肢格构截面有两个轴,一个轴横穿缀条或缀板平面(如图中的轴x-x )称为虚轴,另一个轴横穿两个肢(如图中的 轴y-y )称为实轴。
工程上也用到三肢柱和四肢柱。
这类柱截面的两个轴都是虚轴。
格构式压杆绕实轴失稳时,它的整体稳定性与实腹式压杆相同,因此其整体稳定的实用计算公式可同样采用式(6-22)。
格构式压杆绕虚轴失稳时,其整体稳定性与实腹式压杆不同,应该考虑在剪力作用下,柱肢和缀条或缀板变形的影响。
根据近似的理论分析,两端铰接的缀条压杆在弹性阶段绕虚轴屈曲的临界应力为(6-23)式中:A――杆肢截面面积之和;A1x――压杆截面中垂直于x轴的各斜缀条毛截面面积之和;――斜缀条对压杆横截面的倾角;――两柱肢作为整体对轴x-x(虚轴)的长细比。
上式等号右边分母的第二项表示在剪力作用下,柱肢和缀条变形的影响。
由于一般在45°左右,代入上式可得其中对于缀板式压杆,用同样原理可得缀板式压杆的换算长细比式中:――单肢对平行于x轴的自身形心轴(即上图中的1-1轴)的长细比。
――轴心压杆稳定系数,对于实轴由长细比按实腹截面采用,对于虚轴,式中:按相关知识4求得换算长细比,再查表(b类)求。
(两种不同的格构式构件图)格构式构件的换算长细比计算公式 5-2——整个构件对x和y轴(三)局部失稳破坏●概述●轴心压杆翼缘和腹板的局部稳定 ●轴心受力圆管截面压杆的局部稳定1、概述实腹式轴心压杆的受压翼缘和腹板与受弯构件的受压翼缘和腹板一样,有局部稳定问题。
轴心压杆翼缘和腹板的局部稳定可以作为理想受压平板按屈曲问题来研究,也可以作为有初始挠度的受压平板按稳定极限承载力问题来研究。
我国钢结构设计规范以受压平板的屈曲为失稳准则,不利用受压平板的超屈曲强度,设计时把屈曲应力作为设计应力。
具体方法是限制翼缘和腹板的宽厚比。
(相关知识5)我国薄壁型钢结构设计规范对于四边支承板则利用受压平板的超屈曲强度,设计时采用有效宽厚比和有效截面的概念。
其余情况仍以屈曲为失稳准则,设计时把屈曲应力作为设计应力。
其具方法及有效宽厚比的计算可参见《冷弯薄壁钢结构技术规范》。
2、轴心压杆翼缘和腹板的局部稳定轧制型钢如工字钢、槽钢、角钢等截面中的板厚一般都比较大,局部稳定问题不严重。