基于压缩试验确定真实应力-应变曲线

材料力学压缩实验报告实验目的，通过对不同材料的压缩实验，探究材料在受力情况下的变形规律，分析材料的力学性能。

实验仪器，压力机、标准试样、测力传感器、数据采集系统。

实验材料，铝合金、钢材、塑料。

实验步骤：1. 准备工作，检查实验仪器是否正常，选择合适的试样进行实验。

2. 实验操作，将试样放置在压力机上，施加不同的压力，通过测力传感器和数据采集系统记录试样在受力过程中的压缩变形情况。

3. 数据处理，根据实验数据绘制应力-应变曲线，分析不同材料在压缩过程中的力学性能，如弹性模量、屈服强度等。

实验结果与分析：铝合金，在压缩过程中，铝合金试样表现出较好的弹性，当受到较大压力时，开始出现塑性变形，屈服强度较高。

钢材，钢材试样在受力后表现出较高的屈服强度和延展性，具有良好的塑性变形能力。

塑料，塑料试样在受力后呈现出较大的压缩变形，表现出较低的弹性模量和屈服强度，具有较好的塑性变形特性。

结论，通过本次实验，我们深入了解了不同材料在受力情况下的力学性能，铝合金具有较好的弹性和屈服强度，钢材具有良好的塑性变形能力，而塑料具有较好的塑性变形特性。

这些分析结果对于材料的选择和设计具有一定的指导意义。

实验总结，本次实验通过压缩实验探究了材料的力学性能，为我们深入了解材料的力学特性提供了重要的实验数据和分析结果，也为今后的材料选择和设计提供了参考依据。

实验中遇到的问题及改进措施，在实验过程中，部分试样出现了不同程度的损坏，下一步可以优化试样的制备工艺，提高试样的稳定性和可靠性。

实验的局限性，本次实验仅针对了几种常见的材料进行了压缩实验，后续可以扩大实验范围，对更多材料进行力学性能的研究。

致谢，感谢实验组的成员们在实验过程中的辛勤劳动和合作，也感谢指导老师在实验设计和实施过程中的指导和帮助。

以上就是本次材料力学压缩实验的报告内容，希望对大家有所帮助。

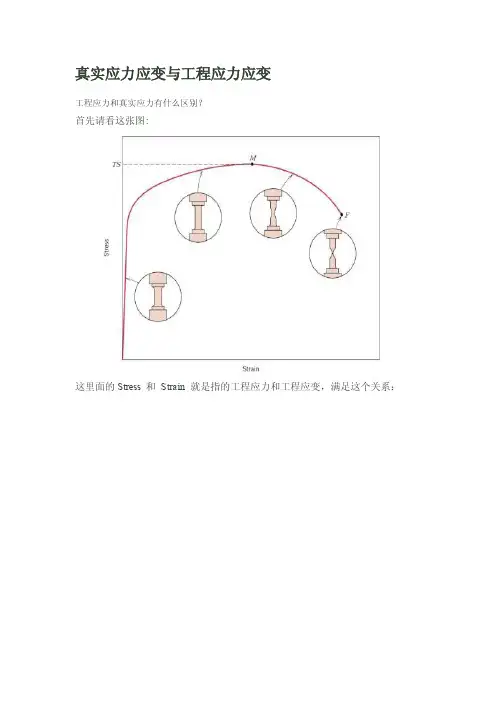
真实应力应变与工程应力应变工程应力和真实应力有什么区别？首先请看这张图:这里面的Stress和Strain就是指的工程应力和工程应变，满足这个关系：但实际上，从前一张图上就可以看出，拉伸变形是有颈缩的，因此单纯的比例关系意义是不大的，因而由此绘出的图也可能给人带来一些容易产生误解的信息，比如让人误认为过了M点金属材料本身的性能会下降。

但其实我们可以看到，在断口处A（这个面积才代表真正的受应力面）是非常小的，因而材料的真实强度时上升了的（是指单位体积或者单位面积上的，不是结构上的）。

因而真实应力被定义了出来：这个是真实应力，其中Ai是代表性区域（cross-sectional area，是这么翻的吧？）前面的例子中是颈缩区截面积。

然后就可以根据某些数学方法推出真实应变：但具体怎么推的别问我，因为我也不知道……但这两个式子在使用上还是不那么直接，因而我们引入体积不变条件Aili＝A 0l0然后可以得到：和但似乎只有在颈缩刚刚开始的阶段这两个式子才成立。

下面这张图是真实应力应变和工程应力引力应变的对照图：其中的Corrected是指的考虑了颈缩区域复杂应力状态后作的修正。

3.6 真实应力－应变曲线单向均匀拉伸或压缩实验是反映材料力学行为的基本实验。

流动应力（又称真实应力）——数值上等于试样瞬间横断面上的实际应力，它是金属塑性加工变形抗力的指标。

一.基于拉伸实验确定真实应力－应变曲线1.标称应力－应变曲线室温下的静力拉伸实验是在万能材料试验机上以小于的应变速率下进行的。

标称应力－应变曲线不能真实地发映材料在塑性变形阶段的力学特征。

2.真实应力－应变曲线A.真实应力－应变曲线分类分三类：Ⅰ．Y －ε；Ⅱ．Y －ψ；Ⅲ．Y －∈；B.第三类真实应力－应变曲线的确定方法步骤如下：Ⅰ．求出屈服点σs（一般略去弹性变形）式中P s——材料开始屈服时的载荷，由实验机载荷刻度盘上读出；A o——试样原始横截面面积。

Ⅱ．找出均匀塑性变形阶段各瞬间的真实应力Y和对数应变Ε式中P——各加载瞬间的载荷，由试验机载荷刻度盘上读出；A——各加载瞬间的横截面面积，由体积不变条件求出；式中Δl——试样标距长度的瞬间伸长量，可由试验机上的标尺上读。

混凝土是一种复合建筑材料，内部组成结构非常复杂。

它是由二相体所组成，即粗细骨料被水泥浆所包裹，靠水泥浆的粘接力，使骨料相互粘接成为整体。

如果考虑到带气泡和毛细孔隙的存在，混凝土实际是一种三相体的混合物，不能认为是连续的整体。

[2]1. 普通高强度混凝土只能测出压应力-应变曲线的上升段，因为混凝土一旦出现出裂缝，承力系统在加压过程中积累的大量弹性能突然急剧释放，使得裂缝迅速扩展，试件即刻发生破坏，无法测得应力-应变曲线的下降段。

[1]2. 拟合本文的高强混凝土和纤维与混杂纤维增强高强混凝土的受压本构方程的参数结果图3和图4为掺杂了纤维与混杂纤维的纤维增强高强混凝土的压缩应力一应变全曲线，由曲线可以看出，纤维与混杂纤维增强高强混凝土则能够准确地测出完整的压应力．应变曲线．纤维增强高强混凝土和混杂纤维增强高强混凝土的这两种曲线具有相同的形状啪，都由三段组成：线性上升阶段、初裂点以后的非线性上升阶段、峰值点以后的缓慢下降阶段．[2]3.[3]再生混凝土设计强度等级为C20，C25，C30，C40，再生骨料取代率100%。

标准棱柱体试件150mm*150mm*300mm，28天强度测试结果。

“等应力循环加卸载试验方法”测定再生混凝土的应力-应变全曲线，即每次加载至预定应力后再卸载至零，再次进行加载，多次循环后达不到预定应力而自动转向包络线时，进行下一级预定应力的加载。

再生粗骨料来源的地域性和差异性使再生骨料及再生混凝土的力学性能有较大差别。

4.通过对普通混凝土和高强混凝土在单轴收压时的应力应变分析发现，混凝土的弹性模量随混凝土的强度的提高而提高，混凝土弹性段的范围随混凝土强度的提高而增大，混凝土应力应变曲线的下降段，随混凝土强度的提高而越来越陡，混凝土的峰值应变与混凝土的抗压强度无正比关系。

图2给出了各组混凝土试件的平均应力应变曲线，从图中可以看出A1-A5试件的曲线为完整的圆滑曲线。

A6，A7由于混凝土试件强度较高实验设备刚度不够，当σc>f c 后，试验机释放的能量迅速传到周围的4个钢柱上，从而引起混凝土突然破坏，所以曲线只有上升段没有下降段，A1-A7试件的应力应变曲线的上升段是相似的，但下降段的曲线形状差别较大。

铝合金压缩应力应变曲线
铝合金压缩应力应变曲线是指在压缩试验中，铝合金样品在受到外部压力作用下所产生的应力与应变之间的关系曲线。

一般来说，铝合金在压缩过程中的应力应变曲线可以分为三个阶段：
1. 弹性阶段：当铝合金样品受到压缩力后，会产生弹性变形，此时应力与应变成正比。

在这个阶段中，应变仅仅是一种恢复形变，断开压力后立刻恢复原状。

这个阶段是铝合金样品的弹性变形阶段，产生的弹性能可以完全恢复。

2. 屈服阶段：当铝合金样品的应变达到一定程度时，它会发生一些内部微观变化，导致它的应力不再与应变成正比关系。

这个临界点叫做屈服点。

在屈服点之后，铝合金样品进入了均匀塑性变形阶段，应力不断增加，但应变增长速度不再加快。

铝合金在这个阶段中，它的应力减少时，其变形能也不会完全恢复。

3. 流动阶段：当铝合金样品达到极限状态并继续应用压力时，铝合金会发生非均匀的塑性变形，且应力下降。

大部分应变发生在铝合金材料的表面。

此时，铝合金已经丧失了大部分它原来的力学性能，会发生显著的减弱。

当铝合金材料达到最后的毁损点时，处于最弱的形态。

基于平面应变压缩试验确定45钢真实应力应变曲线所用工具是一对狭长的窄锤头，所用45钢板料的宽度为W ,而锤头宽度为b ，使10~6=b W ，板料厚度取为（21~41）b 。

压缩式在2轴方向的展宽很小，可忽略不计。

即可认为板料受压部分处于平面应变状态。

板料式样不必精细加工。

实验步骤：①润滑板料表面和锤头表面；②将板料水平放在上、下锤头之间，并使板料的轴线方向1和锤头的轴线方向2保持垂直；③进行压缩，每压缩高度的2%或5%记录一次压力F 并测量出实际板厚，每压缩一次都要重新润滑，压缩到ε≈1为止。

根据每次压缩实验记录下的数据，就可算出每次的压应力p⎪⎭⎫ ⎝⎛=Wb F p 和对数应变ε，（⎪⎭⎫ ⎝⎛≈i h h ln 3ε，h i 为每次压缩后的的高度），于是就可做出此平面应变压缩时的压应力p 与对数应变ε3的关系曲线，如下图中的曲线a 所示。

但是这并不是所求的真实应力-应变曲线，可根据曲线a 并利用下面的方法做出单向应力状态下的真实应力-应变曲线（如下图中曲线b ）。

因为锤头很窄，又有良好的润滑，可认为1轴方向的主应力σ1=0，并设锤头向下压的应力σ3=p 。

因为平面应变，所以ε2=0，2p =31=22+σσσ。

又根据体积不变条件，ε1=-ε3。

这样可求得等效应力σ和等效应变ε，即p p p p p 23)0()2()20(21)3-2122221232221=-+-+-=-+-+=σσσσσσσ（）（）（ []3233232321323222123-00-2323εεεεεεεεεεεε=-+++-=-+-+-=）（）（）（）（）（）（ 在单向应力状态下，有σ=Sε=ε S = p p 866.023= ε=33155.123εε= 这样，可将平面应变压缩状态下的压应力p 和应变ε3分别换算成单向压缩状态下的真实应力S 和真应变ε，如图中曲线a 上的k 1点换算成单向压缩状态时的k 2点。

压缩应力应变曲线引言压缩应力应变曲线是材料力学中常见的实验手段，用于研究材料在受到压缩载荷时的力学性能。

通过对材料施加不同的压缩载荷，可以观察到材料的应变随着应力的变化情况。

这一曲线可以提供关于材料的强度、刚度和塑性等方面的信息，对于材料的设计和工程应用具有重要意义。

实验原理压缩应力应变曲线实验是通过施加垂直于样品截面的压缩载荷，测量材料的应变和应力的关系。

在实验中，通常使用一台万能材料试验机，通过施加压缩载荷并测量应变和应力的变化来绘制应力应变曲线。

实验步骤1.准备样品：根据实验要求，制备合适尺寸和形状的样品。

样品可以是金属、塑料、混凝土等材料。

2.安装样品：将样品固定在万能材料试验机的压缩夹具上。

确保样品被均匀地加载。

3.施加载荷：启动试验机，施加垂直于样品截面的压缩载荷。

载荷的大小可以根据实验要求进行调整。

4.测量应变：通过应变计等设备测量样品的应变。

应变计可以直接粘贴在样品表面或者通过夹具固定在样品上。

5.记录载荷和应变数据：在试验过程中，记录载荷和应变的变化情况。

可以使用数据采集系统来实时记录数据。

6.绘制应力应变曲线：根据记录的载荷和应变数据，绘制出应力应变曲线。

应力应变曲线的特点压缩应力应变曲线通常具有以下几个特点：1.弹性阶段：在开始施加载荷时，材料会发生弹性变形，即应变与应力成正比。

这一阶段的斜率代表了材料的刚度。

2.屈服阶段：当载荷继续增加时，材料会发生塑性变形，即应变与应力不再成正比。

在这个阶段，材料的应力会达到一个最大值，称为屈服强度。

3.塑性阶段：在屈服点之后，材料会发生持续的塑性变形。

应力会随着应变的增加而逐渐减小。

4.断裂阶段：当应力达到材料的极限强度时，材料会发生断裂。

此时，应变会急剧增加，应力会迅速下降。

应力应变曲线的分析通过分析应力应变曲线，可以获得材料的力学性能和变形行为的信息：1.弹性模量：弹性模量是应力应变曲线的斜率，代表了材料的刚度。

材料的弹性模量越大，表示材料的刚度越高。

基于flac^3d模拟的岩石单轴压缩试验应力应变统计规律“基于flac^3d模拟的岩石单轴压缩试验应力-应变统计规律”是研究岩石在单轴压缩试验中应力-应变特性规律的一个重要课题。

本文以FLAC^3D模型为基础，以有限元素方法进行了岩石单轴压缩试验模拟，采集了以应力、应变等作为响应变量的数据，并利用统计学方法对模型数据进行了拟合和分析，探讨了岩石在单轴压缩过程中应力-应变的统计规律。

一、研究背景单轴压缩试验是目前岩石力学性质研究的基本试验，在工程、科研领域中有着至关重要的地位，但传统试验中存在着大量的不确定因素，容易出现偶然性差异。

为了解决传统试验中出现的偶然差异，利用有限元素法进行岩石单轴压缩试验的模拟，再结合统计学技术，分析岩石在单轴压缩试验中的应力-应变关系，已受到包括研究者在内的众多学者的重视。

二、实验方法1.选取模型样品：采用砂岩试样，尺寸为50×50 mm，其表面平整，对其密度、抗拉强度等进行了测定；2.模拟条件：采用FLAC^3D模型，以正常温度、相对湿度和气压下的常用测试机构，应用自由节点模式，实现压缩试验模拟，并设置适当的增量半径修正和初始压力；3.数据采集：在做单轴压缩试验模拟时，实时采集和记录应力、变形、位移、应变等数据；4.拟合分析：根据以上实验数据，以统计学方法对数据进行分析，从数据中汲取所需要的参数，并将参数应用到现有的统计模型中，拟合数据以描述岩石在单轴压缩过程中应力-应变统计规律。

三、实验模拟结果1.岩石在单轴压缩试验中应力-应变随位移的变化趋势：在岩石的单轴压缩实验中，应力随着位移的增加而增加，而应变在位移达到一定程度之后出现稳定的变化态势，其变化曲线在位移方向上大体符合线性变化规律；2.岩石在单轴压缩试验中应力-应变计算结果：应力随压缩距离的增加而增加，最大应力处于压缩距离的末端，而应变的增加则受到压缩距离的影响较小，且应力和应变均为正值；3.应力-应变模型：根据采集的实验数据，选取了由岩石的极限弹性模量E和极限压缩模量σL组成的Ackermann-Kuhn模型作为岩石在单轴压缩过程中应力-应变的拟合模型；4.岩石单轴压缩试验参数拟合结果：拟合得到的参数值为极限弹性模量E=57.1MPa，极限压缩模量σL=62.45MPa，两个参数都满足了90%的拟合要求；5.岩石单轴压缩试验数据分析结果：通过对实验数据的分析，得出在较大的位移范围内，岩石的力学弹性在一定程度上维持不变，而岩石的抗压能力也在适当的范围内维持了一定的稳定性；四、结论本文以FLAC^3D模型作为基础，采用有限元素法进行了岩石的单轴压缩试验模拟，通过对采集数据的统计分析，确定了岩石在单轴压缩实验中的应力-应变曲线规律，提出了一套新的Ackermann-Kuhn应力-应变模型及其参数，从而为岩石力学性质研究提供了新的研究方法。

混凝土轴心抗压试验测得的应力-应变曲线
混凝土轴心抗压试验是评估混凝土材料强度和耐久性的常规方法之一。

在该试验中，混凝土试件沿着其轴心受到均匀的压力载荷，并测量试件的应变（变形）以及所产生的应力（力/面积）。

通过绘制应力-应变曲线，可以分析混凝土在受力过程中的力学性能，并确定其强度特性。

在混凝土轴心抗压试验中，试件通常为长方体或圆柱形。

试件通常从现场制备混凝土中获得，并进行处理和养护以保证试件达到规定的强度等级。

试件应放置在试验室中进行测量，并在试验前进行称重和尺寸测量。

在试验过程中，测试设备应按照规范进行校准和验证，以确保测量精度和可靠性。

试件应慢慢加压，以避免产生冲击载荷并破坏试件。

在试验中，应记录试件受到的载荷和试件内部应变的变化。

在试验完成后，应根据载荷和应变数据确定应力-应变曲线。

应力-应变曲线的形状通常可分为三个阶段：线性弹性区、非线性弹塑性区和极限挤压区。

线性弹性区是指应变增加时应力与应变成比例变化。

应变过大时，混凝土开始发生塑性变形。

在这个阶段，应力-应变曲线不再是直线，而是开始呈现出拐点。

该拐点称为塑性极限。

最后，当应力达到极限压缩应力时，混凝土会发生快速破坏，并且该应力被称为混凝土的抗压强度。

该应力的值通常以每平方米（MPa）为单位表示。

绘制应力-应变曲线是评估混凝土材料性质的关键部分。

该曲线的形状和特征可以用于确定混凝土的强度特性，如抗压强度和抗弯强度。

通过分析该曲线，可以确定混凝土的性质，如刚度、弹性模量和柔软性。

应力-应变曲线是混凝土工程设计和材料质量控制的重要工具。

材料真实应力应变与工程应力应变材料的真实应力应变和工程应力应变是在材料力学中经常使用的两个概念。

真实应力应变是指在材料中根据原子层面的变形计算得到的应力和应变。

在真实应力应变中，考虑了实际变形和应力分布的影响。

材料中的原子在受到外力的作用下会发生位移和旋转，从而导致整个材料的形变。

由于材料的非均匀性，不同位置的应力和应变可能不同。

真实应力应变的计算需要考虑这种分布的差异性。

工程应力应变是指在工程设计中使用的应力和应变。

工程应力应变主要用于设计和分析工程结构的强度和稳定性。

在工程设计中，通常使用的是线性弹性理论，即假设材料的应力和应变是线性关系。

这种假设对于大多数工程设计来说是足够准确的，可以简化计算过程。

工程应力应变还经常用于材料的弯曲、拉伸、压缩等加载情况下的应力和应变计算。

真实应力应变和工程应力应变之间的关系可以通过应力应变曲线来表示。

应力应变曲线是材料在受力过程中应力和应变之间的图形表示。

在弹性阶段，真实应力应变和工程应力应变之间的差别较小，可以忽略不计。

随着应力的增加，材料会发生塑性变形，真实应力应变和工程应力应变之间的差别逐渐增大。

在材料力学中，真实应力应变的计算通常基于拉伸试验或压缩试验得到的应力应变数据。

在拉伸试验中，通过测量试样的变形和受力情况，可以计算出真实应力和真实应变。

然后，将真实应力和真实应变转化为工程应力和工程应变，得到工程应力应变曲线。

这样可以更好地理解材料在受力过程中的行为，并提供准确的设计参数。

总的来说，真实应力应变和工程应力应变是材料力学中重要的概念。

真实应力应变考虑了材料本身的性质和变形行为，而工程应力应变则是在工程设计中常用的近似值。

对于大多数工程设计来说，工程应力应变已经足够准确，可以简化计算过程。

但在一些特殊情况下，如高强度材料和复杂加载条件下的材料行为，真实应力应变的考虑是必要的。

剑桥模型的应力应变关系一、修正剑桥模型的公式剑桥模型的应力应变曲线计算基于压缩试验确定的e-p关系。

εv p=λ−κ1+e0ln(p cp c0)=λ−κ1+e0ln p c−λ−κ1+e0lnp c0（1）式中p c0是e0时（即εv p=0）对应的等效球应力。

对于非等向压缩的应力状态，可由屈服面得到任意应力点对应的屈服面位置变量p c（p c确定了屈服面的大小）。

p c=p(1+η2M2)=p+q2M2p（2）根据公式（1）得到塑性体应变 εv p，然后由塑性应变增量剪胀公式计算塑性偏应变：dεv q=dεv pD=2pqM2p2−q2dεv p=2ηM2−η2dεv p（3）D为剪胀速率：dεv q=2pqM2p2−q2dεv pD=M2p2−q22pq式（1）即为弹塑性模型中的硬化法则，式（2）为屈服准则，式（3）为流动法则，是弹塑性模型的三要素。

再加弹性应变即得到总的应力应变关系曲线。

dp=K dεv edq=3G dεq eK=1+e0κpG=3(1−2ν) 2(1+ν)K模型参数有：λ、κ、M、ν；模型计算需要给定初始孔隙比e0，初始应力状态(p0,q0)。

根据模型公式（1）-（3）可以进行全量的应力应变曲线的计算，示例见Excel文件。

图1 修正剑桥模型屈服面及流动法则示意图图2 修正剑桥模型硬化规律示意图二、增量型求解方法在具体边值问题求解中，需要用增量的应力应变关系。

1. 由应力增量求应变增量（1）塑性应变与屈服面扩大的关系（硬化规律）dεv p =λ−κ1+e 01p c×dp cH p =1+e 0λ−κp cdεvp =1H p×dp cqp c =p +M 2pc00.010.020.030.040.050.060.070.08050100150200250300350400p cεv pH p 称为塑性模量。

（2）求解应力增量引起屈服面的变化dp c =dp −q 2M 2p 2dp +2qM 2p dq=[(1−q 2M 2p 2)2q M 2p ][dp dq]=n f T [dp dq ] n f =[ðf ðσ]=[ 1−q 2M 2p 22q M 2p ]（3）计算屈服面变化引起的塑性应变增量由剪胀公式得到塑性体变和塑性偏应变的比例变化关系dεp=[dεv p dεqp ]=[11D ⁄]dεv p =n g dεv p将屈服面变化引起的塑性体变带入（）：[dεv p dεq p ]=n g 1H p ×dp c =1H pn g n f T [dp dq ]=C p [dp dq ]C p =1H p [11D ⁄][1−q 2M 2p22q M 2p ]=1H p [ 1−q 2M 2p 22qM 2p 1D −q 2DM 2p 22q DM 2p]2. 给定一个应变增量[dεv dεp ]求应力增量[dpdq]（应力积分）（1）用通用弹塑性矩阵的公式增量计算（显式欧拉法）：[dpdq]=D ep [dεv dεp ]弹塑性矩阵为：D ep =D e −D e n g n f T DeH p +n f T D en g矩阵中各元素为：D e =[K3G]n f =[ðf ðσ]=[ 1−q 2M 2p 22q M 2p ]n g =[11D ⁄]D =dεv p dεqp =M 2p 2−q 22pqH p=1+e 0λ−κp c（2）弹性预测-塑性修正的应力积分算法dε=[dεv dεp ], [p q ]，求应力增量[dp dq ],下一步的应力[p n+1q n+1]，同时把应变增量的弹性和塑性部分分开。

岩石三轴压缩任意围压下应力-应变曲线的预测方法研究岩石的力学性质是岩石工程设计中非常重要的参数之一，而岩石的应力-应变曲线可以反映岩石在受到外部作用力时的变形性能。

岩石三轴压缩实验是研究岩石应力-应变关系的常用实验方法之一、在该实验中，岩石试样受到垂直于试样轴向的围压，同时在垂直于轴向的两个方向上施加水平应力。

这样便可以获得岩石三个主应力方向上的应力-应变曲线，进而得到岩石的本构关系。

然而，进行实际岩石三轴压缩试验需要耗费大量的时间和资金，因此，发展一种预测岩石三轴压缩任意围压下应力-应变曲线的方法显得尤为重要。

目前，岩石力学研究中常用的预测岩石三轴压缩应力-应变曲线的方法主要有以下几种：1.细观组织预测方法：这种方法通过对岩石内部细观结构的分析和岩石成分的特性来预测其力学行为。

研究人员通过岩石的微观结构、矿物成分及其排列方式等因素来预测岩石的强度和变形行为。

2. 本构模型方法：本构模型是描述物质变形性能的数学模型，可以通过对实验数据的拟合来得到岩石的应力-应变关系。

常见的本构模型有Mohr-Coulomb模型、Drucker-Prager模型、Hoek-Brown模型等。

通过与实验结果的对比，可以选择适合岩石材料的本构模型。

3.数值模拟方法：使用数值方法进行岩石力学研究是近年来的发展趋势之一、数值模拟方法通过建立岩石的离散模型，将岩石划分为若干个小单元，然后根据材料力学原理和本构关系，通过求解有限元方程来计算岩石的应力-应变状态。

这种方法可以得到较为精确的岩石力学参数和应力-应变曲线。

4.统计学方法：统计学方法通过对大量试验数据的统计分析，建立岩石的力学行为模型。

通过分析不同围压和应变速率下的试验数据，将其拟合为一个函数表达式。

然后，利用拟合出的函数来预测不同围压下的应力-应变关系。

从以上几种方法来看，细观组织预测方法、本构模型方法、数值模拟方法和统计学方法是研究岩石三轴压缩应力-应变曲线的常用方法。

材料拉伸与压缩试验报告一、实验目的1.了解材料在拉伸和压缩状态下的力学性能。

2.通过拉伸试验和压缩试验获取材料的应力-应变曲线。

3.测定材料的屈服点、抗拉强度、断裂强度和弹性模量等力学性能指标。

二、实验仪器和材料1.拉伸试验机。

2.横截面积测量器。

3.试样切割机。

4.金属材料试样。

三、实验步骤1.将待测试样的尺寸测量并记录下来，包括长度、直径等。

2.使用试样切割机将试样切割为适当的长度，并在试样两端做好标记。

3.将试样安装到拉伸试验机上，并设置合适的试验参数，如加载速度、试验时长等。

4.开始拉伸试验，记录试样随时间变化的力和位移数据，并计算出应力和应变值。

5.试验完成后，绘制应力-应变曲线，并通过曲线分析得到屈服点、抗拉强度和断裂强度等力学性能指标。

6.使用横截面积测量器测量试样的横截面积。

7.进行压缩试验，按照相同的步骤测量并记录试样的力和位移数据，计算出应力和应变值。

8.绘制应力-应变曲线，并分析得到压缩材料的力学性能指标。

四、实验结果和分析1.拉伸试验结果：通过该曲线可得到材料的屈服点、抗拉强度和断裂强度等信息，分别对应曲线上的不同点。

屈服点表示材料开始发生塑性变形的特点，抗拉强度表示材料能够承受的最大拉力，而断裂强度表示材料最终断裂的强度。

2.压缩试验结果：通过该曲线同样可以得到材料的力学性能指标。

五、实验结论1.在拉伸状态下，材料发生屈服后，会逐渐进入塑性变形阶段，直至最终断裂。

2.材料的屈服点和抗拉强度等性能指标可以通过应力-应变曲线得到。

3.在压缩状态下，材料同样具有一定的塑性变形能力，并且呈现出与拉伸试验相似的力学行为。

六、实验注意事项1.在进行试验之前，需检查试验设备的工作状态，确保正常运行。

2.选择合适的试样尺寸和试验参数，以获得准确的实验结果。

3.进行试验时需要小心操作，避免试验过程中出现安全事故。

4.在测量数据时，尽量减少误差，确保数据的准确性。

七、实验心得通过本次实验，我深刻认识到材料的拉伸和压缩试验对于研究和了解材料的力学性能非常重要。

侧限压缩试验ep曲线
侧限压缩试验（也称为剪切试验）是一种常用的材料力学试验
方法，用于研究材料在侧向受力下的力学行为。

EP曲线是指在侧限
压缩试验中，应力-应变曲线的形状和特征。

EP曲线通常可以分为以下几个阶段：
1. 弹性阶段，在开始施加侧向压力后，材料会表现出线性弹性
行为，即应力与应变成正比。

这个阶段的EP曲线呈现出直线的形状。

2. 屈服阶段，当施加的侧向压力达到一定程度时，材料会发生
塑性变形，应力不再与应变成正比。

此时，EP曲线会出现明显的非
线性区域，称为屈服阶段。

在这个阶段，材料的应力会逐渐增加，
而应变的增加速度会减缓。

3. 加工硬化阶段，在超过屈服点后，材料会进一步变形，应力
继续增加。

EP曲线在这个阶段会呈现出上升的趋势，表示材料的抗
压性能逐渐增强。

4. 极限强度阶段，当材料接近其极限强度时，应力会达到最大
值，而应变也会趋于饱和。

EP曲线在这个阶段可能会出现平台，表示材料已经达到了其极限状态。

需要注意的是，EP曲线的形状和特征会受到多种因素的影响，包括材料的组成、结构、处理方式等。

不同材料的EP曲线可能会有所不同。

总结起来，侧限压缩试验EP曲线是描述材料在侧向受力下的应力-应变关系的曲线。

它可以帮助我们了解材料的力学性能、塑性变形行为以及其在工程应用中的可靠性。