第十章_logit回归

Number of obs =
LR chi2(1)
=
Prob > chi2
=
Pseudo R2
=
152 30.67 0.0000 0.1455
------------------------------------------------------------------------------
case |
Coef. Std. Err.
z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
exposure | 2.112829 .4228578 5.00 0.000 1.284043 2.941615
2
二分类资料的分析
非条件logistic模型：成组病例对照研究资料 条件logistic模型：配比病例对照研究资料3源自非条件logistic回归模型
lo （ p ） g 0 ＋ i 1 X 1 ＋ t ＝ 2 X 2 k X k
01X1＋ 2X2＋ ＋ kXk
p1ee01X12X2 kXk 1
|------------------------+----------------------
Odds ratio |
8.271605
| 3.4193 21.33091 (exact)
Attr. frac. ex. |
.8791045
| .7075425 .9531197 (exact)
Attr. frac. pop |
.4626866

公式
f(x)=1/(1+e^-x)其中，x是一个实数，源自表示 自然对数的底数。特点
• 输出范围在0-1之间，代 表了一个概率值；
• 函数有单峰性，中心对 称，可以确定最大值和
• 最在小输值入；接近0时函数近 似于线性函数。
应用场景：二元Logistic回归
乳腺癌预测
贷款审核
二元Logistic回归被广泛应用于医 学界用于识别患有乳腺癌的女性。
数据预处理
4
的潜在关系和规律。
对需要进行缩放、归一化、标准化等处
理的变量进行预处理。
5
模型拟合
将数据划分训练集和测试集，通过模型 对训练集进行拟合，并评估模型预测能 力。
模型评估方法
混淆矩阵
将预测结果与真实结果进行比对，计算假正率、假负率、真正率和真负率等指标。
ROC曲线
通过绘制真正率与假正率的曲线，评估模型的预测能力。
AUC指标
ROC曲线下的面积就是AUC，AUC越大说明模型预测结果越准确。
常见模型优化方法
1 数据增强
通过合成数据或者样本扩 增等方法，增加数据量， 提高模型泛化性能。
2 特征选择
选择对于问题最重要的变 量，避免过拟合。
3 模型集成
通过结合多个模型的结果， 提高整体预测能力。
应用探索：Logistic回归的扩展
2 作用
通过逻辑函数将线性变量转化为概率值，从 而进行二元分类。
3 优点
简单易懂、易于解释和使用，对于大规模数 据集有效率。
4 缺点
只适用于二元分类问题，并且在分类较为复 杂的非线性问题上表现较差。
sigmoid函数
介绍
sigmoid函数是Logistic回归模 型中核心的激活函数，将输入 值映射到0-1的概率分布区间内。

0.12
0.13
0.88
0.87
-1.99243
-1.90096
• 以结果变量为二分类变量为例:
– P/(1-P)为比数，定义Y=ln(P/(1-P))
• 其基本思路与多元线性回归分析相同。
– 将应变量由二分类变量转为连续性变量； – 确定m个自变量 (研究因素与混杂因素)。
Logistic模型的构建
（二）Logistic回归的应用条件
• 样本含量足够，一般为自变量个数的5-10倍; • 结果变量满足独立性,常为二分类变量资料， 自变量可以是数值变量/分类变量或等级资料; • 分析前需将分类变量资料与等级资料定量化。
（三）Logistic回归的用途
• 可以在控制1个或多个混杂因素的条件下，探 讨某个事件的发生与研究因素的关系；研究 各因素主效应及其相互间的交互作用； • 在临床研究中多用于鉴别诊断、评价疗效、 分析与疾病预后有关的因素、筛选主要危险 因素、预测不良事件发生。
冠心 病 Total
control case
P=0.029
• 吸烟：
冠 心病 * 吸 烟 C r o s s t a b u l a t i o n Count 吸烟 N 冠心 病 Total control case 10 3 13 Y 18 23 41 Total 28 26 54
P=0.038
0.99 0.98 0.97 0.96
-4.59512 -3.89182 -3.4761 -3.17805
0.05
0.06 0.07
0.95
0.94 0.93
-2.94444
-2.75154 -2.58669
0.08
0.09 0.1 0.11

Logistic回归分析
汕大医学院预防医学教研室
1
第一节 Logistic 回归
Logistic regression：
是研究分类变量统计分析的一种重要方 法。研究两水平或多水平反应变量与其影 响因子间关系的回归分析（线性回归分析： 应变量为连续计量资料）。 Logistic回归模型是一种概率模型, 通常以疾 病,死亡等结果发生的概率为因变量, 影响疾 病发生的因素为自变量建立回归模型。
19
• Logistic回归中的常数项（b0）表示，在不接触任 何潜在危险／保护因素条件下，效应指标发生与 不发生事件的概率之比的对数值。
• Logistic回归中的回归系数（ bi ）表示，某一因 素改变一个单位时，效应指标发生与不发生事件 的概率之比的对数变化值，即OR的对数值。
20
Logistic回归系数的意义
11
• （1）取值问题 • （2）曲线关联 • 反应变量与自变量的关系通常不是直线关
系，而是S型曲线。曲线回归时，往往采用 变量变换，使得曲线直线化，再进行直线 回归方程的拟合。能否考虑对所预测的因 变量加以变换。1970年，COX引入了用于 人口学领域的Logit变换。
12
概率P是以0.5为对称点，分布在0~1的范围内 的，而相应的Logit（P)的大小为
4
实例
试验者术前检查了53例前列腺癌患者，拟 用年龄(AGE)、酸性磷酸酯酶(ACID)两个连 续型的变量，X射线(X-RAY)、术前探针活 检病理分级(GRADE)、直肠指检肿瘤的大小 与位置(STAGE)三个分类变量与手术探查结 果变量NODES（1、0分别表示癌症的淋巴结 转移与未转移 ）建立淋巴结转移的预报模 型。
5
53例接受手术的前列腺癌患者情况

Odds 1 机会比率 Odds 2
若消费支出2000元且有卡 (X1=2,X2=1),则
P (Y 1 | X 1 2, X 2 1) Odds1 1 P (Y 1 | X 1 2, X 2 1)
若消费支出2000元且无卡 (X1=2,X2=0),则
P (Y 1 | X 1 2, X 2 0) Odds2 1 P (Y 1 | X 1 2, X 2 0)
利用机会比率与回归系数之间的关系就容易计算机 会比率的估计值
SPSS 分析结果中的估计机会
Va riable s in the E quation St ep a 1 信用卡 年消费 Co nstant B 1.099 .342 -2.146 S. E. .445 .129 .577 Wald 6.105 7.050 13.82 6 df 1 1 1 Si g. .013 .008 .000 Exp(B ) 3.000 1.407 .117
exp( 2.1464 0.3416X 1 1.098X 2 ) ˆ y 1 exp( 2.1464 0.3416X 1 1.098X 2 )
例如估计去年消费支出为2000元而没有信用卡的顾 客购买商品的概率，此时X1=2，X2=0，代入上式
exp( 2.1464 0.3416 2 1.098 0) p 1 exp( 2.1464 0.3416 2 1.098 0)
已知 X1=2，X2=1，P(Y=1)=0.4099. 已知 X1=2，X2=0，P(Y=1)=0.1880.
0.4099 Odds 1 0.6946 1 0.4099 0.1880 Odds 2 0.2315 1 0.1880
Odds 1 0.6946 机会比率 3.00 Odds 2 0.2315

• 1、举例
• （3）一只球队的成绩
1，胜 Y=
2，负 3，平
二、因变量是离散状态的回归
• 2、离散状态因变量回归方程的意义 （两状态的情况）
Di 0 1X i i
能否进行 这样的回
归呢？
Di 0 或 1
二、因变量是离散状态的回归
• 2、离散状态因变量回归方程的意义 （两状态的情况）
Di的期望值：
所以，应该采用“可行的广义最小二 乘法”，而不是“普通最小二乘法”
二、因变量是离散状态的回归
• 3、离散状态因变量回归遇到的障碍 （2）异方差
步骤： A. 使用OLS进行估计，并得到拟合值 Dˆi
B. 在原方程左右同时除以 Dˆi(1 Dˆi )
之后，再进行OLS估计；
二、因变量是离散状态的回归
二、因变量是离散状态的回归
• 3、离散状态因变量回归遇到的障碍
答案：可以，但有问题！
二、因变量是离散状态的回归
• 3、离散状态因变量回归遇到的障碍 （1）误差非正态分布
i Di (0 1X i ) 其中，Di是1或0的随机变量；
而X是非随机的，或者虽然是随机的，但不 一定是正态的。
即使X是随机的且是正态的，εi也不会是正 态的。
在线性回归与二值结果之间，引入 一个连续取值的潜变量（latent variable）
例如，在前例中，引入一个“实力” 潜变量，Z。
二、因变量是离散状态的回归
• 4、解决方法
“让球数”直接的与“实力”相关联， 而“实力”与“结果”相关联。
Z 0 1X i i
Z 0时，D （ 1 获胜）；注值意不：一阀定 Z 0时，D （ 0 输）； 为0！
What Point Spreads Say About the Probability of Winning in the NFL: I

第十章 logitic 回归本章导读：Logitic 回归模型是离散选择模型之一，属于多重变数分析范畴，是社会学、生物统计学、临床、数量心理学、市场营销、会计与财务等实证分析的常用方法。

10.1 logit 模型和原理Logistic 回归分析是对因变量为定性变量的回归分析。

它是一种非线性模型。

其基本特点是：因变量必须是二分类变量，若令因变量为y ，则常用y=1表示“yes ”，y=0表示“no ”。

[在发放股利与不发放股利的研究中，分别表示发放和不发放股利的公司]。

自变量可以为虚拟变量也可以为连续变量。

从模型的角度出发，不妨把事件发生的情况定义为y=1，事件未发生的情况定义为0，这样取值为0、1的因变量可以写作：⎩⎨⎧===事情未发生事情发生01y 我们可以采用多种方法对取值为0、1的因变量进行分析。

通常以P 表示事件发生的概率（事件未发生的概率为1-P ），并把P 看作自变量x 的线性函数。

由于y 是0-1型Bernoulli 分布，因此有如下分布：P=P （y=1|x ）：自变量为x 时y=1的概率，即发放现金股利公司的概率1-P=P （y=0|x ）：自变量为x 时y=0的概率，即不发放现金股利公司的概率 事件发生和不发生的概率比成为发生比，即相对风险，表现为PP odds -=1.因为是以 对数形式出现的，故该发生比为对数发生比（log odds ），表现为)1ln(P P odds -=。

对数发生比也是事件发生概率P 的一个特定函数，通过logistic 转换，该函数可以写成logistic 回归的logit 模型：)1(log )(log PP P it e -= Logit 一方面表达出它是事件发生概率P 的转换单位；另一方面，它作为回归的因变量就可以自己与自变量之间的依存关系保持传统回归模式。

根据离散型随即变量期望值的定义，可得：E(y)=1(P)+0(1-P)=P进而得到x P y E 10)(ββ+==因此，从以上分析可以看出，当因变量的取值为0、1时，均值x y E 10)(ββ+=总是代表给定自变量时y=1的概率。

第十章 Logistic 回归分析第一节 Logistic 回归基本概念线性回归模型的一个局限性是要求因变量是定量变量(定距变量、定比变量)而不能是定性变量(定序变量、定类变量)。

但是在许多实际问题中，经常出现因变量是定性变量(分类变量)的情况。

可用于处理分类因变量的统计分析方法有：判别分别(Discriminant analysis)、Probit 分析、Logistic 回归分析和对数线性模型等。

在社会科学中，应用最多的是Logistic 回归分析。

Logistic 回归分析根据因变量取值类别不同，又可以分为Binary Logistic 回归分析和Multinomial Logistic 回归分析，Binary Logistic 回归模型中因变量只能取两个值1 和0(虚拟因变量)，而Multinomial Logistic 回归模型中因变量可以取多个值。

本章将只讨论Binary Logistic 回归，并简称Logistic 回归。

因变量只取两个值，表示一种决策、一种结果的两种可能性。

从模型角度出发，不妨把事件发生的情况定义为Y=1，事件未发生的情况定义为Y=0，这样取值为0、1 的因变量可以写为下式：10y ⎧=⎨⎩ 事件发生 事件未发生我们可以采用多种方法对取值为0、1 的因变量进行分析。

通常以p 表示事件发生的概率(事件未发生的概率为1-p )，并把p 看作自变量X i 的线性函数，即p = P ( y = 1) = F (i i X β) i = 1,2,… , k不同形式的F(·)，就有不同形式的模型，最简单的莫过于使F(·)为一线性函数，即01122k k =+++++p X X X ββββε (10-113)我们可能会认为可用普通最小二乘法对上式进行估计，但因p 的值一定在区间[0,1]内，而且当p 接近于0或1时，自变量即使有很大变化p 的值也不可能变化很大，所以对上式直接用普通最小二乘法进行估计是行不通的。

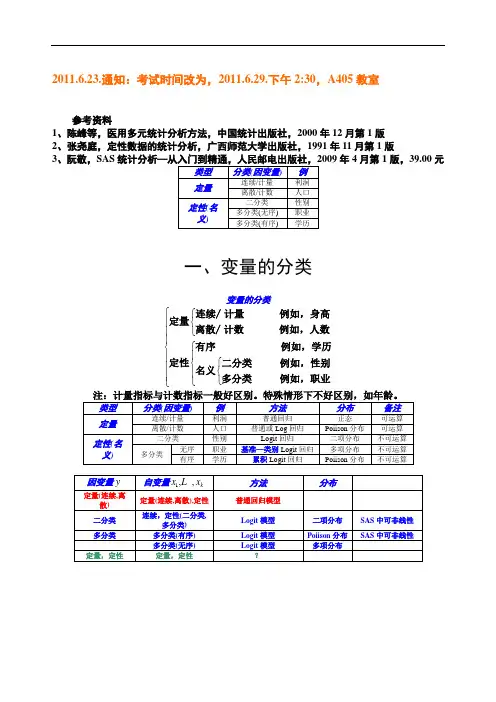
2011.6.23.通知：考试时间改为，2011.6.29.下午2:30，A405教室参考资料1、陈峰等，医用多元统计分析方法，中国统计出版社，2000年12月第1版2、张尧庭，定性数据的统计分析，广西师范大学出版社，1991年11月第1版3、阮敬，SAS年4月第1版，39.00元一、变量的分类变量的分类⎧⎧⎪⎨⎩⎪⎪⎧⎨⎪⎪⎧⎨⎪⎨⎪⎪⎩⎩⎩连续/计量例如，身高定量离散/计数例如，人数有序例如，学历定性二分类例如，性别名义多分类例如，职业二、两分类变量的logistic 回归1、logit 变换考虑上市公司中企业类型（ST 与非ST ）与财务指标的关系。

常常需要研究事件A 发生的概率p 大小与某些因素有关。

例如，讨论某特定人群（例如糖尿病患者）中患动脉硬化的概率与年龄的关系。

显然人群中只有两种状态“动脉硬化”和“非动脉硬化”（简称为“患病”和“不患病”），人群的状态记为y ，则“患病”和“不患病”对应着y 的两个取值：1y =，0y =。

用事件表示即{}1y =—“患病”=“动脉硬化” ， {}0y =—“不患病”=“非动脉硬化”若患病率记为p ，则{}1P y p ==显然{}{}0111P y P y p ==-==-讨论患病率p 与年龄x 的关系，显然，患病率随着年龄x 的增加而增长。

例，观察了123位糖尿病患者，记录了他们的年龄x 以及是否患动脉硬化y 。

数据格式见下表，详细数据见附录—2。

表1、 糖尿病原始数据 （注：此为简表，详见附录3数据）编号 动脉硬化分类 年龄 n y x 132... ... (123)1 78符号说明符号解释 注 n 编号y 是否动脉硬化1——动脉硬化0——动脉非硬化x 年龄根据这些数据如何分析是否患病y 与年龄x 的关系？能否建立y 关于x 的回归方程？不行。

因为y 的取值并无实际意义。

将数据分组，得到各组的患病率i p （见表2），能否建立p 关于x 的回归方程？ （如何将表1的原始数据整理成表2的分组数据？详见附录1）。

2011・6・23通知：考试时间改为，2011・6・29下午2:30, A405教室参考资料1、陈峰等，医用多元统计分析方法，中国统计出版社，2000年12月第1版2、张尧庭，定性数据的统计分析，广西师范大学出版社，佃91年11月第1版年4月第1版，39.00元3、阮敬，SAS变量的分类'宀日’连续/计量例如，身高疋量＜i离散/计数例如，人数■=有序例如，学历定性L v'二分类例如，性别名义彳、‘〔多分类例如，职业注：计量指标与计数指标一般好区别。

特殊情形下不好区别，如年龄】、两分类变量的logistic 回归1、logit 变换考虑上市公司中企业类型（ST 与非ST ）与财务指标的关系。

常常需要研究事件A 发生的概率p 大小与某些因素有关。

例如，讨论某特定人群（例如糖尿病患者）中患动脉硬化的概率与年龄的关系。

显然 人群中只有两种状态“动脉硬化”和“非动脉硬化” （简称为“患病”和“不患病”），人群 的状态记为y ，则“患病”和“不患病”对应着 y 的两个取值：y =1，y = 0。

用事件表示 即{y =1}—“患病”=“动脉硬化” ，{y = 0}—“不患病”=“非动脉硬化”若患病率记为p ，则 显然pfy n_p{y =1丄1一 p讨论患病率p 与年龄X 的关系，显然，患病率随着年龄X 的增加而增长。

例，观察了 123位糖尿病患者，记录了他们的年龄 x 以及是否患动脉硬化y 。

数据格 式见下表，详细数据见附录一2。

表1、 糖尿病原始数据 （注：此为简表，详见附录3数据）编号动脉硬化分类 年龄n y x 132123178符号说明符号 解释 注编号是否动脉硬化年龄根据这些数据如何分析是否患病 y 与年龄X 的关系?能否建立y 关于x 的回归方程？不行。

因为y 的取值并无实际意义。

将数据分组，得到各组的患病率 p （见表2），能否建立p 关于x 的回归方程? （如何将表1的原始数据整理成表2的分组数据？详见附录1）。

03
易于理解和实现： 由于基于逻辑函数，模型输出结 果易于解释，且实现简单。
Logistic回归的优势与不足
• 稳定性好： 在数据量较小或特征维度较高 时，Logistic回归的预测结果相对稳定。
Logistic回归的优势与不足
01
不足：
02
对数据预处理要求高： 需要对输入数据进行标准化或归一化处理，以 避免特征间的尺度差异对模型的影响。
模型假设
01
线性关系
因变量与自变量之间存在线性关系 。
无自相关
因变量与自变量之间不存在自相关 。
03
02
无多重共线性
自变量之间不存在多重共线性，即 自变量之间相互独立。
随机误差项
误差项是独立的，且服从二项分布 。
04
模型参数求解
最大似然估计法
通过最大化似然函数来求解模型参数。
梯度下降法
通过最小化损失函数来求解模型参数。
特征选择与降维
在处理大数据集时，特征选择和降维是提高模 型性能和可解释性的重要手段。
通过使用诸如逐步回归、LASSO回归等方法， 可以自动选择对模型贡献最大的特征，从而减 少特征数量并提高模型的泛化能力。
降维技术如主成分分析（PCA）可以将高维特 征转换为低维特征，简化数据结构并揭示数据 中的潜在模式。
迭代法
通过迭代的方式逐步逼近最优解。
牛顿法
利用牛顿迭代公式求解模型参数。
模型评估指标
准确率
正确预测的样本数占总样本数的比例 。
精度
预测为正例的样本中实际为正例的比 例。
召回率
实际为正例的样本中被预测为正例的 比例。
F1分数
精度和召回率的调和平均数，用于综 合评估模型性能。

3
第一节 非条件logistic回归
一、logistic 回归模型:
设因变量 Y 是一个二分类变量，其取值为 Y =1 和Y =0。 影响 Y 取值的 m 个自变量分别为 X1, X 2 ,, X m 。在 m 个自变量（即暴露因素）作用下阳性结果发生的条件
概率为 P P(Y 1 X1, X 2 ,, X m ) ，则 logistic 回归模
表 1 调查数据
y
x
1
0
1
a
b
0
c
d
合计 a+c b+d
表 2 对应概率
y
x
1
0
1 0 合计
p1 1- p1
1
p2 1- p2
1
9
表 1 调查数据
y
x
1
0
1
a
b
0
c
d
合计 a+c b+d
表 2 对应概率
y
x
1
0
1 0 合计
p1 1- p1
1
p2 1- p2
1
Logistic
模型为：
p1

p( y
1|
（2）多分类资料Logistic回归： 因变量为多项分类的资料，可 用多项分类Logistic回归模型或有序分类Logistic回归模型进 行分析。
2
非条件Logistic回归分析 条件Logistic回归分析 无序分类反应变量Logistic回归分析 有序多分类反应变量Logistic回归分析 Logistic回归分析应用及注意事项
21
对所拟合模型的假设检验：
概率p值均小 于0.05，说明 方程有意义。

logit回归解读
Logit回归是一种用于处理二元分类问题的统计模型。

它是逻辑回归模型的一种形式，逻辑回归模型用于预测一个事件发生的概率。

在logit回归中，我们使用logit函数来将线性回归模型的结果映射到0到1之间的概率值。

这个函数的形式是logit(p) = log(p/(1-p))，其中p是事件发生的概率。

通过logit函数，我们可以将线性回归模型的输出映射到一个概率，然后可以根据这个概率进行分类。

在解读logit回归的结果时，我们通常关注系数的大小和方向，系数的显著性检验以及模型的拟合优度。

系数的大小和方向可以告诉我们自变量对因变量的影响方向和强度，显著性检验可以告诉我们这种影响是否是显著的，而模型的拟合优度则可以告诉我们模型对数据的拟合程度如何。

总的来说，logit回归可以帮助我们理解自变量对于二元分类问题的影响程度，以及预测事件发生的概率。

Logit回归模型（Logit model）也译作“评定模型”，“分类评定模型”，又作Logistic regression，“逻辑回归”，是离散选择法模型之一，属于多重变量分析范畴，是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。

逻辑分布（Logistic distribution）公式其中参数β常用极大似然估计。

具体解释如下：
逻辑分布：假设我们有一个线性回归模型，预测值是介于0和1之间的概率。

当这个线性回归模型的预测值被转换为分类标签时，它被称为逻辑回归模型。

逻辑回归模型的预测值通常通过将预测值与0.5阈值进行比较来转换为二进制分类标签。

参数β：在逻辑回归模型中，参数β被称为逻辑回归系数。

它表示线性回归模型中的斜率，用于解释输入特征对预测结果的影响。

极大似然估计：在统计推断中，极大似然估计是一种参数估计方法，它通过最大化样本数据的似然函数来估计参数的值。

在逻辑回归模型中，极大似然估计用于估计逻辑回归系数β的值。

总之，Logit回归模型是一种用于处理二元分类问题的统计模型，它通过逻辑函数将线性回归模型的预测值转换为介于0和1之间的概率，从而可以用于预测二元分类标签。

二分类自变量 系数为比数比的对数值，由此比数比=eb
多分类自变量 以第i类作参照，比较相邻或相隔的两个类别。
连续型自变量 当自变量改变一个单位时，比数比为eb
2022/11/3
27
输出结果的解释
模型拟合的优劣
自变量与结果变量（因变量）有无关系
确认因变量与自变量的编码 模型包含的各个自变量的临床意义 由模型回归系数计算得到的各个自变 量的比数比的临床意义
3
一般直线回归难以解决的问题
医学数据的复杂、多样
连续型和离散型数据
医学研究中疾病的复杂性
一种疾病可能有多种致病因素或与多种危 险因素有关
疾病转归的影响因素也可能多种多样 临床治疗结局的综合性
2022/11/3
4
简单的解决方法
固定其他因素，研究有影响的一两个因 素； 分层分析：按1~2个因素组成的层进行 层内分析和综合。 统计模型
2022/11/3
28
输出结果的解释
模型的预测结果的评价
敏感度、特异度和阳性预测值
正确选择预测概率界值，简单地以0.5为 界值，但并不是最好的。
C指数
预测结果与观察结果的一致性的度量。 C值越大（最大为1），模型预测结果的
能力越强。
2022/11/3
29
非条件logistic回归
研究对象之间是否发生某事件是 独立的。 适用于：
放入所有变量，再逐个筛选
理论上看，前进法选择变量的经验公式缺乏总体概念，当用于因
素分析时，建议用后退法。当变量间有完全相关性时，后退法无 法使用，可用前进法。
2022/11/3
21
5.交互作用的引入
交互作用的定义
当自变量和因变量的关系随第三个变量 的变化而改变时，则存在交互作用

OR>1,说明 该因素是疾病的危险性增加，为危险因素； OR<1,说明 该因素是疾病的危险性减小，为保护因素；
Logistic回归
举例
例： 为了探讨冠心病发生的有关危险因素， 对26例冠心病病人和28例对照者进行病例 对照 研究，调查记录了8个可能的危险因素，试用 Logistic逐步回归分析方法筛选危险因素，并分 析各自变量的作用大小。
Logit变换
Logit(P) ln( P ) 1 P
Logit(P)
Logistic回归
举例
设有一个应变量 Y 取值为 1 或 0，在一组自变量
X 1,LXog2is,tic模,型X还m有作另一用种下线性阳化性表达结形果式发，称生为的Log概it模率型：为
P
LoPg(iYt ( P)1|
Logistic回归
比数比
是否暴露 暴露组 未暴露组 合计
病例 a c a+c
对照 b d b+d
合计 a+b(n1) c+d(n2) n
比数比（odds ratio、OR）：病例对照研究中表示疾病与暴露间
联系强度的指标，也称比值比。
比数（odds）：发生率与未发生率之比。即阳性率/阴性率。
暴露组发病的比值 a /(a b) 、未暴露组发病的比值 c /(c d )
Xln1(,1XP2P,) ,，则LogimstXicm
回若归记模Z型可表 示1为X1： 2 X 2 m X m Z
则
Z
P与P 之间关系的 Logistic 曲1线为
1 exp ( 1 X1 2 X
2
m
X
m
)
其中，为常数项，
1
,

logit回归结果解读【实用版】目录1.Logit 回归简介2.Logit 回归结果的主要组成部分3.如何解读 Logit 回归结果4.实际案例应用正文1.Logit 回归简介Logit 回归是一种广义线性模型，主要用于解决二分类问题。

与线性回归不同，Logit 回归的输出变量是逻辑斯蒂函数，其取值范围在 0 到 1 之间。

当输出变量大于 0.5 时，我们预测样本属于类别 1；当输出变量小于 0.5 时，预测样本属于类别 0。

Logit 回归可以帮助我们理解两个类别之间的概率关系，为二分类问题提供有效的预测依据。

2.Logit 回归结果的主要组成部分Logit 回归的结果主要包括以下几个部分：（1）系数：系数表示自变量对因变量的影响程度。

正系数表示自变量与因变量正相关，负系数表示负相关。

系数的绝对值越大，相关性越强。

（2）标准误差：标准误差是对系数的一种不确定性度量。

标准误差越小，表示系数的估计越精确。

（3）z 值：z 值表示系数的标准化程度，即系数除以标准误差。

z 值越大，表示自变量对因变量的影响程度越大。

（4）P>|z|：P>|z|表示在零假设成立的情况下，观察到这样的系数的概率。

该值越小，拒绝零假设的证据越强。

3.如何解读 Logit 回归结果当我们得到 Logit 回归的结果后，可以通过以下几个步骤来解读：（1）观察系数：根据系数的正负，可以判断自变量与因变量之间的相关性。

正系数表示正相关，负系数表示负相关。

（2）分析标准误差：标准误差越小，表示对系数的估计越精确。

在实际应用中，可以关注标准误差较小的自变量，因为它们对因变量的影响可能更为显著。

（3）关注 z 值：z 值可以帮助我们判断自变量对因变量的影响程度。

z 值较大的自变量，对因变量的影响可能更为显著。

（4）判断 P>|z|：P>|z|越小，拒绝零假设的证据越强。

可以关注P>|z|较小的自变量，它们对因变量的影响可能具有统计学意义。