北大半导体物理讲义整理
- 格式:doc
- 大小:1.15 MB
- 文档页数:46

半导体物理总结-讲义(1)《半导体物理总结-讲义》是一本关于半导体物理基础知识的讲解材料,其中包括半导体的基本特性、载流子运动、PN结、场效应管等内容。
以下为该书的重点内容概述:一、半导体材料特性1. 能带结构:半导体的能带结构高于导体、低于绝缘体,因此具有介于导体和绝缘体之间的导电和绝缘特性。
2. 晶格结构:半导体具有有序、周期性的晶体结构,能够有效控制电子在晶体内的运动。
3. 掺杂:通过掺杂材料改变半导体的电子浓度,从而使其具有p型或n型半导体的特性。
二、载流子运动1. 热激发:半导体中的电子可以受到能量的激励而被激发到导带中。
热能、光能、电场或磁场都可以起到激发的作用。
2. 离子化:在电场的作用下,半导体中的电子可能与晶格原子碰撞,失去能量而被离子化。
形成的正负离子对在电场作用下会向相反方向漂移。
3. 扩散:电子或空穴在半导体中由高浓度区域向低浓度区域扩散,使浓度逐渐平均,实现电流的流动。
扩散是在没有外电场的情况下发生的。
三、PN结1. 构成:PN结由p型半导体和n型半导体组成。
2. 特性:PN结具有一定的整流特性,能够阻止电流从n型半导体流向p型半导体,但允许反向电流。
3. 工作原理:在PN结中,载流子在电场的作用下发生扩散和漂移,形成电流。
四、场效应管1. 构成:场效应管由栅、漏极和源极三部分构成。
栅极位于n型半导体上,由于n型半导体中的电子易受到电场的影响,因此在栅极上加入电信号可以控制通道的导电性。
2. 工作原理:在没有控制电压的作用下,场效应管的通道是关闭的。
当加入一定电压时,栅极上的电场可以将通道打开,使得电流得以流动。
以上为《半导体物理总结-讲义》的重点内容概述,读者可根据需要深入学习相关内容。

一、半导体物理知识大纲核心知识单元 A:半导体电子状态与能级(课程基础——掌握物理概念与物理过程、是后面知识的基础)半导体中的电子状态(第 1 章)半导体中的杂质和缺陷能级(第 2 章)核心知识单元 B:半导体载流子统计分布与输运(课程重点——掌握物理概念、掌握物理过程的分析方法、相关参数的计算方法)半导体中载流子的统计分布(第 3 章)半导体的导电性(第 4 章)非平衡载流子(第 5 章)核心知识单元 C:半导体的基本效应(物理效应与应用——掌握各种半导体物理效应、分析其产生的物理机理、掌握具体的应用)半导体光学性质(第10 章)半导体热电性质(第11 章)半导体磁和压阻效应(第12 章)二、半导体物理知识点和考点总结第一章半导体中的电子状态本章各节内容提要:本章主要讨论半导体中电子的运动状态。
主要介绍了半导体的几种常见晶体结构,半导体中能带的形成,半导体中电子的状态和能带特点,在讲解半导体中电子的运动时,引入了有效质量的概念。
阐述本征半导体的导电机构,引入了空穴散射的概念。
最后,介绍了Si、Ge 和 GaAs 的能带结构。
在 1.1 节,半导体的几种常见晶体结构及结合性质。
(重点掌握)在 1.2 节,为了深入理解能带的形成,介绍了电子的共有化运动。
介绍半导体中电子的状态和能带特点,并对导体、半导体和绝缘体的能带进行比较,在此基础上引入本征激发的概念。
(重点掌握)在 1.3 节,引入有效质量的概念。
讨论半导体中电子的平均速度和加速度。
(重点掌握)在1.4 节,阐述本征半导体的导电机构,由此引入了空穴散射的概念,得到空穴的特点。
(重点掌握)在 1.5 节,介绍回旋共振测试有效质量的原理和方法。
(理解即可)在 1.6 节,介绍 Si 、Ge 的能带结构。
(掌握能带结构特征)在 1.7 节,介绍Ⅲ -Ⅴ族化合物的能带结构,主要了解GaAs 的能带结构。
(掌握能带结构特征)本章重难点:重点:1、半导体硅、锗的晶体结构(金刚石型结构)及其特点;三五族化合物半导体的闪锌矿型结构及其特点。
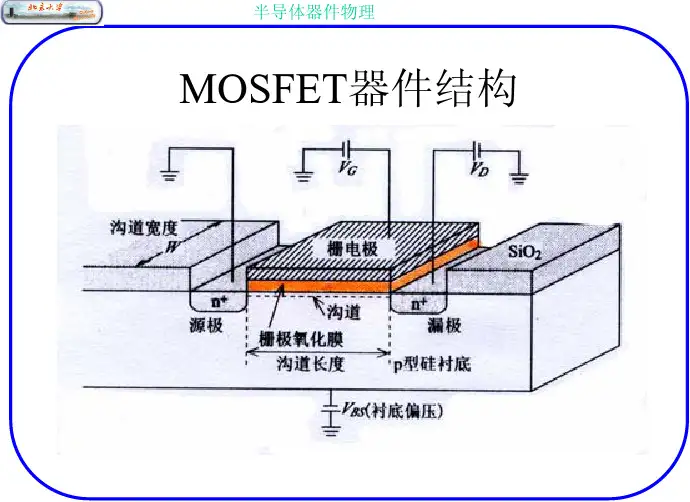





半导体物理讲义-2第二部分半导体中的电子和空穴前面我们讨论了半导体能带结构的一些共同的基本特点。
不同的半导体材料.其能带结构不同,而且往往是各向异件的,即沿不同的被矢k方向,E ~ K关系不同。
由于问题复杂,虽然理论上发展了多种计算的力法.但还不能完全确定出电子的全部能态,尚需借助于实验帮助,采用理论和实验相结合的方法来确定半导体中电子的能态。
本节介绍最初测出载流子有效质量并据此推出半导体能带结构的回旋共振实验及硅和锗的能带结构。
因对大多数半导体,起作用的往往是导带底附近的电子和价带顶附近的空穴,所以只给出导带底和价带顶附近的能带结构一、k空间等能面已知,一维情况下设能带极值在k=0处,则导带底附近和价带顶附近的E ~ K关系:图极值附近E ~K 关系示意图所以,如果知道m*n和m*p ,则极值附近的能带结构便可了解。
对实标的三维晶体,以kx , ky , kz为坐标轴构成k空间,k空间任―矢量代表波矢k(kx , ky , kz) 。
其中简单情况(半导体或晶体具有各向同性时):导带低附近E ~ K关系当E(k)为某一定值时,对应于许多组不同的(kx,ky,kz),将这些组不同的(kx,ky,kz)连接起来构成一个封闭面,在这个面上的能量值均相等,这个面称为等能量面,简称等能面。
容易看出,上式表示的等能面是一系列半径为的球面。
图 k空间球形等能面平面示意图一般情况(半导体或晶体具有各向异性的性质):导带低附近E ~ K关系晶体有各向异性时,E(k)与k的关系沿不同的k方向不一定相同,反映出沿不同的k 方向,电子的有效质量不一定相同,而且能带极值不一定位于k=o处。
设导带底位于k0 ,能量为E(k0),在晶体中选择适当的坐标轴kx , ky , kz,并令m*x , m*y , m*z分别表示沿kx , ky , kz 三个方向的导带底电子的有效质量,用泰勒级数在极值k0附近展开,略去高次项,得:注意:要具体了解这些球面或椭球面的方程,最终得出能带结构,还必须知道有效质量的值。

第二部分半导体中的电子和空穴一、热平衡载流子的统计分布为设计、分析半导体器件,有必要了解半导体单位体积内的载流子浓度(即载流子密度),由前面讲述可知,本征半导体中电子和空穴的浓度大致相等。
掺加施主杂质后,电子为多数载流子的n型半导体,其空穴浓度会怎么样? P型半导体的电子浓度、空穴浓度又如何? 这里,我们以前面获取的知识为基础,以定量方式求出半导体的载流子浓度。
前面已讲过,价带、导带是电子的能级集合体。
在各级能带中,电子按照某种分布概率配置在各能级上。
那么,单位晶体中电子所能利用的能级数有几个,它们在能带中怎样分布呢? 这就需要借助统计力学的一些结论来说明,以帮助我们进一步来理解半导体。
1、电子的分布函数固体中的电子具有下述特征:1)根据泡利不相容原理.若占有同一个能级的电子数超过2个则不能有相同的能量值。
2)不能相互区别。
受此制约,能量为E的电子态(能级)被1个电子占有的概率可由下式的费米-狄拉克分布函数(或者简称费米函数)结出:这里,k为玻尔兹曼常数(k=1.38x10-23 J/K=8.62x10-5 eV/K),T是绝对温度[K],EF 费米能级(费米能)。
可以看出,当能量E与费米能级EF相等时,分布函数为即电子占有率为l/2的能级称为费米能级。
左图表示了T=0K和任意温度T1、T2(T2> T1)时费米分布函数f(E)的情况。
我们注意到f(E)在E=EF时是对称的。
T=0K时,若E < EF , f(E)=1 ; 若E > EF,f(E)=0 。
这意味着比EF小的能级上全部被电子占据,比EF大的能级上全部空着(没有电子)。
图费米分布函数当温度上升,即T>0K时,电于占据比EF高的能级的概率很小,比EF低的能级上电子不存在(能级空着)的概率为1- f(E)。
这意味着EF附近的电子获得热能后,占据了比EF更高的能级,而在原处留下了空位。
当能量E 比E F 大3KT 或小3KT 时,费米分布函数中的指数项分别大于20或小于0.05。


半导体物理知识点汇总总结一、半导体物理基本概念半导体是介于导体和绝缘体之间的材料,它具有一些导体和绝缘体的特性。
半导体是由单一、多层、回交或互相稀释的混合晶形的二元、三元或多元化合物所组成。
它的特点是它的电导率介于导体和绝缘体之间,是导体的电导率∗101~1015倍,是绝缘体的电导率÷102~103倍。
半导体材料具有晶体结构,对它取决于结晶度的大小,织排效应特别大。
由于它的电导率数值在半导体晶体内并不等同,所以它是隔离的,具有相当大的飞行束度,并且不容易受到外界的干扰。
二、半导体晶体结构半导体是晶体材料中最均匀最典型的材料之一,半导体的基本结构是一个由原子排成的一种规则有序的晶体结构。
半导体原子是立方体的晶体,具有600个原子的立方体晶体结构,又称之为立方的晶体结构。
半导体晶体结构的代表性六面体晶体结构,是一种由两个或两个以上的六面全部说构成的立方晶体。
半导体晶体的界面都是由两个或两个以上的六面全部说构成的晶体包围构成,是由两个或两个以上的六面全部说构成的立方晶体。
半导体晶体的界面都是由两个或两个以上的六面全部说构成的晶点构成,是由两个或两个以上的六面全部说构成的晶点构成。
三、半导体的能带结构半导体的能带“带”是指其电子是在“带”中运动的,是光电子带,又称作价带,当其中的自由电子都填满时另一种平面,又称导电带,当其中的自由电子并不填满时其另一种平面在有一些能够使电子轻易穿越的东西。
半导体的能带是由两个非常临近的能带组成的,其中价带的最上一层电子不足,而导电带的下一层电子却相当到往动能,这一些动能可能直到加到电子摆脱它自己体原子,变成自由电子,并且在整体晶体里自由活动。
四、半导体的导电机理半导体的导电机理是在外加电压加大时一部分自由电子均可以在各自能带中加速骚扰,从而增加在给导电子处所需要的电压增大并最终触碰到另一种平面上产生电流就可以。
五、半导体的掺杂掺杂是指在纯净半导体中加入某些以外杂质元素的行为。
半导体物理知识点梳理简介半导体物理学是研究半导体材料的电子结构、载流子动力学和半导体器件工作原理的学科。
它是现代微电子工业的基础和前提,包含了多种复杂的物理过程和电子器件设计原理。
在集成电路中,半导体物理学的研究对于我们理解电子器件的工作原理和提高器件性能至关重要。
一、半导体材料的电子结构1. 能带能带是指材料中的能量电子集合,可以被电子占据或空出来。
常见的能带包括价带和导带。
价带中的电子与原子核共享一个价电子对,导带则含有未占据的电子。
导带和价带之间的区域称为禁带,其中没有可用的能级,这使得该区域没有自由电子。
禁带宽度决定了材料的导电性质。
2. 牛顿力学与量子力学经典物理学,如牛顿力学,不能完全描述电子在原子中的行为,因此计算价带和导带的能量需要借助量子力学。
量子力学通过考虑波粒二象性和不确定性原理,说明电子存在于这两个能带中,以及它们的位置和能量。
3. 材料的类型半导体凭借其调谐电子运动的能力而成为电子器件的主要材料之一。
半导体材料通常可以划分为晶体(单晶或多晶)和非晶体,前者由规则排列的原子构成,后者则表现为无序空间结构。
二、载流子动力学1. 载流子类型在材料中,载流子是指负电荷(电子)或正电荷(空穴),它们的运动是电流传导的主要过程。
半导体中的载流子种类包括电子和空穴。
这些载流子的输运以及它们的沟通将直接影响材料的电学行为。
2. 拉曼散射与荷质比拉曼散射是一种通过材料中的声子色散特性筛选其材料类型和结构的方法。
这可以帮助确定载流子的荷质比,荷质比是电荷与带负荷的质量之比。
荷质比是半导体的一个关键参数,它决定了载流子的涵盖区域和速度。
3. 面掺杂多数半导体材料中的电子和空穴浓度是非常低的,这导致了它们的电导率较低。
通过面掺杂,半导体的电导率可以得到提高。
面掺杂涉及向材料表面引入杂质原子,这些原子具有带电性质以及能影响材料电荷载流子浓度的能力。
三、半导体器件工作原理1. 篱截型场效应晶体管篱截型场效应晶体管(MESFET)是一种单极型晶体管器件,它是通过在材料中形成门结构,控制源引线到漏引线通道上电子流的芯片。
半导体物理学讲义第⼀章半导体中的电⼦状态本章介绍:本章主要讨论半导体中电⼦的运动状态。
主要介绍了半导体的⼏种常见晶体结构,半导体中能带的形成,半导体中电⼦的状态和能带特点,在讲解半导体中电⼦的运动时,引⼊了有效质量的概念。
阐述本征半导体的导电机构,引⼊了空⽳散射的概念。
最后,介绍了Si、Ge和GaAs的能带结构。
在1.1节,半导体的⼏种常见晶体结构及结合性质。
在1.2节,为了深⼊理解能带的形成,介绍了电⼦的共有化运动。
介绍半导体中电⼦的状态和能带特点,并对导体、半导体和绝缘体的能带进⾏⽐较,在此基础上引⼊本征激发的概念。
在1.3节,引⼊有效质量的概念。
讨论半导体中电⼦的平均速度和加速度。
在1.4节,阐述本征半导体的导电机构,由此引⼊了空⽳散射的概念,得到空⽳的特点。
在1.5节,介绍回旋共振测试有效质量的原理和⽅法。
⾃学内容。
在1.6节,介绍Si、Ge的能带结构在1.7节,介绍Ⅲ-Ⅴ族化合物的能带结构,主要了解GaAs的能带结构第⼀节半导体的晶格结构和结合性质本节要点1.常见半导体的3种晶体结构;2.常见半导体的2种化合键。
1. ⾦刚⽯型结构和共价键重要的半导体材料Si、Ge都属于⾦刚⽯型结构。
这种结构的特点是:每个原⼦周围都有四个最近邻的原⼦,与它形成四个共价键,组成⼀个如图1(a)所⽰的正四⾯体结构,其配位数为4。
⾦刚⽯型结构的结晶学原胞,是⽴⽅对称的晶胞如图1(b)图所⽰。
它是由两个相同原⼦的⾯⼼⽴⽅晶胞沿⽴⽅体的空间对⾓线滑移了1/4空间对⾓线长度套构成的。
⽴⽅体顶⾓和⾯⼼上的原⼦与这四个原⼦周围情况不同,所以它是由相同原⼦构成的复式晶格。
其固体物理学原胞和⾯⼼⽴⽅晶格的取法相同,但前者含两个原⼦,后者只含⼀个原⼦。
原⼦间通过共价键结合。
共价键的特点:饱和性、⽅向性。
2. 闪锌矿结构和混合键III-V族化合物半导体绝⼤多数具有闪锌矿型结构。
闪锌矿结构由两类原⼦各⾃组成的⾯⼼⽴⽅晶胞沿⽴⽅体的空间对⾓线滑移了1/4空间对⾓线长度套构成的。
半导体物理知识点梳理半导体物理考点归纳⼀·1.⾦刚⽯1) 结构特点:a. 由同类原⼦组成的复式晶格。
其复式晶格是由两个⾯⼼⽴⽅的⼦晶格彼此沿其空间对⾓线位移1/4的长度形成b. 属⾯⼼晶系,具⽴⽅对称性,共价键结合四⾯体。
c. 配位数为4,较低,较稳定。
(配位数:最近邻原⼦数)d. ⼀个晶体学晶胞内有4+8*1/8+6*1/2=8个原⼦。
2) 代表性半导体:IV 族的C ,Si ,Ge 等元素半导体⼤多属于这种结构。
2.闪锌矿1) 结构特点:a. 共价性占优势,⽴⽅对称性;b. 晶胞结构类似于⾦刚⽯结构,但为双原⼦复式晶格;c. 属共价键晶体,但有不同的离⼦性。
2) 代表性半导体:GaAs 等三五族元素化合物均属于此种结构。
3.电⼦共有化运动:原⼦结合为晶体时,轨道交叠。
外层轨道交叠程度较⼤,电⼦可从⼀个原⼦运动到另⼀原⼦中,因⽽电⼦可在整个晶体中运动,称为电⼦的共有化运动。
4.布洛赫波:晶体中电⼦运动的基本⽅程为:,K 为波⽮,uk(x)为⼀个与晶格同周期的周期性函数,5.布⾥渊区:禁带出现在k=n/2a 处,即在布⾥渊区边界上;允带出现在以下⼏个区:第⼀布⾥渊区:-1/2a第⼆布⾥渊区:-1/aE(k)也是k 的周期函数,周期为1/a,即E(k)=E(k+n/a),能带愈宽,共有化运动就更强烈。
6.施主杂质:V 族杂质在硅,锗中电离时,能够释放电⼦⽽产⽣导电电⼦并形成正电中⼼,称它们为施主杂质或n 型杂质7.施主能级:将施主杂质束缚的电⼦的能量状态称为施主能级,记为ED 。
施主能级离导带很近。
8.受主杂质:III 族杂质在硅,锗中能够接受电⼦⽽产⽣导电空⽳,并形成负电中⼼,称它们为受主杂质或P 型杂质。
9.受主能级:把被受主杂质所束缚的空⽳的能量状态称为受主能级,记为EA 。
受主能级离价带很近。
10.简并半导体&⾮简并半导体:若费⽶能级进⼊了导带,说明n 型杂质掺杂浓度很⾼(即ND 很⼤);也说明了导带底附近的量⼦态基本上被电⼦所占据了。
半导体物理知识点梳理1.半导体材料的能带结构:半导体材料的能带结构是理解其物性的基础。
在二维的能带图中,包含导带和价带之间的能隙。
导带中的电子可以自由移动,而价带中的电子需要外加能量才能进入导带。
2.纯半导体和杂质半导体:纯半导体指的是没有杂质掺杂的半导体材料,其导电能力较弱。
而杂质半导体是通过引入适量的杂质原子来改变半导体材料的导电性质,其中掺入的杂质原子被称为施主或受主。
3.载流子输运:半导体中的电导主要是由自由载流子贡献的,包括n型半导体中的电子和p型半导体中的空穴。
当施主杂质掺杂进入p型半导体时,会产生附加的自由电子;相反,当受主杂质掺杂进入n型半导体时,会产生附加的空穴。
这些自由载流子通过材料中的散射、漂移和扩散等方式进行输运。
4. pn结和二极管:pn结是由p型半导体和n型半导体结合而成的电子器件。
在pn结中,发生了空穴从p区向n区的扩散和电子从n区向p区的扩散,导致p区和n区的空间电荷区形成。
当正向偏置时,电流可以通过pn结,而反向偏置时,电流很小。
这种特性使得二极管可以用作整流器件。
5.晶体管:晶体管是一种三层结构的半导体器件,由一个n型区和两个p型区或一个p型区和两个n型区构成。
晶体管可以用作放大器和开关,其工作原理是通过控制基极电流来调节集电极电流。
6.MOSFET:金属-绝缘体-半导体场效应晶体管,即MOSFET,是一种三层结构的半导体器件。
MOSFET具有较高的输入阻抗和较低的功耗,广泛应用于集成电路中。
MOSFET的工作原理是通过调节栅极电压来调节通道中的电荷密度。
7.光电二极管和光电导:光电二极管和光电导是基于光电效应的半导体器件。
光电二极管是将光信号转换为电压信号的器件,而光电导则是将光信号转换为电流信号。
这两种器件在通信和光电探测等领域有广泛的应用。
8.半导体激光器:半导体激光器是一种利用半导体材料的发光原理来产生激光束的器件。
半导体激光器具有体积小、效率高和工作电流低等优势,广泛应用于光通信和光存储等领域。
第一章晶体结构晶格§1晶格相关的基本概念1.晶体:原子周期排列,有周期性的物质。
2.晶体结构:原子排列的具体形式。
3.晶格:典型单元重复排列构成晶格。
4.晶胞:重复性的周期单元。
5.晶体学晶胞:反映晶格对称性质的最小单元。
6.晶格常数:晶体学晶胞各个边的实际长度。
7.简单晶格&复式晶格:原胞中包含一个原子的为简单晶格,两个或者两个以上的称为复式晶格。
8.布拉伐格子:体现晶体周期性的格子称为布拉伐格子。
(布拉伐格子的每个格点对应一个原胞,简单晶格的晶格本身和布拉伐格子完全相同;复式晶格每种等价原子都构成和布拉伐格子相同的格子。
)9.基失:以原胞共顶点三个边做成三个矢量,α1,α2,α3,并以其中一个格点为原点,则布拉伐格子的格点可以表示为αL=L1α1 +L2α2 +L3α3 。
把α1,α2,α3 称为基矢。
10.平移对称性:整个晶体按9中定义的矢量αL 平移,晶格与自身重合,这种特性称为平移对称性。
(在晶体中,一般的物理量都具有平移对称性)11.晶向&晶向指数:参考教材。
(要理解)12.晶面&晶面指数:参考教材。
(要理解)立方晶系中,若晶向指数和晶面指数相同则互相垂直。
§2金刚石结构,类金刚石结构(闪锌矿结构)金刚石结构:金刚石结构是一种由相同原子构成的复式晶格,它是由两个面心立方晶格沿立方对称晶胞的体对角线错开1/4长度套构而成。
常见的半导体中Ge,Si,α-Sn(灰锡)都属于这种晶格。
金刚石结构的特点:每个原子都有四个最邻近原子,它们总是处在一个正四面体的顶点上。
(每个原子所具有的最邻近原子的数目称为配位数)每两个邻近原子都沿一个<1,1,1,>方向,处于四面体顶点的两个原子连线沿一个<1,1,0>方向,四面体不共顶点两个棱中点连线沿一个<1,0,0,>方向。
金刚石结构的密排面:{1,1,1} 晶面的原子都按六方形的方式排列。
每两层{1,1,1}原子层完全相同,A B C A B C ……在这种结构中,关于任何两个相邻原子连线中点具有反演对称性。
类金刚石结构:GaAs,InSb,GaP等化合物晶体的晶格是由两种不同原子组成的面心立方晶格套构而成的,称为类金刚石结构或闪锌矿结构,显然闪锌矿不再具有反演中心。
§3共价结合§3.1晶体结合的四种基本方式1.离子结合:原子间交换电子,形成正负离子,之间相互库仑作用结合成固体。
2.共价结合:相邻原子共用电子对形成共价键。
(半导体中晶体普遍是共价结合,因此本节重点是共价结合。
)3.金属结合:价电子共有化形成负电子云,正离子浸泡在电子云中。
4.范德瓦尔结合:发生在饱和电子结构中,相互作用靠很弱的瞬时偶极矩。
§3.2成键态与反键态(以H2为例)A,B两原子相互靠近形成分子,两个价电子为A,B共有。
成键态:ψ=C(ψA+ψB) ψA ψB反键态:ψ=C’(ψA-ψB) 其中C和C’为归一常数成键态电子云集中在两原子核之间,同时受到两个原子核的库仑吸引作用,库仑能下降,故形成共价键。
反键态使能量升高△1,成键态能量下降△2且有△1 > △2,只有未成对电子才能形成共价键。
§3.3 SP3杂化(以Si为例)Si的原子组态为:(1S)2 (2S)2 (2P)6(3S)2 (3P)2稳定电子价电子由Si原子组态可知,若不改组的话只能形成2个共价键,但实际上有4个共价键,成四面体,这是因为发生了SP3杂化的缘故。
即价电子的组态发生了如下改组:(3S)2 (3P)2 →(3S1) (3Px) (3Py) (3Pz)组成了新的4个轨道态,实际上四个共价键是以S态和P态波函数线形组合为基础的,这样使得系统能量最低。
杂化的好处:①成键数增多,四个杂化态上全部是未成对电子。
②成键能力增强,电子云集中在四面体方向,电子重叠大,使能量下降更多,抵消杂化的能量,使总能量减小。
§4 晶格缺陷晶格缺陷分3类:●点缺陷:间隙原子和空位。
●线缺陷:位错。
●面缺陷:层错。
点缺陷的类型:●弗兰克尔缺陷:原子热运动,少量原子离开格点位置进入间隙形成空位间隙原子对。
●肖特基缺陷:单一空位的缺陷。
●反肖特基缺陷:单一缺陷原子的缺陷。
第二章 半导体中的电子状态§1 半导体基本能带§1.1布洛赫波在晶体的周期场中,电子波函数的形式为ψk (r )=e i kr μk (r ) ,其中μk (r )= μk (r+αL )其中k 称为简约波束,有波束的量纲,但要在一简约范围内取值。
k 与动量类似,在跃迁过程中守衡,且有外F dtd k= ,故称为准动量。
在晶体中k 取值在一定范围内,这范围称为简约布里渊区,下面以一维为例加以证明。
设晶格周期为α ∵μk (x) = μk (x + n α)∴ψk (x +α) = e ik α·e ikx ·μk (x + n α)= e ik α[e ikx ·μk (x)] =e ik αψk (x)其中e ik α表示相邻原胞之间波函数位相差,因此-π≤k α≤π,三维情形,α1,α2,α3三个基矢有ψk (r +αn )= e i k αn ψk (r ) ,其中n=1,2,3。
定义矢量b 1,b 2,b 3分别等于321213321132321321222αααααb αααααb αααααb ⨯⋅⨯=⨯⋅⨯=⨯⋅⨯=πππ则有αi b j =2πδij (δij 函数表示,当i=j 时为1,不等为0)故称b 1,b 2,b 3为倒矢量,以b 1,b 2,b 3为基矢组成晶格,称为倒格子。
这样定义下有倒格子原胞的体积于原晶格原胞的体积相乘之积为常数(2π)3用K n=n 1b 1+n 2b 2+n 3b 3表示倒格矢,则k 和k +K n 表示相同状态。
因此简约布里渊区也称作不相差任何倒矢量,位相变化单值完备的区域。
对于金刚石结构的面心立方晶格,倒格子为体心立方,通常取倒格子中k =0原点做次近邻,近邻中垂面围成的区域,它称为维格纳—塞兹原胞。
§1.2 周期性边界条件由于实际晶体包含的原子是有限的,故每个能带所包含的状态数是有限的,又由于边界条件的差异对大块晶体性质并无本质影响,故引入周期性边界条件来计算k 空间的取值密度。
一维:设一维晶格总长度L=N α (N 为包含原胞总数) 周期性边界条件为:ψk (0) = ψk (L) = ψk (N α) ψk (0) = μk (0) ψk (N α) = e ikN αμk (N α) = e ikN αμk (0) 所以得到e ikN α = 1 故有kN α = 2n π ( n 为整数)因此k 的可取值为k=(2n π)/N α , 取值密度g k = N α/2π =L/2π对一维,简约布里渊区长度为2π/α,因此布里渊区内包含的状态数为(2π/α)·(L/2π)= L/α = N 正好等于原胞数N所以k 空间的取值密度也可以用原胞总数除以布里渊区长度来计算(对于二维则除以布里渊区面积,三维除以布里渊区体积) 三维:对于三维可以类似地求得k 空间的状态密度 g k =(N 1α1·N 2α2·N 3α3)/(2π)3 (N 1,N 2,N 3表示三个维度上的原胞数)显然,用倒格子原胞的体积 (2π)3/Ω乘以k 空间的密度g k 得到k 空间的状态数为N 1·N 2·N 3,仍等于晶体所包含的原胞总数。
*注:上面公式中Ω表示实际晶体原胞体积,有Ω=α1·α2·α3§2 电子准经典运动§2.1 电子准经典运动的两个基本公式① 外F Pk ==dtd dt d②1=V ▽k E (k )§2.2 加速度和有效质量三维:)()(1))(1(2k k k k k V E F E d d d d t t ∇∇⋅=∇=写成张量形式:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂==222222222222211,)1(zyz x z zy y xy z x yx x t EE E E EEE EE m m d d k k k kk k k k k k k k k k k F V 其中 1/m 可对角化,因此可以写成αααm d d t ⋅⎪⎪⎭⎫⎝⎛=V F{}⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂=222222222*0000z yxE EE m k k k 称为有效质量张量 对于能带底(E k 最小处) 00=⎪⎭⎫ ⎝⎛∂∂k k E 设k 0 = 0 在k = 0处泰勒展开有:()())(2)(21*2*2*2202222222220zz y y x xz zy y x x m m m E E E E E E k k k k k k k k k k k k +++=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+= ∵最小值处0022>⎪⎪⎭⎫⎝⎛∂∂k k E ∴ m x ,m y ,m z 均为正值,在满足上面抛物线性关系的能量范围内,有效质量各个分量可以看作常数,对立方对称性晶体m x = m y = m z = m ,可以写成:mE E 2)()(220k k k +=同理对于能带顶有:mE E 2)()(220k k k +=,此时m 为负值。
§3 导带的电子和空穴§3.1 基本原理1. 满带中电子不导电,未填满能带在有外加场时产生电流。
2. 绝缘体和半导体只有一系列满带和一系列空带,不存在半满带,最上面的满带叫价带,最下面的空带叫导带。
导带底与价带顶之间的能量间隙称为禁带(也叫能隙),禁带宽度用Eg 表示。
可以用两条线代表导带底,和价带顶;能量值分别用E C 和E V 表示。
导带底E C 价带顶E V3.绝缘体,半导体和金属:Eg在1ev附近的称为半导体,热激发时满带不满,空带不空,有一定的导电性;Eg大于10ev的称为绝缘体,电子很少激发,因而几乎不导电,而金属中则存在半满带,因此具有良好的导电性能。
4.近满带的空穴:假想的粒子,等价于2N-1个电子的总体运动。
设空穴处有电子的时候,因为满带电流为0,有J(k) + (-e)V(k) = 0其中J(k)表示2N-1个电子的总电流推出2N-1个电子的总电流J(k) = e V(k)说明2N-1个电子的总电流等效于带正电,速度为V(k)的粒子又因为()*e*ee*2mmddmddttEEFkJv-=-==故而由于空穴出现在价带顶,m*<0,故引入空穴有效质量m h* =|m*|为正,综上,把空穴等价成一个正电荷,正有效质量的粒子。