二元离散选择模型案例

二元logit和多元logit引言二元logit和多元logit是经济学和统计学领域经常使用的两种统计模型。

它们用于分析离散型、有序类变量以及多分类问题。

本文将详细介绍二元logit和多元logit模型的原理、应用领域以及在实际中的应用案例。

二元logit模型原理二元logit模型是一种用于估计和解释两种可能结果的离散型因变量的统计模型。

典型的应用包括预测个体选择两个互斥选项之一的行为，如是否参与劳动力市场、是否购买某个商品等。

二元logit模型的核心思想是通过最大似然估计法估计模型参数。

应用领域二元logit模型在经济学和社会科学的研究中广泛应用。

它可以用于分析个体在选择两个互斥选项之一时的决策过程，从而帮助我们了解个体的行为模式。

例如，研究者可以利用二元logit模型分析个体的劳动力市场参与决策，研究个体特征对参与决策的影响。

应用案例下面通过一个简单的案例来解释二元logit模型的应用。

假设我们想研究个体的购车决策，即个体是否购买一辆新车。

我们收集了一些相关数据，包括个体的年龄、收入、家庭状况等变量。

我们可以使用二元logit模型来分析这个问题。

模型的结果可以告诉我们不同变量对购车决策的影响，并估计它们的影响程度。

多元logit模型原理多元logit模型是一种用于估计和解释多个离散型结果的统计模型。

与二元logit模型相比，多元logit模型可以处理具有三个或更多互斥选项的离散型因变量。

多元logit模型的核心思想是将多个二元logit模型扩展到多个互斥选项之间，并通过最大似然估计法估计模型参数。

应用领域多元logit模型在市场调研、消费者行为研究等领域得到广泛应用。

研究者可以借助多元logit模型分析消费者对多个产品或品牌的选择行为，从而了解消费者的偏好和购买决策。

多元logit模型还可以用于分析投票行为、市场份额预测等问题。

应用案例下面通过一个简单的案例来解释多元logit模型的应用。

假设我们想研究消费者对三个不同品牌的冰淇淋的选择行为。

一．二元离散选择模型1．二元响应模型(Binary response model)我们往往关心响应概率()()()()z G x x G x y x y k k =+++=E ==P βββ...1110，其中x 表示各种影响因素（各种解释变量，包括虚拟变量）。

根据不同的函数形式可以分为下面三类模型：线性概率模型（Linear probability model ，LPM ）、对数单位模型（logit ）、概率单位模型(probit)：三种模型估计的系数大约有以下的关系：L PM probit probit it ββββ5.2,6.1log ==2．偏效应（1）如果解释变量是一个连续型变量，那么他对p(x)=p(y=1|x)的偏效应可以通过求下面的偏导数得出来：()()()()dzz dG z g x g x x p j j =+=∂∂,0βββ，偏效应的符号和该解释变量对应的系数的符号一致；两个解释变量偏效应之比等于它们各自的估计系数之比。

（2）如果解释变量是一个离散性变量，则k x 从k c 变化到k c +1时对概率的影响大小为：()()()k k k k c x G c x G ββββββ+++-++++...1 (110110)上面的其他解释变量的取值往往取其平均值。

3．估计方法与约束检验极大似然估计；三种常见的大样本检验：拉格朗日乘数检验、wald 检验、似然比检验。

4．Stata 程序语法（以Probit 为例）probit depvar [indepvars] [weight] [if exp] [in range] [, level(#) nocoef noconstant robust cluster(varname) score(newvar) asis offset(varname) maximize_options ] predict [type] newvarname [if exp] [in range] [, statistic rules asif nooffset ] where statistic isp predicted probability of a positive outcome; the default xb linear predictionstdp standard error of the prediction二．具体的例子1．数据：美国1988年的CPS 数据2．模型：估计成为工会成员的可能性，模型形式如下：参加工会的概率=F(潜在经验potexp 、经验的平方项potexp2、受教育年限grade 、婚否married 、工会化程度high)；解释变量：Potexp=年龄-受教育年限-5；grade=完成的受教育年限；married ：1表示婚，0未婚；high ：1表示高度工会化的行业，否则为0。

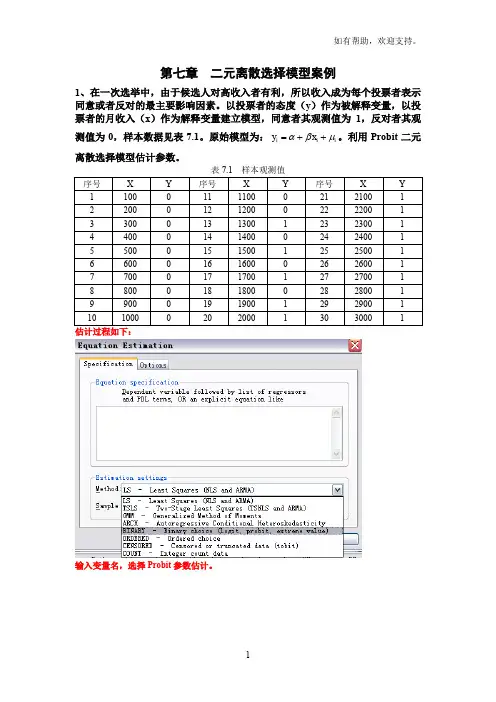
第七章 二元离散选择模型案例1、在一次选举中，由于候选人对高收入者有利，所以收入成为每个投票者表示同意或者反对的最主要影响因素。

以投票者的态度（y ）作为被解释变量，以投票者的月收入（x ）作为解释变量建立模型，同意者其观测值为1，反对者其观测值为0，样本数据见表7.1。

原始模型为：i i i y x αβμ=++。

利用Probit 二元离散选择模型估计参数。

表7.1 样本观测值输入变量名，选择Probit 参数估计。

得到如下输出结果：但是作为估计对象的不是原始模型，而是如下结果：=---+1@[( 4.75390.003067*)]YF CONRM X可以得到不同X值下的Y选择1的概率。

例如，当X=600时，查标准正态分布表，对应于2.9137的累积正态分布为0.9982；于是，Y的预测值YF=1-0.9982=0.0018，即对应于该个人，投赞成票的概率为0.0018。

2、某商业银行从历史贷款客户中随机抽取78个样本，根据涉及的指标体系分别计算它们的“商业信用支持度”（XY）和“市场竞争地位等级”（SC），对它们贷款的结果（JG）采用二元离散变量，1表示贷款成功，0表示贷款失败。

样本观测值见表8.2。

目的是研究JG与XY、SC之间的关系，并为正确贷款决策提供支持。

估计过程如下：输入变量名，选择Logit参数估计。

得到如下输出结果：用回归方程表示如下：JGF CONRM XY SC=---+1@[(16.110.465035*9.379903*)]该方程表示，当XY和SC已知时，带入方程，可以计算贷款成功的概率JGF。

3、某研究所1999年50名硕士考生的入学考试总分数（SCORE）及录取情况见表5。

考生考试总分数用SCORE表示，Y为录取状态，D1为表示应届生与往届生的虚拟变量。

表7.3 50名硕士考生的入学考试总分数（SCORE）及录取状况数据表定义如下：1,0,Y ⎧=⎨⎩录取未录取， 1,10,D ⎧=⎨⎩应届生非应届生 加入D1变量的目的是想考察考生为应届生或往届生是否也对录取产生影响。

二元离散选择模型1.在一次选举中，由于候选人对高收入者有力，所以收入成为每个投票者表示同意或者反对的最主要影响因素。

以投票者的态度（y ）作为被解释变量，以投票者的月收入（x ）作为解释变量建立模型，同意者其观测值为1，反对者其观测值为0，样本数据见表7.1。

原始模型为：i i i y x αβµ=++。

利用Probit 二元离散选择模型估计参数。

表8.1样本观测值序号X Y 序号X Y 序号X Y 11000111100021210012200012120002222001330001313001232300144000141400024240015500015150012525001660001616000262600177000171700127270018800018180002828001990001919001292900110100020200013030001估计过程如下：输入变量名，选择Probit 参数估计。

得到如下输出结果：但是作为估计对象的不是原是模型，而是如下结果：1@[( 4.75390.003067*)]YF CONRM X =−−−+可以得到不通X 值下的Y 选择1的概率。

例如，当X=600时，查标准正态分布表，对应于2.9137的累积正态分布为0.9982；于是，Y 的预测值YF=1-0.9982=0.0018，即对应于该个人，投赞成票的概率为0.0018。

1.某商业银行从历史贷款客户中随机抽取78个样本，根据涉及的指标体系分别计算它们的“商业信用支持度”（XY）和“市场竞争地位等级”（SC），对它们贷款的结果（JG）采用二元离散变量，1表示贷款成功，0表示贷款失败。

样本观测值见表8.2。

目的是研究JG与XY、SC之间的关系，并为正确贷款决策提供支持。

表8.2样本观测值JG XY SC JGF JG XY SC JGF JG XY SC JGF 0125-2001500-20054-10 0599-200960014221 0100-201-80104200.0209 0160-200375-2011821 046-20042-1 6.50E-130801 6.40E-12 080-2015211-501 0133-200172-20032620 0350-101-801026110 12300.9979089-201-2-10.9999 060-200128-20014-2 3.90E-07 070-10160112200.9991 1-8010150-10011310 0400-201542114210.9987 07200028-2015720.9999 0120-1012500.9906014600 14010.999812300.997911501 13510.999911401026-2 4.40E-16 12611049-10089-20 115-10.4472014-10.54981511 069-100610 2.10E-121-9-11 010710140211411 12911030-20054-20 12110112-1013211 13710.9999078-200540 1.40E-07 053-1010010131-20 0194000131-2011501估计过程如下：输入变量名，选择Logit参数估计。

第9讲离散选择模型之二元结果模型参考书目：1．Long, J. S., and J. Freese. 2006. Regression Models for Categorical Dependent Variables Using Stata. 2nd ed. College Station, TX: Stata Press教学视频：Logistic regression, part 1: Binary predictorsLogistic regression, part 2: Continuous predictorsLogistic regression, part 3: Factor variables一、离散被解释变量的例子二元结果模型：考研或不考研；就业或待业；买房或不买房；买保险或不买保险；贷款申请被批准或拒绝；出国或不出国；回国或不回国；战争或和平；医药实验中的生或死。

多元结果模型：对不同交通方式的选择(走路、骑车、坐车上班)；对不同职业的选择。

这类模型被称为“离散选择模型”(discrete choice model) 。

考虑到离散被解释变量的特点，通常不宜用OLS进行回归。

假设个体只有两种选择，比如y=1 (考研)或y=0 (不考研)。

是否考研，取决于研究生毕业后的预期收入、个人兴趣、本科毕业后直接就业的收入前景等。

所有解释变量都包括在向量x中。

二、二元结果模型的微观基础对于二元选择行为，可通过“潜变量”(latent variable)概括该行为的净收益(收益减去成本)。

如果净收益大于0，则选择做；否则，选择不做。

y*=x′β + ε其中，净收益y*为潜变量，不可观测。

选择规则为y=1，若y*>0y=0，若y*≤0如果ε为正态分布，则为Probit；如果ε为逻辑分布，则为Logit。

logistic — Logistic regression, reporting odds ratios (Logistic回归，报告优势比/比值比)对于Logit模型，记p= P(y =1|x ) ，则1-P= P(y =0|x )。