北京课改版五年级数学上册第四单元《统计图表与可能性》知识点汇总

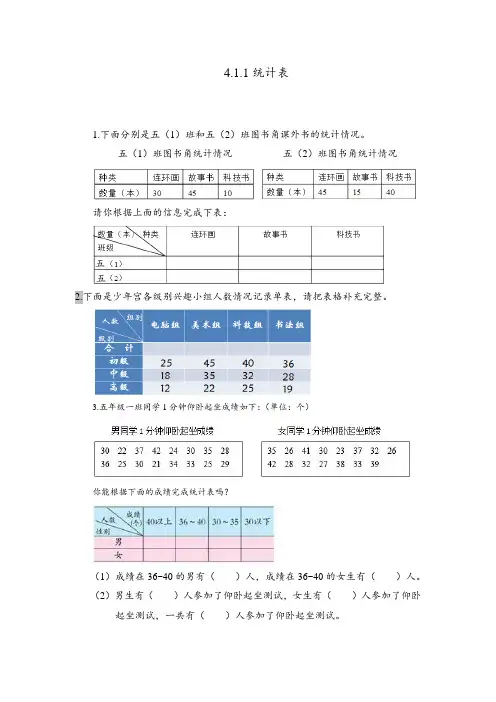
4.1.1统计表1.下面分别是五（1）班和五（2）班图书角课外书的统计情况。

五（1）班图书角统计情况五（2）班图书角统计情况请你根据上面的信息完成下表：2.下面是少年宫各级别兴趣小组人数情况记录单表，请把表格补充完整。

3.五年级一班同学1分钟仰卧起坐成绩如下：（单位：个）你能根据下面的成绩完成统计表吗？（1）成绩在36~40的男有（）人，成绩在36~40的女生有（）人。

（2）男生有（）人参加了仰卧起坐测试，女生有（）人参加了仰卧起坐测试，一共有（）人参加了仰卧起坐测试。

答案：1. 30 45 10 45 15 402. 55 102 97 833. （1）2 3 （2）16 15 314.1.2练习十五1.在绿色环保活动中，五年级三个班积极开展回收废旧报纸的活动。

2012年第一季度各班回收废旧报纸的数量如下。

五(1)班:1月份25千克，2月份31千克，3月份35千克；五(2)班:1月份22千克，2月份24千克，3月份39千克；五(3)班:1月份30千克，2月份41千克，3月份38千克。

完成下面的统计表。

五年级各班回收废旧报纸情况统计表2012年4月2.为了解“文化进社区”活动的开展情况，五年级(1)班同学到和睦街社区图书馆调查到如下信息:2009年购买科技书850本，文艺书723本;2010年购买科技书1012本，文艺书812本;2011年购买科技书1423本，文艺书902本。

请你整理数据，完成下面的统计表。

和睦街社区图书馆购买图书情况统计表2012年2月答案：4.2.1平均数1. 求a、b、c三个数的平均数,列式是( )。

A. a+b+cB. (a+b+c)×3C. (a+b+c)÷32.计算下面一组数据的平均数。

55178152253.先完成下面的统计表,再回答下面的问题。

(可以使用计算器)班级人数存书/本人均存书/本合计五(1)班30 360五(2)班28 420五(3)班32 576五(4)班30 480(1)人均存书最多的是哪个班?人均存书最少的是哪个班?(2)全年级人均存书多少本?4.商店蓝气球有43只，黄气球有21只，绿气球有33只，红气球和蓝气球同样多，平均每种气球有多少只？答案：1. C2. 113. 120 1836 15.3 12 15 18 16 （1）五（3）班五（1）班（2）15.34. （43+21+33+43）÷4=35（只）答：平均每种气球35只。

五年级数学上册第4课可能性必备知识点五年级数学上册第4课《可能性》的必备知识点主要包括以下几个方面：一、事件发生的确定性和不确定性1. 确定性：生活中有些事件的发生是确定的，一般用“一定”或“不可能”来描述。

例如，太阳一定从东方升起；在地球上，人不可能不借助外力而在空中悬浮。

2. 不确定性：生活中有些事件的发生是不确定的，一般用“可能”来描述。

例如，明天可能会下雨；掷一枚硬币，可能正面朝上，也可能反面朝上。

二、可能性的大小与数量的关系1. 基本关系：当某种情况的个体在总数中占的数量越多时，发生的可能性就越大；数量越少时，发生的可能性就越小。

2. 实例说明：例如，一个盒子里有5个红球和3个蓝球，任意摸出一个球，摸出红球的可能性大于摸出蓝球的可能性，因为红球的数量比蓝球多。

三、可能性的表示与计算1. 表示方法：可能性的大小可以用分数来表示。

具体地，把几种可能的情况的份数相加做分母，单一的这种可能性做分子，即可求出相应事件发生的可能性大小。

2. 计算实例：如在一个盒子里装有3个红球、6个黄球、1个蓝球，求摸出每种颜色球的可能性。

此时，分母为3（红球）+6（黄球）+1（蓝球）=10，摸出红球的可能性为3/10，摸出黄球的可能性为6/10（即3/5），摸出蓝球的可能性为1/10。

四、可能性的应用1. 设计游戏规则：在设计游戏规则时，可以利用可能性的大小来保证游戏的公平性。

例如，设计一个转盘游戏，将转盘分成若干等份，分别涂上不同的颜色，根据颜色区域的大小来确定转到不同颜色的可能性大小，从而制定相应的游戏规则。

2. 做出决策：在生活中，可以根据可能性的大小来做出决策。

例如，天气预报说明天有80%的可能性会下雨，那么我们可以考虑带上雨具出门。

五、可能性的进一步理解1. 必然事件与不可能事件：在一定条件下，一定会发生的事件称为必然事件，其发生的可能性为1；在一定条件下，一定不会发生的事件称为不可能事件，其发生的可能性为0。

北京课改版五年级数学上册知识手册学校________________班级________________姓名________________一小数乘法一、小数乘整数1.积的变化规律:(1)一个因数不变,另一个因数扩大到原来的几倍(或缩小到原来的几分之几),它们的积也扩大到原来的几倍(或缩小到原来的几分之几)。

(2)如果一个因数扩大到原来的几倍,另一个因数缩小到原来的几分之几 ,它们的积不变。

2.小数乘整数的计算方法:先按整数乘法算出积,再看因数中一共有几位小数,有几位小数,就从积的右边起数出几位,点上小数点。

如果积的小数部分末尾有0,可以把0去掉,把小数化简。

二、小数乘小数1.小数乘小数的计算方法:(1)按照整数乘法的计算方法算出积。

(2)看因数中一共有几位小数,有几位小数,就从积的右边起数出几位,点上小数点。

(3)如果积的小数位数不够,就在积的前面用0补位。

(4)如果积的小数部分末尾有0,可以把0去掉。

2.因数与积的大小关系:一个因数大于．．．．．．1,．．积大于另一个因．．．．．．．重点提示:小数乘整数的意义与整数乘法的．．．．．．．．．．．．．．意义相同．．．．,．都是求几个相同加数的和的简便运算。

要点提示:小数乘整数的积的末尾有0时,一定要先点积中的小数点．．．．．．．．,．再去掉小数部．．．．．．分末尾的．．．．0．。

．知识巧记:小数乘法并不难,关键点好小数点;因数小数位数和,等同积中小数位;积中位数如不够,用0补足再点点;如果因数不为0,一个因数大于1,另一个因数小于积;一个因数小于1,二小数除法一、小数除法的计算方法1.小数除以整数的计算方法。

按照整数除法的计算方法进行计算;商的小数点要与被除数的小数点对齐;如果被除数小于除数,个位上不够商1,应在商的个位上写0占位,点上商的小数点后继续除;如果除到被除数的末尾仍有余数,要在后面添0继续除;除到哪一位不够除时,要在商的那一位上写0占位,然后继续除。

五年级数学上册第四单元的必背知识点一、可能性1. 事件发生的三种情况：可能发生不可能发生一定发生2. 可能性大小的计算：计算方法：把几种可能的情况的份数相加做分母，单一的这种可能性做分子，即可求出相应事件发生可能性大小。

二、图形面积1. 图形面积的比较：借助方格纸能直接判断图形面积的大小。

图形面积相同，其形状可以是不同的。

2. 不规则图案面积的计算：数方格法：直接通过数方格的方法得出答案的面积。

“化整为零”法：将整体的图案分割为若干个相同面积的小图案，通过求小图案的面积，得出整个图案的面积。

“大面积减小面积”法：通过计算相关图形的面积，得到所求的面积。

三、平面图形的认识与面积计算1. 平行四边形：底和高的定义：从平行四边形一边的某一点到对边画垂直线段，这条垂直线段就是平行四边形的高，这条对边是平行四边形的底。

面积公式：平行四边形面积= 底× 高，用字母表示为S = ah。

2. 三角形：底和高的定义：三角形的一个顶点到对边的垂直线段是三角形的高，这条对边是三角形的底。

面积公式：三角形面积= 两个相同三角形拼成的平行四边形的面积÷ 2 = 底× 高÷ 2，用字母表示为S = ah ÷ 2。

3. 梯形：底和高的定义：从梯形的两条平行线中的一条上的某一点到对边画垂直线段，这条垂直线段就是梯形的高，这条对边就是梯形的底。

面积公式：梯形面积= 两个相同梯形拼成的平行四边形的面积÷ 2 = (上底+ 下底) × 高÷ 2，用字母表示为S =(a + b)h ÷ 2。

四、运算定律与公式1. 加法运算定律：加法交换律：a + b = b + a加法结合律：(a + b) + c = a + (b + c)2. 乘法运算定律：乘法交换律：a × b = b × a乘法结合律：(a × b) × c = a × (b × c)乘法分配律：(a + b) × c = a × c + b × c 或a × c + b × c =(a + b) × c (b=1时，省略b)3. 用字母表示计算公式：长方形的周长公式：c = (a + b) × 2长方形的面积公式：s = ab五、方程与数量关系1. 方程的定义：含有未知数的等式称为方程。

五年级数学上册《统计与可能性》知识点
汇总
五年级数学上册《统计与可能性》知识点汇总
1、平均数=总数量÷总份数
2、中位数的优点是不受偏大或偏小数据的影响，用它代表全体数据的一般水平更合适。

3、求一组数据中位数的方法：
先将这一组数据按照大小顺序排列好，如果这一组
数据是单数个，中间的数就是这一组数据的中位数，如
果这一组数据是双数个，中间两个数的和除以2就是这
一组数据的中位数。

数学广角
1、数不仅可以用来表示数量和顺序，还可以用来编码。

2、邮政编码：由6位数组成，前2位表示省（直辖市、自治区），前3位表示邮区，前4位表示县（市），最后2位表示投递局。

3、身份证号码：18位
前六位表示省（自治区、直辖市）、市、县，7—14位表示出生年月日，倒数第二位的数字用来表示
性别，单数表示男，双数表示女，最后一位是校验码。

四统计图表与可能性一、统计表1.认识复式统计表。

某电器连锁店2011年四种家用电器销售情况统计表2012年2月为了便于分析和比较,有时需要把几个有联系的简单统计表合并成一个比较复杂的统计表,即复式统计表。

是表头,店别表示竖栏的类别;种类表示横栏的类别,即四种家用电器的名称;销售额/万元表示栏中的数据。

“合计”是指两家分店每种家用电器的销售总额。

2.简单统计表和复式统计表的联系与区别。

提示: 如果表头中已标明单位名称,填写栏中数据时不需要加单位名称;如果没有标明,填写栏中数据时,数据后要加单位名称。

重点提示: 计算时,将同一竖栏中的数据合在一起,填在对应竖栏的合计处。

区别:简单统计表只对某一项目的数量．．．．．．．．．．．．．．进行统计．．．．;．复式统计表的统计项目在两个或．．．．．．．．．．．．．．两个以上。

复式统．．．．．．．．计表的表内部分比简单统．．．．．．．．．．．计表的表内部分复杂。

．．．．．．．．．．联系:都分为表外和表内两部分．．．．．．．．．．．,．表外部．．．分都包括统计表的名称和制作时间。

．．．．．．．．．．．．．．．．二、平均数求较复杂的平均数的方法: 先求出每组数据的总数量．．．．．．．．．．．(．用每组数据．．．．．的平均数．．．．×．数据个数．．．．),．．然后求出全部数据的．．．．．．．．．总数量及总份数．．．．．．．,．最后用“总数量．．．．．．．÷．总份．．数”求出平均数。

．．．．．．．．三、统计图认识并绘制复式统计图: 1复式条形统计图: 用两种(或两种以上)直条表示不同数量的条形统计图,称为复式条形统计图。

方法总结: 总数量÷总份数=平均数平均数×总份数=总数量总数量÷平均数=总份数提示: 1.画直条时,一般先画一种直条,再画另一种直条。

2.在绘制复式条形统计图时,要写出统计图的名称和制图时间,并注2.复式条形统计图的绘制方法: 与单式条形统计图的绘制方法基本相同,只是每组中表示两组(或两组以上)数据,需要用不同颜色(或底纹)的直条来表示,同时要注明图例。

小学数学北京版新五年级上册《统计表表与可能性》教案教学目标一、知识与技能1.经历可能性的试验过程，知道事件发生的可能性与数量多少有关。

2.结合生活实际，体会生活中事件发生的不确定性。

二、过程与方法1.培养学生通过实验获取数据、利用数据进行猜测与推理的能力；并能列出简单试验所有可能发生的结果。

2.培养学生合作学习和数学应用的意识。

三、情感态度和价值观1.体会数学与生活的联系，经历统计的全过程，进一步认识统计的意义。

2.体会数学与生活的联系，培养学生的创新意识。

教学重点学生通过试验、收集和分析试验数据知道事件发生的可能性是有大小的。

教学难点利用可能性的知识解决实际问题。

教学方法“自主探究”教学模式、小组合作课前准备多媒体课件、使用“学乐师生”APP拍照，和同学们分享课时安排第 4 课时教学过程一、导入新课（一）创设游戏情境，初步感受游戏公平的重要性。

1、猜球比赛（袋子里装有 4 个红球、 1 个黄球）师：（出示袋子）老师在袋子里装了一些球，你们想不想进行一次摸球比赛？（1）、规则：全班分两组，男生一组、女生一组，男女生各派10 个代表摸球，每人各摸1次。

摸到红球多算女生赢、摸到黄球多算男生赢，其余学生记录每次摸球的结果。

看看会有什么果出？（2）、可要有方法，你想用怎方法行呢？（学生介）（3）、匀袋子，男女生依次摸球；同桌合作：一人，另一人督他的是否正确。

（指名一上台）摸到球几次？摸到黄球几次 ?： ?女生，在大家把烈的掌声送她。

（4）、男生好像有些疑惑了，想什么？你怎么得不公平了？（5）、（出示袋子里的球）如果再摸下去，果会怎呢？什么？体会：球个数比黄球多，所以摸球的可能性大，摸黄球的可能性小，也就是女生的可能性比男生大。

男生想些什么？2.揭示：你用了一个“公平”，到底怎的游是公平、合理的呢？今天，我就一同研究、出一份公平的游。

二、新学1、想想：怎改口袋里黄球的个数，使得比得公平呢？2、老也每准了一些球，你先想想装球的方法再合作装一装黄球的个数，使得游得公平。

统计图与可能性总结
一·统计图
1.三种统计图得比较：用点、线、面等来表示相关联的量之间的关系的图形，
叫做统计图。

常见的统计图有条形统计图、折线统计图、扇形统计图三种。

2.统计图结构如下：
统计图
1.复式折线统计图：
制作：与复式条形统计图的步骤基本相同
特点：能表示数量的多少级增减变化情况
作用：分析、决策
2.扇形统计图：
制作：1.算个部分所占百分数；2.算各部分的扇形的圆角；3.在圆里画出各个扇形；4.标注各部分名称、百分数。

特点：表示部分数量与总数量的关系
3.统计图的绘制：
绘制条形统计图：A。

整理数据，会看统计表；B。

画出横轴、纵轴，用一个长度单位表示一定的数量；C。

根据数量的多少画成宽一样、长不
同的直条，并按一定的顺序排列起来；D。

写出统计图的名称、制图日
期，并标出图例。

折线统计图：A。

整理数据；B。

画出纵轴和横轴，用一个长度单位表示一定的数量；C。

根据数量的多少描出各点，再把各点用线段顺次连接
起来；D。

写出统计图的名称、制图日期，并标出图例。

绘制扇形统计图：A。

现正确计算统计图的各部分占总数得百分比；B。

去适当半径画个圆用量角器画出扇形的圆角，做出扇形；C。

注明各扇形，表示的内容和所占的百分比并用不同标记加以区别；D。

写上标题及制图日期。

可能性
可能性表示一件事情或物体的结果的可能占所有可能的多少。

可能性用数字表示通常以分数表示，而文字通常有3个答案：一定、可能、不可能。