MATLAB讲义第五、六章

本讲义详细介绍了控制系统的matlab仿真与设计，重点围绕控制系统CAD和经典控制理论CAD展开。在控制系统固有特性分析方面，讲义首先探讨了时域分析，通过二阶系统闭环传函的标准形式，分析了阻尼比变化对系统闭环极点位置的影响，并展示了simulink的仿真结果。此讲义深入探讨了频域分析，介绍了频率特性法的基本概念和实用价值，详细阐述了伯德图、奈奎斯特图和尼克尔斯图等频率特性图的应用。特别是，通过伯德图命令的详细示例，展示了如何生成幅频特性和相频特性图，并提供了相应的matlab代码。这些分析方法和示例代码，有助于读者深入理解和掌握控制系统的matlab仿真与设计技术。

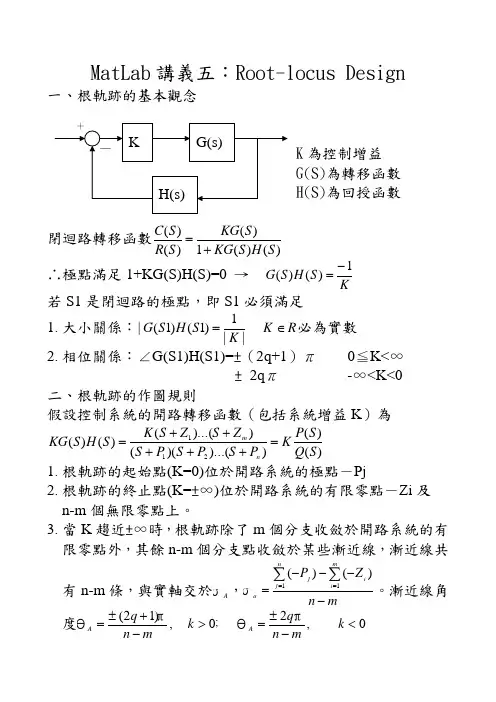
MatLab 講義五：Root-locus Design一、根軌跡的基本觀念K 為控制增益 G(S)為轉移函數H(S)為回授函數閉迴路轉移函數)()(1)()()(S H S KG S KG S R S C +=∴極點滿足1+KG(S)H(S)=0 → KS H S G 1)()(-=若S1是閉迴路的極點，即S1必須滿足1. 大小關係：||1)1()1(|K S H S G = R K ∈必為實數2. 相位關係：∠G(S1)H(S1)=±（2q+1）π 0≦K<∞ ± 2q π -∞<K<0 二、根軌跡的作圖規則假設控制系統的開路轉移函數（包括系統增益K ）為)()())...()(())...(()()(211S Q S P KP S P S P S Z S Z S K S H S KG n m =+++++= 1. 根軌跡的起始點(K=0)位於開路系統的極點－Pj 2. 根軌跡的終止點(K=±∞)位於開路系統的有限零點－Zi 及n-m 個無限零點上。

3. 當K 趨近±∞時，根軌跡除了m 個分支收斂於開路系統的有限零點外，其餘n-m 個分支點收斂於某些漸近線，漸近線共有n-m 條，與實軸交於A σ，mn Z P nj mi i j a ----=∑∑==11)()(σ。

漸近線角度0,20,)12(<-±=>-+±=k mn q k m n q A A π；　θ　πθ 4. 根軌跡兩分支或兩分支以上相交的點稱為分離點。

分離點滿足0)()(=dSS H S dG 5. 根軌跡與S 平面上虛軸的交點，可由系統閉迴路方程式)()()(S KP S Q S +=∆建立羅斯表，令某列為零為K ，代入輔助方程解得純虛根即為所求。

二、根軌跡的推廣觀念與變化型1. 由特性方程式→改寫為1+KG(S)=0，定義G(S)為單位開迴路轉移函數，利用此來做根軌跡。

例5-12 根据输入参数的个数将例5-11中参数个数使用 varargin和varargout函数，绘制不同线型的曲线，绘制的 曲线与图5-6相同。 function varargout=ex5_12(varargin) x=0:10; lin=length(varargin); %取输入参数个数 在命令窗口中输入 y=lin*ones(11,1); 调用命令： hold on >> y=ex5_12('y','o') if lin==0 varargout = plot(x,y) [2] elseif lin==1 y= plot(x,y,varargin{1}) 2 else >> ex5_12('y','o') plot(x,y,[varargin{1} varargin{2}]) varargout = end [2] varargout{1}=lin ans = 2
5.3.2 函数的输入输出参数
1. 参数的传递 函数的参数传递是将主调函数中的变量值 传给被调函数的输入参数 （1）函数参数传递的是数值 （2）被调函数的输入参数是存放在函数 的工作空间中，与MATLAB的工作空间是 独立的，当调用结束时函数的工作空间被清 除，输入参数也被清除。
2. 输入输出参数的个数
例5-2 使用switch结构判断学生成绩的等级，90分以上 为优，80～90为良，70～80为中，60～70为及格，60分以 下为不及格。
>> score=98; >> s1=fix(score/10); >> switch s1 case {9,10} s='优' case 8 s='良' case 7 s='中' case 6 s='及格' otherwise s='不及格' end

由Cleve Moler和John Little于1980 年代初期开发，用于解决线性代数课 程的数值计算问题。
MATLAB的优势
易于学习、使用灵活、高效的数值计 算和可视化功能、强大的工具箱支持。
发展历程
从最初的数值计算工具，逐渐发展成 为一款功能强大的科学计算软件，广 泛应用于工程、科学、经济等领域。
MATLAB工作环境与界面
MATLAB工作环境
包括命令窗口、工作空间、命令历史窗口、当 前文件夹窗口等。
界面介绍
详细讲解MATLAB界面的各个组成部分，如菜 单栏、工具栏、编辑器窗口等。
基本操作
介绍如何在MATLAB环境中创建、保存、运行脚本和函数，以及如何进行基本 的文件操作。
基本数据类型与运算
矩阵大小
使用`size`函数获取矩阵的行数 和列数。
矩阵元素访问
通过下标访问矩阵元素，如 `A(i,j)`表示访问矩阵A的第i行第j 列元素。
矩阵基本操作
包括矩阵的加、减、数乘、转置 等操作。
矩阵运算及性质
矩阵乘法 满足乘法交换律和结合律，但不满足 乘法交换律。
矩阵的逆
对于方阵，若存在一矩阵B，使得 AB=BA=I（I为单位矩阵），则称B 为A的逆矩阵。
Hale Waihona Puke 03 数据分析与可视化数据导入、导出及预处理
数据导入
介绍如何使用MATLAB导入各种格式的数据文件， 如.csv、.txt、.xlsx等。
数据导出
讲解如何将MATLAB中的数据导出为常见的数据文件格式，以 便于数据共享和交换。
数据预处理
阐述数据清洗、数据变换、数据规约等预处理技术，为后续的数 据分析和可视化奠定基础。
01
02

图5-4中间的下拉框可以选择拟合算法，可以 试用多种拟合算法，以找出最佳拟合图形。例 如选择Smoothing Spline（平滑样条函数）， 观察Curve Fitting Tool窗口，如图5-5所示。
图5-5 拟合曲线
第5章 MATLAB数值计算
第5章 MATLAB数值计算
5.4.4 图形窗口的拟合和统计工具
第5章 MATLAB数值计算
在图5-6中的“绘制拟合图”中选择拟合方 法（可同时选多种）；
“显示方程”复核框可以选择是否在图形上 显示拟合多项式；
“绘制残差图”复核框选中时会产生第二幅 图形，该图形显示了每一个数据点与计算出来的 拟合曲线之间的距离。
例如选择“线性”和“三次方”拟合方法， 同时选中两个复核框，产生图形如图5-7所示。
MATLAB的图形窗口中提供了简单方便的数 据拟合和基本统计工具。
数据拟合工具可以对所绘制的曲线使用多种 方法进行拟合；
基本统计工具可提供最小值、最大值、平均 值、中位值、标准差、数据范围等统计运算。
1．数据拟合工具
第5章 MATLAB数值计算
使用数据拟合工具首先需要创建一幅图形，在 命令行窗口输入以下程序：
两个矩阵x和y的相关系 数
第5章 MATLAB数值计算
5.2 数值运算 一、 多项式
名称
创建多项 式
求根
求值
多项式乘 法
多项式除 法
多项式求 导
函数格式 P=[ a0 a1 a2 …an-1
an] P=poly(A) roots(P) polyval(P，A)
polyvalm(P,m)
说明
P为多项式（以下各函数中P均为多项式），a0 a1 a2 … an-1 an为按降幂顺序排列的多项式系数 A为向量。创建以向量A中元素为根的多项式

《MA TLAB软件应用》讲义[第2 / 16次课]第1章基础准备及入门一点名二作业讲评三复习提问MATLAB界面由几大组件组成？MATLAB的搜索路径主要有什么应用途径？四上机练习内容启动MATLAB。

在D盘根目录下，以“学号_姓名”的格式创建文件夹，并在Matlab中将该目录设置为Current Folder。

（利用MA TLAB Toolbar中Current Folder组合框后的按钮）。

以下为本章教学必须掌握的知识点。

在MA TLAB的Command Window中练习以下代码，并观察系统输出，并逐行进行注释。

本次课结束后将代码文件上传。

在MA TLAB程序界面中进行以下操作：1 上机实习内容提示及要求启动MATLAB后，依次练习MA TLAB的菜单项、工具栏和Command Window、Current Folder、Command History、Workspace等主要组件的基本功能，按指定内容在MA TLAB程序界面下进行操作练习。

2 上机实习内容在MATLAB程序界面中进行以下操作：1) Command Window指令窗口在集成窗体和独立窗体之间切换（Undock/Dock按钮）2) 在Command Window中运行以下指令，掌握换行符(...)的使用>> (12+2*(7-4))/3^2>> S=1-1/2+1/3-1/4+1/5-1/6+1/7-1/8>> S=1-1/2+1/3-1/4+…+1/5-1/6+1/7-1/83）在Command Window中分别输入以下数值，并按回车，观察MA TLAB的输出（数值如3, -99, 0.001, 9.456, 1.3e-3, 4.5e33, eps, 等）4）以下实例涉及变量的定义规则，在Command Window中分别输入并按回车，观察MA TLAB的输出结果.输出结果为错误提示时,分析出现错误的原因.>> xyz_4=32.75>> var1=3.09e-5*1028>> 4xyz=32.75>> 4*xyz=198.28>>4,xyz=198.285) 在Command Window中输入下列数学常数，并按回车：eps, i, j, Inf, inf, intmax, NaN, nan, pi, realmax, realmin，观察并分析系统的输出。

4
5.1 概述
根据程序运行方式的不同，可以将MATLAB程序设计分为
两种方式：
一种是在命令窗口中逐条输入命令，另一种是将相关
的命令存储在一个M文件中。
前者称为命令行方式，又称为指令驱动模式。后者称
为M文件的程序运行方式。
命令行方式 M文件编程方式 命令逐条解释执行 自动一次执行完文件中所有命令 简单，直观 不直观 速度慢，执行过程不能保留， 速度快，可以重复执行文件 不能重复执行
25
2、while语句
while语句的一般格式为： while 表达式 循环体语句 end while语句为条件循环语句，循环次数不确定，只要循环条件
表达式的结果非零，语句体就重复执行，直到循环条件表达 式的结果为零，则跳出循环
26
5.3.4 程序流的控制
与控制程序执行过程相关的语句主要有break语句、
5.3 MATLAB程序结构
MATLAB程序的控制结构有3种：
顺序结构、选择结构和循环结构。
按照程序设计的观点, 任何算法功能都可以通过由程序模
块组成的三种基本程序结构的组合来实现。
11
5.3.1 顺序结构
顺序结构是指程序按程序语句或模块在执行流中的顺序逐
个执行，直到执行到程序的最后一个语句。
函数式M文件 接受输入参数，有返回值 文件中定义变量为局部变量， 文件执行完毕时，局部变量 清除，不保留在工作空间
要通过函数调用的方式调用 才能运行 用户需要自定义某种具体算 法时使用
5.2.3 M文件操作
对M文件常用的操作有：打开M文件、新建M文件、编辑
M文件、保存M文件和运行M文件等。
10
例5.8：判断读取矩阵是否正确。 解：程序如下 n=4; a=magic(3) try a_n=a(n,:), %取a的第n 行元素 catch a_n=a(end, : ), %如取a的第n 行出错，则改取a的最后一行 end lasterr %显示出错原因 执行结果如下; a= 8 1 6 3 5 7 4 9 2 a_n = 9 2 ans = Attempted to access a(4,:); index out of bounds because size(a)=[3,3].

《MATLAB教案》PPT课件第一章：MATLAB概述1.1 MATLAB简介介绍MATLAB的历史和发展解释MATLAB的含义（Matrix Laboratory）强调MATLAB在工程和科学计算中的应用1.2 MATLAB界面介绍MATLAB的工作空间解释MATLAB的菜单栏和工具栏演示如何创建、打开和关闭MATLAB文件1.3 MATLAB的基本操作介绍MATLAB的数据类型演示如何进行矩阵运算解释MATLAB中的向量和矩阵运算规则第二章：MATLAB编程基础2.1 MATLAB脚本编程解释MATLAB脚本文件的结构演示如何编写和运行MATLAB脚本强调注释和代码的可读性2.2 MATLAB函数编程介绍MATLAB函数的定义和结构演示如何创建和使用MATLAB函数强调函数的重用性和模块化编程2.3 MATLAB编程技巧介绍变量和函数的命名规则演示如何进行错误处理和调试强调代码的优化和性能提升第三章：MATLAB数值计算3.1 MATLAB数值解算介绍MATLAB中的数值解算工具演示如何解线性方程组和不等式解释MATLAB中的符号解算和数值解算的区别3.2 MATLAB数值分析介绍MATLAB中的数值分析工具演示如何进行插值、拟合和数值积分解释MATLAB中的误差估计和数值稳定性3.3 MATLAB优化工具箱介绍MATLAB优化工具箱的功能演示如何使用优化工具箱进行无约束和约束优化问题解释MATLAB中的优化算法和参数设置第四章：MATLAB绘图和可视化4.1 MATLAB绘图基础介绍MATLAB中的绘图命令和函数演示如何绘制二维和三维图形解释MATLAB中的图形属性设置和自定义4.2 MATLAB数据可视化介绍MATLAB中的数据可视化工具演示如何绘制统计图表和散点图解释MATLAB中的数据过滤和转换4.3 MATLAB动画和交互式图形介绍MATLAB中的动画和交互式图形功能演示如何创建动画和交互式图形解释MATLAB中的图形交互和数据探索第五章：MATLAB应用案例5.1 MATLAB在信号处理中的应用介绍MATLAB在信号处理中的基本概念演示如何使用MATLAB进行信号处理操作解释MATLAB在信号处理中的优势和应用场景5.2 MATLAB在控制系统中的应用介绍MATLAB在控制系统中的基本概念演示如何使用MATLAB进行控制系统分析和设计解释MATLAB在控制系统中的优势和应用场景5.3 MATLAB在图像处理中的应用介绍MATLAB在图像处理中的基本概念演示如何使用MATLAB进行图像处理操作解释MATLAB在图像处理中的优势和应用场景《MATLAB教案》PPT课件第六章：MATLAB Simulink基础6.1 Simulink简介介绍Simulink作为MATLAB的一个集成组件解释Simulink的作用：模型化、仿真和分析动态系统强调Simulink在系统级设计和多领域仿真中的优势6.2 Simulink界面介绍Simulink库浏览器和模型窗口演示如何创建、编辑和运行Simulink模型解释Simulink中的块和连接的概念6.3 Simulink仿真介绍Simulink仿真的基本过程演示如何设置仿真参数和启动仿真解释Simulink仿真结果的查看和分析第七章：MATLAB Simulink高级应用7.1 Simulink设计模式介绍Simulink的设计模式，包括连续、离散、混合和事件驱动模式演示如何根据系统特性选择合适的设计模式解释不同设计模式对系统性能的影响7.2 Simulink子系统介绍Simulink子系统的概念和用途演示如何创建和管理Simulink子系统解释子系统在模块化和层次化设计中的作用7.3 Simulink Real-Time Workshop介绍Simulink Real-Time Workshop的功能演示如何使用Real-Time Workshop进行代码解释代码对于硬件在环仿真和嵌入式系统开发的重要性第八章：MATLAB Simulink库和工具箱8.1 Simulink库介绍Simulink库的结构和分类演示如何访问和使用Simulink库中的块解释Simulink库对于模型构建和功能复用的意义8.2 Simulink工具箱介绍Simulink工具箱的概念和功能演示如何安装和使用Simulink工具箱解释Simulink工具箱在特定领域仿真和分析中的作用8.3 自定义Simulink库介绍如何创建和维护自定义Simulink库演示如何将自定义块添加到库中解释自定义库对于个人和组织级模型共享的重要性第九章：MATLAB Simulink案例分析9.1 Simulink在控制系统中的应用介绍控制系统模型在Simulink中的构建演示如何使用Simulink进行控制系统设计和分析解释Simulink在控制系统教育和研究中的应用9.2 Simulink在信号处理中的应用介绍信号处理模型在Simulink中的构建演示如何使用Simulink进行信号处理仿真解释Simulink在信号处理领域中的优势和实际应用9.3 Simulink在图像处理中的应用介绍图像处理模型在Simulink中的构建演示如何使用Simulink进行图像处理仿真解释Simulink在图像处理领域中的优势和实际应用第十章：MATLAB Simulink项目实践10.1 Simulink项目实践流程介绍从需求分析到模型验证的Simulink项目实践流程演示如何使用Simulink进行项目规划和实施解释Simulink在项目管理和协作中的作用10.2 Simulink与MATLAB的交互介绍Simulink与MATLAB之间的数据交互方式演示如何在Simulink中使用MATLAB函数和脚本解释混合仿真模式对于复杂系统仿真的优势10.3 Simulink项目案例分析具体的Simulink项目案例演示如何解决实际工程问题解释Simulink在工程教育和项目开发中的应用价值《MATLAB教案》PPT课件第十一章：MATLAB App Designer入门11.1 App Designer简介介绍App Designer作为MATLAB中的应用程序开发环境解释App Designer的作用：快速创建跨平台的MATLAB应用程序强调App Designer在简化MATLAB代码部署和用户交互中的优势11.2 App Designer界面介绍App Designer的用户界面和工作流程演示如何创建新应用和编辑应用界面解释App Designer中的组件和布局的概念11.3 App Designer编程介绍App Designer中的MATLAB编程模式演示如何使用App Designer中的MATLAB代码块解释App Designer中事件处理和应用程序生命周期管理的重要性第十二章：MATLAB App Designer高级功能12.1 App Designer用户界面设计介绍App Designer中用户界面的定制方法演示如何使用样式、颜色和主题来美化应用界面解释用户界面设计对于提升用户体验的重要性12.2 App Designer数据模型介绍App Designer中的数据模型和模型视图概念演示如何创建、使用和绑定数据模型和视图解释数据模型在应用程序中的作用和重要性12.3 App Designer部署和分发介绍App Designer应用程序的部署和分发流程演示如何打包和发布应用程序解释如何为不同平台安装和运行App Designer应用程序第十三章：MATLAB App Designer案例研究13.1 图形用户界面(GUI)应用程序设计介绍使用App Designer设计的GUI应用程序案例演示如何创建交互式GUI应用程序来简化MATLAB脚本解释GUI应用程序在数据输入和结果显示中的作用13.2 数据分析和可视化应用程序设计介绍使用App Designer进行数据分析和可视化的案例演示如何创建应用程序来处理和显示大型数据集解释App Designer在数据分析和决策支持中的优势13.3 机器学习和深度学习应用程序设计介绍使用App Designer实现机器学习和深度学习模型的案例演示如何将MATLAB中的机器学习和深度学习算法集成到应用程序中解释App Designer在机器学习和深度学习应用部署中的作用第十四章：MATLAB App Designer实战项目14.1 App Designer项目规划和管理介绍App Designer项目的规划和管理方法演示如何组织和维护大型应用程序项目解释项目管理和版本控制对于团队协作的重要性14.2 App Designer与MATLAB的集成介绍App Designer与MATLAB之间的数据和功能集成演示如何在App Designer中调用MATLAB函数和脚本解释集成MATLAB强大计算和分析能力的重要性14.3 App Designer项目案例实现分析具体的App Designer项目案例实现过程演示如何解决实际工程项目中的问题解释App Designer在工程项目实践中的应用价值第十五章：MATLAB App Designer的未来趋势15.1 App Designer的新功能和技术介绍App Designer的最新功能和技术发展演示如何利用新功能和技术提升应用程序的性能和用户体验强调持续学习和适应新技术的重要性15.2 App Designer在跨平台开发中的应用介绍App Designer在跨平台应用程序开发中的优势演示如何创建适用于不同操作系统的应用程序解释跨平台开发对于扩大应用程序市场的重要性15.3 App Designer的未来趋势和展望讨论App Designer在未来的发展趋势和潜在应用领域激发学生对于应用程序开发和创新的兴趣强调持续探索和创造新应用的重要性重点和难点解析本文档为您提供了一份详尽的《MATLAB教案》PPT课件，内容涵盖了MATLAB 的基本概念、编程基础、数值计算、绘图和可视化、应用案例、Simulink的基础知识、高级应用、库和工具箱的使用、案例分析以及项目实践、App Designer 的基础知识、高级功能、案例研究、实战项目和未来趋势等方面的内容。

要退出Matlab系统，也有3种常见方法： (1) 在Matlab主窗口File菜单中选择Exit Matlab命令。 (2) 在Matlab命令窗口输入Exit或Quit命令。 (3) 单击Matlab主窗口的“关闭”按钮。
2013-8-21
17
1.3.2 主窗口及子窗口
Matlab主窗口是Matlab的主要工作界面。主窗口除了嵌入一些子 窗口外，还主要包括菜单栏和工具栏。 1．菜单栏 在Matlab 6.5主窗口的菜单栏，共包含File、Edit、View、Web、 Window和Help 6个菜单项。 (1) File菜单项：File菜单项实现有关文件的操作。 (2) Edit菜单项：Edit菜单项用于命令窗口的编辑操作。 (3) View菜单项：View菜单项用于设置Matlab集成环境的显示方 式。 (4) Desktop菜单项：在MATLAB中，Desktop主菜单用于设置工作 空间和工具栏等的显示项。单击Desktop主菜单或按下快捷键 Alt+D，可以弹出Desktop下拉菜单。 (5) Window菜单项：主窗口菜单栏上的Window菜单，只包含一个 子菜单Close all，用于关闭所有打开的编辑器窗口，包括Mfile、Figure、Model和GUI窗口。 (6) Help菜单项：Help菜单项用于提供帮助信息。
2013-8-21
10
1.2.2 Matlab的安装
安装Matlab 7.0系统，需运行系统自带的安装程序setup.exe,一般只
要用鼠标双击安装图标，就会启动安装程序,你只需按照安装提示 正确输入（或粘贴）安装序列号后点击《确认》键，并按提示修改 安装路径（或默认安装到C盘）就能完成安装。 安装完毕后，在开始-程序-Matlab.exe菜单中,双击Matlab图标,即可 运行程序。

6.3.2 仿真结果分析 为了观察仿真结果的变化轨迹可以采用3种方法。 （1）把输出结果送给Scope模块或者XY Graph模块。 Scope模块显示系统输出量对于仿真时间的变化曲线，XY Graph模块显示送到该模块上的两个信号中的一个对另一 个的变化关系。 （2）把仿真结果送到输出端口并作为返回变量，然后使用 MATLAB命令画出该变量的变化曲线。 （3）把输出结果送到To Workspace模块，从而将结果直接 存入工作空间，然后用MATLAB命令画出该变量的变化曲 线。
（3）保存选项（Save options） 在保存选项栏中的“Format”下拉列表中有矩阵、结构和包 含时间的结构3种选择。“Limit data points to last”用来限 定保存到工作空间中的数据的最大长度。 输出选项（Output options）有： ① Refine output（细化输出） output ② Produce additional output（产生附加输出） ③ Produce specified output only（仅在指定的时刻产生输 出）
6.3.3 系统仿真实例 【例6.3】有初始状态为0的二阶微分方程 y" + 1.5y' + 10y = 2u'(t) + 10u(t)，其中u(t)是单位阶跃函数，试建立 系统模型并仿真。 方法1：用微分/积分器直接构造求解微分方程的模型。 把原微分方程改写为 y" = 2u' (t) + 10u(t) − 1.5y' − 10y u经微分作用得u'，y"经积分作用得y'，y'再经积分模块作用就得y，而u'、 u、y'和y经代数运算又产生y"，据此可以建立系统模型并仿真。 （1）利用Simulink模块库中的基本模块建立系统模型 （2）设置系统仿真参数。 在模型编辑窗口的 Simulation stop time栏把仿 真的停止时间设置为5。 （3）仿真操作。

SIMULINK库浏览器：SIMULINK是一个仿真工具，它不是MATLAB的一个部分 ，所有如果您没有安装SIMULINK，就不会有此图标。
在线帮助：此图标打开MATLAB的在线帮助窗口，您可以一路单击所要的类别或 命令，直到得到所需要的帮助信息。
中北大学 信息与通信工程学院
1.3 MATLAB 第六版外观
交互界面分类目录窗口
View | Profiler
程序性能解析窗口
中北大学 信息与通信工程学院
1.3 MATLAB 第六版外观
mand Window 命令窗口是MATLAB操作最主要的窗口。在这个窗口中可以键入各种MATLAB的 命令、函数、表达式，并显示除图形以外的所有结果。命令窗口的每一行前有提 示符>>。命令窗口内显示的字符和数值采用不同的颜色。输入的命令、表达式和 计算结果采用黑色字体，字符串用红色，if ，for等关键词采用蓝色。MATLAB 把命令窗口中输入的命令都记录在Command History中，因此MATLAB的命令 窗口不仅可以对输入的命令编辑和运行，而且可以对已输入的命令进行回调、编 辑、重新运行。 2. Command History 历史命令窗口出现在MATLAB界面的左下方，用来记录并显示已运行的命令、函 数、表达式，并允许用户对它们进行选择、复制和重运行。用户可以方便地输入 和修改长命令，选择多行命令产生M文件。
进 入 夏 天 ，少 不了一 个热字 当头， 电扇空 调陆续 登场， 每逢此 时，总 会想起 那 一 把 蒲 扇 。蒲扇 ，是记 忆中的 农村， 夏季经 常用的 一件物 品。 记 忆 中 的故 乡 ， 每 逢 进 入夏天 ，集市 上最常 见的便 是蒲扇 、凉席 ，不论 男女老 少，个 个手持 一 把 ， 忽 闪 忽闪个 不停， 嘴里叨 叨着“ 怎么这 么热” ，于是 三五成 群，聚 在大树 下 ， 或 站 着 ，或随 即坐在 石头上 ，手持 那把扇 子，边 唠嗑边 乘凉。 孩子们 却在周 围 跑 跑 跳 跳 ，热得 满头大 汗，不 时听到 “强子 ，别跑 了，快 来我给 你扇扇 ”。孩 子 们 才 不 听 这一套 ，跑个 没完， 直到累 气喘吁 吁，这 才一跑 一踮地 围过了 ，这时 母 亲总是 ，好似 生气的 样子， 边扇边 训，“ 你看热 的，跑 什么？ ”此时 这把蒲 扇， 是 那 么 凉 快 ，那么 的温馨 幸福， 有母亲 的味道 ！ 蒲 扇 是 中 国传 统工艺 品，在 我 国 已 有 三 千年多 年的历 史。取 材于棕 榈树， 制作简 单，方 便携带 ，且蒲 扇的表 面 光 滑 ， 因 而，古 人常会 在上面 作画。 古有棕 扇、葵 扇、蒲 扇、蕉 扇诸名 ，实即 今 日 的 蒲 扇 ，江浙 称之为 芭蕉扇 。六七 十年代 ，人们 最常用 的就是 这种， 似圆非 圆 ， 轻 巧 又 便宜的 蒲扇。 蒲 扇 流 传 至今， 我的记 忆中， 它跨越 了半个 世纪， 也 走 过 了 我 们的半 个人生 的轨迹 ，携带 着特有 的念想 ，一年 年，一 天天， 流向长

聚合矩阵的特殊函数
下表列出了聚合矩阵的一些特殊函数。
函数
cat horzcat vertcat repmat blkdiag
描述
沿指定的维聚合矩阵 水平聚合矩阵 垂向聚合矩阵 通过复制和叠置矩阵来创建新矩阵 用已有矩阵创建块对角矩阵
获取矩阵的元素
使用编号索引 使用线性索引 使用冒号 使用end关键字
用索引生成多维数组
创建多维数组的方法之一是先创建一个 二维数组，然后扩展它。如：
A = [5 7 8; 0 1 9; 4 3 6];
A是一个3×3的数值，即它的行维和列 维都是3。给A添加第三维。
A(:,:,2) = [1 0 4; 3 5 6; 9 8 7]
用特殊函数生成多维数组
可以使用与生成二维数组相同的方式， 用randn,ones和zeros函数等生成多维数 组。提供的每个变量表示生成的数组中 对应维的大小。如：要创建一个正态分 布随机数的4×3×2的数组，可以输入：
其中，变量为字段名和它们的对应值。
单元数组
创建单元数组 获取单元数组的数据 删除单元和重塑单元数组
创建单元数组
用赋值语句创建单元数组 可以使用单元索引和内容索引两种方
式创建单元数组。 用cell函数创建单元数组
使用cell函数，可以预分配指定大小的 空单元数组，如，下面的语句创建一个 空的单元数组：
B = cell(2,3);
然后可以用赋值语句填充B单元。
函数句柄
函数句柄是一种MATLAB数据类型， 它包含用于引用函数的信息。创建函数 句柄时，MATLAB在句柄中保存所有与 要运行的函数有关的信息。
第3章将对函数句柄进行比较详细的介 绍。
第3章 M文件设计

第一章 Matlab 基本介绍一、数学建模常用软件简介数值计算 Matlab符号计算 Maple , Mathematica统计软件 SPSS, SAS优化软件 LINGOOFFICE 软件 Word , Excel二、matlab 界面介绍1、command window （命令窗口）2、wordspace （工作空间）3、command history （历史命令窗口）4、菜单(1)File->import data(2)View->desklayout->default(3)Help三、一些常用命令1、clc (清空命令窗口)2、clear （清空工作空间变量）3、save （保存工作空间中变量到指定文件）4、load （导入文件中数据）（注：双击数据文件也可）5、help （帮助）6、doc （查询帮助文档）第二章 数值计算一、数据类型1、主要四大类数据类型：数值型，字符串，符号型（代数式），逻辑型1⎧⎪⎧⎨⎨⎪⎩⎩、浮点数值型长整2、整型短整 字符串 name=’lisan ’a=’x ’符号型 用syms ， sym 定义逻辑型 取值只能为0或1，即真或假2 常用运算符数值运算：+ , - ,* , / , \, ^,.*, ./, .^关系运算 （运算结果为逻辑型，即0或1）>,<,>=,<=,==,~=逻辑运算（运算结果为逻辑型，即0或1）与或非，&，|，~any, all基本数学函数三角sin ,asin,cos,acos,tan,atan,cot,acot指数exp,log,log2,log10,sqrt其他abs,real,imag,sign,mod,floor,ceil特殊字符, ; . : [] () @ %2、变量命名规则（1）以字母开头，可包含字母、数字、下划线，不超过31位字符。

（2）区分大小写。

3、常量i, j 虚数单位pi , 圆周率eps,infNaN4、数字的输入输出格式format 格式参数shortlongrat5、字符串（1）字符串生成name=’lisan’a=char(‘l’,’i’)size(name) 查看字符串长度length(name) 查看字符串长度（2）字符与数组之间的转换double 字符转换为ASC码num2str 数字转化为字符str2num 字符转位数字a=’2’b=a*2b=double(a)*2b=str2num(a)*2（3）字符串操作相关函数。

《Matlab仿真应用详解》一、基本概念1．1、什么是计算机仿真1、仿真定义基本思想：仿真的基本思想是利用物理的或数学的模型来类比模仿现实过程，以寻求过程和规律。

它的基础是相似现象，相似性一般表现为两类：几何相似性和数学相似性。

当两个系统的数学方程相似，只是符号变换或物理含义不同时，这两个系统被称为“数学同构”。

仿真的方法可以分为三类：(1)实物仿真。

它是对实际行为和过程进行仿真，早期的仿真大多属于这一类。

物理仿真的优点是直观、形象，至今在航天、建筑、船舶和汽车等许多工业系统的实验研究中心仍然可以见到。

比如：用沙盘仿真作战，利用风洞对导弹或飞机的模型进行空气动力学实验、用图纸和模型模拟建筑群等都是物理仿真。

但是要为系统构造一套物理模型，不是一件简单的事，尤其是十分复杂的系统，将耗费很大的投资，周期也很长。

此外，在物理模型上做实验，很难改变系统参数，改变系统结构也比较困难。

至于复杂的社会、经济系统和生态系统就更无法用实物来做实验了。

(2)数学仿真。

就是用数学的语言、方法去近似地刻画实际问题，这种刻画的数学表述就是一个数学模型。

从某种意义上，欧几里德几何、牛顿运动定律和微积分都是对客观世界的数学仿真。

数学仿真把研究对象(系统)的主要特征或输入、输出关系抽象成一种数学表达式来进行研究。

数学模型可分为：●解析模型(用公式、方程反映系统过程)；●统计模型(蒙特卡罗方法)；●表上作业演练模型然而数学仿真也面临一些问题，主要表现在以下几个方面：●现实问题可能无法用数学模型来表达，即刻画实际问题的表达式不存在或找不到；●找到的数学模型由于太复杂而无法求解；●求出的解不正确，可能是由模型的不正确或过多的简化近似导致的。

(3)混合仿真。

又称为数学—物理仿真，或半实物仿真，就是把物理模型和数学模型以及实物联合在一起进行实验的方法，这样往往可以获得较好的效果。

2、计算机仿真计算机仿真也称为计算机模拟，就是利用计算机对所研究系统的结构、功能和行为以及参与系统控制的主动者——人的思维过程和行为，进行动态性的比较和模仿，利用建立的仿真模型对系统进行研究和分析，并可将系统过程演示出来。

MATLAB王春兴编物理与电子科学学院2009.9第一章MATLAB简介MA TLAB的原意为MATrix LABoratory,即矩阵实验室，是由在数值线性代数领域颇有影响的Cleve Moler博士首创的。

后来由Moler博士等一批数学家和软件专家组建了MathWorks软件公司，专门从事MATLAB的扩展与改进。

MA TLAB不仅具有强大的数值计算能力，而且具有数据图示功能和符号运算功能。

特别是大量的工具箱，扩展了应用领域，是高校学生、教师、科研人员和工程计算人员的最好选择，是数学建模必不可少的工具。

1.1MATLAB的主要特点1．功能强大MATLAB以复数矩阵作为基本编程单元，可以方便地处理诸如矩阵变换及运算、多项式运算、微积分运算、线性与非线性方程求解、常微分方程求解、偏微分方程求解、插值与拟合、特征值问题、统计及优化问题。

2．语言简单MATLAB语句书写简单，表达式的书写如同在稿纸中演算一样，允许用户以数学形式的语言编写程序，控制语句同C语言相近，并提供了强大的帮助功能。

3．扩充能力强MATLAB本身就像一个解释系统，用户可以方便地看到函数的源程序，也可以方便地开发自己的程序。

另外，MATLAB可以方便地和FORTRAN、C等语言进行接口，还和Maple有很好的接口。

4．编程易从形式上看，MATLAB程序文件是一个纯文本文件，扩展名为M，调试方便。

1.2MATLAB的窗口1．启动MATLAB2．工具栏3．命令窗口MATLAB的输入命令和输出结果的窗口，在这里输入的命令会立即执行并输出结果。

可用UP键盘将以前执行的命令调出。

1.3MATLAB的通用命令1.管理命令和函数：2.管理变量和工作空间3.控制命令窗口4.使用文件和工作环境5.启动和退出MA TLAB第二章数值计算2.1数字及运算1．数值MA TLAB中采用十进制数，并可用科学表示法，虚数用i或j 表示。

5 -39 0.0025 1.52e-20 6.9e13 3.0i -3+4i浮点数的范围大致为10-308~10308。

指 令 \downarrow \leftarrow \leftrightarrow \rightarrow \uparrow \circ \bullet
符



\exists \forall \in \infty \perp \prime \cdot



字符
\Nu \xi \Xi \pi \Pi \rho









6
\Delta \epsilon


\zeta 指 令 'sin\beta'

效果
\lambda \Lambd a \mu 指 令 '\zeta\omega'


\sigma \Sigma \tau
5
Normal and Grid on 4 2 0 -2 -4 -2 2
Equal 4 2 0 -2 0 -2 -4 -2
Square
0 Image and Box off 2 0 -2 -1 0 1
2
-2
0
2
0 Tight
2
Image and Fill 1 0.5 0 -0.5 -1 -1 0 1 -2 -1 0 2
一 坐标轴的控制
【例 5.2-3】观察各种轴控制指令的影响。演示采用长轴为 3.25，短轴为 1.15 的椭圆。注意： 采用多子图（图 5.2-3）表现时，图形形状不仅受“控制指令”影响，而且受整个图面“宽 高比”及“子图数目”的影响。本书这样处理，是出于篇幅考虑。读者欲想准确体会控制指 令的影响，请在全图状态下进行观察。

π
y′′ − µ 1 − y 2 y′ + y = 0 y (0) = 1, y′(0 ) = 0, µ = 2
函数ode23和ode45是对一阶常微分方程组设计的，因此，对高阶常微 和 是对一阶常微分方程组设计的， 函数 是对一阶常微分方程组设计的 因此， 分方程，需先将它转化为一阶常微分方程组，即状态方程。 分方程，需先将它转化为一阶常微分方程组，即状态方程。 则可写出Van der Pol 方程的状态方程形式： 方程的状态方程形式： 令 x1 = y , x2 = y ′, 则可写出
求解器 Ode23 Ode45 Ode113 Ode23t Ode15s Ode23s Ode23tb ode15i 采用方法 2-3阶Runge-Kutta算法，低精度 算法， 阶 算法 4-5阶Runge-Kutta算法，中精度 阶 算法， 算法 Adams算法，精度可到 10 −3 ~ 10 −6 算法， 算法 梯形算法 Gear’s方向数值微分算法，中精度 方向数值微分算法， 方向数值微分算法 2阶Rosebrock算法，低精度 阶 算法， 算法 梯形算法，低精度 梯形算法， 可变秩方法 适用场合 非刚性 非刚性 非刚性， 非刚性， 适度刚性 刚性 刚性 刚性 完全隐式微分方程
∫
1
0
ln xdx .
（1）建立被积函数文件 ）建立被积函数文件feln.m. function y=feln(x) y=exp(x).*log(x); （2）调用数值积分函数 求定积分。 ）调用数值积分函数quadgk求定积分。 求定积分 format long; I=quadgk(@ feln,0,1) 3.梯形积分法 梯形积分法 在MATLAB中，对由表格形式定义的函数关系的求定积分问题用梯 中 形积分函数trapz.该函数调用格式如下。 该函数调用格式如下。 形积分函数 该函数调用格式如下 ●T=trapz(Y).例如：trapz([1:5;2:6]’) 例如： 例如 ●T=trapz(X,Y).