当前位置：文档之家 › matlab讲义第2章

matlab讲义第2章

  • 格式：ppt
  • 大小：799.00 KB
  • 文档页数：85

下载文档原格式

  / 85

合集下载

Matlab第2章讲稿

Matlab第2章讲稿
• 矩阵除法运算又左除和右除之分，运算规则 矩阵除法运算又左除和右除之分，
A/B：右除。相当于A*inv（B） ：右除。相当于 （ ） A\B: 左除。相当于 左除。相当于inv(A)*B；一般用于求解线性代数 ； 方程组
A=[1 2;3 4]; B=[3 5;8 6]; A./B 和B.\A比较 比较 ans = 0.3333 0.4000 0.3750 0.6667 A/B和B/A比较 和 比较 ans = 0.4545 -0.0455 0.6364 0.1364 ans = 1.5000 0.5000 -7.0000 5.0000
3、数组和矩阵的除运算 、 （1）数组、矩阵与标量间的除法运算：规则是标量 ）数组、矩阵与标量间的除法运算： 与数组的每个元素进行除法运算； 与数组的每个元素进行除法运算；矩阵和标量只 有矩阵右除标量可运算（即矩阵/标量 标量）。 有矩阵右除标量可运算（即矩阵 标量）。 （2）数组、矩阵的除法运算：规则不同 ）数组、矩阵的除法运算： • 维数相同的两数组除法是对应元素之间相除。 维数相同的两数组除法是对应元素之间相除。 如 A./B（右除）与B.\A（左除）结果相同 （右除） （左除）
2.2.2
数组、 数组、矩阵操作
1、元素提取 、 A是m行n列矩阵 是 行 列矩阵 A(i,j) (i<=m且j<=n)由A中i指定行，j指定列的元素 且 指定行， 由 中 指定行 指定列的元素 A(i,:)由数组或矩阵中 指定行所对应的所有列元素组 由数组或矩阵中i指定行所对应的所有列元素组 由数组或矩阵中 成的子数组 A(:,j)由数组或矩阵中 指定列所对应的所有行元素组 由数组或矩阵中j指定列所对应的所有行元素组 由数组或矩阵中 成的子数组 A(:)由数组 的各个列按从左到右的次序首末相接的 由数组A的各个列按从左到右的次序首末相接的 由数组 一维长列” “一维长列”子数组

MATLAB课件-第二讲

MATLAB课件-第二讲

A（r,c）
访问A的由r指定行和c指定列上元素构 成的子数组；r，c可取多行或列
A（r, :）
访问A的r指定行上全部元素构成的子 数组；此处冒号表示全部列
A（:,c）
访问A的c指定列上全部元素的子数 组；此处冒号表示全部行
【例1】单下标的使用 >>a=zeros(2, 5); >>a(:)=-1:8
【例4】>> diag (diag(D)) %外面diag含义为利用一维数组生 成对角阵
ans= 100 010 001
【例5】>>命令栏输入:magic(3) ans =
816 357 492 说明:magic(3)生成一3x3魔方矩阵,即该矩阵横、竖、斜 各列元素总和相等
2.4 数组操作
常见的数组操作函数
命令 permute repmat
reshape
flipud
fliplr
rot90
含义
重排数组的维度次序
按指定的“行数、列数”铺放模块数组，以形成更大 的数组
在总元素数不变的前提下，改变数组的“行数、列 数” 以数组“水平中线”为对称轴，交换上下对称位置上 的数组元素
以数组“垂直中线”为对称轴，交换左右对称位置上 的数组元素
>>a([1 3 5 5 3 1])
ans = 0 5 10 10 5 0
>>a(6)
??? Index exceeds matrix dimensions. 索引超出矩阵维度。 下标值超出了数组的维数，导致错误
>>a(2.1)
??? Subscript indices must either be real positive integers or logicals.

matlab课件 第二章 Matlab基础

matlab课件 第二章 Matlab基础

2017/1/10
19
矩阵操作
1、矩阵下标
A(m,n)：提取第m行，第n列元素 A(:,n)：提取第n列元素 A(m,:)：提取第m行元素 A(m1:m2,n1:n2)：提取第m1行到第m2行和第 n1列到第n2列的所有元素（提取子矩阵）。 A(:)：得到一个长列矢量，该矢量的元素按矩阵的 列进行排列。
2017/1/10
14
3．建立大矩阵 大矩阵可由方括号中的小矩阵或向量建立起来。 4．利用冒号表达式建立一个向量 冒号表达式可以产生一个行向量，一般格式是 e1:e2:e3 其中，e1为初始值，e2为步长（可以为负数），e3 为终止值。
例如：>>a=[1:2:10] a= 1 3 5 7 9
2017/1/10 15
短格式，5位有效数字浮点数
长格式，15位有效数字浮点数 3.333333333333334e+001 十六进制格式 2个十进制位 正、负或零 有理格式 4040aaaaaaaaaaab 33.33 + 100/3
10
复数和复数矩阵
MATLAB的矩阵元素可以是复数或复数表达式，在matlab 中，用i或j字元来表示虚部。 x=1-2*i 注意是2*i而不是2i real(x) 列出实部 imag(x) 列出虚部 conj(x) 计算共轭复数 abs(x) 计算复数大小 angle(x) 计算复数向量的夹角（弧度表示） y=exp(x) 以指数方式表示一个复数
命令语句的输入,也就完成了它的执行，直接便可得 到最终结果。例如
>>a=5; >>b=6; >>c=a*b,
结果显示
c= 30
2017/1/10
7

MATLAB讲义第2讲

MATLAB讲义第2讲
4
2013-7-27
2.2 命令窗口 （续）
>>who
Your variables are: circle_len area radius
>>whos
Name Size Bytes Class area 1x1 8 double array circle_len 1x1 8 double array radius 1x1 8 double array Grand total is 3 elements using 24 bytes
Matlab Language
20
பைடு நூலகம்
2013-7-27
2.1 数值表示、变量及表达式 （续）
Matlab预定义的变量
变量名 ans eps pi inf i或j NaN 意义 最近的计算结果的变量名 MATLAB定义的正的极小值=2.2204e-16 圆周率π ∞值，无限大 虚数单元，sqrt(-1) 非数，0/0、∞/ ∞
11
2.6 获取在线帮助
MATLAB提供的帮助信息有两类
简单纯文本帮助信息
help
lookfor（条件比较宽松）例：inverse
窗口式综合帮助信息（文字、公式、图形）
doc
helpwin
2013-7-27
Matlab Language
12
〘功能演示-1〙求方程的根
5 3 2 求方程 2 x 3 x 71 x 9 x 13 0 的全部根。
2013-7-27
Matlab Language
6
2.2 命令窗口 （续）
数值显示格式设置 缺省显示格式：简洁的短（short g，7位有效数字）格式 窗口命令及语法格式：format 显示格式关键字 如：format long %15位数字显示 常见通用命令 命令 clc clear who或whos dir cd type help或doc quit或exit

matlab讲义2

matlab讲义2
1 18/10/1012
例3：编写一个脚本文件将华氏温度转化为摄氏温度 5 c ( f 32) 9 新建一个 M 文件 f2cs.m，内容如下：
clear; % 清除当前工作空间中的变量 f=input('Please input Fahrenheit temperature:'); c=5*(f-32)/9;
1
18/10/1012
所谓M脚本文件是指： （1）该文件中的指令形式和前后位置，与解决 同一个问题时在指令窗中输入的那组指令没有 任何区别。 （2）MATLAB在运行这个脚本时，只是简单地从 文件中读取那一条条指令，送到MATLAB中去执 行。 （3）与在指令窗中直接运行指令一样，脚本文 件运行产生的变量都是驻留在MATLAB基本工作 空间中。 （4）文件扩展名是“.m”。
1 18/10/1012
3．程序的暂停 暂停程序的执行可以使用pause函数，其调 用格式为： pause(延迟秒数) 如果省略延迟时间，直接使用pause，则将 暂停程序，直到用户按任一键后程序继续 执行。 若要强行中止程序的运行可使用Ctrl+C命 令。
1
18/10/1012
选择结构 是根据给定的条件成立或不成立，分别执 行不同的语句。Matlab 用于实现选择结构的语句有 if 语句和 switch 语句。
1 18/10/1012
输出：
a= 11 12 13 14 15 16 17 18 b= 1 2 3 4 5 6
7
8
9 10
调用该命令文件时，不用输入参数，也没有 输出参数，文件自身建立需要的变量。当文 件执行完毕后，可以用 whos 查看工作空间中 的变量。这里会发现a,b,c仍然保留在工作空间 中。

MATLAB第二讲.ppt

MATLAB第二讲.ppt

Matrix Operations – Eigenstates –
China University of Petroleum
❖ 例：求矩阵的特征值对角阵。 >> a=[-2 1 1；0 2 0；-4 1 3]； >> [v,d]=eig(a) %列向量是特征值对应的特征向量的矩阵 % Eigenvectors … v = -0.7071 -0.2425 0.3015
0 0 0.9045 -0.7071 -0.9701 0.3015
d = -1 0 0 020 002
%矩阵的特征值对角阵 % Eigenvalues …
Matrix Operations
China University of Petroleum

– Eigenstates –
❖例： 1 2 0 ,求矩阵的特征值。
-1 0 1
❖Multiplication (*) >>X =[1 2 3]; >> Z = 2 * X Z= 24 6
Division (/) >>X =[1 2 3]; >> Z = X / 2 Z= 0.5000 1.0000 1.5000
Vector Operators – Scalar Operations –
❖4. 位操作数 ❖5. 集合操作
1、数学操作
China University of Petroleum
❖数学操作之优先级: ❖1. ’（矩阵转置）、^（矩阵幂）、和.’
（数组转置）、.^（数组幂） ❖2. ~（逻辑非） ❖3. （乘）、\（左除）、/（右除）和.*（点
乘）、.\（点左除）、./（点右除） ❖4. +、-（加减） ❖5.冒号（:）（例如：x = 1:2:5 等） ❖同一类的操作数均具有相同的优先度，因

Matlab第2章

Matlab第2章
2 2 2 2
程序控制结构
3．break语句和continue语句 break语句用于终止循环的执行。当在循环体内执行到该语 句时，程序将跳出循环，继续执行循环语句的下一语句。 continue语句控制跳过循环体中的某些语句。当在循环体内 执行到该语句时，程序将跳过循环体中所有剩下的语句，继 续下一次循环。 【例2.11】输入两个整数，求它们的最小公倍数。 程序如下： x=input('请输入第一个数:'); y=input('请输入第二个数:'); z=max(x,y); while or(rem(z,x)~=0,rem(z,y)~=0) z=z+1; end disp([num2str(x),'和',num2str(y),'的最小公倍数是： ',num2str(z)])
3．try语句 try语句是一种试探性执行语句，为开发人员提供了一种捕获错误的机制，其语 句格式为 try 语句块1 catch 语句块2 end try语句先试探性执行语句块1，如果语句块1在执行过程中出现错误，则将错误 信息赋给保留的lasterr变量，并转去执行语句块2。 【例2.6】矩阵乘法运算要求两矩阵的维数相容，否则会出错。先求两矩阵的乘 积，若出错，则自动转去求两矩阵的点乘。 A=input('请输入A矩阵：'); B=input('请输入B矩阵：'); lasterr(''); %清除原有的错误信息 try C=A*B; catch C=A.*B; end C disp(lasterr) %显示出错原因
2.2 程序控制结构
3．程序的暂停 当程序运行时，为了查看程序的中间结果或者观看输出的图 形，有时需要暂停程序的执行。这时可以使用pause函数， 其调用格式为 pause（延迟秒数) 如果省略延迟时间，则将暂停程序，直到用户按任一键后程 序继续执行。 若要强行中止程序的运行可使用Ctrl+C组合键。

matlab教学讲义

matlab教学讲义

第二章 MATLAB 运算基础(1)主要内容：①变量的定义及赋值；②数值数组、字符串数组、元胞数组和构架数组等数据类型；③矩阵运算的定义和规则；④数组运算的定义和规则。

2.1 概述2.1.1 数据术语1）矩阵：由m×n个数组成的排成m行n列的一个矩形的数表，其中0×0矩阵为空矩阵([])。

数表中第i(1≤i≤m)行第j(1≤j≤n)列的数据称为矩阵元素2）标量：1×1的矩阵，即为只含一个数的矩阵。

3）向量：1×n或n×1的矩阵，即只有一行的或者一列的矩阵。

只有一行的矩阵称为行向量，只有一列的矩阵称为列向量。

数表中第i(1≤i≤n)个数据称为向量元素。

4）数组：矩阵的延伸，一般指多维数组，其中标量、向量和矩阵都是数组的特例。

2.1.2 数据类型数据类型包括数值型、字符串型、元胞型、构架型等。

数值型有单精度型、双精度型和整数型。

整数型有uint8,uint16,uint32和uint64等无符号型和int8，int16，int32和int64等符号型整数。

数值型数据可以用带小数点的形式和科学计数法表示，数值的表示范围是10-309～10+309。

-20、1.25、2.88e-56(表示2.88×10-56)、7.68e204(表示7.68×10204) 都是合法的数据表示。

一般在计算时采用双精度型，在输出时有多种数值显示格式可供选择。

数值显示格式的设置通过format 命令，格式如下：format short 默认设置，以5位数字形式输出format long 以15位十进制数形式输出format short e 以5位十进制数加指数形式输出format long e 以16位十进制数加指数形式输出format short g 从format short和format short eformat long g 从format long和format long e中自动选择最佳输出形式format hex 以16位十六进制数形式输出format + 以正号、负号和零形式输出format bank 以两位小数形式输出format rat 以近似分数形式输出format loose 以稀疏格式（变量与执行结果之间有空行）输出format compact 以紧凑格式（变量与执行结果之间无空行）输出2.2 变量2.2.1变量的命名变量的命名规则为:1 变量名必须以字母开头，变量名的组成可以是任意字母、数字或者下划线，但不能含有空格和标点符号。

第二章(2) MATLAB课件

第二章(2) MATLAB课件
16
>> flipdim(c,2)
>> flipdim(c,3) ans = 1 2 3 3 4 5 4 5 7 3 5 8
4 6 9 0
3. 矩阵的抽取 对角元素抽取函数diag diag(X,k) 抽取矩阵X的第k条对角线的元素向量。k为0时抽取 主对角线，k 为正值时为上方第k条对角线，k 为负 值时为下方第k条对角线。 diag(X) 相当于diag(X,0)，即抽取主对角线元素。 此函数还可以用来建立对角矩阵，其形式如下： diag(v,k) 使得向量v为所得矩阵的第k条对角线元素。 diag(v) 使得向量v为矩阵的对角线元素。 例如：矩阵抽取示例。 >> a=pascal(4) %4阶pascal矩阵
>> x=linspace(1,6,7) %创建一维数组 %创建一维数组 x= 1.0000 1.8333 2.6667 3.5000 4.3333 >> x(5) %索引访问数组元素 %索引访问数组元素 ans = 4.3333 >> x(1:5) %访问一块数据 %访问一块数据 ans = 1.0000 1.8333 2.6667 3.5000 4.3333
7
>>[v,d]=eig(a) v= 0.3162 -0.4041 -0.1391 -0.9487 0.9091 0.9740 -0.0000 0.1010 -0.1789 d= 1.0000 0 0 0 2.0000 0 0 0 3.0000 2. 其它分解 （自看）
>>[v,d]=eig(a,b) v= -1.0000 -0.3305 -0.0202 0.4204 1.0000 -1.0000 0.5536 -0.0046 0.3485 d= 12.9030 0 0 0 -0.0045 0 0 0 0.0706

《MATLAB第二讲》PPT课件

《MATLAB第二讲》PPT课件
有了足够多的函数，可以生成一个工具箱，放在一个固定的目录下，并在MATLAB中 加入这个目录路径即可。
37
2 参数传递
在MATLAB中，参数具有自己的专有工作空间。函数中 的参数和命令行参数不在一个空间中，它们的唯一联系 为函数的输入输出变量。输入参数在函数中是可读的， 但在函数中的任何改动不会传递回上一级空间。
35
• 下面举一个递归调用的例子 function y=factorial(k) if k>1
y=k*factorial(k-1); elseif k==1
y=1; elseif k==0;
y=1; else error('输入参数只能为非负整数') end %大家试着读读这是用来求这么的函数
36
11
1.创建m文件
• 这三行命令可以在command window中输入并且执行，但是如果想保存 起来，以便下次使用，需要编辑成m文件
12
• 2.保存m文件：File Save As
13
关于保存路径：一般默认 在安装路径matlab7\work,
也可以保存在自己需要的 路径
把这个m文件命名为graph_sin.m存放在 c:\matlab7\work中
x=0:2*pi/180:2*pi; %x为一个行向量,第一个元素为0,最后一个元素为2π,步长2π/180 y=sin(x); %y也为一个向量，每个元素是x对应元素的正弦值 plot(x,y) %画图，x中的元素为横坐标,y中相应的元素为纵坐标 %所以在本例中画的是y=sinx的图像，自变量取值[0, 2π]
19
2.1.4 函数m文件
• 一.函数m文件的几种格式及调用 • 格式1（无返回值函数） function 函数名(输入表) %称为函数头 函数体

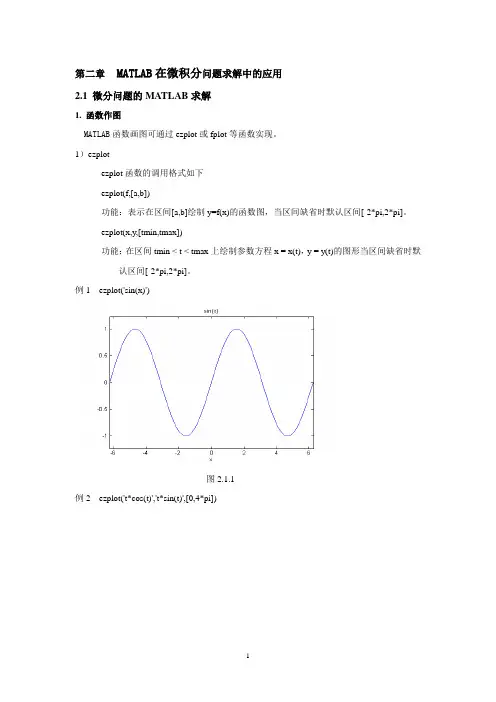
matlab简明教程 第二章

matlab简明教程 第二章

第二章 MATLAB在微积分问题求解中的应用2.1 微分问题的MATLAB求解1. 函数作图MATLAB函数画图可通过ezplot或fplot等函数实现。

1）ezplotezplot函数的调用格式如下ezplot(f,[a,b])功能：表示在区间[a,b]绘制y=f(x)的函数图，当区间缺省时默认区间[-2*pi,2*pi]。

ezplot(x,y,[tmin,tmax])功能：在区间tmin < t < tmax上绘制参数方程x = x(t)，y = y(t)的图形当区间缺省时默认区间[-2*pi,2*pi]。

例1 ezplot('sin(x)')图2.1.1例2 ezplot('t*cos(t)','t*sin(t)',[0,4*pi])图2.1.22) fplotfplot 函数的调用格式如下fplot(fun,lims)功能：绘制函数fun在区间lims上的图形。

例３fplot('tan(x)',[-pi/4 pi/4])图2.1.32 极限的符号运算极限是高等数学中基本概念之一，在微积分中，很多概念是用极限定义的，例如导数和定积分。

因此，掌握极限的运算对学好高等数学是极为重要的。

在MATLAB中，极限的求解可由limit 函数来实现，limit 函数的格式及功能见表2.2.1。

表2.2.1 1limit 函数的格式及功能因为数列()n x f n =实际上就是定义在正整数集合上的函数，因此数列的极限可看成x →+∞时的特殊函数的极限；多元函数的极限可化为累次极限实现。

例1 求下列数列的极限1）lim n n→∞ 2）n →∞ 3）lim 3sin 3n n n π→∞ 4）1123lim 32n n n n n ++→∞-- 5）)n →∞6）1lim()1n n n n →∞-+ 7）2(1)lim 1n n n →∞-+ 8）lim(1)n n →∞- 9）lim(2)nn →∞-解：syms n ar1=limit(sqrt(n^2+a^2)/n,n,inf,'left') 输出 r1 =1 r2=limit(sqrt(n^2+3)-sqrt(n^2-3),n,inf,'left') 输出r2 =0 r3=limit(3^n*sin(pi/3^n),n,inf,'left') 输出r3 =pir4=limit((2^n-3^(n+1))/(3^n-2^(n+1)),n,inf,'left') 输出r4 =-3 r5=limit(sin(pi*sqrt(n^2+1)),n,inf,'left') 输出r5 =1 .. 1 r6=limit(((n-1)/(n+1))^n,n,inf,'left') 输出r6 =exp(-2) r7=limit((n-1)^2/(n+1),n,inf,'left') 输出r7 =Infr8=limit((-1)^n,n,inf,'left') 输出r8 =-1 .. 1 r9=limit((-2)^n,n,inf,'left') 输出r9 =NaN 例2 求下列函数的极限 1）0sin()sin()limh x h x h →+- 2）3113lim()11x x x →--- 3）01lim sin x x x→ 4）3lim 2x tx →-5）0lim x x x-→ 6）lim (1)3x x t x →-∞+ 7）123lim()21x x x x +→∞+- 8）11lim sin 1x x x →- 9）lim sin x x x →∞解： syms x h tf1=limit((sin(x+h)-sin(x))/h,h,0) 输出f1 =cos(x) f2=limit(1/(1-x)-3/(1-x^3),x,1) 输出 f2 =-1 f3=limit(x*sin(1/x)) 输出 f3 =0 f4=limit(t/(x-2),3) 输出f4 =t f5=limit(abs(x)/x,x,0,'left') 输出f5 =-1f6=limit((1+t/(-3*x))^(-x),x,inf,'left') 输出f6 =exp(1/3*t) f7=limit(((2*x+3)/(2*x+1))^(x+1),x,inf) 输出f7 =exp(1) f8=limit(x*sin(1/(x-1)),x,1) 输出f8 =-1 .. 1 f9=limit(x*sin(x),x,inf) 输出f9 =NaN 例3 求下列函数的极限1）(,)(0,0)lim x y → 2）(,)lim y x y →解： syms x y;p1=limit(limit((2-sqrt(x*y+4))/(x*y),x,0),y,0) 输出p1 =-1/4 p2=limit(limit(log(x+exp(y))/sqrt(x^2+y^2),x,1),y,0) 输出p2 =log(2) 3. 一阶微商的计算由导数的定义可知，一切导数的问题，都可以用极限的方法求得，例如上面例2中的第1题。

matlab讲稿 第二讲

matlab讲稿 第二讲

A(i,j,k,:)
A(:)
2.5 操作和特殊字符
3.特殊字符
［］ 用于形成向量和矩阵,空格用于行元素的间 隔，分号或回车表示一行的结束。 ［］内还可以采用矩阵和向量， 例如只要A、B、C 的维数适当，就可利用D=［A B; C］产生更大的 矩阵。
A=［］表示产生空矩阵A A(m, :)=［］表示从A中删去第m行 A(:, n)=［］表示从A中删去第n列 A(:)表示将A重新排列成列向量
2.5 操作和特殊字符
A′可求出矩阵转置， 对复数阵A， 则可 求出其复共轭转置； A.′可求出阵列转置， 对复数阵A也不涉 及到共轭运算。
2.5 操作和特殊字符
2. 冒号(∶) 冒号是MATLAB中最常用的操作符之一, 它 可用于建立向量、 下标阵列和迭代。
表 2.3 冒号使用格式(1) 格式 j:k j:k j:i:k j:i:k 功 能 当j<=k时，等同 于［j, j+1,…,k］ 当j>k时为空 等同于［ j+i, j+2i, …, k］ j, 当i>0且j>k, 或者 i<0且j<k时为空
4.关系操作符 关系操作符可完成两个阵列之间元素对元素的比 较，其结果为同维数的阵列。当关系成立时相应 的元素置为逻辑真(1)，否则置为逻辑假(0)。 操作符<、<=、>、>=只用于比较操作数的实部， 而==、~=用于比较实部和虚部。 测试两个字符串是否相同可采用strcmp， 这时 可比较不同长度的字符串。 strcmpi将忽略大小写 strncmp,strncmpi可以比较前n个字符
2.6 基本矩阵和矩阵操作
阵 作 矩 操 diag reshape rot90 fliplr flipud tril triu cat repmat 功 能 对 矩 角 阵和 阵 矩 的对 角 化 阵 列重 新排 列 矩 阵旋 转90° 矩 阵左 右翻 转 矩 阵上 下翻 转 矩 的下三 阵 阵 角 矩 的上三 阵 阵 角 阵列 接 连 复 并平铺 列 制 阵

MATLAB实用教程第二章

MATLAB实用教程第二章
1．矩阵的合并 2．矩阵行列的删除
1．矩阵的合并
矩阵的合并就是把两个或者两个以上的矩阵 连接成一个新矩阵矩阵构造符 可用于构造矩阵并 可以作为一个矩阵合并操作符 ➢ 表达式C=A B在水平方向合并矩阵A和B； ➢ 表达式C=A;B在竖直方向合并矩阵A和B
具有相同行数的两个矩阵合并为一个新矩阵
12 34 56 3×2
1．访问单个元素
2．线性引用元素
➢ 对于矩阵A线性引用元素的格式为 Ak通常这样的引用用于行向量或列 向量但也可用于二维矩阵
➢ MATLAB按列优先排列的一个长列向量格 式线性引用元素来存储矩阵元素
3．访问多个元素
操作符：可以用来表示矩阵的多个元 素若A是二维矩阵其主要用法如下： ➢ A:: 返回矩阵A的所有元素 ➢ Ai: 返回矩阵A第i行的所有元素
3．用满矩阵和稀疏矩阵存储方式分别构造下述矩 阵：
4．采用向量构造符得到向量159…41 5．按水平和竖直方向分别合并下述两个矩阵：
6． 分别删除第5题两个结果的第2行 7． 分别将第5题两个结果的第2行最后3列的数值
改为11 12 13 8． 分别查看第5题两个结果的各方向长度 9． 分别判断pi是否为字符串和浮点数 10．分别将第5题两个结果均转换为29的矩阵 11．计算第5题矩阵A的转秩 12．分别计算第5题矩阵A和B的A+B、A.* B和
行运算; ➢ 不同优先级的运算符采用先进行优先高的
运算
运算符的优先等级表
由表中可以看到括号的优先级别最高因此可 以用括号来改变默认的优先等级
2.4 字符串处理函数
2.4.1 字符串的构造 2.4.2 字符串的比较 2.4.3 字符串的查找和替换 2.4.4 字符串与数值间的转换

Matlab讲义第二章 matlab语言基础

Matlab讲义第二章 matlab语言基础

七、使用帮助
1、help命令，在命令窗口中显示 • MATLBA的所有函数都是以逻辑群组方式进行组 织的，而MATLAB的目录结构就是以这些群组方 式来编排的。 • help matfun ：矩阵函数－数值线性代数 • help general：通用命令 • help graphics：通用图形函数 • help elfun：基本的数学函数 • help elmat：基本矩阵和矩阵操作 • help datafun：数据分析和傅立叶变换函数 • help ops：操作符和特殊字符
• 如果结果为整数，则显示没有小数；如果结果不是 整数，则输出形式有： format (short)：短格式（5位定点数）99.1253 format long：长格式（15位定点数 99.12345678900000 format short e：短格式e方式 9.9123e+001 format long e：长格式e方式 9.912345678900000e+001 format bank：2位十进制 99.12 format hex：十六进制格式
》a=[1 2 3; 4 5 6; 2 3 5]; 》b=inv(a)
4、了解矩阵超越函数 •在MATLAB中exp、sqrt等命 令也可以作用到矩阵上，但 这种运算是定义在矩阵的单 个元素上的，即分别对矩阵 的每一个元素进行计算。 •超越数学函数可以在函数后 加上m而成为矩阵的超越函 数，例如：expm,sqrtm。矩 阵的超越函数要求运算矩阵 为方阵。
2、命令行编辑器 （1）方向键和控制键可以编辑修改已输入的命令 ：回调上一行命令 ：回调下一行命令 （2）命令窗口的分页输出 • more off：不允许分页 more on：允许分页 • more(n)：指定每页输出的行数 • 回车前进一行，空格键显示下一页，q结束当前显 示。 （3）多行命令（…） • 如果命令语句超过一行或者太长希望分行输入，则 可以使用多行命令继续输入。 • S=1-12+13+4+… 9-4-18;
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5
3．Debug主菜单项 （1）Open M-Files when Debugging：调试时打开M文件 （2）Step：单步调试程序 （3）Step In：单步调试进入子程序 （4）Step Out：单步调试从子程序跳出 （5）Continue：程序执行到下一断点 （6）Clear Breakpoints in All Files：清除所有打开文件中的断点 （7）Stop if Errors/Warnings：在程序出错或报警处停止往下执行 （8）Exit Debug Mode：退出调试模式
4
2．Edit主菜单项 （1）Undo：撤销上一步操作 （2）Redo：重新执行上一步操作 （3）Cut：剪切选中的对象 （4）Copy：复制选中的e to Workspace：粘贴到工作区 （7）Select All：全部选择 （8）Delete：删除所选的对象 （9）Find：查找所需选择的对象 （10）Find Files：查找所需文件 （11）Clear Command Window：清除命令窗口区的对象 （12）Clear Command History：清除命令窗口区的历史记录 （13）Clear Workspace：清除工作区的对象
精品
matlab第2章
2、MATLAB系统构成：五部分
MATLAB开发环境 MATLAB数学函数库 MATLAB语言 MATLAB图形处理系统 MATLAB应用程序接口（API）
3、工具箱是MATLAB的关键部分
MATLAB每年都会增加一些新的工具箱，所以，在一般情况下，工具箱的列表不是 固定不变的。 有关MATLAB工具箱的最新信息可以在http://www. /products中看到。
8
5．Window主菜单项 （1）Close All documents：关闭所有文档 （2）0 Command Window：选定命令窗口为当前活动窗口 （3）1 Command History：选定历史命令窗口为当前活动窗口 （4）2 Current Directory：选定当前路径窗口为当前活动窗口 （5）3 Workspace：选定工作空间窗口为当前活动窗口
9
6．Help主菜单项 （1） Product Help：显示所有MATLAB产品的帮助消息 （2）Using the Desktop：启动Desktop的帮助 （3）Using the Command Window：启动命令窗口帮助 （4）Web Resources：显示internet上一些相关的资源网址 （5）Check for Updates：检查软件是否更新 （6）Demos：调用MATLAB所提供的范例程序 （7）About MATLAB：显示有关MATLAB的信息
10
MATLAB窗口
MATLAB有多个显示窗口，默认的有四个窗口：
命令窗口（command window）
工作空间窗口(workspace) 当前路径窗口(current directory)
当前路径
历史命令窗口(command history)。
工作空间
历史命令
命令窗口
11
历史命令窗口(command history)：记录所有运行过的命令。 退出MATLAB时，命令窗口将被清空，但历史命令窗口仍然 会保存所有运行过的命令。 使用编辑菜单可以清空所有历史命令。
7
（6）Command History：历史命令窗口项 （7）Current Directory：当前路径窗口项 （8）Workspace：工作窗口项 （9）Help：帮助窗口项 （10）Profiler：轮廓图窗口项 （11）Toolbar：显示或隐藏工具栏 （12）Shortcuts Toolbar：显示或隐藏快捷方式选项 （13）Titles：显示或隐藏标题栏选项
2
2.3 MATLAB 桌面操作环境
2.3.1 matlab启动和退出
启动：2种方法
1、以windows操作系统为例，进入windows后，选择“开始” →“程序” →“matlab”； 2、单击桌面上的图标。 一旦matlab被启动，可以看到matlab的提示符（>>）
退出：3种方法
1、在file菜单项中选择“exit matlab” 2、用鼠标单击窗口右上角图标（×） 3、在提示符后输入“exit”
3
2.3.2 MATLAB主菜单及功能
打开MATLAB主窗口后，即弹出其主菜单栏。 1．File主菜单项 （1）New：建立新的.m文件、图形、模型和图形用户界面 （2）Open：打开.m文件、.fig文件、.mat文件、.mdl文件等 （3）Close Command Window：关闭命令窗口 （4）Import Data：从其它文件导入数据 （5）Save Workspace As：把工作空间的数据存放到相应的路径文件中 （6）Set Path：设置工作路径 （7）Preferences：设置命令窗口的属性 （8）Page Setup：页面设置
6
4．Desktop主菜单项 （1）Undock Command window：将命令窗口变为全屏显示，
并设为当前活动窗口 （2）Desktop Layout：用于工作区的设置，设置选项包括：
Default：系统默认设置项 Command Window Only：单独命令窗口项 History and Command Window：命令历史窗口和命令窗口项 All Tabbed：全部标签项显示 （3）Save Layout：保存选定的工作区设置 （4）Organize Layouts：管理保存的工作区设置 （5）Command Window：命令窗口项
当前路径窗口(current directory)：列出了该路径下计算机文 件夹里的所有文档。 MATLAB存储或打开文件都要使用当前路径窗口。
12
2.3.3 MATLAB命令窗口
主要两大功能： （1）用户通过命令窗口输入命令和数据 （2）显示命令执行的结果 命令窗口（command window）:可以保存计算结果，但不能保存命令。 MTATLAB语句形式为：>>变量=表达式 通过等号将表达式的值赋予变量。当输入回车键时，该语句被执行。 语句执行后，窗口自动显示语句执行的结果。