关于“平面弹性悬臂梁剪切挠度问题”的进一步研究

如何在理论力学中解决梁的挠曲问题？在理论力学中，梁的挠曲问题是一个非常重要的研究领域。

梁在受到外力作用时会发生弯曲变形，这种变形会影响梁的强度、刚度以及稳定性等性能。

因此，准确地解决梁的挠曲问题对于工程设计和实际应用具有重要意义。

要解决梁的挠曲问题，首先我们需要了解一些基本的概念和理论。

梁是一种常见的结构构件，其主要承受横向载荷。

当梁受到载荷作用时，梁内会产生弯矩和剪力。

弯矩是导致梁弯曲的主要因素，而剪力则会对梁的剪切变形产生影响。

在研究梁的挠曲时，我们通常会引入一些假设来简化问题。

例如，我们假设梁的材料是均匀、连续和各向同性的，梁的横截面在弯曲过程中始终保持平面，并且忽略梁的横向剪切变形。

这些假设在大多数实际情况中是合理的，可以帮助我们更方便地分析和解决问题。

解决梁挠曲问题的一个重要方法是利用梁的弯曲方程。

梁的弯曲方程描述了梁的挠度与弯矩之间的关系。

对于等截面梁，常见的弯曲方程有欧拉伯努利梁理论和铁木辛柯梁理论。

欧拉伯努利梁理论假设梁的弯曲变形很小，并且忽略了剪切变形的影响。

在这种理论下，梁的弯曲方程可以表示为：＄EI\frac{d^2y}｛dx^2} ＝ M(x)＄其中，＄E$ 是梁材料的弹性模量，＄I$ 是梁横截面的惯性矩，＄y$ 是梁的挠度，＄x$ 是梁的轴向坐标，＄M(x)＄是梁在＄x$ 处的弯矩。

通过求解这个微分方程，结合梁的边界条件和连续条件，我们可以得到梁的挠度曲线和转角曲线。

然而，欧拉伯努利梁理论在一些情况下并不适用，例如对于短粗梁或者梁的剪切变形不能忽略的情况。

这时就需要用到铁木辛柯梁理论。

铁木辛柯梁理论考虑了剪切变形的影响，其弯曲方程相对更加复杂。

除了利用弯曲方程求解梁的挠曲问题，还可以采用能量法。

能量法的基本思想是利用梁在变形过程中的能量守恒原理来求解。

常见的能量法有单位载荷法和卡氏定理。

单位载荷法是通过在梁上施加一个单位虚拟载荷，然后根据虚拟载荷所做的功等于实际载荷所产生的应变能来求解梁的挠度和转角。

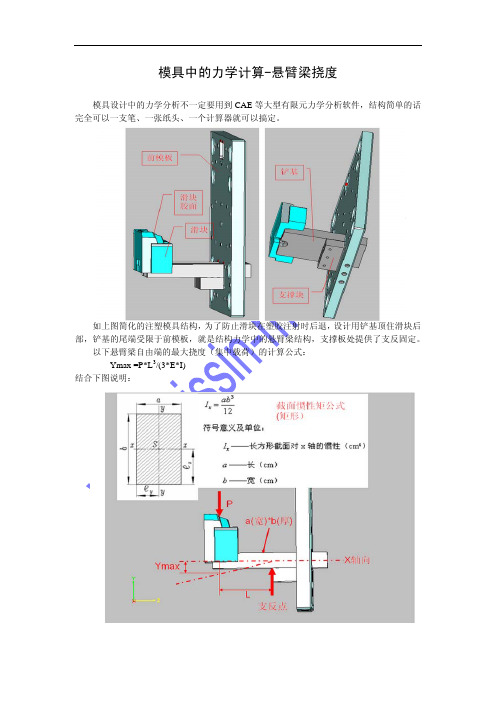
模具中的力学计算-悬臂梁挠度模具设计中的力学分析不一定要用到CAE等大型有限元力学分析软件，结构简单的话完全可以一支笔、一张纸头、一个计算器就可以搞定。

如上图简化的注塑模具结构，为了防止滑块在塑胶注射时后退，设计用铲基顶住滑块后部，铲基的尾端受限于前模板，就是结构力学中的悬臂梁结构，支撑板处提供了支反固定。

以下悬臂梁自由端的最大挠度（集中载荷）的计算公式：Ymax =P*L3/(3*E*I)结合下图说明：P为加在悬臂梁自由端的载荷，就是塑胶注射导致滑块后退的力，在本套模具塑胶投影在滑块上的面积为（4.5cm*13cm=58.5cm2）,最大射胶压力的注塑机上的指示值是75，这个值不是Mpa值，要经过换算，注塑机厂家提供的最大指示值是140，告知的最大注塑压力是200Mpa，则最大射胶压力为75/140*200Mpa=107.1Mpa=1071Kg/cm2。

这样P=1071*58.5=62653Kg。

L是集中载荷点到支反固定端的距离，本模具是9cm。

E是铲基模具钢材的弹性模量，这需要问下钢材供应商，拿比较容易查到的大同的DC53（未热处理时参数接近718钢材）,这里有3个数据要记住，弹性模量E=21700Kg/mm2,刚性模量G=8480 Kg/mm2，泊松比u=0.28（指与应力垂直的方向的变形量和应力方向的变形量的比值）。

刚性模量又叫剪切（切变）弹性模量，其实刚性模量可以通过G=E/(2*(1+u))大致推算出来，此处我们只要有E = 21700Kg/mm2 = 2170000Kg/cm2这个数据就可以了。

在此顺便提下材料的弹性模量，弹性模量是施加的应力除以产生的应变值，这个应变值是材料的变形的百分比，没有量纲（单位），所以弹性模量的单位还是Mpa。

根据施加的应力形式不同，弹性模量分为拉伸、压缩、弯曲、剪切、扭转等弹性模量，基本没有厂家会公示所有的弹性模量试验值。

通常未特别说明的弹性模量指拉伸弹性模量用E表示，剪切弹性模量用G表示，压缩弹性模量用K表示。

第一章绪论1.1研究意义与国内外研究现状对于弹塑性悬臂梁的研究作为力学科研的基础，已经广泛应用于水利水电、建筑工程结构、建筑材料，机械设计制造等方面。

特别是在建筑工程结构领域，大部分组成均为弹塑性悬臂梁，其由于材料的不同，应用领域的差异等情况，需要从实际工程角度考虑进行研究与分析，从而为以上所述领域提供相关的资讯信息。

因此，研究好弹塑性悬臂梁的性质是对社会生活、工农业生产等方面具有极为深刻的意义。

目前，弹塑性悬臂梁的研究已经完全计算机化，特别是ANSYS，MARC，PRO/E等大型有限元商用软件的广泛运用，更使其研究简便化、通用化，从最广泛研究的方向——工程设计角度的计算方向考虑，对弹塑性悬臂梁内力按暂不考虑塑性内力重分布的弹塑性力学方法计算[1]。

弹塑性悬臂梁在实际应用中已经发展了多种适应不同领域发展方向研究成果，我国长安大学在此项领域里发挥着重要作用，典型的诸如该校发明的抗侧力结构体系——钢板悬臂梁；其利用有限元分析软件分析了两侧加劲钢板悬臂梁的弹塑性屈曲性能，讨论了悬臂俩梁跨高比、宽厚比等参数对钢板悬臂梁屈曲性能的影响。

得出了较为优化的结果[2]。

为实现结构刚度可在一定范围内渐变,同时充分发挥组合钢板的性能,该校还对此研发出了新型高层抗震加固结构体系一组合悬臂梁【3】，并用实际证明该结构恢复力模型可用于组合悬臂梁结构的弹塑性反应分析。

1.2通用有限元软件MSC.Marc软件简介作为国际上第一个通用非线性商用有限元软件MSC.Marc软件从20世纪70年代处诞生，一直紧跟有限元理论和计算机硬，软件发展的最新进展。

MSC.Marc是功能齐全的高级非线性有限元软件的求解器，体现了有限元分析的理论方法和软件实践的完美结合。

它具有极强的结构分析能力。

可以处理各种线性和非线性结构分析包括：线性/非线性静力分析、模态分析、简谐响应分析、频谱分析随机振动分析、动力响应分析、自动的静/动力接触、屈曲/失稳、失效和破坏分析等。

基于机械力学的悬臂梁研究悬臂梁是一种常见的结构形式，由于其在工程应用中的广泛性和重要性，成为力学研究的热点之一。

本文将基于机械力学的角度，对悬臂梁的特性、应变分析、挠度计算及在工程中的应用进行探讨。

一、悬臂梁的特性悬臂梁是一种只有一端支撑的梁，另一端呈自由悬挂状态。

由于其结构特点，悬臂梁在实际工程中具有许多独特的特性。

首先，悬臂梁上存在最大弯矩点和零弯矩点，对于结构设计和承载能力的考虑至关重要。

其次，悬臂梁的应力分布不均匀，呈现出梁根部的应力较大，而梁端部的应力较小的特点。

此外，悬臂梁在受外力作用下会产生挠度和转角，研究这些特性对于悬臂梁的设计和分析至关重要。

二、应变分析应变分析是研究悬臂梁特性的重要手段之一。

在悬臂梁的弯曲过程中，由于受力，其纵向发生应变。

应变分析可以帮助工程师了解和评估悬臂梁的变形情况，并进一步优化结构设计。

应变分析主要包括线弹性理论、材料非线性理论和梁的几何非线性理论等方面。

在实际应用中，结合实验方法进行对比验证，可以进一步提高应变分析的准确性。

三、挠度计算挠度是评估悬臂梁变形程度的重要指标之一。

通过准确计算悬臂梁的挠度，工程师可以判断梁是否满足承载要求，并进行合理的结构设计。

挠度计算主要依据弯曲理论和力学方程等方法，结合悬臂梁的几何形状、材料性质和外力作用情况来进行。

在实际应用中，悬臂梁的挠度计算不仅关注其最大挠度值，还需要考虑挠度的分布和变化趋势等。

四、悬臂梁在工程中的应用悬臂梁所具有的独特特性和性能，使其在工程中有广泛的应用。

在建筑结构中，悬臂梁常用于支撑大跨度的屋顶或悬挂空间。

在桥梁工程中，悬臂梁常用于支撑桥梁的主梁结构，承担桥梁承载的重要任务。

此外，在飞机、船舶以及机械装置上，悬臂梁的应用也非常广泛。

通过合理的结构设计和力学分析，可以进一步提高悬臂梁在工程中的性能和安全性。

总结机械力学是研究悬臂梁的核心领域，应变分析和挠度计算是研究悬臂梁特性的重要方法。

悬臂梁凭借其独特的特性，在建筑、桥梁、航空航天等工程中得到了广泛的应用。

深梁理论的研究现状与工程应用夏桂云;曾庆元【摘要】综述了深梁理论、截面剪切修正系数计算理论、深梁线性与几何非线性有限元、深梁材料非线性分析、深梁振动理论、深梁稳定理论、箱梁结构分析中弯曲、剪力滞、畸变分析时考虑剪切变形影响的计算理论、钢腹板桥梁考虑剪切变形的研究成果、弹性地基深梁、深梁理论在工程结构中的应用等.提出了杆系结构的静力、振动和稳定分析方法都可用Timoshenko深梁理论进行重建和重写.【期刊名称】《力学与实践》【年(卷),期】2015(037)003【总页数】15页(P302-316)【关键词】深梁理论;剪切修正系数;有限元;振动;稳定【作者】夏桂云;曾庆元【作者单位】长沙理工大学土木与建筑学院,长沙410076;中南大学土木工程学院,长沙410075;西安交通大学航天航空学院,西安710049;中南大学土木工程学院,长沙410075【正文语种】中文【中图分类】U441.3夏桂云，长沙理工大学土木与建筑学院教授、湖南省普通高校青年骨干教师.主要从事考虑剪切变形影响的杆系结构理论与应用、箱梁结构的多重耦合分析理论、桥梁结构非线性分析理论等的研究.先后主持国家自然科学基金项目、中国博士后基金项目、湖南省科技计划项目及横向项目等10余项课题的研究.获湖南省科技进步一、二、三等奖、中国公路学会科技进步二等奖等4项.在国内外主要期刊上发表学术论文30余篇（其中SCI数据库收录1篇、EI数据库收录20余篇），出版《考虑剪切变形影响的杆系结构理论与应用》专著1部.经典的Bernoulli一一Euler初等梁理论应用非常广泛，是《材料力学》、《结构力学》、《结构振动》、《结构稳定》所论述杆系结构的理论基础，但该理论引入直法线假定［1］，没有考虑剪切变形的影响，故只能适用于长梁情况.随着工程技术的发展，应考虑剪切变形影响的深梁问题越来越多，如结构截面尺寸相对于跨径来说较大情况、梁的高阶振动、局部高度承载、弹性地基梁的地基沉降等问题，应用初等梁理论分析将导致计算挠度偏小［2］、计算精度不足等问题.为解决这些问题，各国学者提出了多种深梁理论［3］，出现了大量的研究成果和工程应用，促进了深梁理论的发展.到目前为止，可以说凡是利用Bernoulli一一Euler初等梁理论研究的杆系问题都可以利用考虑剪切变形影响的深梁理论进行分析，以提高计算精度.从 1921年 Timoshenko提出著名的两广义位移深梁理论以来［2-3］，深梁理论一直在快速发展当中，按剪切变形的位移场模式，深梁理论主要有零阶剪切变形理论［4-5］、一阶剪切变形理论［2-3］和高阶剪切变形理论［6］（主要是二阶和三阶剪切变形理论）；按广义位移的个数主要有单广义位移梁理论［7］、两广义位移梁理论［2-3］和多广义位移梁理论［8-9］；按理论建立的方式主要有经典理论、双挠度理论和精化理论［10］.在这些理论中，一阶剪切变形的经典理论是Timoshenko梁理论，三阶剪切变形理论主要有Bickford［6］、Levinson［8］、Jemielita［11］、Reddy［12-13］等所建立的理论和模型.在这些深梁理论中，由于Timoshenko梁理论简单、求解方便、应用最广而成为经典.考虑剪切变形影响后，如图1所示，受竖向均布载荷q、均布弯矩载荷m和轴压力共同作用的深梁的经典微分方程为［2］式中，抗弯劲度D=EI、抗剪劲度C=GA/k，k为剪切修正系数［1-2，14-15］、q为竖向均布载荷、m为均布弯矩.Timoshenko梁理论从《弹性力学》的观点看，仍然是一种近似理论，即有些方面仍不符合《弹性力学》的要求，主要缺点有3个［2］：（1）同一截面上各点的竖向位移并不相等，而这里假定为常数；（2）截面在变形后实际上并不再保持为平面，而这里继续假定它为一平面；（3）同一截面上假定剪应变为常数而剪应力却不是常数，因而不满足本构关系.为缓和上述矛盾，Cowper指出，可以把挠度w理解为截面上各点的平均挠度，转角ψ理解为截面上各点的平均转角［2］，即式中，A和I分别为截面的面积和惯性矩.经过上式的平均处理，这样w′-ψ可以理解为平均剪应变，于是剪应变与剪应力之间不符合本构关系的矛盾得到缓解［2］.一般认为，高跨比h/L≥1/5或弯剪刚度比D/（L2C）≥1/30的杆系结构都是深梁理论研究的范畴.利用 Timoshenko梁理论进行结构分析时，最为关键的问题是截面剪切修正系数（shear correction factor）的计算问题.截面剪切修正系数又称为剪切变形系数（shear deformation coefficients）、剪应力不均匀系数、剪切系数等.其定义有按式（1）中C=GA/k定义的，也有按C=kGA定义的［2］，此时的剪切修正系数与式（1）定义的剪切修正系数互为倒数.引入这个系数的目的主要是克服假定剪切应变沿梁截面均匀分布、剪应力却非均匀分布间的误差影响.历史上有多种计算理论和方法，有的根据深梁振动频谱来定义剪切修正系数，有的根据深梁静力分析理论来定义剪切修正系数.目前主要有 Timoshenko方法、Cowper方法、Stephen一一Hutchinson方法、梯形分块算法、材料力学方法、有限元方法、弹性力学方法等.一般认为，截面剪切修正系数受截面形式、结构材料、边界条件和作用载荷等的影响.Timoshenko最早提出剪切修正系数计算方法，其采用最大剪切应力与平均剪切应力之比作为剪切修正系数，并计算了矩阵、圆形、薄壁圆管、工字型、箱型等截面的剪切修正系数［14-15］.剪切修正系数的计算理论中最有影响的是能量法.最常用、最简单的能量公式如式（3）所示此式的实质就是不均匀分布的剪应力所做功与假定的平均剪切应变所做功之比.根据此计算式，得到了众多截面的剪切修正系数.1966年Cowper根据《弹性力学》中悬臂梁的剪应力分布形式及能量原理建立了计算公式［16］.对于一些简单截面，Cowper利用Love解给出的剪应力分布解析解得到了剪切修正系数的解析式，对于某些复杂截面Cowper给出了近似解，其给出的 11种常见截面剪切修正系数当今应用极为广泛［2，17］.Cowper建立其计算公式时利用截面的主弯矩轴，其Iyz=0，这样导致截面有两个剪切修正系数，即αyy，αzz.因此Cowper方法只适应于有对称轴的截面.1968年，Mason等将Cowper方法扩展到任意截面的剪切修正系数计算中，起始坐标系统可以任意定义，其计算理论中多出了两个相关剪切修正系数αyz，αzy［18］.1980年 Stephen［19］采用与 Cowper相同的过程，但采用自重作用下的剪应力分布，对Cowper理论进行修正，提出了新的剪切修正系数，将其应用于圆形、矩形截面杆的固有频率估算，其结果比Cowper方法精确，但是对于一般截面情形未能得出相同结论.2001年Hutchinson［20］利用Hellinger一一Reissner变分原理建立了另一种新的剪切修正系数公式，后来证明与Stephen方法是同一种公式，只要经过复杂的推导就可互相转化，被称为S一一H系数［21-22］. 2013年王乐等［23］采用《弹性力学》方法，得到悬臂梁纯弯曲变形条件下截面剪应力分布的精确解，基于能量原理得到了各种梁截面剪切修正系数新的表达式，然后推导了弯扭耦合变形条件下截面剪应力分布的精确解，进一步获得了该条件下截面的剪切修正系数.2008年夏桂云在截面面积、抗弯惯性矩特性计算的梯形分块算法［24］基础上提出了截面剪切修正系数的算法，其假定截面的剪应力分布服从《材料力学》中剪应力分布规律，应用最小能量原理建立剪切修正系数的计算公式，即取式（3）中的单轴向剪应力所做功，采用Gauss数值积分方法进行积分计算，用Fortran编制了截面剪切修正系数的梯形分块计算程序［25-26］，可适应于截面可梯形分块的实心截面剪切修正系数计算.推导的10种截面计算公式与Cowper公式相比，只是没有考虑泊松比效应，对桥梁工程常用的T型截面、工字型截面计算的剪切修正系数数值结果与理论结果一致.该方法和计算程序适应于常规复杂截面的剪切修正系数计算.用《弹性力学》方法来确定剪切修正系数也是一种不错的途径，其做法大致为先用《弹性力学》的方法确定简单结构的解，如挠度等，将其与考虑剪切变形影响的《材料力学》解进行比较，即可得到剪切修正系数［17］.但此方法存在同一结构由于《弹性力学》有精度不同的多种解，导致同一截面有多种剪切修正系数值［27-30］.黄文彬［27-28］、王敏中［29］、唐玉花等［30］等先后讨论了平面弹性悬臂梁剪切挠度问题，得到了不同的计算结果.用有限元方法确定截面剪切修正系数是一种简便的数值方法.Mason等［18］在基于假定的位移场，使用最小势能原理，建立了针对任意截面三角形单元划分的有限元方程.Schramm等［31］、Wagner等［32］根据弹性梁理论，用加权残值法建立了截面几何特性计算的有限元方法.Sapountzakis等［33］根据弹性梁理论建立了截面几何特性计算方法，但是使用了边界元方法求解；Chana等［34］从频率角度，提出了剪切修正系数的计算方案.陈常松等［35］利用目前成熟的弹性梁理论，建立了悬臂梁受自由扭转、约束扭转、横向剪力下的弹性方程，推导出截面翘曲函数的调和方程.引入圆柱自由边界条件，采用Galerkin方法，解出离散截面节点处的函数值，利用高斯积分计算截面几何特性，采用4节点等参元编写任意梁截面几何特性值计算的有限元程序. Pilkey［36-37］系统地介绍了利用有限元法计算截面几何特性的理论、程序编制方法等，是截面几何特性数值计算的经典著作，在国际上有广泛的影响.1992年郑泉水等［38-39］提出了Hilbert空间上用子空间变分原理来提高本构方程精度，以解决投影类型梁本构方程精度比平衡方程精度低的缺点，其研究生卢小抒［40］在此基础上利用子空间变分原理和有限元方法建立梁的深化本构方程，并利用子空间变分原理进行深梁剪切修正系数的有限元计算.1996年杜丹旭等［41］通过简化子空间变分原理的数学结构，用修正子空间变分原理消除子空间变分原理的奇异性，计算了单材料多种截面的剪切修正系数，并对圆环截面剪切修正系数的有限元结果与Cowper理论结果进行了比较，指出了修正子空间变分原理的有限元法可处理复杂截面以及层状或复合材料截面的能力.周凌远［42］采用将梁截面离散化的方式，用数值积分方法计算截面的几何特性，并根据梁的剪切变形和扭转理论，利用变分原理建立截面几何特性计算的有限元方程，求解任意形状截面的扭转常数、剪切中心、剪切修正系数等.目前大型商业软件，如Ansys，Midas，SAP，桥梁博士等都有截面几何特性计算功能.Ansys采用9节点平面单元计算截面的面积、抗弯惯性矩、中心轴、剪心、抗扭惯性矩、翘曲惯性矩、剪切修正系数等［43］.Midas软件也具备相同功能，略为不同的是采用4节点平面单元计算截面几何特性［44］.曹志远等［45］在研究中厚板的振动问题时指出，只要对板中剪切变形和挤压变形的分布作出不同假定，就可导出中厚板的Hencky理论、Reissner理论、Vlasov理论、Mindlin理论等，这些经典的中厚板理论都可退化成深梁理论，利用其偏离位移分布函数和挤压变形函数可确定剪切修正系数.4种经典中厚板理论中，剪切修正系数分别为1，6/5，6/5，12/π2.但由于其偏离位移分布函数和挤压变形函数是从中厚板理论中得来，故只能用于矩形截面梁.瞿履谦等［46］利用截面剪应力分布特征建立了剪切修正系数的计算公式，此公式的实质是截面实际分布剪应力所做剪切功与平均剪应力所做剪切功之比.经过公式推导，其建立了建筑结构中常用的对称与不对称的工字型、十字型和T型截面的剪切修正系数，并制作了大量的计算表格以供查询，得到剪切修正系数的另一种数学解释为“剪切修正系数可表示为截面剪应力与平均剪应力之比的方差再加1、也就是截面剪应力的变异系数的平方再加1”，剪应力分布越不均匀，则剪切修正系数就越大.随着深梁研究的深入，其有限元发展也很迅速.深梁有限元列式中最简单的模式是1977年Hughes提出的线性插值单元［47-48］，此单元的缺点是整个单元的弯矩和曲率为常数，单元网格必须划分较密才能获得较好的精度，而且剪切刚度过硬，存在剪切闭锁问题.1968年 Przemieniecki［49］采用工程梁理论中梁的位移微分方程，分别考虑剪切变形和弯曲变形，导出了均匀梁的刚度矩阵，该方法中挠度采用三次插值函数、转角位移采用二次插值函数，精度高、适应性强，导出的刚度矩阵是一般意义上深梁单元的精确刚度矩阵，因此广为使用.1981年胡海昌［2］根据Timoshenko两广义位移梁理论，假定深梁单元横向位移为三次插值、转角位移为二次插值，应用最小势能原理消去内部自由度，导出了深梁单元位移插值函数，是深梁单元插值函数的标准形式，并被广泛使用.但此方法由于要消除内部自由度，理论推导繁杂.Oral［50］提出了高阶等参数杂交Timoshenko梁单元.1994年周世军等［51］利用最小势能原理得到了考虑剪切变形影响的Timoshenko梁单元位移函数表达式，并导出了单元刚度矩阵、一致质量矩阵和几何刚度矩阵.2000年龚克［7］提出了单广义位移深梁理论，并利用该理论建立深梁单元，是对二广义位移梁理论的发展.2004年夏桂云等［52］从深梁的二广义位移理论出发，利用解析试函数［2］直接建立深梁单元横向位移、转角、剪切应变的插值函数，进而导出了考虑剪切变形影响的单元线弹性刚度矩阵、一致质量矩阵和几何刚度矩阵.Przemieniecki［49］、胡海昌［2］、周世军等［51］、夏桂云等［52］推导的单元位移模式、线弹性刚度矩阵都相同，是深梁单元的标准形式，为多数商业软件所采用，能克服剪切闭锁问题.2008年杜柏松等［53］从工程梁理论中的梁位移微分方程出发直接推导出考虑剪切变形影响的空间梁单元的刚度矩阵，并从动力载荷的虚功原理出发推导出考虑剪切变形影响的质量矩阵，通过实例分别比较考虑剪切变形影响和不考虑剪切变形影响对结构固有频率的影响，结果表明在剪切修正系数较大时，不考虑剪切效应会引起较大的误差.1998年李华［54］将深梁单元横向位移分解为弯曲位移和剪切位移，都采用三次插值函数，成功构造了深梁的有限元列式和刚度，是一种双挠度理论.1999年王荣辉［55］通过引入剪切转角和弯曲转角，假定横向位移为三次插值函数，导出了一种新的单元模式.此单元引入了剪切转角和弯曲转角2个自由度，比一般深梁单元的自由度多.初等梁结构几何非线性分析主要有两种方法，一种是基于T.L.列式或U.L.列式的非线性有限元方法（单元的位移函数取多项式）；另一种是稳定函数方法，其经典方法主要有Saafan理论、Brotton理论、Fleming理论，这些理论被称为有限位移理论，是大跨度杆系结构分析的主流方法［56］.对于深梁结构的几何非线性来说，李国强等［57］指出主要有4种影响因素：（1）轴力的影响（轴力对横向变形的影响）；（2）剪切变形的影响；（3）初始弯曲的影响；（4）弓形效应的影响（弯矩对轴向变形的影响）.准确地说，剪切变形不是梁的几何非线性影响因素，而是梁弯曲理论简化缺陷所带来的问题.分析轴力对杆件弯曲的影响时，一般指其 P一一δ或P一一∆效应，目前主要采用Von-Karman的大挠度理论［58-59］，建立基于 T.L.或 U.L.列式下的刚度，并结合拖动坐标来实现大位移效应的求解.刘永华等［59］利用 Ansys用户可编程特性（user programmable features，UPFS）研究考虑剪切变形后的弓形效应实用方法，研究了空间梁单元转角位移函数的级数展开形式，给出了弯曲缩短与轴力间的近似函数关系，避免迭代运算.钱若军等［60］讨论了空间梁柱的几何非线性分析方法，并对剪切闭锁产生的原因、防止剪锁的方法进行了详细探讨.2006年夏桂云［61］在其博士论文中参考初等梁的有限位移理论［62-63］，利用Timoshenko深梁的解析函数，建立了Timoshenko深梁相应的Saafan理论、Brotton理论、Fleming理论，将有限位移理论从初等梁推广至深梁.并对单元轴力N=0时的特殊情况进行了处理，建立了通用的弓形效应分析方法.李国强等［64］以考虑剪切变形影响的深梁双挠度理论为基础，建立了考虑轴力影响的几何非线性分析方法，导出了包含剪切变形影响的深梁单元刚度矩阵，为解决数值计算中当轴力很小时可能出现不稳定现象，给出了刚度的级数展开形式［65］.深梁单元刚度展开后，如同初等梁一样，取前两项时，第一项为线弹性刚度、第二项为初应力刚度（或称几何刚度）［56］.1992年笹川和郎［66］利用考虑剪切变形影响的深梁双挠度理论，建立了有轴力作用下的单元刚度矩阵，其与夏桂云、李国强等建立的刚度矩阵一致.并推导了多种深梁单元在轴力和横向载荷共同作用下的固端力表达式.2004年赵红华等［67］通过分析横向剪切变形对梁单元的影响、轴心力的二次影响以及约束扭转时翘曲引起的二次剪应力效应，引入了翘曲函数及三次多项式的扭转模式，得到了7个自由度的杆系结构精确模型.在几何非线性分析中，考虑了轴向载荷、平面弯曲、剪切、约束扭转翘曲以及载荷一一变形各效应的耦合，建立了变形状态几何非线性分析的切线刚度矩阵.利用基于弧长法的球面显式迭代一一增量法，进行了空间结构的几何非线性全过程分析.1995年黄文等［68-69］以三维连续体的虚功增量方程为基础，采用平动、转角位移分别插值方法，导出了深梁结构大位移、大转动问题分析的U.L.列式方法，其考虑了轴力、剪切变形、弯曲、扭转等效应，提出了新的几何刚度矩阵.1988 年Dvorkin等［70］提出考虑大位移、大转角的Timoshenko梁增量分析的T.L.方法，并推导了相应的切线刚度矩阵，文中采用了Argyris提出的描述大转动的转换方法.1979年Bathe等［71］根据三维连续体虚功方程，提出了适应大转动效应的Timoshenko空间梁的T.L.列式和U.L.列式方法，通过增加两个附加自由度来考虑剪切变形影响，单元结点有7个自由度，非线性刚度通过三维积分得到，积分点多达254个［72］，工作量非常大，其据此编制了Adina 的4号梁单元，材料可以为线弹性和弹塑性.1992年陈政清等［72］以三维连续体的虚功增量方程为基础，导出了空间梁单元大挠度问题分析的U.L.列式法，提出了新的几何刚阵形式.理论与算例表明其新建立的方法与ADINA的4号梁单元精度相同，但计算时间大大减少，并能适用于任意形状截面的杆件.其编制的NACS程序具有分析大型空间柔性结构在非常规载荷作用下的强非线性行为的能力，可用于斜拉桥、悬索桥的非线性分析中，并得到了工程界的青睐.1994年舒兴平［73］在试验基础上认识到钢框架结构的剪切变形较大，其影响不应忽略，后基于有限变形理论，利用空间梁单元模式，采用考虑剪切变形影响的3次多项式位移插值函数，建立了考虑剪切变形影响的空间钢框架结构几何非线性、材料非线性分析方法，并分析了一个6层的钢框架结构.在框架结构分析中，考虑剪切变形影响、几何和材料非线性的高等分析还有刘坚［74］、郑廷银［75］、万金国［76］所做的类似系列工作等.考虑剪切变形影响的杆系结构材料非线性分析中，Hinton等［77］研究了深梁的弯曲变形，并编制了计算程序.崔世杰等［78］也做了相同的工作，其研制的程序与文献［77］相近.舒兴平［73］在空间钢框架结构的非线性分析中考虑了材料非线性，并分析了一个6层的钢框架结构.李国强等［64］、郑廷银［75］利用深梁理论，同时考虑材料和几何非线性特性，对框架结构的双重非线性分析方法进行了系统的研究.笹川和郎［66］在研究框架结构的材料非线性时也同时考虑了剪切变形影响.黄侨等［79-80］根据混凝土的塑性理论及极限分析的上限方法，探讨了求解钢筋混凝土简支深梁的抗剪强度的数值计算方法，分析了钢筋混凝土简支深梁发生塑性剪切破坏时屈服线的形状以及屈服线上混凝土和钢筋的能量耗散情况，建立了钢筋混凝土简支深梁的2个剪切破坏机构的模型，通过对这2个破坏机构的计算分析，求出了与破坏机构对应的极限载荷.庞苗等［81］为提高钢筋混凝土梁的计算效率和精度，提出了一种基于梁截面弯矩一一曲率关系的宏观有限元方法，在此基础上利用Timoshenko梁弯曲理论建立考虑横向剪切变形影响的钢筋混凝土梁的有限元分析模型，通过对试验梁的分析、对比，验证了所提出的分析方法的适用性.夏桂云等［25］通过假定单元的统一位移场，建立了可以考虑材料非线性的钢筋混凝土Timoshenko深梁组合单元，来分析桥梁结构等非线性特征和极限承载力.梁结构振动理论的研究历史较长，研究成果丰富［82］.自 18世纪以来，各国学者提出一系列理论，经典的理论主要有：（1）基于直法线和截面不变形条件下的Bernoulli一一Euler梁振动理论［82］，目前绝大多数结构振动书藉论述杆系结构振动时都采用此理论，尤其在桥梁、建筑等土木工程中最为典型；（2）考虑梁弯曲引起转动惯量的Rayleigh梁振动理论［83］；（3）考虑剪切变形影响的剪切梁振动理论［84］；（4）同时考虑剪切变形和转动惯量的Timoshenko梁振动理论［85］，此为经典的Timoshenko梁振动理论；（5）陈镕等［86］既考虑剪切变形影响和转动惯量，又考虑剪切变形引起转动惯量影响的修正Timoshenko深梁振动理论.陈镕认为，传统的Timoshenko深梁振动理论没有考虑到剪切变形引起的转动，导致振动方程非常复杂，考虑剪切变形引起的转动后，所建立的方程形式简单，并且只有一个相速度系、一个群速度系、一个固有频谱，克服了经典Timoshenko梁理论一个振型对应两个振动频率的困惑.1973年Dym等［85］应用变分原理导出了传统的Timoshenko梁的振动方程，分析中考虑了剪切变形影响及截面转动惯量影响，比较了简支初等梁、深梁自由振动频率的差别，讨论了分别只考虑转动惯量和剪切变形影响时的深梁自由振动频率解的近似程度.1983年曹志远［87］推导了简支一一简支、自由一一自由、固支一一固支、固支一一自由、固支一一简支、简支一一自由等6种边界条件下深梁振动频率的特征方程.1961年 Huang［83］也进行了相同的工作，计算中考虑了剪切变形影响和截面转动惯矩的影响，并对悬臂梁等的自由振动频率进行了计算.夏桂云等［25］利用变分原理建立了Timoshenko振动方程，导出了单梁多种边界条件下的深梁振动频率的特征方程.夏桂云等［52］建立了深梁单元的位移模式，分析了悬梁梁的振动频率.2002年楼梦麟等［88］应用模态摄动法求解Timoshenko梁的振动模态特性，对两端简支的Timoshenko梁得到了精确理论解，对比了两端简支的Timoshenko梁、Euler梁、纯剪切梁的模态特性及其影响因素，讨论了Timoshenko简支梁自由振动频率随长细比及模态数的变化情况.楼梦麟等［89］还讨论了固端Timoshenko梁振动频率求解的近似方法.周平等［90］采用Timoshenko梁动态刚度矩阵研究船体的总振动问题，导出了Timoshenko梁动态刚度矩阵的显示表达式.陈准［91］建立了考虑梁单元剪切变形和转动惯量影响的框架结构动力分析的动态有限元方法，阐述了框架结构有限单元各阶振动约束模态函数的概念，并用它组成结构有限单元各阶动态形函数矩阵，说明了使用递推方法计算结构的各阶振动特性以及利用动态有限元方法求解框架结构动态响应和动应力的方法.Eisenberger［92］同样建立了 Timoshenko梁动态刚度矩阵.韩博宇等［93］应用直接模态摄动法研究了变截面 Timo-shenko固端及简支梁的自由振动特性，并通过算例，讨论了这两种支撑条件下梁高的斜率及长细比对梁各阶主频率的影响.张汝清等［94］建立了Timoshenko梁振动的对偶变量求解体系，提出了分离变量法.芮筱亭等［95］系统研究了多体系统传递矩阵法，其中就包括了Timoshenko梁系统.刘庆潭等［96］也广泛研究了深梁振动的传递矩阵法.李。

第二个问题的实作范例1——悬臂梁受均布压力载荷的弯曲问题1.问题描述与解析解有一个如图0所示的悬臂梁（截面为10mm*10mm的矩形，长度100mm），受均布压力载荷10N/m2。

试求出该悬臂梁的最大应力和最大挠度。

（它的解析解已经解完了，在图0的下面，挠度7.5e-6mm，应力0.003MPa，即3000Pa。

）图0 悬臂梁的问题描述2. 用CATIA中的工程分析模块（即CAE模块）求解该问题的思路1）. 启动CATIA，建立一个悬臂梁的3D模型，设置单位，加材料。

（这一步已经做完了。

）2）. 然后，进入工程分析模块，加固定约束，加均布载荷，求解，查看结果。

3）. 分析两次计算，第一次线性单元的边长为6mm，计算精度很低。

第二次抛物线单元的边长为3mm，CATAI得到的挠度、应力与解析解基本一致。

3 在CATIA求解该问题的操作指导1）. 启动CATIA，打开xuanbiliang目录下的xuanbiliang.CATPart文件，在该文件中的几何模型中已经加好了材料（钢）。

2）. 进入创成式零件有限元分析模块，如图1。

之后点击“确定”，如图2。

图1图23）. 在零件的有限元模块中选择工具条中的按钮，按照如图3所示的方式选择梁的一个端面，点击“确定”，即可完成悬臂约束的施加。

（该约束限制了空间中的6各自由度。

）图34）. 选择工具条中的按钮，并选择悬臂梁的上表面，在pressure中输入10N_m2，如图4、图5。

施加了载荷与约束的悬臂梁如图6。

图4图5图65）. 在特征树的finite element model.1——nodes and elements 下的上双击，如图7。

弹出如图8的对话框，在size中输入6mm的单元边长，点击确定。

图7 图86）. 选择工具条中的按钮，在弹出的对话框中分别点击“确定”、YES，即可自动完成计算，如图9。

如图9 7）. 选择工具条中按钮查看受力后的变形形状。

悬臂梁ansys有限元分析求最大挠度（一） 悬臂梁ansys 有限元分析求最大挠度问题：悬臂梁长1000mm ，宽50mm ，高10mm ，左端固定，求其在自重作用下的最大挠度？解：弯矩方程：221)()(x l q x M --=微分方程： 221'')(x l q y EI z-=积分求解：DCx qx qlx x ql y EI Cqx qlx x ql y EI z z +++-=++-=4322322'2416125.0615.05.0由边界条件：0;0,0''====A A A y y x θ 得：C=0，D=0I=1/12*h^3*b,h 为梁截面的高，b 为梁截面的宽。

q=ρ*g*a*h*l材料力学公式求：Y=EI85gahl^ρ=5.733mmq EILANSYS 模拟求：Y=5.5392mm，详细见下步骤ANSYS 软件设置及其具体过程如下：步骤1：建立一个模型，在model下creat一个长1，宽0.05，高0.01的长方体实体。

（单位默认为m）步骤2：材料属性设置。

密度：7800，杨氏模量：2E11，泊松比0.3。

步骤3：划分网格。

设置网格单元为structure solid brick 8node 185，mesh tool中设置网格大小为0.002，HEX下点击mesh。

步骤4：施加载荷；在preprocessor中inertia中设置重力加速度Y方向为9.8。

在左面施加固定约束（三个方向固定）步骤5:：求解。

在solve下solve current LS。

步骤6：后处理查看。

在result中plot result，查看nodes displacement。

List查看文本，观察nodes的最大位移点。

从化职称改革职称论文发表-薄壁铝板|工装平台|平面度|工作孔论文选题题目从化职称改革职称论文发表-以下是薄壁铝板|工装平台|平面度|工作孔职称论文发表选题参考题目，均采用云论文发表选题题目软件，经过大数据搜索对比精心整理而成，各职称论文发表题目均为近年来所发表论文题目，可供薄壁铝板|工装平台|平面度|工作孔职称论文发表选题参考题目，也可以作为薄壁铝板|工装平台|平面度|工作孔毕业论文撰写选题参考。

更多论文选题，论文发表题目可登陆“云发表”网站自主选择！关键词：医学论文编辑，化学教学论文发表，法学学年论文选题1……平面机构运动输出精度可靠性及寿命2……平面二自由度七连杆机构分支自动识别研究3……基于动态极值理论和Copula函数的极端海平面高度预测建模4……基于均匀试验设计的平面度误差测量技术5……基于改进蚁群算法的薄壁件柔性工装布局优化(英文)6……7050铝合金厚板平面应变断裂韧度的研究7……3D打印工作台平面度的差分式光电检测与补偿8……平面光学元件平面度动态干涉拼接测量9……高精度平面气浮导轨的误差均化效应研究10……疏导式热控结构温度分布研究11……平板压电除冰系统中压电元件排布规律研究12……平面度误差检测平台设计与数据处理13……断块油藏平面动用均衡程度实验研究14……圆柱薄壁筒件典型工装数字化设计系统研究15……基于Deform的热轧3003铝板带温度场的三维有限元模拟16……平面铝板上的压电振动除冰方法17……基于B_z(p_(max))相轨迹的电磁涡流无损检测方法18……铸轧Al-Mn合金板材的各向异性分析19……基于空间分布熵的电磁脉冲涡流无损检测方法20……水声无源材料回声降低测量时反聚焦方法21……基于多元线性回归的6016汽车铝板FLD_0预测模型22……平面2自由度并联机器人的解耦控制和仿真分析23……不同强度系列钢铝板材压力连接成形规律研究24……一种平面二自由度并联机器人机构刚度性能与运动学参数关系研究25……盘类薄壁零件车削加工减震工装设计及应用26……利用MATLAB进行焦平面探测器的In柱高度自动统计27……一种检查机载LiDAR平面精度的新方法28……多国研究指出南极冰融化致海平面上升幅度超预期29……新型平面折展机构柔性铰链等效刚度分析30……基于最小区域平面度评定的三维曲面构建31……不同压力梯度平面库埃特流中扰动涡动力学特性32……平面连杆机构运动精度可靠性及灵敏度分析33……基于微分进化算法的平面度误差评定34……平面2自由度并联机构动力学性能优化35……平面2自由度冗余驱动并联机构的工作空间(英文)36……静电纺丝法制备定向排列微/纳米纤维及其机理37……薄板台阶断面件FCF加工硬化特性38……铝合金-聚合物复合层板弯曲回弹理论分析39……基于有限元分析的大跨度平面闸门设计研究40……激光扫描多平面动态测量下颈椎椎间高度退变后椎间孔的变化41……激光声表面波检测材料表面微缺陷数值研究42……静电纺定向排列微/纳米纤维束的湿热牵伸43……三自由度永磁同步平面电机的控制策略44……平面内压力和侧向压力组合作用下预测连续加劲铝板极限强度的经验公式45……局部平面波叠前深度偏移46……基于单程波动方程平面波叠前深度偏移47……基于数据预处理的平面不确定度评定技术研究48……飞行器薄壁件柔性工装定位/支承阵列优化自生成研究49……High precision measurement method of parameters of plane circle based on stereo vision基于立体视觉的平面圆参数高精度测量算法*50……平面镜多次反射的二维高精度小角度偏转测量51……固定角度平面镜标定方法与不确定度分析52……Reflectivity uncertainty analysis of planar mirror calibration in BSRF同步辐射标定平面镜反射率不确定度分析方法研究53……平面三自由度惯性压电叠堆移动机构研究54……均匀受压工字型等截面三铰圆弧钢拱的平面内稳定性和极限强度55……基于Geant4的介质深层充电电场计算56……3-RRR平面并联机构刚度分析57……平面内压力和侧向压力组合作用下连续加劲铝板弹性屈曲和极限强度的敏感性分析58……对称切口拉伸法评价高强度涂层及平面应力有限元分析59……TDLAS测量甲烷/空气预混平面火焰温度和H_2O浓度60……一种改进的位平面复杂度分割算法61……弹性铰平面并联三自由度机器人连续刚度映射研究62……超精密平面研磨加工压力对精度的影响63……FFT在平面机械结构声学灵敏度分析中的应用64……Virtue Plane Mapping: A Method of Rendering into Depth Images虚平面映射:深度图像内部视点的绘制技术65……平面尺寸链灵敏度分析的区间方法66……三自由度绳牵引平面并联机器人力/位控制研究67……三维情况下平面介质交界面处二阶精度FDTD方程68……Measurement of Temperature Field in a Fast Liquid-Liquid Mixing Process byPLIF平面激光诱导荧光技术用于快速液液混合过程温度场测量69……基于相位相关与块匹配的纳米精度微器件平面动态测量70……真空吸附在薄板加工中的应用71……柱面波分解测量反射系数的一些分析72……基于VC环境下求平面度误差的编程技术73……平面二自由度全铰链五杆轨迹机构综合方法的研究74……表面垂直裂痕诱发瑞利波散射的数值分析75……条状功能梯度材料中偏心裂纹对反平面简谐波的散射问题76……直线度平面度公差的快速评定测点分类法77……双自由度平面五杆机构机电系统的轨迹控制78……激光超声在缺陷材料中散射波形的声谱分析79……新型平面三自由度冗余并联机构的动力学分析80……给定平面内直线度误差评定的实用方法81……平面应变状态下基于统一强度理论的土压力计算82……混合驱动平面两自由度七杆机构最优运动规划83……长白山阔叶红松林的零平面位移和粗糙度84……大型硅晶片平面度精密纳米计量技术(英文)85……平面串联型冗余度机器人的混沌运动研究86……平面三自由度并联机构的惯性力平衡87……保证和提高磨削薄弱零件两端平面平行度精度的新途径88……单自由度平面闭链机构构型方法的研究89……无限长条功能梯度材料的反平面裂纹问题90……平面四杆机构运动精度可靠性分析与数字仿真91……可视化平面度自动检测系统92……HB型共永磁体二自由度平面直线电动机的研究93……基于平面波合成的傅里叶有限差分叠前深度偏移94……一种自适应的平面线轮廓度误差评定方法95……机械加工过程中网孔大薄板平面度工艺控制研究96……平面弹性悬臂梁剪切挠度的进一步研究97……平面型载体催化元件制作过程中的温度自控系统98……极点迭代法──一个求最小条件平面度误差的快速、精确算法99……浅析高等级公路平面控制导线网精度对实地放线的影响100……平面包络环面蜗杆加工误差诊断及提高制造精度的研究。