悬臂梁挠度计算公式

为保证承重结构的承载能力和防止在一定条件下出现脆性破坏，应根据结构的重要性、荷载特征、结构形式、应力状态、连接方法、钢材厚度和工作环境等因素综合考虑，选用合适的钢材牌号和材性。

承重结构的钢材宜采用Q235钢、Q345钢、Q390钢和Q420钢，其质量应分别符合现行国家标准《碳素结构钢》GB/T700和《低合金高强度结构钢》GB/T 1591的规定。

当采用其他牌号的钢材时，尚应符合相应有关标准的规定和要求。

对Q235钢宜选用镇静钢或半镇静钢。

承重结构的钢材应具有抗拉强度、伸长率、屈服强度和硫、磷含量的合格保证，对焊接结构尚应具有碳含量的合格保证。

焊接承重结构以及重要的非焊接承重结构的钢材还应具有冷弯试验的合格保证。

对于需要验算疲劳的焊接结构的钢材，应具有常温冲击韧性的合格保证。

当结构工作温度等于或低于0℃但高于-20℃时，Q235钢和Q345钢应具有0℃C冲击韧性的合格保证；对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。

当结构工作温度等于或低于-20℃时，对Q235钢和Q345钢应具有-20℃冲击韧性的合格保证；对Q390钢和Q420钢应具有-40℃冲击韧性的合格保证。

对于需要验算疲劳的非焊接结构的钢材亦应具有常温冲击韧性的合格保证，当结构工作温度等于或低于-20℃时，对Q235钢和Q345钢应具有0℃冲击韧性的合格保证；对Q390钢和Q420钢应具有-20℃冲击韧性的合格保证。

当焊接承重结构为防止钢材的层状撕裂而采用Z向钢时，其材质应符合现行国家标准《厚度方向性能钢板》GB/T 5313的规定。

钢材的强度设计值（材料强度的标准值除以抗力分项系数），应根据钢材厚度或直径按表1采用。

钢铸件的强度设计值应按表2采用。

连接的强度设计值应按表3~5采用。

1钢材的强度设计值（N/mm2）表1注：表中厚度系指计算点的钢材厚度，对轴心受力构件系指截面中较厚板件的厚度。

2钢铸件的强度设计值（N/mm2）表23焊缝的强度设计值（N/mm2）表3注：1．自动焊和半自动焊所采用的焊丝和焊剂，应保证其熔敷金属的力学性能不低于现行国家标准《碳素钢埋弧焊用焊剂》GB/T 5293和《低合金钢埋弧焊用焊剂》GB/T 12470中相关的规定；2．焊缝质量等级应符合现行国家标准《钢结构工程施工质量验收规范》GB 50205的规定。

材料力学挠度计算公式：
1、在跨中单个荷载F作用下的挠度是：F*L^3/(48EI)
2、在均不荷载q作用下的挠度是：5*q*L^4/(384EI)
3、在各种荷载作用下，利用跨中弯矩M可以近似得到统一的跨中挠度计算公式：0。

1*M*L^2/(EI)。

其中：p=kN=1000N，L=8。

16m=8 160mm，E=2。

1x10^5N/mm^2=210000N/mm^ 2，Ix=5280cm^4=52800000mm^4，计算结果单位= mm。

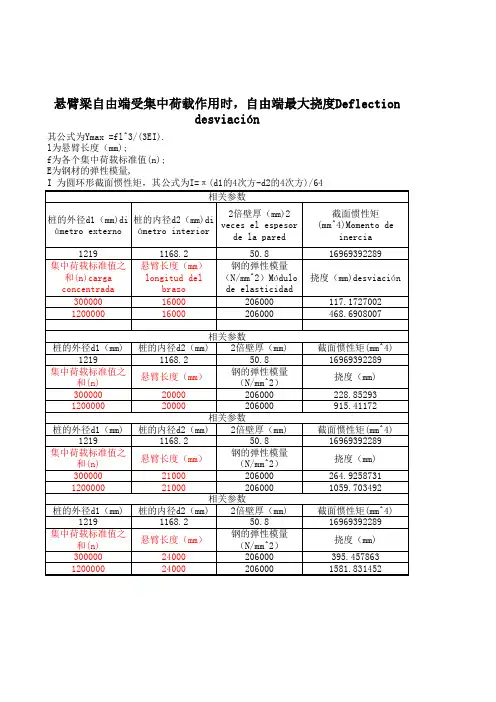
悬臂梁受均布荷载或自由端受集中荷载作用时，自由端最大挠度分别为的,其计算公式:
Ymax=1ql^4/(8EI)。

;Ymax=1pl^3/(3EI)。

q为均布线荷载标准值(kn/m)。

;p为各个集中荷载标准值之和(kn)。

你可以根据最大挠度控制1/400，荷载条件25kn/m以及一些其他荷载条件。

扩展资料
挠度是在受力或非均匀温度变化时，杆件轴线在垂直于轴线方向的线位移或板壳中面在垂直于中面方向的线位移。

细长物体（如梁或柱）的挠度是指在变形时其轴线上各点在该点处轴线法平面内的位移量。

薄板或薄壳的挠度是指中面上各点在该点处中面法线上的位移量。

物体上各点挠度随位置和时间变化的规律称为挠度函数或位移函数。

通过求挠度函数来计算应变和应力是固体力学的研究方法之一。

工字钢挠度计算公式工字钢是一种常见的结构钢材，广泛应用于建筑、桥梁、机械制造等领域。

在使用过程中，我们常常需要了解工字钢的挠度情况，以便评估其承载能力和结构稳定性。

工字钢的挠度计算是基于悬臂梁的理论基础上进行的。

悬臂梁是指梁的一端固定，另一端自由悬挂。

工字钢在实际应用中常常处于悬臂状态，因此可以采用相应的悬臂梁挠度计算公式进行计算。

工字钢的挠度计算公式如下：δ = (5 * q * L^4) / (384 * E * I)其中，δ表示工字钢的挠度，q表示悬臂梁上的集中载荷，L表示悬臂梁的长度，E表示工字钢的弹性模量，I表示工字钢截面的惯性矩。

在实际应用中，我们需要根据具体的工字钢尺寸和载荷情况来计算挠度。

首先，我们需要测量工字钢的长度L，并计算出截面的惯性矩I。

惯性矩是描述截面形状对于承载能力的影响的重要参数，可以通过工字钢的几何尺寸计算得出。

接下来，我们需要确定悬臂梁上的集中载荷q。

集中载荷是指作用在悬臂梁上的单点力或集中力，可以通过实际测量或结构设计参数得出。

我们需要知道工字钢的弹性模量E。

弹性模量是描述材料对外力作用下变形程度的物理量，可以通过实验测量或查阅资料得到。

根据上述计算公式，我们可以将具体数值代入进行计算，从而得出工字钢的挠度。

挠度的数值可以帮助我们评估工字钢的承载能力，如果挠度过大，则可能存在结构安全隐患，需要采取相应的加固措施。

工字钢挠度的计算也对工字钢的设计和选型具有重要意义。

通过计算不同尺寸和材质的工字钢的挠度，可以比较不同方案的承载能力和结构稳定性，从而选择合适的工字钢材料和尺寸。

工字钢的挠度计算是工程设计和结构评估中重要的一环。

通过合理计算工字钢的挠度，可以评估其承载能力和结构稳定性，为工程安全提供重要参考。

同时，工字钢挠度的计算也对工字钢的设计和选型具有指导意义，帮助选择合适的工字钢材料和尺寸。

梁的刚度计算范文梁的刚度是指材料在受到外力作用时的抵抗变形的能力。

在工程中，刚度是一个非常重要的参数，它决定了梁的强度和稳定性。

梁的刚度计算可以通过不同的方法进行，下面将介绍两种常用的计算方法：简支梁的刚度计算和悬臂梁的刚度计算。

一、简支梁的刚度计算简支梁是指两个端点都可以转动的梁，它的刚度可以通过弯曲刚度来计算。

弯曲刚度是指单位长度下的梁的抵抗弯曲变形的能力。

1.简支梁的弯曲刚度公式简支梁的弯曲刚度可以通过以下公式进行计算：EI=(WL^3)/(48D)其中，EI为弯曲刚度，W为作用在梁上的力或负荷，L为梁的长度，D为梁的挠度。

2.弯曲刚度的单位和性质弯曲刚度的单位是N.m^2，它的数值越大，梁的刚度越高。

弯曲刚度与梁的材料属性有关，即与材料的弹性模量E和惯性矩I有关。

E表示材料的刚度，单位为N/m^2，I表示梁的惯性矩，单位为m^4、弯曲刚度EI 的数值越大，表示材料的刚度越高。

二、悬臂梁的刚度计算悬臂梁是指只有一个端点可以转动的梁，它的刚度可以通过挠度和力矩进行计算。

1.悬臂梁的挠度计算悬臂梁的挠度是指梁在受到外力作用时的弯曲变形。

悬臂梁的挠度可以通过以下公式进行计算：δ=(FL^3)/(3EI)其中，δ为悬臂梁的挠度，F为作用在梁上的力或负荷，L为梁的长度，E为梁的弹性模量，I为梁的惯性矩。

2.悬臂梁的刚度计算悬臂梁的刚度可以通过力矩和挠度的比值来计算：K=M/δ其中，K为悬臂梁的刚度，M为悬臂梁上的力矩，δ为悬臂梁的挠度。

总结：梁的刚度是指梁在受到外力作用时的抵抗变形的能力。

梁的刚度可以通过弯曲刚度和挠度进行计算。

简支梁的刚度可以通过弯曲刚度进行计算，悬臂梁的刚度可以通过力矩和挠度的比值进行计算。

两种方法都可以用来计算梁的刚度，根据具体的梁结构和受力情况选择适当的计算方法。

工程力学挠度计算公式在工程力学领域中，挠度是一个重要的参数，用来描述结构在受力作用下的变形情况。

挠度计算公式是工程师在设计和分析结构时必须掌握的基本知识之一。

通过挠度计算公式，可以帮助工程师预测结构在实际工作中的变形情况，从而确保结构的安全性和稳定性。

挠度计算公式的推导通常是基于梁的弹性理论。

在弹性理论中，假设结构受到的载荷是小幅度的，且结构材料具有线弹性特性。

根据这些假设，可以得到梁的挠度计算公式，其基本形式为：δ = (F * L^3) / (3 * E * I)其中，δ表示梁的挠度，F表示作用在梁上的外力，L表示梁的长度，E表示梁的弹性模量，I表示梁的惯性矩。

这个公式是工程力学中常用的简化形式，适用于许多工程实际问题的分析。

在实际工程中，为了更准确地计算结构的挠度，有时还需要考虑结构的边界条件、截面形状等因素。

对于不同形状和受力条件的结构，挠度计算公式可能会有所差异。

例如，对于悬臂梁、简支梁、悬臂梁等不同类型的梁，其挠度计算公式会有所不同。

除了梁的挠度计算公式外，对于其他类型的结构如板、壳、柱等，也有相应的挠度计算公式。

这些公式通常是基于结构的几何形状、材料性质和受力条件等因素推导而来的。

工程师在实际工作中需要根据具体情况选择合适的挠度计算公式，并结合有限元分析等方法进行结构的挠度分析。

总的来说，挠度计算公式是工程力学中的重要概念，对于工程师设计和分析结构具有重要意义。

掌握挠度计算公式可以帮助工程师更好地理解结构的变形特性，从而设计出更安全、稳定的工程结构。

在工程实践中，工程师需要灵活应用挠度计算公式，结合实际情况进行分析，确保结构的安全性和可靠性。

常用挠度公式常用的挠度公式指的是用于计算结构物挠度的公式，挠度是指结构物在受力作用下发生的形变。

挠度公式的应用十分广泛，涉及到工程、建筑、力学等领域。

在工程中，我们经常需要计算结构物的挠度，以评估其受力性能和安全性。

挠度公式是用来描述结构物在受力作用下发生的弯曲变形的数学公式。

常用的挠度公式有梁的挠度公式和杆的挠度公式。

我们来看梁的挠度公式。

梁是一种常见的结构物，在很多工程中起着承载和支撑作用。

梁的挠度是指梁在受力作用下发生的弯曲形变程度。

梁的挠度公式可以根据梁的几何形状、材料性质和受力情况进行推导。

常用的梁的挠度公式有三种，分别是简支梁的挠度公式、悬臂梁的挠度公式和悬臂梁的挠度公式。

简支梁的挠度公式是根据梁的几何形状和受力情况推导出来的。

简支梁的挠度公式可以用来计算在梁两端施加集中力或均布力时梁的挠度。

简支梁的挠度公式是根据梁的受力平衡方程和弯矩-挠度关系推导出来的。

简支梁的挠度公式可以表述为：挠度=（集中力或均布力乘以梁的长度的平方）/（48倍的弹性模量和惯性矩的乘积）。

悬臂梁的挠度公式是用来计算在梁一端施加集中力或均布力时梁的挠度的公式。

悬臂梁的挠度公式可以根据悬臂梁的受力平衡方程和弯矩-挠度关系推导出来。

悬臂梁的挠度公式可以表述为：挠度=（集中力或均布力乘以梁的长度的平方）/（3倍的弹性模量和惯性矩的乘积）。

杆的挠度公式是用来计算杆在受力作用下发生的挠度的公式。

杆的挠度公式可以根据杆的几何形状、材料性质和受力情况进行推导。

常用的杆的挠度公式有两种，分别是短杆的挠度公式和长杆的挠度公式。

短杆的挠度公式是用来计算短杆在受力作用下发生的挠度的公式。

短杆的挠度公式可以根据短杆的受力平衡方程和弯矩-挠度关系推导出来。

短杆的挠度公式可以表述为：挠度=（集中力或均布力乘以杆的长度的平方）/（2倍的弹性模量和截面面积的乘积）。

长杆的挠度公式是用来计算长杆在受力作用下发生的挠度的公式。

长杆的挠度公式可以根据长杆的受力平衡方程和弯矩-挠度关系推导出来。

三跨连续梁 内力计算公式(一)三跨连续梁 内力计算公式1. 弯矩计算公式•综合法：根据对称轴原理，可以得到弯矩计算公式为：M =qL 28，其中q 为荷载值，L 为跨度。

• 悬臂法：对于三跨连续梁中两个悬臂梁的弯矩计算，可以使用悬臂法，其公式为：M =qL 212，其中q 为荷载值，L 为悬臂梁的长度。

2. 剪力计算公式• 剪力平衡法：根据剪力平衡原理，可以得到剪力计算公式为：V =qL 2，其中q 为荷载值，L 为跨度。

• 弯矩法：根据弯矩和剪力的关系，可以得到剪力计算公式为：V =−dM dx ，其中M 为弯矩，x 为跨度上的任意位置。

3. 梁的挠度计算公式• 三跨连续梁的挠度计算可以使用弹性力学理论，其中常用的公式是梁的挠度计算公式为：δ=5qL 4384EI ，其中q 为荷载值，L 为跨度，E 为梁的弹性模量，I 为梁的惯性矩。

• 对于三跨连续梁中两个悬臂梁的挠度计算，可以使用悬臂梁挠度计算公式为：δ=qL 4192EI ，其中q 为荷载值，L 为悬臂梁的长度，E 为梁的弹性模量，I 为梁的惯性矩。

举例解释假设有一根三跨连续梁，其总跨度为10米，其中两个悬臂梁的长度为2米，受到均匀分布荷载为10kN/m 的作用。

根据上述计算公式，可以得到以下结果：1. 弯矩计算：• 综合法：M =10×1028=125 kNm • 悬臂法：M =10×2212=103 kNm ，对应两个悬臂梁 2. 剪力计算：• 剪力平衡法：V =10×102=50 kN• 弯矩法：根据弯矩和剪力的关系，可以在弯矩计算的基础上求得剪力分布。

例如，在距离支座2米处的剪力为V =−dM dx =−1255=−25 kN 。

3. 梁的挠度计算：• 综合法：δ=5×10×104384×E×I ，需要进一步提供梁的弹性模量E 和惯性矩I 来计算。

• 悬臂法：δ=10×24192×E×I ，同样需要提供梁的弹性模量E 和惯性矩I 。

2023年第08期总第315期薄壁箱型悬臂梁挠度计算方法探讨袁春辉杨继湖北佳恒科技股份有限公司，湖北十堰，442500摘要：在起重机结构设计中，薄壁箱型结构应用较多，以吊臂和支腿为典型，而吊臂和支腿设计计算中，挠度是重要的考量指标，因此薄壁箱型结构的挠度计算较为关键。

据此，从理论计算和有限元计算两种方法入手，针对某个车型的具体尺寸及载荷数据分别计算不同工况下的挠度值，分析说明计算结果的差异，从而得到两种贴合实际工况的计算方式。

关键词：起重机；薄臂箱型悬臂梁；挠度计算；有限元法中图分类号：U462收稿日期：2023-06-10DOI：10 19999/j cnki 1004-0226 2023 08 0121前言起重机的吊臂、支腿一般都设计为伸缩式薄壁箱型结构，类似于悬臂梁受力方式。

设计中均需校核吊臂和支腿的挠度。

在产品概念设计阶段，一般会根据粗算的受力情况，通过理论计算来确定截面尺寸。

计算过程中发现采用不同方法得到的挠度值有一定偏差，尤其是采用初等梁理论的计算值偏差较大。

本文以某一个支腿截面为例，将支腿的受力简化为悬臂梁计算模型（图1），相关截面参数见图2，分别采用理论计算和有限元计算两种方法。

理论计算时考虑了初等梁理论的挠度计算及考虑剪切变形影响的挠度计算；有限元计算则分别采用梁单元、板壳单元和实体单元三种单元得到对应结构的挠度值。

图1支腿受力简化为悬臂梁2理论计算挠度值2 1初等梁理论挠度计算参考刘鸿文撰写的《材料力学》［1］计算公式，则集中力作用下自由端最大挠度为：W max=FL 33EI（1）2 2考虑剪切变形效应的薄壁箱型悬臂梁挠度计算初等梁理论未考虑剪切变形效应，对于薄壁箱型结构，需考虑剪切变形效应。

考虑剪切变形效应时悬臂梁的挠度计算公式如下：W max=FL 33EI +FLGA w（2）式中，G 为剪切模量；A w 为箱型截面腹板面积。

2 3薄壁箱型悬臂梁挠度理论计算值假设悬臂梁长度为3100mm ，自由端受集中力为100000N ，采用上面两种方法计算得到挠度的数值如表1所示。

梁的挠度公式
梁的挠度公式是描述材料在作用力下产生的弯曲变形程度的数学公式。

挠度是指材料在受力作用下产生的弯曲变形的程度，即材料在受到扭矩或弯矩作用后的弯曲程度。

梁的挠度公式可以用来计算梁的挠度值。

对于简支梁来说，梁的挠度公式可以表示为：
δ = 5 * q * L^4 / (384 * E * I)
其中，δ是梁的挠度，q是分布载荷，L是梁的长度，E是杨氏模量，I是梁的截面转动惯量。

这个公式的推导基于梁的弯曲理论和力学原理，并假设梁的截面在弯曲时保持平面和线性弹性。

这个公式适用于简支梁，并不适用于其他类型的梁，如悬臂梁或连续梁。

梁的挠度公式在工程设计中具有重要的应用价值。

通过计算梁的挠度，工程师可以评估材料在受力作用下的变形程度，进而确定梁的设计参数，以确保结构的安全性和稳定性。

需要注意的是，梁的挠度公式是基于一些假设和理论前提推导得出的近似解，并不能考虑材料的非线性和复杂载荷情况。

在实际工程中，需要结合实际情况、材料特性和精确计算方法来评估梁的挠度和结构的性能。

总之，梁的挠度公式是描述梁的弯曲变形程度的数学公式，它在工程设计中具有重要的应用价值，但在实际应用中需要结合实际情况进行准确的分析和计算。

挠度计算例题
为了解答您的问题，我们首先需要知道定义"挠度"是指弹性体在受到外力作用下发生形变时的偏移量，即物体的弯曲程度。

挠度计用来测量物体弯曲的程度。

以下是一个例题：
假设有一根长度为L的均匀悬臂梁（只有一端固定，另一端自由），受到一个向下的集中力F作用在梁的自由端上。

我们希望计算该悬臂梁的挠度。

首先，我们需要知道四个参数：
1. 梁的长度L
2. 集中力F的大小
3. 梁的弯曲刚度EI (E为弹性模量，I为截面惯性矩，测量悬臂梁材料的抗弯能力)
4. 材料的横向拉伸系数v (悬臂梁材料的纵向和横向伸缩性之间的比例)
根据理论分析和边界条件，可以得到悬臂梁的挠度公式为：d = (dd^3)/(3dd)
其中，
- d为悬臂梁的挠度
- F为作用在悬臂梁自由端的集中力
- L为悬臂梁的长度
- E为悬臂梁材料的弹性模量
- I为悬臂梁的截面惯性矩
根据给定的参数，将其代入公式即可计算出悬臂梁的挠度。

机械设计跨度计算公式
机械设计中，跨度是指两个支撑点之间的距离。

在设计机器或设备时，需要确定跨度以确定杆件尺寸和材料，以确保机器或设备的稳定性和安全性。

以下是机械设计跨度计算公式。

1. 悬臂梁跨度计算公式
悬臂梁指只有一个支撑点的梁。

其跨度计算公式为：
L = (W × L^3) / (3 × E × I)
其中，L为梁的跨度，W为悬挂在梁上的负载，E为材料的弹性
模量，I为梁的截面惯性矩。

2. 简支梁跨度计算公式
简支梁指有两个支撑点的梁。

其跨度计算公式为：
L = (W × L^4) / (8 × E × I)
其中，L为梁的跨度，W为悬挂在梁上的负载，E为材料的弹性
模量，I为梁的截面惯性矩。

3. 梁的自由端挠度计算公式
梁的自由端挠度是指梁的一端受力后的弯曲程度。

其计算公式为：δ = (F × L^3) / (3 × E × I)
其中，δ为梁的自由端挠度，F为受力，L为梁的长度，E为材
料的弹性模量，I为梁的截面惯性矩。

以上是机械设计跨度计算公式。

在实际应用中，需要根据具体情况选择适当的公式和参数，以确保机器或设备的安全性和稳定性。

- 1 -。

当荷载作用在任意一点时挠度的计算方式在工程力学中，荷载作用在结构上时会引起结构的变形和挠度。

挠度是指结构在受到荷载后，由于弯曲或扭转而产生的变形量。

计算挠度的方式取决于结构的类型和受力条件，下面将介绍几种常见的挠度计算方法。

1.集中力的作用下的挠度计算：当集中力作用在结构上时，挠度的计算可以通过弹簧公式来实现。

弹簧公式基于胡克定律，即弹性体的变形与施加力成正比。

根据弹簧公式，挠度可以通过以下公式计算：δ=F*L/(k*A)其中，δ表示挠度，F表示作用于结构上的集中力，L表示作用点到支座的距离，k表示弹簧刚度系数，A表示截面积。

2.均匀分布载荷下的挠度计算：当均匀分布载荷作用在结构上时，挠度的计算可以通过梁的静力学方程和边界条件来实现。

根据梁的静力学方程，挠度可以通过以下公式计算：δ=(q*L^4)/(8*E*I)其中，δ表示挠度，q表示单位长度的均匀分布载荷，L表示梁的长度，E表示弹性模量，I表示梁的截面惯性矩。

3.杆件受轴向力和弯矩作用下的挠度计算：当杆件同时受轴向力和弯矩作用时，挠度的计算可以通过求解受弯方程来实现。

如果材料是线弹性的，挠度可以通过下面的方程计算：δ=(P*L)/(A*E)+(M*L^2)/(2*E*I)其中，δ表示挠度，P表示轴向力，L表示杆件的长度，A表示截面积，E表示弹性模量，M表示弯矩，I表示截面惯性矩。

4.悬臂梁的挠度计算：对于悬臂梁，挠度的计算可以通过函数法或力学中心法来实现。

函数法适用于特定的载荷和边界条件，通过求解相关的微分方程来计算挠度。

力学中心法适用于具有对称荷载和几何形状的结构，它利用力学中心理论，将梁替代为集中力和力矩的组合，从而计算挠度。

总之，在计算挠度时，我们必须考虑诸如荷载形式、结构类型、材料性质和边界条件等因素。

以上介绍的方法是一些常见的挠度计算方式，工程师在实际工作中可以根据具体情况选择适用的计算方法。

在装修行业中往往有自己的通用术语和计算方法，很多人很难达到专业水平，但是想要装修如果合适，应该使用一些更好的公式将其与其他部分进行比较正确，整个过程将顺利实施，那么悬臂梁挠度的计算公式是什么？因为梁在弯曲后会在一定压力下变形，那么这个弧度就是挠度，只有其只有经过计算，我们才能确保安全，而且还要在下一步执行特定操作时，使整个设计变得更加集成原因。

在建筑学的研究中，这是必须理解的，通过简单的学习可以解决许多实际问题。

悬臂梁的挠度公式为：ymax = 8pl ^ 3 /（384ei）= 1pl ^ 3 /（48ei）首先，ymax是光束跨度中间的最大挠度（mm），而P主要用于集中载荷的标准值（KN）之和，然后e主要是指钢的弹性模量。

针对不同情况有不同的标准，例如对于工程结构钢，e为2100000 n / mm ^ 2，I为钢的截面惯性矩，可在截面钢表中找到（mm ^ 4），这是整体的公式，可以完全使用。

挠度计算公式：ymax = 5ql ^ 4 /（384ei）（EI是在均布载荷q下长度为L的简支梁的抗弯刚度）挠度与构件的载荷，截面尺寸和材料物理特性有关。

挠曲变形时，截面质心在垂直于轴的方向上的线性位移称为挠度，用γ表示。

旋转角在弯曲变形期间相对于其原始位置的旋转角度称为角度，用θ表示。

挠曲曲线方程式-挠曲和旋转角度的值随截面的位置而变化。

在讨论弯曲变形问题时，我们通常选择坐标轴X朝右为正，y选择为朝下为正。

选择坐标轴后，梁的每个截面的挠度γ将是截面位置坐标X的函数，其表达式称为梁的挠度曲线方程，即γ= f （X）。

扩展数据：传统的桥梁挠度测量大多使用百分表或位移计直接测量。

目前，它在中国仍广泛用于桥梁维护，旧桥安全评估或新桥验收。

该方法的优点是设备简单，可以进行多点检测，可以直接获得每个测量点的挠度值，测量结果稳定可靠。

另外，由于缺乏直接测量桥在水下的挠度的方法，因此不可能直接测量桥在水下的挠度。

无论部署或拆除多少米，它们都非常复杂且耗时-消耗。

机械悬臂梁的设计计算公式悬臂梁是一种常见的机械结构，在工程设计中经常会用到。

悬臂梁的设计需要考虑到受力情况、材料强度等因素，因此需要进行一系列的计算和分析。

本文将介绍机械悬臂梁的设计计算公式，帮助读者更好地了解和应用悬臂梁的设计原理。

首先，我们来看一下悬臂梁的基本结构。

悬臂梁是一种横截面呈“L”形的梁，其中一端固定在支撑点上，另一端悬挂在空中。

在受力分析中，我们需要考虑悬臂梁在受外力作用下的弯曲和剪切情况，以确定梁的尺寸和材料。

在设计悬臂梁时，我们首先需要计算梁的受力情况。

根据力学原理，悬臂梁在受外力作用下会产生弯矩和剪力。

弯矩是梁在受力点附近产生的弯曲效应，而剪力则是梁在受力点附近产生的剪切效应。

为了确保梁的安全性，我们需要计算出梁在受力点处的最大弯矩和最大剪力。

弯矩的计算公式为：M = F L。

其中，M表示弯矩，F表示受力，L表示梁的长度。

根据这个公式，我们可以计算出梁在受力点处的最大弯矩，从而确定梁的截面尺寸和材料强度。

剪力的计算公式为：V = F。

其中，V表示剪力，F表示受力。

根据这个公式，我们可以计算出梁在受力点处的最大剪力，也可以用来确定梁的截面尺寸和材料强度。

除了弯矩和剪力，我们还需要考虑悬臂梁的挠度和应力。

挠度是梁在受外力作用下产生的变形，而应力则是梁在受力点处产生的内部应力。

为了确保梁的安全性，我们需要计算出梁的最大挠度和最大应力，并根据这些数据来确定梁的尺寸和材料强度。

挠度的计算公式为：δ = (F L^3) / (3 E I)。

其中，δ表示挠度，F表示受力，L表示梁的长度，E表示弹性模量，I表示惯性矩。

根据这个公式，我们可以计算出梁在受力点处的最大挠度，从而确定梁的尺寸和材料强度。

应力的计算公式为：σ = M y / I。

其中，σ表示应力，M表示弯矩，y表示截面的距离，I表示惯性矩。

根据这个公式，我们可以计算出梁在受力点处的最大应力，也可以用来确定梁的截面尺寸和材料强度。

通过上述计算公式，我们可以确定悬臂梁的尺寸和材料强度，从而设计出符合安全要求的悬臂梁结构。

变截面悬臂梁的挠度计算公式及系数表
宋相道
【期刊名称】《结构工程师》
【年(卷),期】1991(000)003
【摘要】本文根据对三种变截面悬臂梁导出的挠度计算公式,编制成供设计计算用的挠度系数表,是对过去在这方面的工作的补充。

【总页数】2页(P1-2)
【作者】宋相道
【作者单位】青岛市建筑设计研究院
【正文语种】中文
【中图分类】TU3
【相关文献】
1.N段变截面悬臂梁的挠度公式 [J], 杨宝清;张立明;王晓琨
2.变截面悬臂梁大挠度分析与计算 [J], 江五贵;谢亚清
3.一种变截面悬臂梁挠度计算方法研究 [J], 王利平
4.四类变截面悬臂梁在侧向三角形载荷下的挠度 [J], 廖晗;姜吕锋;李恒达;杨兴昌;李映辉
5.矩形变截面悬臂梁的挠度计算公式 [J], 宋相道
因版权原因，仅展示原文概要，查看原文内容请购买。