2.1 等式性质与不等式性质

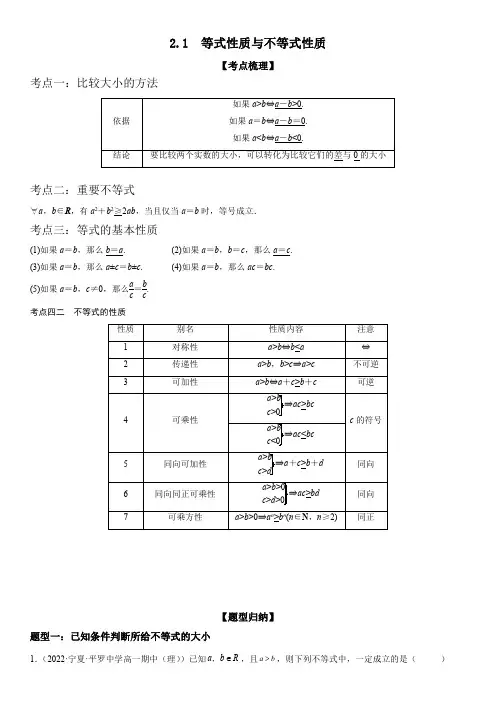
2.1等式性质与不等式性质【考点梳理】考点一：比较大小的方法依据如果a>b⇔a－b>0.如果a＝b⇔a－b＝0.如果a<b⇔a－b<0.结论要比较两个实数的大小，可以转化为比较它们的差与0的大小考点二：重要不等式∀a，b∈R，有a2＋b2≥2ab，当且仅当a＝b时，等号成立．考点三：等式的基本性质(1)如果a＝b，那么b＝a.(2)如果a＝b，b＝c，那么a＝c.(3)如果a＝b，那么a±c＝b±c.(4)如果a＝b，那么ac＝bc.(5)如果a＝b，c≠0，那么ac＝b c .考点四二不等式的性质性质别名性质内容注意1对称性a>b⇔b<a⇔2传递性a>b，b>c⇒a>c不可逆3可加性a>b⇔a＋c>b＋c可逆4可乘性a>bc>0⇒ac>bcc的符号a>bc<0⇒ac<bc5同向可加性a>bc>d⇒a＋c>b＋d同向6同向同正可乘性a>b>0c>d>0⇒ac>bd同向7可乘方性a>b>0⇒a n>b n(n∈N，n≥2)同正【题型归纳】题型一：已知条件判断所给不等式的大小1．（2022·宁夏·平罗中学高一期中（理））已知,a b R∈，且a b>，则下列不等式中，一定成立的是（）A ．11a b<B ．||||a b >C ．22a b >D ．33a b >2．（2022·内蒙古·赤峰市元宝山区第一中学高一期中）若0a b <<，则下列不等式不能成立的是（）A ．22a b >B ．11a b>C ．a b>D ．11a b a>-3．（2022·四川省峨眉第二中学校高一期中（理））若110a b<<，则下列不等式正确的是（）A ．a b>B ．a b<C ．3311a b >D ．a b ab+<题型二：不等式的性质比较数的大小4．（2022·浙江省淳安中学高一期中）已知实数,a b 满足0a b >>，则“0c b <<”是“1111a b a c b c+<++-”（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件5．（2022·重庆巴蜀中学高一期末）若0a b >>，则下列不等式一定成立的是（）A ．b aa b>B ．11b b a a +>+C ．11a b b a->-D ．11ba>6．（2022·山东青岛·高一期末）已知0,0,0a b c d e >><<<，则下述一定正确的是（）A ．ae be >B ．22c d <C ．0e ea c d b+>--D ．()ea d c b->题型三：作差法或作商法比较不等式的大小7．（2022·甘肃张掖·高一期末）若(1)(3)a x x =++，22(2)b x =+，则下列结论正确的是（）A ．a b>B ．a b<C ．a b≥D ．a ，b 大小不确定8．（2021·山东·泰安一中高一期中）设()121p a a -=++，21q a a =-+，则（）．A ．p q>B ．p q<C ．p q≥D ．p q≤9．（2022·河北沧州·高一期末）下列说法正确的是（）A ．若a b >，c d >，则22a c b d ->-B ．若a ，b ∈R ，则2ab ba +≥C ．若0ab >>，0m n >>，则b b ma a n+<+D ．若||a b >，则22a b >题型四：利用不等式求取值范围10．（2022·吉林延边·高一期末）已知12a ≤≤，14b -≤≤，则2a b -的取值范围是（）A ．724a b -≤-≤B ．629a b -≤-≤C ．629a b ≤-≤D ．228a b -≤-≤11．（2022·江苏·高一）已知23,21<<-<<-a b ，则2a b -的取值范围为（）A ．(0,2)B ．(2,5)C ．(5,8)D ．(6,7)12．（2021·全国·高一专题练习）下列选项中，使不等式21x x x<<成立的x 的取值范围是（）A ．1x <-B ．10x -<<C ．01x <<D ．1x >题型五：由不等式性质证明不等式13．（2022·湖南·高一课时练习）利用不等式的性质证明下列不等式：(1)若a b <，0c <，则()0a b c ->；(2)若0a <，10b -<<，则2a ab ab <<．14．（2022·湖南·高一课时练习）求证：(1)若0a b >>，且0c d <<，则ac bd <；(2)若a b >，且a ，b 同号，0c >，则c ca b<；(3)若0a b >>，且0c d >>，则a bd c>．15．（2021·湖南·衡阳市田家炳实验中学高一阶段练习）（1）已知a ，b ，c ，d 均为正数.求证：()a b +()()()16b c c d d a abcd+++≥（2）已知0xy >.求证：1x <1y的充要条件为x >y 【双基达标】一、单选题16．（2022·内蒙古·赤峰二中高一阶段练习（理））下列命题正确的是（）A ．若ac bc >，则a b >B ．若ac bc =，则a b =C ．若a b >，则11a b<D ．若22ac bc >，则a b>17．（2022·江苏·高一）已知a b <，3x a b =-，2y a b a =-，则,x y 的大小关系为（）A ．x y>B ．x y<C ．x y=D ．无法确定18．（2022·湖南·新化县教育科学研究所高一期末）已知a ，b ，c ，d 均为实数，则下列命题正确的是（）A ．若a b >，c d <，则a c b d -<-B ．若0a b >>，0c d <<，则ac bd <C ．若0a b >>，则2211a b >D ．若0a b c >>>，则c c a b>19．（2022·广东珠海·高一期末）对于任意实数a b c d ,,,，给定下列命题正确的是（）A ．若a b >，则ac bc >B ．若,a b c d >>，则a c b d ->-C ．若22ac bc >，则a b>D ．若a b <，则11a b>20．（2022·湖南·高一课时练习）已知0<a 1<1，0<a 2<1，记M ＝a 1a 2，N ＝a 1＋a 2－1，则M 与N 的大小关系是（）A ．M <NB ．M >NC ．M ＝ND ．无法确定21．（2022·湖南·高一课时练习）比较下列各题中两个代数式值的大小：(1)()21m -与()21m +；(2)()()222121x x x x ++-+与()()2211x x x x ++-+．22．（2022·湖南·高一课时练习）证明不等式：(1)若0a b <<，0c d <<，则ac bd >；(2)若0a b >>，0c d >>，则22a c b d >．【高分突破】一：单选题23．（2022·湖南永州·高一期末）若m n >，则下列不等式一定成立的是（）A ．m c n c->-B ．m n>C ．mc nc>D ．11m n<24．（2022·北京顺义·高一期末）已知||||0m n >>，则下列不等式一定成立的是（）A ．m n >B ．||0m n +>C ．0m n +<D ．11m n<25．（2022·山西运城·高一期末）如果,,a b c ∈R ，且0abc ≠，那么下列命题中正确的是（）A ．若11a b<，则a b >B ．若ac bc >，则a b >C ．若33a b >，则11a b<D ．若a b >，则22a b>26．（2022·湖南·高一期末）已知1,0a b c >>>，则下列不等式一定成立的是（）A ．1a bcb ac c+<+B ．1a bcb ac a+<+C ．a bcc b ac+<+D ．a bca b ac+<+27．（2021·四川成都·高一期末（文））若a ，b 为实数，下列命题正确的是（）A ．若a b >，则22a b >B ．若a b >，则22a b >C ．若22a b >，则a b>D ．若a b >，则22a b >28．（2022·山东滨州·高一期末）一家商店使用一架两臂不等长的天平称黄金．一位顾客到店里购买12g 黄金，售货员先将6g 的砝码放在天平左盘中，取出x g 黄金放在天平右盘中使天平平衡；再将6g 的砝码放在天平右盘中，再取出y g 黄金放在天平左盘中使天平平衡；最后将两次称得的黄金交给顾客，则（）A ．12x y +>B ．12x y +=C ．12x y +<D ．以上选项都有可能29．（2022·上海虹口·高一期末）设a 、b 都是实数，则“1a >且2b >”是“3a b +>且2ab >”的（）条件A ．充分非必要B ．必要非充分C ．充要D ．既非充分也非必要30．（2022·北京平谷·高一期末）已知a ，b ，c ∈R ，那么下列命题中正确的是（）A ．若a b >，则22ac bc >B ．若a bc c>，则a b >C ．若a b >，0ab <，则11a b>D ．若22a b >，0ab >，则11a b<二、多选题31．（2022·湖北·测试·编辑教研五高一）下列命题为真命题的是（）A ．若23,12a b -<<<<，则42a b -<-<B ．若22ac bc >，则a b >C ．若0,0b a m <<<，则m ma b>D ．若,a b c d >>，则ac bd>32．（2022·广东·深圳科学高中高一期中）下列说法正确的是（）A ．若0a b >>，则11a b<B ．若0a b >>，0m >，则b m ba m a+>+C ．0a b >>，则3322a b a b ab ->-D ．若0a b >>，则22ac bc >33．（2022·贵州贵阳·高一期末）下列说法正确的有（）A ．若,a b c d ><，则a c b d ->-B ．若0,0a b c d >><<，则ac bd <C ．若0a b c >>>，则c ca b >D ．若0a b c >>>，则a a cb b c+<+34．（2022·黑龙江·齐齐哈尔市第八中学校高一开学考试）十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“=”作为符号使用，后来英国数学家哈利奥特首次使用“<”和“>”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远．若a ，b ，R c ∈，则下列命题正确的是（）A ．若0b a >>，则11a b>B ．若a b >，则ac bc >C ．若a b >，c d >，则a c b d+>+D ．若22ac bc >，则a b>35．（2022·辽宁·育明高中高一期末）若实数a b <，则下列不等关系正确的是（）A ．若1a >，则log 2a ab >B ．若0ab ≠，则11a b>C ．若0a >，则2211b a a b>++D ．22ac bc <36．（2022·湖南衡阳·高一期末）下列命题为假命题的是（）A ．若a b >，则11a b<B ．若a b >，c d >，则a c b d +>+C ．若a b <，c d <，则ac bd<D ．若0a b c <<<，则b bc a a c+<+37．（2022·辽宁丹东·高一期末）如果a ，b ，c ，d R ∈，那么（）A ．若a b >，则11a b<B ．若22ac bc >，则a b>C ．若a b >，c d >，则ac bd>D ．若a b >，c d >，则a c b d+>+38．（2022·浙江·杭州市富阳区江南中学高一开学考试）下列命题是真命题的是（）A ．若0a b >>，则22ac bc >B ．若0a b >>，且0c d <<，则ac bd <C ．若11a b>，则a b <D ．若0a b c >>>，则a c ab c b+<+39．（2022·江苏镇江·高一期末）对于实数a ，b ，c ，正确的命题是（）A ．若a b >，则2a ba b +>>B ．若0a b >>，则a ab b >>C ．若11a b>，则0a >，0b <D ．若0a b >>，0c >，则a a cb b c+>+40．（2022·湖南张家界·高一期末）下列命题为真命题的是（）A ．若a b >，则a c b c ->-B ．若a b >，c d >，则ac bd >C ．若a b >，则33a b >D ．若0a b >>，则22a ab b >>三、填空题41．（2022·全国·高一）下列四个代数式①4mn ，②224+m n ，③224m n +，④22m n +，若0m n >>，则代数式的值最大的是______．（填序号）．42．（2022·全国·高一）已知14a -<<，12b <<，则-a b 的取值范围是__________．43．（2022·全国·高一）若a 、b ∈R ，则下列不等式：①a 2＋3＞2a ；②a 2＋b 2≥2(a －b －1)；③a 5＋b 5＞a 3b 2＋a 2b 3；④a ＋1a≥2中一定成立的是__________．(填序号)44．（2021·天津市滨海新区大港第八中学高一期中）比较大小：239x x -+___(2)(1)x x --.（填;≤≥<>；；）45．（2021·全国·高一专题练习）给出以下四个命题：①*()n n a b a b n N >⇒>∈；②*||()n n a b a b n N >⇒>∈；③110a b a b<<⇒>；④110a b a b a <<⇒>-．其中真命题的序号是________．46．（2021·山东·济南市章丘区第四中学高一阶段练习）某新农村为加强体育文化建设，购买了一批体育器材.已知在该批次器材中，4个排球和5个足球的价格之和小于400元，而6个排球和3个足球的价格之和大于450元.设1个排球的价格为A 元，1个足球的价格为B 元，则A ___________B （填“>”､“<”或“=”）.47．（2022·江苏·高一）若0a b <<，则下面有六个结论：①22a b >，②33a b >，③11a b <，④1a b>，⑤11a b a >-，⑥a b >-中，正确结论的序号是_______．四、解答题48．（2021·湖北·车城高中高一）（1）已知23x <<，23y <<，求x y -和xy的取值范围；（2）已知24<+≤x y ，13x y -<-<，求3x y +的取值范围.49．（2021·全国·高一专题练习）（1）若bc －ad ≥0，bd >0，求证：a b b +≤c dd+；（2）已知c >a >b >0，求证：a bc a c b>--50．（2021·全国·高一）已知0a b >>，0c d <<，0m <，求证：(1)11a cb d<--；(2)m ma cb d>--.51．（2021·全国·高一）（1）若bc－ad≥0，bd>0，求证：a bb+≤c dd+；（2）已知c>a>b>0，求证：a bc a c b>--；（3）观察以下运算：1×5＋3×6>1×6＋3×5，1×5＋3×6＋4×7>1×6＋3×5＋4×7>1×7＋3×6＋4×5.①若两组数a1，a2与b1，b2，且a1≤a2，b1≤b2，则a1b1＋a2b2≥a1b2＋a2b1是否成立，试证明；②若两组数a1，a2，a3与b1，b2，b3且a1≤a2≤a3，b1≤b2≤b3，对a1b3＋a2b2＋a3b1，a1b2＋a2b1＋a3b3，a1b1＋a2b2＋a3b3进行大小顺序(不需要说明理由【答案详解】1．D 【详解】对A ，当2,1a b ==-时，11a b<不成立，故A 错误；对B ，当1,2a b ==-时，||||a b >不成立，故B 错误；对C ，当1,2a b ==-时，22a b >不成立，故C 错误；对D ，因为3y x =为增函数，故a b >时33a b >一定成立，故D 正确；故选：D 2．D 【解析】【分析】根据条件，结合结合不等式性质判断A ，B ，C 正确，再举例说明D 错误..【详解】因为0a b <<，所以0a b +<，0a b -<，0ab >，0b a ->，又22()()a b a b a b -=-+，所以220a b ->，所以22a b >成立，110b aa b ab --=>，所以11a b >，0a b a b -=-+>，所以a b >，取2,1a b =-=-可得11=121a b =---+，112a =-，11a b a <-，所以11a b a>-不成立，故选：D.3．D 【解析】【分析】根据不等式的性质判断．【详解】110a b<<0b a ⇔<<a b ⇒<，A 错，B 错；331111()()a b a b <⇒<即3311a b<，C 错；0a b ab +<<，D 正确．故选：D ．4．A 【解析】【分析】由11a b a b ab++=，()11a c b c ab c b c a a b ++=+-+--，依题意可得只需比较()c b c a --与0的大小，再根据充分条件、必要条件的定义判断可得；【详解】解：因为11a b a b ab++=，()()()11a c b c a c b a a b a b c ab c b c +==+--+++--+又0a b >>，则0a b +>，所以要比较11a b +与11a c b c++-的大小，即比较1ab 与()1ab c b c a +--的大小，即比较()c b c a --与0的大小，当0a b >>且0b c >>时()0c b c a --<，且()()0a c b c +->，即()0ab c b c a ab <+--<，所以()11ab ab c b c a <+--，即1111a b a c b c+<++-，故充分性成立，当0c b >>时()()0c b c a c a b c ⎡⎤--=---<⎣⎦，此时也满足1111a b a c b c+<++-，故必要性不成立；即“0c b <<”是“1111a b a c b c+<++-”充分不必要条件；故选：A 5．D 【解析】【分析】利用不等式的性质可判断ABD ，取特殊值可判断C 选项.【详解】选项A ：因为0a b >>，所以10a b>⋅，220a b >>所以a bb a>，故A 错误；选项B ：因为0a b >>，则0ab >，所以a ab b ab +>+，即()()11a b b a +>+，又()101a a >+，所以不等式()()11a b b a +>+两侧同时乘以()11a a +，则11b ba a+>+，故B 错误；选项C ：当11,23a b ==时，此时0a b >>，115322a b -=-=-，115233b a -=-=-，11b aa b -<-，故C 错误；选项D ：因为0a b >>，所以0a b >>，则11b a >，故D 正确.故选：D.6．C【详解】解：因为0,0,0a b c d e >><<<，所以ae be <，22c d >，故AB 错误；0c d ->->，所以0a c b d ->->，所以11a c b d <--，所以e e a c b d >--，即0e e a c d b+>--，故C 正确；对于D ，若12,1,1,,12a b c d e ===-=-=-时，则()2e a d c b-==，故D 错误.故选：C.7．B【详解】解：因为22(2)(1)(3)b a x x x -=+-++()2228843x x x x =++-++245x x =++()2210x =++>，所以a b <．故选：B.8．D【解析】【分析】首先配方判断p 、q 均大于零，然后作商即可比较大小.()1222110132411p a a a a a -==>⎛⎫++ ⎪⎭+⎝=+++，22131024q a a a ⎛⎫=-+=-+> ⎪⎝⎭，则()()()222121111a a a a a a a q a p --+-++++=+=()()222222111a a a a =+-=++≥.故p q ≤，当且仅当0a =时，取等号，故选：D【点睛】本题考查了作商法比较两个式子的大小，属于基础题.9．C【解析】【分析】结合特殊值、差比较法确定正确选项.【详解】A ：令2a =，1b =；1c =，0d =，则20a c -=，21b d -=，不满足22a c b d ->-，故A 错误；B ：a ，b 异号时，不等式不成立，故B 错误；C ：()()()()b m b b m a b a n ma nb a n a a n a a n a++-+--==+++，0a b >>，0m n >>，0am bm ∴->，即b m b a n a+>+，故C 正确；D ：令1a =，2b =-，22a b >不成立，故D 错误.故选：C10．A【解析】【分析】先求2b -的范围，再根据不等式的性质，求2a b -的范围.【详解】因为14b -≤≤，所以822b -≤-≤，由12a ≤≤，得724a b -≤-≤.故选：A.【解析】【分析】由不等式的性质求解【详解】23,21<<-<<-a b ，故426a <<，12b <-<，得528<-<a b 故选：C12．A【解析】【分析】根据给定条件解不等式2x x <，再分类等价转化即可求解作答.【详解】因21x x x<<，则有2x x <，解得：0x <或1x >，当1x >时，22311x x x x x ⇔<<<<，显然21x <不成立，无解，当0x <时，22311x x x x x⇔>><<，不等式31x >恒成立，解21x >得1x <-或1x >，则有1x <-，所以使不等式21x x x <<成立的x 的取值范围是1x <-.故选：A13．(1)证明见解析(2)证明见解析【解析】【分析】（1）可知0a b ->，而0c <，即可得证；（2）可知2101b b >>>>-，而0a <，即可得证；(1)证明：a b >，0a b ∴->，又0c <，()0a b c ∴-<；(2)证明：10b -<<，201b ∴<<2101b b ∴>>>>-，又0a <，2a ab ab ∴<<．14．(1)证明见解析(2)证明见解析(3)证明见解析【解析】【分析】（1）将0c d <<变为0c d ->->，利用不等式同向正值的可乘性，即可证明结论；（2）由a b >以及0c >，可得ac bc >，再根据a ，b 同号，得10ab >，利用不等式同向正值的可乘性证明结论；（3）由0c d >>可得110d c >>，继而可得0a b d c >>,利用不等式的性质可得结论.(1)证明：因为0c d <<，所以0c d ->->，又0a b >>，故()()0a c b d ->->，即ac bd <；(2)证明：因为a b >，0c >，所以ac bc >，因为a ，b 同号，所以0ab >，10ab >，故11ac bc ab ab ⨯>⨯，即c c b a >，所以c c a b <；(3)证明：因为0c d >>，所以110d c >>，又0a b >>，所以0a b d c>>，故a b d c >.15．详见解析.【解析】【分析】（1）利用基本不等式即证；（2）利用不等式的性质，由x y >，0xy >可得1x <1y ，由1x <1y，0xy >，可得x y >，即证.【详解】（1）∵a ，b ，c ，d 均为正数，∴20,a b ab +≥>当且仅当a b =时取等号，同理可得20,20,20b c bc c d cd d a da +≥>+≥>+≥>，∴()()()()16a b b c c d d a abcd ++++≥，当且仅当a b c d ===时取等号；（2）充分性，因为x y >，0xy >，10xy >，∴1x <1y，必要性，因为1x <1y ，0xy >，所以x y >，综上，1x <1y的充要条件为x >y .16．D【解析】【分析】由不等式性质依次判断各个选项即可.【详解】对于A ，若0c <，由ac bc >可得：a b <，A 错误；对于B ，若0c =，则0ac bc ==，此时a b =未必成立，B 错误；对于C ，当0a b >>时，110a b>>，C 错误；对于D ，当22ac bc >时，由不等式性质知：a b >，D 正确.故选：D.17．B【解析】【分析】作差可得x-y 的表达式，根据题意，分析可得x-y 的正负，即可得答案.【详解】()()3221x y a b a b a a b a -=--+=-+，因为a b <，所以0a b -<，又210a +>，所以2()(1)0a b a -+<，即x y <.故选：B18．B【解析】【分析】利用不等式的性质逐项判断可得出合适的选项.【详解】对于A 选项，若a b >，c d <，则c d ->-，故a c b d ->-，A 错；对于B 选项，若0a b >>，0c d <<，则0c d ->->，所以，ac bd ->-，故ac bd <，B 对；对于C 选项，若0a b >>，则220a b >>，则2211a b <，C 错；对于D 选项，若0a b c >>>，则110b a >>，所以，c c a b<，D 错.故选：B.19．C【解析】【分析】利用特殊值判断A 、B 、D ，根据不等式的性质证明C ；【详解】解：对于A ：当0c =时，若a b >则0ac bc ==，故A 错误；对于B ：若0a =，1b =-，1c =-，10d =-，满足,a b c d >>，则1a c -=，9b d -=，a c b d ->-不成立，故B 错误；对于C ：若22ac bc >，则20c >，所以a b >，故C 正确；对于D ：若1a =-，1b =满足a b <，但是11a b<，故D 错误；故选：C20．B【解析】【分析】采用作差法，将M ＝a 1a 2，N ＝a 1＋a 2－1相减，根据条件判断差的符号，即可比较大小.【详解】∵0<a 1<1，0<a 2<1，∴－1<a 1－1<0，－1<a 2－1<0，∴M －N ＝a 1a 2－(a 1＋a 2－1)＝a 1a 2－a 1－a 2＋1＝a 1(a 2－1)－(a 2－1)＝(a 1－1)(a 2－1)>0，∴M >N ，故选：B.21．(1)22(1)(1)m m ≤-+(2)()()222121x x x x ++-+()()2211x x x x ≤++-+【解析】【分析】利用作差法得出大小关系.(1)()()()()221121214m m m m m m m --+=-+-++=-因为0m ≥，所以22(1)(1)0m m --+≤，当且仅当0m =时，取等号.即22(1)(1)m m ≤-+(2)()()222121x x x x ++-+()()2211x x x x -++-+()()2222222121x x x x x ⎡⎤⎡⎤=+--+-=-⎢⎥⎢⎥⎣⎦⎣⎦因为0x ≥，所以()()2222221210x x x x ⎡⎤⎡⎤+--+-≤⎢⎥⎢⎥⎣⎦⎣⎦，当且仅当0x =时，取等号.故()()222121x x x x ++-+()()2211x x x x ≤++-+.22．(1)证明见解析；(2)证明见解析；【解析】【分析】（1）利用不等式的性质可证得结论；（2）由0a b >>，知220a b >>，利用0c d >>，即可证得结论；(1)0a b <<Q ，两边同乘以0c <，则ac bc>又0c d <<，两边同乘以0b <，则bc bd>即ac bd>(2)0a b >>，两边同乘以0a >，得20a ab >>；两边同乘以0b >，得20ab b >>，所以220a ab b >>>又0c >，则220a b c c >>，又0cd >>，则22b c b d >，即22a c b d>23．A【解析】选项A.根据不等式的基本性质可判断；选项B.当,m n 为负数时，根式无意义可判断；选项C.当0c ≤时的情况可判断；选项D.举特例可判断.【详解】选项A.由m n >，根据不等式的基本性质可得m c n c ->-成立，故选项A 正确.选项B.当,m n 为负数时，根式无意义，则m n >不成立.故选项B 不正确.选项C.当0c ≤时，mc nc >不成立.故选项C 不正确.选项D.取2,1m n ==-，显然m n >满足，但11m n <不成立，故选项D 不正确.故选：A24．B【解析】【分析】对于ACD ，举例判断，对于B ，分0,0n n ><两种情况判断【详解】对于A ，若2,1m n =-=时，满足||||0m n >>，而不满足m n >，所以A 错误，对于B ，当0n >时，则||0m n +>一定成立，当0n <时，由||||0m n >>，得m n >-，则||0m n +>，所以B 正确，对于C ，若2,1m n ==时，满足||||0m n >>，而不满足0m n +<，所以C 错误，对于D ，若2,1m n =-=-时，则满足||||0m n >>，而不满足11m n<，所以D 错误，故选：B25．D【解析】【分析】根据不等式的性质逐项分析判断即可.【详解】对于A ，若1a =-，1b =，满足11a b <，但a b >不成立，错误；对于B ，若0c <，则a b <，错误；对于C ，若2a =，1b =-，满足33a b >，但11a b<不成立，错误；对于D ，由指数函数的单调性知，正确.故选：D.【解析】【分析】通过作差法来判断每一个选项.【详解】对于A ，()()()2211b c a bc ac bc b ac b ac c b ac c b ac c -++---==+++，当1c >时，()()210b c b ac c ->+，即1a bc b ac c +>+，则A 错误；对于B ，()()()()211a a c b ac a bc a abc b ac b ac a b ac a b ac a-+-++---==+++，当1a c >>时，0,1a c ac ->>，则()()()10a a c b ac b ac a -+->+，即1a bc b ac a+>+，则B 错误；对于C ，()221a c a bc a bc bc ac c b ac b ac b ac -++---==+++，当01c <<时，210c ->，则()210a c b ac ->+，即a bc c b ac+>+，则C 错误；对于D ，()()221a b b a c a bc a bc ab a c a b ac b ac b ac -+-++---==+++，因为1,0a b c >>>，所以()()210,0a b b a c -<-<，所以()()210a b b a cb ac -+-<+，即a bc a b ac+<+，则D 正确.故选：D27．D【解析】【分析】据特值可说明ABC 不正确；根据不等式的性质可得D 正确.【详解】对于A ，当1,2a b =-=-时，满足a b >，不满足22a b >，故A 不正确；对于B ，当1,2a b =-=-时，满足||a b >，不满足22a b >，故B 不正确；对于C ，当2,1a b =-=-时，满足22a b >，不满足a b >，故C 不正确；对于D ，若a b >0≥，则222||a b b >=，故D 正确.故选：D.28．A【解析】【分析】由于天平的两臂不等长，故可设天平左臂长为a ，右臂长为b （不妨设)a b >，先称得的黄金的实际质量为1m ，后称得的黄金的实际质量为2m ，利用杠杆的平衡原理可得16a m b=，26b m a =，再利用作差法比较12m m +与12的大小即可．【详解】由于天平的两臂不等长，故可设天平左臂长为a ，右臂长为b （不妨设)a b >，先称得的黄金的实际质量为1m ，后称得的黄金的实际质量为2m ，由杠杆的平衡原理：16bm a =⨯，26am b =⨯，解得16a m b =，26b m a=，则1266a b m m b a +=+，下面用作差法比较12m m +与12的大小，212666()()1212a b b a m m b a ab-+-=+-=，又a b ≠，∴26()0b a ab->，1212m m ∴+>，∴顾客实际购买的黄金大于12克．故选：A ．29．A【解析】【分析】利用充分条件和必要条件的定义结合不等式性质即可判断作答.【详解】a 、b 都是实数，若1a >且2b >，由不等式性质得：3a b +>且2ab >成立，若3a b +>且2ab >成立，取1,52a b ==，而1a >且2b >不成立，所以“1a >且2b >”是“3a b +>且2ab >”的充分非必要条件.故选：A30．C【解析】【分析】根据不等式的性质或通过举反例，对四个选项进行分析．【详解】A ．若a b >，当0c =时，22ac bc =，所以A 不成立；B ．若a b c c>，当0c <时，则a b <，所以B 不成立；C ．因为0ab <，将a b >两边同除以ab ，则11a b >，所以C 成立D ．若22a b >且0ab >，当00a b <⎧⎨<⎩时，则a b <，所以11a b >，则D 不成立．故选：C ．31．ABC【解析】【分析】对于A ：利用同向不等式相加，即可证明；对于B 、C ：利用不等式的可乘性可以证明；对于D ：取特殊值2,1;2,3a b c d ===-=-即可否定结论.【详解】对于A ：因为12b <<，所以21b -<-<-.因为23a -<<，利用同向不等式相加，则有42a b -<-<.故A 正确；对于B ：因为22ac bc >，所以20c ≠，所以210c >，对22ac bc >两边同乘以21c，则有a b >.故B 正确；对于C ：因为0b a <<，所以110a b <<.因为0m <，所以0m ->.对11a b <两边同乘以m -，有m m a b --<，所以m m a b >.故C 正确；对于D ：取2,1;2,3a b c d ===-=-，满足,a b c d >>，但是4,3ac bd =-=-，所以ac bd >不成立.故D 错误.故选：ABC32．ABC【解析】【分析】根据不等式的性质判断AD ，结合作差法比较大小判断BC.【详解】解：对于A 选项，因为0a b >>，故10ab>，故110a b <<，正确；对于B 选项，由于0a b >>，0m >，故0a b ->，0a m +>，故()()()()()0a b m b a m m a b b m b a m a a a m a a m +-+-+-==>+++，即b m b a m a+>+，正确；对于C 选项，由于0a b >>，故0a b ->，故()()()()332222220a b a b ab a a b b a b a b a b --+=-+-=-+>，即3322a b a b ab ->-，正确；对于D 选项，当0c =时，220ac bc ==，故错误.故选：ABC33．AB【解析】【分析】对于A ：利用同向不等式相加可以证明；对于B ：利用同向不等式相乘可以证明；对于C ：利用不等式的可乘性可以判断；对于D ：取特殊值3,2,1a b c ===可以判断.【详解】对于A ：因为c d <，所以c d ->-，利用同向不等式相加可以得到：a c b d ->-.故A 正确；对于B ：因为0c d <<，所以0c d ->->，又因为0a b >>，利用同向不等式相乘可以得到：ac bd ->-，所以ac bd <.故B 正确；对于C ：因为0a b c >>>，所以11a b <.因为0c >，所以c c a b<.故C 错误；对于D ：取特殊值3,2,1a b c ===满足0a b c >>>，但是32a b =，43a cbc +=+，所以a a c b b c +>+.故D 错误.故选：AB34．ACD【解析】【分析】分别由不等式的同加同乘性质可得，注意选项B 中c 为0的情况.【详解】选项A ：0b a >>，0.ab ∴>在不等式b a >两边同除以ab 得11a b>，A 正确；选项B ：当0c =时，ac bc =，B 错误；选项C ：同向不等式相加，不等号方向不变，C 正确；选项D ：22ac bc >，20c ∴>，两边同除以2c 得，a b >，D 正确.故选：ACD.35．AC【解析】【分析】直接利用不等式的性质、构造函数、作差法等进行逐项判断即可．【详解】对于A ：由于1b a >>，∴22log 2log log log 0a a a aab ab ab a a -=-=>，故A 正确；对于B ：由于a b <，且0ab ≠，则b －a ＞0，∴11b a a b ab --=不一定大于0，故B 错误；对于C ：设2()(1)f x x x =+，由于函数在(0,)+∞上单调递增，故f (b )＞f (a )，可得2211b a a b>++成立，故C 正确；对于D ：当0c =时，22ac bc =，故D 错误．故选：AC ．36．AC【解析】【分析】对于AC ，举例判断，对于B ，利用不等式的性质判断，对于D ，利用作差法判断【详解】对于A ，若1,1a b ==-，则1111a b=>=-，所以A 错误，对于B ，因为a b >，c d >，所以由不等式的性质可得a c b d +>+，对于C ，若2,1,1,2a b c d =-=-==，则2ac bd =-=，所以C 错误，对于D ，因为0a b c <<<，所以()0,()0c a b a a c ->+>，所以()()()0()()b c b a b c b a c c a b a c a a a c a a c ++-+--==>+++，所以b b c a a c+<+，所以D 正确，故选：AC37．BD【解析】【分析】根据举例说明即可判断选项A 、C ，根据不等式的基本性质即可判断选项B 、D.【详解】A ：令11a b ==-，，满足a b >，但11a b>，故A 错误；B ：因为2220ac bc c >>，，所以a b >，故B 正确；C ：令11a b ==-，，11c d ==-，，满足a b >，c d >，但ac bd =，故C 错误；D ：因为a b >，c d >，由不等式的性质，得a c b d +>+，故D 正确.故选：BD38．BD【解析】【分析】举出反例可判断AC ，利用不等式的性质即可判断B ，利用作差法即可判断D.【详解】解：对于A ，若0a b >>，当0c =时，22ac bc =，故A 错误；对于B ，若0a b >>，且0c d <<，则0c d ->->，所以ac bd ->-，所以ac bd <，故B 正确；对于C ，若11a b>，当1,1a b ==-时，a b >，故C 错误；对于D ，若0a b c >>>，则()()()()()0b a c a b c c b a a c a b c b b b c b b c +-+-+-==<+++，所以a c a b c b+<+，故D 正确.故选：BD.39．ABD【解析】【分析】利用作差法，作商法和特值法依次判断选项即可.【详解】对选项A ，因为a b >，所以022a b a b a +--=>，022a b a b b +--=>，所以2a b a b +>>，故A 正确；对选项B ，0a b >>，1aaab b =>，所以a ab >，因为1ab a b b=>，所以ab b >，即a ab b >>，故B 正确；对选项C ，令2a =，3b =，满足11a b>，不满足0a >，0b <.对选项D ，因为0a b >>，0c >，所以()()()()()0a b c b a c c a b a a c b b c b b c b b c +-+-+-==>+++，故D 正确.故选：ABD40．ACD【解析】【分析】利用不等式的性质或举反例的方法来判断各选项中不等式的正误.【详解】由不等式性质知若a b >，则+()()a c b c ->+-，即a c b c ->-，A 对，取2,1,1,2a b c d ===-=-，则a b >，c d >，=ac bd ，B 错，因为a b >，所以0a b ->，所以2332223=()()()024b a b a b a ab b a b a b ⎡⎤⎛⎫---+=--+≥⎢⎥ ⎪⎝⎭⎢⎥⎣⎦(当且仅当0a b ==时等号成立)，而a b >，故33a b >，C 对，因为0a b >>，所以2a ab >，2ab b >，所以22a ab b >>，D 对，故选：ACD.41．③【解析】【分析】利用作差法比较大小即可．【详解】∵0m n >>，令②-①得：()2224042mn m n m n -=-+＞，∴②＞①，令③-②得：22222244330m n m n m n +--=-＞，∴③＞②，令③-④得：22222430m n m n m +--=＞，∴③＞④，∴代数式的值最大的是③.故答案为：③42．()3,3-【解析】【分析】利用不等式的基本性质可得答案.【详解】因为14a -<<，12b <<，则21b -<-<-，所以1241--<-<-a b ，即-a b 的取值范围是33a b -<-<．故答案为：()3,3-.43．①②【解析】【分析】利用作差法及不等式性质，即可作出判断.【详解】①a 2－2a ＋3＝(a －1)2＋2＞0，正确；②a 2＋b 2－2a ＋2b ＋2＝(a －1)2＋(b ＋1)2≥0，正确；③a 5－a 3b 2＋b 5－a 2b 3＝a 3(a 2－b 2)＋b 3(b 2－a 2)＝(a 2－b 2)(a 3－b 3)＝(a ＋b )(a －b )2(a 2＋ab ＋b 2)，若a ＝b ，则上式＝0，不正确；④若a ＜0，则a ＋1a＜0不正确.∴①②一定成立.故答案为：①②44．>【解析】【分析】利用差比较法确定正确答案.【详解】()()()2223921393270x x x x x x x x -+---=-+--+=>，所以()()23921x x x x -+>--故答案为：>45．②③【解析】【分析】利用不等式的基本性质及特殊值法，判断命题的真假即可．【详解】解：①当1a =-，2b =-，2n =时，满足a b >，当时n n a b <，所以①不正确；②因为0b >，所以*||()n n a b a b n N >⇒>∈，所以②正确；③1100a b a b <<⇒>>；所以③正确；④110a b a b a<<⇒>-．反例2a =-，1b =-，满足条件但是结论不成立．所以④不正确；故答案为：②③．46．>【解析】【分析】依题意可得4540063450A B A B +<⎧⎨+>⎩，再根据不等式的性质即可得到25A B ->，即可判断；【详解】解：由题意得4540063450A B A B +<⎧⎨+>⎩，所以4540063450A B A B -->-⎧⎨+>⎩，所以250A B ->>，则A B >.故答案为：>47．①④⑥【解析】【分析】利用不等式的基本性质及作差法，对结论逐一分析，选出正确结论即可.【详解】因为0a b <<，则0a b ->->，所以()()22a b ->-，即22a b >，故①正确；由22a b >，不等式两边同时乘a 时，32a b a <，对于a b <，两边同乘2b ，可得23b a b <，故323a b a b <<，即33a b <，则②错误；因为0a b <<，所以0ab >，则10ab >，所以11a b ab ab ⋅<⋅，即11b a <，则③错误；由11b a <，不等式边同时乘a ，得1a a b a>=，故④正确；由()()()11a a b b a b a a b a a b a---==---，因为0,0a b a -<<，所以()0a b a ->，又因为0b <，所以110a b a-<-，即11a b a <-，故⑤错误；由0a b <<可得，a b b >=-，故⑥正确；因此，正确结论的序号是①④⑥.故答案为：①④⑥.48．（1）11x y -<-<，2332x y <<；（2）3311x y <+<.【解析】【分析】（1）根据不等式的性质求解（2）由待定系数法配凑后求解【详解】（1）23y <<，32∴-<-<-y又23x <<，11∴-<-<x y 23y <<，11132y <<又23x <<，2332∴<<x y （2）设3()()x y a x y b x y +=++-，得3211a b a a b b +==⎧⎧⇒⎨⎨-==⎩⎩即32()()+=++-x y x y x y 而42()8<+≤x y ，13x y -<-<3311∴<+<x y 49．（1）证明见解析；（2）证明见解析.【解析】【分析】（1）由不等式的性质，先得到c ad b ≥，两边同时+1，即得证；（2）由不等式的性质，先得到11a b <，两边乘以c,可得c c a b <，两边同时-1，可得c a c b a b --<，再两边取倒数，即得证.【详解】证明：（1）∵bc ≥ad ，bd >0，∴c ad b ≥，∴c d ＋1≥a b ＋1，∴a b b +≤c d d+.（2）∵c >a >b >0，∴c －a >0，c －b >0.∵a >b >0，∴11a b <又∵c >0，∴c c a b <，∴c a c b a b--<，又c －a >0，c －b >0，∴a b c a c b >--.50．(1)证明见解析(2)证明见解析【解析】【分析】（1）根据不等式的性质证明即可；（2）结合（1）和不等式的性质求解.(1)证明：因为0a b >>，0c d ->->，所以0a cb d ->->所以11a c b d <--；(2)证明：由（1）得11a c b d <--，又0m <，所以m m a c b d>--.51．（1）证明见解析；（2）证明见解析；（3）①成立，证明见解析；②a 1b 3＋a 2b 2＋a 3b 1≤a 1b 2＋a 2b 1＋a 3b 3≤a 1b 1＋a 2b 2＋a 3b 3【详解】证明：（1）因为0bd >，所以10bd >，又0bc ad -≥，即bc ad ≥，所以c a d b ≥，所以11c a d b +≥+，即a b b +≤c d d+；（2）因为0c a b >>>，所以0,0,c a c b c a c b ->->-<-，11a b <，所以c a c b a b --<，所以a b c a c b>--；（3）解：①成立，证明如下：∵a 1b 1＋a 2b 2－(a 1b 2＋a 2b 1)＝a 1(b 1－b 2)＋a 2(b 2－b 1)＝(a 1－a 2)(b 1－b 2)，又a 1≤a 2，b 1≤b 2，∴(a 1－a 2)(b 1－b 2)≥0，即a 1b 1＋a 2b 2≥a 1b 2＋a 2b 1；②a 1b 3＋a 2b 2＋a 3b 1≤a 1b 2＋a 2b 1＋a 3b 3≤a 1b 1＋a 2b 2＋a 3b 3。