第六章-简单超静定问题-习题选解
- 格式:doc
- 大小:441.00 KB
- 文档页数:7

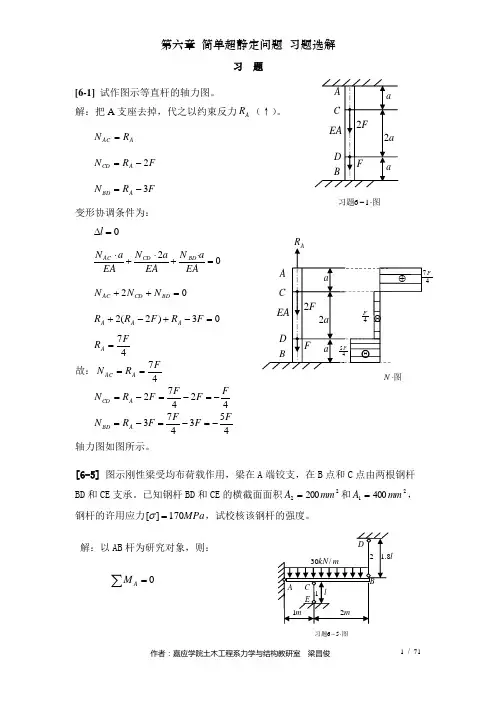
图习题⋅-16图⋅N l 图习题⋅-56习 题[6-1] 试作图示等直杆的轴力图。
解:把A 支座去掉,代之以约束反力A R (↑)。
A AC R N = F R N A CD 2-=F R N A BD 3-=变形协调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)2(2=-+-+F R F R R A A A47FR A =故:47F R N A AC == 42472FF F F R N A CD -=-=-= 453473FF F F R N A BD-=-=-= 轴力图如图所示。
[6-5] 图示刚性梁受均布荷载作用,梁在A 端铰支,在B 点和C 点由两根钢杆BD 和CE 支承。
已知钢杆BD 和CE 的横截面面积22200mm A =和21400mm A =,钢杆的许用应力MPa 170][=σ,试校核该钢杆的强度。
解:以AB 杆为研究对象,则:0=∑AM1023)330(3121=⨯⨯-⨯+⨯N N 135321=+N N (1)变形协调条件:3121=∆∆l l 123l l ∆=∆112238.1EA lN EA l N ⨯=⋅ 40032008.112N N =⋅ 212.1N N = (2)(2)代入(1)得:13532.122=+N N)(143.322.41352kN N ≈=(拉力) )(571.38143.322.12.121kN N N ≈⨯== (压力)按轴力正负号的规定,记作:kN N 571.381-=;kN N 143.322=强度校核:MPa MPa mm N A N 170][4275.9640038571||||2111=<===σσ,符合强度条件。
图习题⋅-156 MPa MPa mm NA N 170][715.160200321432122=<===σσ,符合强度条件。

第六章简单的超静定问题知识要点1.超静定问题的概念(1)静定问题结构或结构的约束反力或内力均能通过静力学平衡方程求解的问题。
(2)超静定问题结构或构件的约束反力或内力不能仅凭静力学平衡方程全部求解的问题。
(3)超静定次数未知力(约束反力或内力)数超过独立的静力平衡方程书的数目。
(4)多余约束力超静定问题中,多余维持静力平衡所必需的约束(支座或杆件)。
(5)多余未知力与多余(支座或杆件)相应的支座反力或内力。
(6)基本静定系在求解静定结构时,解除多余约束,并代之以多余未知力,从而得到一个作用有荷载和多余未知力的静定结构,称之为原超静定结构的基本体静定系。
2.静不定问题的解题步骤(1) 静力平衡条件——利用静力学平衡条件,列出平衡方程。
(2) 变形相容条件——根据结构或杆间变形后应保持连续的变形相容条件,作出位移图,由位移图的几何关系列出变形间的关系方程。
(3) 物理关系——应用胡克定律列出力与变形间的关系方程。
(4) 将物理关系代入变形相容条件,得补充方程 。
补充方程和静力平衡方程,二者方程数之和正好等于未知数的个数,联立平衡方程和补充方程,求解全部未知数。
习题详解6-1 试作题6-1图(a )所示等直杆的轴力图。
解 解除题6-1图(a )所示等直杆的约束,代之以约束反力,作受力图,如题6-1图(b )所示。
由静力学平衡条件,03,0=-+=∑F F F FB A Y和变形协调条件0=∆+∆+∆DB CD AC 并将()EAa F EA a F F EA a F B DB A CD A AC -=∆-=∆=∆,22,代入式②,可得 联立式①,③,解得45,47F F F F B A == 轴力如图6-1图(c )所示6-2 题6-2图(a )所示支架承受荷载F=10 kN,1,2,3各杆由同一材料制成,其横截面面积分别为232221200,150,100mm A mm A mm A ===。
试求各杆的轴力。

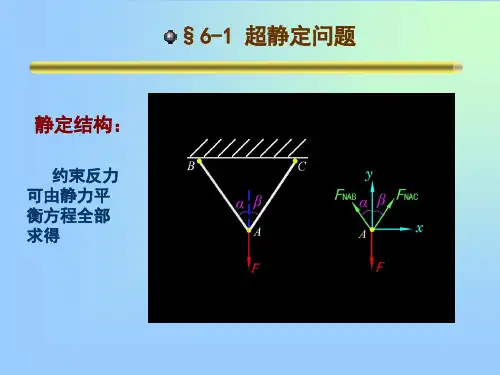

轴力图1234-5-4-3-2-11234567N(F/4)x(a)第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C , F 作用点为D ,则:B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=(实际方向与假设方向相反,即:↑) 故:45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。



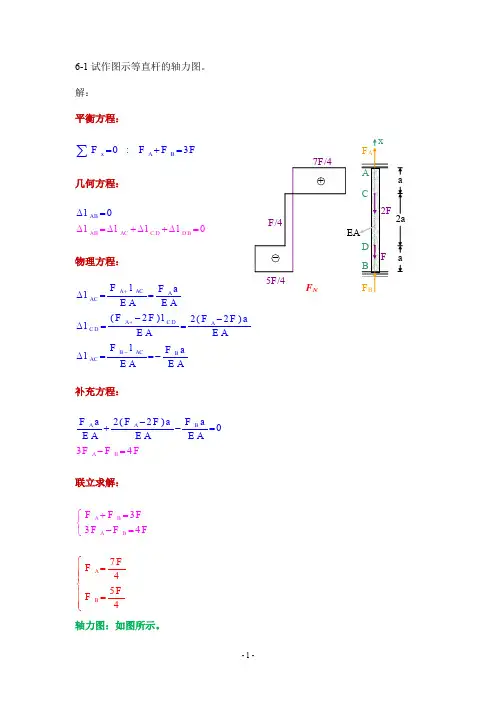
6-1试作图示等直杆的轴力图。
解:平衡方程:0:3xA B FF F F =+=∑几何方程:00ABACD D AB C B l lll l ∆=∆+∆+∆==∆物理方程:(2)2(2)A AC AAC A C D A C D B ACB AC F l F al E A E AF F l F F al E AE AFlF a lE AE A++-∆==--∆==∆==-补充方程:(32)042A A A B B F a F F a F aE A E A FA E F F -+--==联立求解:7453344A B A A B B F F F F FF F F F F +=⎧⎨-=⎩⎧=⎪⎪⎨⎪=⎪⎩轴力图:如图所示。
F N7F /4 - +F /4 5F /46-2如图所示托架承受载荷10kN F =,等直杆1、2、3由同一材料制成,各杆横截面面积分别为21100mm A =、22150mm A =、23200mm A =。
试求1、2、3轴力。
解:平衡方程(如图所示):oo0:()cos3000:()cos600x D B C y D B F F F F F F F F ⎧=--=⎪⎨=+-=⎪⎩∑∑几何方程(如图所示):123o o13oo 2321o2;;cos(60)cos(90)cos(60)cos(60)1(ctg sin 2cos(60)1(ctg sin 2l l l l l l l l l l θθθθθθθθθ∆∆∆=∆=∆=∆--+⎧∆-==⎪∆⎪∆-∆⇒⎨∆+⎪==∆⎪⎩物理方程: 123oo123;;cos30cos30B C D F l F l F ll l l E A E A E A ∆=∆=∆=补充方程:1323222B D CB DC F F F F F F A A A -=⇒-=联立求解:8.4530kN 2.6795kN 11.5470kN(220(02)2B C B D C D D B C D B F F F F F F F F F F F F ⎧-=⎪+-=⇒⎨⎪-=⎧⎩=⎪=⎨⎪=⎩ll 1 D x6-3如图所示刚性板由四根截面形状、大小及杆长相同的支柱支撑。
补充内容:第六章简单超静定问题§6-1 超静定问题及其解法•一、静定和超静定问题静定问题:约束反力(轴力)可由静力平衡方程求得用平衡方程可求两杆轴力,为静定问题。
§6-2 拉、压超静定问题超静定度(次)数:平面平行力系:2个平衡方程共线力系:1个平衡方程§6-2 拉、压超静定问题拉压超静定结构的求解方法:5、求解方程组得αα3221cos 21cos +==F F F N N α33cos 21+=F F N 1l ∆2l ∆3l ∆§6-2 拉、压超静定问题§6-2 拉、压超静定问题§6-2 拉、压超静定问题o30BC o 30D123§6-2 拉、压超静定问题o30BC o 30D123F§6-2 拉、压超静定问题o30BC o 30D123F拉压超静定问题例 图示刚性梁AB受均布载荷作用,梁在A端铰支,在B点和C点由两根钢杆BD和CE支承。
已知钢杆的横截面面积ADB=200mm2, 例题 6.2 A =400mm2,其许用应力[σ]=170MPa,试校核钢杆的强度。
CE 1)列静力平衡方程 2)变形协调方程1.8L∑MA=0FNCE = 135kN − 3FNBDFNBD × 1.8l 5 3× F × l FNCE= 3∆L− 30kN / m × 3m × 1.56 + FNBD= 3m = 0 NCE 2 ×1m m 2 = × ∆LDB CE NCE 200 × 10 −FNBD × E F400 × 10 −6 m × E mD630kN / mBFNBD = 32.2kNFNCE = 38.4kNALC1m2mEDFBD32.2 × 103 N FNBD = = 161MPa2p [σ ] σ BD = 200mm ADBσ CEB′ FBD1m 2m30kN / mF = NCE ACE38.4 × 103 N = = 96MPa p [σ ] 400mm 2ABCE∆LCE∆ LDB例题 6.3 图示结构中的三角形板可视为刚性板。
图
习题⋅-16
图
⋅
N l 图
习题⋅-56习 题
[6-1] 试作图示等直杆的轴力图。
解:把A 支座去掉,代之以约束反力A R (↑)。
A AC R N = F R N A CD 2-=
F R N A BD 3-=
变形协调条件为:
0=∆l
02=⋅+⋅+⋅EA a
N EA a N EA a N BD CD AC 02=++BD CD AC N N N
03)2(2=-+-+F R F R R A A A
4
7F
R A =
故:4
7F R N A AC =
= 42472F
F F F R N A CD -=-=-= 4
53473F
F F F R N A BD
-
=-=-= 轴力图如图所示。
[6-5] 图示刚性梁受均布荷载作用,梁在A 端铰支,在B 点和C 点由两根钢杆BD 和CE 支承。
已知钢杆BD 和CE 的横截面面积22200mm A =和21400mm A =,钢杆的许用应力MPa 170][=σ,试校核该钢杆的强度。
解:以AB 杆为研究对象,则:
0=∑A
M
1
02
3
)330(3121=⨯
⨯-⨯+⨯N N 135321=+N N (1)
变形协调条件:
3
1
21=∆∆l l 123l l ∆=∆
1
12238.1EA l
N EA l N ⨯=⋅ 400
32008.11
2N N =⋅ 212.1N N = (2)
(2)代入(1)得:
13532.122=+N N
)(143.322
.4135
2kN N ≈=
(拉力) )(571.38143.322.12.121kN N N ≈⨯== (压力)
按轴力正负号的规定,记作:
kN N 571.381-=;kN N 143.322=
强度校核:
MPa MPa mm N A N 170][4275.9640038571||
||2
111=<===σσ,符合强度条件。
图
习题⋅-15
6 MPa MPa mm N
A N 170][715.160200321432
122=<===
σσ,符合强度条件。
因此,钢杆符合强度条件,即安全。
[6-15(a)] 试求图示超静定梁的支反力。
解:把B 支座去掉,代之以约束反力B R ,则变形协调方程为:
0=B w 0=+B e R BM w w
查附录IV ,得:
EI
a M EI a M w e e BM e
2222)2(-=-=
EI
a R a a EI a R w B B R B
38)223(6)2(3
2-=-⨯-=
故, 03823
2=--=+EI
a R EI a M w w B e R BM B e
03
4=+
a
R M B e a
M R e
B 43-
= (负号表示方向向下,即↓) 由0=∑Y 得:a
M R e
A 43=
(↑)
B
图
习题⋅-176
B
由0=∑A M 得:e e A M a a M M +⋅-243,a
M
M e A 2=(逆时针方向转动)
[习题6-17] 梁AB 因强度和刚度不足,用同一材料和同样截面的短梁AC 加固,如图所示。
试求:
(1)二梁接触处的压力C F ;
(2)加固后梁AB 的最大弯矩和B 点的挠度减小的百分数。
解:(1)求二梁接触处的压力C F
以AB 为研究对象,把C 处的圆柱垫去掉,代之以约束反力C F (↑);以AC 为研究对象,作用在C 处的力为'C F (↓)。
C F 与'C F 是一对作用与反作用力,
'C C F F =。
受力如图所示。
AB 梁在C 处的挠度:
C CF CF AB C w w w +=,。
查附录IV 得:
EI
Fl l l EI l F w CF
48523(6)2(32
=
-=
B
B
FL
图
M EI
l F l l EI l F w C C CF C
24)223(6)2(32
-
=-⋅-= 故,EI
l F EI Fl w w w C CF CF AB C C 244853
3,-=+= AC 梁在C 处的挠度:
EI
l F EI l F w C C AC
C 243)2(33
',=
= 变形协调方程:
AC C AB C w w ,,=
EI
l F EI l F EI Fl C C 242448533
3=- 2424485C
C F F F =- C C F F F 225=-
4
5F
F C =
(↑) (2)求加固后梁AB 的最大弯矩和B 点的挠度减小的百分数 ① 弯矩的变化情况
加固前:2
2Fl l F M C -=⋅
-= max M Fl M A =-=
B
A
图
M Fl 3Fl 加固后:
max '
2
2M Fl l F M C
=-=⋅-=
8
3245'
Fl
l F Fl M A -
=⋅+
-= 显然,AB 梁的最大弯矩
减小:%5021=-Fl Fl
Fl (负弯矩只表示AB 梁上侧受拉) ② B 点挠度的变化情况
加固前:
EI
Fl w B 33
=
加固后:2
'
l w w w C C CF CF CF B ⋅++=θ
EI
Fl w CF
33= EI Fl EI l F EI l F l l EI l F w C C CF C
965244524)223(6)2(333
2-
=⋅-=-=-⋅-= EI
Fl EI l F EI l F EI l F EI l l F C C C CF C
3258458]2)2(22[222
2-
=⋅-=-=-⋅⋅-=θ 故,2
'
l w w w C C CF CF CF B ⋅++=θ
23259653233l
EI Fl EI Fl EI Fl ⋅--=
EI
Fl 192393
=
B 点挠度减小的百分数为:
%3964251926419225319239333
333===-EI
Fl EI Fl EI Fl EI Fl EI Fl。