下载文档原格式
单因素方差分析的计算步骤Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】一、 单因素方差分析的计算步骤假定实验或观察中只有一个因素（因子）A ,且A 有m 个水平，分别记为,,,21m A A A 在每一种水平下，做n 次实验，在每一次试验后可得一实验值，记做ij x 表示在第j 个水平下的第i 个试验值()m j n i ,2,1;,2,1==。
结果如下表：m A A A ,,21看成是m 个正态总体，而()m j n i x ij ,2,1;,2,1==看成是取自第j 总体的第i 个样品，因此，可设()m j n i a N x j ij ,2,1;,2,1,,~2==σ。
可以认为j j j a εεμ,+=是因素A 的第j 个水平j A 所引起的差异。
因此检验因素A 的各水平之间是否有显着的差异，就相当于检验：μ====m a a a H 210:或者 具体的分析检验步骤是：（一）计算水平均值令j x 表示第j 种水平的样本均值，式中，ij x 是第j 种水平下的第i 个观察值，j n 表示第j 种水平的观察值次数（二）计算离差平方和在单因素方差分析中，离差平方和有三个，它们分别是总离差平方和，组内离差平方和以及组间平方和。
首先，总离差平方和，用SST 代表，则，其中,n x x ij ∑∑=它反映了离差平方和的总体情况。
其次，组内离差平方和，用SSE 表示，其计算公式为：其中j x 反映的是水平内部或组内观察值的离散状况，即反映了随机因素带来的影响。
最后，组间平方和，用SSA 表示，SSA 的计算公式为：用各组均值减去总均值的离差的平方，乘以各组观察值个数，然后加总，即得到SSA 。
可以看出，它所表现的是组间差异。
其中既包括随机因素，也包括系统因素。
根据证明，SSA SSE SST ,,之间存在着一定的联系，这种联系表现在： 因为：在各组同为正态分布，等方差的条件下，等式右边最后一项为零，故有，即 SSA SSE SST +=（三）计算平均平方用离差平方和除以各自自由度即可得到平均平方。
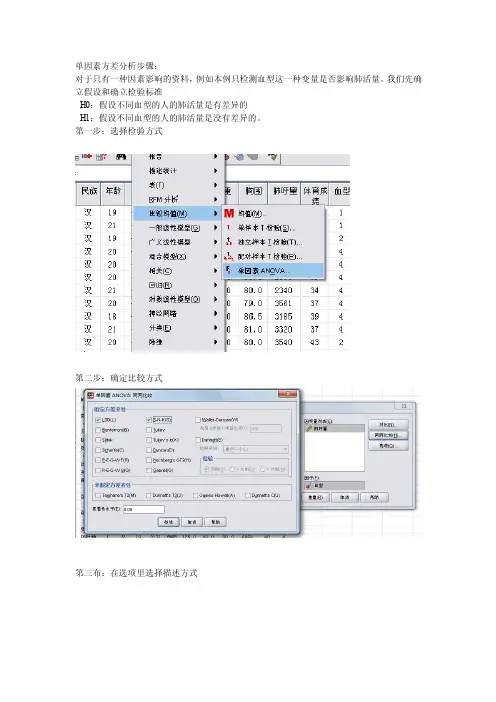
单因素方差分析步骤：对于只有一种因素影响的资料，例如本例只检测血型这一种变量是否影响肺活量。
我们先确立假设和确立检验标准H0：假设不同血型的人的肺活量是有差异的H1：假设不同血型的人的肺活量是没有差异的。
第一步：选择检验方式第二步：确定比较方式第三布：在选项里选择描述方式第四步：得出结果：由本图可知，p》0.05，可知肺活量的总体方差无差异，方差齐则可做方差分析再有下图可知：p= 0.789是大与0.05的，所以不是小概率事件，不拒绝H0，所以认为不同血型的人的肺活量是没有差异的。
随机区组设计资料的方差分析2.如果对四种饲料对猪体重增加量有无差异进行分析，则可将猪随机分组，本例中以a代表分组，b代表饲料，x代表体重增加量如图：对于这种资料分析，应选用单变量方差分析，主要是影响因素是多样的，主要描述的是体重增加量。
那么我们首先应1、确定假设：对于处理组：H0，假设三种处理方式体重增加量是相等的H1，假设三种处理方式体重增加量是不等的。
对于区组：H0，假设三组之间体重增加量是相等的H1，假设三组之间体重增加量是不等的。
2、确立检验标准a=0.053、计算统计量F F1=MS处理/MS误差F2=MS区组/MS误差4、确定p值，做出推断结论。
第一步：选择分析方式第二步：选择确立因变量，本题描述的是体重增加量，故选用x，确立区间，处理措施。
如图：第三步：确定模型，本题为确定区组a与处理措施b的交互作用，因此选用a，b交互模式。
如图：如需作图比较分组a 与处理措施b 的交互作用对体重影响有无差异可添加对比组，如图：确定观察均值的两两比较，主要针对与各分组的均值比较，及各处理方式的均值比较：在选项里设定输出，描述统计及方差齐性检验，显示分组及处理方式的均值。
最后得出结果：有本图可知F＜3，p＞0.05，可知各组间方差齐，可做方差检验。
如下图所示，可知p≥0.05，统计无差异，所以可知，三种处理方式对体重增加是无差异的。
