单因素方差分析列表计算 (1)
- 格式:doc
- 大小:61.00 KB
- 文档页数:2


单因素方差分析的计算步骤Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】一、 单因素方差分析的计算步骤假定实验或观察中只有一个因素(因子)A ,且A 有m 个水平,分别记为,,,21m A A A 在每一种水平下,做n 次实验,在每一次试验后可得一实验值,记做ij x 表示在第j 个水平下的第i 个试验值()m j n i ,2,1;,2,1==。
结果如下表:m A A A ,,21看成是m 个正态总体,而()m j n i x ij ,2,1;,2,1==看成是取自第j 总体的第i 个样品,因此,可设()m j n i a N x j ij ,2,1;,2,1,,~2==σ。
可以认为j j j a εεμ,+=是因素A 的第j 个水平j A 所引起的差异。
因此检验因素A 的各水平之间是否有显着的差异,就相当于检验:μ====m a a a H 210:或者 具体的分析检验步骤是:(一)计算水平均值令j x 表示第j 种水平的样本均值,式中,ij x 是第j 种水平下的第i 个观察值,j n 表示第j 种水平的观察值次数(二)计算离差平方和在单因素方差分析中,离差平方和有三个,它们分别是总离差平方和,组内离差平方和以及组间平方和。
首先,总离差平方和,用SST 代表,则,其中,n x x ij ∑∑=它反映了离差平方和的总体情况。
其次,组内离差平方和,用SSE 表示,其计算公式为:其中j x 反映的是水平内部或组内观察值的离散状况,即反映了随机因素带来的影响。
最后,组间平方和,用SSA 表示,SSA 的计算公式为:用各组均值减去总均值的离差的平方,乘以各组观察值个数,然后加总,即得到SSA 。
可以看出,它所表现的是组间差异。
其中既包括随机因素,也包括系统因素。
根据证明,SSA SSE SST ,,之间存在着一定的联系,这种联系表现在: 因为:在各组同为正态分布,等方差的条件下,等式右边最后一项为零,故有,即 SSA SSE SST +=(三)计算平均平方用离差平方和除以各自自由度即可得到平均平方。



Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题,需要应用方差分析。
方差分析是把试验看成一个整体,分解各种变异的原因。
从总的方差中,将可能的变异原因逐个分出,并用误差的方法作为判断其他方差是否显著的标准,如果已知变异原因的方差比误差方差大得多,那么,该方差就不是随机产生的,试验的处理间的差异不会是由于误差原因造成的,这时处理的效应是应该肯定的。
通过学习Excel中方差分析,掌握基本的分析操作,能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法2、例:在五个硼肥试验处理中测得苹果叶内硼含量(ppm),试比较各处理苹果叶内平均含硼量的差异显著性。
3、操作步骤:在Excel统计中,完全随机试验设计的方差分析,只须经过单因素方差分析即可得出结果,具体步骤如下:①打开Excel,向单元格中输入文字与数字,建立表格;②单击“工具”,在出现的对话框中,选择“数据分析”,选取“方差分析: 单因素方差分析”;③单击“确定”,单击“输入区域:”框右边的按钮,用鼠标选中数据,再次单击按钮;其他设置选择a为0.05。
分组方式:行。
点选标志位于第一列④单击“确定”,即可输出单因素方差分析结果。
4、方差分析输出结果: SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.55、多重比较:由方差分析的结果,采用新复极差测验法,再稍加计算比较处理, 即可得出:新复极差测验的LSR值6结论:由方差分析结果F=94.17>F o.o5=Fcrit=2.76,可知5种喷硼处理间差异显著,并可知除E与B二处理间无极显著差异外,其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析,是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题,如各组之间有显著差异,说明这个因素(分类变量)对因变量是有显著影响的,因素的不同水平会影响到因变量的取值。



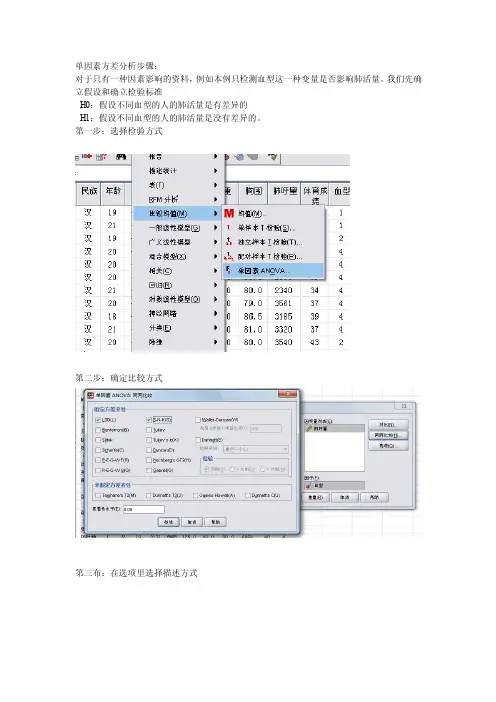
单因素方差分析步骤:对于只有一种因素影响的资料,例如本例只检测血型这一种变量是否影响肺活量。
我们先确立假设和确立检验标准H0:假设不同血型的人的肺活量是有差异的H1:假设不同血型的人的肺活量是没有差异的。
第一步:选择检验方式第二步:确定比较方式第三布:在选项里选择描述方式第四步:得出结果:由本图可知,p》0.05,可知肺活量的总体方差无差异,方差齐则可做方差分析再有下图可知:p= 0.789是大与0.05的,所以不是小概率事件,不拒绝H0,所以认为不同血型的人的肺活量是没有差异的。
随机区组设计资料的方差分析2.如果对四种饲料对猪体重增加量有无差异进行分析,则可将猪随机分组,本例中以a代表分组,b代表饲料,x代表体重增加量如图:对于这种资料分析,应选用单变量方差分析,主要是影响因素是多样的,主要描述的是体重增加量。
那么我们首先应1、确定假设:对于处理组:H0,假设三种处理方式体重增加量是相等的H1,假设三种处理方式体重增加量是不等的。
对于区组:H0,假设三组之间体重增加量是相等的H1,假设三组之间体重增加量是不等的。
2、确立检验标准a=0.053、计算统计量F F1=MS处理/MS误差F2=MS区组/MS误差4、确定p值,做出推断结论。
第一步:选择分析方式第二步:选择确立因变量,本题描述的是体重增加量,故选用x,确立区间,处理措施。
如图:第三步:确定模型,本题为确定区组a与处理措施b的交互作用,因此选用a,b交互模式。
如图:如需作图比较分组a 与处理措施b 的交互作用对体重影响有无差异可添加对比组,如图:确定观察均值的两两比较,主要针对与各分组的均值比较,及各处理方式的均值比较:在选项里设定输出,描述统计及方差齐性检验,显示分组及处理方式的均值。
最后得出结果:有本图可知F<3,p>0.05,可知各组间方差齐,可做方差检验。
如下图所示,可知p≥0.05,统计无差异,所以可知,三种处理方式对体重增加是无差异的。

单因素⽅差分析(one-wayANOVA)单因素⽅差分析(⼀)单因素⽅差分析概念是⽤来研究⼀个控制变量的不同⽔平是否对观测变量产⽣了显著影响。
这⾥,由于仅研究单个因素对观测变量的影响,因此称为单因素⽅差分析。
例如,分析不同施肥量是否给农作物产量带来显著影响,考察地区差异是否影响妇⼥的⽣育率,研究学历对⼯资收⼊的影响等。
这些问题都可以通过单因素⽅差分析得到答案。
(⼆)单因素⽅差分析步骤第⼀步是明确观测变量和控制变量。
例如,上述问题中的观测变量分别是农作物产量、妇⼥⽣育率、⼯资收⼊;控制变量分别为施肥量、地区、学历。
第⼆步是剖析观测变量的⽅差。
⽅差分析认为:观测变量值的变动会受控制变量和随机变量两⽅⾯的影响。
据此,单因素⽅差分析将观测变量总的离差平⽅和分解为组间离差平⽅和和组内离差平⽅和两部分,⽤数学形式表述为:SST=SSA+SSE。
第三步是通过⽐较观测变量总离差平⽅和各部分所占的⽐例,推断控制变量是否给观测变量带来了显著影响。
(三)单因素⽅差分析原理总结在观测变量总离差平⽅和中,如果组间离差平⽅和所占⽐例较⼤,则说明观测变量的变动主要是由控制变量引起的,可以主要由控制变量来解释,控制变量给观测变量带来了显著影响;反之,如果组间离差平⽅和所占⽐例⼩,则说明观测变量的变动不是主要由控制变量引起的,不可以主要由控制变量来解释,控制变量的不同⽔平没有给观测变量带来显著影响,观测变量值的变动是由随机变量因素引起的。
(四)单因素⽅差分析基本步骤1、提出原假设:H0——⽆差异;H1——有显著差异2、选择检验统计量:⽅差分析采⽤的检验统计量是F统计量,即F值检验。
3、计算检验统计量的观测值和概率P值:该步骤的⽬的就是计算检验统计量的观测值和相应的概率P值。
4、给定显著性⽔平,并作出决策(五)单因素⽅差分析的进⼀步分析在完成上述单因素⽅差分析的基本分析后,可得到关于控制变量是否对观测变量造成显著影响的结论,接下来还应做其他⼏个重要分析,主要包括⽅差齐性检验、多重⽐较检验。

单因素方差分析的计算步骤步骤1:制定假设首先,我们需要明确研究的问题以及相应的假设。
通常,单因素方差分析的研究问题是判断不同组之间均值是否存在显著差异,即研究问题可以被表述为"不同组的均值是否相等"。
根据问题,我们可以制定空假设和备择假设。
空假设通常是"不同组的均值相等",而备择假设通常是"不同组的均值不相等"。
步骤2:收集数据在进行单因素方差分析之前,我们需要收集相关数据。
收集数据的过程可能涉及实验设计、随机采样等方法。
数据的收集应该遵循一定的数据收集原则,以保证数据的真实性和可靠性。
步骤3:计算平均值第一步是计算每个组的平均值。
对于每个组,将其所有观测值相加,然后除以观测值的总数,即可得到该组的平均值。
计算每个组的平均值是了解数据分布和比较不同组均值的重要步骤。
步骤4:计算组内平方和接下来,我们需要计算组内平方和。
组内平方和表示每个组内各个观测值与该组平均值之差的平方的总和。
具体计算方法如下:-对于每个观测值,将其与该组的平均值相减,然后将结果平方。
-对于每个组,将每个观测值得到的平方差加起来,即得到该组的组内平方和。
-最后,将所有组的组内平方和相加,得到总的组内平方和。
步骤5:计算组间平方和接下来,我们需要计算组间平方和。
组间平方和表示不同组平均值之间的差异的平方的总和。
具体计算方法如下:-对于每个组,将其平均值与总体平均值相减,然后将结果平方。
-对于每个组,将每个计算得到的平方差相加,即得到该组的组间平方和。
-最后,将所有组的组间平方和相加,得到总的组间平方和。
步骤6:计算均方接下来,我们需要计算组内均方和组间均方。
组内均方是组内平方和除以自由度(总观测值数减去组数)得到的结果,而组间均方是组间平方和除以自由度(组数减去1)得到的结果。
步骤7:计算F值计算F值是判断组间均方和组内均方之间差异是否显著的重要步骤。
F值是组间均方除以组内均方计算得到的结果。
单因素方差分析方法首先在单因素试验结果的基础上,求出总方差V 、组内方差vw、组间方差vB。
总方差 v=()2ijx x -∑组内方差 v w =()2ij x x i-∑ 组间方差 v B=b ()2ix x -∑从公式可以看出,总方差衡量的是所有观测值xij对总均值x 的偏离程度,反映了抽样随机误差的大小,组内方差衡量的是所有观测值xij对组均值x 的偏离程度,而组间方差则衡量的是组均值x i对总均值x 的偏离程度,反映系统的误差。
在此基础上,还可以得到组间均方差和组内均方差: 组间均方差2Bs∧=1B-a v组内均方差2ws∧=aab vw-在方差相等的假定下,要检验n 个总体的均值是否相等,须首先给定原假设和备择假设。
原假设 H:均值相等即μ1=μ2=…=μn备择假设H 1:均值不完全不相等则可以应用F 统计量进行方差检验:F=)()(b ab a vv w--1B =22∧∧ss WB该统计量服从分子自由度a —1,分母自由度为ab-a 的F 分布。
给定显著性水平a ,如果根据样本计算出的F 统计量的值小于等于临界值)(a ab 1a F --,α,则说明原假设H不成立,总体均值不完全相等,差异并非仅由随机因素引起。
下面通过举例说明如何在Excel 中实现单因素方差分析。
例1:单因素方差分析某化肥生产商需要检验三种新产品的效果,在同一地区选取3块同样大小的农田进行试验,甲农田中使用甲化肥,在乙农田使用乙化肥,在丙地使用丙化肥,得到6次试验的结果如表2所示,试在0.05的显著性水平下分析甲乙丙化肥的肥效是否存在差异。
表2 三块农田的产量甲 50 46 49 52 48 48 乙 49 50 47 47 46 49 丙515049465050要检验三种化肥的肥效是否存在显著差异,等同于检验三者产量的均值是否相等:给定原假设H:三者产量均值相等;备择假设H 1:三者的产量均不相等,对于影响产量的因素仅化肥种类一项,因此可以采用单因素方差分析进行多总体样本均值检验. ⑴新建工作表“例1”,分别单击B3:D8单元格,输入表2的产量数值。
方差分析公式单因素与多因素方差分析的关键公式方差分析是一种统计方法,用于比较不同因素对变量的影响是否显著。
通过方差分析,我们可以确定不同因素之间是否存在统计学差异,并进一步研究这些差异的来源。
在方差分析中,单因素与多因素方差分析是两种常见的方法。
本文将介绍这两种方差分析中的关键公式。
一、单因素方差分析公式在单因素方差分析中,我们只考虑一个因素对变量的影响。
假设我们有k个水平(或组),每个水平下有n个观测值。
那么总观测值的个数为N=k*n。
在进行单因素方差分析之前,我们需要计算以下几个统计量:1. 总平方和(SST):表示所有观测值与整体均值之间的差异的总和。
计算公式为:SST = Σ(Σ(x_ij - X¯)^2)其中,x_ij表示第i组的第j个观测值,X¯表示所有观测值的均值。
2. 组间平方和(SSB):表示各组均值与整体均值之间的差异的总和。
计算公式为:SSB = Σ(n_i * (X¯_i - X¯)^2)其中,n_i表示第i组的观测值个数,X¯_i表示第i组的均值。
3. 组内平方和(SSW):表示每组内个体与组内均值之间的差异的总和。
计算公式为:SSW = Σ(Σ(x_ij - X¯_i)^2)其中,x_ij表示第i组的第j个观测值,X¯_i表示第i组的均值。
根据以上统计量,我们可以计算方差分析的F值,来判断组间差异是否显著。
F值的计算公式为:F = (SSB / (k-1)) / (SSW / (N - k))其中,k表示组数,N表示总观测值的个数。
二、多因素方差分析公式在多因素方差分析中,我们考虑两个或两个以上的因素对变量的影响。
假设我们有r个因素,每个因素有k个水平(或组)。
那么总观测值的个数为N = k^r。
在进行多因素方差分析之前,我们需要计算以下几个统计量:1. 总平方和(SST):表示所有观测值与整体均值之间的差异的总和。