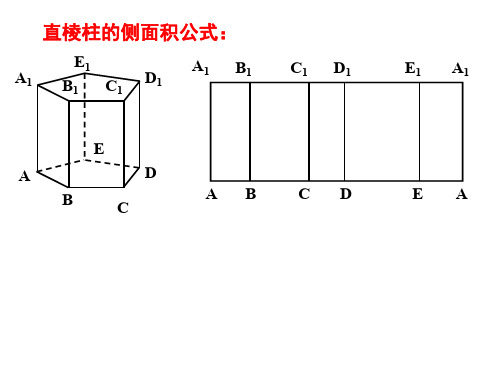
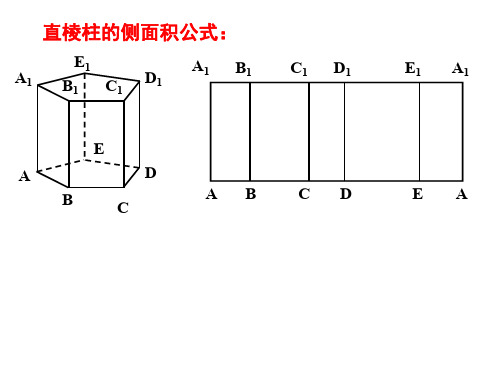
棱柱的面积和体积
- 格式:ppt
- 大小:277.50 KB
- 文档页数:13

三棱柱的体积和表面积公式
【原创版】
目录
1.引言
2.三棱柱的体积公式
3.三棱柱的表面积公式
4.结论
正文
【引言】
三棱柱是一种有六个面的立体图形,其中三个面为三角形,另外三个面为矩形。
了解三棱柱的体积和表面积公式,有助于我们更好地计算与三棱柱相关的数学问题。
本文将为大家介绍三棱柱的体积和表面积公式。
【三棱柱的体积公式】
三棱柱的体积可以通过以下公式进行计算:
V = (1/3) × S × h
其中,V 表示三棱柱的体积,S 表示底面的面积,h 表示三棱柱的高。
【三棱柱的表面积公式】
三棱柱的表面积可以通过以下公式进行计算:
S = 2 × (1/2 × a × b + 1/2 × a × c + 1/2 × b × c) + 3 × S 底
其中,S 表示三棱柱的表面积,a、b、c 分别表示三棱柱的三条棱的长度,S 底表示底面的面积。
【结论】
通过上述公式,我们可以方便地计算三棱柱的体积和表面积。
在实际应用中,这些公式为我们解决与三棱柱相关的数学问题提供了有力的工具。

棱柱与棱锥的体积与表面积比棱柱和棱锥是几何学中常见的立体图形,它们在我们日常生活和工作中都有广泛的应用。
了解它们的体积和表面积比可以帮助我们更好地理解它们的特性和应用。
本文将深入探讨棱柱与棱锥的体积和表面积比,并从数学和实际应用的角度进行阐述。
一、棱柱的体积与表面积首先,我们来看一下棱柱的定义和特性。
棱柱是由两个平行的多边形底面和连接它们的矩形侧面组成的立体图形。
如果底面是正多边形,我们称之为正棱柱。
棱柱的两个底面平行且相等,侧面是矩形,而顶面和底面是相同的正多边形。
棱柱的体积可以通过将底面积乘以高来计算得出。
设底面积为A,高度为h,则棱柱的体积V可以表示为:V = A * h棱柱的表面积可以通过将底面积加上底面周长与侧面面积的两倍来计算得出。
设底面积为A,底面周长为P,侧面积为S,则棱柱的表面积S可以表示为:S = A + 2P * h二、棱锥的体积与表面积接下来,我们来看一下棱锥的定义和特性。
棱锥是由一个多边形底面和连接它们的三角形侧面组成的立体图形。
如果底面是正多边形,我们称之为正棱锥。
棱锥的底面为一个多边形,顶点位于底面上方,连接底面和顶点的线段称为棱。
棱锥的体积可以通过将底面积乘以高再除以3来计算得出。
设底面积为A,高度为h,则棱锥的体积V可以表示为:V = A * h / 3棱锥的表面积可以通过将底面积加上底面周长与侧面积的两倍来计算得出。
设底面积为A,底面周长为P,侧面积为S,则棱锥的表面积S可以表示为:S = A + P * l其中,l为棱的长度。
三、体积与表面积比的计算与应用现在,我们可以来计算棱柱与棱锥的体积和表面积比了。
1. 体积比我们先来计算棱柱的体积与棱锥的体积比。
设棱柱的底面积为A1,高度为h1,棱锥的底面积为A2,高度为h2,则体积比V_ratio可以表示为:V_ratio = (A1 * h1) / (A2 * h2)2. 表面积比接下来,我们计算棱柱的表面积与棱锥的表面积比。

棱柱的表面积公式
【原创实用版】
目录
1.棱柱的定义和特点
2.棱柱表面积公式的推导
3.棱柱表面积公式的应用举例
4.棱柱的体积公式
5.总结
正文
一、棱柱的定义和特点
棱柱是一种几何体,它的特点是有两个平行且全等的底面,侧棱平行且相等。
棱柱的底面可以是任意多边形,常见的有矩形、三角形等。
根据底面的不同,棱柱可以分为不同的类型,如三棱柱、四棱柱等。
二、棱柱表面积公式的推导
棱柱的表面积由底面积和侧面积两部分组成。
底面积为底面的面积,侧面积为所有侧面的面积之和。
假设棱柱的底边长为 a,高为 h,侧面积为 s 侧,底面周长为 l,底面面积为 s 底,那么棱柱的表面积公式为:表面积 = s 侧 + 2s 底
三、棱柱表面积公式的应用举例
以一个正三棱柱为例,底边长为 a,高为 h。
首先计算底面积:
s 底 = (根号 3 / 4) * a^2
底面周长:
l = 3a
侧面积:
s 侧 = l * h = 3ah
将底面积和侧面积代入表面积公式:
表面积 = 3ah + 2 * (根号 3 / 4) * a^2
四、棱柱的体积公式
棱柱的体积公式为:
体积 = 底面积 * 高 = (根号 3 / 2) * a^2 * h
五、总结
本文介绍了棱柱的定义、特点和表面积公式,以及体积公式。
通过推导表面积公式,我们可以更好地理解棱柱的表面积组成,并应用到实际问题中。

计算棱柱的体积和表面积之比在几何学中,棱柱是一种具有两个平行且等面积多边形底面的立体形状。
它的侧面由多条平行的边连接底面的对应顶点而构成。
本文将介绍如何计算棱柱的体积和表面积,并探讨它们之间的比例关系。
1. 棱柱的定义和特征棱柱是一个多面体,它由两个平行的多边形底面和连接底面对应顶点的若干矩形侧面构成。
棱柱的特征主要包括底面的形状、边的数量和高度。
2. 计算棱柱的体积棱柱的体积可以通过底面积和高度的乘积得出。
设底面的面积为A,高度为h,则棱柱的体积V可以表示为:V = A * h根据底面形状的不同,我们可以计算出不同类型的棱柱体积。
下面将以正方形底面和圆形底面的棱柱为例进行说明。
2.1 正方形底面棱柱的体积计算设正方形底面的边长为a,则底面积A = a * a = a^2。
棱柱的体积V可以表示为:V = A * h = a^2 * h2.2 圆形底面棱柱的体积计算设圆形底面的半径为r,则底面积A = π * r^2。
棱柱的体积V可以表示为:V = A * h = π * r^2 * h3. 计算棱柱的表面积棱柱的表面积由底面和侧面的面积之和构成。
设底面的面积为A,侧面的总面积为P,则棱柱的表面积S可以表示为:S = A + P3.1 正方形底面棱柱的表面积计算除了底面积A = a^2之外,正方形底面的棱柱还有四个矩形的侧面,每个矩形的长宽分别为a和h。
所以侧面的总面积P = 4 * a * h。
棱柱的表面积S可以表示为:S = A + P = a^2 + 4 * a * h3.2 圆形底面棱柱的表面积计算除了底面积A = π * r^2之外,圆形底面的棱柱还有一个圆筒形侧面。
圆筒的侧面积为2πrh,其中r为底面的半径,h为棱柱的高度。
所以侧面的总面积P = 2πrh。
棱柱的表面积S可以表示为:S = A + P = π * r^2 + 2πrh = π(r^2 + 2rh)4. 体积和表面积之比根据上述计算公式,我们可以得到棱柱的体积和表面积之比。
计算七棱柱的体积和表面积七棱柱是一种具有七个相等侧面的多面体。
它的形状类似于圆柱,但有七个侧面而不是一个圆面。
本文将介绍如何计算七棱柱的体积和表面积。
一、七棱柱的定义和特点七棱柱是由两个底面和七个侧面组成的多面体。
它的底面是正七边形,而侧面是矩形。
七棱柱的特点是侧面的数目和底面的形状。
二、计算七棱柱的体积七棱柱的体积可以通过以下公式计算:体积 = 底面积 ×高首先,我们需要计算底面的面积。
由于七棱柱的底面是正七边形,我们可以使用以下公式计算正七边形的面积:底面积 = (7 × a^2) / (4 × tan(π/7))其中,a表示正七边形的边长。
接下来,我们需要确定七棱柱的高。
七棱柱的高是两个底面之间的距离,可以通过测量或已知给定的数值获得。
最后,将底面积与高相乘,即可计算出七棱柱的体积。
三、计算七棱柱的表面积七棱柱的表面积可以通过以下公式计算:表面积 = 2 ×底面积 + 7 ×侧面积首先,我们已经知道如何计算底面积。
接下来,我们需要计算侧面的面积。
七棱柱的侧面是矩形,它们的长度等于正七边形的边长,宽度等于七棱柱的高。
侧面积 = 底面边长 ×高最后,将底面积乘以2,再将侧面积乘以7,然后将两者相加,即可得到七棱柱的表面积。
四、总结在本文中,我们介绍了如何计算七棱柱的体积和表面积。
七棱柱是一种多面体,由两个底面和七个侧面构成。
通过使用相应的公式,我们可以准确地计算出七棱柱的体积和表面积。
这些计算方法可以应用于解决相关的几何问题,以及在实际生活中的测量和设计中。
例求斜三棱柱的体积
1、三棱柱表面积公式:3个侧面(一般都是长方形的)+2个底面面积(三角形)
2、三棱柱体积公式是:V=SH,体积=底面积×高,底面积=三角形的底×高÷2
由于三棱柱也可以视为三面体截去2个顶点,故又称截角三面体,另外,因为正三棱柱具有对称性,且由2种正多边形组成,因此有人称正三棱柱为半正五面体。
一般三棱柱有5个面、9个边和6个顶点。
扩展资料
棱柱是几何学中的一种常见的三维多面体,指平面上的一个多边形平行投影到与该平面平行的平面所截得的封闭几何体。
棱柱的两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行。
若用于截平行平面的平面数为n,那么该棱柱便称为n-棱柱。
如三棱柱就是由两个平行的平面被三个平面所垂直截得的封闭几
何体。
一些特殊的棱柱
1、斜棱柱
侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时,一般将侧棱画成不与底面垂直。
2、直棱柱
侧棱垂直于底面的棱柱叫做直棱柱。
画直棱柱时,应将侧棱画成与底面垂直。
3、正棱柱
底面是正多边形的直棱柱叫做正棱柱。