下载文档原格式
第四章 准静态电磁场4．1 准静态电磁场1．电准静态场由麦克斯韦方程组知，时变电场由时变电荷和时变磁场产生的感应电压产生。
时变电荷产生库仑电场，时变磁场产生感应电场。
在低频情况下，一般时变磁场产生的感应电场远小于时变电荷产生的库仑电场，可以忽略。
此时，时变电场满足ρ=∙∇≈⨯∇D 0E 称为电准静态场。
可见，电准静态场与静电场类似，可以定义时变电位函数ϕ ，即ϕ-∇=E且满足泊松方程ερϕ-=∇2 与电准静态场对应的时变磁场满足 0t =∙∇∂∂+=⨯∇B DE H γ 2．磁准静态场由麦克斯韦方程组知，时变磁场由时变传导电流和时变电场产生的位移电流产生。
在低频情况下，一般位移电流密度远小于时变传导电流密度，可以忽略。
此时，时变磁场满足0=∙∇≈⨯∇B J H c称为磁准静态场。
可见，磁准静态场与恒定磁场类似，可以定义时变矢量位函数A ，即A B ⨯∇=且满足矢量泊松方程c J A μ-=∇2与磁准静态场对应的时变电场满足ρ=∙∇∂∂-=⨯∇D B E t例1：图示圆形平板电容器，极板间距d = 0.5 cm ，电容器填充εr =5.4的云母介质。
忽略边缘效应，极板间外施电压t t u 314cos 2110)(=V ，求极板间的电场与磁场。
[解]：极板间的电场由极板上的电荷和时变磁场产生。
在工频情况下，忽略时变磁场的影响，即极板间的电场为电准静态场。
在如示坐标系下，得()()()V/m t 31410113t 31410501102d u z 4z 2z e e e E -⨯=-⨯⨯=-=-cos .cos . 由全电流定律得出，即由()z z 20r 4Sl t 31431410113d t H 2d e e S D l H ∙-π⨯⨯-=∙∂∂=π=∙⎰⎰ρεερφsin . 极板间磁场为φφφρe e H t 314103352H 4sin .-⨯== A/m也可以由麦克斯韦方程直接求解磁场强度，如下tt 0r ∂∂=∂∂=⨯∇E D H εε 展开，得t 314106694H 14sin .)(-⨯=∂∂φρρρ 解得φφφρe e H t 314103352H 4sin .-⨯== A/m 讨论：若考虑时变磁场产生的感应电场，则有tt ∂∂-=∂∂-=⨯∇H B E 0μ 展开，得t E z 314cos 103.231440ρμρ-⨯⨯-=∂∂- 解得 t E z 314cos 10537.428ρ-⨯= V/m可见，在工频情况下，由时变磁场产生的感应电场远小于库仑电场。
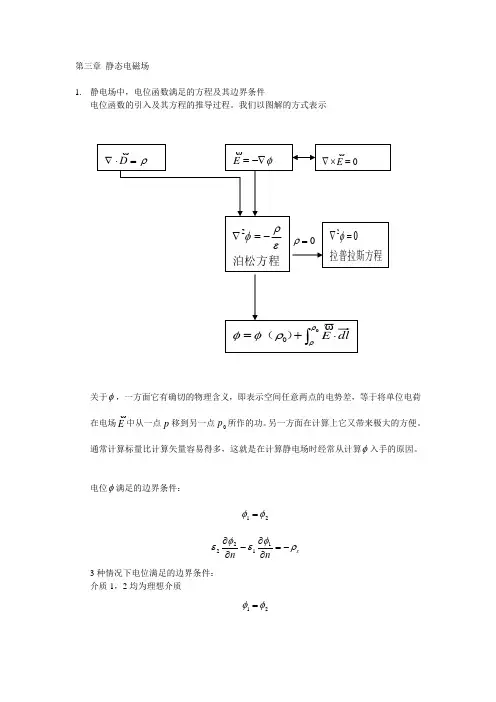
第三章 静态电磁场1. 静电场中，电位函数满足的方程及其边界条件电位函数的引入及其方程的推导过程。
我们以图解的方式表示关于φ，一方面它有确切的物理含义，即表示空间任意两点的电势差，等于将单位电荷在电场E中从一点p 移到另一点0p 所作的功。
另一方面在计算上它又带来极大的方便。
通常计算标量比计算矢量容易得多，这就是在计算静电场时经常从计算φ入手的原因。
电位φ满足的边界条件：21φφ=s nn ρφεφε-=∂∂-∂∂11223种情况下电位满足的边界条件： 介质1，2均为理想介质21φφ=s nn ρφεφε-=∂∂-∂∂1122介质1为导体，介质2为理想介质)(0常数φφ=s nρφε-=∂∂ 介质1，2均为导电介质，在恒定电流情况21φφ=01122=∂∂-∂∂nn φσφσ2. 静电场的能量，能密度；导体上的静电力与一个电荷分布相联系的势能可写成：⎰=v e dv W ρφ21或 ⎰⋅=ve dv E D W21其中第一个积分中的v 包含所有的电荷分布，第二式则包含所有E不为零的空间。
能量密度为：E D W e ⋅=21 当E D ε=时：221E W e ε=导体上的静电力分两种情况：常=∇=φe W F常=-∇=q eW F3. 恒定电场的方程和边界条件微分方程：0=⨯∇E0=⋅∇J)(K E J+=σ积分方程：0=⋅⎰E L0=⋅⎰sJ其中K表示电源作用在单位正电荷上的非静电力。
电位φ所满足的方程⎩⎨⎧⋅∇=∇)()(02电源内部电源外部K φ在两导体交界面上的边界条件：21φφ=nn ∂∂=∂∂2211φσφσ4. 恒定电流的磁场磁失势所满足的方程及边界条件磁失势的引入及方程的推导过程我们以图解的方式表示磁失势满足的边界条件：12A A =s A A nτμμ=⨯∇-⨯∇⨯)11(ˆ1122磁失势所满足的方程及边界条件：磁失势的引入及方程的推导过程我们以图解的方式表示其中m φ引入的条件是无传导电流的单连通区域如电流是环形分布的，磁标势适合的区域只能是挖去环形电流所围成的壳形之后剩下的区域。
