地震倾覆力矩的计算

物理参数:圬工砌体容重: 20.500(kN/m3)圬工之间摩擦系数: 0.800地基土摩擦系数: 0.577墙身砌体容许压应力: 580.000(kPa)墙身砌体容许剪应力: 58.000(kPa)墙身砌体容许拉应力: 110.000(kPa)墙身砌体容许弯曲拉应力: 56.000(kPa)挡土墙类型: 抗震区浸水挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)墙背与墙后填土摩擦角: 23.000(度)地基土容重: 18.000(kN/m3)修正后地基土容许承载力: 300.000(kPa)地基土容许承载力提高系数:墙趾值提高系数: 1.200墙踵值提高系数: 1.300平均值提高系数: 1.000地震作用墙趾值提高系数: 1.500地震作用墙踵值提高系数: 1.625地震作用平均值提高系数: 1.250墙底摩擦系数: 0.300地基土类型: 土质地基地基土内摩擦角: 30.000(度)地震烈度: 设计烈度7度面侧地震动水压力系数: 1.000背侧地震动水压力系数: 1.000水上地震角: 1.50水下地震角: 2.50水平地震系数: 0.13重要性修正系数: 1.00综合影响系数: 0.25抗震基底容许偏心距:B/5地震力调整系数: 1.000墙后填土浮容重: 12.500(kN/m3)地基浮力系数: 0.700土压力计算方法: 库仑第 2 种情况: 地震情况[土压力计算] 计算高度为 5.500(m)处的库仑主动土压力按实际墙背计算得到:第1破裂角： 27.000(度)Ea=103.732 Ex=95.486 Ey=40.531(kN) 作用点高度 Zy=1.898(m) 墙身截面积 = 22.250(m2) 重量 = 456.125 kN地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m) 墙面坡侧: 54.78 -17.24 -1.99 -4.40墙背坡侧: -54.78 -9.05 2.75 -4.40墙底面: -0.00 127.43 0.25 -5.50全墙地震力=11.403(kN) 作用点距墙顶高度=3.140(m)(一) 滑动稳定性验算基底摩擦系数 = 0.300滑移力= 106.889(kN) 抗滑力= 118.654(kN)滑移验算满足: Kc = 1.110 > 1.000(二) 倾覆稳定性验算相对于墙趾点，墙身重力的力臂 Zw = 3.035 (m)相对于墙趾点，Ey的力臂 Zx = 5.000 (m)相对于墙趾点，Ex的力臂 Zy = 1.898 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 502.292(kN-m) 抗倾覆力矩= 1586.833(kN-m)倾覆验算满足: K0 = 3.159 > 1.300(三) 地基应力及偏心距验算基础为天然地基，验算墙底偏心距及压应力作用于基础底的总竖向力 = 395.513(kN) 作用于墙趾下点的总弯矩=1084.541(kN-m) 基础底面宽度 B = 5.500 (m) 偏心距 e = 0.008(m)基础底面合力作用点距离基础趾点的距离 Zn = 2.742(m)基底压应力: 趾部=72.530 踵部=71.293(kPa)最大应力与最小应力之比 = 72.530 / 71.293 = 1.017作用于基底的合力偏心距验算满足: e=0.008 <= 0.200*5.500 = 1.100(m)墙趾处地基承载力验算满足: 压应力=72.530 <= 450.000(kPa)墙踵处地基承载力验算满足: 压应力=71.293 <= 487.500(kPa)地基平均承载力验算满足: 压应力=71.911 <= 375.000(kPa)(四) 基础强度验算基础为天然地基，不作强度验算(五) 墙底截面强度验算验算截面以上地震力=11.403(kN) 作用点距墙顶高度=3.140(m)地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 54.78 -17.24 -1.99 -4.40墙背坡侧: -54.78 -9.05 2.75 -4.40验算截面以上，墙身截面积 = 22.250(m2) 重量 = 456.125 kN相对于验算截面外边缘，墙身重力的力臂 Zw = 3.035 (m)相对于验算截面外边缘，Ey的力臂 Zx = 5.000 (m)相对于验算截面外边缘，Ex的力臂 Zy = 1.898 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 522.945(kN) 作用于墙趾下点的总弯矩=1434.981(kN-m) 相对于验算截面外边缘，合力作用力臂 Zn = 2.744(m)截面宽度 B = 5.500 (m) 偏心距 e1 = 0.006(m)截面上偏心距验算满足: e1= 0.006 <= 0.400*5.500 = 2.200(m)截面上压应力: 面坡=95.700 背坡=94.462(kPa)压应力验算满足: 计算值= 95.700 <= 870.000(kPa)切向应力检算:剪应力验算满足: 计算值= -56.630 <= 58.000(kPa)(六) 台顶截面强度验算[土压力计算] 计算高度为 4.000(m)处的库仑主动土压力按实际墙背计算得到:第1破裂角： 27.000(度)Ea=56.994 Ex=52.463 Ey=22.269(kN) 作用点高度 Zy=1.369(m)墙身截面积 = 14.750(m2) 重量 = 302.375 kN地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 16.38 -8.19 -1.70 -3.40墙背坡侧: -16.38 -1.55 2.75 -3.40墙底面: -0.00 63.35 0.50 -4.00全墙地震力=7.559(kN) 作用点距墙顶高度=2.244(m)[强度验算]验算截面以上地震力=7.175(kN) 作用点距墙顶高度=2.190(m)地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 16.38 -8.19 -1.70 -3.40墙背坡侧: -16.38 -0.00 2.50 -3.40验算截面以上，墙身截面积 = 14.000(m2) 重量 = 287.000 kN相对于验算截面外边缘，墙身重力的力臂 Zw = 2.702 (m)相对于验算截面外边缘，Ey的力臂 Zx = 4.500 (m)相对于验算截面外边缘，Ex的力臂 Zy = 1.369 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 317.459(kN) 作用于墙趾下点的总弯矩=793.474(kN-m) 相对于验算截面外边缘，合力作用力臂 Zn = 2.499(m)截面宽度 B = 4.500 (m) 偏心距 e1 = -0.249(m)截面上偏心距验算满足: e1= -0.249 <= 0.400*4.500 = 1.800(m)截面上压应力: 面坡=47.083 背坡=94.010(kPa)压应力验算满足: 计算值= 94.010 <= 870.000(kPa) 切向应力检算:剪应力验算满足: 计算值= -43.184 <= 58.000(kPa)。

地震倾覆力矩测试抗震设计时，地震造成的对房屋的倾覆力矩是由框架和剪力墙两部分共同承担的。

若由框架承担的部分大于总倾覆力矩的一定比例时，说明框架部分已居于较主要地位，应加强其抗震能力的储备。

另外，对于近年兴起的短肢剪力墙结构，新规程要求设置剪力墙筒体（或一般剪力墙），形成短肢剪力墙与筒体（或一般剪力墙）共同抵抗水平力的结构。

同时对短肢剪力墙结构中抗震设计时筒体和一般剪力墙承受的地震倾覆力矩作了相应的规定。

为便于操作，本次规范修订给出了框架部分承受的地震倾覆力矩的具体计算公式。

1. 规范、规程相关规定和测试内容1．1．规范、规程相关规定1． 抗震规范6.1.3-1和高规8.1.3条文，用于判定框剪结构的框架部分抗震等级的提高。

具体内容为“框架抗震墙结构，在基本振型地震作用下，若框架部分承受的地震倾覆力矩大于结构总倾覆力矩的50%，其框架部分的抗震等级应按框架结构确定，（柱轴压比限值宜按框架结构的规定采用）；最大适用高度可比框架结构适当增加”； 框架部分承受的地震倾覆力矩可按下式计算：11n mc ij i i j M V h ===∑∑式中 Mc ——框剪结构在基本振型地震作用下框架部分承受的地震倾覆力矩 n ——结构层数m ——框架i 层的柱根数Vij ——第i 层j 根框架柱的计算地震剪力 hi ——第i 层层高 2． 高规7.1.2-2，用于限定短肢剪力墙结构中短肢剪力墙的数量。

具体内容为“抗震设计时，筒体和一般剪力墙承受的第一振型底部地震倾覆力矩不宜小于结构总底部地震倾覆力矩的50%”；2. 测试例题2.1．例1-框架-剪力墙SOF15层框剪，层高均为3.3M ，总高度16.5M 。

无地下室。

地震信息 ............................................振型组合方法: CQC12345678123456789101112131415161718192021222324252627282930313233343536123456789Xm=8.00Ym=8.00Xs=8.00Ys=8.00Rx=0.56Ry=7.96第 2 层墙柱 墙梁编号及节点简图梁总数 = 36 柱总数 = 9 墙梁数 = 0 墙柱数 = 82.1.1 SATWE 计算取15个振型，刚性楼板假定。

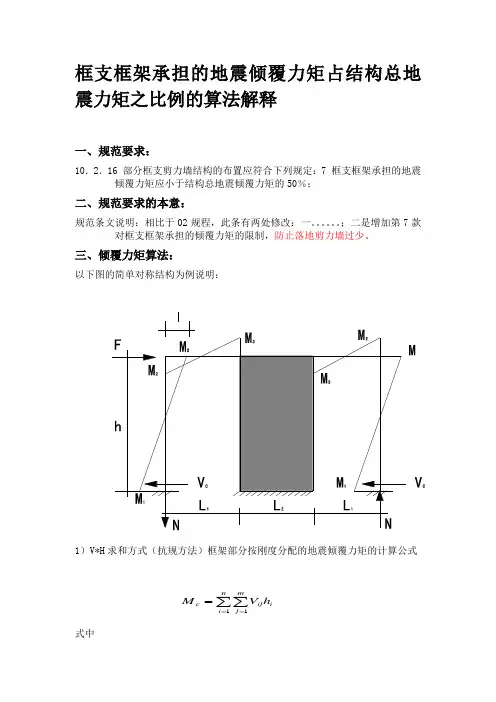
框支框架承担的地震倾覆力矩占结构总地震力矩之比例的算法解释一、规范要求：10．2．16 部分框支剪力墙结构的布置应符合下列规定：7 框支框架承担的地震倾覆力矩应小于结构总地震倾覆力矩的50％；二、规范要求的本意：规范条文说明：相比于02规程，此条有两处修改：一。

；二是增加第7款对框支框架承担的倾覆力矩的限制，防止落地剪力墙过少。

三、倾覆力矩算法：以下图的简单对称结构为例说明：1）V*H 求和方式（抗规方法）框架部分按刚度分配的地震倾覆力矩的计算公式in i mj ij c h V M ∑∑===11式中c M ——框架-抗震墙结构在规定的侧向力作用下框架部分分配的地震倾覆力矩；n ——结构层数； m ——框架i 层的柱根数；ij V ——第i 层第j 根框架柱的计算地震剪力； i h ——第i 层层高。

对一根框架柱来讲，根据其平衡条件，21M M h V c += （8） 同样根据平衡条件，此时梁上剪力N V b = （9） 在梁内由梁的平衡条件有Nl l V M b ==2 （10） 则按照抗规方法计算得到的柱倾覆力矩为：Nl M h V M c c 2221'+== （11）2）力学标准方式（即PKPM 中提供的轴力方式）按力学方法计算倾覆力矩，需要先计算合力作用点，然后用底部轴力对合力作用点取距。

SATWE 中的合力作用点计算方法为 ∑∑=ii i o N x N x （5） 其中o x ——x 向合力作用点i N ——x 向规定水平力下各构件的轴力 i x ——柱的x 坐标或者墙柱的中心点x 坐标。

则框架柱承担的倾覆力矩为： ()[]∑=+-=ni yi o ii cx M x x N M 1（6）即倾覆力矩为轴力产生的倾覆力矩与柱底弯矩之和，墙的计算方法与柱相同。

图6所示框剪结构在水平力F 作用下，在框架柱底部产生的轴力为N ，柱底弯矩为1M ，显然框架承担的倾覆力矩应该为：()12122M L L N M c ++= （7）四结论：从计算结果可以看出：1抗规方式算出的柱底部弯矩占结构总弯矩的比例与墙数量的相关性更强（主要跟墙柱的刚度在总刚度的占比有关），而轴力方式算出的柱底部弯矩的占结构总弯矩的比例与墙位置的相关性也有很大关系，甚至占主导的关系（根据轴力计算弯矩时的墙柱与结构合力作用点的距离（即力臂）的有关）。

挡土墙抗倾覆稳定性验算例题假设挡土墙的高度为6米,墙后填土的重度为18kN/m³,填土面与墙面摩擦角为30度,水平地震分析加速度为0.15g,垂直地震分析加速度为0.1g。

现在来计算挡土墙的抗倾覆稳定性。

步骤如下：1.计算填土的横向作用力填土的横向作用力 = 填土重度 x 墙高 x 墙宽= 18 kN/m³ x 6m x 1m= 108 kN/m2.计算填土与墙面之间的摩擦力填土与墙面之间的摩擦力 = 填土的横向作用力 x 摩擦系数= 108kN/m x tan(30度)= 62.4 kN/m3.计算水平方向的地震作用力水平方向的地震作用力 = 0.15g x 1g x 填土重度 x 墙高 x 墙宽= 0.15 x 1 x 18 kN/m³ x 6m x 1m= 16.2 kN/m4.计算垂直方向的地震作用力垂直方向的地震作用力 = 0.1g x 1g x 填土重度 x 墙高 x 墙宽= 0.1 x 1 x 18 kN/m³ x 6m x 1m= 10.8 kN/m5.计算倾覆力矩倾覆力矩 = 填土的横向作用力 x 墙高/2 + 填土与墙面之间的摩擦力 x 墙高/3+ 水平方向的地震作用力 x 墙高/3 + 垂直方向的地震作用力 x 墙高/3 = 108 kN/m × 6m/2 + 62.4 kN/m × 6m/3 + 16.2 kN/m × 6m/3 + 10.8 kN/m × 6m/3= 876.6 kN·m6.计算抗倾覆稳定系数抗倾覆稳定系数 = 倾覆力矩 / 抵抗倾覆力矩= 倾覆力矩 / (填土的横向作用力 x 墙高/2)= 876.6 kN·m / (108 kN/m × 6m/2)= 2.04因此,挡土墙的抗倾覆稳定系数为2.04,满足抗倾覆的要求。

框剪倾覆力矩比的权威解惑结构设计中,倾覆力矩是一个关乎结构体系合理性控制的重要概念.高规8.1.3条、抗规6.1.3条,利用框架倾覆力矩占结构总倾覆力矩的百分比,来界定结构性质,规定不同的控制和设计方法；高规7.1.8条,通过限制短肢墙倾覆力矩占结构总倾覆力矩的百分比,以控制结构中布置足够的普通墙,从而保证短肢墙结构体系的合理性；高规10.2.16条,通过控制框支框架倾覆力矩占结构总倾覆力矩的百分比,防止落地剪力墙过少造成的薄弱层,来保证部分框支剪力墙结构体系的合理性；显然,所有这些体系指标的控制,都建立在框架倾覆力矩正确计算的基础上.目前关于框架倾覆力矩的计算,有两种基本方法：规范算法与轴力算法一、《建筑抗震设计规范》6.1.3条文说明推荐的方法框架部分按刚度分配的地震倾覆力矩的计算公式：式中M－框架-抗震墙结构在规定的侧向力作用下框架部分c分配的地震倾覆力矩；n—结构层数；m—框架i层的柱根数；V—第i层第j根框架柱的计算地震剪力；ij—第i层层高.hi规范算法的影响因素：1）框架柱的计算剪力Vc,ij —取决于柱与墙的相对刚度2）建筑层高hi—与结构布局无关二、轴力算法以外力作用下结构嵌固端的内力响应为依据,统计嵌固端所有框架柱实际产生的总体弯矩Moc“真实”的弯矩,不是“需要”的弯矩！轴力算法的影响因素：1）框架柱嵌固部位的计算弯矩Mcj和轴力Ncj——取决于柱与墙的相对刚度、相对位置、楼盖（梁）刚度等因素2）框架柱距倾覆点的距离Lcj——取决于柱子的平面布局三、规范算法与轴力算法的关系轴力算法的结果Moc,除了包含框架部分按侧向刚度分配的倾覆力矩Mc外,还包括由于结构整体的变形协调而额外负担的一部分抗震墙的倾覆力矩Mcw‘,即轴力算法的结果应为：Moc=Mc+Mcw‘Mow=Mw-Mcw'举例：5层,H=3m,平动周期：0.18s,墙体刚度相对大,框架的刚度比重下降规范算法MC=617.16kN-m框架比重下降轴力算法Moc=1036.91kN-m框架比重上升5层,H=3m,平动周期：0.294s,墙体相对刚度变小,框架的刚度比重上升规范算法MC=2081.64kN-m 框架比重上升轴力算法Moc=-206.08kN-m 框架比重下降四、规范的目的1、规范对结构底层框架部分的倾覆力矩分担比例提出要求,实质上是为了控制框架与抗震墙侧向刚度的相对大小；2、规范公式反映了结构体系中框架的刚度贡献量3、轴力公式的影响因素众多,无法对两种构件的相对刚度做出正确的评价.4、实际工程应以规范公式的计算结果为准.规范给定的计算公式是基于结构倾覆的基本概念和结构内外水平力相互平衡的条件得到的.按规范公式计算的框架部分分担的倾覆力矩百分比反映了结构体系中框架的刚度贡献量,规范对结构底层框架部分的倾覆力矩分担比例提出要求,实质上是为了控制框架与抗震墙侧向刚度的相对大小,当底层框架部分的倾覆力矩分担比例小于50%时,说明框架部分对结构整体抗侧刚度的贡献较小,抗震墙提供了大部分抗侧刚度,是主要的抗侧力构件,框架为次要抗震构件,是结构的二道防线.严格意义上讲,我们要求计算倾覆力矩分担比的目的是为了判别框架-抗震墙结构等双重体系的属性的,即是偏向墙的属性还是偏向框架的属性.欧洲规范采用的抗剪承载能力,我们的规范采用的倾覆力矩,本质上是考虑了层高修正的剪力分担比.。

第二十三届全国高层建筑结构学术会议论文 2014年关于倾覆弯矩规范法与轴力法计算结果不同的分析与讨论隋庆海(中国建筑东北设计研究院有限公司深圳分公司深圳 518040)摘要：按照《建筑抗震设计规范》和《高层建筑混凝土结构技术规程》，在框剪结构设计中，框架部分承担的地震力倾覆弯矩占结构总地震倾覆力矩的比例是结构设计必须考虑的重要指标。

然而，目前设计中有两种说法，一种是按规范计算，一种是按柱底轴力计算。

两种计算方法计算的结果不同，有时还相差很大。

本文笔者从不同角度对其进行了推导，当扣除轴力法结果中剪力墙的贡献后，轴力法与规范法计算结果一致，可以认为规范法正确，软件的轴力法值得商榷。

关键词：倾覆力矩轴力法1规范及STAWE软件对倾覆弯矩的计算规定根据《高规》[1]7.1.8、8.1.3、10.2.16条，《抗规》[2]6.1.3、6.1.9条的有关规定，倾覆力矩的计算是结构设计中极其重要的指标，且抗规6.1.3条的条文说明中明确规定，框架部分地震力倾覆弯矩的计算公式为：除此之外，SATWE中还提供了一种倾覆弯矩的算法即轴力法[3]。

其计算方法如图1所示。

按力学方法计算倾覆弯矩需先计算合力作用点，然后用底部轴力对合力作用点取矩：（2）2不同计算方法的计算结果工程实践表明，同一工程按照上述两种不同计算方法计算的框架部分承担的倾覆力矩结果不同，有时差别还比较大，以SATWE培训的图2所示简单的框筒结构工程为例，SATWE的计算结果如下：图1 轴力法计算简图图2 框筒结构算例平面图上述计算结果表明，同一框剪结构框架部分承担的倾覆力矩相差达两倍之多。

对此，有人认为规范算法正确，有人认为轴力法计算合理，也有人说由设计人员根据实际情况判断使用，这样在工程设计中易造成有倾向选择计算方法来满足规范对框剪结构中框架部分承担倾覆弯矩比例规定的情况出现。

3不同方法计算结果产生差异的原因分析力学有几个特点，一是无论对体系还是对体系内的任何构件，力永远是平衡的；二无论采用什么样的计算方法，计算的结果是一致的。

物理参数:圬工砌体容重: 20.500(kN/m3)圬工之间摩擦系数: 0.800地基土摩擦系数: 0.577墙身砌体容许压应力: 580.000(kPa)墙身砌体容许剪应力: 58.000(kPa)墙身砌体容许拉应力: 110.000(kPa)墙身砌体容许弯曲拉应力: 56.000(kPa)挡土墙类型: 抗震区浸水挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)墙背与墙后填土摩擦角: 23.000(度)地基土容重: 18.000(kN/m3)修正后地基土容许承载力: 300.000(kPa)地基土容许承载力提高系数:墙趾值提高系数: 1.200墙踵值提高系数: 1.300平均值提高系数: 1.000地震作用墙趾值提高系数: 1.500地震作用墙踵值提高系数: 1.625地震作用平均值提高系数: 1.250墙底摩擦系数: 0.300地基土类型: 土质地基地基土内摩擦角: 30.000(度)地震烈度: 设计烈度7度面侧地震动水压力系数: 1.000背侧地震动水压力系数: 1.000水上地震角: 1.50水下地震角: 2.50水平地震系数: 0.13重要性修正系数: 1.00综合影响系数: 0.25抗震基底容许偏心距:B/5地震力调整系数: 1.000墙后填土浮容重: 12.500(kN/m3)地基浮力系数: 0.700土压力计算方法: 库仑第 2 种情况: 地震情况[土压力计算] 计算高度为 5.500(m)处的库仑主动土压力按实际墙背计算得到:第1破裂角： 27.000(度)Ea=103.732 Ex=95.486 Ey=40.531(kN) 作用点高度 Zy=1.898(m) 墙身截面积 = 22.250(m2) 重量 = 456.125 kN地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m) 墙面坡侧: 54.78 -17.24 -1.99 -4.40墙背坡侧: -54.78 -9.05 2.75 -4.40墙底面: -0.00 127.43 0.25 -5.50全墙地震力=11.403(kN) 作用点距墙顶高度=3.140(m)(一) 滑动稳定性验算基底摩擦系数 = 0.300滑移力= 106.889(kN) 抗滑力= 118.654(kN)滑移验算满足: Kc = 1.110 > 1.000(二) 倾覆稳定性验算相对于墙趾点，墙身重力的力臂 Zw = 3.035 (m)相对于墙趾点，Ey的力臂 Zx = 5.000 (m)相对于墙趾点，Ex的力臂 Zy = 1.898 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 502.292(kN-m) 抗倾覆力矩= 1586.833(kN-m)倾覆验算满足: K0 = 3.159 > 1.300(三) 地基应力及偏心距验算基础为天然地基，验算墙底偏心距及压应力作用于基础底的总竖向力 = 395.513(kN) 作用于墙趾下点的总弯矩=1084.541(kN-m) 基础底面宽度 B = 5.500 (m) 偏心距 e = 0.008(m)基础底面合力作用点距离基础趾点的距离 Zn = 2.742(m)基底压应力: 趾部=72.530 踵部=71.293(kPa)最大应力与最小应力之比 = 72.530 / 71.293 = 1.017作用于基底的合力偏心距验算满足: e=0.008 <= 0.200*5.500 = 1.100(m)墙趾处地基承载力验算满足: 压应力=72.530 <= 450.000(kPa)墙踵处地基承载力验算满足: 压应力=71.293 <= 487.500(kPa)地基平均承载力验算满足: 压应力=71.911 <= 375.000(kPa)(四) 基础强度验算基础为天然地基，不作强度验算(五) 墙底截面强度验算验算截面以上地震力=11.403(kN) 作用点距墙顶高度=3.140(m)地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 54.78 -17.24 -1.99 -4.40墙背坡侧: -54.78 -9.05 2.75 -4.40验算截面以上，墙身截面积 = 22.250(m2) 重量 = 456.125 kN相对于验算截面外边缘，墙身重力的力臂 Zw = 3.035 (m)相对于验算截面外边缘，Ey的力臂 Zx = 5.000 (m)相对于验算截面外边缘，Ex的力臂 Zy = 1.898 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 522.945(kN) 作用于墙趾下点的总弯矩=1434.981(kN-m) 相对于验算截面外边缘，合力作用力臂 Zn = 2.744(m)截面宽度 B = 5.500 (m) 偏心距 e1 = 0.006(m)截面上偏心距验算满足: e1= 0.006 <= 0.400*5.500 = 2.200(m)截面上压应力: 面坡=95.700 背坡=94.462(kPa)压应力验算满足: 计算值= 95.700 <= 870.000(kPa)切向应力检算:剪应力验算满足: 计算值= -56.630 <= 58.000(kPa)(六) 台顶截面强度验算[土压力计算] 计算高度为 4.000(m)处的库仑主动土压力按实际墙背计算得到:第1破裂角： 27.000(度)Ea=56.994 Ex=52.463 Ey=22.269(kN) 作用点高度 Zy=1.369(m)墙身截面积 = 14.750(m2) 重量 = 302.375 kN地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 16.38 -8.19 -1.70 -3.40墙背坡侧: -16.38 -1.55 2.75 -3.40墙底面: -0.00 63.35 0.50 -4.00全墙地震力=7.559(kN) 作用点距墙顶高度=2.244(m)[强度验算]验算截面以上地震力=7.175(kN) 作用点距墙顶高度=2.190(m)地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 16.38 -8.19 -1.70 -3.40墙背坡侧: -16.38 -0.00 2.50 -3.40验算截面以上，墙身截面积 = 14.000(m2) 重量 = 287.000 kN相对于验算截面外边缘，墙身重力的力臂 Zw = 2.702 (m)相对于验算截面外边缘，Ey的力臂 Zx = 4.500 (m)相对于验算截面外边缘，Ex的力臂 Zy = 1.369 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 317.459(kN) 作用于墙趾下点的总弯矩=793.474(kN-m) 相对于验算截面外边缘，合力作用力臂 Zn = 2.499(m)截面宽度 B = 4.500 (m) 偏心距 e1 = -0.249(m)截面上偏心距验算满足: e1= -0.249 <= 0.400*4.500 = 1.800(m)截面上压应力: 面坡=47.083 背坡=94.010(kPa)压应力验算满足: 计算值= 94.010 <= 870.000(kPa) 切向应力检算:剪应力验算满足: 计算值= -43.184 <= 58.000(kPa)。

框架-剪力墙结构体系中总地震倾覆力矩比关键信息项1、框架剪力墙结构体系的定义与特点定义：＿___________________________特点：＿___________________________2、总地震倾覆力矩的计算方法计算公式：＿___________________________相关参数说明：＿___________________________3、倾覆力矩比的确定标准标准值：＿___________________________允许偏差范围：＿___________________________4、协议适用的建筑类型与规模建筑类型：＿___________________________规模限制：＿___________________________5、责任与义务设计方责任：＿___________________________施工方责任：＿___________________________监管方责任：＿___________________________6、违反协议的处理方式违约责任：＿___________________________赔偿标准：＿___________________________7、争议解决途径协商方式：＿___________________________仲裁机构：＿___________________________诉讼法院：＿___________________________11 引言在建筑结构设计中，框架剪力墙结构体系因其在抗震性能和空间利用方面的优势而得到广泛应用。

然而，其中的总地震倾覆力矩比是评估结构抗震性能的重要指标之一。

为了明确在框架剪力墙结构体系中总地震倾覆力矩比的相关要求和各方的责任义务，特制定本协议。

111 框架剪力墙结构体系的定义与特点框架剪力墙结构是由框架和剪力墙共同承担水平和竖向荷载的结构体系。

框支框架承担的地震倾覆力矩占结构总地震力矩之比例的算法说明一、标准要求：10．2．16 部份框支剪力墙结构的布置应符合以下规定：7 框支框架承担的地震倾覆力矩应小于结构总地震倾覆力矩的50％；二、标准要求的本意：标准条文说明：相较于02规程，此条有两处修改：一。

；二是增加第7款对框支框架承担的倾覆力矩的限制，避免落地剪力墙过少。

三、倾覆力矩算法：以以下图的简单对称结构为例说明：1）V*H求和方式（抗规方式）框架部份按刚度分派的地震倾覆力矩的计算公式in i mj ij c h V M ∑∑===11式中c M ——框架-抗震墙结构在规定的侧向力作用下框架部份分派的地震倾覆力矩；n ——结构层数； m ——框架i 层的柱根数；ij V ——第i 层第j 根框架柱的计算地震剪力； i h ——第i 层层高。

对一根框架柱来讲，依照其平稳条件，21M M h V c += （8） 一样依照平稳条件，现在梁上剪力N V b = （9） 在梁内由梁的平稳条件有Nl l V M b ==2 （10） 那么依照抗规方式计算取得的柱倾覆力矩为：Nl M h V M c c 2221'+== （11）2）力学标准方式（即PKPM 中提供的轴力方式）按力学方式计算倾覆力矩，需要先计算合力作用点，然后用底部轴力对合力作用点取距。

SATWE 中的合力作用点计算方式为 ∑∑=ii i o N x N x （5） 其中o x ——x 向合力作用点i N ——x 向规定水平力下各构件的轴力 i x ——柱的x 坐标或墙柱的中心点x 坐标。

那么框架柱承担的倾覆力矩为： ()[]∑=+-=ni yi o ii cx M x x N M 1（6）即倾覆力矩为轴力产生的倾覆力矩与柱底弯矩之和，墙的计算方式与柱相同。

图6所示框剪结构在水平力F 作用下，在框架柱底部产生的轴力为N ，柱底弯矩为1M ，显然框架承担的倾覆力矩应该为：()12122M L L N M c ++= （7）四结论：从计算结果能够看出：1抗规方式算出的柱底部弯矩占结构总弯矩的比例与墙数量的相关性更强（要紧跟墙柱的刚度在总刚度的占比有关），而轴力方式算出的柱底部弯矩的占结构总弯矩的比例与墙位置的相关性也有专门大关系，乃至占主导的关系（依照轴力计算弯矩时的墙柱与结构合力作用点的距离（即力臂）的有关）。

基础稳定验算1.基本资料筏板宽度/厚度B1=22.6 /1.6米，建筑总高度H=86.45，建筑宽度B=85.7/23.6米地震烈度6度（0.05g,罕遇地震水平地震响响系数最大值αmax=0.28），基本风压ω0=0.3（50年一遇）结构自重G=517800KN,结构自震周期X=3.00s,Y=3.00s2.抗倾覆验算2.1地震作用Fek =Geq*α1 (抗规5.2.1-1)α1=[η2*0.2r-η1(T-5Tg)] αmax (抗规5.1.5)=（1*0.2349-0.025）*0.28=0.058772Fek=G*0.058772=30432.1416KN2.2地震作用产生的倾覆力矩M震=H/2*Fek=2.54G=77297.6356KN.m2.3风荷载Fk=B*H*ωkωk=βzμsμzω0取:μz=1.25 μs=1.4 ξ=1.5785 ν=0.43 ζz=0.38Βz=1+(ξνζz/μz)Βz=1+(1.5785*0.43*0.38/1.25)=1.206ωk =1.206*1.25*1.4*0.3=0.63315Fk=85.7*86.45*0.63315(取最不利方向计算)=4691KN2.4风荷载产生的倾覆力矩M风=H/2*Fk=4691*43.224=202762.4KN.m2.5地推力F土=B*0.5*h1*r (h1取4.5米平均值，r土容重取18) =85.7*0.5*4.5*18=3470.85KN2.5地推力产生的倾覆力矩M土=F土*h1/2=7809KN.m2.6基础抗倾覆力矩M抗=G*B1/2=11.3G=5851140 KN.m结论M抗> M震+ M土安全M抗> M风+ M土安全3.抗滑移验算取基底摩擦系数为0.4，抗滑移力F=G*0.4=517800*0.4=207120KNF/（Fek+F土）=207120/33903=6.11>1.2 安全F/（F风+F土）=207120/8161.85=25.4>1.2 安全。

框架承担倾覆力矩的合理计算方法全文共四篇示例，供读者参考第一篇示例：框架结构在建筑设计中扮演着重要的角色，它可以承担一定的倾覆力矩，确保建筑物的稳定性和安全性。

在设计过程中，如何合理计算框架结构所需承担的倾覆力矩是一个关键问题。

本文将探讨框架结构承担倾覆力矩的合理计算方法，以及其中涉及的相关理论和技术。

一、倾覆力矩的定义和作用倾覆力矩是指外部作用力（如风载和地震作用）对建筑物产生的侧向力矩，是导致建筑物倾覆的主要力矩之一。

倾覆力矩的大小取决于建筑物的高度、形状、结构类型等因素。

在设计过程中，需要计算建筑物能够承受的最大倾覆力矩，以保证建筑物在外部作用力的影响下不会倾覆。

二、框架结构承担倾覆力矩的原理框架结构在承担倾覆力矩时，其主要作用是通过牢固的连接和合理的结构布局将外部作用力传递到基础中，使建筑物保持稳定。

框架结构的承载能力取决于其结构形式、材料特性和连接方式等因素。

在计算框架结构承担倾覆力矩时，需要考虑框架结构的整体刚度和受力性能，以确定其受力状态和承载能力。

1. 确定设计参数：在计算框架结构承担倾覆力矩时，首先需要确定设计参数，包括建筑物的高度、结构形式、设计风载或地震作用等参数。

2. 选择合适的理论方法：根据建筑物的特点和设计要求，选择合适的计算方法，常用的有静力分析法、动力分析法和有限元分析等方法。

3. 进行结构分析：对框架结构进行力学分析，计算其在外部作用力作用下的受力状态和承载能力。

4. 校核设计方案：根据计算结果对设计方案进行校核，确保框架结构能够承担倾覆力矩，满足设计要求。

5. 考虑安全系数：在计算框架结构承担倾覆力矩时，需要考虑安全系数，确保建筑物在实际使用中不会发生倾覆事故。

四、结论框架结构在建筑设计中承担着重要的倾覆力矩，其合理计算方法是确保建筑物稳定性和安全性的关键。

设计师在进行框架结构设计时，应根据建筑物的特点和设计要求，选择合适的计算方法，并进行严谨的结构分析和校核，以确保框架结构能够承担倾覆力矩，保证建筑物的安全稳定。

笔者在接受设计咨询以及浏览相关结构网页时，发现有相当一部分设计者对《抗规》第6.1.3条第1款的理解和应用存在误区，在此谈谈个人的理解，并请网友发表高见。

1．规范原文：《抗规》第6.1.3条第1款：框架－抗震墙结构，在基本振型地震作用下，若框架部分承受的地震倾覆力矩大于结构总地震倾覆力矩的50％，其框架部分的抗震等级应按框架结构确定，最大适用高度可比框架结构适当增加。

《砼高抗》第8.1.3条：抗震设计的框架－剪力墙结构，在基本振型地震作用下，框架部分承受的地震倾覆力矩大于结构总地震倾覆力矩的50％时，其框架部分的抗震等级应按框架结构确定，柱轴压比限值宜按框架结构的规定采用；其最大适用高度和高宽比限值可比框架结构适当增加。

《抗规》第6.1.3条第1款的条文说明：当框架－抗震墙结构有足够的抗震墙时，其框架部分是次要抗侧力构件，可按框架－抗震墙结构中的框架确定抗震等级。

89规范要求抗震墙底部承受的地震倾覆力矩不小于结构底部总地震倾覆力矩的50％。

为了便于操作，本次修订改为在基本振型地震作用下，框架承受的地震倾覆力矩小于结构总地震倾覆力矩的50％时，其框架部分的抗震等级按框架－抗震墙结构的规定划分。

关于框架部分承受的地震倾覆力矩的计算可按附件中的第1条的公式进行计算。

2．从规范原文及其条文说明来看，对于一般比较规则的常规框架－剪力墙结构，只要满足“在基本振型地震作用下，框架承受的地震倾覆力矩小于结构总地震倾覆力矩的50％”这一条件，其框架部分的抗震等级就可按框架－剪力结构中的框架确定抗震等级。

从附件的第1条所附的框架部分承受的地震倾覆力矩计算公式可以看出：框架部分承受的地震倾覆力矩的计算是针对结构整体而言，表面上并没有要求“在基本振型地震作用下，每一层框架所承受的地震倾覆力矩均小于结构总地震倾覆力矩的50％”；但是实际上对于正常设计的比较规则的框架－剪力墙结构，只要结构的底部楼层框架部分承受的地震倾覆力矩小于结构总地震倾覆力矩的50％，其上部各层必定满足“在基本振型地震作用下，框架承受的地震倾覆力矩小于结构总地震倾覆力矩的50％”这一条件。

框支框架承担的地震倾覆力矩占结构总地震力矩之比例的算法解释一、规范要求：10．2．16 部分框支剪力墙结构的布置应符合下列规定：7 框支框架承担的地震倾覆力矩应小于结构总地震倾覆力矩的50％；二、规范要求的本意：规范条文说明：相比于02规程，此条有两处修改：一。

；二是增加第7款对框支框架承担的倾覆力矩的限制，防止落地剪力墙过少。

三、倾覆力矩算法：以下图的简单对称结构为例说明：1）V*H 求和方式（抗规方法）框架部分按刚度分配的地震倾覆力矩的计算公式in i mj ij c h V M ∑∑===11式中c M ——框架-抗震墙结构在规定的侧向力作用下框架部分分配的地震倾覆力矩；n ——结构层数； m ——框架i 层的柱根数；ij V ——第i 层第j 根框架柱的计算地震剪力； i h ——第i 层层高。

对一根框架柱来讲，根据其平衡条件，21M M h V c += （8） 同样根据平衡条件，此时梁上剪力N V b = （9） 在梁内由梁的平衡条件有Nl l V M b ==2 （10） 则按照抗规方法计算得到的柱倾覆力矩为：Nl M h V M c c 2221'+== （11）2）力学标准方式（即PKPM 中提供的轴力方式）按力学方法计算倾覆力矩，需要先计算合力作用点，然后用底部轴力对合力作用点取距。

SATWE 中的合力作用点计算方法为 ∑∑=ii i o N x N x （5） 其中o x ——x 向合力作用点i N ——x 向规定水平力下各构件的轴力 i x ——柱的x 坐标或者墙柱的中心点x 坐标。

则框架柱承担的倾覆力矩为： ()[]∑=+-=ni yi o ii cx M x x N M 1（6）即倾覆力矩为轴力产生的倾覆力矩与柱底弯矩之后，墙的计算方法与柱相同。

图6所示框剪结构在水平力F 作用下，在框架柱底部产生的轴力为N ，柱底弯矩为1M ，显然框架承担的倾覆力矩应该为：()12122M L L N M c ++= （7）四结论：从计算结果可以看出：1抗规方式算出的柱底部弯矩占结构总弯矩的比例与墙数量的相关性更强（主要跟墙柱的刚度在总刚度的占比有关），而轴力方式算出的柱底部弯矩的占结构总弯矩的比例与墙位置的相关性也有很大关系，甚至占主导的关系（根据轴力计算弯矩时的墙柱与结构合力作用点的距离（即力臂）的有关）。