第三节 销轴连接

1.销轴连接的轴向限位方式
1.1过盈连接
过盈连接就是在销轴和轴套之间有一定的过盈量，装配时销轴结合面被压缩产生周向压应力和径向压应力，轴套由于被撑大而产生周向拉应力和径向拉应力，使销轴和轴套牢固地连接在一起，不产生轴向运动和转动，以达到轴向定位和防转的目的。

1.2 限位块
在销轴上铣出一个平面，在侧壁上焊上或用螺钉紧固一个限位块，是较简略避免销轴向窜动与旋转的有用办法，因为铣出的平面不大，故避免旋转的扭矩较小，通常选用轻载或中等载荷。

1.3 改变销结构
改动原销轴的布局，加大一端直径并铣扁，卡在焊于侧壁的防转套中，可有用地避免销轴的轴向窜动与旋转，其效果强于上述布局。

1.4 轴端挡圈
这种结构是在支座的侧面焊接一个内径与销轴相同的圆环，在圆环上攻出螺纹孔或圆锥孔，同时在销轴伸出的一端钻出一个定位槽或与定位销配合的孔，销轴装上之后用螺钉拧如螺纹孔或用定位销插入销孔以达到防转和轴向定位的目的。

a. 使用紧定螺钉固定
b. 使用定位销固定
c. 开口销限位
1.5 采用防转曲拐
这种结构的销轴有两部分组成，一部分是销轴，另一部分则是曲拐。

在曲拐的一端钻出一个与销轴直径一样的孔，另一端攻螺纹，然后将曲拐和销轴焊接到一起形成一个整体。

装配时在支座的侧面加工出一个螺纹孔，用螺栓将曲拐上的螺纹孔和侧壁上的螺纹孔连接到一起，这样便可防止销轴转动和阻止销轴的轴向运动。

2.限位销的选择
2.1弹性开口销（DIN 11024）
2.2安全销（DIN11203）
2.3插销。

正页教学内容第三节销连接的装配教学目的1、了解销连接的主要作用2、掌握圆柱销的装配要点3、掌握圆锥销的装配要点重、难点1、圆柱销的装配要点2、圆锥销的装配要点教法选择用挂图分析讲解教具挂图教学进程由旧课引入新课：上两次课我们学习了第二节键连接的装配知识，使我们掌握了松键连接的装配、紧键连接的装配及花键连接的装配等内容，这一次课我们将学习第三节销连接的装配知识。

第三节销连接的装配比较讲解一、概述联系实际1、作用销连接的主要作用是定位、连接或锁定零件，有时还可以作为安全装置中的过载剪断元件。

2、分类（1）、销是一种标准件，形状和尺寸已标准化。

（2）、销的种类较多，应用广泛，其中最多的是圆柱销及圆锥销。

重、难点二、圆柱销的装配举例讲解1、应用及作用圆柱销一般依靠过盈固定在孔中，用以定位和连接。

2、装配要点（1）、对销孔尺寸、形状、表面粗糙度要求较高，故销孔在装配前须铰削。

（2）、一般被连接件的两孔应同时钻、铰，并使孔壁表面粗糙度值不高于R a1.6μm，以保证连接质量。

（3）、在装配时，应在销子表面涂机油，用铜棒将销子轻轻打入。

（4）、圆柱销不宜多次装拆，否则会降低定位精度和连接的紧固程度。

重、难点三、圆锥销的装配1、圆锥销的规格以小头直径和长度表示规格。

2、圆锥销的装配要点（1）、圆锥销装配时，两连接件的销孔也应一起钻、铰。

（2）、钻孔时按圆锥销小头直径选用钻头，用1﹕50锥度的铰刀铰孔。

（3）、铰孔时，用试装法控制孔径；一般以圆锥销自由地插入全长的80%~85%为宜。

（4）、然后，用手锤敲入，销子大头可稍微露出，或与被连接件表面平齐。

3、拆卸时的注意事项（1）、拆卸普通圆柱销和圆锥销时，可从小头（圆锥销）向外敲出。

（2）、有螺尾的圆锥销可用螺母旋出。

（3）、拆卸带内螺纹的圆柱销和圆锥销时，可用拔销器拔出。

课堂小结一、概述1、作用2、分类二、圆柱销的装配1、应用及作用2、装配要点三、圆锥销的装配1、圆锥销的规格2、装配要点2、拆卸时的注意事项布置作业P15213、14课后效果销连接的内容较少，在进行讲解时，多进行举例讲解，并联分析系实际，使同学们容易接受、理解，但由于学生基础较差，又不愿意学习，故掌握得不太好。

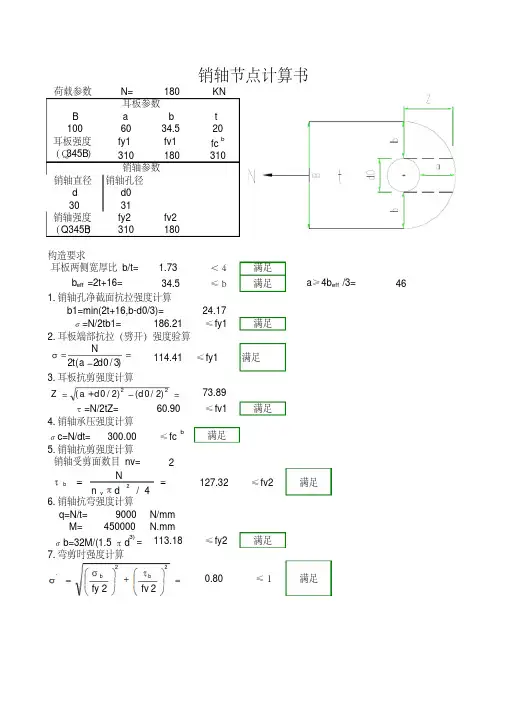
销轴强度校核第三节销轴连接销轴连接是起重机金属结构常用的连接形式，例如起重机臂架根部的连接（图4-30a）以及拉杆或撑杆的连接等（图4-30b），通常都采用销轴连接。

图4-30 销轴连接示例(a) 臂架根部；(b) 拉杆。

一、销轴计算（一）销轴抗弯强度验算[]WW WMσσ≤=（4-43）式中M──销轴承受的最大弯矩；323dWπ=──销轴抗弯截面模数；[]Wσ──许用弯曲应力，对于45号钢[]Wσ = 360MPa。

（二）销轴抗剪强度验算[]τππτ≤⋅=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛==243max3166412dQdddQIbQS（4-44）式中Q──把销轴当作简支梁分析求得的最大剪力；[]τ──销轴许用剪应力，45号钢[]τ=125MPa。

二、销孔拉板的计算（一）销孔壁承压应力验算[]c c d Pσδσ≤⋅=（4-45）式中 P ──构件的轴向拉力，即销孔拉板通过承压传给销轴的力； δ──销孔拉板的承压厚度；d ──销孔的直径；[]c σ──销孔拉板的承压许用应力，[][]σσ4.1=c 。

（二）销孔拉板的强度计算首先根据销孔拉板承受的最大拉力P 求出危险截面（图4-31a 中的水平截面b -b 及垂直截面a -a ）上的内力，然后用弹性曲梁公式求出相应的应力，并进行强度校核。

图4-31 销孔拉板计算简图1. 内力计算拉板承受的拉力P 是通过销孔壁以沿孤长分布压力P 的形式传给销轴，假定P 沿弧长按正弦规律分布，即ϕsin max ⋅=p p（4-46）由图4-31a ，根据拉板的平衡条件可得2sin 2sin 2max202max 20rp d rp rd p P π=ϕ⋅ϕ⋅=ϕ⋅ϕ⋅=⎰⎰ππ 则rP p π=2max（4-47）根据拉板结构和受力的对称性，可知拉板上反对称的内力（即剪力）等于零。

若沿销孔中心线截开拉板，则截面上只有轴力N b 及弯矩M b ，如图4-31b 所示。

根据平衡条件0=∑Y ，得2P N b =（4-48）由于根据平衡方程解不出M b ，故是一次超静定问题，须根据变形条件求M b 。

第三节 销轴连接销轴连接是起重机金属结构常用的连接形式，例如起重机臂架根部的连接（图4-30a ）以及拉杆或撑杆的连接等（图4-30b ），通常都采用销轴连接。

图4-30 销轴连接示例 (a ) 臂架根部；(b ) 拉杆。

一、销轴计算（一）销轴抗弯强度验算[]W W WMσσ≤=（4-43）式中 M ──销轴承受的最大弯矩； 323d W π=──销轴抗弯截面模数；[]W σ──许用弯曲应力，对于45号钢[]W σ = 360MPa 。

（二）销轴抗剪强度验算[]τππτ≤⋅=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛==243max 3166412d Q d d d Q Ib QS （4-44）式中 Q ──把销轴当作简支梁分析求得的最大剪力；[]τ──销轴许用剪应力，45号钢[]τ=125MPa 。

二、销孔拉板的计算 （一）销孔壁承压应力验算[]c c d Pσδσ≤⋅=（4-45）式中 P ──构件的轴向拉力，即销孔拉板通过承压传给销轴的力； δ──销孔拉板的承压厚度；d ──销孔的直径；[]c σ──销孔拉板的承压许用应力，[][]σσ4.1=c 。

（二）销孔拉板的强度计算首先根据销孔拉板承受的最大拉力P 求出危险截面（图4-31a 中的水平截面b -b 及垂直截面a -a ）上的内力，然后用弹性曲梁公式求出相应的应力，并进行强度校核。

图4-31 销孔拉板计算简图1. 内力计算拉板承受的拉力P 是通过销孔壁以沿孤长分布压力P 的形式传给销轴，假定P 沿弧长按正弦规律分布，即ϕsin max ⋅=p p（4-46）由图4-31a ，根据拉板的平衡条件可得 2sin 2sin 2max202max 20rp d rp rd p P π=ϕ⋅ϕ⋅=ϕ⋅ϕ⋅=⎰⎰ππ则rP p π=2max（4-47）根据拉板结构和受力的对称性，可知拉板上反对称的内力（即剪力）等于零。

若沿销孔中心线截开拉板，则截面上只有轴力N b 及弯矩M b ，如图4-31b 所示。

补充内容：切向键连接切向键由两个斜度为 1:100 的普通楔键组成，见图。

装配时两个楔键分别从轮毂一端打入，使其两个斜面相对，共同楔紧在轴与轮毂的键槽内。

其上、下两面为工作面，其中一个工作面在通过轴心线的平面内，工作时工作面上的挤压力沿轴的切线作用。

因此，切向键的工作原理是靠工作面的挤压来传递转矩。

一个切向键只能传递单向转矩，若要传递双向转矩，必须用两个切向键，并错开 120º～135º 反向安装。

切向键主要用于轴径大于 100mm 、对中性要求不高且载荷较大的重型机械中。

销连接销连接主要是用来固定零件之间的相对位置，也用于轴与毂的连接或其它零件的连接，并可传递不大的载荷。

还可以作为安全装置中的过载剪断元件，如图。

1、销连接的作用方式销连接是靠形状起作用的连接，在任何时候都能拆卸而不会损坏连接元件。

销大都以一定的过盈打入被连接件的同心孔中。

在这种情况下，被连接的构件就被强制地销住在所要求的位置。

2、销的种类销也是一种标准件，形状和尺寸标准化。

销的种类较多，应用广泛。

下表列出了常用销的类型、特点和应用场合。

销的类型、特点和应用第三节：键连接和销连接一、填空题：1、键连接的主要用途是 和 。

2、按照键的外形键连接分为 、 、 和 四种类型。

3、普通平键的规格选择，宽度与厚度主要由决定。

4、平键、半圆键的工作面是，而普通楔键的工作面是。

5、能起自动定心作用，加工工艺和齿轮相同的键是。

6、销连接是靠起作用的连接。

7、按照形状，销可以分为、和。

8、主要用于定位的销有和。

9、平键连接根据配合公差不同可分为、和。

10、按照用途，销可以分为、和。

二、判断题：1、普通平键连接能够实现轴上零件的轴向固定和周向固定。

（）2、平键都是标准件。

（）3、平键连接在传递转矩时，受到挤压和剪切两种力的作用。

（）4、键都是靠侧面来工作的。

（）5、普通楔键连接只适用于低速转动。

（）6、圆锥销有1：50的锥度，定位精度比圆柱销高，但安装不便。

第三节销轴连接销轴连接是起重机金属结构常用的连接形式，例如起重机臂架根部的连接（图4-30a）以及拉杆或撑杆的连接等（图4-30b），通常都采用销轴连接。

图4-30 销轴连接示例(a) 臂架根部；(b) 拉杆。

一、销轴计算（一）销轴抗弯强度验算[]WW WMσσ≤=（4-43）式中M──销轴承受的最大弯矩；323dWπ=──销轴抗弯截面模数；[]Wσ──许用弯曲应力，对于45号钢[]Wσ= 360MPa。

（二）销轴抗剪强度验算[]τππτ≤⋅=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛==243max3166412dQdddQIbQS（4-44）式中Q──把销轴当作简支梁分析求得的最大剪力；[]τ──销轴许用剪应力，45号钢[]τ=125MPa。

二、销孔拉板的计算（一）销孔壁承压应力验算[]c c d Pσδσ≤⋅=（4-45）式中 P ──构件的轴向拉力，即销孔拉板通过承压传给销轴的力； δ──销孔拉板的承压厚度；d ──销孔的直径；[]c σ──销孔拉板的承压许用应力，[][]σσ4.1=c 。

（二）销孔拉板的强度计算首先根据销孔拉板承受的最大拉力P 求出危险截面（图4-31a 中的水平截面b -b 及垂直截面a -a ）上的内力，然后用弹性曲梁公式求出相应的应力，并进行强度校核。

图4-31 销孔拉板计算简图1. 内力计算拉板承受的拉力P 是通过销孔壁以沿孤长分布压力P 的形式传给销轴，假定P 沿弧长按正弦规律分布，即ϕsin max ⋅=p p（4-46）由图4-31a ，根据拉板的平衡条件可得 2sin 2sin 2max202max 20rp d rp rd p P π=ϕ⋅ϕ⋅=ϕ⋅ϕ⋅=⎰⎰ππ则rP p π=2max（4-47）根据拉板结构和受力的对称性，可知拉板上反对称的内力（即剪力）等于零。

若沿销孔中心线截开拉板，则截面上只有轴力N b 及弯矩M b ，如图4-31b 所示。

根据平衡条件0=∑Y ，得2P N b =（4-48）由于根据平衡方程解不出M b ，故是一次超静定问题，须根据变形条件求M b 。

销轴连接常用于两个结构构件之间的连接，以满足构件之间的相对转动的需要，也用于一些结构构件吊装过程中。

无论是构件连接节点还是吊装节点，其节点都需要进行必要的验算，以满足结构安全及吊装安全的需要。

销轴连接方式多种多样，最常采用的连接的结构方式为单剪连接、双剪连接和多耳板连接。

而建筑结构销轴连接的结构形式受到加工精度的限制比较单一，多为三耳板（下二上一或下一上二）组成的双剪结构，这种结构形式由一根销轴将一侧耳板与另一侧耳板连接起来，销轴与耳板之间可以发生相对转动，相互间的荷载通过销轴和耳论。

1把销轴当作简支梁进行分析销轴弯曲强度验算最大弯矩值：销轴弯曲强度计算计算满足。

公式中：M——把销轴作为简支梁分析所求得的最大弯矩值W——销轴截面的抗弯模量，——销轴的许用弯曲应力，这里采用45号钢2d3、平均剪应力复核：将销轴按双剪进行平均剪应力计算计算满足。

二、耳板强度验算首先耳板的尺寸必须满足构造要求（这里我们可以参照螺栓构造要求其满足1.5~2d，在此构造满足的情况下，可不进行耳板孔周的抗拉验算，直接进行抗剪验算，此理解可供大家讨论，此处仅为笔者个人理解），在满足这一条件下进行计算。

1、耳板孔壁承压应力验算上耳板：——构件的承压面积，为销轴直径，为孔壁的承压总厚度钢取值为1/4范围更为准确，即：2、耳板抗剪验算上耳板：计算满足。

公式中：耳板抗剪强度设计值，采用Q345钢取值为下耳板：计算满足。

公式中：耳板抗剪强度设计值，采用Q345钢取值为采用何种焊公式中：当为等强剖口焊缝连接时，计算(焊缝和母材等强计)：计算满足。

当为双面角焊缝连接时，（焊脚高度16mm）计算：计算满足。

若焊缝为直角角焊缝时，净截面模量为0.7倍焊脚尺寸作为焊缝有效厚度进行计算。

参数说明：为构件所受轴力；为构件净截面面积；为与为与=295=200。

1、销轴直径相对于耳板厚度越粗壮，销轴刚度越大，销轴以剪切变形为主；销轴直径相对于耳板厚度比较细，销轴刚度较小，销轴逐渐转变为以弯曲变形为主。