电磁场与电磁波课程知识点总结

电磁场与电磁波课程知识点总结与主要公式1 麦克斯韦方程组的理解和掌握 （1）麦克斯韦方程组⎰⎰⎰⎰⎰⎰=•=•∇=•=•∇•∂∂-=•∂∂-=⨯∇•∂∂+=•∂∂+=⨯∇ss l s l s s d B B Q s d D D s d t B l d E t B E s d tD J l d H t D J H 0)(ρ本构关系： E J H B EDσμε===（2）静态场时的麦克斯韦方程组（场与时间t 无关）⎰⎰⎰⎰=•=•∇=•=•∇=•=⨯∇=•=⨯∇ss l l s d B B Q s d D D l d E E I l d H JH 000ρ2 边界条件（1）一般情况的边界条件nn n sT t t sn s n n sn tt n B B B B a J H H J H H a D D D D a E E E E a 21212121212121210)())(0)==-•=-=-⨯=-=-•==-⨯（（ρρ（2）介质界面边界条件（ρs = 0 J s = 0）nn n t t n n n n t t n B B B B a H H H H a D D D D a E E E E a 21212121212121210)(0)0)(0)==-•==-⨯==-•==-⨯（（3 静电场基本知识点 （1）基本方程0022=•==∇-=∇=•=•∇=•=⨯∇⎰⎰⎰A Apsl ld E Qs d D D l d E E ϕϕϕερϕρ本构关系： E Dε=（2）解题思路● 对称问题（球对称、轴对称、面对称）使用高斯定理或解电位方程（注意边界条件的使用）。

● 假设电荷Q ——> 计算电场强度E ——> 计算电位φ ——>计算能量ωe =εE 2/2或者电容（C=Q/φ）。

（3）典型问题● 导体球（包括实心球、空心球、多层介质）的电场、电位计算；● 长直导体柱的电场、电位计算；● 平行导体板（包括双导体板、单导体板）的电场、电位计算； ● 电荷导线环的电场、电位计算； ● 电容和能量的计算。

电磁场与电磁波知识点总结知乎
电磁场和电磁波是物理学中的重要基础知识，涉及到电学、磁学、波动光学等多个领域。

下面是对电磁场和电磁波的一些重要知识点总结：
1. 电场和磁场：电场是指空间中由电荷引起的电力作用，磁场是指空间中由电流引起的磁力作用。

电场和磁场都是矢量场，可以用矢量图形表示。

2. 麦克斯韦方程组：麦克斯韦方程组是描述电磁场行为的基本方程，包括四个方程：高斯定理、高斯磁定理、法拉第电磁感应定律和安培环路定理。

3. 电磁波：电磁波是由电场和磁场相互作用引起的一种波动现象，包括无线电波、可见光、紫外线、X射线等。

电磁波具有波长、频率等特征，可以用波动方程表示。

4. 偏振：偏振是指电磁波中电场矢量的振动方向。

根据电场矢量的振动方向，电磁波可以分为线偏振、圆偏振和不偏振等。

5. 折射和反射：当电磁波从一种介质传播到另一种介质时，会发生折射现象，即波的传播方向改变。

同时，当电磁波遇到介质的边界时，会发生反射现象，即波发生反向传播。

折射和反射现象可以用斯涅尔定律和菲涅尔公式计算。

6. 衍射和干涉：电磁波在经过小孔或射缝等障碍物时，会发生衍射现象，即波扩散后形成干涉条纹。

同时，当两束电磁波相遇时，会发生干涉现象，即波的振幅会增强或减弱。

衍射和干涉现象可以用
菲涅尔衍射和双缝干涉等理论进行描述。

以上是电磁场和电磁波的一些重要知识点总结。

熟练掌握这些知识，对于理解电学、磁学、波动光学等学科都具有重要意义。

电磁场与电磁波课程知识点总结1 麦克斯韦方程组的理解和掌握 （1）麦克斯韦方程组⎰⎰⎰⎰⎰⎰=∙=∙∇=∙=∙∇∙∂∂-=∙∂∂-=⨯∇∙∂∂+=∙∂∂+=⨯∇ss l s l s s d B B Q s d D D s d t B l d E t B E s d tD J l d H t D J H 0)(ρ本构关系： E J HB EDσμε===（2）静态场时的麦克斯韦方程组（场与时间t 无关）⎰⎰⎰⎰=∙=∙∇=∙=∙∇=∙=⨯∇=∙=⨯∇ss l l s d B B Qs d D D l d E E Il d H J H 0000ρ2 边界条件（1）一般情况的边界条件nn n sT t t sn s n n sn tt n B B B B a J H H J H H a D D D D a E E E E a 21212121212121210)())(0)==-∙=-=-⨯=-=-∙==-⨯（（ρρ（2）介质界面边界条件（ρs = 0 J s = 0）nn n t t n n n n t t n B B B B a H H H H a D D D D a E E E E a 21212121212121210)(0)0)(0)==-∙==-⨯==-∙==-⨯（（（1）基本方程0022=∙==∇-=∇=∙=∙∇=∙=⨯∇⎰⎰⎰A Apsl ld E Qs d D D l d E E ϕϕϕερϕρ本构关系： E Dε=（2）解题思路● 对称问题（球对称、轴对称、面对称）使用高斯定理或解电位方程（注意边界条件的使用）。

● 假设电荷Q ——> 计算电场强度E ——> 计算电位φ ——> 计算能量ωe =εE 2/2或者电容（C=Q/φ）。

（3）典型问题● 导体球（包括实心球、空心球、多层介质）的电场、电位计算； ● 长直导体柱的电场、电位计算；● 平行导体板（包括双导体板、单导体板）的电场、电位计算； ● 电荷导线环的电场、电位计算； ● 电容和能量的计算。

已经将文本间距加为24磅,第18章:电磁场与电磁波一、知识网络二、重、难点知识归纳1．振荡电流和振荡电路（1）大小和方向都随时间做周期性变化的电流叫振荡电流。

能够产生振荡电流的电路叫振荡电路。

自由感线圈和电容器组成的电路，是一种简单的振荡电路，简称LC 回路。

在振荡电路里产生振荡电流的过程中，电容器极板上的电荷，通过线圈的电流以及跟电荷和电流相联系的电场和磁场都发生周期性变化的现象叫电磁振荡。

（2）LC 电路的振荡过程:在LC 电路中会产生振荡电流，电容器放电和充电，电路中的电流强度从小变大，再从大变小，振荡电流的变化符合正弦规律．当电容器上的带电量变小时，电路中的电流变大，当电容器上带电量变大时，电路中的电流变小(3)LC 电路中能量的转化 :a 、电磁振荡的过程是能量转化和守恒的过程．电流变大时，电场能转化为磁场能，LC 回路中电磁振荡过程中电荷、电场。

电路电流与磁场的变化规律、电场能与磁场能相互变化。

分类：阻尼振动和无阻尼振动。

振荡周期：LC T π2=。

改变L 或C 就可以改变T 。

电磁振荡 麦克斯韦电磁场理论 变化的电场产生磁场 变化的磁场产生电场 特点：为横波，在真空中的速度为3.0×108m/s 电磁波 电磁场与电磁波 发射接收 应用：电视、雷达。

目的：传递信息 调制：调幅和调频 发射电路：振荡器、调制器和开放电路。

原理：电磁波遇到导体会在导体中激起同频率感应电流 选台：电谐振 检波：从接收到的电磁波中“检”出需要的信号。

接收电路：接收天线、调谐电路和检波电路电流变小时，磁场能转化为电场能。

b 、电容器充电结束时，电容器的极板上的电量最多，电场能最大，磁场能最小；电容器放电结束时，电容器的极板上的电量为零，电场能最小，磁场能最大．c 、理想的LC 回路中电场能E 电和磁场能E 磁在转化过程中的总和不变。

回路中电流越大时，L 中的磁场能越大。

极板上电荷量越大时，C 中电场能越大（板间场强越大、两板间电压越高、磁通量变化率越大）。

电磁场与电磁波知识点整理一、电磁场的基本概念电磁场是由电场和磁场相互作用而形成的一种物理场。

电场是由电荷产生的，而磁场则是由电流或者变化的电场产生的。

电荷是产生电场的源。

正电荷会产生向外辐射的电场，负电荷则产生向内汇聚的电场。

电场强度 E 用来描述电场的强弱和方向，其单位是伏特每米（V/m）。

电流是产生磁场的源。

电流产生的磁场方向可以通过右手螺旋定则来确定。

磁场强度 H 用来描述磁场的强弱和方向，其单位是安培每米（A/m）。

法拉第电磁感应定律表明，变化的磁场会产生电场。

麦克斯韦进一步提出，变化的电场也会产生磁场。

这两个定律共同揭示了电磁场的相互联系和相互转化。

二、电磁波的产生电磁波是电磁场的一种运动形态。

当电荷加速运动或者电流发生变化时，就会产生电磁波。

例如，在一个开放的电路中，电荷在电容器和电感之间来回振荡，就会产生电磁波。

这种振荡电路是产生电磁波的一种简单方式。

电磁波的频率和波长之间存在着一定的关系，即光速 c ＝λf，其中c 是光速（约为 3×10^8 m/s），λ 是波长，f 是频率。

不同频率的电磁波具有不同的特性和应用。

例如，无线电波频率较低，用于通信和广播；而X 射线频率较高，用于医学成像和材料检测。

三、电磁波的传播电磁波在真空中可以无需介质传播，在介质中传播时，其速度会发生变化。

电磁波在传播过程中遵循反射、折射和衍射等规律。

当电磁波遇到障碍物时，会发生反射。

如果电磁波从一种介质进入另一种介质，会发生折射，折射的程度取决于两种介质的电磁特性。

衍射则是指电磁波绕过障碍物传播的现象。

当障碍物的尺寸与电磁波的波长相当或较小时，衍射现象较为明显。

电磁波的极化是指电场矢量的方向在传播过程中的变化。

常见的极化方式有线极化、圆极化和椭圆极化。

四、电磁波的特性1、电磁波是横波，电场和磁场的振动方向都与电磁波的传播方向垂直。

2、电磁波具有能量，其能量密度与电场强度和磁场强度的平方成正比。

3、电磁波的传播速度是恒定的，在真空中为光速。

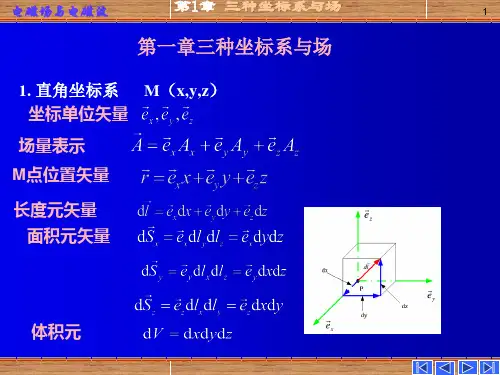
电磁场与电磁波总结第一章一、矢量代数 A ∙B =AB cos θA B ⨯=AB e AB sin θA ∙(B ⨯C ) = B ∙(C ⨯A ) = C ∙(A ⨯B )()()()C A C C A B C B A ⋅-⋅=⨯⨯二、三种正交坐标系 1. 直角坐标系 矢量线元x y z =++le e e d x y z矢量面元=++Se e e x y z d dxdy dzdx dxdy体积元d V = dx dy dz 单位矢量的关系⨯=e e e x y z ⨯=e e e y z x ⨯=e e e z x y2. 圆柱形坐标系 矢量线元=++l e e e z d d d dz ρϕρρϕl 矢量面元=+e e z dS d dz d d ρρϕρρϕ体积元dz d d dVϕρρ=单位矢量的关系⨯=⨯⨯=e e e e e =e e e e zz z ρϕϕρρϕ3. 球坐标系 矢量线元d l = e r d r e θr d θ+e ϕr sin θd ϕ矢量面元d S = e r r 2sin θd θd ϕ体积元ϕθθd drd r dVsin 2=单位矢量的关系⨯=⨯⨯=e e e e e =e e e e r r r θϕθϕϕθ三、矢量场的散度和旋度 1. 通量与散度=⋅⎰A SSd Φ0lim∆→⋅=∇⋅=∆⎰A S A A Sv d div v2. 环流量与旋度=⋅⎰A l ld Γmaxn 0rot =lim∆→⋅∆⎰A lA e lS d S3. 计算公式∂∂∂∇=++∂∂∂⋅A y x z A A A x y z11()z A A A z ϕρρρρρϕ∂∂∂∇=++∂∂∂⋅A 22111()(sin )sin sin ∂∂∂∇=++∂∂∂⋅A r A r A A r r r r ϕθθθθθϕxy z∂∂∂∇⨯=∂∂∂e e e A x y z x y zA A A 1zzzA A A ρϕρϕρρϕρ∂∂∂∇⨯=∂∂∂e e e A 21sin sin r r zr r A r A r A ρϕθθθϕθ∂∂∂∇⨯=∂∂∂e e e A4. 矢量场的高斯定理与斯托克斯定理⋅=∇⋅⎰⎰A S A SVd dV⋅=∇⨯⋅⎰⎰A l A S lSd d四、标量场的梯度 1. 方向导数与梯度00()()lim∆→-∂=∂∆l P u M u M u ll 0cos cos cos ∂∂∂∂=++∂∂∂∂P u u u ulx y zαβγcos ∇⋅=∇e l u u θgrad ∂∂∂∂==+∂∂∂∂e e e +e n x y zu u u uu n x y z2. 计算公式∂∂∂∇=++∂∂∂e e e xy z u u u u x y z 1∂∂∂∇=++∂∂∂e e e z u u u u z ρϕρρϕ11sin ∂∂∂∇=++∂∂∂e e e r u u uu r r r zθϕθθ 五、无散场与无旋场1. 无散场()0∇⋅∇⨯=A =∇⨯F A2. 无旋场()0∇⨯∇=u -u =∇F 六、拉普拉斯运算算子 1. 直角坐标系22222222222222222222222222222222∂∂∂∇=++∇=∇+∇+∇∂∂∂∂∂∂∂∂∂∂∂∂∇=++∇=++∇=++∂∂∂∂∂∂∂∂∂A e e e x x y y z zyyyx x x z z z x y zu u uu A A A x y zA A A A A A A A A A A A x y z x y z x y z，，2. 圆柱坐标系22222222222222111212⎛⎫∂∂∂∂∇=++ ⎪∂∂∂∂⎝⎭∂∂⎛⎫⎛⎫∇=∇--+∇-++∇ ⎪ ⎪∂∂⎝⎭⎝⎭A e e e z z u u uu zA A A A A A A ϕρρρρϕϕϕρρρρρϕρρϕρρϕ3. 球坐标系22222222111sin sin sin ⎛⎫∂∂∂∂∂⎛⎫∇=++ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭u u uu r r r r r r θθθϕθϕ ⎪⎪⎭⎫⎝⎛∂∂+-∂∂+∇+⎪⎪⎭⎫⎝⎛∂∂--∂∂+∇+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂---∇=∇ϕθθθϕθϕθθθθϕθθθθϕϕϕϕθθθϕθθA r A r A r A A r A r A r A A r A r A r A r A r r r r r 222222222222222222sin cos 2sin 1sin 2sin cos 2sin 12sin 22cot 22e e e A 七、亥姆霍兹定理如果矢量场F 在无限区域中处处是单值的，且其导数连续有界，则当矢量场的散度、旋度和边界条件（即矢量场在有限区域V’边界上的分布）给定后，该矢量场F 唯一确定为()()()=-∇+∇⨯F r r A r φ其中1()()4''∇⋅'='-⎰F r r r r V dV φπ1()()4''∇⨯'='-⎰F r A r r r V dV π第二章一、麦克斯韦方程组 1. 静电场 真空中：001d ==VqdV ρεε⋅⎰⎰SE S （高斯定理） d 0⋅=⎰l E l 0∇⋅=E ρε0∇⨯=E 场与位：3'1'()(')'4'V dV ρπε-=-⎰r r E r r r r ϕ=-∇E 01()()d 4πV V ρϕε''='-⎰r r |r r |介质中：d ⋅=⎰D S Sqd 0⋅=⎰lE l ∇⋅=D ρ0∇⨯=E极化：0=+D E P εe 00(1)=+==D E E E r χεεεε==⋅P e PS n n P ρ=-∇⋅P P ρ2. 恒定电场 电荷守恒定律：⎰⎰-=-=⋅Vsdv dtd dt dq ds J ρ0∂∇⋅+=∂J tρ传导电流与运流电流：=J E σρ=J v恒定电场方程：d 0⋅=⎰J S Sd 0⋅=⎰J l l 0∇⋅=J 0∇⨯J =3. 恒定磁场 真空中：0 d ⋅=⎰B l lI μ（安培环路定理） d 0⋅=⎰SB S 0∇⨯=B J μ0∇⋅=B场与位：03()( )()d 4π ''⨯-'='-⎰J r r r B r r r VV μ=∇⨯B A 0 ()()d 4π'''='-⎰J r A r r r V V μ 介质中：d ⋅=⎰H l lId 0⋅=⎰SB S ∇⨯=H J 0∇⋅=B磁化：0=-BH M μm 00(1)=+B H =H =H r χμμμμm =∇⨯J M ms n =⨯J M e4. 电磁感应定律() d d in lC dv B dl dt ⋅=-⋅⨯⋅⎰⎰⎰SE l B S +）（法拉第电磁感应定律∂∇⨯=-∂B E t5. 全电流定律和位移电流全电流定律： d ()d ∂⋅=+⋅∂⎰⎰D H l J S lSt∂∇⨯=+∂DH J t 位移电流：d=DJ d dt6. Maxwell Equationsd ()d d d d d 0∂⎧⋅=+⋅⎪∂⎪∂⎪⋅=-⋅⎪∂⎨⎪⋅=⎪⎪⋅=⎪⎩⎰⎰⎰⎰⎰⎰⎰D H J S B E S D S B S lS l SS V Sl tl t V d ρ 0∂⎧∇⨯=+⎪∂⎪∂⎪∇⨯=-⎨∂⎪∇⋅=⎪⎪∇⋅=⎩D H J BE D B t t ρ()()()()0∂⎧∇⨯=+⎪∂⎪∂⎪∇⨯=-⎨∂⎪∇⋅=⎪⎪∇⋅=⎩E H E H E E H t t εσμερμ 二、电与磁的对偶性e m e m eme e m m e e m mm e 00∂∂⎫⎧∇⨯=-∇⨯=⎪⎪∂∂⎪⎪∂∂⎪⎪∇⨯=+∇⨯=--⎬⎨∂∂⎪⎪∇=∇=⎪⎪⎪⎪∇=∇=⎩⎭⋅⋅⋅⋅B D E H DB H J E J D B D B t t&tt ρρm e e m ∂⎧∇⨯=--⎪∂⎪∂⎪∇⨯=+⇒⎨∂⎪∇=⎪⎪∇=⎩⋅⋅B E J D H J D B t t ρρ 三、边界条件1. 一般形式12121212()0()()()0n n S n Sn σρ⨯-=⨯-=→∞⋅-=⋅-=（）e E E e H H J e D D e B B2. 理想导体界面和理想介质界面111100⨯=⎧⎪⨯=⎪⎨⋅=⎪⎪⋅=⎩e E e H J e D e B n n S n S n ρ12121212()0()0()0()0⨯-=⎧⎪⨯-=⎪⎨⋅-=⎪⎪⋅-=⎩e E E e H H e D D e B B n n n n 第三章一、静电场分析 1. 位函数方程与边界条件 位函数方程：220∇=-∇=ρφφε电位的边界条件：121212=⎧⎪⎨∂∂-=-⎪∂∂⎩s nn φφφφεερ111=⎧⎪⎨∂=-⎪∂⎩s const nφφερ（媒质2为导体） 2. 电容定义：=qCφ两导体间的电容：=C q /U 任意双导体系统电容求解方法：3. 静电场的能量N 个导体：112ne i i i W q φ==∑连续分布：12e VW dV φρ=⎰电场能量密度：12ω=⋅D E e二、恒定电场分析1.位函数微分方程与边界条件位函数微分方程：20∇=φ边界条件：121212=⎧⎪⎨∂∂=⎪∂∂⎩nn φφφφεε12()0⋅-=e J J n 1212[]0⨯-=J J e n σσ 2. 欧姆定律与焦耳定律欧姆定律的微分形式： =J E σ 焦耳定律的微分形式： =⋅⎰E J VP dV3. 任意电阻的计算2211d d 1⋅⋅====⋅⋅⎰⎰⎰⎰E lE l J S E SSSU R G I d d σ（L R =σS ） 4.静电比拟法：G C —，σε—2211⋅⋅===⋅⋅⎰⎰⎰⎰D S E S E lE lS S d d qC Ud d ε2211d d d ⋅⋅===⋅⋅⎰⎰⎰⎰J S E SE lE lS S d I G Uσ三、恒定磁场分析 2211⋅⋅===⋅⋅⎰⎰⎰⎰D S E S E lE lS S d d qC Ud d ε1. 位函数微分方程与边界条件矢量位：2∇=-A J μ12121211⨯⨯⨯A A e A A J n s μμ()=∇-∇=标量位：20m φ∇=211221∂∂==∂∂m m m m n nφφφφμμ 2. 电感定义：d d ⋅⋅===⎰⎰B S A lSlL IIIψ0=+i L L L3. 恒定磁场的能量N 个线圈：112==∑Nmj j j W I ψ连续分布：m 1d 2=⋅⎰A J V W V 磁场能量密度：m 12ω=⋅H B第四章一、边值问题的类型（1）狄利克利问题：给定整个场域边界上的位函数值()=f s φ （2）纽曼问题：给定待求位函数在边界上的法向导数值()∂=∂f s nφ（3）混合问题：给定边界上的位函数及其向导数的线性组合：2112()()∂==∂f s f s nφφ （4）自然边界：lim r r φ→∞=有限值二、唯一性定理静电场的惟一性定理：在给定边界条件（边界上的电位或边界上的法向导数或导体表面电荷分布）下，空间静电场被唯一确定。

电磁场与电磁波知识点整理一、电磁场的基本概念电磁场是有内在联系、相互依存的电场和磁场的统一体的总称。

电荷会产生电场，而电流会产生磁场。

电场是由电荷产生的，它对处在其中的电荷有力的作用。

电场强度是描述电场强弱和方向的物理量，用 E 表示，单位是伏特每米（V/m）。

电场线可以形象地描绘电场的分布，其疏密程度表示电场强度的大小，切线方向表示电场的方向。

磁场是由运动电荷或电流产生的，对处在其中的运动电荷或电流有力的作用。

磁感应强度是描述磁场强弱和方向的物理量，用 B 表示，单位是特斯拉（T）。

磁感线可以形象地描绘磁场的分布，其疏密程度表示磁感应强度的大小，切线方向表示磁场的方向。

二、麦克斯韦方程组麦克斯韦方程组是电磁场理论的核心，它由四个方程组成，分别描述了电场和磁场的产生、变化和相互关系。

1、高斯定律：描述了电场的散度与电荷量之间的关系。

对于静电场，通过任意闭合曲面的电通量等于该闭合曲面所包围的电荷量除以真空中的介电常数。

数学表达式：∮E·dS ＝ q ／ε₀2、高斯磁定律：表明磁场的散度恒为零，即磁感线总是闭合的，没有磁单极子存在。

数学表达式：∮B·dS ＝ 03、法拉第电磁感应定律：指出时变磁场会产生感应电场，感应电场的环流等于磁通量的变化率的负值。

数学表达式：∮E·dl ＝dΦ/dt4、安培麦克斯韦定律：修正了安培环路定律，不仅电流会产生磁场，时变电场也会产生磁场。

数学表达式：∮B·dl ＝μ₀（I ＋ε₀dΦₑ/dt）三、电磁波的产生与传播电磁波是由时变的电场和磁场相互激发而产生的，并在空间中以波动的形式传播。

变化的电流或电荷是电磁波的源。

电磁波的传播不需要介质，可以在真空中传播。

在真空中，电磁波的传播速度为光速 c，约为 3×10⁸米每秒。

电磁波具有波的特性，如波长、频率、波速之间的关系：v ＝fλ，其中 v 是波速，f 是频率，λ 是波长。

电磁场与电磁波知识点总结电磁场知识点总结篇一电磁场知识点总结电磁场与电磁波在高考物理中属于非主干知识点，多以选择题的形式出现，题目难度较低，属于必得分题目，重点考察考生对基本概念的理解和掌握情况。

下面为大家简单总结一下高中阶段需要大家掌握的电磁场与电磁波相关知识点。

电磁场知识点总结一、电磁场麦克斯韦的电磁场理论：变化的电场产生磁场，变化的磁场产生电场。

理解：* 均匀变化的电场产生恒定磁场，非均匀变化的电场产生变化的磁场，振荡电场产生同频率振荡磁场* 均匀变化的磁场产生恒定电场，非均匀变化的磁场产生变化的电场，振荡磁场产生同频率振荡电场* 电与磁是一个统一的整体，统称为电磁场（麦克斯韦最杰出的贡献在于将物理学中电与磁两个相对独立的部分，有机的统一为一个整体，并成功预言了电磁波的存在）二、电磁波1、概念：电磁场由近及远的传播就形成了电磁波。

（赫兹用实验证实了电磁波的存在，并测出电磁波的波速）2、性质：* 电磁波的传播不需要介质，在真空中也可以传播* 电磁波是横波* 电磁波在真空中的传播速度为光速* 电磁波的波长=波速*周期3、电磁振荡LC振荡电路：由电感线圈与电容组成，在振荡过程中，q、I、E、B 均随时间周期性变化振荡周期：T = 2πsqrt[LC]4、电磁波的发射* 条件：足够高的振荡频率；电磁场必须分散到尽可能大的'空间* 调制：把要传送的低频信号加到高频电磁波上，使高频电磁波随信号而改变。

调制分两类：调幅与调频# 调幅：使高频电磁波的振幅随低频信号的改变而改变# 调频：使高频电磁波的频率随低频信号的改变而改变（电磁波发射时为什么需要调制？通常情况下我们需要传输的信号为低频信号，如声音，但低频信号没有足够高的频率，不利于电磁波发射，所以才将低频信号耦合到高频信号中去，便于电磁波发射，所以高频信号又称为“载波”）5、电磁波的接收* 电谐振：当接收电路的固有频率跟收到的电磁波频率相同时，接受电路中振荡电流最强（类似机械振动中的“共振”）。