数字电子技术基础第五版

《数字电子技术基础（第5版）》是2006年高等教育出版社出版的图书，作者是阎石、清华大学电子学教研组。

本书是普通高等教育“十五”国家级规划教材。

本书以前各版曾分别获得北京市教育教学成果一等奖、国家教委优秀教材一等奖、国家级优秀教材奖。

新版教材是在基本保持第四版教材内容、理论体系和风格的基础上，按照教育部2004年修订的“数字电子技术基础课程教学基本要求”修订而成的。

本次修订除改写了部分章节外，还增加了硬件描述语言和EDA软件应用的基础知识。

此外，还在多数小节后面增设了复习思考题。

为了便于教学，也为了便于读者今后阅读外文教材和使用外文版的EDA软件，书中采用了国际上流行的图形逻辑符号。

全书主要内容有：数制和码制、逻辑代数基础、门电路、组合逻辑电路、触发器、时序逻辑电路、半导体存储器、可编程逻辑器件、硬件描述语言、脉冲波形的产生和整形、数-模和模-数转换等共11章。

本书可作为电气信息类、仪器仪表类各专业的教科书，也可供其他相关理工科专业选用以及社会选者阅读。

阎石，清华大学教授、全国高等学校电子技术研究会理事长。

1937年生人。

1958年毕业于清华大学自动控制系，其后一直在清华大学从事电子技术的教学与科研工作。

曾任国家教委工科本科基础课程教学指导委员会第一、二届委员，华北地区高等学校电子技术教学研究会理事长。

1989年与童诗白教授等一起获得普通高等学校优
秀教学成果国家级特等奖。

主编的《数字电子技术基础》第二版获国家教委优秀教材一等奖，第三版获国家优秀教材奖，第四版获北京市教育教学成果一等奖。

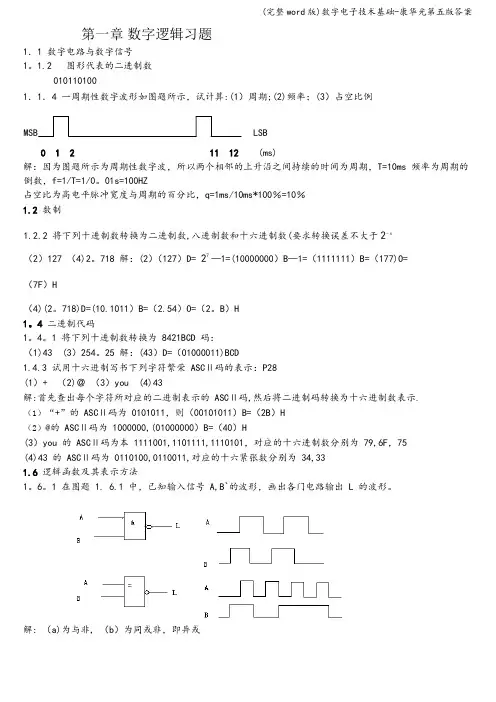
第一章数字逻辑习题1．1 数字电路与数字信号1。

1.2 图形代表的二进制数0101101001．1．4 一周期性数字波形如图题所示，试计算:(1）周期;(2)频率；(3）占空比例MSB LSB0 1 2 11 12 (ms)解：因为图题所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/0。

01s=100HZ占空比为高电平脉冲宽度与周期的百分比，q=1ms/10ms*100％=10％1.2 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4（2）127 （4)2。

718 解：(2）（127）D= 27 —1=(10000000）B—1=（1111111）B=（177)O=（7F）H（4)(2。

718)D=(10.1011）B=（2.54）O=（2。

B）H1。

4 二进制代码1。

4。

1 将下列十进制数转换为 8421BCD 码：（1)43 (3）254。

25 解：(43）D=（01000011)BCD1.4.3 试用十六进制写书下列字符繁荣ASCⅡ码的表示：P28(1）+ （2)＠（3）you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示.（1）“+”的ASCⅡ码为 0101011，则（00101011）B=（2B）H（2）@的ASCⅡ码为 1000000,(01000000）B=（40）H(3）you 的ASCⅡ码为本 1111001,1101111,1110101，对应的十六进制数分别为 79,6F，75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,331.6 逻辑函数及其表示方法1。

6。

1 在图题 1. 6.1 中，已知输入信号 A,B`的波形，画出各门电路输出 L 的波形。

解: （a)为与非, （b）为同或非，即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式（3)A⊕ =B AB AB+(A⊕B)=AB+AB解：真值表如下由最右边2栏可知，A⊕B与AB+AB的真值表完全相同。

数字电子技术基础第五版习题解答本文档为《数字电子技术基础第五版》习题解答，共计五个习题的解答内容。

习题一：布尔代数问题描述：将以下布尔代数表达式化简。

(A + B) · (A + C) · (B + C)解答：按照展开公式，并根据布尔运算规则简化表达式，可以得到以下计算步骤：(A + B) · (A + C) · (B + C)= (A·A + A·C + B·A + B·C) · (B + C)= (A + A·C + B·A + B·C) · (B + C)然后使用分配律的规则继续化简：= A·(1 + C) + B·(A + C) · (B + C)= A + AC + AB + BC= A + AB + BC + AC所以，原始表达式(A + B) · (A + C) · (B + C)可以化简为A + AB + BC + AC。

习题二：逻辑门问题描述：给定逻辑电路图如下，请确定其逻辑功能，并列出该电路的真值表。

____ ____A -----| |---| || | | |--- YB -----|and | |or ||____| |____|解答：根据逻辑电路图，可以判断该电路为两个输入 A 和 B 的AND 门和 OR 门的组合，输出为 Y。

该电路的真值表如下：A B Y000010101111习题三：数字编码问题描述：将以下十进制数转换为二进制数。

45解答：对于十进制数转换为二进制数，可以采用除以2取余法，将余数逆序排列即可。

使用该方法将数字 45 转换为二进制数的计算步骤如下：45 ÷ 2 = 22 余 122 ÷ 2 = 11 余 011 ÷ 2 = 5 余 15 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷2 = 0 余 1将余数倒序排列得到的二进制数为101101。

第1章数制和码制1.1复习笔记一、数字信号与数字电路1.模拟信号和数字信号模拟信号：幅度和时间连续变化的信号。

例如，正弦波信号。

数字信号：在幅度和时间上取值离散的信号。

例如，统计一座桥上通过的汽车数量。

模拟信号经过抽样、量化、编码后可转化为数字信号。

数字信号的表示方式：（1）采用二值数字来表示，即0、1数字；0为逻辑0，1为逻辑1。

（2）采用逻辑电平来表示，即H（高电平）和L（低电平）。

（3）采用数字波形来表示。

2.模拟电路和数字电路模拟电路：工作在模拟信号下的电路统称为数字电路。

数字电路：工作在数字信号下的电路统称为数字电路。

数字电路的主要研究对象是电路的输入和输出之间的逻辑关系；主要分析工具是逻辑代数关系；表达电路的功能的方法有真值表，逻辑表达式及波形图等。

二、几种常用的进制不同的数码既可以用来表示不同数量的大小，又可以用来表示不同的事物。

在用数码表示数量的大小时，采用的各种计数进位制规则称为数制，主要包括进位制、基数和位权三个方面。

进位制：多位数码每一位的构成以及从低位到高位的进位规则。

基数：在进位制中可能用到的数码个数。

位权：在某一进位制的数中，每一位的大小都对应着该位上的数码乘上一个固定的数，这个固定的数就是这一位的权数，权数是一个幂。

常用的数制有十进制、二进制、八进制和十六进制几种。

1.十进制在十进制数中，每一位有0～9十个数码，所以计数基数为10。

超过9的数必须用多位数表示，其中低位和相邻高位之间的关系是“逢十进一”，故称为十进制。

十进制的展开形式为式中，是第i位的系数，可以是0～9十个数码中的任何一个。

任意N进制的展开形式为式中，是第i位的系数，N为计数的基数，为第i位的权。

2.二进制在二进制数中，每一位仅有0和1两个可能的数码，计数基数为2。

低位和相邻高位间的进位关系是“逢二进一”。

二进制的展开形式为例如，（101.11）2=1×22＋0×21＋1×20＋1×2-1＋0×2-2=（5.75）10。

第一章数字逻辑习题1．1 数字电路与数字信号1.1.2 图形代表的二进制数0101101001．1．4 一周期性数字波形如图题所示，试计算：（1）周期；（2）频率；（3）占空比例MSB LSB0 1 2 11 12 （ms）解：因为图题所示为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比，q=1ms/10ms*100%=10%1.2 数制1.2.2 将下列十进制数转换为二进制数，八进制数和十六进制数（要求转换误差不大于2−4（2）127 （4）2.718 解：（2）（127）D= 27 -1=（10000000）B-1=（1111111）B=（177）O=（7F）H（4）（2.718）D=(10.1011)B=(2.54)O=(2.B)H1.4 二进制代码1.4.1 将下列十进制数转换为 8421BCD 码：（1）43 （3）254.25 解：（43）D=（01000011）BCD1.4.3 试用十六进制写书下列字符繁荣 ASCⅡ码的表示：P28（1）+ （2）@ （3）you (4)43解：首先查出每个字符所对应的二进制表示的 ASCⅡ码，然后将二进制码转换为十六进制数表示。

（1）“+”的 ASCⅡ码为 0101011，则（00101011）B=（2B）H（2）@的 ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的 ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的 ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,331.6 逻辑函数及其表示方法1.6.1 在图题 1. 6.1 中，已知输入信号 A，B`的波形，画出各门电路输出 L 的波形。

解: (a)为与非， (b)为同或非，即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)A⊕ =B AB AB+ （A⊕B）=AB+AB解：真值表如下由最右边2栏可知，A⊕B与AB+AB的真值表完全相同。