当前位置：文档之家 › 材料力学典型题解

材料力学典型题解

  • 格式：doc
  • 大小：3.62 MB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

材料力学典型例题及解析 12.冲击问题典型习题解析

材料力学典型例题及解析 12.冲击问题典型习题解析

击构件瞬间的速度为 υ
，只须将前面（a）式右端改为
1 2
⋅
Pυ2 g
= Vε
，即可导出 kd
=
υ2 。 g∆st
（4）、前面推导过程中，冲击物的势能取为 Ep = P(h + ∆d ) ，一般情况下 ∆d << h ，可将其忽
略，取 Ep = Ph ，读者可仿照上面推导一下，并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为： kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论：（1）、在线弹性范围内，载荷、变形、应变、应力之间都是线性关系，也就是说，当
外载荷被放大 kd 倍，则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解：设小球离开木拍瞬间速度为υ ，则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ；而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ，其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形，
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ，于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数，则有
Fd P
=
∆d ∆st
= σd σ st

材料力学试题及答案解析7套

材料力学试题及答案解析7套

材料力学试卷1一、结构构件应该具有足够的 、 和 。

（本题3分） 二、低碳钢拉伸破坏经历了四个典型阶段： 阶段、 阶段、 阶段和 阶段。

衡量材料强度的指标是 、 。

（本题6分） 三、在其他条件不变的前提下，压杆的柔度越大，则临界应力越 、临界力越 ；材料的临界柔度只与 有关。

（本题3分） 四、两圆截面杆直径关系为：123D D =，则12Z Z I I =；12Z Z W W =；12P P I I =；12P P W W =； （本题8分）五、已知构件上危险点的应力状态，计算第一强度理论相当应力；第二强度理论相当应力；第三强度理论相当应力；第四强度理论相当应力。

泊松比3.0=μ。

（本题15分）六、等截面直杆受力如图，已知杆的横截面积为A=400mm 2， P =20kN 。

试作直杆的轴力图；计算杆内的最大正应力；材料的弹性模量E =200Gpa ，计算杆的轴向总变形。

（本题15分）七、矩形截面梁，截面高宽比h=2b，l=4米，均布载荷q=30kN/m许用应力[]MPa100=σ，1、画梁的剪力图、弯矩图2、设计梁的截面(本题20分)。

八、一圆木柱高l=6米，直径D=200mm ，两端铰支，承受轴向载荷F=50kN，校核柱子的稳定性。

已知木材的许用应力[]MPa10=σ，折减系数与柔度的关系为：23000λϕ=。

(本题15分)九、用能量法计算结构B 点的转角和竖向位移，EI 已知。

（本题15分）材料力学试卷2一、（5分）图（a ）与图（b ）所示两个矩形微体，虚线表示其变形后的情况，确定该二微体在A 处切应变b aγγ的大小。

二、（10分）计算图形的惯性矩yz I I 。

图中尺寸单位：毫米。

三、（15分）已知构件上危险点的应力状态，计算第三强度理论相当应力；第四强度理论相当应力。

四、（10分）画图示杆的轴力图；计算横截面上最大正应力；计算杆最大轴向应变ε。

已知杆的横截面积A =400 mm 2，E =200GPa 。

材料力学考试典型题目

材料力学考试典型题目

2
(4)
Fx 2 EIw Flx C1 (3) 2 2 3 Flx Fx EIw C 1x C 2 2 6 边界条件 x 0, w 0
x 0, w 0
(4)
将边界条件代入（3）（4）两式中,可得 C1 0 梁的转角方程和挠曲线方程分别为
C2 0
ql 2 q 3 EIw x x C 4 6
ql 3 q 4 EIw x x Cx D 12 24
边界条件x=0 和 x=l时, w
0
x
q
wmax B
梁的转角方程和挠曲线方程 A 分别为
A
l
B
q 2 3 3 (6lx 4 x l ) 24 EI qx w (2lx 2 x 3 l 3 ) 24 EI
FN 3 l3 -4 1.58 10 m uB ΔlCD Δl BC -0.3mm EA3
-4
Δl AD Δl AB Δl BC ΔlCD -0.47 10 mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa，DB=1°. 试求：
x= l , M = 0
M 0
+
Mb l
梁上集中力偶作用处左、右两侧
FRA
A a
M
FRB
C b l B
横截面上的弯矩值(图)发生突变，其
突变值等于集中力偶矩的数值.此处 剪力图没有变化.
M /l
+ +
Mb l
Ma l
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F 作用.试求梁的挠曲线方程和转角方程, 并确定其最大挠度 wmax 和最大转角 max w

工程力学材料力学-知识点-及典型例题

工程力学材料力学-知识点-及典型例题

作出图中AB杆的受力图。

A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。

B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。

AB杆：二力杆E处固定端C处铰链约束（1）运动效应：力使物体的机械运动状态发生变化的效应。

（2）变形效应：力使物体的形状发生和尺寸改变的效应。

3、力的三要素：力的大小、方向、作用点。

4、力的表示方法：（1）力是矢量，在图示力时，常用一带箭头的线段来表示力；（注意表明力的方向和力的作用点！）（2）在书写力时，力矢量用加黑的字母或大写字母上打一横线表示，如F、G、F1等等。

5、约束的概念：对物体的运动起限制作用的装置。

6、约束力（约束反力）：约束作用于被约束物体上的力。

约束力的方向总是与约束所能限制的运动方向相反。

约束力的作用点，在约束与被约束物体的接处7、主动力：使物体产生运动或运动趋势的力。

作用于被约束物体上的除约束力以外的其它力。

8、柔性约束：如绳索、链条、胶带等。

(1)约束的特点：只能限制物体原柔索伸长方向的运动。

(2)约束反力的特点：约束反力沿柔索的中心线作用，离开被约束物体。

（）9、光滑接触面：物体放置在光滑的地面或搁置在光滑的槽体内。

（1）约束的特点：两物体的接触表面上的摩擦力忽略不计，视为光滑接触面约束。

被约束的物体可以沿接触面滑动，但不能沿接触面的公法线方向压入接触面。

（2）约束反力的特点：光滑接触面的约束反力沿接触面的公法线，通过接触点，指向被约束物体。

（）10、铰链约束：两个带有圆孔的物体，用光滑的圆柱型销钉相连接。

约束反力的特点:是方向未定的一个力；一般用一对正交的力来表示，指向假定。

（）11、固定铰支座（1）约束的构造特点：把中间铰约束中的某一个构件换成支座，并与基础固定在一起，则构成了固定铰支座约束。

（2）约束反力的特点：固定铰支座的约束反力同中间铰的一样，也是方向未定的一个力；用一对正交的力来表示，指向假定。

()12、可动铰支座（1）约束的构造特点把固定铰支座的底部安放若干滚子，并与支撑连接则构成活动铰链支座约束，又称锟轴支座。

材料力学典型例题与详解(经典题目)

材料力学典型例题与详解(经典题目)
G = [σ ]A(l) − F
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大

材料力学典型例题及解析7.应力应变状态典型习题解析

材料力学典型例题及解析7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。

绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。

b = 60 mm ，h = 100 mm 。

解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。

则各点处的应力状态如图示。

2、梁截面惯性矩为点微体上既有正应力又有切应力。

解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。

材料力学典型例题及解析 3.扭转典型习题解析

材料力学典型例题及解析 3.扭转典型习题解析

的切向内力所形成的力偶矩将由哪个力偶矩来平衡？
A M
B
A
M
B
C
z
D
A
(a)
C
dρ
ρ
R
(c)
D
题2图
BC Dx
(b)
θ dθ
(d)
解题分析：由切应力互等定理可知截面ABCD上的切向内力分布及其大小。该截面上切向内
力形成一个垂直向上的力偶矩。在图b中，左右两个横截面上的水平切向内力分量形成垂直
于截面ABCD的竖直向下的力偶矩，正好与截面ABCD上切向内力的合力偶矩平衡。
应力相等的条件下，试确定空心轴的外径，并比较实心轴和空心轴的重量。
解题分析：用空心轴代替实心轴，须保证二者强度相同。根据强度条件可求出D值，再用面
积比得出重量比。
解：1、根据两轴切应力相等的条件，确定空心轴外径
Tmax = Tmax = [τ ] WP实 WP空
πd 3 = πD3 (1 − α 4 ) 16 16
解得 D = 107.7 ×10−3 m = 107.7 mm
δ = D − d = 107.7mm −100mm = 3.85 mm
2
2
比较可知，两种设计的结果非常接近。
讨论: 当 δ ≤ R0 /10 时，即认为是薄壁圆管，可以直接使用薄壁管扭转公式。
2 图示受扭圆杆，沿平面ABCD截取下半部分为研究对象，如图b所示。试问截面ABCD上
4
即在强度相同条件下，空心轴可以节约近30％的材料。
讨论：在实际工程中常用空心圆轴代替实心圆轴，在保障安全运行的前提下，可以节约材料。
5 已知钻探机杆的外径D = 60 mm，内径d = 50 mm，功率P = 7.46 kW，转速n =180 r/min， 钻杆入土深度l = 40 m，G = 80 GPa，[τ]= 40 MPa。设土壤对钻杆的阻力是沿长度均匀分布 的，试求：(1) 单位长度上土壤对钻杆的阻力矩M；(2) 作钻杆的扭矩图，并进行强度校核； (3) 求A、B两截面相对扭转角。 解题分析：根据题意，为圆轴扭转问题。土壤对钻杆的阻力形成扭力矩作用在钻杆上，并沿

材料力学力法典型例题解

材料力学力法典型例题解

l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图，EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1）选图示相当系统（：一次超静定）
2）力法方程：
X 0
11 1
1P
3）利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2）力法方程
F
X 0
11 1
1P
3）图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4）解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1）选图示相当系统 （一次超静定）
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解：1）选图示静定基及相当系统

材料力学典型例题及难题详解

材料力学典型例题及难题详解

材料力学典型例题及难题详解材料力学是力学领域中极其重要的科学分支，它研究材料物理性质和力学性质之间的关系，用以确定物体在外力作用下的变形和应力分布。

材料力学的研究对于我们了解材料的性能和研制新材料有着重要的意义。

为了更好地探索材料力学，本文将从材料力学典型例题及难题详解入手，介绍一些典型例题以及相关技术，从而加深大家对材料力学的理解。

首先，我们从材料力学中最基础的问题剪切强度的测定入手，剪切强度指的是材料在剪切力作用下的应力值，一般来讲，材料的剪切强度越大，说明该材料具有更好的抗剪强度能力。

剪切强度的测定方法有很多种，最常用的是双螺旋测试仪，这种测试仪由一个上螺旋和下螺旋组成，上螺旋设定所需的应力，下螺旋逐渐拧紧，当材料断裂时，就可以读取到该材料的剪切强度。

其次，我们再来介绍材料力学中的其他重要参数，如伸长率、断裂伸长率、表面硬度和屈服应力等。

伸长率指的是材料在外力作用下，它长度变化的比例，通常用拉伸法来测定；断裂伸长率指的是材料在外力作用下，它断裂的长度变化的比例；表面硬度则是指材料表面的硬度，断裂伸长率一般用硬度测试仪来测定；屈服应力是指材料在拉伸或压缩下的临界应力，也就是材料在超过这个屈服应力时就会断裂的应力。

此外，还有一些材料力学难题，比如受曲应力的刚性体、晶界移动和材料缺陷等。

受曲应力的刚性体是指刚性体在受到曲应力作用时，会产生剪切变形，因此，一般就采用有限元分析，以准确解算复杂的受曲应力的刚性体的问题；晶界移动则是指在材料的塑性变形过程中，晶格面内的原子会发生移动，这种移动会产生更多的晶格缺陷；而材料缺陷则是指材料中所存在的导致开裂或断裂的缺陷。

最后，总结材料力学的研究状况，材料力学是一个庞大而广阔的学科，它涉及到材料物理性质、力学性质和结构力学等方面。

本文介绍了典型例题和材料力学难题，以帮助大家加深对材料力学的理解，但这些只是材料力学的冰山一角，希望大家能够更多地接触材料力学，加深对它的理解，为材料力学的发展做出贡献。

材料力学典型例题及解析 1.拉伸应力典型习题解析

材料力学典型例题及解析 1.拉伸应力典型习题解析

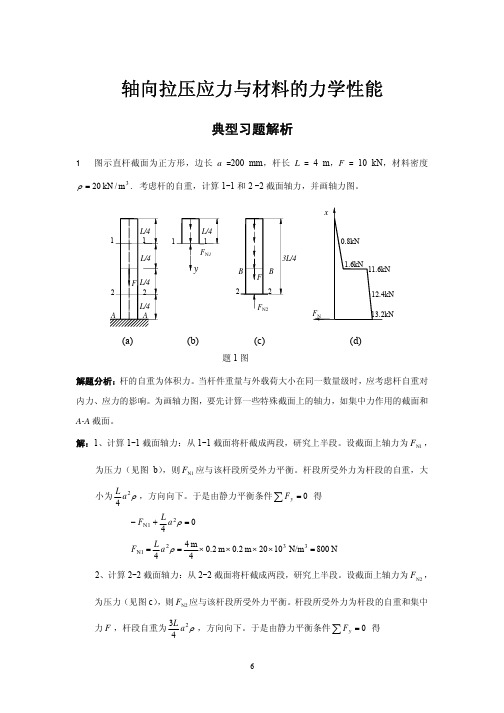
轴向拉压应力与材料的力学性能典型习题解析1　图示直杆截面为正方形，边长a =200 mm ，杆长L = 4 m ，F = 10 kN ，材料密度3m /kN 20=ρ. 考虑杆的自重，计算1-1和2 -2截面轴力，并画轴力图。

解题分析：杆的自重为体积力。

当杆件重量与外载荷大小在同一数量级时，应考虑杆自重对内力、应力的影响。

为画轴力图，要先计算一些特殊截面上的轴力，如集中力作用的截面和A-A 截面。

解：1、计算1-1截面轴力：从1-1截面将杆截成两段，研究上半段。

设截面上轴力为1N F ，为压力（见图b ），则1N F 应与该杆段所受外力平衡。

杆段所受外力为杆段的自重，大小为ρ24a L ，方向向下。

于是由静力平衡条件∑=0y F 得 042N1=+−ρa L F N 800N/m 1020m 2.0m 2.04m 44332N1=××××==ρa L F 2、计算2-2截面轴力：从2-2截面将杆截成两段，研究上半段。

设截面上轴力为N2F ，为压力（见图c ），则N2F 应与该杆段所受外力平衡。

杆段所受外力为杆段的自重和集中力F ，杆段自重为ρ243a L ，方向向下。

于是由静力平衡条件∑=0y F 得(c)(a) (b)题1图(d)kN 12.4N 104.12N/m 1020m 2.0m 2.04m43N 10104333332N2=×=×××××+×=+=ρa L F F 3、计算集中力F 作用截面上的轴力：首先将杆沿力F 作用截面（B-B ）上侧截开，设截面上轴力为压力+B F N ，研究上半部分杆段。

由于只受本身重量作用，所以由静力平衡条件得F 作用截面上侧轴力为kN 1.6N 106.1N/m 1020)m 2.0(2m 4233322N =×=×××==+ρa L F B 然后将杆沿F 作用截面（B-B ）下侧截开，设截面上轴力为压力−B F N ，研究上半部分杆段。

《材料力学》第11章典型习题解析

《材料力学》第11章典型习题解析

第11章典型习题解析1.用卡氏第二定理求图12.3所示刚架A 截面的位移和B 截面的转角。

略去剪力Q 和轴力N 的影响，E Ⅰ为已知.解：（1）A 截面的位移AB 段弯矩：M(x)=-Px （0≤x ≤l ） ∂M(x) /∂P=-x在A 处虚加一水平力向右的力Q,之后，再令其为0.那么,BC 段弯矩：M(y)=-2P l - Q l +(P+Q)y∂M(y) /∂P=-2l +y ∂M(y) /∂ Q=-l +yA 截面的竖直位移:Y A ==∂∂∑⎰EI P Mdx ML 0 ()()()()⎰⎰+-+-+--L LEIdy y L Py PL EI dx x Px 00222 =EIPL 223A 截面的水平位移: X A =EI Q M M L ∂∂∑⎰0dx=()()EI dy y L Qy Py QL PL L 200+-++--⎰ 积分，令Q=0得 ()()EIPL EI dy y L Py PL XA L 1252230=+-+-=⎰(2)B 截面的转角在B 处虚加一力偶M B,AB 段弯矩：M(x)=-Px （0≤x<l ）BC 段弯矩：M(y)=-2P l -B M +Py （0<y<l ）∂M(x) /∂MB=0 ∂M(y) /∂MB =-1 ∑⎰∂∂=L B B EI dx M M M 0θ =()()⎰-+--L B EI dxPy M PL 0212 EIPL 432= 2.用卡氏第二定理求图示的A 截面的位移和B 截面的转角。

略去剪力Q 和轴力N 的影响，E Ⅰ为已知。

解：（1）A 截面的位移在A 点虚加一向下的力F ，支反力2qL F P Y B ++= （L 为AB 和AD 的长度） P X qL P Y C C -=--=,2AB 段弯矩： M1=0∂ M1 /∂F=0AD 段弯矩：M2(x)=2qL P F qx 2++⋅1（）x-2∂M2(x) /∂F=xCD 段弯矩：M3(y)=PyaⅠⅠ2ⅠC DA 截面的竖直位移:∑⎰∂∂=L A EIdx F M M Y 0=⎰⋅⎥⎦⎤⎢⎣⎡-⋅⎪⎭⎫ ⎝⎛++L EI xdx qx x F qL P 02222 积分，令F=0得34A PL qL Y 6EI 24EI =+求A 截面的水平位移时， 在A 处虚加一水平力向右的力Q, 再令其为0.那么, 支反力B qL Y P Q 2=++ （L 为AB 和AD 的长度）C C qL Y P Q X P Q 2=-+=-+（）+，（） AB 段弯矩： M1=0∂ M1 /∂Q=0AD 段弯矩：M2(x)=(P+Q)x ⋅∂M2(x) /∂Q=xCD 段弯矩：M3(y)=（P+Q ）y∂M3(y) /∂Q=yA 截面的水平位移∑⎰∂∂=L A EI dx Q M M X 0=()⎰⋅+L EIdx x Q P 022=()⎰⋅+L EI ydy y Q P 0积分，令Q=0得 EIPL X A 23= (2) B 截面的转角在B 处虚加一顺时针的力偶M B, 积分，并令其为零。

材料力学典型例题及解析 6.弯曲变形典型习题解析

材料力学典型例题及解析 6.弯曲变形典型习题解析

弯曲变形典型习题解析1 试用积分法写出图示梁的挠曲轴方程，说明用什么条件决定方程中积分常数，画出挠曲轴大致形状。

图中C 为中间铰。

为已知。

I E解题分析：梁上中间铰处，左、右挠度相等，转角不相等。

解：设支反力为，如图示。

yB A yA FM F、、1、建立各段挠曲轴近似微分方程并积分 将梁分为AC 、CB 、BD 段。

AC 段 a x ≤≤10挠曲轴近似微分方程 11x FM w I E yA A ⋅−=′′转角方程1211'12C x Fx Mw IE yA A+−= (a) 挠度方程1113121162D x C x F x M w I E y A A ++−=(b)CB 段 )(2b a x a +≤≤挠曲轴近似微分方程2"2x FMw I E yA A ⋅−=转角方程 222222C x F xM w I E yA A+−=′(c)挠度方程2223222262D x C xFx M w I E yA A++−= (d)BD 段 l x b a ≤≤+3)(挠曲轴近似微分方程[])(333b a x Fx FM w I E yB yA A+−+−=′′转角方程[]32323332)(2C b a x F x F x M w I E yB yA A++−+−=′ (e) 挠度方程[]33333332336)(62D x C b a x FxFxM w I E yB yA A+++−+−= (f)2、确定积分常数共有6个积分常数。

需要6个位移边界条件和光滑连续条件。

332211D C D C D C 、、、、、题1图M A边界条件：，代入(b)得 01=x 01=w 01=D (g)0'1=w 代入(a)得 01=C(h)b a x +=2，02=w (i)连续条件： ， a x x ==2121w w =(j) b a x x +==32， 32w w ′=′ (k) 32w w =(l)联立(i)、(j)、(k)、(l)，可求出。

材料力学典型例题及解析 7.应力应变状态典型习题解析

材料力学典型例题及解析 7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。

绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。

b = 60 mm ，h = 100 mm 。

解题分析： 从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。

则各点处的应力状态如图示。

2、 梁截面惯性矩为 点微体上既有正应力又有切应力。

解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z1点处弯曲正应力（压应力）MPa 100Pa 10100m 10500m1050m N 101064833−=×=×××⋅×==−−zI My σ 1点为单向压缩受力状态，所以 021==σσ，MPa 1003−=σ 2点为纯剪切应力状态， MPa 30Pa 1030m10100602N 1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa 303−=σ 3点为一般平面应力状态弯曲正应力MPa 50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−zI My σ 弯曲切应力F S =120 kN题图1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−z z bI S F τ MPa 6.8MPa 6.58Pa)105.22()2Pa 1050(2Pa 1050)2(22626622min max −=×+×±×=+−±+=xy x y x τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1轴向拉伸与压缩例1-1 如图所示的等截面直杆，受轴向力F 1=15kN ，F 2=10kN 的作用。

试分别求出杆件1-1、2-2截面的轴力，并画出轴力图。

F 2F 2C 22 22F 111 11B F 1AF RF RF N1F 1F N2F R F N10kN5kN图1-1解：（1）外力分析 先解除约束，画出杆件的受力图。

120,0xR FF F F = -+=∑得：()121510kN 5kN R F F F =-=-=（2）内力分析 外力F R 、F 1、F 2将杆件分为AB 段和BC 段，在AB 段，用1-1截面将杆件截分为两段，取左段为研究对象，右段对截面的作用力用F N1来代替。

假定内力F N1为正，列平衡方程10,0xN R FF F = +=∑得：15kN N R F F =-=-负号表示F N1的方向和假定方向相反，截面受压。

在BC 这一段，用任意2-2截面将杆件分为两段，取左段为研究对象，右段对左段截面的作用力用F N2来代替。

假定轴力F N2为正，有平衡方程2100xN R FF F F = +-=∑得： ()21515kN N R F F F =-+=-+=10kN （3）画轴力图由以上例题可以总结出求截面轴力的简捷方法：杆件任意截面的轴力F N （x ）等于截面一侧所有外力的代数和。

即1nN i i F F ==∑，外力背离该截面的时取正，指向该截面时取负。

例1-2 如图所示为正方形截面阶梯杆，受力及尺寸如图所示。

试分析杆上1截面处和2截面处的正应力。

FF2hh12（a ）FFF N 11122N hh σ==F F F N 1222244N h h σ==F F（b ） 图1-2解：先求出杆两截面处的轴力F N 1和F N 2，在用截面上的轴力除以相应的截面面积，如图（b ）所示，不难求出σ1=F/h 2，σ2=F/（4h 2）。

例1-3 如图所示，斜杆AB 为直径d =20mm 的钢杆，载荷Q =15kN 。

求此时斜杆AB 横截面上的正应力。

F AB F ABBAdAC0.8m1.9m0.5mB QBQCF CyF CxF ABαα图1- 3解：BC 杆受力分析如图1-3所示。

()0CMF =∑， (1.9sin )(1.90.5)0AB F a Q --=所以 1.41.9sin AB Q F a=又sin 0.388a ==所以1.41528.5kN 1.90.388AB F ⨯==⨯又因斜杆的内力（轴力）为28.5kN N A B F F == 由此得出AB 杆横截面上的应力为：228.5kN90.76MPa (20mm)4N F A == 例1-4 一构件如图所示，已知：F 1=30kN ，F 2=10kN ，A AB =A BC =500mm 2，A CD =200mm 2，E =200GPa 。

试求：（1）各段杆横截面上的内力和应力；（2）杆的总伸长。

BCD F 1F 2A100 100 100（a ）BCDF 1F 2 1 F 112 2F N 2F N 1xF N30kN20k N（b ）图1-4解：（1）整个杆共在三处受外力，每两各外力作用点之间的轴力都相等（即AB 段内轴力是一定值，BD 段内轴力也是一定值）。

所以只要在AB 段内任求一截面1-1处的轴力F N1，就知道整段AB 上的内力。

同样只要在BC 段内任求一截面2-2处的轴力就可知道整段BC 上的内力。

整杆的内力分布如图1-4所示。

虽然BD 段上的轴力都等于30kN ，但是由于BC 段和CD 段横截面不等。

所以它们的应力也不等。

320kN 2010N40MP 500mm 500mm NAB AB AB F A σ⨯==== 330kN 3010N 60MP 500mm 500mm NBC BC BC F A σ⨯==== 330kN 3010N 150MP 200mm 200mmNCD CDCD F A σ⨯==== （2）虽然杆对于整杆AD 不满足胡克定律的适用条件，但AB 段、BC 段和CD 却能分别满足胡克定律，因此，我们可按胡克定律分别求AB 、BC 、CD 三段杆的伸长量，然后相加得到杆AD 的总伸长量。

又根据公式（3-2）和（3-6）可推得：L L L Eσε∆==所以40MPa100mm 0.02mm 200GPaABAB AB L L Eσ∆=⨯=⨯= 60MPa100mm 0.03mm 200GPaBCBC BC L L Eσ∆=⨯=⨯= 150MPa100mm 0.075mm 200GPaCDCD BC L L Eσ∆=⨯=⨯= 0.02mm 0.03mm 0.075mm 0.125mm AB BC CD L L L L ∆=∆+∆+∆=++=例1-5 如图所示为某铣床工作台进给油缸图，缸内工作油压P =2MPa ，油缸内径D =75mm ，活塞杆直径d =18mm ，已知活塞杆材料的许用应力[σ]=50MPa ，试校核该活塞杆的强度。

FPDd图1-5解：（1）求活塞杆的轴力22221π()π(7518)244N D d F pA p --===⨯（2）按强度条件校核222π(7518)24MPa 32.6MPa π184N F Aσ-⨯===⨯ 显然σ＜[σ]。

所以活塞杆的强度足够。

例1-6 如图6所示为一钢木结构。

AB 为木杆，其截面A 1=10×103mm 2，许用压应力[σ]1=7MPa ；BC 为钢杆，其截面积A 2=600mm 2，许用应力[σ]2=160MPa 。

（1）若吊起重物为45kN ，试校核AB 和BC 杆的强度；（2）试求B 处可吊的最大载荷W ；（3）若吊起重物为50kN ，则两杆的截面面积至少为多少才能保证两杆能安全的工作？CA 拉杆 30︒B WN BC N AByB xW（a ） （b ）图1- 6解：（1）AB 、BC 为二力杆件，取B 为研究对象，受力分析如图1-6（b ）所示。

由平衡条件可求得N BC 及N AB 与载荷W 的关系为0yF=∑，sin300BC N W ︒-=由此得2245kN 90kN sin30BC WN W ===⨯=︒0xF=∑c o s 30A B B CN N-︒=由此得cos302 1.73245kN 77.94kN AB BC N N W =︒===⨯= 则132177.94kN7.8MPa 1010mmAB N A σ===⨯22290kN150MPa 600mm BC N A σ=== 因为[]117.8MPa 7MPa σσ=>=，[]22150MPa 160MPa σσ=<=所以AB 杆不满足强度要求，BC 杆满足强度要求。

（2）由（1）可得N BC 及N AB 与载荷W 的关系为2BC N W =AB N =又117MPa AB N A σ== 所以3340.410N 40.4kN W =⨯=同样2222160MPa 600mm BC N WA σ==≤ 160600N 48kN 2W ⨯=≤因此，为了保证此结构的安全，B 处可吊的最大许可载荷W =40.4kN 。

（3）根据强度公式[]111ABN A σσ=≤可得 []42111.210mm ABN A σ==⨯≥同样可得[]2222250k N625m m160M P a 160M P aBCN W A σ⨯===≥2剪切与挤压例2-1 试校核如图2-1所示中齿轮与轴的平键连接的强度。

已知装齿轮处轴的直径d =48mm ，A 型平键的尺寸为b =14mm ，h =9mm ，L =45mm ，传递的转矩M T ＝l81481 N·mm ，键的许用切应力[τ]=60MPa ，许用挤压应力[σ jy ]＝130MPa 。

hbdd +t 1d -t t t 1（a ） （b ）bR=b /2A 型h L（c ）d O mM Tbmh /2M TFLl（d ） （e ）图 2- 1解：由于键是A 型键，其形状如图2-1（c ）所示。

此类型键的两个圆头与轮毂上的键槽并不接触，所以该键的有效工作长度为l L b =-。

（1）以键和轴整体为研究对象，其受力分析如图2-1（d ）所示。

求键所受的力。

()0O M F =∑，即02d F T ⨯-=，所以221814817561.7N 48T F d ⨯=== 键连接的破坏可能是键沿m -m 截面被切断及键与键槽工作面间的挤压破坏。

则用截面法可求得剪切力和挤压力为7561.7N s jy F F F ===。

（2）校核键的强度计算如下：键的剪切面积()s A bl b L b ==-，挤压面积为()22jy h h A l L b ==-[]7561.7MPa 17.4MPa 60MPa 14(4514)s s F A ττ===<=⨯- ()7561.7MPa 54.2MPa 945142jy jy jy jyF A σσ⎡⎤===<⎣⎦- 键的剪切和挤压强度均满足要求。

例2-2 如图2-2所示为螺栓连接，已知钢板的厚度σ = 10mm ，设上下两钢板与螺栓实际接触高度近似都等于钢板的厚度。

螺栓的许用切应力[σ]=100MPa ，许用挤压应力[σjy ]= 200MPa ，F=28kN ，试选择该螺栓的直径。

FFFδd 0Fδd 0m m（a ） （b ）图2-2解：（1）分析破坏形式从图可以看出，螺栓的破坏可能是沿m -m 截面被切断及与孔壁间的挤压变形。

（2）求切力和挤压力。

用截面法可求得28kN Q jy F F F ===（3）按剪切强度条件设计螺杆配合直径d 0018.9mm d = （4）按挤压强度条件设计螺杆配合直径d 00jy jy jy F A d δσ=⎡⎤⎣⎦≥028000mm 14mm 20010jy jy F d σ==⨯⎡⎤δ⎣⎦≥若要螺栓同时满足剪切和挤压强度的要求，则其螺杆配合直径应为d0=18.9mm。

按此直径从设计手册中选用M18的六角头铰制孔用螺栓，其螺杆配合直径d0=19mm。

3扭转例3-1 如图3-1所示圆截面杆各截面处的外力偶大小分别为1e M =6M ，2e M =M ，3e M =2M ，4e M =3M 。

求杆在截面1-1、2-2、3-3处的扭矩。

（a ）M e 12 M e 2 M e3 M e 41 3 A2 B 13 C DM e 1 M e 2 1 T 1xA B 1 （b ）（c ）（d ）M e 1 2 T 2xA 2 M e 1 M e 2M e 3T 3xA BC（e ）T 6M 5M3M+xO图3-1解：由截面法，沿各所求截面将杆件切开，取左段为研究对象，并以T 1、T 2、T 3表示相应截面上的扭矩。