材料力学精编例题word资料11页

第二章2-1试求图示各杆11，22，33截面上的轴力,并作轴力图。

(a)(b)题2-1图解：（）受力分析,如图2-1。

各个截面上的轴力取拉力为正，压力为负， a 由轴向平衡条件，0X =∑321200203002030400N N N +=⎧⎪+−=⎨⎪+−−=⎩ ⇒1350(10(20(N kN kN N kN =⎧⎪=⎨⎪=−⎩2拉力）N 拉力）压力）作轴力图如上。

（b ）各截面上的轴力，均按其正方向设出，由轴向受力平衡：由0X =∑可得 作轴力图如上。

13(0(N P N P =⎧⎪=⎨⎪=⎩2拉力）N 拉力）2-2在图示简易吊车的横梁上P 力可以左右移动。

试求截面11上的内力及其最大值。

解：如图所示，题2-2图构件在1截面处“断开”，以下方的部分为研究对象，轴力和力作用在研究对象上，由平衡条件：1−1N P 0AM=∑1(sin )P x N l 0α⋅+−⋅= 11()sin P xN N x l α⋅==（P l α、、均为常数）1N 最大值为 1,max1()sin sin P l PN N l l αα⋅===⋅ 2-3图示为简易起重机。

已知钢丝绳子AC 的横截面积24AC A cm =,吊杆AB 的横截左面积26AB A cm =,当起重量P=20KN 时,求钢丝绳子AC 和吊杆AB 的正应力。

题2-3图解：先假设吊杆AB 、均受拉力作用，则对AC A 点进行受力分析可知，两杆对A 的作用力如图示方向。

AB AC T T 、由受力平衡得:0AB AC P T T ++=J G JJJ G JJJ GX Y ⎧=⎪⎨=⎪⎩∑∑ cos30cos 450cos 45cos600AC AB AB AB T T P T T ⋅°+⋅°=⎧⇒⎨+⋅°+⋅°=⎩20P k =N N =⎧⎨=−⎩54.6466.93AC AB N kNN kN=⎧⎨=−⎩ ⇒54.6466.93AC AB T k T kN 可见，杆受拉，而AC AB 杆实际受压。

材料力学（一）轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。

为设计既安全可靠又经济合理的构件，提供有关强度、刚度与稳定性分析的基本理论与方法。

【重点、难点】重点考察基本概念，掌握截面法求轴力、作轴力图的方法，截面上应力的计算。

【内容讲解】一、基本概念强度——构件在外力作用下，抵抗破坏的能力，以保证在规定的使用条件下，不会发生意外的断裂或显著塑性变形。

刚度——构件在外力作用下，抵抗变形的能力，以保证在规定的使用条件下不会产生过分的变形。

稳定性——构件在外力作用下，保持原有平衡形式的能力，以保证在规定的使用条件下，不会产生失稳现象。

杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件，称为杆件或简称杆。

根据轴线与横截面的特征，杆件可分为直杆与曲杆，等截面杆与变截面杆。

二、材料力学的基本假设工程实际中的构件所用的材料多种多样，为便于理论分析，根据它们的主要性质对其作如下假设。

(一)连续性假设——假设在构件所占有的空间内均毫无空隙地充满了物质，即认为是密实的。

这样，构件内的一些几何量，力学量(如应力、位移)均可用坐标的连续函数表示，并可采用无限小的数学分析方法。

(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。

按此假设通过试样所测得的材料性能，可用于构件内的任何部位(包括单元体)。

(三)各向同性假设——沿各个方向均具有相同力学性能。

具有该性质的材料，称为各向同性材料。

综上所述，在材料力学中，一般将实际材料构件，看作是连续、均匀和各向同性的可变形固体。

三、外力内力与截面法(一)外力对于所研究的对象来说，其它构件和物体作用于其上的力均为外力，例如载荷与约束力。

外力可分为：表面力与体积力；分布力与集中力；静载荷与动载荷等。

当构件(杆件)承受一般载荷作用时，可将载荷向三个坐标平面(三个平面均通过杆的轴线，其中两个平面为形心主惯性平面)内分解，使之变为两个平面载荷和一个扭转力偶作用情况。

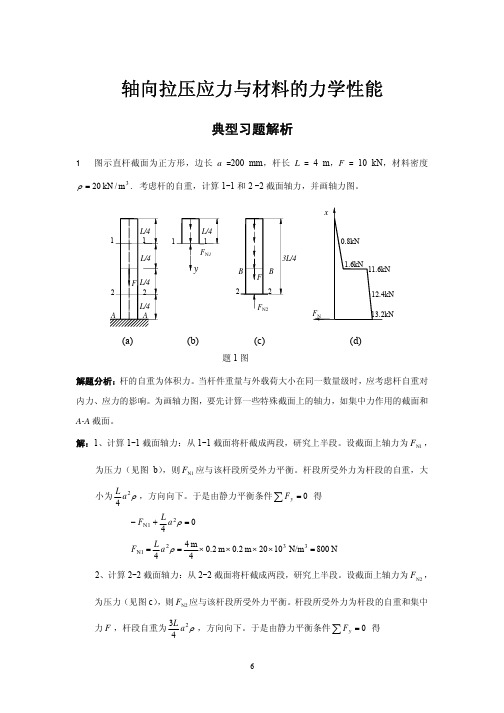
习题1-1图示拆卸工具的爪钩（见图），若已知顶压力F=20kN ，求m-m 截面上的内力.1-2试求图示m-m ，n-n 截面上的内力.习题1-1图习题1-2图1-3图示简易托架横梁上有吊车移动。

试求截面1－1和2－2(位于集中力F 左侧)上的内力及其最大值.ACB5kNnnm 2mm 1m1mFB21 21CAmm3232Fd习题1-3图1-4图示圆形薄板半径为R=100mm,变形后半径R 的增量为ΔR=2×10.3mm,.分别求出沿半径和外圆周两个方向的平均应变。

1-5图示三角形薄板受外力作用而变形,角点B 垂直向上位移为0.06mm, AB 和OB 仍保持为直线.试求：1）OB 的平均应变; 2)AB 和OB 两边在B 点的角度改变。

习题1-4图习题1-5图思考题2-1 若杆件横截面上各点处的正应力都相等，则该截面上的法向分布内力的合力必通过横截面形心吗？又若杆件法向分布内力的合力通过横截面形心，横截面上各点处的正应力必相等吗？2-2 闭合薄壁截面杆受轴向拉伸如下图所示。

若已知A 、B 两点间距离为a,材料的横向变形系数。

试证明该两点距离改变量为aAB。

2-3 试说明公式A F N,EA lF lN 的应用条件，并说明E 的物理意义和量纲。

2-4 三根杆件尺寸相同但材料不同，材料的曲线如图所示，试问哪一种（1）强度高？B240OA4545ΔＲR思考题2-2图σσBA（2）刚度大？（1）塑性好？2-5 杆件弹性模量E =210GPa ，比例极限σp =200MPa; 在轴向拉力作用下，纵向线应变为ε＝8×10—4，求此时横截面上的正应力。

若拉力加大使杆件的纵向线应变增加到ε＝5×10—3，问此时横截面上的正应力能否再由胡克定律确定？2-6 若已测得受力物体内x 和y 两方向均有线应变，问在x 和y 两方向是否都必有正应力? 若测得x 和y 两方向均无线应变，则在x 和y 两方向是否都必无正应力?2-7 低碳钢试样的拉伸图中，拉断时的应力为何比强度极限低？2-8 两根杆件，同样材料制成但横截面积不同，它们的强度极限相同吗？2-9 脆性材料制成的轴向拉伸矩形截面杆，若有方向平行于轴线的裂纹，问杆的强度是否因此降低？若裂纹方向垂直于轴线，杆的强度是否因此降低？2-10 在图示杆系中,钢杆1和铜杆2的许用应力分别为1和2,横截面面积分别为A 1和A 2 ；且1>2,而A 2>A 1; 能断定铜杆2先破坏吗？若根据节点C 的平衡条件ΣY=0求结构的许可荷载，则2201130cos ][45cos ][][A A F ，这种结论对吗？2-11在图示杆系中,若1、2、3三杆的材料及横截面面积均相同，问可否有办法使各杆同时达到材料的许用应力值？习题思考题2-10图 21CAB F3045FC AB D 123思考题2-11图123思考题2-4图2-1求图示各杆1－1、 2－2和3－3截面上的轴力，并作轴力图。

第1章1－1 什么是构件的强度、刚度和稳定性？1－2 材料力学对变形固体有哪些假设？第2章2－1 试作图示各杆的轴力图，并确定最大轴力| FN |max 。

2－2 试求图示桁架各指定杆件的轴力。

2－3 试作图示各杆的扭矩图，并确定最大扭矩| T|max 。

2－4 图示一传动轴，转速n＝200 r/min ，轮C为主动轮，输入功率P＝60 kW ，轮A、B、D均为从动轮，输出功率为20 kW，15 kW，25 kW。

（1）试绘该轴的扭矩图。

（2）若将轮C与轮D对调，试分析对轴的受力是否有利。

2－5 试列出图示各梁的剪力方程和弯矩方程。

作剪力图和弯矩图，并确定| Fs |max及|M |max值。

2－6 试用简易法作图示各梁的剪力图和弯矩图，并确定| F s |max及| M|max值，并用微分关系对图形进行校核。

2－7 图示起重机横梁AB承受的最大吊重F P＝12kN，试绘出横梁A B的内力图。

2－8 图示处于水平位置的操纵手柄，在自由端C处受到一铅垂向下的集中力F p作用。

试画出AB段的内力图。

第3章3－1图示圆截面阶梯杆，承受轴向荷载F1＝50kN与F2的作用，AB与BC段的直径分别为d1＝20mm与d2＝30mm，如欲使AB与BC段横截面上的正应力相同，试求荷载F2之值。

3－2变截面直杆如图所示。

已知A1＝8cm2，A2＝4cm2，E＝200GPa 。

求杆的总伸长量。

3－3 在图示结构中，AB为刚性杆，CD为钢斜拉杆。

已知F P1＝5kN ，F P2＝10kN ，l＝1m ，杆CD的截面积A＝100mm2 ，钢的弹性模量E＝200GPa 。

试求杆CD的轴向变形和刚性杆AB在端点B的铅垂位移。

3－4 一木柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E＝10GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

拉伸与压缩1.图示结构，4F为刚性杆，CD杆为钢制，其面积A = 200mm2,弹性模量E=2.0X 105MPa o B处弹簧刚度^=3X103N/mm,匸lm。

若CD杆的许用应力［B = 160MPa,试求荷载F的容许值。

（西南交大2003年）2.图示结构C结点与滑块餃接，不计滑块与滑槽间摩擦力，滑块只可能沿滑槽上下自由移动,4C与BC两杆面积均为A=100mm2,材料的弹性模量均为E=2.0x 105MPa,膨胀系数 a =12x10-6（1/1）。

求当BC杆升温50°C ,而4C杆温度不变时C处的位移值。

（西南交大2002 年）3.图示杆系中AC、BC杆的直径分别为Ji=10mm、J2=20mm,两杆材料均为0235钢, 许用应力= 170MPa,试按强度条件确定容许F值。

（西南交大2001年）4.图示两端固定的杆件，在距左端x处作用一轴向力F，杆横截面面积为4,材料的许用拉应力为［况，许用压应力为［创，且［创=3［5］。

求x为何值时F的许可值最大?其值［FUx 为多少？（西南交大1999年）X5.图示结构中①、②、③三杆的材料相同，弹性模量均为E，线膨胀系数均为a。

三杆的横截面面积分别为旳、A2、A3 ,各杆的长度如图所示。

横杆CD为钢杆。

受力如图所示, 各杆温度同时上升&°C。

求①、②、③三杆的轴力。

（西南交大1998年）6.图示结构中，BC为刚性梁，杆①、②、③的材料、横截面面积均相同，在横梁BC ± 作用一可沿横梁移动的载荷F,其活动范围为0 <x<2«o计算各杆的最大轴力值。

（西南交大1997年）p7、空心圆截面钢杆,其外径D=40mm,内径d=20mm,承受轴向拉力F=180kN,钢材的弹性常数E=2.0x 105MPa及v=0.3。

求m—m横截面上a、b两点的相对位移和b、c两点的相对位移。

（西南交大1991年）D8、AC及BC两钢杆的抗拉刚度为EA,在C点較接处受一铅垂向下的力F作用。

一、空心钢轴的外径D =100mm ，内径d =50mm ，若要求轴在单位长度内的最大转角不超过0.75°，试求它所承受的最大扭矩，并求此时轴内的最大切应力。

已知G =80GPa 。

二、两杆AC 和BC 两端均为铰支，且在C 处承受F =200kN 力的作用。

两杆的材料均为钢，直径均为mm 50=d ，许用应力MPa 100][=σ，弹性模量E =200GPa ，试校核两杆的强度；并求C 点的垂直位移。

F
C 30°
F F C
C'4
1
2
3
AC ∆l BC
∆l N,AC
N,BC
三、作梁和刚架的内力图。

16 kN
a 2a
q = 2 kN/m
(d)F
a 2a
a
q (e)
q
(a)
q
a
a
F
(b)
MPa ，截面对形心轴c z 的惯性矩F 。

0.8F (+)
0.6F (-)
(a)
五、求图示刚架自由端C 点的垂直位移和水平位移。

EI 为常数，拉压和剪切变
形不计。

（提示：跨度为l 的悬臂梁自由端受集中力偶e M 作用，该处转角为EI l
M e ，
挠度为EI l M e 22
；跨度为l 的悬臂梁自由端受集中载荷F 作用，该处转角为EI
Fl 22
，
挠度为EI
Fl 33
）
六、图示铝柱用青铜芯加强，置于刚性支承上，加在刚性盖板上的轴向压力F =40kN ，已知两种材料的弹性模量分别为E al =70GPa ，E br =100GPa ，求横截面上两种材料的正应力。

习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

习题2-1图习题2-2图习题2-3图习题2-4图1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）d d Q x F d M（B ）d d Q x F （C ）d d Q x F （D ）d d Q xF 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。

材料力学习题选及其解答精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】5-1. 矩形截面悬臂梁如图所示，已知l =4m ，h/b=2/3，q=10kN/m ，[]=10MPa ，试确定此梁横截面的尺寸。

解：（由弯矩图知：（2）计算抗弯截面模量（3）强度计算5-2. 20a工字钢梁的支承和受力情况如图所示，若[]=160MPa ，试求许可载荷。

解：（1（2）查表得抗弯截面模量（3）强度计算取许可载荷5-3. 图示圆轴的外伸部分系空心轴。

试作轴弯矩图，并求轴内最大正应力。

qxMql 2x解：（1（2C截面：B 截面：（3）轴内的最大正应力值5-8. 压板的尺寸和载荷如图所示。

材料为45钢，s =380MPa ，取安全系数n=1.5。

试校核压板的强度。

（3）强度计算许用应力Mx强度校核压板强度足够。

5-12. ⊥形截面铸铁梁如图所示。

若铸铁的许用拉应力为[t ]=40MPa ，许用压应力为[c ]=160MPa ，截面对形心z c 的惯性矩I zc =10180cm4，h 1=96.4mm ，试求梁的许用载荷P 。

解：（1（2A 截面的最大压应力A 截面的最大拉应力C 截面的最大拉应力取许用载荷值5-15. 铸铁梁的载荷及截面尺寸如图所示。

许用拉应力[l ]=40MPa ，许用压应力[c ]=160MPa 。

试按正应力强度条件校核梁的强度。

若载荷不变，但将T 形截面倒置成为⊥形，是否合理何故x0.6解：（1）画梁的弯矩图截面（2形心位置和形心惯性矩（3）强度计算B 截面的最大压应力B 截面的最大拉应力C 截面的最大拉应力梁的强度足够。

（4）讨论：当梁的截面倒置时，梁内的最大拉应力发生在B 截面上。

梁的强度不够。

5-20. 试计算图示工字形截面梁内的最大正应力和最大剪应力。

解：（1A No16Mx QMx最大剪力和最大弯矩值是（2）查表得截面几何性质（3）计算应力最大剪应力最大正应力5-22. 起重机下的梁由两根工字钢组成，起重机自重Q=50kN，起重量P=10kN。

实用文档第一章绪论【例 1-1 】钻床如图1-6a 所示，在载荷P 作用下，试确定截面m-m上的内力。

【解】（ 1）沿 m-m 截面假想地将钻床分成两部分。

取m-m 截面以上部分进行研究（图1-6b ），并以截面的形心O为原点。

选取坐标系如图所示。

（ 2）为保持上部的平衡，m-m 截面上必然有通过点O的内力 N 和绕点 O的力偶矩M。

（ 3）由平衡条件∴【例 1-2 】图 1-9a 所示为一矩形截面薄板受均布力p 作用，已知边长=400mm，受力后沿 x 方向均匀伸长=0.05mm。

试求板中 a 点沿 x 方向的正应变。

【解】由于矩形截面薄板沿x 方向均匀受力，可认为板内各点沿x 方向具有正应力与正实用文档应变，且处处相同，所以平均应变即 a 点沿 x 方向的正应变。

x 方向【例 1-3 】图 1-9b 所示为一嵌于四连杆机构内的薄方板，b=250mm。

若在 p 力作用下CD杆下移b=0.025，试求薄板中 a 点的剪应变。

【解】由于薄方板变形受四连杆机构的制约，可认为板中各点均产生剪应变，且处处相同。

第二章拉伸、压缩与剪切【例题 2.1 】一等直杆所受外力如图 2. 1 (a)所示，试求各段截面上的轴力，并作杆的轴力图。

解：在 AB段范围内任一横截面处将杆截开，取左段为脱离体( 如图 2. 1 (b)所示)，假定轴力 F N1为拉力 ( 以后轴力都按拉力假设) ，由平衡方程F x0 ， F N1300得F N130kN结果为正值，故 F N1为拉力。

同理，可求得BC段内任一横截面上的轴力( 如图 2. 1 (c)所示)为F N230 4070(kN)在求 CD段内的轴力时，将杆截开后取右段为脱离体( 如图 2. 1 (d)所示)，因为右段杆上包含的外力较少。

由平衡方程F x0 ，F N330 200.得F N330 20 10(kN)结果为负值，说明 F N3 为压力。

同理，可得段内任一横截面上的轴力F N4 为DEF N4 20kN30kN 40kN80kN30kN 20kN(a)40kN 80kN 30kN 20kN30kNA (a)CDEB20kN30kN40kN80kN30kN(b) 30kN (a)A (a)BC DE40kN 80kN F30kN20kN30kN40kN 80kN 30kN 30kN20kNCDE(a)B30kN30kN(b) 40kN A F N1(a)(c)BD F N2EA30kN C(b)40kN(b)FABC D30kN20kN30kN80kNE30kN30kN(c)40kNF N2(b)F N330kN 20kN30kN(a)F(d)F 30kN40kN(b)F N2(c) BCDE30kN20kN30kNA(d)F N340kNF N2(c)30kN(c)30kN (b)e)F N420kN40kN(d)20kN(c)F N2 FF N330kN(d)30kN (e)F N370kN 30kN 20kN F N420kN(d) (c)F N3 40kN 30kN F N2 20kN(e) 30kN70kN20kN(f)(d)20kN F N4 (e)FN420kNN3 70kN30kN(e)(d)(f)F20kN 30kN20kN20kNF N470kN10kN30kN(f)20kN70kN(f) (e) 30kN(e) 20kN FN410kN20kN(f)30kN70kN20kN10kN10kN(f)30kN 10kN20kN10kN(f)图 2.1 例题 2.1 图【例题 2.2 】 一正方形截面的阶梯形砖柱，其受力情况、各段长度及横截面尺寸如图 2.8(a) 所示。

一、简答题1、轴向拉压时杆件受力和变形的特点？答： 外荷载必须是轴向荷载，其内力只有轴力。

变形特点是轴向伸长或缩短。

2、什么是最大拉应力理论？如何选择？答：最大拉应力理论认为引起材料断裂的主要因素是最大拉应力，而且，不论材料处于何种应力状态，只要最大拉应力达到材料单向拉伸断裂时的最大拉应力，材料即发生断裂。

脆性材料在二向或三向受拉断裂时；当存在压应力的情况下，只在最大压应力值不超过最大拉应力值，可选用最在拉应力理论。

3、低碳钢拉伸试验时分哪几个变形阶段？答：有弹性阶段、屈服阶段、强化阶段和缩颈阶段等。

4、什么是应力集中？应力集中对构件强度有何影响？答：应力应力集中：由于截面急剧变化所引起的应力局部增大现象，称为应力集中。

在设计脆性材料构件时，应考虑应力集中的影响。

在设计塑性材料构件的静强度问题时，通常可以不考虑应力集中的影响。

应力集中对构件的疲劳强度影响极大。

所以，在工程设计中，要特别注意减小构件的应力集中。

5、若直径和长度相同，而材料不同的两根轴，在相同的扭矩作用下，它们的最大切应力是否相同？扭转角是否相同？ 答：轴扭转时最大剪应力p W T =τ，因为两根轴直径d 和长度l 都相同，所以p W 相同。

因此，最大剪应力max τ相同。

扭转角不同。

6、铸铁T 形截面悬臂梁，在自由端上作用向下的集中荷载。

若保证在任何情況下都无扭转（画出截面放置图，并说明理由。

）所以截面（在图中示意）？。

最大压应力发生在固定端左下角。

8、什么是疲劳破坏？图示交变应力循环特征r ，应力振幅σa 和平均应力σm 分别为多少？答：在交变应力作用下，构件产生可见裂纹或完全断裂的现象，称为疲劳破坏。

r =0, σa =50Mpa ,σm =50Mpa9、构件说明图示结构中，AD杆发生什么变形？答：发生弯曲和压缩的组合变形。

10、什么是最大拉应变理论？如何选择？11、梁截面合理强度设计的原则是什么？举例说明抗拉强度低于抗压强度的脆性材料梁，宜采用哪种截面？答：从弯曲强度考虑，合理的截面形状，是使用较小的截面面积，能获得较大抗弯截面系数的截面。

精选材料力学试题卷与含答案解析全1 / 51------- --- ------ -- - -- -- - 号- -- 学- -- _- - _ - - _- _- _ - _ - - _ - _ - - _ - _ - - _ - _- -- 名- -- 姓- - --- ---级 题班答准不内线业 封专密_ - _- _ - -_ - _ -- _- _ - - _ - _ - - _ - _ - - _- _- - _- _- - -- 院- -- 学- -- 术- -- 技 - -- 程- -- 工- - ----- -----江 苏 科 技 大 学学年第二学期资料力学试(A 题卷)题 号 一二三四五六总分得 分一、 选择题 （20 分 ）1、图示刚性梁AB 由杆 1 和杆 2 支承，已知两杆的资料相同，长度不等，横截面积分别为 A 1 和 A 2，若载荷 P 使刚梁平行下移，则其横截面面积（ ）。

A 、A 1〈 A 2B 、A 1 〉A 2C 、A 1=A 2题一、 1 图D 、A 1、 A 2 为任意2、建立圆周的扭转应力公式τ ρ =M ρ ρ/I ρ 时需考虑以下因素中的哪几个答：（ ）（ 1） 扭矩 M T 与剪应力τ ρ的关系 M T =∫A τρ ρdA （ 2） 变形的几何关系（即变形协调条件） （ 3） 剪切虎克定律（ 4） 极惯性矩的关系式 I T =∫A ρ 2dAA 、（1）B 、（ 1）（2）C 、（1）（2）（ 3）D 、全部3、二向应力状态以下列图，其最大主应力σ 1 =（）A 、σB 、 2σC 、 3σ题一、 3 图D、4σ4、高度等于宽度两倍 (h=2b)的矩形截面梁，承受垂直方向的载荷，若仅将竖放截面改为平放截面，其他条件都不变，则梁的强度（）A、提高到原来的 2 倍B、提高到原来的 4 倍题一、 4C、降低到原来的1/2 倍D、降低到原来的1/4 倍5.已知图示二梁的抗弯截面刚度 EI 相同，若二者自由端的挠度相等，则 P1/P2=（）A、2B、 4C、8题一、5图D、16二、作图示梁的剪力求、弯矩图。

一、试作出图示各杆的轴力图。

二、图示结构中，1、2两杆的横截面直径分别为mm 10和mm 20，试求两杆的应力。

设两根横梁皆为刚体。

三、桁架的尺寸及受力如图所示，若kN 300=F ，AB杆的横截面面积2mm 6000=A ，试求AB杆的应力。

()a四、在图示简易吊车中，BC 为钢杆，AB为木杆。

木杆AB的横截面面积21cm 100=A ，许用应力[]MPa 71=σ；钢杆BC 的横截面面积22cm 6=A ，许用应力[]MPa 1602=σ。

试求许可吊重[]F 。

五、在低碳钢拉伸实验用的力与变形曲线及应力应变曲线中分别标出p F 、s F 、b F 和p σ、s σ、b σ，并回答在εσ-曲线中的p σ、s σ、b σ是否是构件中的真实应力，如果不是请另绘出强化阶段与颈缩阶段真实应力曲线的大致形状。

六、像矿山升降机钢缆这类很长的拉杆，应考虑其自重的影响。

设材料单位体积的重量为γ，许用应力为[]σ。

钢缆下端所受拉力为F ，且钢缆截面不变。

试求钢缆的允许长度及其总伸长。

钢缆横截面面积为A 。

B七、图示结构中，AB 为刚体，杆1、杆2、杆3的材料和横截面面积均相同，在杆AB 的中点C 作用铅垂方向的载荷F，试计算C 点的水平位移和铅垂位移。

已知：kN 20=F ，2321mm 100====A A A A ，mm 1000=l ，GPa 200=E 。

八、设横梁ABCD为刚体。

横截面面积为2mm 36.76的钢索绕过无摩擦的滑轮。

设kN 20=P ，试求钢索内的应力和C九、图示结构中，AB 为刚体，1、2杆的抗拉（压）刚度均为EA 。

试求两杆的轴力。

十、图示杆系的两杆同为钢杆，GPa200=E，C 061105.12-⨯=α。

两杆的横截面面积同为2cm 10=A 。

若AC 杆的温度降低C 200，而AB 杆的温度不变，试计算两杆的轴力。

十一、图示支架中的三根杆件材料相同，杆1的横截面面积为2mm 200，杆2的横截面面积为2mm 300，杆3的横截面面积为2mm 400。