小学奥数有余数的除法专题培训课件
- 格式:ppt
- 大小:145.50 KB
- 文档页数:16


课件contents•引入与概念•运算方法与步骤目录•实例分析与计算•应用场景与拓展•练习题与答案解析引入与概念01如何分配物品,使得每个人得到的数量不同?在日常生活中,遇到不能整除的情况怎么办?有余数除法在实际问题中的应用有哪些?引入问题有余数除法定义有余数除法的概念两个整数相除,不能整除时,商为整数,余数为非零整数的除法运算。
余数的定义在整数除法中,被除数减去除数与商的乘积后所得的数。
有余数除法表示方法a ÷b =c …… r,其中a为被除数,b 为除数,c为商,r为余数。
无余数除法中,被除数能被除数整除,商为整数;有余数除法中,被除数不能被除数整除,商为整数,余数为非零整数。
结果差异无余数除法满足结合律和交换律;有余数除法不满足这些运算性质。
运算性质无余数除法常用于等分、计算比例等问题;有余数除法常用于解决分配、周期等问题。
应用场景与无余数除法区别运算方法与步骤02将被除数、除数和商按照竖式格式排列。
列竖式如果余数大于除数,说明试商偏小,需要调大;如果余数小于除数,说明试商偏大,需要调小。
调整根据被除数和除数的大小,估计一个接近的商。
试商将试商与除数相乘,得到积。
相乘将被除数减去积,得到余数。
相减0201030405竖式运算方法运算步骤详解观察被除数和除数的大小关系,确定商的位数。
从被除数的最高位开始,依次与除数相除,得到每一位的商和余数。
将每一位的商相加,得到最终的商。
根据被除数的最高位和除数的最高位进行试商,确定商的最高位。
010204注意事项在列竖式时,要保证被除数、除数和商的位数对齐。
在试商时,要根据被除数和除数的大小关系进行估计,避免过大或过小的试商。
在相乘和相减时,要注意运算顺序和符号问题。
在得到最终的商后,要检查余数是否为零,以确保运算的正确性。
03实例分析与计算03例子1:23 ÷5 = 4...3计算过程:23 -5 ×4 = 3被除数为17,除数为3,商为5,余数为2。


有余数的除法课件完整版•有余数除法基本概念•有余数除法运算规则•有余数除法性质探讨•有余数除法在实际问题中应用目录•课程总结与回顾除法与有余数除法定义除法定义除法是四则运算之一,已知两个因数的积与其中一个非零因数,求另一个因数的运算,叫做除法。
有余数除法定义在整数除法中,除数除以被除数,商为整数而余下的部分,称为余数。
有余数的除法就是指在除法算式中,除不尽的情况。
余数产生原因及意义余数产生原因在整数除法中,由于除数和被除数都是整数,当被除数不能被除数整除时,就会产生余数。
余数意义余数在数学中有着重要的意义,它可以表示除法运算后的剩余部分,也可以用来判断一些数学问题的解是否存在。
生活中有余数除法实例分配物品当需要将一定数量的物品平均分给若干个人时,如果物品数量不能被人数整除,就会产生余数。
时间计算在计算时间时,由于时间的单位是60进制,当进行除法运算时,很容易产生余数。
周期性现象在自然界和社会生活中,有很多周期性现象,如一年四季、一周七天等。
当这些周期性现象进行除法运算时,也可能会产生余数。
数学符号表示方法除法符号除法可以用符号“÷”表示,也可以用分数形式表示,如a÷b或a/b。
余数符号在数学中,余数通常用符号“r”表示,如a÷b=q……r,其中a表示被除数,b 表示除数,q表示商,r 表示余数。
被除数、除数、商和余数关系被除数=除数×商+余数这是有余数除法的基本公式,表示被除数可以被分解为除数乘以商再加上余数。
除数、商和余数的确定在有余数的除法中,除数和商都是根据被除数和除法运算规则来确定的,而余数则是被除数除以除数后剩余的数。
写出竖式确定商计算余数检查结果竖式计算方法步骤01020304将被除数、除数、商和余数按照竖式格式写出来,方便计算。
根据被除数和除数的大小关系,确定商的大小。
用被除数减去商乘以除数的积,得到余数。
检查竖式计算的结果是否正确,特别是商和余数的位置是否写错。





优质课件•课程介绍与目标•有余数除法基本概念•有余数除法计算方法•有余数除法在生活中的应用目录•练习题与课堂互动环节•课程总结与拓展延伸课程介绍与目标课件背景及目的知识与技能过程与方法情感态度与价值观030201教学目标与要求教学内容与方法教学内容教学方法有余数除法基本概念有余数除法定义0102除法算式各部分名称被除数余数除数商除法运算中被另一个数所除的数,是被除数。
被除数除以除数所得的结果叫做商,如24÷8=3举例说明有余数除法例子1例子2有余数除法计算方法逐步逼近法从高位开始试商,逐步逼近准确值,直到找到合适的商为止。
估算试商法通过估算被除数与除数的商,得到一个近似值,作为试商的起点。
折半试商法当被除数的前几位与除数相除时,若余数小于除数的一半,则商为0或1;若余数大于或等于除数的一半,则商为除数或被除数的下一位数字。
试商方法增减调整法倍数调整法分数调整法直接观察法通过观察被除数与除数的运算过程,直接得出余数。
运算求余法通过计算被除数与除数的乘积再减去被除数,得到余数。
公式求余法根据除法运算的公式,将被除数和除数代入公式进行计算,得出余数。
有余数除法在生活中的应用生活中常见问题类型周期问题分配问题某些现象或事件按照固定的周期循环出现,需要计算特定周期内的事件次数。
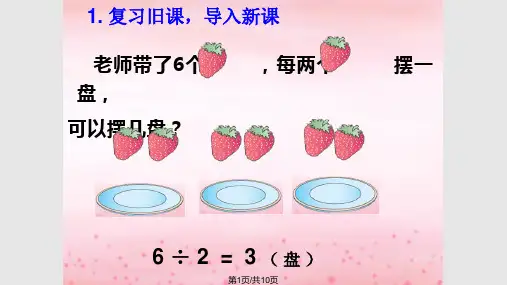
图形与几何问题解析17÷5=3…2,每个小朋友能得到还剩2个。
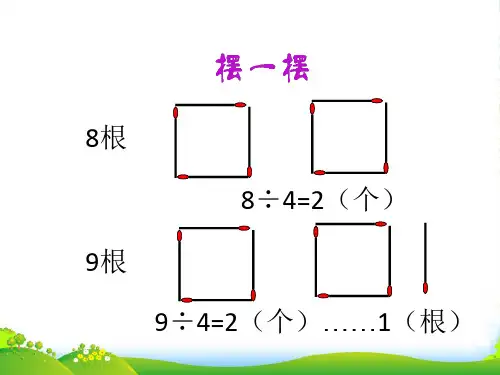
解析解析去掉中间一个小正方形后,剩下正方形。
可以拼成4个小正方形组成。
分配问题举例个小朋友,每个小朋友能得到几个苹果,还剩几个?周期问题举例图形与几何问题举例个相同的小正方形,如果去掉中间的一个小正方形,剩下的部分能拼成几个长方形?010203040506应用举例与解析明确余数在实际问题中的含义和作用,如分配问题中的剩余数量、周期问题中的额外天数等。
理解有余数除法的意义掌握基本计算方法灵活运用数学知识加强实践应用训练熟练掌握有余数除法的计算方法,包括商和余数的确定、不同进制下的计算等。