圆柱和圆锥体积中的典型题 等积变形
- 格式:ppt
- 大小:139.50 KB
- 文档页数:5
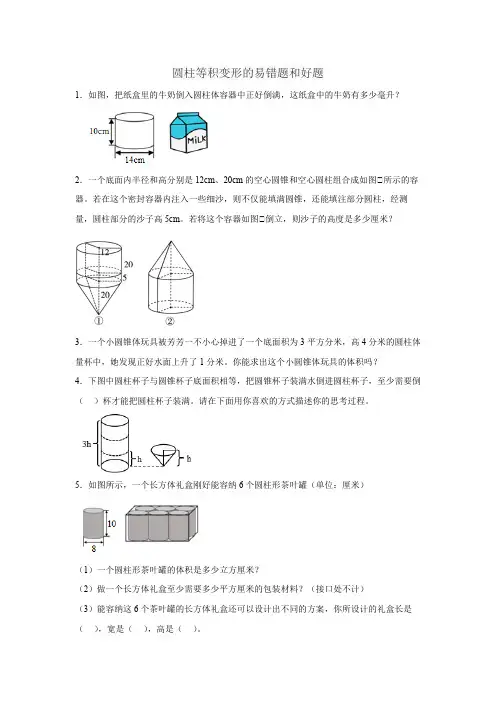
圆柱等积变形的易错题和好题1.如图,把纸盒里的牛奶倒入圆柱体容器中正好倒满,这纸盒中的牛奶有多少毫升?2.一个底面内半径和高分别是12cm、20cm的空心圆锥和空心圆柱组合成如图①所示的容器。
若在这个密封容器内注入一些细沙,则不仅能填满圆锥,还能填注部分圆柱,经测量,圆柱部分的沙子高5cm。
若将这个容器如图①倒立,则沙子的高度是多少厘米?3.一个小圆锥体玩具被芳芳一不小心掉进了一个底面积为3平方分米,高4分米的圆柱体量杯中,她发现正好水面上升了1分米。
你能求出这个小圆锥体玩具的体积吗?4.下图中圆柱杯子与圆锥杯子底面积相等,把圆锥杯子装满水倒进圆柱杯子,至少需要倒()杯才能把圆柱杯子装满。
请在下面用你喜欢的方式描述你的思考过程。
5.如图所示,一个长方体礼盒刚好能容纳6个圆柱形茶叶罐(单位:厘米)(1)一个圆柱形茶叶罐的体积是多少立方厘米?(2)做一个长方体礼盒至少需要多少平方厘米的包装材料?(接口处不计)(3)能容纳这6个茶叶罐的长方体礼盒还可以设计出不同的方案,你所设计的礼盒长是(),宽是(),高是()。
6.一个底面半径是10厘米的圆柱形玻璃杯,原来水深15厘米,现在把一块长和宽都是8厘米,高是42厘米的长方体铁块垂直放入水中,水没有溢出,求水面上升了多少厘米?7.袁隆平爷爷,世界上第一个成功利用水稻杂交优势的科学家,被誉为“杂交水稻之父”,发展杂交水稻,造福世界人民是袁降平院士毕生的追求。
目前,我国杂交水稻年种植积约2.57亿亩,非杂交水稻年种植面积约1.94亿亩,2020年我国稻谷总产量约为120亿千克,其中杂交水稻产量与非杂交水稻产量的比为13①7,杂交水稻每年增产的稻谷,可为中国多养活8000万人。
(1)2020年杂交水稻产量约多少亿千克?,那么问题为___________________。
(2)根据上面的信息,如果列式为1.94 2.57(3)如下图,已知圆锥形谷堆的底面直径是圆柱形铁桶底面直径的2倍,它们的高一样,把这些稻谷装在铁桶中(铁桶厚度忽略不计),装得下吗?请把你的想法写下来。


人教版数学六年级下册第三单元《圆柱与圆锥》“等积变形”教学预案永川区望城路小学何开莲教材分析数学六年级下册第三单元《圆柱与圆锥》是整个小学阶段最后一个“几何与图形”的内容。
包括圆柱圆锥的认识、圆柱的表面积、圆柱的体积和圆锥体积。
圆柱、圆锥是人们在生产、生活中经常遇到的几何形体。
教学这一部分内容,有利于发展学生的空间观念,为进一步应用几何知识解决实际问题打下基础。
几何知识一向是小学生学习的难点。
特别是圆柱的表面积、圆柱圆锥体积的应用问题更是让学生忘而却步。
造成这种现象的原因除了计算复杂繁琐外,就是学生对立体图形的空间思维能力差。
不能根据文字叙述想象立体图形的样子,找不到解题的关键。
我的思考本次教研主题是“提高立体图形空间思维能力”。
围绕这个主题,我确定从“等积变形”思想方法来落实。
“等积变形”是小学阶段要渗透落实的重要思想方法之一。
生活中大量存在其身影。
在实际生活中有些物质如金属、橡皮泥、或装在容器里的液体等,可以通过熔铸、锻造、重塑或更换容器等改变原来的形状,在这个变换的过程中物体的形状发生了变化,体积不变,这就是形体的“等积变形”。
围绕“等积变形”,我设计“面积变形”和“体积变形(重点)”两个内容。
“面积变形”是为了使计算简便。
“体积变形”设计为稍复杂的体积变形:不规则物体体积计算(看图计算)和未完全浸没(解决问题)。
利用“化曲为直”、“动画重现”“割补剪拼”、“移花接木”“数形结合”等方式,让学生体会转化思想在数学中的广泛应用,提高学生的立体图形空间观念。
教学目标1.优化圆柱体表面积计算公式,能够解决稍复杂的体积的“等积变形”问题。
2.在不同情境中,找准“形变”与“体积不变”的关系,在变化中找不变的量,抓住解决问题的关键,从而正确解决实际问题。
3.发展空间观念,提高学生立体图形空间思维能力。
体会转化的思想价值。
教学重、难点重点:运用多种方法通过“等积变形”解决实际问题。
难点:在不同题目情境中,找准不变的量,抓住“等积”这一解题关键。


圆柱与圆锥的等体积变化练习题一、填空。
1、 一个圆柱和一个圆锥等底等高。
已知圆柱的体积是9立方米,圆锥的体积是(3)立方米。
2、 一个圆锥的体积是1.2立方分米,和它底面直径相等,高也相等的圆柱的体积是(3.6)立方分米。
二、选择。
1、 把一个圆柱形状的木块切削成一个和它等底等高的圆锥形状的木块。
削掉的部分是这个圆柱体积的(B )A .31 B. 32 C.3倍 2、一个圆柱和一个圆锥体积相等,底面积也相等。
如果圆柱的高是2.4厘米,那么圆锥的高是(A )厘米。
A.7.2B.2.4C.0.83、把一个棱长为4厘米的正方体铸件切削成尽可能大的圆柱形状的机器零件。
这个零件的体积是(B)立方厘米。
A.5.024B.50.24C.200.96三、解决问题。
1、一个圆锥形麦堆,底面周长是25.12米,高3米。
把这些小麦装入一个底面直径是4米的圆柱形粮囤内,正好装满。
这个粮囤的高是多少米?(25.12÷3.14÷2)²×3.14×3÷3=50.24(m³)50.24÷((4÷2)²×3.14)=4(m)答:这个粮囤的高是4m。
2、一个底面直径为20厘米的圆柱形的玻璃杯装有一些水,水中放着一个底面直径为6厘米、高20厘米您的圆锥形铅锤。
当取出铅锤后,杯里的水下降几厘米?(6÷2)²×3.14×20=565.2(cm³)3、把50个底面直径都是30厘米,高20厘米的圆锥形钢坯,熔铸成一根底面直径是60厘米的圆柱形钢材。
求钢材长多少厘米?4、一个圆锥形的沙堆的沙堆,底面积是12.56平方米,高是1.2米。
用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?。




巧解等积变形题
作者:唐擘
来源:《数学小灵通·5-6年级》2015年第04期
[题目一]如图1所示,一个底面直径是10cm的圆柱形容器装满水,先将一个底面直径是8cm的圆锥形铁块放入容器中,铁块全部浸入水中,再将铁块取出,这时水面的高度下降了3.2cm。
则圆锥形铁块高 cm。
(第十二届小学“希望杯”全国数学邀请赛六年级第1试第15题)我是这样解的
取出铁块后,圆柱里的水面下降了3.2 cm,说明圆锥形铁块的体积是л( 10÷2)z×3.2。
已知圆锥形铁块的底面直径是8cm,那么它的底面积就是这时由圆锥的体积计算公式可
[题目二]用底面内半径和高分别是12cm、20cm的空心圆锥和空心圆柱各一个组合成如图2所示竖放的容器。
在这个容器内注入一些细沙,能填满圆锥,还能填部分圆柱,经测量,圆柱部分的沙子高5cm。
若将这个容器倒置,则沙子的高度是____cm。
(第十一届小学“希望杯”全国数学邀请赛六年级第1试第9题)我的方法很巧妙
因为空心圆锥和空心圆柱等底等高,所以空心圆锥里沙子的体积是空心圆柱容积的。
由此可知,将圆锥里的沙子倒入圆柱后的高度是20×31=62(cm)。
进而可知,若将这个容器倒置,则沙子的高度是62+5=112(cm)。
“数学漫画”参考答案既爱吃萝卜又爱吃青菜的小兔子有4只。

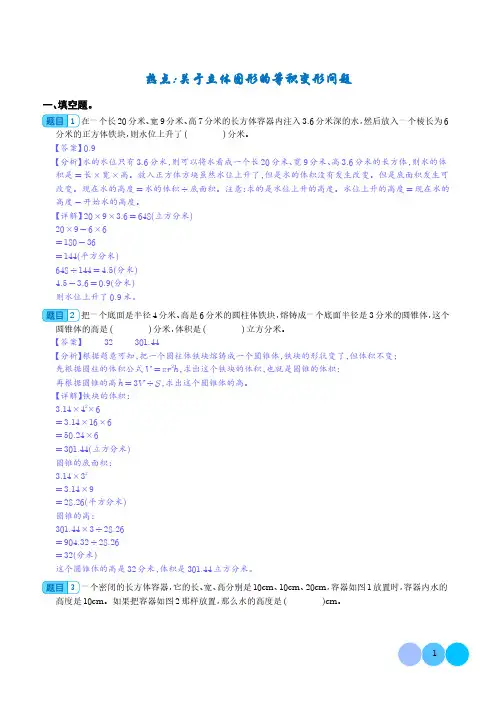
热点:关于立体图形的等积变形问题一、填空题。
1在一个长20分米、宽9分米、高7分米的长方体容器内注入3.6分米深的水,然后放入一个棱长为6分米的正方体铁块,则水位上升了()分米。
【答案】0.9【分析】水的水位只有3.6分米,则可以将水看成一个长20分米、宽9分米、高3.6分米的长方体,则水的体积是=长×宽×高。
放入正方体方块虽然水位上升了,但是水的体积没有发生改变。
但是底面积发生可改变。
现在水的高度=水的体积÷底面积。
注意:求的是水位上升的高度。
水位上升的高度=现在水的高度-开始水的高度。
【详解】20×9×3.6=648(立方分米)20×9-6×6=180-36=144(平方分米)648÷144=4.5(分米)4.5-3.6=0.9(分米)则水位上升了0.9米。
2把一个底面是半径4分米、高是6分米的圆柱体铁块,熔铸成一个底面半径是3分米的圆锥体,这个圆锥体的高是()分米,体积是()立方分米。
【答案】32301.44【分析】根据题意可知,把一个圆柱体铁块熔铸成一个圆锥体,铁块的形状变了,但体积不变;先根据圆柱的体积公式V=πr2h,求出这个铁块的体积,也就是圆锥的体积;再根据圆锥的高h=3V÷S,求出这个圆锥体的高。
【详解】铁块的体积:3.14×42×6=3.14×16×6=50.24×6=301.44(立方分米)圆锥的底面积:3.14×32=3.14×9=28.26(平方分米)圆锥的高:301.44×3÷28.26=904.32÷28.26=32(分米)这个圆锥体的高是32分米,体积是301.44立方分米。
3一个密闭的长方体容器,它的长、宽、高分别是10cm、10cm、20cm,容器如图1放置时,容器内水的高度是10cm。
形体的等积变形
把一个圆锥状油泥块,经过揉搓之后可变成一个圆柱或一个长方体,无论它的形状如何变化,它们的体积大小是恒等不变的,这就是等积变形。
例题:如图所示,一个底面直径为20厘米的装有一部分水的圆柱形容器, 水中放着一个底面直径为12厘米、高为10厘米的圆锥体铅锤,当铅锤从水中取出后,容器中水面高度下降了几厘米?
[思路]铅锤取出后,水面就会下降,下降的体积与圆锥状铅锤的体积相同,这样依据等积变形的方法可知水的体积,从而可求得水面高度变化的情况。
[详解]铅锤的体积为 )立方厘米(8.3761021214.3312
=⨯⎪⎭
⎫ ⎝⎛⨯⨯ 圆柱体的底面积为()平方厘米31422014.32=⎪⎭
⎫ ⎝⎛⨯ 所以水面下降的高度为376.8÷314=1.2(厘米)
答:容器中水面高度下降了1.2厘米。
[诀窍]形体的等积变形的解题关键是确定两个体积相等的物体,或两个体积相等的部分,从而从体积相等中推算出另一个物体或部分的底或高。
A 用直径为20厘米的圆钢,锻造成长、宽、高分别为30厘米、20厘米、5厘米的长方体钢板,应截取圆钢多长?(精确到0.1厘米)
B 、把一块长15.7厘米、宽8厘米、高5厘米的长方体铝锭,和一块底面直径6厘米、高24厘米的圆柱形铝块,熔铸成一个底面半径为8厘米的圆锥形铝块,求这个圆锥形铝块高是多少厘米?。
奥数等积变形题目一、一个长方体水箱,长、宽、高分别为3米、2米、1米。
若将其变形为正方体,且体积保持不变,则正方体的边长为多少米?A. 1米B. 2米C. 3米D. 根号6米(答案)B二、有一个圆柱体,底面半径为2厘米,高为5厘米。
若将其等体积变形为圆锥体,且底面半径保持不变,则圆锥体的高为多少厘米?A. 5厘米B. 10厘米C. 15厘米D. 20厘米(答案)C三、一个正方体纸盒,棱长为4厘米。
若将其等体积变形为长方体,且新长方体的长、宽、高均为整数,则新长方体的可能的长、宽、高组合为?A. 1厘米、2厘米、8厘米B. 2厘米、2厘米、4厘米C. 1厘米、4厘米、4厘米D. 3厘米、3厘米、3厘米(答案)A四、有一个圆锥体,底面半径为3厘米,高为4厘米。
若将其等体积变形为圆柱体,且圆柱体的高为2厘米,则圆柱体的底面半径为多少厘米?A. 3厘米B. 4厘米C. 5厘米D. 6厘米(答案)A五、一个长方体水槽,长、宽、高分别为6分米、4分米、2分米。
若将其等体积变形为正方体水槽,则新水槽的表面积比原水槽的表面积减少了多少平方分米?A. 16平方分米B. 32平方分米C. 48平方分米D. 64平方分米(答案)C六、一个圆柱体,底面半径为1厘米,高为10厘米。
若将其等体积变形为圆锥体,且圆锥体的高保持不变,则圆锥体的底面半径为多少厘米?A. 1厘米B. 根号3厘米C. 2厘米D. 3厘米(答案)B七、有一个正方体,棱长为5厘米。
若将其切割成若干个小正方体,且小正方体的棱长均为整数,这些小正方体的体积之和最大为多少立方厘米?(小正方体可以大小不同)A. 125立方厘米B. 100立方厘米C. 75立方厘米D. 50立方厘米(答案)A八、一个圆锥体,底面半径为4厘米,高为6厘米。
若将其等体积变形为圆柱体,且圆柱体的底面半径为2厘米,则圆柱体的高为多少厘米?A. 6厘米B. 8厘米C. 12厘米D. 24厘米(答案)D。
等积变形法等积变形法是指几何形体的形状发生变化后,变化后的物体和原物体相比较,体积与原来相等。
练习:1、一个圆柱形铁块的底面半径是10厘米,高是5厘米,把它熔铸成一个底面积是157平方厘米的圆锥形铁块,圆锥形铁块的高是多少厘米?2、一个圆锥形的沙堆,底面积是12.56平方米,高是6米。
用这堆沙在10米宽的公路上铺20厘米厚的路面,能铺多少米长?3、一个圆锥形的麦堆,底面半径为2米,高1.5米,如果把这些小麦装入一个圆柱形粮囤里,只占粮囤容积的94。
已知粮囤底面积是9平方米,粮囤的高是多少米?4、将一个底面半径是20厘米,高是27厘米的圆锥形铝材和一个底面半径是30厘米,高是20厘米的圆柱形铝材熔铸成一个底面半径是15厘米的圆柱形铝材,这个圆柱形铝材的高是多少厘米?5、一个圆柱形容器与一个圆锥形容器的底面积都是15平方厘米,用圆锥形容器盛水倒入圆柱形容器中,4次正好装满。
已知圆锥形容器的高是9厘米,圆柱形容器的高是多少?6、把一块长为18.84厘米,宽为8.4厘米,高为6厘米的长方体铝块和一块底面直径为8.4厘米,高为10厘米的圆柱形铝块,熔铸成一个底面半径为4.2厘米的圆锥形铝块,这块圆锥形铝块的高是多少厘米?不规则物体体积的计算方法1、一个圆柱形量杯,底面直径是10厘米,杯中浸没一块不规则的铁块,当铁块取出时,水面下降了4厘米,这块铁块的体积是多少立方厘米?2、在一个圆柱形水桶里,把一段底面是5厘米的圆柱形钢材全部放入水中,水面就上升9厘米。
把圆柱形钢材竖着拉出水面8厘米长后,水面就下降4厘米。
这个圆柱形钢材的体积是多少?3、如下图,a、b是两个棱长为8厘米的正方体盒子。
a盒中放入一个直径为8厘米、高为8厘米的圆柱形铁块,b盒中放入四个直径为4厘米、高为8厘米的圆柱形铁块。
现在把两个盒子注满水,哪个盒子中的水多?。
人教版六年级数学下册第三单元专项训练《等积变形》(含答案)1.把一个圆柱底面平均分成若千个扇形,沿高切开拼成一个近似长方体。
这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?2.把一个棱长是8分米的正方体铁块熔铸成一个底面直径是10分米的圆柱,这个圆柱的高大约是多少?(得数保留一位小数)3.一个圆柱形水池装满水,它的底面积是12.56平方米,深3米,将水池的水全部倒入一个长8米、宽3米、深2米的长方体水池,长方体的水面高是多少米?4.把一个棱长8分米的正方体木块加工成一个最大的圆柱,圆柱的体积是多少立方分米?5.一个圆柱体,如果把它的高截短2厘米,它的表面积就减少94.2平方厘米,这个圆柱体的体积减少多少立方厘米?6.将一个底面直径是20厘米,高为12厘米的金属圆锥体,全部浸没在直径是20厘米的圆柱形水槽中,水槽水面会升高多少厘米?7.一个圆锥形沙堆,底面积12.56平方米,高1.2米。
用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?8.一个圆锥形沙堆,底面积是24平方米,高是1.8米。
用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?9.把一个长、宽、高分别是7厘米、3厘米、9厘米的长方体铁块和一个棱长是5厘米的正方体铁块,熔铸成一个底面直径是10厘米的圆柱,这个圆柱的高是多少?10.机灵狗有一块体积是753.6立方厘米的绿色橡皮泥,它用这块橡皮泥捏成了等底等高的一个圆柱体和一个圆锥体。
则这个圆柱体体积是多少立方分米?11.在底面半径为5厘米、高为18厘米的圆柱形玻璃缸中,放入一个底面半径3厘米、高为10厘米的圆锥形铅块,放水将铅块全部淹没。
当铅块取出后,玻璃缸中的水面下降了多少厘米?12.学校的跳远沙池长6.28米,宽2米,学校运来一堆沙子(堆放如图)。
如果把这些沙子均匀地铺在跳远沙池中,可以铺多厚?13.把一个棱长6分米的正方体木块削成一个最大的圆锥,需要削去多少立方分米的木头?14.把一个长是10厘米,宽和高都是5厘米的长方体铁块和一个棱长是4厘米的正方体铁块,一起熔铸成一个底面周长是314厘米的圆柱。