第13章习题分析
- 格式:doc
- 大小:1.65 MB
- 文档页数:13

第13章时间序列分析和预测13.1 考点归纳【知识框架】【考点提示】(1)时间序列构成要素及平稳序列、非平稳序列的含义(简答题考点);(2)时间序列的描述性分析(简答题、计算题考点);(3)平稳序列的预测,重点是移动平均法、一次平滑指数法(选择题、简答题、计算题考点)。
【核心考点】考点一:时间序列1.成分分解表13-1 时间序列的成分2.分解模型表13-2 时间序列构成因素的组合模型【注意】四种因素不一定同时存在于每个时间序列中。
一般情况下,经常存在的是长期趋势,季节变动因素和周期变动因素则不一定存在。
3.平稳序列与非平稳序列(1)平稳序列平稳序列是基本上不存在趋势的序列。
这类序列中的观察值基本上在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,其波动可以看成是随机的。
(2)非平稳序列非平稳序列是包含趋势、季节性或周期性的序列,它可能只含有其中的一种成分,也可能是几种成分的组合。
其又可以分为有趋势的序列、有趋势和季节性的序列、几种成分混合而成的复合型序列。
考点二:时间序列的描述性分析1.速度分析指标(1)增长率环比增长率:G i =(Y i -Y i -1)/Y i -1=Y i /Y i -1-1(i =1,…,n )定基增长率:G i =(Y i -Y 0)/Y 0=Y i /Y 0-1(i =1,…,n )式中,Y 0表示用于对比的固定基期的观察值。
(2)平均增长率(平均增长速度)111n n Y G Y -=⨯⨯-=- 式中,G _表示平均增长率;n 为环比值的个数。
(3)增长率分析中应注意的问题①当时间序列中的观察值出现0或负数时,不宜计算增长率,此时直接用绝对数进行分析;②增长1%的绝对值表示增长率每增长一个百分点而增加的绝对数量,其计算公式为:增长1%的绝对值=前期水平/100。
2.水平分析指标【考点拓展】表13-3考点三:平稳序列的预测1.简单平均法112111()t t t i i F Y Y Y Y t t +==+++=∑ 12121111()11t t t t i i F Y Y Y Y Y t t +++==++++=++∑2.移动平均法对于t+1期的简单移动平均预测值为:F t+1=Y_t=(Y t-k+1+Y t-k+2+…+Y t-1+Y t)/k【注意】移动平均后的序列项数较原序列减少,当k为奇数时,新序列首尾各减少(k -1)/2项;当k为偶数时,首尾各减少k/2项。

第十三章双变量关联性分析【思考与习题】一、思考题1.两变量间的关联性是否可解释为因果关系2.2⨯2列联表的关联性分析与两样本率比较的2χ检验有何不同3.相关系数r经假设检验有统计学意义,且得到的P值很小,是否表示两变量间一定有很强的直线关系4.简述Pearson积矩相关与Spearman秩相关的区别与联系。
二、案例辨析题为研究年龄与牙齿AKP酶反应活性之间的关系,某医生在其接诊的患者中随机抽取281例,按年龄(岁)分为三组进行观测,测量各患者牙齿的AKP酶反应活性,如表13-1所示。
问年龄与牙齿AKP酶反应活性之间有无关系表13-1 281例患者年龄与牙齿AKP酶反应活性的分布年龄AKP酶反应活性合计—+++<31517365831~234549051~249712133合计31148102 281按照R×C表的2χ检验结果,得2χ=,005.0<P,故按α=水准,拒绝H,可认为不同年龄患者的AKP酶反应活性不同,两者之间有关系。
以上分析正确吗三、最佳选择题1.Pearson积矩相关系数的假设检验,其自由度为A.1-nB.2-nC .12-nD .)1(2-nE .n2.积矩相关系数的计算公式是 A .xy xy yyl r l l =B.r =C.l r =D.l r =E.r =3. 直线相关分析中,若0.05,||r r ν>,则可认为两变量之间 A. 有一定关系B. 不存在直线相关关系C. 有直线相关关系D. 有直线相关关系,且为正相关E. 有直线相关关系,且为负相关 4.下列指标中可正可负的是 A .F 统计量 B .2χ统计量 C .21()nxx i l x x ==-∑D .1()()nxy i l x x y y ==--∑E .21()nyy i l y y ==-∑5.研究18岁女大学生体重和肺活量的关系时,表达正确的无效假设是 A .体重与肺活量无关联 B .体重与肺活量有关联 C .体重与肺活量有直线关系 D .体重与肺活量有因果关系 E .体重与肺活量无因果关系 6.计算Pearson 列联系数的公式为 A.l r =B .nr +=22χχC .22χχnr +=D .12-=n r χE .nr +=22χχ7.某放射科医师收集脑外伤患者30例,观察脑出血直径和病人昏迷的程度(轻度、中度、重度),欲分析昏迷程度是否与病灶大小有关,可进行 A .Pearson 相关分析 B .Spearman 秩相关分析 C .两小样本比较的t 检验 D .方差分析 E .2χ检验8.对两个分类变量的频数表资料作关联性分析,可用 A .积矩相关或等级相关B .积矩相关或列联系数C .列联系数或等级相关D .积矩相关E .等级相关9.两组数据分别进行直线相关分析,对1r 进行假设检验得到P <,对2r 进行假设检验,得到P <,可以认为A .第一组的两个变量关系比第二组密切B .第二组的两个变量关系比第一组密切C .更有理由认为第一组的两个变量之间有直线关系D .更有理由认为第二组的两个变量之间有直线关系E .两组变量关系同样密切四、综合分析题1.为研究某病成年男性患者血浆清蛋白含量与血红蛋白含量的关系,某医生测得10名患者血浆清蛋白含量(g/L)及血红蛋白含量(g/L)见表13-2所示,试分析二者是否有关联。


第十三章《国际战略和外交政策》习题一、单项选择题1、和平共处五项原则由()最先提出A、毛泽东 B 、周恩来C、乔冠华2、在我国外交政策上,确定“真正的不结盟”战略的是()A、毛泽东B、邓小平C、江泽民3、和平共处五项原则的精髓是()A、国家主权平等B、互不侵犯C、互不干涉内政4、我国对外政策的立足点是():A、独立自主B、发展与大国关系C、加强同发展中国家的团结与合作5、威胁世界和平稳定的主要根源是()A、贫穷B、水资源缺乏C、霸权主义和强权政治6、当今世界的核心问题是()A、和平与发展 B 、霸权主义C、第三世界7、中国外交政策的宗旨是()A、维护世界和平,促进共同发展B、反对霸权主义C、实现人类的解放8、中国外交政策的崇高目标是()A、提高中国的国际地位B、维护世界和平,促进人类共同繁荣和发展C、实现人类的解放9、1974年毛泽东提出了三个世界划分的战略。
他指出,亚洲除了(),都是第三世界。
A、日本B、中国C、韩国10、在世界格局多极化与单边主义的斗争中,关键因素是()A、军事力量B、经济技术C、政治力量11、经济全球化在本质上是()的跨国流动。
A、资本B、人才C、货物12、不论在理论上还是在实践上,人权的保护责任,主要还是由()来承担的A、大国B、主权国家的政府C、国际组织13、在处理国际关系和外交关系方面,我国坚持的外交工作布局是:A、大国是首要,周边是关键,发展中国家是基础,多边是舞台B、大国是关键,周边是首要,发展中国家是基础,多边是舞台C、大国是关键,发展中国家是首要,周边是基础,多边是舞台14、当今世界的核心问题是()A、和平B、发展C、世界多极化D、经济全球化15、和平共处五项基本原则中的核心和最重要原则是()A、互相尊重主权和领土完整B、互不侵犯C、互不干涉内政D、平等互利、和平共处16、我国对外政策的根本原则是()A、和平共处B、不干涉他国内政C、独立自主D、发展经济17、世界和平与发展的主要障碍()A、贫富差距B、民族矛盾C、宗教问题D、霸权主义和强权政治18、处理国与国之间关系的最好方式是()A、大家庭方式B、和平共处五项原则C、集团政治方式D、势力范围方式二、多项选择题1、和平共处五项原则的是()A、互相尊重主权和领土完整B、互不侵犯C、互不干涉内政D、平等互利E、和平共处2、坚持独立自主的和平外交政策包含着哪些内容()A、反对霸权主义B、维护世界和平C、独立自主D、和平共处五项原则3、和平与发展这两大主题至今一个都没有解决,天下仍不太平。

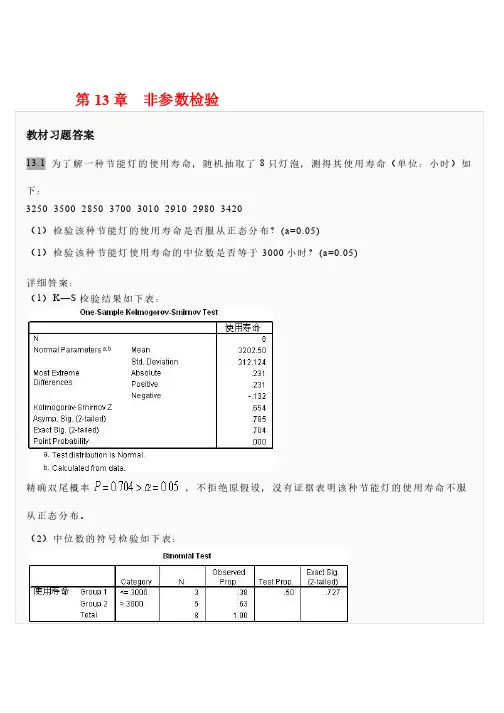
第13章非参数检验教材习题答案13.1 为了解一种节能灯的使用寿命,随机抽取了8只灯泡,测得其使用寿命(:小时时)如命(单单位:小下:3250 3500 2850 3700 3010 2910 2980 3420 (1)检验该种节能灯的使用寿命是否服从正态分布?(a=0.05) (1)检验该种节能灯使用寿命的中位数是否等于3000小时?(a=0.05) 详细答案:(1)K—S检验结果如下表:精确双尾概率,不拒绝原假设,没有证据表明该种节能灯的使用寿命不服从正态分布。
(2)中位数的符号检验如下表:精确的双尾概率为,不拒绝原假设,没有证据表明该种节能灯的使用寿命的实际中位数与3000有显著差异。
13.2 利用13.1题的数据,采用Wilcoxon符号秩检验该种节能灯使用寿命的中位数是否等于3000小时?(a=0.05) 详细答案:检验结果如下表精确的双尾概率,不拒绝原假设。
没有证据表明该种节能灯的使用寿命的实际中位数与3000有显著差异。
13.3 为分析股票的每股收益状况,在某证券市场上随机抽取10只股票,得到2005年和2006股收益年的每股收益数据如下表,采用Wilcoxon符号秩检验分析:2007年与2006年相比,每,每股是否有显著提高?(a=0.05) 股票代码2006年每股收益(元)2007年每股收益(元)1 0.12 0.26 2 0.95 0.87 3 0.20 0.24 4 0.02 0.12 5 0.05 0.13 6 0.56 0.51 7 0.31 0.35 8 0.25 0.42 9 0.16 0.37 10 0.06 0.05 详细答案:配对样本的Wilcoxon符号秩检验如下表:精确的单尾,拒绝,2006年与2005年相比每股收益有显著提高。
13.4 某种品牌的彩电在两个城市销售,其中在A城市有6个商场销售,在B城市有8个商场销售,下表是各商场一年的销售量(单位:台)。

第十三章 详析分析与偏相关练习题:1.一学者研究了青年人的文化程度与社区参与的关系,获得下表13-4的数据, 为了进一步分析两者之间的关系,研究者引进了性别变量,获得表13-5的数据。
表13-4 文化程度与社区参与的关系社区参与 文化程度合计 高 低 高 145 78 223 中 97 80 177 低 58 102 160 合计300260560表13-5 控制性别后文化程度与社区参与的关系男女根据上面两表计算:(1)根据表13-4计算青年人的受教育程度与社区参与的相关系数Gamma 。
(2)计算表13-5各分表的Gamma 值,并与表13-1的结果进行比较。
(3)计算偏相关系数。
(4)根据所得到的结果作出研究结论。
解:(1)同序对:N s =145×(80+102)+97×102=36284异序对:N d =78×(97+58)+80×58=1673036284167300.3683628416730s d s d N N G N N --===++ 这一结果说明青年人文化程度越高,其社区参与程度越高,或者说,根据青年人的文化程度来预测社区参与程度时可以减少36.8%的误差。
(2)根据计算同序对与异序对的方法,可得:男:同序对:N s1=80×(25+70)+40×70=10400异序对:N d1=45×(40+28)+25×28=3760111111040037600.469104003760s d s d N N G N N --===++女:同序对:N s2=65×(55+32)+57×32=7479异序对:N d2=33×(57+30)+55×30=452122222747945210.24774794521s d s d N N G N N --===++与(1)的计算结果相比可知:○1在男性青年人中,依据文化程度来预测其社区参与程度可以减少47%的误差,在女性青年人中,依据文化程度来预测其社区参与程度可以减少25%的误差。

人教版八年级数学上册第13章等腰三角形(讲义)➢ 课前预习1. 已知:如图,在△ABC 中,AB =AC .(1)若∠1=∠2,则BD ____DC (填“>”,“<”或“=”); (2)若BD =CD ,则AD ____BC (填“⊥”或“∥”); (3)若AD ⊥BC ,则∠1____∠2(填“>”,“<”或“=”).D CB A 212. 已知等腰三角形的两边长分别为5和8,则这个三角形的周长为_________.➢ 知识点睛1. ______________的三角形叫做等腰三角形.2. 等腰三角形是_________图形.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“__________”),它们所在的直线都是等腰三角形的_________.3. 等腰三角形的两个底角________,简称______________.如果一个三角形有两个角相等,那么它们所对的边也______,简称_________________.4. 三边都______的三角形是等边三角形.等边三角形三边都相等,三个内角都是________. 5. “三线合一”模块书写:已知:如图,在△ABC 中,AB =AC ,AD 平分∠BAC 交BC 于点D .求证:BD =CD . 证明:➢ 精讲精练1. 在下面的等腰三角形中,∠A 是顶角,请分别将它们底角的度数标注在相应的图上.CB C B C B AAA108°60°2. 如图,在△ACD 中,AD =BD =BC ,若∠C =25°,则∠ADB =____.D CB ADCBAEDCBA第2题图第3题图3. 如图,在△ABC 中,AB =AC ,BD 平分∠ABC ,BD =BE ,∠A =100°,则∠DEC =________.4. 如图,在等腰三角形ABC 中,AB =AC ,D 为边BC 上一点,CD =AC ,AD =BD ,则∠BAC =______.CD B AABCE第4题图第5题图5. 如图,在△ABC 中,AB =AC ,点D 是BC 的中点,点E 在AC 上,AD =AE ,若∠BAD =50°,则∠CDE =________.6. 如图,在△ABC 中,已知AB =AC ,AD ⊥BC 于点D ,过点D 作DE ∥AB 交AC 于点E .求证:AE =ED .7. 已知:如图,在△ABC 中,AB =AC ,点D 在△ABC 外,CD ⊥AD于点D ,12CD BC.求证:∠ACD =∠B . E CB AAB CD8. 已知:如图,△ABC 是等边三角形,D 是BC 的中点,DF ⊥AC 于F ,延长DF 到E ,使EF =DF ,连接AE .求∠E 的度数.FE DCBA9. 若等腰三角形的周长为13 cm ,其中一边长为3 cm ,则该等腰三角形的底边长为_______________.10. 若等腰三角形的一个内角为40°,则此等腰三角形的顶角为______________.11.若等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°,则此等腰三角形的顶角为______________.12.已知:如图,线段AB的端点A在直线l上(AB与l不垂直),请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请你找出所有符合条件的点.13.已知:如图,线段AB的端点A在直线l上,AB与l的夹角为60°,请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请你找出所有符合条件的点.➢课前预习1.(1)=(2)⊥(3)=2.18或21➢知识点睛1.有两边相等2.轴对称,三线合一,对称轴3.相等,等边对等角相等,等角对等边4.相等,60°5.证明:如图∵AB=AC,AD平分∠BAC∴D为BC的中点(等腰三角形三线合一)∴BD=CD➢精讲精练1.60°,60°;45°,45°;36°,36°2.80°3.100°4.108°5.25°6.证明略提示:根据等腰三角形三线合一可得∠BAD=∠CAD,再由平行可以得到∠CAD=∠BAD=∠ADE,从而AE=DE7.证明略提示:过点A作AE⊥BC于点E,根据等腰三角形三线合一可得BE=CD,再证△ABE≌△ACD即可.8.∠E=60°提示:连接AD,利用垂直平分线定理得AD=AE,从而∠E=∠ADE9.3cm10.40°或100°11.50°或130°12.这样的点能找4个,作图略13.这样的点能找2个,作图略等腰三角形(随堂测试)1.如图,在△ABC中,D为AC边上一点,且AD=BD=BC.若∠A=40°,则∠DBC=______.CDB 2.已知等腰三角形的周长为28cm,其中一边长为10cm,则该等腰三角形的底边长为_______________.3. 已知:如图,在△ABC 中,E 为BC 边上一点,连接AE ,D 为AE 的中点,连接BD ,∠BAD =∠EAC +∠C .求证:AD ⊥BD .【参考答案】1. 20°2. 10cm 或8cm3. 证明略提示:利用外角可以得到∠AEB =∠BAD ,根据等角对等边,得BA =BE ,因为D 是AE 的中点,利用等腰三角形三线合一,可以得到AD ⊥BD等腰三角形(习题)➢ 例题示范E DCB A例1:如图,在△ABC 中,AB =AC ,点D 在△ABC 外,CD ⊥AD 于点D ,12CD BC =.求证:∠ACD =∠B . 【思路分析】 ① 读题标注:② 梳理思路:由条件12CD BC =,可尝试取BC 的中点E ,此时结合等腰构造三线合一的线AE ,如图所示.要证∠ACD =∠B ,可以证明△ABE ≌△ACD .【过程书写】证明:如图,取BC 的中点E ,连接AE .∵E 是BC 的中点∴12BE BC =∵12CD BC = ∴BE =CD∵AB =AC ,E 是BC 的中点 ∴AE ⊥BC ∴∠AEB =90° ∵CD ⊥AD ∴∠D =90°∴∠AEB =∠D =90°在Rt △ABE 和Rt △ACD 中 AB AC BE CD =⎧⎨=⎩(已知)(已证)∴Rt △ABE ≌Rt △ACD (HL ) ∴∠ACD =∠B例2:等腰三角形的周长为12cm ,其中一边长为5cm ,则该等腰三角形的底边长为__________cm .【思路分析】ACDEA B C D A CD等腰三角形一边长为5cm ,这一边可能是底,也可能是腰,故需分类讨论: ① 如果5cm 为底,则根据周长为12cm ,可知腰长为3.5cm .此时两边之和大于第三边,这个三角形存在.② 如果5cm 为腰,则根据周长为12cm ,可知底边长为2cm .此时两边之和大于第三边,这个三角形存在.综上,该等腰三角形的底边长为5cm 或2cm . ➢ 巩固练习1. 已知:如图,在△ABC 中,AB =AC ,∠A =80°,求∠C 的度数.2. 如图,在△ABC 中,AB =AC ,BE ∥AC ,∠BDE =100°,∠BAD =70°,则∠E =______.第2题图第3题图3. 已知:如图,在△ABC 中,AB =AC ,D 为AB 边上一点,若CD =AD =BC ,则∠A =_________.4. 如图,在△ABC 中,∠ABC 的平分线和∠ACB 的平分线相交于点E ,过点E作MN ∥BC ,交AB 于点M ,交AC 于点N .若BM +CN =9,则线段MN 的长为()CBAED CB ADB AA .6B .7C .8D .95. 已知:如图,在△ABC 中,AB =AC ,AD 是BC 边上的中线,点P 在AD 上.求证:PB=PC .6. 已知:如图,B ,D ,E ,C 在同一直线上,AB =AC ,AD =AE .求证:BD =CE .N M EC BADCBAPA B CD E7.已知等腰三角形的两边长分别为4和8,则该等腰三角形的周长为_________________.8.若等腰三角形的一个角比另一个角大30°,则该等腰三角形的顶角的度数为_____________.9.已知:如图,线段AB的端点A在直线l上,AB与l的夹角是30°,请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请找出所有符合条件的点.➢思考小结1.要证明边相等或角相等,可以考虑两种思路:①如果边或者角在两个三角形里面,则证明两个三角形__________;②如果边或角在一个三角形里面,证明三角形是_______三角形.2.将两个含30°角的三角板如图放置,则△ABD是_________三角形(“等腰”或“等边”),故AB_____BD,BC=____BD,所以BC=____AB,从而得到对于含有30°角的直角三角形,30°角所对的直角边是斜边的_______.【参考答案】➢巩固练习 1.50° 2.50° 3.36° 4. D5. 证明略提示:利用等腰三角形三线合一的性质,得AD 垂直平分BC ,从而得到PB =PC6. 证明略提示:根据等边对等角可得∠B =∠C ,∠ADE =∠AED ,进而可得∠BAD =∠CAE ,从而证明△ABD ≌△ACE ,根据全等三角形对应边相等,可得BD =CE7. 20 D C B A8.80°或40°9.这样的点能找4个,作图略➢思考小结1.①全等②等腰2.等边,=,12,12,一半。

AHA12GAGGAGAGGAFFFFAFAF第 十 三 章 习 题1、在293K 时,把半径为1mm 的水滴分散成半径为1μm 的小水滴,问比表面增加了多少倍?表面吉布斯自由能增加了多少?完成该变化时,环境至少需做功若干?已知293K 时水的表面张力为0.07288N ·m -1。
解 设半径为1mm 水滴的表面积为A 1,体积为V 1,半径为R 1;半径为1μm 小水滴的表面积为A 2,体积为V 2,半径为R 2。
大水滴分散成小水滴后,设分散成小水滴后的数目为N ,则V 1=N V 2,所以32313434R N R ππ=, 9363321101010=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=--m m R R N1000101010442639212212=⎪⎪⎭⎫ ⎝⎛==--m m R R N A A ππJ m N R NR m N A G A442122110145.910145.9)(407288.0---⨯=⋅⨯=-⨯⋅=∆=∆πγJ G W A f 410145.9-⨯-=∆-=。
2、已知汞溶胶中粒子(设为球形)的直径为22nm ,每dm 3溶胶中含Hg 为8×10-5kg ,试问每1cm 3的溶胶中粒子数为多少?其总表面积为若干?把8×10-5kg 的汞滴分散成上述溶胶时表面吉布斯自由能增加多少?已知汞的密度为13.6kg ·dm -3,汞-水界面张力为0.375N ·m -1。
解 直径为22nm 的汞的粒子的体积为AHA12GAGGAGAGGAFFFFAFAF32439310576.5102223434m m R V --⨯=⎪⎭⎫ ⎝⎛⨯⨯==ππ每1cm 3的溶胶中粒子数N(为每1cm 3的溶胶中含汞的体积再除以直径为22nm 的汞的粒子的体积)123243333510054.110576.516.13101108⨯=⨯⨯⋅⨯⨯⋅⨯=-----m dm kg dm dm kg N232912210603.110222410054.14m m R N A --⨯=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=⋅=ππ总 8×10-5kg 的汞滴的半径R 0,m dm dm kg kg V R 32313531001012.11012.14)]6.13/(108[343----⨯=⨯=⎪⎪⎭⎫ ⎝⎛⋅⨯⨯=⎪⎭⎫ ⎝⎛=ππ J R NR m N A G A 420211095.5)(4375.0--⨯=-⨯⋅=∆=∆πγ。
习 题13-1 如图13-16所示,一飞机以匀加速度a 沿与水平线成仰角b 的方向作直线运动。
已知装在飞机上的单摆的悬线与铅垂线所成的偏角为f ,摆锤的质量为m 。
试求此时飞机的加速度a 和悬线中的张力F T 。
图13-16ma F =I 0cos sin 0I T =-=∑βϕF F F xϕβsin cos IT F F =0sin cos 0I T =--=∑mg F F F y βϕ0sin cos sin cos I I =--mg F F βϕϕβ0sin )cos(I=-+mg F ϕβϕ mgma=+ϕβϕsin )cos()cos(sin βϕϕ+=g amg maF F )cos(cos sin cos sin cos I T βϕβϕβϕβ+===13-2 球磨机的简图如图13-17所示,滚筒作匀速转动,内装钢球及被粉碎的原料,当钢球随滚筒转到某一角度f 时,将脱离筒壁作抛射运动,由于钢球的撞击,从而破碎与研磨原料。
已知钢球脱离筒壁的最佳位置'4054︒=ϕ,滚筒半径R =0.6m 。
试求使钢球在'4054︒=ϕ处脱离滚筒的滚筒转速。
图13-172n I ωmR ma F == 0cos 0I N n =-+=∑F mg F F ϕ)cos (cos cos 22I N ϕωϕωϕg R m mg mR mg F F -=-=-=令0N =F0cos 2=-ϕωg RR g ϕωcos =min r/35.296.00454cos 8.9π30cos π30π30='︒⨯===R g n ϕω13-3 一质量为m 的物块A 放在匀速转动的水平转台上,如图13-18所示。
已知物块的重心距转轴的距离为r ,物块与台面之间的静摩擦因数为s μ。
试求物块不致因转台旋转而滑出时水平转台的最大转速。
图13-182n I ωmr ma F == 00N =-=∑mg F F ymg F =N00I =-=∑F F F x0N s 2=-F mr μω 0s 2=-mg mr μωrgs μω=rgn s max π30π30μω==13-4 离心调速器的主轴以匀角速度w 转动,如图13-19所示。
曼昆《经济学原理(微观经济学分册)》(第6版)第5篇企业行为与产业组织第13章生产成本课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
一、概念题1.总收益(total revenue)答:总收益指一定时期内厂商从一定量产品的销售中得到的货币总额,它等于单位产品的价格P乘以销售量Q,即:=⋅TR P Q由于完全竞争的厂商所面对的是一条水平的需求曲线,厂商增减一单位产品的销售所引起的总收益的变化(TR∆)总是等于固定不变的单位产品的价格P,所以总收益曲线是一条从原点出发的直线,其斜率就是固定不变的价格。
完全竞争市场外其他类型市场的总收益曲线是先上升达到最大后再下降的。
2.总成本(total cost)答:总成本指企业购买生产投入所支付的货币量,它包括两个部分,即固定成本(FC)与可变成本(VC)。
固定成本是在短期内不随产量变动而变动的生产费用,如厂房费用、机器折旧费用、一般管理费用及厂部管理人员的工资等。
只要建立了生产单位,不管产量多少,都需要支出固定成本。
可变成本是随产量变动而变动的生产费用,如原材料、燃料和动力支出及生产工人的工资等。
这些费用在短期内是随着产量的变动而变动的。
其变动的规律是:最初,在产量开始增加时,由于各种生产要素的投入比例不合理,不能充分发挥生产效率,故可变成本增加的幅度较大;以后随着产量的增加,各种生产要素的投入比例趋于合理,其效率得以充分发挥,故可变成本增加的幅度依次变小;最后由于可变要素的边际收益递减,可变成本增加的幅度依次变大。
这一变动趋势正好同边际收益递减规律所描述的总产量的变动趋势相反。
第十三章组织设计一、教学要点1、管理幅度、管理层次与组织形态的关系。
2、扁平形组织结构的基本特点。
3、锥形组织结构的基本特点。
4、影响管理幅度的因素。
5、组织设计的任务。
6、组织设计的基本原则。
7、组织设计的影响因素。
8、经营环境如何影响组织设计?9、经营战略如何影响组织设计?10、企业技术类型与组织结构特征间的相互关系。
11、信息技术对组织结构的影响。
12、企业发展阶段与组织结构特征间的关系。
13、经营规模如何影响组织设计?14、职能部门化的依据、优点和局限性。
15、产品部门化的依据、优点和局限性。
16、区域部门化的依据、优点和局限性。
17、矩阵组织的依据、优点和局限性。
18、权力的性质和特征。
19、组织中集权倾向的产生原因。
20、组织过分集权的弊端。
21、判断分权程度的标准。
22、组织中促进分权及不利于分权的因素。
23、制度分权与授权的概念以及两者间的区别。
24、关键名词:组织设计、管理幅度、管理层次、组织结构、扁平形结构、锥形结构、因事设职、因人设职、权责对等、命令统一、保守型战略、风险型战略、分析型战略、组织发展五阶段理论、Parkinson法则、部门化、横向分工、纵向分工、职能部门化、产品部门化、区域部门化、矩阵组织、权力、集权、分权、制度分权、授权二、习题(一)填充题1.组织设计的实质是对管理人员的管理劳动进行__________和____________的分工。
2.管理中的组织职能就是在________的基础上,设计出组织所需的________及其之间的关系。
3.组织结构的必要性和重要性是随着___________和___________而不断提高。
4.管理层次受到_________和__________的影响。
它与组织规模成_____比,在组织规模已定的条件下,它与管理幅度成_____比。
5.组织设计的任务是提供企业的________________和编制________________。
第十三章习题解答13-1 如题图13-1所示,两条平行长直导线和一个矩形导线框共面,且导线框的一个边与长直导线平行,到两长直导线的距离分别为r 1,r 2;已知两导线中电流都为0sin I I t ω=,其中I 0和ω为常数,t 为时间;导线框长为a 宽为b ,求导线框中的感应电动势;分析:当导线中电流I 随时间变化时,穿过矩形线圈的磁通量也将随时间发生变化,用法拉第电磁感应定律d d i tΦε=-计算感应电动势,其中磁通量s B d S Φ=⎰,B 为两导线产生的磁场的叠加;解:无限长直电流激发的磁感应强度为02IB rμ=π;取坐标Ox 垂直于直导线,坐标原点取在矩形导线框的左边框上,坐标正方向为水平向右;取回路的绕行正方向为顺时针;由场强的叠加原理可得x 处的磁感应强度大小00122()2()IIB r x r x μμ=+π+π+, 垂直纸面向里通过微分面积dS adx =的磁通量为00122()2()I I d B dS B dS adx r x r x μμππ⎡⎤Φ===+⎢⎥++⎣⎦通过矩形线圈的磁通量为000122()2()bI I adx r x r x μμΦ⎡⎤=+⎢⎥π+π+⎣⎦⎰ 012012ln ln sin 2a r b r b I t r r μω⎛⎫++=+ ⎪π⎝⎭感生电动势012012012012d ln ln cos d 2()()ln cos 2i a r b r b I t t r r ar b r b I t r r μωΦεωμωω⎛⎫++=-=-+ ⎪π⎝⎭⎡⎤++=-⎢⎥π⎣⎦0i ε>时,回路中感应电动势的实际方向为顺时针;0i ε<时,回路中感应电动势的实际方向为逆时针;题图13-1 题图13-213-2 如题图13-2所示,有一半径为r =10cm 的多匝圆形线圈,匝数N =100,置于均匀磁场B 中B =;圆形线圈可绕通过圆心的轴O 1O 2转动,转速n =600rev/min;求圆线圈自图示的初始位置转过/2π时,1 线圈中的瞬时电流值线圈的电阻为R =100Ω,不计自感;2 感应电流在圆心处产生的磁感应强度;分析:应用法拉第电磁感应定律求解感应电动势;应用载流圆环在其圆心处产生的磁场公式求出感应电流在圆心处产生的磁感应强度; 解:1 圆形线圈转动的角速度2=2060nπωπ= rad/s 设t =0时圆形线圈处在图示位置,取顺时针方向为回路绕行的正方向;则t 时刻通过该回路的全磁通2cos cos NB S NBS t NB r t ψωπω===电动势 2d sin d i NB r t tψεπωω=-= 感应电流 2sin ii NB r t I R Rεπωω== 将圆线圈自图示的初始位置转过/2π时,2t πω=代入已知数值 得: 0.99i I A =2 感应电流在圆心处产生的磁感应强度的大小为40 6.2210T 2ii I B Nrμ-==⨯i B 的方向与均匀外磁场B 的方向垂直;13-3 均匀磁场B 被限制在半径R =10cm 的无限长圆柱形空间内,方向垂直纸面向里;取一固定的等腰梯形回路abcd ,梯形所在平面的法向与圆柱空间的轴平行,位置如题图13-3所示;设磁场以d 1T/s d B t =的匀速率增加,已知6cm Oa Ob ==,3πθ=,求等腰梯形回路abcd 感生电动势的大小和方向;分析:求整个回路中的电动势,采用法拉第电磁感应定律,本题的关键是确定回路的磁通量;解:设顺时针方向为等腰梯形回路绕行的正方向.则t 时刻通过该回路的磁通量题图13-3 题图13-4B S BS Φ==其中S 为等腰梯形abcd 中存在磁场部分的面积,其值为2211()sin 22S R oa θθ=- 电动势d d d d i B St t Φε=-=-2211d ()sin 22d BR oa tθθ⎡⎤=--⎢⎥⎣⎦ 代入已知数值 33.6810V i ε-=-⨯“–”说明,电动势的实际方向为逆时针,即沿adcba 绕向;用楞次定律也可直接判断电动势的方向为逆时针绕向;13-4 如题图13-4所示,有一根长直导线,载有直流电流I ,近旁有一个两条对边与它平行并与它共面的矩形线圈,以匀速度v 沿垂直于导线的方向离开导线.设t =0时,线圈位于图示位置,求:1 在任意时刻t 通过矩形线圈的磁通量m Φ;2 在图示位置时矩形线圈中的电动势i ε;分析:线圈运动,穿过线圈的磁通量改变,线圈中有感应电动势产生,求出t 时刻穿过线圈的磁通量,再由法拉第电磁感应定律求感应电动势;解:1 设线圈回路的绕行方向为顺时针;由于载流长直导线激发磁场为非均匀分布,02IB xμπ=;因此,必须由积分求得t 时刻通过回路的磁通量; 取坐标Ox 垂直于直导线,坐标原点取在直导线的位置,坐标正方向为水平向右,则在任意时刻t 通过矩形线圈的磁通量为00d d ln22b vtSa vtI Il b vtl x x a vtμμΦππ+++===+⎰⎰B S 2在图示位置时矩形圈中的感应电动势00()d d 2i t Ilv b a tabμΦεπ=-=-=电动势的方向沿顺时针绕向;13-5 如题图13-5所示为水平面内的两条平行长直裸导线LM 与L M '',其间距离为l ,其左端与电动势为0ε的电源连接.匀强磁场B 垂直于图面向里,一段直裸导线ab 横嵌在平行导线间并可保持在导线上做无摩擦地滑动,电路接通,由于磁场力的作用,ab 从静止开始向右运动起来;求:1 ab 达到的最大速度;2 ab 到最大速度时通过电源的电流I ;分析:本题是包含电磁感应、磁场对电流的作用和全电路欧姆定律的综合性问题;当接通电源后,ab 中产生电流;该通电导线受安培力的作用而向右加速运动,由于ab 向右运动使穿过回路的磁通量逐渐增加,在回路中产生感应电流,从而使回路中电流减小,当回路中电流为零时,直导线ab 不受安培力作用,此时ab 达到最大速度;解:1电路接通,由于磁场力的作用,ab 从静止开始向右运动起来;设ab 运动的速度为v ,则此时直导线ab 所产生的动生电动势i Blv ε=,方向由b 指向a .由全电路欧姆定理可得此时电路中的电流为0Blv i Rε-=ab 达到的最大速度时,直导线ab 不受到磁场力的作用,此时0i =;所以ab 达到的最大速度为max v Blε=2ab 达到的最大速度时,直导线ab 不受到磁场力的作用,此时通过电路的电流i =0;所以通过电源的电流也等于零;13-6 如题图13-6所示,一根长为L 的金属细杆ab 绕竖直轴O 1O 2以角速度ω在水平面内旋转,O 1O 2在离细杆a 端L /5处;若已知均匀磁场B 平行于O 1O 2轴;求ab 两端间的电势差U a -U b . 分析:由动生电动势表达式先求出每段的电动势,再将ab 的电动势看成是oa 和ob 二者电动势的代数和,ab 两端的电势差大小即为ab 间的动生电动势大小;求每段的电动势时,由于各处的运动速度不同,因此要将各段微分成线元dl ,先由动生电动势公式计算线元dl 的两端的动生电动势i d ε,再积分计算整段的动生电动势;解:设金属细杆ab 与竖直轴O 1O 2交于点O ,将ab 两端间的动生电动势看成ao 与ob 两段动生电动势的串联;取ob 方向为导线的正方向,在铜棒上取极小的一段线元dl ,方向为ob 方向;线元运动的速度大小为v l ω=;由于,,v B dl 互相垂直;所以dl 两端的动生电动势()i d v B dl vBdl B ldl εω=⨯=-=-ob 的动生电动势为242501416d d 2550L ob i abL Bl l B B L εεωωω⎛⎫==-=-=- ⎪⎝⎭⎰⎰动生电动势ob ε的方向由b 指向O ;同理oa 的动生电动势为题图13-5 题图13-6225011d d 2550L oa i baL Bl l B B L εεωωω⎛⎫==-=-=- ⎪⎝⎭⎰⎰动生电动势oa ε的方向由a 指向O ;所以ab 两端间的的动生电动势为2310ab ao ob oa ob B L εεεεεω=+=-+=-动生电动势ab ε的方向由a 指向了b ;a 端带负电,b 端带正电;ab 两端间的电势差2310a b ab U U B L εω-==-b 端电势高于a 端;13-7 如题图13-7所示,导线L 以角速度ω绕其端点O 旋转,导线L 与电流I 在共同的平面内,O 点到长直电流I 的距离为a ,且a >L ,求导线L 在与水平方向成θ角时的动生电动势的大小和方向;分析:载流长直导线产生磁场,导线L 绕O 旋转切割磁力线;由于切割是不均匀的磁场,而且导体各处的运动速度不同,所以要微分运动导线,先由动生电动势公式计算线元dl 的两端的动生电动势i d ε,再积分计算整段的总动生电动势;解:取OP 方向为导线的正方向,在导线OP 上某处取极小的一段线元dl ,方向为OP 方向;线元运动的速度大小为v l ω=;由于,,v B dl 互相垂直;所以dl 两端的动生电动势()d v B dl vBdl B ldl εω=⨯=-=-将载流长直导线在该处激发磁场02(cos )IB a l μπθ=+代入,积分得导线L 在与水平方向线成θ角时的动生电动势为:()00d 2cos L i OP i I ldla l ωμεεπθ==-+⎰⎰020(cos )(cos )2cos (cos )LI a l ad l a l ωμθθπθθ+-=+⎰题图13-7 题图13-802+cos cos In 2cos I a L L a a ωμθθπθ⎛⎫=--⎪ ⎭⎝ 动生电动势的方向由P 指向O ;13-8 如题图13-8所示半径为r 的长直密绕空心螺线管,单位长度的绕线匝数为n ,所加交变电流为I =I 0sin ωt ;今在管的垂直平面上放置一半径为2r ,电阻为R 的导线环,其圆心恰好在螺线管轴线上;1计算导线环上涡旋电场E 的值且说明其方向; 2计算导线上的感应电流i I ;3计算导线环与螺线管间的互感系数M ;分析:电流变化,螺线管内部磁场也变化,由磁场的柱对称性可知,由变化磁场所激发的感生电场也具有相应的对称性,感生电场线是一系列的同心圆;根据感生电场的环路定理,可求出感生电场强度;由法拉第电磁感应定律及欧姆定律求感应电流,由互感系数定义式求互感系数; 解:1以半径为2r 的导线环为闭合回路L ,取回路L 的绕行正方向与B 呈右旋关系,自上向下看为逆时针方向;由于长直螺线管只在管内产生均匀磁场0B nI μ=,导线环上某点涡旋电场E 的方向沿导线环的切向;所以由规律LS BE dl dS t∂=-∂⎰⎰可得 22(2)dB E r r dtππ=-导线环上涡旋电场E 的值为00cos 44n r r dBE I t dt μωω=-=- 若cos ωt >0,E 电场线的实际走向与回路L 的绕行正方向相反,自上向下看为顺时针方向;若cos ωt <0,E 电场线的实际走向与回路L 的绕行正方向相同,自上向下看为逆时针方向; 2 导线上的感应电流i I22001cos ii d r dB r I nI t R R dt R dt RεππμωωΦ==-=-=3导线环与螺线管间的互感系数为220B r M n r I IπμπΦ===13-9 电子感应加速器中的磁场在直径为0.50m 的圆柱形区域内是匀强的,若磁场的变化率为×10-2T/S;试计算离开中心距离为0.10m 、0.50m 、1.0m 处各点的感生电场; 分析:由磁场的柱对称性可知,变化磁场所激发的感生电场分布也具有相应的对称性,即感生电场的电场线是一系列以圆柱体中心为轴的同心圆;根据LS BE dl dS t∂=-∂⎰⎰可求出感生电场强度;解:以圆柱形的区域的中心到各点的距离为半径,作闭合回路L ;取回路L 的绕行正方向与B呈右旋关系,为顺时针方向;由于回路上各点处的感生电场E 沿L 的切线方向;所以由规律LS BE dl dS t∂=-∂⎰⎰可得 22()2()LdB r r R dtE dl E r dB R r R dtπππ⎧-<⎪⎪==⎨⎪->⎪⎩⎰得 2d ()2d d ()2d r Br R tE R B r R r t⎧-<⎪⎪=⎨⎪->⎪⎩式中“-”说明:若d 0d Bt>,E 的实际方向与假定方向相反,否则为一致; r =0.10m 时,r <R , 4d || 5.010V/m 2d r BE t-==⨯r =0.50m 时, r >R , 24d || 6.2510V/m 2d R BE r t -==⨯ r =1.10m 时,r >R , 24d || 3.1310V/m 2d R BE r t-==⨯ 13-10 如题图13-10所示,一个限定在半径为R 的圆柱体内的均匀磁场B 以10-2T/s 的恒定变化率减小;电子在磁场中A 、O 、C 各点处时,它所获得的瞬时加速度大小、方向各为若干 设r =5.0cm; 分析:根据对称性,由感生电场的环路定理求出感生电场强度,由感生电场力及牛顿第二定律求出瞬时加速度;解:以圆柱形区域的中心到各点的距离为半径,作闭合回路L ;取回路L 的绕行正方向与B 呈右旋关系,由于回路上各点处的感生电场E 沿L 的切线方向;所以由规律题图13-10 题图13-11d d Ll t∂=-∂⎰⎰S BE S 可得 2d d 2d LB E r r t=π=-π⎰E l r <R 得 d 2d r BE t=-由于圆柱体内的均匀磁场B 以10-2T/s 的恒定变化率减小.所以d 0d Bt<,E 的实际方向与假定方向一致,为顺时针方向的切线方向;电子受到的电场力为e F eE =-,其方向为逆时针的切线方向; 瞬时加速度的大小为:d 2d eE e r B a m m t== 由于r A =0.05m,所以A 处的瞬时加速度的大小为:724.410/A a m s =⨯,方向为水平向右; 由于r C =0.05m,所以C 处的瞬时加速度的大小为:724.410/C a m s =⨯,方向为水平向左;由于r O =0,所以O 处的瞬时加速度:0O a =13-11 真空中的矩形截面的螺线环的总匝数为N ,其它尺寸如题图13-11所示,求它的自感系数;分析:自感系数一般可由LI ψ=计算,可见计算自感系数关键是确定穿过自感线圈的磁通量;假设螺线管通有电流,求出磁感应强度,再求出磁通量、磁通链,即可求出自感系数; 解:设螺绕管通有电流I ,由安培环路定理可得管内距轴线r 处的磁场强度为2NI H r =π, 2NI B H rμμ==π 通过某一截面的磁通量210021d d ln22R SR NINIhR B S h r rR μμΦ===ππ⎰⎰⎰螺绕管的磁通链2021ln2N N IhR N R μψΦ==π 自感系数:2021ln 2NN hR L IR ψμ==π13-12 设一同轴电缆由半径分别为1r 1和2r 的两个同轴薄壁长直圆筒组成,电流由内筒流入,由外筒流出,如题图13-12所示;两筒间介质的相对磁导率r 1μ=,求同轴电缆1 单位长度的自感系数;2单位长度内所储存的磁能;分析:先求磁场、磁通量,由自感系数定义式求自感系数,再由自感磁能表达式求磁能; 解:1电流由内筒流入,由外筒流出时,在内外筒之间产生的磁场为B=02Irμπ见11-19;通过内外筒之间单位长度截面的磁通量为212121d 1d lnln r Sr IIr x xr r L r μμΦμΦI 000===2π2π∴==2π⎰⎰S B2单位长度内所储存的磁能220211ln 24m I r W LI r μπ==13-13 一无限长直导线通以电流I =I 0sin ωt ,和直导线在同一平面内有一矩形线框,其短边与直导线平行,线框的尺寸及位置如题图13-13所示,且b /c =3;求: 1 直导线和线框的互感系数; 2 线框中的互感电动势;分析:互感系数由MI =φ计算,计算互感系数关键是确定穿过互感线圈的磁通量; 解:1 无限长直导线产生的磁场02IB r μπ=;取矩形线框的正法线方向为垂直纸面向里,通过矩形线框的磁通量为d d d ln ln 3bcSIIa x a xxxIa Ia b c μμΦμμ0000==-2π2π==2π2π⎰⎰⎰S B∴ 0ln 32aM IμΦ==π2线框中的互感电动势00ln 3d cos d 2i a I IMt t μωεω=-=-πi ε为正时,电动势的方向沿顺时针绕向;i ε为负时,电动势的方向沿逆时针绕向;13-14 一圆环,环管横截面的半径为a ,中心线的半径为R Ra ;有两个彼此绝缘的导线圈题图13-12 题图13-13都均匀地密绕在环上,一个N 1匝,另一个N 2匝,求: 1两线圈的自感L 1和L 2; 2两线圈的互感M ; 3M 与L 1和L 2的关系; 分析:由于Ra ,环中的磁感应强度可视为均匀;设两个线圈通有电流1I 、2I ,求出穿过螺线管线圈的磁通链数,进而求出自感、互感系数;解:1设N 1匝螺绕管线圈中通有电流I 1,由于中心线的半径R 环管横截面的半径a ,所以螺绕管内的磁场01112N I B Rμ=π,通过螺绕管线圈的磁通链数为222011011111122N I N a N B S N a I RRμμψ==π=πN 1匝螺绕管线圈自感系数:22011112N a L I Rμψ==同理,N 2匝螺绕管线圈自感系数:22022222N a L I Rμψ==2N 1匝螺绕管线圈产生的磁场B 1,通过N 2匝螺绕管线圈的磁通链数为2201101221212122N I N N a N B S N a I RRμμψ==π=π两线圈的互感20122112N N a M I Rμψ==3M 与L 1和L 2的关系22220120222N N a N aM RRμμ===13-15 一圆柱体长直导线,均匀地通有电流I ,证明导线内部单位长度储存的磁场能量为2m 0/(16)W I μ=π设导体的相对磁导率r 1μ≈;分析:均匀通有电流的长直导线,其内部和外部均存在磁场,且磁场分布呈轴对称性;据题意,只需求得单位长度导线内所储存的磁能,因此根据磁能密度公式,求得体元内的磁能,然后对圆柱内部的磁能进行积分即可;解:设圆柱形导体的半径为R .由安培环路定律可得长直导线内的磁场02,2rB I R μ=π r<R导线内的磁能密度222200m 2240012228r I r B w I R R μμμμ⎛⎫===⎪ππ⎝⎭在导线内取单位长度的同轴薄圆柱筒体元d 2d V r r =π 其磁能为 230m m 4d d d 4I W w V r r R μ==π单位长度导体柱内储存的磁场能量为22300m m 4d d 416RI I W W r r R μμ===ππ⎰⎰13-16 平行板电容器的电容为C=μF,两板上的电压变化率为dU/dt =×105V/s,则该平行板电容器中的位移电流为多少;分析:根据平行板电容器的性质,平行板间为均匀电场,电位移D 均匀分布,由平行板电容器场强与电压关系式,求出电位移通量ψ与电压U 的关系,并求出位移电流; 解:设平行板电容器的极板面积S 、间距d ,其间电位移通量为00U DS ES S dψεε=== 对平行板电容器,其电容为0SC dε=,代入上式得CU ψ= 位移电流为65d d d 2010 1.5103A d d UI C t tψ--===⨯⨯⨯= 13-17 一平行板电容器,极板是半径为R 的两圆形金属板,极板间为空气,此电容器与交变电源相接,极板上电量随时间变化的关系为q =q 0sin ωt ω为常量,忽略边缘效应,求: 1电容器极板间位移电流及位移电流密度;2极板间离中心轴线距离为rr <R 处的b 点的磁场强度H 的大小;3当/4t ω=π时,b 点的电磁场能量密度即电场能量密度与磁场能量密度之和; 分析:根据电流的连续性,电容器极板间位移电流等于传导电流求解位移电流;忽略边缘效应,极板间位移电流均匀分布求解位移电流密度;根据全电流安培环路定理求出磁场强度极板间的磁场强度;由极板间电场强度、磁场强度可求得电磁场能量密度; 解:1电容器极板间位移电流d 00d cos cos d UI CCU t q t tωωωω=== 或由电流连续性得:0cos d dqI q t dtωω== 位移电流密度02cos d d I q t S R ωωδπ== 2以中心轴线为圆心,过b 点作一半径为rr <R 的圆为回路,由全电流安培环路定理'd LH dl I =⎰,有2202cos 2d q t H r r r R ωωπδπππ==解得02cos 2q r tH Rωωπ=3 t ω=π/4时,0022cos 24q rrH R Rωπωππ/4== 0022000sin /412q E R R πσεεππε=== b 点的电磁场能量密度22222000024012244e mw w w E H q r R εμμωπε=+⎛⎫=+=+ ⎪⎝⎭13-18 由一个电容C =μF 的电容器和一个自感为L =10mH 的线圈组成的LC 电路,当电容器上电荷的最大值Q=×10-5C 时开始作无阻尼自由振荡;试求 1电场能量和磁场能量的最大值;2当电场能量和磁场能量相等时,电容器上的电荷量; 分析:由电容器储能,自感磁能,求电场能量,磁场能量;解:1由初始条件可知,电磁振荡的初相位0ϕ=.所以电容器上的电量振荡表达式为0cos q Q t ω=自感线圈上的电流振荡表达式为0sin dqI Q t dtωω==- 系统固有振动角频率ω=由于电场能量为2220cos 22e Q Q W t C Cω==,所以电场能量的最大值为 240 4.510J 2eMAXQ W C-==⨯ 由于磁场能量为2220sin 22m LI LI W t ω==,所以磁场能量最大值为 22400 4.510J 22mMAXLI Q W C-===⨯电场能量和磁场能量的最大值相同,都与系统总能量相等;2 电场能量和磁场能量相等时,e m W W = 解得2cos 2t ω=±所以电容器上的电荷量为5024.310C 2q Q -=±=±⨯ 13-19 一个沿负z 方向传播的平面电磁波,其电场强度沿x 方向,传播速度为c ;在空间某点的电场强度为300cos 2V /m 3x E vt ππ⎛⎫=+ ⎪⎝⎭试求在同一点的磁场强度表达式,并用图表示电场强度和传播速度之间相互关系;分析:根据电场强度与磁场强度的定量关系可得该点的磁场强度; 解:由于平面电磁波沿负z 方向传播,某点电场强度E 的振动方向沿x 轴正方向,根据电场强度、磁场强度和传播方向三者满足右旋关系,则该点磁场强度的振动方向沿负y 轴方向;由此,根据电场强度与磁场强度的定量关系式可得该点的磁场强度表示式为000.8cos 2A/m 3y x H E vt εππμ⎛⎫=-=-+ ⎪⎝⎭ 用坡印廷矢量S 的方向表示电磁波的传播方向;电场强度、磁场强度和电磁波的传播方向坡印廷矢量三者满足关系S E H =⨯;题13-19解图。
第十三章 可见分光光度法和紫外分光光度法 首 页 难题解析 学生自测题 学生自测答案 章后习题解答 难题解析例13-1用邻二氮杂菲光度法测定一含铁样品,已知其大致浓度在5×10-7 g ⋅mL -1,此时ε摩尔吸光系数为1.1×104 L ⋅mol -1⋅cm -1,问欲使测定时吸光度在0.2~0.3之间,该选用多厚的比色皿(Fe = 55.85 g ⋅mol -1) 解 当c 用mol ⋅L -1表示有A=ε b c已知浓度为5×10-7 g ⋅mL -1则 1-611317L mol 1095.8molg 85.55L mL 10mL g 105⋅×=⋅⋅×⋅×==−−−−−M a c ∴ cA b ε= 当A =0.2时,cm 2cmmol L 101.1L mol 1095.82.011416=⋅⋅××⋅×=−−−−b 当A =0.3时,cm 3cmmol L 101.1L mol 1095.83.011416=⋅⋅××⋅×=−−−−b 例13-2 某有色溶液在1cm 比色皿中的 A =0.400。
将此溶液稀释到原浓度的一半后,转移至3 cm 的比色皿中。
计算在相同波长下的A 和T 值。
解 设 b 1=1 cm b 2=3 cm A 1=0.400 c 2=0.5 c 1A 1=ε b 1 c 1,A 2=ε b 2 c 2得 A 2=0.60T =10-A 2=10-0.6=25 %例13-3未知相对分子质量的胺试样,通过用苦味酸(Mr =229)处理后转化为胺苦味酸盐(1:1加成化合物)。
当波长为380 nm 时,胺苦味酸盐在95%乙醇中的摩尔吸光系数为1.35×104 L·mol -1·cm -1。
现将0.0300 g 胺苦味酸盐溶于95%乙醇中,准确配制1.00 L 溶液,在380 nm ,b =1.00 cm 时,测得溶液吸光度A =0.800,试计算未知胺的相对分子质量。
尼科尔森《微观经济理论-基本原理与扩展》(第9版)第5篇 不完全竞争模型第13章 垄断市场模型课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.垄断者的平均成本与边际成本是常数5AC MC ==。
厂商面对的市场需求曲线为:53Q P =-。
(1)计算垄断者利润最大化的价格—数量组合与垄断者的利润。
(2)在完全竞争(其中价格=边际成本)情况下这个产业的产出水平是多少?(3)计算在情形(2)中消费者获得的消费者剩余。
证明它超过垄断者利润与情形(1)中的消费者剩余的和。
垄断的“无谓损失”值是多少?解:(1)垄断企业的利润函数为:()()253548PQ C Q Q Q Q Q Q π=-=--=-利润最大化一阶条件为:480d d 2QQ π=-=,解得24Q =。
于是5329P Q =-=,利润为248576Q Q π=-=。
(2)由5MC P ==可得,完全竞争下的市场价格为5P =,因而完全竞争的产出水平为:5348Q P =-=。
(3)如图13-7所示,完全竞争下的消费者剩余为:20.5481152⨯=;垄断下的消费者剩余为:20.524288⨯=,垄断利润为:2424576⨯=;因而完全竞争下的消费者剩余超过了垄断下的消费者剩余与垄断利润之和,其超过的部分构成了垄断的无谓损失(20.524288=⨯=)。
图13-7 垄断的福利损失2.垄断者面对的市场需求曲线为:70Q P =-。
(1)如果垄断者以不变的平均成本与边际成本6AC MC ==生产,为了利润最大化,垄断者选择什么产出小平?在这个产出水平上价格是多少?垄断者的利润是多少?(2)假设垄断者的成本结构变化了,总成本为:20.255300TC Q Q =-+。
第13章直流稳压电源一、填空题1、(1-1,低)把P型半导体N型半导体结合在一起,就形成。
2、(1-1,低)半导体二极管具有单向导电性,外加正偏电压,外加反偏电压。
3、(1-1,低)利用二极管的,可将交流电变成。
4、(1-1,低)根据二极管的性,可使用万用表的R×1K挡测出其正负极,一般其正反向的电阻阻值相差越越好。
5、(1-1,低)锗二极管工作在导通区时正向压降大约是,死区电压是。
6、(1-1,低)硅二极管的工作电压为,锗二极管的工作电压为。
7、(1-1,中)整流二极管的正向电阻越,反向电阻越,表明二极管的单向导电性能越好。
8、(1-1,低)杂质半导体分型半导体和型半导体两大类。
9、(1-1,低)半导体二极管的主要参数有、,此外还有、、等参数,选用二极管的时候也应注意。
10、(1-1,中)当加到二极管上的反向电压增大到一定数值时,反向电流会突然增大,此现象称为现象。
11、(1-1,中)发光二极管是把能转变为能,它工作于状态;光电二极管是把能转变为能,它工作于状态。
12、(1-2,中)整流是把转变为。
滤波是将转变为。
电容滤波器适用于的场合,电感滤波器适用于的场合。
答:交流电,脉动的直流电,脉动的直流电,平滑的直流电,负载电流较小且变化不大,负载电流较大13、(1-1,中)设整流电路输入交流电压有效值为U2,则单相半波整流滤波电路的输出直流电压U L(A V)= ,单相桥式整流电容滤波器的输出直流电压U L(A V)= ,单相桥式整流电感滤波器的输出直流电压U L(A V)= 。
14、(1-1,中)除了用于作普通整流的二极管以外,请再列举出2种用于其他功能的二极管:,。
15、(1-1,低)常用的整流电路有和。
16、(1-2,中)为消除整流后直流电中的脉动成分,常将其通过滤波电路,常见的滤波电路有,,复合滤波电路。
17、(1-2,难)电容滤波器的输出电压的脉动τ与有关,τ愈大,输出电压脉动愈,输出直流电压也就愈。
18、(1-2,中)桥式整流电容滤波电路和半波整流电容滤波电路相比,由于电容充放电过程(a.延长,b.缩短),因此输出电压更为(a.平滑,b.多毛刺),输出的直流电压幅度也更(a.高,b.低)。
二、选择题1、(1-1,低)具有热敏特性的半导体材料受热后,半导体的导电性能将。
A、变好B、变差C、不变D、无法确定2、(1-1,中)P型半导体是指在本征半导体中掺入微量的。
A、硅元素B、硼元素C、磷元素D、锂元素3、(1-1,中)N型半导体是指在本征半导体中掺入微量的。
A、硅元素B、硼元素C、磷元素D、锂元素4、(1-1,难)PN结加正向电压时,空间电荷区将。
A、变窄B、基本不变C、变宽D、无法确定5、(1-1,低)二极管正向电阻比反向电阻。
A、大B、小C、一样大D、无法确定6、(1-1,中)二极管的导通条件。
A、u D>0B、u D>死区电压C、u D>击穿电压D、以上都不对7、(1-1,中)晶体二极管内阻是。
A、常数B、不是常数C、不一定D、没有电阻8、(1-1,中)电路如图所示,输出电压U O应为。
A、0.7VB、3.7VC、10VD、0.3V9、(1-1,中)把一个二极管直接同一个电动势为1.5V,内阻为零的电池正向连接,该二极管。
A、击穿B、电流为零C、电流正常D、电流过大使管子烧坏10、(1-1,中)下面列出的几条曲线中,哪条表示的理想二极管的伏安特性曲线。
A B C D11、(1-1,低)二极管的反向饱和电流在室温20o C时是5 μA,温度每升高10o C,其反向饱和电流值增大一倍,当温度为30o C时,反向饱和电流值为。
A、5 μAB、10 μAC、20 μAD、30 μA12、(1-1,中)将交流电压Ui经单相半波整流电路转换为直流电压Uo的关系是。
A、Uo=UiB、Uo=0.45UiC、Uo=0.5UiD、13、(1-1,中)三极管三个极的对地电位分别是-6 V、-3 V、-3.2 V,则该管是。
A、PNP硅管B、NPN锗管C、NPN硅管D、PNP锗管14、(1-1,中)NPN型三极管,三个电极的电位分别有V C=3.3 V,V E=3 V,V B=3.7 V,则该管工作在。
A、饱和区B、截止区C、放大区D、击穿区15、(1-1,中)用万用表欧姆挡测量小功率晶体二极管性能好坏时,应把欧姆挡拨到。
A、R×100Ω或R×1KΩB、R×1ΩC、R×10ΩD、R×100Ω16、(1-1,中)当环境温度升高时,二极管的反向电流将。
A、减少B、增大C、不变D、缓慢减少17、(1-1,中)如图所示,设二极管为理想状态,则电压V AB为。
A、3VB、6VC、-3VD、-6V18、(1-1,难)如图所示的电路中,理想二极管D1、D2的工作状态为。
A、D1、D2均导通B、D1截止,D2导通C、D1、D2均截止D、D1导通,D2截止19、(1-1,中)二极管从反向到正向导通所需时间t1,从正向导通到反向截止所需要的时间t2,则t1和t2的关系是A、相等B、t1远大于t2C、t1远小于t2D、t1略小于t220、(1-1,中)将交流220V经单相半波整流电路转换为直流电压的值为。
A、110VB、0.45×220V C220V D、220V21、(1-1,中)问以下哪种情况中,二极管会导通。
A、B、C、D、22、(1-1,难)用万用表测量小功率二极管极性时,应选用。
A、直流电压挡量程5VB、直流电流挡量程100mAC、交流电压挡量程10VD、电阻挡量程R×10023、(1-1,中)当万用表不同欧姆挡去测量二极管正反向电阻时,获得的结果差异较大,这是因为。
A、该管已坏B、万用表各挡有差异C、二极管的电阻可变D、二极管的伏安特性是非线性24、(1-1,难)二极管在反向截止区的反向电流。
A、随反向电压升高而升高B、随反向电压升高而急剧升高C、基本保持不变D、随反向电压升高而减少25、(1-1,中)某晶体二极管的正、反向电阻都很小或为零时,则该二极管。
A、正常B、已被击穿C、内部短路D、内部开路26、(1-1,难)已知输入正弦波Ui,欲获取图示输出波形Uo,应选取的合适电路是。
A、B、C、 D27、(1-1,难)两只相同的灯泡L1、L2接在如图所示的电路中,则。
A、L1比L2亮B、L2比L1亮C、L1、L2一样亮D、以上答案都不对28、(1-1,低)在单相半波整流电路中,所用整流二极管的数量是。
A、四只B、三只C、二只D、一只29、(1-1,难)在整流电路中,设整流电流平均值为I0,则流过每只二极管的电流平均值I ID0的电路是。
A、单相桥式整流电路B、单相半波整流电路C 、单 相 全 波 整 流 电 路D 、以上都不行30、(1-1,难)设 整 流 变 压 器 副 边 电 压u U t 222=sin ω,欲 使 负 载 上 得 到 图 示 整 流 电 压 的 波 形,则 需 要 采 用 的 整 流 电 路 是 。
A 、 单 相 桥 式 整 流 电 路B 、 单 相 全 波 整 流 电 路C 、 单 相 半 波 整 流 电 路D 、以上都不行2U31、(1-2,难)整 流 滤 波 电 路 如 图 所 示, 负 载 电 阻 R L 不 变, 电 容 C 愈 大, 则 输 出 电 压 平 均 值U O 应 。
A 、不 变B 、愈 大C 、愈 小D 、无法确定u O-32、(1-2,难)单 相 半 波 整 流 、 电 容 滤 波 电 路 中, 设 变 压 器 副 边 电 压 有 效 值 为U 2, 则 整 流 二 极管 承 受 的 最 高 反 向 电 压 为 。
A 、222UB 、22UC 、U 2 D 、2 U 2~u O-三、 判断题1、(1-1,低)二极管的内部结构实质就是一个PN 结。
( )2、(1-1,低)在N 型半导体中如果掺入足够量的三价元素,可将其改型为P 型半导体。
( )3、(1-1,中)因为N 型半导体的多子是自由电子,所以它带负电。
( )4、(1-1,中)PN 结在无光照、无外加电压时,结电流为零。
( )5、(1-1,低)硅二极管的热稳定性比锗二极管好。
( )6、(1-1,低)普通二极管正向使用也有稳压作用。
()7、(1-1,低)P型半导体带正电,N型半导体带负电。
()8、(1-1,中)二极管反向漏电流越小,表明二极管单向导电性越好。
()9、(1-1,低)二极管仅能通过直流,不能通过交流。
()10、(1-1,中)对于实际的晶体二极管,当加上正向电压时它立即导通,当加上反向电压时,它立即截止。
()11、(1-1,中)用数字万用表识别晶体二极管的极性时,若测的是晶体管的正向电阻,那么与标有“+”号的表笔相连接的是二极管正极,另一端是负极。
()12、(1-2,低)任何电子电路都需要直流电源供电,因此需要直流稳压电源()13、(1-2,中)电容滤波效果是由电容器容抗大小决定的()14、(1-2,中)电容滤波器广泛运用于负载电流小且变化量不大的场合()四、简答题1、(1-1,低)什么是PN结?PN结有什么特性?2、(1-1,低)欲使二极管具有良好的单向导电性,管子的正向电阻和反向电阻分别为大一些好,还是小一些好?3、(1-1,中)为什么说二极管是一种非线形元件?什么是二极管的伏安特性?它的伏安特性曲线是如何绘制的?4、(1-1,低)什么是二极管的死区电压?硅管和锗管的死区电压值约为多少?5、(1-1,低)为什么二极管可以当着一个开关来使用?6、(1-1,中)选用二极管时候主要考虑哪些参数?这些参数的含义是什么?7、(1-2,中)什么叫整流?什么叫滤波?五、 计算题1、(1-1,低)电路如图1.1所示,试确定二极管是正偏还是反偏。
设二极管正偏时的正向压降为0.7V ,估算U A 、U B 、U C 、U D 、U AB 、U CD 。
2、(1-1,低)电 路 如 图 所 示 , 试 分 析 当 u I V =3 时, 哪 些 二 极 管 导 通? u I V =0时, 哪 些 二 极 管 导 通?( 写 出 分 析 过 程 并 设 二 极 管 正 向 压 降 为0.7 V)。
D 1D 2D 343、(1-1,低)根据图(b)中给出的U A、U B,分析图(a)所示电路中二极管的工作状态,求U o的值,并将结果添入图(b)中。
设二极管正向压降为0.7V。
4、(1-1,低)计算下图所示电路的电位U Y(设D为理想二极管)。
(1)U A=U B=0时;(2)U A=E,U B=0时;(3)U A=U B=E时。
5、(1-1,中)在下图所示电路中,设D为理想二极管,已知输入电压u i的波形。