2020-2021年新高三数学开学摸底考试卷详解(一)

2020-2021学年高三下学期数学开学摸底考试（新课标全国卷理科）【满分：150分】一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}21220,log (1)0A xx x B x x ⎧⎫=-=+>⎨⎬⎩⎭∣∣，则A B ⋂=( ) A.(1,0)- B.(1,0]- C.(2,)+∞ D.[2,)+∞2.已知复数z 满足(1i)22i z -=--，则||z =( )A.2C.13.已知12,F F 为双曲线22:2C x y -=的左、右焦点,点 P 在C 上,122PF PF =,则12cos F PF ∠等于( ) A.14B.35C.34D.454.设双曲线22221(0)x y a b a b-=>>的两条渐近线与圆2210x y +=相交于A B C D ，，，四点，若四边形ABCD 的面积为12，则双曲线的离心率是( )D ．5.根据下表中的数据可以得到线性回归直线方程0.70.35y x =+,则实数,m n 应满足( )A.0.7 1.7n m -=B.0.7 1.5n m -=C.0.7 1.7n m +=D.0.7 1.5n m +=6.函数()432f x x x =-的图像在点()()1,1f 处的切线方程为( ) A.21y x =-- B.21y x =-+C.23y x =-D.21y x =+7.621(1)(1)x x++展开式中2x 的系数为( ) A .15B .20C .30D .358.若cos(2π)α-=且π,02α⎛⎫∈- ⎪⎝⎭，则sin(π)α-=( )A. B.23- C.13- D.23±9.已知函数()π6f x x +⎛⎫ ⎪⎝⎭在区间(),0ααα->［］上是增函数，则α的最大值是( ) A.π6B.π3C.π2D.5π610.在三棱锥P ABC -中,2,2,AB AC BC PA PB PC ======,若三棱锥P ABC -的顶点均在球O 的表面上，则球O 的半径为( )D.311.已知椭圆2221(02)4x y b b+=<<，直线1x y +=与椭圆交于,P Q 两点，若OP OQ ⊥，则椭圆的离心率为( )12.设函数()f x 的定义域为R,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-，则m 的取值范围是( )A ．9,4⎛⎤-∞ ⎥⎝⎦B ．7,3⎛⎤-∞ ⎥⎝⎦C ．5,2⎛⎤-∞ ⎥⎝⎦D ．8,3⎛⎤-∞ ⎥⎝⎦二、填空题：本题共4小题，每小题5分，共20分.13.若x y ,满足约束条件210501x y x y y --≥⎧⎪+-≤⎨⎪≥⎩，则2244z x x y =-++的取值范围是 .14.已知向量,,|||2==a b a b ,且()-⊥a b a ,则向量 a 和 b 的夹角是____________,()⋅+=a a b _______________.15.ABC 的内角,,A B C 的对边分别为,,a b c 。

最新高三第一次模拟考试数学试题(考试时间：120分钟 总分：160分)注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．已知集合{}21A x x =≤，集合{}2,1,0,1,2B =--，则A B = ▲ ．2．如图，在复平面内，点A 对应的复数为1z ，若21i z z =（i 为虚数单位）， 则2z = ▲ ．3．在平面直角坐标系xOy 中，双曲线2212x y -=的实轴长为 ▲ ．4．某校共有教师200人，男学生800人，女学生600人，现用分层抽样的方法从所有师生中抽取一个容量为n 的样本，已知从男学生中抽取的人数为100 人，那么n = ▲ ．5．执行如图所示的伪代码，当输入,a b 的值分别为1,3时，最后输出的a的值为 ▲ ．6．甲乙两人下棋，若甲获胜的的概率为15，甲乙下成和棋的概率为25，则乙不输棋的概率为▲ ．7．已知直线(0)y kx k =>与圆22:(2)1C x y -+=相交于,A B 两点，若255AB =， 则k = ▲ ．8．若命题“存在20,4R x ax x a ∈++≤”为假命题，则实数a 的取值范围是 ▲ ． 9．如图，长方体1111ABCD A B C D -中，O 为1BD 的中点，三棱锥O ABD -的体积为1V ，四棱锥11O ADD A -的体积为2V ，则12VV的值为 ▲ ．10．已知公差为2的等差数列{}n a 及公比为2的等比数列{}n b 满足11220,0a b a b +>+<，Read ,1While 21End WhilePrint a b i i a a b b a bi i a ←≤←+←-←+（第5题） （第9题）OCDBC 1A B 1A 1D 1（第2题）则33a b +的取值范围是 ▲ ．11．设()f x 是R 上的奇函数，当0x >时，()2ln4x xf x =+，记(5)n a f n =-，则数列 {}n a 的前8项和为 ▲ ．12．在平面直角坐标系xOy 中，已知点,A B 分别为x 轴，y 轴上一点，且2AB =，若点P ，则AP BP OP ++的取值范围是 ▲ ．13．若正实数,x y 满足2(21)(52)(2)xy y y -=+-，则12x y+的最大值为 ▲ ．14．已知函数π()sin()cos cos()262x x f x A x θ=+--（其中A 为常数，(π,0)θ∈-），若实数123,,x x x 满足：①123x x x <<，②31x x -<2π，③123()()()f x f x f x ==，则θ的值为 ▲ ．二、解答题：（本大题共6小题，共90分．解答应写出文字说明，证明过程或演算步骤．） 15．（本题满分14分）在ABC ∆中，角,A B 的对边分别为,a b ，向量(cos ,sin ),(cos ,sin )A B B A ==m n ． （1）若cos cos a A b B =，求证：//m n ； （2）若⊥m n ,a b >，求tan2A B-的值．如图，在三棱锥P ABC -中，90PAC BAC ∠=∠=︒，PA PB =，点D ，F 分别为BC ，AB 的中点．（1）求证：直线//DF 平面PAC ；（2）求证：PF ⊥AD ．17．（本题满分14分）一个玩具盘由一个直径为2米的半圆O 和一个矩形ABCD 构成，1AB =米，如图所示．小球从A 点出发以v 5的速度沿半圆O 轨道滚到某点E 处后，经弹射器以6v 的速度沿与点E 切线垂直的方向弹射到落袋区BC 内，落点记为F ．设AOE θ∠=弧度，小球从A 到F 所需时间为T ． （1）试将T 表示为θ的函数()T θ，并写出定义域；（2）求时间T 最短时cos θ的值．18．（本题满分16分）已知数列{},{}n n a b 满足2(2)n n n S a b =+，其中n S 是数列{}n a 的前n 项和．（1）若数列{}n a 是首项为23，公比为13-的等比数列，求数列{}n b 的通项公式； （2）若n b n =，23a =，求数列{}n a 的通项公式；（3）在（2）的条件下，设n n nac b =，求证：数列{}n c 中的任意一项总可以表示成该数列其他两项之积．如图，在平面直角坐标系xOy 中， 已知圆:O 224x y +=，椭圆:C 2214x y +=， A 为椭圆右顶点．过原点O 且异于坐标轴的直线与椭圆C 交于,B C 两点，直线AB 与圆O 的另一交点为P ，直线PD 与圆O 的另一交点为Q ，其中6(,0)5D -．设直线,AB AC 的斜率分别为12,k k ．（1）求12k k 的值； （2）记直线,PQ BC 的斜率分别为,PQ BC k k ，是否存在常数λ，使得PQ BC k k λ=？若存在，求λ值；若不存在，说明理由；（3）求证：直线AC 必过点Q ．20．（本题满分16分） 已知函数()4212f x ax x =-，(0,)x ∈+∞，()()()g x f x f x '=-． （1） 若0a >，求证：（ⅰ）()f x 在()f x '的单调减区间上也单调递减； （ⅱ）()g x 在(0,)+∞上恰有两个零点；（2） 若1a >，记()g x 的两个零点为12,x x ，求证：1244x x a <+<+．数学试题（附加题）21.【选做题】请考生在A 、B 、C 、D 四小题中任选两题作答.如果多做，按所做的前两题记分. A ．（几何证明选讲，本题满分10分）如图,圆O 是ABC ∆的外接圆,点D 是劣弧BC 的中点,连结AD 并延长,与以C 为切点的切线交于点P ,求证:PC BDPA AC=.B ．（矩阵与变换，本题满分10分）已知矩阵1252M x -⎡⎤⎢⎥=⎢⎥⎣⎦的一个特征值为2-,求2M .C ．（坐标系与参数方程，本题满分10分）在平面直角坐标系xoy 中,已知直线11:()72x t C t y t=+⎧⎨=-⎩为参数与椭圆2cos :(0)3sin x a C a y θθθ=⎧>⎨=⎩为参数,的一条准线的交点位于y 轴上,求实数a 的值.D ．（不等式选讲，本题满分10分）已知正实数,,a b c 满足231a b c ++=，求证：24627111a b c ++≥.P22．【必做题】（本题满分10分）如图，在直三棱柱ABC —A 1B 1C 1中，AC = 3，BC = 4，AB = 5，AA 1 = 4． （1）设AB AD λ=，异面直线AC 1与CD，求λ的值； （2）若点D 是AB 的中点，求二面角D —CB 1—B 的余弦值．23. 【必做题】（本题满分10分）已知,N*k m ∈，若存在互不相等的正整数12,,a a …,m a ，使得1223,,a a a a …11,,m m m a a a a -同时小于k ，则记()f k 为满足条件的m 的最大值． （１） 求(6)f 的值；（２） 对于给定的正整数n (1)n >，（ⅰ）当(2)(1)(2)n n k n n +<≤++时，求()f k 的解析式； （ⅱ）当(1)(2)n n k n n +<≤+时，求()f k 的解析式．1A高三数学参考答案一、填空题1．}{1,0,1-； 2．2i --； 3． 4．200； 5．5； 6．45； 7．12； 8．(2,)+∞； 9．12； 10．(,2)-∞-； 11．16-； 12．[7,11]； 13．12- ； 14．23π-. 二、解答题15. 证明：（1）因为cos cos a A b B =，所以sin cos sin cos A A B B =，所以//m n . ……………7分 （2）因为⊥m n ，所以cos cos sin sin 0A B A B +=，即cos()0A B -=， 因为a b >，所以A B >，又,(0,)A B π∈，所以(0,)A B π-∈，则2A B π-=，…12分所以tantan 124A B π-==. ……………14分 16. 证明（1）∵点D ，F 分别为BC ，AB 的中点，∴//DF AC ，又∵DF ⊄平面PAC ，AC ⊂平面PAC ，∴直线//DF 平面PAC ． ……………6分（２）∵90PAC BAC ∠=∠=︒， ∴AC AB ⊥，AC AP ⊥，又∵AB AP A =，,AB AP 在平面PAB 内， ∴AC ⊥平面PAB ， ……………8分 ∵PF ⊂平面PAB ，∴AC PF ⊥，∵PA PB =，F 为AB 的中点，∴PF AB ⊥，∵AC PF ⊥，PF AB ⊥，AC AB A =，,AC AB 在平面ABC 内，∴PF ⊥平面ABC ， ……………12分∵AD ⊂平面ABC ，∴AD PF ⊥． ……………14分17. 解：（1）过O 作OG BC ⊥于G ，则1OG =，1sin sin OG OF θθ==，11sin EF θ=+，AE θ=， 所以11()5656sin 6AE EF T v v v v v θθθ=+=++，[,]44θ∈π3π．……7分 （写错定义域扣1分）（2）11()56sin 6T v v v θθθ=++，22221cos 6sin 5cos (2cos 3)(3cos 2)()56sin 30sin 30sin T v v v v θθθθθθθθθ-+-'=-==-，…………9分 记02cos 3θ=，0[,]44θ∈π3π，θ0(,)4πθ 0θ 03(,)4πθ ()T θ' - 0 +()T θ故当2cos 3θ=时，时间T 最短． …………14分 18. 解：（1）因为1211()2()333n n n a -=-=--，21[(1()]1133[(1()]1231()3n n n S --==----， …………2分 所以11()2131222()23nn n n n S b a --===+--+． …………4分（2）若n b n =，则22n n S na n =+，∴112(1)2n n S n a ++=++， 两式相减得112(1)2n n n a n a na ++=+-+，即1(1)2n n na n a +=-+， 当2n ≥时，1(1)(2)2n n n a n a --=-+，两式相减得11(1)(1)2(1)n n n n a n a n a -+-+-=-，即112n n n a a a -++=， …………8分 又由1122S a =+，22224S a =+得12a =，23a =， 所以数列{}n a 是首项为2，公差为321-=的等差数列， 故数列{}n a 的通项公式是1n a n =+．…………10分 （3）由（2）得1n n c n+=， 对于给定的*n N ∈，若存在*,,,k t n k t N ≠∈，使得n k t c c c =⋅，只需111n k t n k t+++=⋅，即1111(1)(1)n k t +=+⋅+，即1111n k t kt =++，则(1)n k t k n +=-， …………12分 取1k n =+，则(2)t n n =+，∴对数列{}n c 中的任意一项1n n c n +=，都存在121n n c n ++=+和2222212n n n n c n n +++=+使得212n n n n c c c ++=⋅． …………16分 19．解：（1）设00(,)B x y ，则00(,)C x y --，220014x y += 所以22000012220000111422424x y y y k k x x x x -=⋅===--+--． …………4分 （2）联立122(2)4y k x x y =-⎧⎨+=⎩得2222111(1)44(1)0k x k x k +-+-=，解得211122112(1)4,(2)11P P P k k x y k x k k --==-=++，联立122(14y k x x y ⎧=⎪⎨+=⎪⎩得2222111(14)164(41)0k x k x k +-+-=，解得211122112(41)4,(1414B B Bk k x y k x k k --===++， …………8分 所以121241B BC B y k k x k -==-，121122112141562(1)641515P PQ P k y k k k k k x k -+-===--+++， 所以52PQ BC k k =，故存在常数52λ=，使得52PQ BC k k =． …………10分（3）当直线PQ 与x 轴垂直时，68(,)55Q --，则28156225AQ k k -===--，所以直线AC 必过点Q ． 当直线PQ 与x 轴不垂直时，直线PQ 方程为：12156()415k y x k -=+-， 联立1212256()4154k y x k x y -⎧=+⎪-⎨⎪+=⎩，解得21122112(161)16,161161Q Q k k x y k k --==++， 所以1212211211616112(161)42161AQk k k k k k k +==-=---+，故直线AC 必过点Q ． …………16 分（不考虑直线PQ 与x 轴垂直情形扣1分）20. 证：（1）因为()()42102f x ax x x =->，所以3()4f x ax x '=-， 由32(4)1210ax x ax '-=-<得()f x '的递减区间为， …………2 分 当x ∈时，32()4(41)0f x ax x x ax '=-=-<， 所以(f x 在()f x '的递减区间上也递减． …………4 分（2）解1：()()()42343211(4)422g x f x f x ax x ax x ax ax x x '=-=---=--+， 因为0x >，由()4321402g x ax ax x x =--+=得3214102ax ax x --+=，令321()412x ax ax x ϕ=--+，则21()382x ax ax ϕ'=--，因为0a >，且1(0)02ϕ'=-<，所以()x ϕ'必有两个异号的零点，记正零点为0x ，则0(0,)x x ∈时，()0x ϕ'<，()x ϕ单调递减；0(,)x x ∈+∞时，()0x ϕ'>，()x ϕ单调递增，若()x ϕ在(0,)+∞上恰有两个零点，则0()0x ϕ<， …………7 分由20001()3802x ax ax ϕ'=--=得2001382ax ax =+，所以0003217()939x ax x ϕ=--+，又因为对称轴为4,3x =所以81()(0)032ϕϕ==-<，所以08733x >>，所以0003217()()0933x ax x ϕ=---<，又3222111()41(8)(1)1222x ax ax x ax x x ax ϕ=--+=-+-+，中的较大数为M ，则()0M ϕ>， 故0a >()g x 在(0,)+∞上恰有两个零点． …………10 分解2：()()()42343211(4)422g x f x f x ax x ax x ax ax x x '=-=---=--+， 因为0x >，由()4321402g x ax ax x x =--+=得3214102ax ax x --+=，令321()412x ax ax x ϕ=--+，若()g x 在(0,)+∞上恰有两个零点，则()x ϕ在(0,)+∞上恰有两个零点，当2x =时， 由()0x ϕ=得0a =，此时1()12x x ϕ=-+在(0,)+∞上只有一个零点，不合题意； 当2x ≠时，由321()4102x ax ax x ϕ=--+=得321422x x a x -=-， …………7 分 令322148()2422x x x x x x x ϕ-==-----，则22122572[()]2(58)24()0(2)(2)x x x x x x x x ϕ-+-+'==>--， 当(0,2)x ∈时，()x ϕ单调递增，且由2824,2y x x y x =--=--值域知 ()x ϕ值域为(0,)+∞；当(2,)x ∈+∞时，1()x ϕ单调递增，且1(4)0ϕ=，由2824,2y x x y x =--=--值域知()x ϕ值域为(,)-∞+∞； 因为0a >，所以102a >，而12y a=与1()x ϕ有两个交点，所以1()x ϕ在(0,)+∞上恰有两个零点． …………10 分（3）解1：由（2）知，对于321()412x ax ax x ϕ=--+在(0,)+∞上恰有两个零点12,x x ， 不妨设12x x <，又因为(0)10ϕ=>，11()(67)028a ϕ=-<，所以1102x <<，……12 分又因为(4)10ϕ=-<，91()(65710)028a ϕ=->，所以2942x <<， 所以121945422x x a <+<+=<+． …………16 分 解2：由（2）知321422x x a x -=-， 因为[0,2)x ∈时，1()x ϕ单调递增，17()212ϕ=，111111(0)0()()22x a ϕϕϕ=<=<， 所以1102x <<， …………12 分 当(2,)x ∈+∞时，1()x ϕ单调递增，1981()220ϕ=，112119(4)0()()22x a ϕϕϕ=<=<， 所以2942x <<， 所以121945422x x a <+<+=<+． …………16 分附加题参考答案21.A ．证明：连结CD ，因为CP 为圆O 的切线，所以PCD PAC ∠=∠,又P ∠是公共角，所以PCD ∆～PAC ∆， ……………5分 所以PC CD PA AC = , 因为点D 是劣弧BC 的中点,所以CD BD =,即PC BD PA AC =. ……………10分21.B . 解：2λ=-代入212(1)(5)052x x x λλλλ+-=---+=--，得3x =矩阵12532M -⎡⎤⎢⎥=⎢⎥⎣⎦……………5分∴264514M ⎡⎤=⎢⎥⎣⎦ ……………10分21.C . 解：直线1C ：29x y +=，椭圆2C :2221(03)9y x a a +=<<， …………………………5分准线：29y a =±-由299a =-得，22a = …………………………10分21.D .证明：因为正实数,,a b c 满足231a b c ++=，所以32313ab c ≥，即23127ab c ≤， …………………………5分 所以23127ab c ≥因此，32462461111327a b c a b c ++≥≥ ……………………10分22. 解：（１）由AC = 3，BC = 4，AB = 5得090ACB ∠= ……………１分以CA 、CB 、CC 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系．则Ａ(3,0,0)，1C (0,0,4)，B(0,4,0)，设D(x,y,z)，则由AB AD λ=得(33,4,0)CD λλ=-，而1(3,0,4)AC =-，根据2910||50525189λλ=-+解得，15λ=或13λ=- ……………５分 （２）13(,2,0),(0,4,4)2CD CB ==，可取平面1CDB 的一个法向量为1(4,3,3)n =-；…………………………７分而平面1CBB 的一个法向量为2(1,0,0)n =，并且12,n n <>与二面角D —CB 1—B 相等， 所以二面角D —CB 1—B的余弦值为12cos cos ,n n θ=<>= ………１０分 （第（１）题中少一解扣１分；没有交代建立直角坐标系过程扣1分．第（２）题如果结果相差符号扣１分．）23. 解：（1）由题意，取121,2a a ==，126a a <，满足题意，若33a ∃≥，则必有236a a ≥，不满足题意，综上所述：m 的最大值为2，即(6)2f =． ………………4分 （２）由题意，当(1)(1)(2)n n k n n +<≤++时，设1{1,2,A =…,}n ，2{1,2,3,A n n n =+++…}，显然，∀11,i i a a A +∈时，满足1(1)(1)i i a a n n n n k +≤-<+<，∴从集合1A 中选出的i a 至多n 个，∀12,j j a a A +∈时，1(1)(2)j j a a n n k +≥++≥，∴从集合2A 中选出的j a 必不相邻，又∵从集合1A 中选出的i a 至多n 个，∴从集合2A 中选出的j a 至多n 个，放置于从集合1A 中选出的i a 之间，∴()2f k n ≤， ………………6分 （ⅰ）当(2)(1)(2)n n k n n +<≤++时，取一串数i a 为：1,2,2,21,3,22,n n n --…,1,2,,1n n n n -++， 或写成1, 221,2i i i a i n i +⎧⎪=⎨⎪+-⎩为奇数为偶数，（12i n ≤≤），此时1(2)i i a a n n k +≤+<，(121i n ≤≤-),211n a a n k =+<，满足题意，∴()2f k n =， ………………8分 （ⅱ）当(1)(2)n n k n n +<≤+时，从1A 中选出的n 个i a ：1,2,…,n ，考虑数n 的两侧的空位，填入集合2A 的两个数,p q a a ，不妨设p q na na >，则(2)p na n n k ≥+≥，与题意不符，∴()21f k n ≤-，取一串数i a 为：1,21,2,22,3,23,n n n ---…,2,2,1,1,n n n n n -+-+ 或写成1,22,2i i i a i n i +⎧⎪=⎨⎪-⎩为奇数为偶数，（121i n ≤≤-），此时1(1)i i a a n n k +≤+<，（122i n ≤≤-），211n a a n k -=<，满足题意，∴()21f k n =-， ………………10分 （写出（ⅰ）、（ⅱ）题的结论但没有证明各给１分．）。

2021年高三上学期开学摸底考试数学（理）试题含答案第Ⅰ卷（选择题）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项符合题意的）1.已知集合，，则（）A． B． C． D．2.如果复数（其中为虚数单位，为实数）的实部和虚部互为相反数，那么等于（）A．-6 B． C． D．23.设等差数列的前项和为，若，则的值为（）A． 27 B．36 C．45 D．544.下列命题错误的是（）A．命题“若，则”的逆否命题为“若中至少有一个不为0，则”B．若命题，则C．中，是的充要条件D．若向量满足，则与的夹角为钝角5.某几何体的三视图如上图所示（单位：），则该几何体的体积是（）A． B． C． D．6.若用下边的程序框图求数列的前100项和，则赋值框和判断框中可分别填入（）A． B．C．D．7.已知函数的图象与直线的三个相邻交点的横坐标分别是2，4，8，则的单调递增区间是（）A． B． C．D．8.已知实数满足约束条件，则的最小值是（）A． B．2 C． D．19. 若函数y＝（a＞0，且a≠1）的值域为{y｜0＜y≤1}，则函数y＝的图像大致是10.已知双曲线与抛物线相交于两点，公共弦恰过它们的公共焦点，则双曲线的一条渐近线的倾斜角所在的区间可能是（）A． B． C． D．11.已知满足，，，则（）A． B． C． D．12.已知是定义在上的单调函数，且对任意的，都有，则方程的解所在的区间是（）A． B． C． D．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每题5分，满分20分．）13.已知的展开式中的各项系数的和为2，则该展开式中的常数项为．14.曲线在点处的切线与坐标轴围成的三角形的外接圆方程是．15.已知两个小孩和甲、乙、丙三个大人排队，不排两端，3个大人有且只有两个相邻，则不同的排法种数有．16.在正方体中，是棱的中点，是侧面内的动点，且平面，则与平面所成角的正切值的取值范围是．三、解答题：本大题共6小题，共70分。

高三摸底考试数学卷（满分120分，考试时间120分钟）一、选择题：（本题共20小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知F 是双曲线C：22145x y -=的一个焦点，点P 在C 上，O 为坐标原点，若=OP OF ，则OPF△的面积为（）A．32B．52C．72D．922．记不等式组6,20x y x y +⎧⎨-≥⎩ 表示的平面区域为D.命题:(,),29p x y D x y ∃∈+ ；命题:(,),212q x y D x y ∀∈+ .下面给出了四个命题（）①p q ∨②p q ⌝∨③p q ∧⌝④p q⌝∧⌝这四个命题中，所有真命题的编号是A．①③B．①②C．②③D．③④3．下列函数中，为增函数的是()A．ln(1)y x =-+B．21y x =-C．2xe y =D．|1|y x =-4、0=b 是直线b kx y +=过原点的（）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5、方程43)22(log =x 的解为（）A .4=xB .2=xC .2=xD .21=x 6.设,“X>0”是“”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件7.函数的图象如图所示,则最大、最小值分别为()A. B.C. D.8.设,,,其中为自然对数的底数,则a,b,c 的大小关系是()A. B. C. D.9.设a,b,c,d 都为正数,且不等于1,函数,,,在同一坐标系中的图象如图所示,则a,b,c,d 的大小顺序是()A. B. C. D.10.某单位有15名成员,其中男性10人,女性5人,现需要从中选出6名成员组成考察团外出参观学习,如果按性别分层,并在各层按比例随机抽样,则此考察团的组成方法种数是()A. B. C. D.11、已知定义在R 上的函数12)(-=-m x x f (m 为实数)为偶函数，记)3(log 5.0f a =，)5(log 2f b =，)2(m f c =，则c b a ,,的大小关系为()A、cb a <<B、b ac <<C、bc a <<D、a b c <<12、不等式152x x ---<的解集是（）A、(,4)-∞B、(,1)-∞C、(1,4)D、(1,5)13、函数x x y 2cos sin =是()A、偶函数B、奇函数C、非奇非偶函数C、既是奇函数，也是偶函数14、若(12)a＋1<(12)4－2a，则实数a 的取值范围是()A、(1，＋∞)B、(12，＋∞)C、(－∞，1)D、(－∞，12)15、化简3a a 的结果是()A、a B、12a C、41a D、83a16、下列计算正确的是()A、(a3)2＝a9B、log36－log32＝1C、12a -·12a ＝0D、log3(－4)2＝2log3(－4)17．定义一种运算bc ad d c b a -=*),(),(，若函数))51(,413(tan )log 1()(3x x x f π*=，，0x 是方程0)(=x f 的解，且010x x <<，则)(1x f 的值（）A．恒为正值B．等于0C．恒为负值D．不大于018.已知函数⎩⎨⎧>+-≤-=2,3)1(log 2,1)(x x x ax x f a 是定义域上的单调函数，则的取值范围是（）A.()+∞,1B.[)+∞,2C.()2,1D.(]2,119．已知函数()sin (0)f x x x ωωω=->的图象与轴的两个相邻交点的距离等于2π，若将函数()y f x =的图象向左平移6π个单位得到函数()y g x =的图象，则()y g x =是减函数的区间为（）A.(,0)3π- B.(,)44ππ- C.(0,)3π D.(,43ππ20.已知集合U ={(x，y)|x ∈R,y ∈R},M ={(x，y)||x |+|y |<a }，P ={(x，y)|y =f (x )}，现给出下列函数：①y =ax ,②y =logax ,③y =sin(x +a),④y =cos a x，若0<a <1时，恒有P∩CUM =P，则f (x)可以取的函数有（）A.①②③B.①②④C.①③④D.②③④二、填空题：（共20分）1、若04x <<，则当且仅当x =______时，(4)x x -的最大值为______2、从8位女生和5位男生中，选3位女生和2位男生参加学校舞蹈队，共有_______种不同选法.3．已知)2,1(A ，)4,3(B ，直线0:1=x l ，0:2=y l 和013:3=-+y x l 设i P 是i l （3,2,1=i ）上与A ，B 两点距离平方和最小的点，则△321P P P 的面积是_________；4．如右图将网格中的三条线段沿网格线上下或左右平移，组成一个首尾相连的三角形，则三条线段一共至少需要移动__________格；三、解答题：（本题共3小题，共50分．解答应写出文字说明、证明过程或演算步骤．）1.计算：34cos 49()15(4log 2102π+--+.2.下面是王倩同学的作业及自主探究笔记，请认真阅读并补充完整.【作业】如图①，直线L1//L2，△ABC与ΔDBC的面积相等吗?为什么?设L1与L2之间的距离为h，则:S∆ABC=S∆DBC.【探究】(1)如图②，当点D在L1，L2之间时，设点A,D到直线L2的距离分别为h，证明:·S∆ABC=____.(2)如图③，当点D在4，以之间时，连接AD并延长交于点M，则。

2021年高三数学上学期第一次摸底考试试题理（含解析）新人教A版【试卷综评】本试卷试题主要注重基本知识、基本能力、基本方法等当面的考察，覆盖面广，注重数学思想方法的简单应用，试题有新意，符合课改和教改方向，能有效地测评学生，有利于学生自我评价，有利于指导学生的学习，既重视双基能力培养，侧重学生自主探究能力，分析问题和解决问题的能力，突出应用，同时对观察与猜想、阅读与思考等方面的考查。

第I卷一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的）（1）集合A={x|log3（x-1）<1},B={x|},则(A)(1,2) (B)(1,4) (C)(-2,0) (D)(0,2)【知识点】交集及其运算．A1（x﹣1）＜1}={x|}={x|1＜x＜4}，【答案解析】A 解析：∵A={x|log3B={x|＜2﹣x＜1}={x|0＜x＜2}，∴A∩B={x|1＜x＜2}=（1，2）．故选：A．【思路点拨】利用交集的性质和不等式的性质求解．【题文】(2)命题“对任意的，都有”的否定是（A）对任意的，都有(B)存在，使（C）不存在，使（D）存在，使【知识点】命题的否定．A2【答案解析】B 解析：由全称命题的否定方法得：“对任意的x∈R，都有2x2﹣x+1≥0”的否定是“存在x0∈R，使得2x2﹣x+1＜0成立．故选B．【思路点拨】将量词改为“存在”，将结论否定当结论．由此得到原命题的否定．【题文】（3）曲线在点处的切线与坐标轴所围成的三角形的面积为（A）（B）（C）(D)【知识点】利用导数研究曲线上某点切线方程． B11【答案解析】D 解析：∵曲线y=，∴y′=×，切线过点（4，e2）∴f（x）|x=4=e2，∴切线方程为：y﹣e2=e2（x﹣4），令y=0，得x=2，与x轴的交点为：（2，0），令x=0，y=﹣e2，与y轴的交点为：（0，﹣e2），∴曲线y=在点（4，e2）处的切线与坐标轴所围三角形的面积s=×2×|﹣e2|=e2，故选D．【思路点拨】利用导数求曲线上点切线方程，求直线与x轴，与y轴的交点，然后求切线与坐标轴所围三角形的面积．【题文】(4)下列函数中是偶函数且在上单调递增的是（A）（B）（C）（D）【知识点】函数奇偶性的性质． B4【答案解析】D 解析：A，y=2﹣x定义域是{x|x≠0}，是偶函数，且在（0，+∞）上单调递减，则A不符合；B，函数y=lnx的定义域是（0，+∞），则是非奇非偶函数，B不符合题意；C，函数y=x﹣2的定义域是{x|x≠0}，但在（0，+∞）单调递减，C不符合题意；D，y=|x|﹣1为偶函数，在（0，+∞）上单调递增，D正确．故选：D．【思路点拨】根据基本初等函数的单调性奇偶性，逐一分析答案四个函数在（0，+∞）上的单调性和奇偶性，逐一比照后可得答案．【题文】（5）“”是“”的（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必要条件【知识点】充要条件． A2【答案解析】A 解析：由得：当a＞0时，有1＜a，即a＞1；当a＜0时，不等式恒成立．所以⇔a＞1或a＜0，从而a＞1是的充分不必要条件．故应选：A【思路点拨】可以把不等式“”变形解出a的取值范围来，然后再作判断，具体地来说，两边同乘以分母a要分类讨论，分a＞0，a＜0两类来讨论，除了用符号法则，这是解答分式不等式的另一种重要方法．【题文】（6）若，则下列不等式成立的是（A）（B）（C）（D）【知识点】不等式的基本性质．E1【答案解析】C 解析：b=，a=，则ab=，b2=，故A不正确；a2=，ab=，故D不正确；log=﹣2，log=﹣1，故B不正确；∵0＜b＜a＜1，2＞1，∴2b＜2a＜2，故选：C．【思路点拨】取特殊值，确定A，B，D不正确，0＜b＜a＜1，2＞1，利用指数函数的单调性，可得C正确．【题文】（7）如图，已知直线l和圆C，当l从l0开始在平面上绕O匀速旋转（转动角度不超过90°）时，它扫过的圆内阴影部分的面积y是时间x的函数，这个函数的图象大致是(A) (B) (C) (D)【知识点】直线与圆相交的性质．H4【答案解析】B 解析：观察可知面积S变化情况为“一直增加，先慢后快，过圆心后又变慢”对应的函数的图象是变化率先变大再变小，由此知D符合要求，故选B【思路点拨】由图象可以看出，阴影部分的面积一开始增加得较慢，面积变化情况是先慢后快然后再变慢，由此规律找出正确选项。

2020-2021学年⾼三数学第⼀次模拟考试试题及答案解析最新⾼三第⼀次模拟考试数学试题(考试时间：120分钟总分：160分)注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的⽆效．⼀、填空题：（本⼤题共14⼩题，每⼩题5分，共70分．请将答案填⼊答题纸填空题的相应答题线上．）1．已知集合{}21A x x =≤，集合{}2,1,0,1,2B =--，则A B = ▲．2．如图，在复平⾯内，点A 对应的复数为1z ，若21i z z =（i 为虚数单位），则2z = ▲．3．在平⾯直⾓坐标系xOy 中，双曲线2212x y -=的实轴长为▲．4．某校共有教师200⼈，男学⽣800⼈，⼥学⽣600⼈，现⽤分层抽样的⽅法从所有师⽣中抽取⼀个容量为n 的样本，已知从男学⽣中抽取的⼈数为100 ⼈，那么n = ▲．5．执⾏如图所⽰的伪代码，当输⼊,a b 的值分别为1,3时，最后输出的a的值为▲．6．甲⼄两⼈下棋，若甲获胜的的概率为15，甲⼄下成和棋的概率为25，则⼄不输棋的概率为▲．7．已知直线(0)y kx k =>与圆22:(2)1C x y -+=相交于,A B 两点，若255AB =，则k = ▲．8．若命题“存在20,4R x ax x a ∈++≤”为假命题，则实数a 的取值范围是▲． 9．如图，长⽅体1111ABCD A B C D -中，O 为1BD 的中点，三棱锥O ABD -的体积为1V ，四棱锥11O ADD A -的体积为2V ，则12VV的值为▲．10．已知公差为2的等差数列{}n a 及公⽐为2的等⽐数列{}n b 满⾜11220,0a b a b +>+<，Read ,1While 21End WhilePrint a b i i a a b b a bi i a ←≤←+←-←+（第5题）（第9题）OCDBC 1A B 1A 1D 1（第2题）则33a b +的取值范围是▲．11．设()f x 是R 上的奇函数，当0x >时，()2ln4x xf x =+，记(5)n a f n =-，则数列 {}n a 的前8项和为▲．12．在平⾯直⾓坐标系xOy 中，已知点,A B 分别为x 轴，y 轴上⼀点，且2AB =，若点P ，则AP BP OP ++的取值范围是▲．13．若正实数,x y 满⾜2(21)(52)(2)xy y y -=+-，则12x y+的最⼤值为▲．14．已知函数π()sin()cos cos()262x x f x A x θ=+--（其中A 为常数，(π,0)θ∈-），若实数123,,x x x 满⾜：①123x x x <<，②31x x -<2π，③123()()()f x f x f x ==，则θ的值为▲．⼆、解答题：（本⼤题共6⼩题，共90分．解答应写出⽂字说明，证明过程或演算步骤．） 15．（本题满分14分）在ABC ?中，⾓,A B 的对边分别为,a b ，向量(cos ,sin ),(cos ,sin )A B B A ==m n ．（1）若cos cos a A b B =，求证：//m n ；（2）若⊥m n ,a b >，求tan2A B-的值．如图，在三棱锥P ABC -中，90PAC BAC ∠=∠=?，PA PB =，点D ，F 分别为BC ，AB 的中点．（1）求证：直线//DF 平⾯PAC ；（2）求证：PF ⊥AD ．17．（本题满分14分）⼀个玩具盘由⼀个直径为2⽶的半圆O 和⼀个矩形ABCD 构成，1AB =⽶，如图所⽰．⼩球从A 点出发以v 5的速度沿半圆O 轨道滚到某点E 处后，经弹射器以6v 的速度沿与点E 切线垂直的⽅向弹射到落袋区BC 内，落点记为F ．设AOE θ∠=弧度，⼩球从A 到F 所需时间为T ．（1）试将T 表⽰为θ的函数()T θ，并写出定义域；（2）求时间T 最短时cos θ的值．18．（本题满分16分）已知数列{},{}n n a b 满⾜2(2)n n n S a b =+，其中n S 是数列{}n a 的前n 项和．（1）若数列{}n a 是⾸项为23，公⽐为13-的等⽐数列，求数列{}n b 的通项公式；（2）若n b n =，23a =，求数列{}n a 的通项公式；（3）在（2）的条件下，设n n nac b =，求证：数列{}n c 中的任意⼀项总可以表⽰成该数列其他两项之积．如图，在平⾯直⾓坐标系xOy 中，已知圆:O 224x y +=，椭圆:C 2214x y +=， A 为椭圆右顶点．过原点O 且异于坐标轴的直线与椭圆C 交于,B C 两点，直线AB 与圆O 的另⼀交点为P ，直线PD 与圆O 的另⼀交点为Q ，其中6(,0)5D -．设直线,AB AC 的斜率分别为12,k k ．（1）求12k k 的值；（2）记直线,PQ BC 的斜率分别为,PQ BC k k ，是否存在常数λ，使得PQ BC k k λ=？若存在，求λ值；若不存在，说明理由；（3）求证：直线AC 必过点Q ．20．（本题满分16分）已知函数()4212f x ax x =-，(0,)x ∈+∞，()()()g x f x f x '=-．（1）若0a >，求证：（ⅰ）()f x 在()f x '的单调减区间上也单调递减；（ⅱ）()g x 在(0,)+∞上恰有两个零点；（2）若1a >，记()g x 的两个零点为12,x x ，求证：1244x x a <+<+．数学试题（附加题）21.【选做题】请考⽣在A 、B 、C 、D 四⼩题中任选两题作答.如果多做，按所做的前两题记分. A ．（⼏何证明选讲，本题满分10分）如图,圆O 是ABC ?的外接圆,点D 是劣弧BC 的中点,连结AD 并延长,与以C 为切点的切线交于点P ,求证:PC BDPA AC=.B ．（矩阵与变换，本题满分10分）已知矩阵1252M x -??=的⼀个特征值为2-,求2M .C ．（坐标系与参数⽅程，本题满分10分）在平⾯直⾓坐标系xoy 中,已知直线11:()72x t C t y t=+??=-?为参数与椭圆2cos :(0)3sin x a C a y θθθ=?>?=?为参数,的⼀条准线的交点位于y 轴上,求实数a 的值.D ．（不等式选讲，本题满分10分）已知正实数,,a b c 满⾜231a b c ++=，求证：24627111a b c ++≥.P22．【必做题】（本题满分10分）如图，在直三棱柱ABC —A 1B 1C 1中，AC = 3，BC = 4，AB = 5，AA 1 = 4．（1）设AB AD λ=，异⾯直线AC 1与CD，求λ的值；（2）若点D 是AB 的中点，求⼆⾯⾓D —CB 1—B 的余弦值．23. 【必做题】（本题满分10分）已知,N*k m ∈，若存在互不相等的正整数12,,a a …,m a ，使得1223,,a a a a …11,,m m m a a a a -同时⼩于k ，则记()f k 为满⾜条件的m 的最⼤值．（１）求(6)f 的值；（２）对于给定的正整数n (1)n >，（ⅰ）当(2)(1)(2)n n k n n +<≤++时，求()f k 的解析式；（ⅱ）当(1)(2)n n k n n +<≤+时，求()f k 的解析式．1A⾼三数学参考答案⼀、填空题1．}{1,0,1-； 2．2i --； 3． 4．200； 5．5； 6．45； 7．12； 8．(2,)+∞； 9．12； 10．(,2)-∞-； 11．16-； 12．[7,11]； 13．12- ； 14．23π-. ⼆、解答题15. 证明：（1）因为cos cos a A b B =，所以sin cos sin cos A A B B =，所以//m n . ……………7分（2）因为⊥m n ，所以cos cos sin sin 0A B A B +=，即cos()0A B -=，因为a b >，所以A B >，⼜,(0,)A B π∈，所以(0,)A B π-∈，则2-=，…12分所以tantan 124A B π-==. ……………14分 16. 证明（1）∵点D ，F 分别为BC ，AB 的中点，∴//DF AC ，⼜∵DF ?平⾯PAC ，AC ?平⾯PAC ，∴直线//DF 平⾯PAC ． ……………6分（２）∵90PAC BAC ∠=∠=?，∴AC AB ⊥，AC AP ⊥，⼜∵AB AP A =，,AB AP 在平⾯PAB 内，∴AC ⊥平⾯PAB ， ……………8分∵PF ?平⾯PAB ，∴AC PF ⊥，∵PA PB =，F 为AB 的中点，∴PF AB ⊥，∵AC PF ⊥，PF AB ⊥，AC AB A =，,AC AB 在平⾯ABC 内，∴PF ⊥平⾯ABC ， ……………12分∵AD ?平⾯ABC ，∴AD PF ⊥． ……………14分17. 解：（1）过O 作OG BC ⊥于G ，则1OG =，1sin sin OG OF θθ==，11sin EF θ=+，AE θ=，所以11()5656sin 6AE EF T v v v v v θθθ=+=++，[,]44θ∈π3π．……7分（写错定义域扣1分）（2）11()56sin 6T v v v θθθ=++，1cos 6sin 5cos (2cos 3)(3cos 2)()56sin 30sin 30sin T v v v v θθθθθθθθθ-+-'=-==-，…………9分记02cos 3θ=，0[,]44θ∈π3π，θ0(,)4πθ 0θ 03(,)4πθ ()T θ' - 0 +()T θ故当2cos 3θ=时，时间T 最短． …………14分 18. 解：（1）因为1211()2()333n n n a -=-=--，21[(1()]1133[(1()]1231()3n n n S --==----， …………2分所以11()2131222()23nn n n n S b a --===+--+． …………4分（2）若n b n =，则22n n S na n =+，∴112(1)2n n S n a ++=++，两式相减得112(1)2n n n a n a na ++=+-+，即1(1)2n n na n a +=-+，当2n ≥时，1(1)(2)2n n n a n a --=-+，两式相减得11(1)(1)2(1)n n n n a n a n a -+-+-=-，即112n n n a a a -++=， …………8分⼜由1122S a =+，22224S a =+得12a =，23a =，所以数列{}n a 是⾸项为2，公差为321-=的等差数列，故数列{}n a 的通项公式是1n a n =+．…………10分（3）由（2）得1n n c n+=，对于给定的*n N ∈，若存在*,,,k t n k t N ≠∈，使得n k t c c c =?，只需111n k t n k t即1111(1)(1)n k t +=+?+，即1111n k t kt =++，则(1)n k t k n +=-， …………12分取1k n =+，则(2)t n n =+，∴对数列{}n c 中的任意⼀项1n n c n +=，都存在121n n c n ++=+和2222212n n n n c n n +++=+使得212n n n n c c c ++=?． …………16分 19．解：（1）设00(,)B x y ，则00(,)C x y --，2 20014x y += 所以22000012220000111422424x y y y k k x x x x -====--+--． …………4分（2）联⽴122(2)4y k x x y =-??+=?得2222111(1)44(1)0k x k x k +-+-=，解得211122112(1)4,(2)11P P P k k x y k x k k --==-=++，联⽴122(14y k x x y ?=??+=??得2222111(14)164(41)0k x k x k +-+-=，解得211122112(41)4,(1414B B Bk k x y k x k k --===++， …………8分所以121241B BC B y k k x k -==-，1211141562(1)641515P PQ P k y k k k k k x k -+-===--+++，所以52PQ BC k k =，故存在常数52λ=，使得52PQ BC k k =． …………10分（3）当直线PQ 与x 轴垂直时，68(,)55Q --，则28156225AQ k k -===--，所以直线AC 必过点Q ．当直线PQ 与x 轴不垂直时，直线PQ ⽅程为：12156()415k y x k -=+-，联⽴1212256()4154k y x k x y -?=+?-??+=?，解得21122112(161)16,161161Q Q k k x y k k --==++，所以1212211211616112(161)42161AQk k k k k k k +==-=---+，故直线AC 必过点Q ． …………16 分（不考虑直线PQ 与x 轴垂直情形扣1分）20. 证：（1）因为()()42102f x ax x x =->，所以3()4f x ax x '=-，由32(4)1210ax x ax '-=-<得()f x '的递减区间为， …………2 分当x ∈时，32()4(41)0f x ax x x ax '=-=-<，所以(f x 在()f x '的递减区间上也递减． …………4 分（2）解1：()()()42343211(4)422g x f x f x ax x ax x ax ax x x '=-=---=--+，因为0x >，由()4321402g x ax ax x x =--+=得3214102ax ax x --+=，令321()412x ax ax x ?=--+，则21()382x ax ax ?'=--，因为0a >，且1(0)02'=-<，所以()x ?'必有两个异号的零点，记正零点为0x ，则0(0,)x x ∈时，()0x ?'<，()x ?单调递减；0(,)x x ∈+∞时，()0x ?'>，()x ?单调递增，若()x ?在(0,)+∞上恰有两个零点，则0()0x ?<， (7)分由20001()3802x ax ax ?'=--=得2001382ax ax =+，所以0003217()939x ax x ?=--+，⼜因为对称轴为4,3x =所以81()(0)032??==-<，所以08733x >>，所以0003217()()0933x ax x ?=---<，⼜3222111()41(8)(1)1222x ax ax x ax x x ax ?=--+=-+-+，中的较⼤数为M ，则()0M ?>，故0a >()g x 在(0,)+∞上恰有两个零点． …………10 分解2：()()()42343211(4)422g x f x f x ax x ax x ax ax x x '=-=---=--+，因为0x >，由()4321402g x ax ax x x =--+=得3214102ax ax x --+=，令321()412x ax ax x ?=--+，若()g x 在(0,)+∞上恰有两个零点，则()x ?在(0,)+∞上恰有两个零点，当2x =时，由()0x ?=得0a =，此时1()12x x ?=-+在(0,)+∞上只有⼀个零点，不合题意；当2x ≠时，由321()4102x ax ax x ?=--+=得321422x x a x -=-， …………7 分令322148()2422x x x x x x x ?-==-----，则22122572[()]2(58)24()0(2)(2)x x x x x x x x ?-+-+'==>--，当(0,2)x ∈时，()x ?单调递增，且由2824,2y x x y x =--=--值域知 ()x ?值域为(0,)+∞；当(2,)x ∈+∞时，1()x ?单调递增，且1(4)0?=，由2824,2y x x y x =--=--值域知()x ?值域为(,)-∞+∞；因为0a >，所以102a >，⽽12y a=与1()x ?有两个交点，所以1()x ?在(0,)+∞上恰有两个零点． …………10 分（3）解1：由（2）知，对于321()412x ax ax x ?=--+在(0,)+∞上恰有两个零点12,x x ，不妨设12x x <，⼜因为(0)10?=>，11()(67)028a ?=-<，所以11 02x <<，……12 分⼜因为(4)10?=-<，91()(65710)028a ?=->，所以2942x <<，所以121945422x x a <+<+=<+． …………16 分解2：由（2）知321422x x a x -=-，因为[0,2)x ∈时，1()x ?单调递增，17()212?=，111111(0)0()()22x a =<=<，所以1102x <<， …………12 分当(2,)x ∈+∞时，1()x ?单调递增，1981()220?=，112119(4)0()()22x a =<=<，所以2942x <<，所以121945422x x a <+<+=<+． …………16 分附加题参考答案21.A ．证明：连结CD ，因为CP 为圆O 的切线，所以PCD PAC ∠=∠,⼜P ∠是公共⾓，所以PCD ?～PAC ?， ……………5分所以PC CDPA AC=, 因为点D 是劣弧BC 的中点,所以CD BD =,即PC BDPA AC=. ……………10分 21.B . 解：2λ=-代⼊212(1)(5)052x x xλλλλ+-=---+=--，得3x =矩阵12532M -??= ……………5分∴264514M ??=??……………10分 21.C . 解：直线1C ：29x y +=，椭圆2C :2221(03)9y x a a+=<<， …………………………5分准线：29y a =±-由299a=-得，22a = …………………………10分 21.D .证明：因为正实数,,a b c 满⾜231a b c ++=，所以32313ab c ≥，即23127ab c ≤， …………………………5分所以23127ab c ≥ 因此，32462461111327a b c a b c++≥≥ ……………………10分22. 解：（１）由AC = 3，BC = 4，AB = 5得090ACB ∠= ……………１分以CA 、CB 、CC 1所在直线分别为x 轴、y 轴、z 轴建⽴如图所⽰的空间直⾓坐标系．则Ａ(3,0,0)，1C (0,0,4)，B(0,4,0)，设D(x,y,z)，则由AB AD λ=得(33,4,0)CD λλ=-，⽽1(3,0,4)AC =-，根据2910||50525189λλ=-+解得，15λ=或13λ=- ……………５分（２）13(,2,0),(0,4,4)2CD CB ==，可取平⾯1CDB 的⼀个法向量为1(4,3,3)n =-；…………………………７分⽽平⾯1CBB 的⼀个法向量为2(1,0,0)n =，并且12,n n <>与⼆⾯⾓D —CB 1—B 相等，所以⼆⾯⾓D —CB 1—B的余弦值为12cos cos ,n n θ=<>=………１０分（第（１）题中少⼀解扣１分；没有交代建⽴直⾓坐标系过程扣1分．第（２）题如果结果相差符号扣１分．）23. 解：（1）由题意，取121,2a a ==，126a a <，满⾜题意，若33a ?≥，则必有236a a ≥，不满⾜题意，综上所述：m 的最⼤值为2，即(6)2f =． ………………4分（２）由题意，当(1)(1)(2)n n k n n +<≤++时，设1{1,2,A =…,}n，2{1,2,3,A n n n =+++…}，显然，?11,i i a a A +∈时，满⾜1(1)(1)i i a a n n n n k +≤-<+<，∴从集合1A 中选出的i a ⾄多n 个，12,j j a a A +∈时，1(1)(2)j j a a n n k +≥++≥，∴从集合2A 中选出的j a 必不相邻，⼜∵从集合1A 中选出的i a ⾄多n 个，∴从集合2A 中选出的j a ⾄多n 个，放置于从集合1A 中选出的i a 之间，∴()2f k n ≤， ………………6分（ⅰ）当(2)(1)(2)n n k n n +<≤++时，取⼀串数i a 为：1,2,2,21,3,22,n n n --…,1,2,,1n n n n -++，或写成1, 221,2i i i a i n i +??=??+-?为奇数为偶数，（12i n ≤≤），此时1(2)i i a a n n k +≤+<，(121i n ≤≤-),211n a a n k =+<，满⾜题意，∴()2f k n =， ………………8分（ⅱ）当(1)(2)n n k n n +<≤+时，从1A 中选出的n 个i a ：1,2,…,n ，考虑数n 的两侧的空位，填⼊集合2A 的两个数,p q a a ，不妨设p q na na >，则(2)p na n n k ≥+≥，与题意不符，∴()21f k n ≤-，取⼀串数i a 为：1,21,2,22,3,23,n n n ---…,2,2,1,1,n n n n n -+-+或写成1,22,2i i i a i n i +??=??-?为奇数为偶数，（121i n ≤≤-），此时1(1)i i a a n n k +≤+<，（122i n ≤≤-），211n a a n k -=<，满⾜题意，∴()21f k n =-， ………………10分（写出（ⅰ）、（ⅱ）题的结论但没有证明各给１分．）。

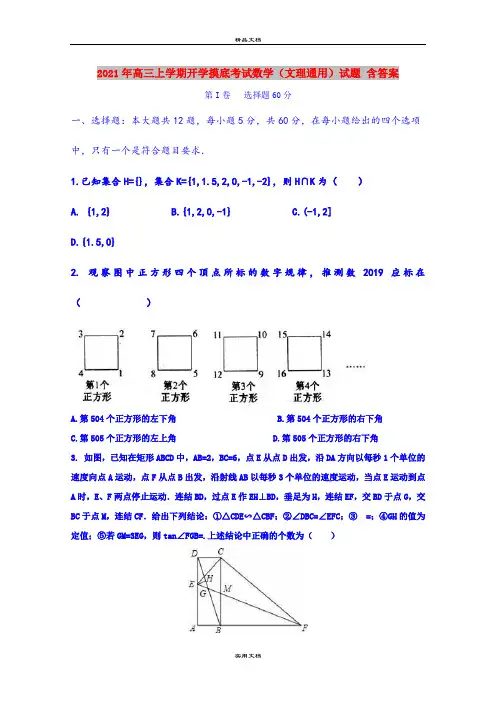
2021年高三上学期开学摸底考试数学（文理通用）试题含答案第I卷选择题60分一、选择题：本大题共12题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求．1.已知集合H={}，集合K={1,1.5,2,0,-1,-2}，则H∩K为（）A. {1,2}B.{1,2,0,-1}C.(-1,2]D.{1.5,0}2. 观察图中正方形四个顶点所标的数字规律，推测数2019应标在（）A.第504个正方形的左下角B.第504个正方形的右下角C.第505个正方形的左上角D.第505个正方形的右下角3. 如图，已知在矩形ABCD中，AB=2，BC=6，点E从点D出发，沿DA方向以每秒1个单位的速度向点A运动，点F从点B出发，沿射线AB以每秒3个单位的速度运动，当点E运动到点A时，E、F两点停止运动．连结BD，过点E作EH⊥BD，垂足为H，连结EF，交BD于点G，交BC于点M，连结CF．给出下列结论：①△CDE∽△CBF；②∠DBC=∠EFC；③=；④GH的值为定值；⑤若GM=3EG，则tan∠FGB=.上述结论中正确的个数为（）A．2 B.3 C.4D.54. 设分别是方程和的根(其中), 则的取值范围是( )A. B. C. D.5. 已知函数.若方程有两个不相等的实根，则实数的取值范围是（）A． B．C． D．6. 若关于的方程恒有实数解，则实数m的取值范围是（）A. B. C.D.7. 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈L2h，它实际上是将圆锥体积公式中的圆周率π近似取为3，那么，近似公式V≈L2h相当于将圆锥体积公式中的π近似取为（）A． B． C．D．8. 函数f(x)＝2x＋sin x的部分图像可能是( )9. 已知O为坐标原点，双曲线的左焦点为，以OF为直径的圆交双曲线C的渐近线于A,B，O 三点，且.关于的方程的两个实数根分别为和，则以为边长的三角形的形状是（）A.钝角三角形 B.直角三角形 C. 锐角三角形 D. 等腰直角三角形10. 已知直线l⊥平面α，直线m⊂平面β，则下列四个命题：①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β；④l⊥m⇒α∥β其中正确命题的序号是（）A.①②B.②④C.③④D.①③11. 已知F1、F2分别是双曲线（，）的左、右焦点，且F2是抛物线（p＞0）的焦点，双曲线C1与抛物线C2的一个公共点是P．若线段的中垂线恰好经过焦点F1，则双曲线C1的离心率是（）A． B． C． D．12. 若复数满足，其中为虚数为单位，则=（）A.1-iB.1+iC. -1-iD. i-1第II卷非选择题90分二、填空题：本大题共4小题，每小题5分，共20分．13.执行如图所示的程序框图，若输出S的值为﹣18，则输入的S值为___________.14.已知等差数列{a n}中，a1=1，S11=33，则公差d等于______________.15. 函数y=f（x）为R上可导函数，则f′（x0）=0是x0为函数f（x）极值点的_____________条件.16. 已知椭圆+=1(a>b>0)上一点A关于原点的对称点为B，F为其右焦点，若AF⊥BF，设∠ABF=α，且α∈，则该椭圆离心率的取值范围为_______________.三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（12分）函数()的最大值为3, 其图像相邻两条对称轴之间的距离为.(1)求函数的解析式;(2)设,则,求的值18．（12分）如图1，在正方形中，，是边的中点，是边上的一点，对角线分别交、于、两点．将折起，使重合于点，构成如图2所示的几何体．（Ⅰ）求证：面；（Ⅱ）试探究：在图1中，在什么位置时，能使折起后的几何体中／／平面，并给出证明．19．（12分）在某大学自主招生考试中，所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A，B，C，D，E五个等级．某考场考生的两科考试成绩的数据统计如图所示，其中“数学与逻辑”科目的成绩为B的考生有10人．（Ⅰ）求该考场考生中“阅读与表达”科目中成绩为A的人数；（Ⅱ）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分，求该考场考生“数学与逻辑”科目的平均分；（Ⅲ）已知参加本考场测试的考生中，恰有两人的两科成绩均为A．在至少一科成绩为A的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为A的概率．20．（12分）已知椭圆E：+=1（a＞b＞0）的离心率e=，并且经过定点P（，）．（Ⅰ）求椭圆E的方程；（Ⅱ）问是否存在直线y=﹣x+m，使直线与椭圆交于A、B两点，满足•=，若存在求m值，若不存在说明理由．21.（12分）已知函数。

第Ⅰ卷（选择题）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集}5,4,3,2,1{=U ,集合}23{<-∈=x Z x A ，则集合=A C U （ ）A ． {1, 2, 3, 4}B ．{2, 3, 4}C ．{1,5}D ．{5}2．设函数)2()1()(2-+=x x x f ，则=')1(f （ ）A ． 1-B ． 0C ．1D ．43． 曲线22x y =在点P(1,2)处的切线方程是（ ）A ． 024=--y xB ．024=-+y xC ．024=++y xD ．024=-+-y x4．已知α、β是两个不同平面，m 、n 是两不同直线，下列命题中的假命题是（ ）A ．αα⊥⊥n m n m 则若,,//B ．n m n m //,,//则若=βααIC ．βαβα//,,则若⊥⊥m mD ．βαβα⊥⊂⊥则若,,m m5．曲线x x y +=331在点)34,1(处的切线与坐标轴围成的三角形面积为（ ）A ．91B ．92C ．31D ．326． 函数433123--+=x x x y 在[0, 2]上最小值是 （ ）A ．317-B ．310-C ．4-D ．364-7．已知一个球的直径为3，则此球的表面积为 （ ）A ．π3B ． π4C ．π33D ．π68．若n xx )1(+的展开式的二项式系数之和为64，则展开式的常数项为 （ ）A ． 10B ． 20 C．30D ．1209．由数字1，2，3，4，5所组成的三位数中，其各个数字之和为9的三位数共有 （ ） A ．16个 B ．18个C．19个D ．21个10．P 为抛物线2x y =上的任意一点，则P 到直线02=--y x 的最短距离为 （ ）A ．2B ．827 C ．22 D ．011．设函数)(x f 是R 上以5为周期的可导偶函数，则曲线)(x f y =在5=x 处的切线的斜率为（ ）A ． 51- B ． 0C ．51D ．512．设]1,1[,,2141)(2124-∈-=x x x x x f ，且()1x f ()2x f <，则下列结论必成立的是A ．1x ＞2xB ．1x +2x ＞0C ．1x ＜2xD ．21x ＞22x第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，共20分． 13．2323)(x x x f +=的单调减区间是14．从4名男生和6名女生，选出3名奥运火炬手，要求至少包含1名男生，则不同的选法共有15．某校现有高一学生210人，高二学生270人，高三学生300人，校学生会采用分层抽样的方法从这三个的学生中随机抽取n 名学生进行问卷调查，如果已知从高一学生中抽取的人数为7，那么从高三学生中抽取的人数为16．在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是 （写出所有正确结论的编号．．）. ①矩形；②不是矩形的平行四边形；③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；④每个面都是等边三角形的四面体； ⑤每个面都是直角三角形的四面体.三、解答题（本大题共6小题，共70分。

最新高三年级第一次模拟考试数 学 试 题(总分160分，考试时间120分钟)参考公式锥体的体积公式：13V Sh =，其中S 为底面积,h 为高. 一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上） 1．已知集合{}210A x x =-=，{}1,2,5B =-，则A B I = ▲ .2．已知复数21iz i+=-（i 是虚数单位），则||z = ▲ . 3．书架上有3本数学书，2本物理书，从中任意取出2本，则取出的两本书都是数学书的概率为 ▲ . 4．运行如图所示的伪代码，其结果为 ▲ .5．某校高一年级有学生400人，高二年级有学生360人， 现采用分层抽样的方法从全校学生中抽出55人，其中 从高一年级学生中抽出20人，则从高三年级学生中抽 取的人数为 ▲ .6．在平面直角坐标系xOy 中，已知抛物线C 的顶点在坐标原点，焦点在x 轴上，若曲线C 经过点(1,3)P ，则其焦点到准线的距离为 ▲ .7．已知实数,x y 满足50,220,0,x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩则目标函数z x y =-的最小值为 ▲ .8．设一个正方体与底面边长为▲ . 9．在ABC ∆中，设,,a b c 分别为角,,A B C 的对边，若5a =，4A π=，3cos 5B =，则边c = ▲ .10．设n S 是等比数列{}n a 的前n 项和，0n a >，若6325S S -=，则96S S -的最小值为 ▲ .11．如图，在ABC ∆中，3AB AC ==，1cos 3BAC ∠=，2DC BD =u u u r u u u r ，则AD BC ⋅u u u r u u u r的值为 ▲ .12．过点(4,0)P -的直线l 与圆22:(1)5C x y -+=相交于,A B 两点，若点A 恰好是线段PB 的中点，则直线l 的方程为 ▲ .13．设()f x 是定义在R 上的奇函数，且()22x x mf x =+，设(),1,()(),1,f x x g x f x x >⎧=⎨-≤⎩若函数()y g x t =-有且只有一个零点，则实数t 的取值范围是 ▲ .14．设函数32,,ln ,x x x e y a x x e ⎧-+<=⎨≥⎩的图象上存在两点,P Q ，使得POQ ∆是以O 为直角顶点的直角三角形（其中O 为坐标原点），且斜边的中点恰好在y 轴上，则实数a 的取值范围是 ▲ .二、解答题（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．(本小题满分14分)设函数()sin()(0,0,,)22f x A x A x R ππωϕωϕ=+>>-<<∈的部分图象如图所示.（1）求函数()y f x =的解析式； （2）当[,]22x ππ∈-时，求()f x 的取值范围.16．(本小题满分14分)如图，已知直三棱柱111ABC A B C -的侧面11ACC A 是正方形，点O 是侧面11ACC A 的中心，2ACB π∠=，M 是棱BC 的中点.（1）求证：//OM 平面11ABB A ； （2）求证：平面1ABC ⊥平面1A BC .17．(本小题满分14分)如图所示，,A B 是两个垃圾中转站，B 在A 的正东方向16千米处，AB 的南面为居民生活区. 为了妥善处理生活垃圾，政府决定在AB 的北面建一个垃圾发电厂P . 垃圾发电厂P 的选址拟满足以下两个要求（,,A B P 可看成三个点）：①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比，比例系数相同；②垃圾发电厂应尽量远离居民区（这里参考的指标是点P 到直线AB 的距离要尽可能大）. 现估测得,A B 两个中转站每天集中的生活垃圾量分别约为30吨和50吨，问垃圾发电厂该如何选址才能同时满足上述要求？6318．(本小题满分16分)如图，在平面直角坐标系xOy 中，设点00(,)M x y 是椭圆22:14x C y +=上一点，从原点O 向圆22200:()()M x x y y r -+-=作两条切线分别与椭圆C 交于点,P Q ，直线,OP OQ 的斜率分别记为12,k k .（1）若圆M 与x 轴相切于椭圆C 的右焦点，求圆M 的方程；（2）若r =. ①求证：1214k k =-； ②求OP OQ ⋅的最大值.19．(本小题满分16分)已知函数()xaxf x e =在0x =处的切线方程为y x =. （1）求a 的值；（2）若对任意的(0,2)x ∈，都有21()2f x k x x <+-成立，求k 的取值范围；（3）若函数()ln ()g x f x b =-的两个零点为12,x x ，试判断12()2x x g +'的正负，并说明理由.20．(本小题满分16分)设数列{}n a 共有(3)m m ≥项，记该数列前i 项12,,,i a a a L 中的最大项为i A ，该数列后m i -项12,,,i i m a a a ++L 中的最小项为i B ，(1,2,3,,1)i i i r A B i m =-=-L .（1）若数列{}n a 的通项公式为2nn a =，求数列{}i r 的通项公式；（2）若数列{}n a 满足11a =，2i r =-，求数列{}n a 的通项公式；（3）试构造一个数列{}n a ，满足n n n a b c =+，其中{}n b 是公差不为零的等差数列，{}n c 是等比数列，使得对于任意给定的正整数m ，数列{}i r 都是单调递增的，并说明理由.高三年级第一次模拟考试数学附加题部分（本部分满分40分，考试时间30分钟）21．[选做题]（在A 、B 、C 、D 四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内）A .（选修4—1：几何证明选讲）如图，AB 为⊙O 的直径，直线CD 与⊙O 相切于点D ，AC ⊥CD ，DE ⊥AB ，C 、E 为垂足，连接,AD BD . 若4AC =，3DE =，求BD 的长.B .（选修4—2：矩阵与变换）设矩阵 02 1a ⎡⎤=⎢⎥⎣⎦M 的一个特征值为2，若曲线C 在矩阵M 变换下的方程为221x y +=，求曲线C 的方程.C ．（选修4—4：坐标系与参数方程）在极坐标系中，已知点A 的极坐标为)4π-，圆E 的极坐标方程为4cos 4sin ρθθ=+，试判断点A 和圆E 的位置关系.D ．(选修4—5：不等式选讲）已知正实数,,,a b c d 满足1a b c d +++=.[必做题]（第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内） 22．（本小题满分10分）直三棱柱111ABC A B C -中，AB AC ⊥，2AB =，4AC =，12AA =，BD DC λ=u u u r u u u r. （1）若1λ=，求直线1DB 与平面11AC D 所成角的正弦值； （2）若二面角111B AC D --的大小为60︒，求实数λ的值.23．（本小题满分10分）设集合{}1,2,3,,(3)M n n =≥L ，记M 的含有三个元素的子集个数为n S ，同时将每一个子集中的三个元素由小到大排列，取出中间的数，所有这些中间的数的和记为n T .（1）求33T S ，44TS ，55T S ，66T S 的值； （2）猜想n nTS 的表达式，并证明之.数学参考答案一、填空题：本大题共14小题，每小题5分，计70分.1.{}1-2.3. 3104. 175. 176. 927. 3- 8. 29. 7 10. 20 11. 2- 12. 340x y ±+= 13. 33[,]22- 14. 1(0,]1e + 二、解答题：本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内.15．解：（1）由图象知，2A =， …………2分又54632T πππ=-=，0ω>，所以22T ππω==，得1ω=. …………4分 所以()2sin()f x x ϕ=+，将点(,2)3π代入，得2()32k k Z ππϕπ+=+∈，即2()6k k Z πϕπ=+∈，又22ππϕ-<<，所以6πϕ=. ………6分所以()2sin()6f x x π=+. …………8分（2）当[,]22x ππ∈-时，2[,]633x πππ+∈-， …………10分所以sin()[6x π+∈，即()[2]f x ∈. …………14分 16．证明：（1）在1A BC ∆中，因为O 是1A C 的中点，M 是BC 的中点，所以1//OM A B . ..............4分 又OM ⊄平面11ABB A ，1A B ⊂平面11ABB A ，所以//OM 平面11ABB A . ............6分 （2）因为111ABC A B C -是直三棱柱，所以1CC ⊥底面ABC ，所以1CC BC ⊥，又2ACB π∠=，即BC AC ⊥，而1,CC AC ⊂面11ACC A ，且1CC AC C =I ，所以BC ⊥面11ACC A . .............8分 而1AC ⊂面11ACC A ，所以BC ⊥1AC ，又11ACC A 是正方形，所以11A C AC ⊥，而,BC 1AC ⊂面1A BC ，且1BC AC C =I ， 所以1AC ⊥面1A BC . .............12分 又1AC ⊂面1ABC ，所以面1ABC ⊥面1A BC . .............14分 17．解法一：由条件①，得505303PA PB ==. ..............2分 设5,3PA x PB x ==，则222(5)16(3)8cos 2165105x x x PAB x x+-∠==+⨯⨯， ..............6分所以点P 到直线AB的距离sin 5h PA PAB x =∠=== ...............10分所以当234x =，即x =h 取得最大值15千米.即选址应满足PA =PB =. ...........14分 解法二：以AB 所在直线为x 轴，线段AB 的中垂线为y 轴，建立平面直角坐标系. .......2分则(8,0),(8,0)A B -. 由条件①，得505303PA PB ==. ...............4分 设(,)(0)P x y y >，则=化简得，222(17)15(0)x y y -+=>， ...............10分 即点P 的轨迹是以点（17,0）为圆心、15为半径的圆位于x 轴上方的半圆. 则当17x =时，点P 到直线AB 的距离最大，最大值为15千米.所以点P 的选址应满足在上述坐标系中其坐标为(17,15)即可. ............14分 18．解：（1）因为椭圆C右焦点的坐标为0)，所以圆心M的坐标为1)2±， .......2分从而圆M的方程为2211(()24x y +±=. …………4分 （2）①因为圆M 与直线1:OP y k x ==， 即222010010(45)10450x k x y k y -++-=， ………6分 同理，有222020020(45)10450x k x y k y -++-=，所以12,k k 是方程2220000(45)10450x k x y k y -++-=的两根， ………8分从而222000122220001545(1)1451444545454x x y k k x x x ---+-====----. …10分②设点111222(,),(,)P x y P x y ，联立12214y k xx y =⎧⎪⎨+=⎪⎩，解得222111221144,1414k x y k k ==++， ……12分同理，222222222244,1414k x y k k ==++，所以222212222211224444()()14141414k k OP OQ k k k k ⋅=+⋅+++++ 22221211222212114(1)4(1)4411614141414k k k k k k k k ++++=⋅=⋅++++ ……………14分 221221520()252(14)4k k +≤=+， 当且仅当112k =±时取等号. 所以OP OQ ⋅的最大值为52. ……16分 19. 解：（1）由题意得(1)()xa x f x e -'=，因函数在0x =处的切线方程为y x =，所以(0)11af '==，得1a =. ……………4分（2）由（1）知21()2x x f x e k x x =<+-对任意(0,2)x ∈都成立，所以220k x x +->，即22k x x >-对任意(0,2)x ∈都成立，从而0k ≥. ………6分又不等式整理可得22x e k x x x <+-，令2()2x e g x x x x=+-， 所以22(1)()2(1)(1)(2)0x xe x e g x x x x x-'=+-=-+=，得1x =， ……………8分当(1,2)x ∈时，()0g x '>，函数()g x 在(1,2)上单调递增，同理，函数()g x 在(0,1)上单调递减，所以min ()(1)1k g x g e <==-， 综上所述，实数k 的取值范围是[0,1)e -. ……………10分 （3）结论是12()02x x g +'<. …………11分 证明：由题意知函数()ln g x x x b =--，所以11()1xg x x x-'=-=，易得函数()g x 在(0,1)单调递增，在(1,)+∞上单调递减，所以只需证明1212x x +>即可. ……12分因为12,x x 是函数()g x 的两个零点，所以1122ln ln x b x x b x +=⎧⎨+=⎩，相减得2211ln xx x x -=，不妨令211x t x =>，则21x tx =，则11ln tx x t -=，所以11ln 1x t t =-，2ln 1t x t t =-，即证1ln 21t t t +>-，即证1()ln 201t t t t ϕ-=->+， ……………14分因为22214(1)()0(1)(1)t t t t t t ϕ-'=-=>++，所以()t ϕ在(1,)+∞上单调递增，所以()(1)0t ϕϕ>=，综上所述，函数()g x 总满足12()02x x g +'<成立. …………16分20．解：（1）因为2n n a =单调递增，所以2ii A =，12i i B +=，所以1222i i ii r +=-=-，11i m ≤≤-. ……………4分（2）根据题意可知，i i a A ≤，1i i B a +≤，因为20i i i r A B =-=-<，所以i i A B <可得1i i i i a A B a +≤<≤即1i i a a +<，又因为1,2,3,,1i m =-L ，所以{}n a 单调递增， ……7分则i i A a =，1i i B a +=，所以12i i i r a a +=-=-，即12i i a a +-=，11i m ≤≤-， 所以{}n a 是公差为2的等差数列，12(1)21n a n n =+-=-，11i m ≤≤-. ……………10分（3）构造1()2n n a n =-，其中n b n =，1()2n n c =-. ………12分下证数列{}n a 满足题意.证明：因为1()2n n a n =-，所以数列{}n a 单调递增，所以1()2i i i A a i ==-，1111()2i i i B a i ++==+-， ……………14分所以1111()2i i i i r a a ++=-=--，11i m ≤≤-， 因为2121111[1()][1()]()0222i i i i i r r ++++-=-----=>，所以数列{}i r 单调递增，满足题意. ……………16分（说明：等差数列{}n b 的首项1b 任意，公差d 为正数，同时等比数列{}n c 的首项1c 为负，公比(0,1)q ∈，这样构造的数列{}n a 都满足题意.）附加题答案21. A 、解：因为CD 与O e 相切于D ，所以CDA DBA ∠=∠， ……2分又因为AB 为O e 的直径，所以90ADB ∠=︒.又DE AB ⊥，所以EDA DBA ∆∆:，所以EDA DBA ∠=∠，所以EDA CDA ∠=∠. ………4分又90ACD AED ∠=∠=︒，AD AD =，所以ACD AED ∆≅∆.所以4AE AC ==，所以5AD ==， ……… 6分又DE AE BD AD =，所以154DE BD AD AE =⋅=. …………10分 B 、由题意，矩阵M 的特征多项式()()((1)f a λλλ=--，因矩阵M 有一个特征值为2，(2)0f =，所以2a =. …………4分所以 2 0M 2 1x x x y y y '⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦，即22x xy x y'=⎧⎨'=+⎩， 代入方程221x y +=，得22(2)(2)1x x y ++=，即曲线C 的方程为22841x xy y ++=. ………10分C 、解：点A 的直角坐标为(2,2)-， …………2分圆E 的直角坐标方程为22(2)(2)8x y -+-=， ………6分 则点A 到圆心E的距离4d r ==>=，所以点A 在圆E 外. ………10分D、解：因24(12121212)a b c d ≤+++++++， (6)分又1a b c d +++=，所以224≤，≤ ………10分22．解：分别以1,,AB AC AA 所在直线为,,x y z 轴建立空间直角坐标系.则(0,0,0)A ，(2,0,0)B ，(0,4,0)C ，1(0,0,2)A ，1(2,0,2)B ，1(0,4,2)C ………2分 （1）当1λ=时，D 为BC 的中点，所以(1,2,0)D ，1(1,2,2)DB =-u u u u r ，11(0,4,0)AC =u u u u r ，1(1,2,2)A D =-u u u u r ，设平面11AC D 的法向量为1(,,)n x y z =u r 则4020y x z =⎧⎨-=⎩，所以取1(2,0,1)n =u r，又111111cos ,||||DB n DB n DB n ⋅<>===u u u u r u r u u u u r u r u u u u r u r ， 所以直线1DB 与平面11AC D…………6分 （2）BD DC λ=u u u r u u u r Q ，24(,,0)11D λλλ∴++，11(0,4,0)AC ∴=u u u u r ，124(,,2)11A D λλλ=-++u u u u r ， 设平面11AC D 的法向量为1(,,)n x y z =u r ，则402201y x z λ=⎧⎪⎨-=⎪+⎩， 所以取1(1,0,1)n λ=+u r . …………8分又平面111A B C 的一个法向量为2(0,0,1)n =u u r ，由题意得121|cos ,|2n n <>=u r u u r ，12=，解得1λ=或1λ=（不合题意，舍去）， 所以实数λ1. …………10分23.解：（1）332T S =，4452T S =，553T S =，6672T S =. ……………4分 （2）猜想12n n T n S +=. ……………5分 下用数学归纳法证明之.证明：①当3n =时，由（1）知猜想成立；②假设当(3)n k k =≥时，猜想成立，即12k k T k S +=，而3k k S C =，所以得312k k k T C +=. ……6分则当1n k =+时，易知311k k S C ++=， 而当集合M 从{}1,2,3,,k L 变为{}1,2,3,,,1k k +L 时，1k T +在k T 的基础上增加了1个2，2个3，3个4，…，和(1)k -个k ， ……………8分所以1k k T T +=+213243(1)k k ⨯+⨯+⨯++-L 3222223412[]2k k k C C C C C +=++++⋅⋅⋅+ 3322233412[]2k k k C C C C C +=++++⋅⋅⋅+3311222k k k C C ++-=+3122k k C ++=1(1)12k k S +++=， 即11(1)12k k T k S ++++=. 所以当1n k =+时，猜想也成立. 综上所述，猜想成立. ……………10分（说明：未用数学归纳法证明，直接求出n T 来证明的，同样给分.）。

原创精品资源学科网独家享有版权，侵权必究！12020年秋季高三开学摸底考试（一）一、单选题（共8小题，满分40分，每小题5分）1、（2020届山东省潍坊市高三上期中）已知集合{}220A x x x =-≥，{}03B x x =<<，则AB =（ ）A ．()1,3-B ．(]0,2C ．[)2,3D ．()2,3【答案】C 【解析】{|0A x x =≤或2}x ≥，{|03}B x x =<<，[2,3)A B ∴⋂=．故选：C.2、（2020届山东省烟台市高三上期末）设0.5log 3a =，30.5b =，0.513c -⎛⎫= ⎪⎝⎭，则,,a b c 的大小关系为（ ）A ．a b c <<B ．a c b <<C ．b a c <<D ．b c a <<【答案】A 【解析】由题,因为0.5log y x =单调递减,则0.50.5log 3log 10a =<=；因为0.5xy =单调递减,则3000.50.51b <=<=；因为3xy =单调递增,则0.50.5013313c -⎛⎫==>= ⎪⎝⎭,所以01a b c <<<<,原创精品资源学科网独家享有版权，侵权必究！2故选：A3、（2020届山东省日照市高三上期末联考）如图，《九章算术》中记载了一个“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？意思是：有一根竹子原高一丈（一丈10=尺），现被风折断，尖端落在地上，竹尖与竹根的距离三尺，问折断处离地面的高是（ ）A ．2.55尺B ．4.55尺C ．5.55尺D ．6.55尺【答案】B 【解析】已知一直角边为3尺，另两边和为10尺，设另一直角边为x 尺，则斜边为10x -尺，由勾股定理可得：()222310x x +=-，可得 4.55x =尺.故选：B4、（2020届山东省泰安市高三上期末）函数()3ln xf x x =的部分图象是（）原创精品资源学科网独家享有版权，侵权必究！3A ．B ．C ．D ．【答案】A 【解析】()()()33ln ln ,x xf x f x f x x x =-==--， ()f x 为奇函数，排除B 当1x >时，()3ln 0xf x x=>恒成立，排除CD 故答案选A5、（2020届山东省潍坊市高三上期末）已知345sin πα⎛⎫-= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，则cos α=（ ）A ．210B ．3210C ．22D ．7210【答案】A原创精品资源学科网独家享有版权，侵权必究！4【解析】0,2πα⎛⎫∈ ⎪⎝⎭，,444πππα⎛⎫-∈- ⎪⎝⎭24cos 1sin 445ππαα⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭，cos cos cos cos sin sin 444444ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=-+=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦42322525210=⨯-⨯=. 故选：A6、（2020届山东省泰安市高三上期末）已知圆22:10210C x y y +-+=与双曲线22221(0,0)x y a b a b-=>>的渐近线相切，则该双曲线的离心率是（ ）A 2B ．53C ．52D 5【答案】C 【解析】由双曲线22221(0,0)x y a b a b -=>>，可得其一条渐近线的方程为b y x a=，即0bx ay -=，又由圆22:10210C x y y +-+=，可得圆心为(0,5)C ，半径2r，则圆心到直线的距离为2255()a a d c b a -==+-，则52a c =，可得52c e a ==， 故选C.原创精品资源学科网独家享有版权，侵权必究！57、（2020届山东省泰安市高三上期末）已知正三棱锥S ABC -的侧棱长为36，则该正三棱锥外接球的表面积是（ ） A ．16π B ．20πC ．32πD ．64π【答案】D 【解析】如图所示，因为正三棱锥S ABC -的侧棱长为436，则236233AE ==2222(43)(23)6SE SA AE =-=-=, 又由球心O 到四个顶点的距离相等，在直角三角形AOE 中，,6AO R OE SE SO R ==-=-，又由222OA AE OE =+，即222(23)(6)R R =+-，解得4R =， 所以球的表面积为2464S R ππ==， 故选D.原创精品资源学科网独家享有版权，侵权必究！68、（2020届山东省枣庄、滕州市高三上期末）已知ln ,1()(2),1x x f x f x k x ≥⎧=⎨-+<⎩若函数()1y f x =-恰有一个零点，则实数k 的取值范围是（ ） A ．(1,)+∞ B ．[1,)+∞C ．(,1)-∞D ．(,1]-∞【答案】B 【解析】1x ≥时，()ln 1f x x ==，x e =，所以函数()1y f x =-在1x ≥时有一个零点，从而在1x <时无零点，即()1f x =无解．而当1x <时，21x ->，()(2)f x f x k =-+ln(2)x k =-+，它是减函数，值域为(,)k +∞， 要使()1f x =无解．则1k ．故选：B.二、多选题（共4小题，满分20分，每小题5分，少选的3分，多选不得分）9、（2020届山东省泰安市高三上期末）已知a b c d ,,,均为实数，则下列命题正确的是（ ） A ．若,a b c d >>，则ac bd > B ．若0,0ab bc ad >->，则0c da b-> C ．若,,a b c d >>则a d b c ->- D ．若,0,a b c d >>>则a b d c> 【答案】BC 【解析】原创精品资源学科网独家享有版权，侵权必究！7若0a b >>，0c d >>，则ac bd <，故A 错； 若0ab >，0bc ad ->，则0bc ad ab ->，化简得0c da b->，故B 对； 若c d >，则d c ->-，又a b >，则a d b c ->-，故C 对； 若1a =-，2b =-，2c =，1d =，则1a d =-，1b c =-，1a bd c==-，故D 错； 故选：BC ．10、（2020届山东师范大学附中高三月考）已知函数，是函数的极值点，以下几个结论中正确的是（ ） A ． B ． C ． D ．【答案】AC 【解析】函数,,∵是函数的极值点，∴，即，,,,即A 选项正确,B 选项不正确;,即C 正确,D 不正确.故答案为:AC.2()ln f x x x x =+0x ()f x 010x e<<01x e>00()20f x x +<00()20f x x +>2()l (),n 0f x x x x x =+>()ln 12f x x x '∴=++0x ()f x ()'00f x =00ln 120x x ∴++=120f e e'⎛⎫∴=> ⎪⎝⎭0,()x f x '→→-∞010x e∴<<()()()2000000000002ln 2l 21n 0f x x x x x x x x x x x +=++==-+++<原创精品资源学科网独家享有版权，侵权必究！811、（2020·江苏省徐州一中高二月考）下列关系中，能成立的是（ ）A ．11m m n n m C C n--=B ．!()!!mn n C n m m =-C ．!m nm nA m C =D ．11m m mn n n A mA A -++=【答案】BCD【解析】对A ，令3,1n m ==，可得等式103213C C =不成立，故A 错误；对B ，利用组合数的计算公式知正确，故B 正确； 对C ，利用排列数与组合数的定义，故C 正确； 对D ，∵11!!(1)!()!(1)!(1)!mm mn n n n m n n A mA A n m n m n m -+⋅++=+==--+-+，故D 正确；故选：BCD.12、（2020届山东省潍坊市高三上学期统考）下列判断正确的是（ ） A ．若随机变量ξ服从正态分布()21,N σ，()40.79P ξ≤=，则()20.21P ξ≤-=；B ．已知直线l ⊥平面α，直线//m 平面β，则“//αβ”是“l m ⊥”的充分不必要条件；C ．若随机变量ξ服从二项分布：414,B ξ⎛⎫~ ⎪⎝⎭,则()1E ξ=； D ．22am bm >是a b >的充分不必要条件. 【答案】ABCD 【解析】A ．已知随机变量ξ服从正态分布N （1，σ2），P （ξ≤4）＝0.79，则曲线关于x ＝1对称，可得P （ξ＞4）＝1﹣0.79＝0.21，P （ξ≤﹣2）＝P （ξ＞4）＝0.21，故A 正确；B ．若α∥β，∵直线l ⊥平面α，∴直线l ⊥β，∵m ∥β，∴l ⊥m 成立．原创精品资源学科网独家享有版权，侵权必究！9若l ⊥m ，当m ∥β时，则l 与β的位置关系不确定，∴无法得到α∥β． ∴“α∥β”是“l ⊥m ”的充分不必要条件．故B 对；C ．由于随机变量ξ服从二项分布：ξ～B （4，14），则Eξ＝4×0.25＝1，故C 对； D ．“am 2>bm 2”可推出“a >b ”，但“a >b ”推不出“am 2>bm 2”，比如m ＝0，故D 对； 故选：ABCD ．三、填空题（共4小题，满分20分，每小题5分，一题两空，第一空2分）13、（2020江苏苏州五校联考）设公比不为1的等比数列{}n a 满足1231a a a =-，且2a ，4a ，3a 成等差数列，则数列{}n a 的前4项和为______．【答案】54【解析】由等比数列的性质可知312321a a a a ==- ，21a ∴=-，243,,a a a 成等差数列，4232a a a ∴=+，22222a q a a q =+，2210q q ∴--=，解得：1q =(舍)或12q =-，212a a q ∴==，()4414121121112a q S q⎛⎫⎛⎫-- ⎪ ⎪ ⎪-⎝⎭⎝⎭==-⎛⎫-- ⎪⎝⎭54=．故答案为：54． 14、（2020届浙江省之江教育评价联盟高三第二次联考）若实数,x y 满足0x y >>，且22log log 1x y +=，则22x y x y -+的最大值为______. 【答案】14【解析】原创精品资源学科网独家享有版权，侵权必究！10实数x 、y 满足x ＞y ＞0，且log 2x +log 2y ＝1，则xy ＝2，则()()2222114()2()4442x y x y x y x y x y xy x y x y x y x yx y---===≤=+-+-+-+---，当且仅当x ﹣y 4x y=-，即x ﹣y ＝2时取等号 故22x y x y -+的最大值为14，故答案为14．15、（2020届山东省潍坊市高三上期中）已知函数()f x 是定义在R 上的偶函数，且在[)0,+∞上是减函数，10,3f ⎛⎫-= ⎪⎝⎭则不等式18log 0f x ⎛⎫> ⎪⎝⎭的解集为__________． 【答案】1,22⎛⎫⎪⎝⎭【解析】()f x 是定义在R 上的偶函数，且在[0,)+∞上是减函数，1()03f -=，11()()033f f ∴=-=，则不等式18(log )0f x >等价为不等式181(|log |)()3f x f >， 即181|log |3x <⇒1811log 33x -<<⇒122x <<，原创精品资源学科网独家享有版权，侵权必究！11即不等式的解集为1(,2)2，故答案为：1(,2)2.16、（2020·浙江省温州市新力量联盟高三上期末）在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c .已知3b =3c =，3A C π+=，则cos C ________，ABC S ∆=________.【答案】332【解析】由于3A C π+=，则3A C A B C +=++，解得2B C =， 由于3b =3c =，利用正弦定理sin sin b cB C=， 则sin 2sin b c C C =233sin C=， 解得3cos 3C =，∴26sin 1cos 3C C =-=， 由3A C π+=，所以3A C π=-所以()339sin sin 3sin 33sin 4sin 6664333A C C C C π==⎛⎫-⨯= ⎪ ⎪⎝⎭-=-=⨯ 则116sin 2332229ABC S b c A ∆=⋅⋅=⨯⨯=原创精品资源学科网独家享有版权，侵权必究！12故答案为：32.四、解答题（共6小题，满分70分，第17题10分，其它12分）17、（2020·全国高三专题练习（文））在ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且满()(sin sin )(3sin )b a B A c B C -+=-.（1）求A 的大小； （2）再在①2a =，②4B π=，③3=c b 这三个条件中，选出两个使ABC 唯一确定的条件补充在下面的问题中，并解答问题.若________，________，求ABC 的面积. 【答案】（1）6A π=；（2）见解析【解析】（1）因为()(sin sin )3sin )b a B A c B C -+=-，又由正弦定理sin sin sin a b cA B C==，得 ()()3)b a b a c b c -+=-，即2223b c a bc +-=，所以22233cos 2b c bc A bc a +===-， 因为0A π<<，原创精品资源学科网独家享有版权，侵权必究！13所以6A π=.（2）方案一：选条件①和②.由正弦定理sin sin a b A B=，得sin 22sin ab B A == 由余弦定理2222cos b a c ac B =+-，得222(22)222cos4c c π=+-⨯，解得26c =所以ABC 的面积112sin 2(26)31222S ac B ==⨯⨯⨯=. 方案二：选条件①和③.由余弦定理2222cos a b c bc A =+-，得222433b b b =+-，则24b =，所以2b =. 所以23c =，所以ABC 的面积111sin 2233222S bc A ==⨯⨯=18、（2020届山东省烟台市高三上期末）如图，在四棱锥S ABCD -中，ABCD 为直角梯形，//AD BC ，BC CD ⊥，平面SCD ⊥平面ABCD ，SCD ∆是以CD 为斜边的等腰直角三角形，224BC AD CD ===，E 为BS 上一点，且2BE ES =.原创精品资源学科网独家享有版权，侵权必究！14（1）证明：直线//SD 平面ACE ； （2）求二面角S AC E --的余弦值. 【答案】（1）证明见解析 （2）13【解析】（1）连接BD 交AC 于点F ,连接EF , 因为//AD BC ,所以AFD ∆与BCF ∆相似,所以2BF BCFD AD==, 又=2BE BFES FD=,所以//EF SD , 因为EF ⊂平面ACE ,SD ⊄平面ACE , 所以直线//SD 平面ACE（2）由题,因为平面SCD ⊥平面ABCD ,平面SCD 平面ABCD CD =,BC ⊂平面ABCD ,BC CD ⊥,所以BC ⊥平面SCD ,以C 为坐标原点,,CD CB 所在的方向分别为y 轴、z 轴的正方向,与,CD CB 均垂直的方向作为x 轴的正方向,建立如图所示的空间直角坐标系C xyz -,原创精品资源学科网独家享有版权，侵权必究！15因为224BC AD CD ===,2BE ES =, 则(0,0,0)C ,(1,1,0)S ,(0,2,2)A ,224(,,)333E ,所以(0,2,2)CA =,(1,1,0)CS =,224(,,)333CE =,设平面SAC 的一个法向量为(,,)m x y z =,则00m CA m CS ⎧⋅=⎨⋅=⎩,即00y z x y +=⎧⎨+=⎩, 令1z =,得1x =,1y =-,于是(1,1,1)m =-,设平面EAC 的一个法向量为(,,)n x y z =,则00n CA n CE ⎧⋅=⎨⋅=⎩,即020y z x y z +=⎧⎨++=⎩, 令1z =,得1x =-,1y =-,于是(1,1,1)m =--,设二面角S AC E --的平面角的大小为θ,则1cos 3m n m nθ⋅==, 所以二面角S AC E --的余弦值为1319、（2020届山东省潍坊市高三上期末）读书可以使人保持思想活力，让人得到智慧启发，让人滋养浩然正原创精品资源学科网独家享有版权，侵权必究！16气书籍是文化的重要载体，读书是承继文化的重要方式某地区为了解学生课余时间的读书情况，随机抽取了n名学生进行调查，根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图，将日均课余读书时间不低于40分钟的学生称为“读书之星”，日均课余读书时间低于40分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于10分钟的有10人(1)求,n p的值;(2)根据已知条件完成下面的22⨯列联表，并判断是否有95%以上的把握认为“读书之星”与性别有关?非读书之星读书之星总计男女1055总计(3)将上述调查所得到的频率视为概率，现从该地区大量学生中，随机抽取3名学生，每次抽取1名，已知每个人是否被抽到互不影响，记被抽取的“读书之星”人数为随机变量X，求X的分布列和期望()E X附：()()()()()22n ad bcKa b c d a c b d-=++++，其中n a b c d=+++.原创精品资源学科网独家享有版权，侵权必究！17()20P K k ≥ 0.100.05 0.025 0.010 0.005 0.0010k 2.706 3.841 5.024 6.635 7.879 10.828【答案】（1）0.01P =,n =100,（2）表见解析，没有95%以上的把握认为“读书之星”与性别有关（3）分布列见解析，()34E X = 【解析】 【分析】（1）首先根据频率和为1求P ，再根据频率，频数和样本容量的关系求n ；（2）首先计算“读书之星”的人数，然后再依次填写22⨯列联表；并根据公式计算2K 和3.841比较大小，做出判断；（3）从该地区学生中抽取一名学生是“读书之星”的概率为14，由题意可知1~3,4X B ⎛⎫⎪⎝⎭并求分布列和数学期望. 【详解】（1）()0.0050.0180.0200.0220.025101P +++++⨯= 解得：0.01P =， 所以100.1010n ==. (2)因为100n =，所以“读书之星”有1000.2525⨯= 从而22⨯列联表如下图所示:原创精品资源学科网独家享有版权，侵权必究！18非读书之星 读书之星 总计男 301545女 45 10 55 总计7525100将22⨯列联表中的数据代入公式计算得()2210030101545100 3.0304555752533K ⨯⨯-⨯==≈⨯⨯⨯因为3.030 3.841<，所以没有95%以上的把握认为“读书之星”与性别有关 (3)将频率视为概率，即从该地区学生中抽取一名学生是“读书之星”的概率为14. 由题意可知1~3,4X B ⎛⎫ ⎪⎝⎭所以()30301127041464P X C ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭-=⎝⎭==()3211271146414P X C ⎛==-=⎫⨯ ⎪⎝⎭， ()223192146414P X C ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭==-=()333413641P X C ⎛⎫ ⎪⎭=⎝==原创精品资源学科网独家享有版权，侵权必究！19所以X 的分布列为X 0123P27642764964164故()13344E X =⨯=. 20、（2020届山东省九校高三上学期联考）已知数列{}1n a +是等比数列，11a =且2a ，32a +，4a 成等差数列.（1）求数列{}n a 的通项公式；（2）设11n nn n n a a b a a ++-=，求数列{}n b 的前n 项和n S .【答案】(1) 21nn a =- (2) 112221n n n S ++-=- 【解析】（1）设数列{}1n a +的公比为q ，∵112a +=，∴22334121212a q a q a q +=⎧⎪+=⎨⎪+=⎩，∴22334212121a q a q a q =-⎧⎪=-⎨⎪=-⎩， ∵()32422a a a +=+，∴()232212121q q q +=-+-，原创精品资源学科网独家享有版权，侵权必究！20∴2342222q q q +=+-，即：()()224121q q q +=+， 解得：2q.∴11222n nn a -+=⋅=，∴21nn a =-.（2）()()1121121212121n nn n n n b ++==-----，∴1231n n n S b b b b b -=+++++122334111111212121212121⎛⎫⎛⎫⎛⎫=-+-+- ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭11111121212121n n n n -+⎛⎫⎛⎫++-+- ⎪ ⎪----⎝⎭⎝⎭11112212121n n n +++-=-=--. 21、（2020届山东省潍坊市高三上期中）已知函数． （1）当时，求曲线在点处的切线方程； （2）若函数处有极小值，求函数在区间上的最大值．【答案】（1）；（2）. 【解析】()32112f x x x ax =-++2a =()y f x =()()0,0f ()1f x x =在()f x 32,2⎡⎤-⎢⎥⎣⎦210x y -+=4927原创精品资源学科网独家享有版权，侵权必究！21 （1）当时，，， 所以，又，所以曲线在点处切线方程为，即. （2）因为，因为函数处有极小值，所以， 所以由，得或， 当或时，， 当时，， 所以在，上是增函数，在上是减函数， 因为，， 所以的最大值为. 22、（2020届山东省潍坊市高三上期末）在平面直角坐标系中，()()1 ,0,1,0A B -，设ABC 的内切圆分别与边,,AC BC AB 相切于点,,P Q R ，已知1CP =，记动点C 的轨迹为曲线E .(1)求曲线E 的方程;(2)过()2,0G 的直线与y 轴正半轴交于点S ，与曲线E 交于点,H HA x ⊥轴，过S 的另一直线与曲线E 交2a =321()212f x x x x =-++2()32f x x x '=-+(0)2f '=(0)1f =()y f x =()()0,0f 12y x -=210x y -+=2()3f x x x a '=-+()1f x x =在(1)202f a a '=+=⇒=-2()32f x x x '=--()0f x '=23x =-1x =23x <-1x >()0f x '>213x -<<()0f x '<()f x 22,3⎛⎫--⎪⎝⎭31,2⎛⎫ ⎪⎝⎭2,13⎛⎫- ⎪⎝⎭249327f ⎛⎫-= ⎪⎝⎭3124f ⎛⎫= ⎪⎝⎭()f x 249327f ⎛⎫-= ⎪⎝⎭原创精品资源学科网独家享有版权，侵权必究！22 于M N 、两点，若6SMG SHN S S =，求直线MN 的方程. 【答案】（1）221(0)43x y y +=≠（2）61y x =+或61y x =+. 【解析】 (1)由内切圆的性质可知CP CQ =，AP AR =，BQ BR =， ∴CA CB CP CQ AP BQ +=+++24CP AB AB =+=>.所以曲线E 是以,A B 为焦点，长轴长为4的椭圆(除去与x 轴的交点).设曲线2222:1(0,0)x y E a b y a b +=>>≠则1,24c a ==，即2222,3a b a c ==-=所以曲线E 的方程为221(0)43x y y +=≠.(2)因为HA x ⊥轴，所以31,2H ⎛⎫- ⎪⎝⎭，设()00,S y ，所以03223y --=-，所以01y =，则()0,1S因为2a c =，所以2SG SH =，原创精品资源学科网独家享有版权，侵权必究！23 所以1sin 2261sin 2SMG SMN SM SG MSGSM S S SN SN SH NSH ∠===∠ 所以3SM SN =，所以3SM SN =-设()()1122,, ,,M x y N x y 则()11,1SM x y =- ()22,1SN x y =-，所以123x x =-①直线MN 斜率不存在时， MN 方程为0x = 此时32331SM SN ==+-. ②直线MN 的斜率存在时，设直线MN 的方程为1y kx =+.联立221143y kx x y =+⎧⎪⎨+=⎪⎩，得()2234880,k x kx ++-=所以122122834834kx x k k x x k -⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩，将123x x =-代入得222228348334kx k k x k -⎧=⎪⎪+⎨⎪=⎪+⎩，所以2224833434k k k k ⎛⎫=⎪⎭+⎝+.原创精品资源学科网独家享有版权，侵权必究！24所以236 ,2k k==所以直线MN的方程为612y x=+或612y x=-+.。

2021年高三数学第一次摸底考试理（含解析）【试卷综评】本试卷试题主要注重基本知识、基本能力、基本方法等当面的考察，覆盖面广，注重数学思想方法的简单应用，试题有新意，符合课改和教改方向，能有效地测评学生，有利于学生自我评价，有利于指导学生的学习，既重视双基能力培养，侧重学生自主探究能力，分析问题和解决问题的能力，突出应用，同时对观察与猜想、阅读与思考等方面的考查。

一、选择题：本大题共12题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求．【题文】1．计算：=（）A． i+1 B．i﹣1 C．﹣i+1 D．﹣i﹣1【知识点】复数代数形式的乘除运算．L4【答案解析】C 解析：化简可得===1﹣I,故选：C【思路点拨】分子分母同乘以分母的共轭复数﹣i﹣1，化简可得．【题文】2．已知A⊆B，A⊆C，B={1，2，3，5}，C={0，2，4，8}，则A可以是（）A． {1，2} B．{2，4} C．{2} D．{4}【知识点】集合的包含关系判断及应用.A1【答案解析】C 解析：∵A⊆B，A⊆C，∴A⊆（B∩C），∵B={1，2，3，5}，C={0，2，4，8}，∴B∩C={2}，而A⊆（B∩C）则A={2}或∅，故选C。

【思路点拨】先根据A⊆B，A⊆C可知A⊆（B∩C），然后求出B∩C，最后求出所求满足条件的A，最后得到结论．【题文】3．已知条件p：x2﹣2ax+a2﹣1＞0，条件q：x＞2，且q是p的充分而不必要条件，则a的取值范围是（）A．a≥1B．a≤1C．a≥﹣3 D．a≤﹣3【知识点】必要条件、充分条件与充要条件的判断。

A2【答案解析】B 解析：∵条件p：x2﹣2ax+a2﹣1＞0，条件q：x＞2，且q是p的充分而不必要条件，∴q⊊p，即a≤2且4﹣4a+a2﹣1≥0，解不等式组可得：a≤1，故选：B。

【思路点拨】把充分性问题转化为结合关系，再利用不等式求解．【题文】4．某程序图如图所示，该程序运行后输出的结果是（）A． 3 B． 4 C． 5 D． 6【知识点】程序框图．L1【答案解析】C 解析：当S=1时，满足进入循环的条件，执行完循环体后，S=2，k=2；当S=2时，满足进入循环的条件，执行完循环体后，S=22，k=3；当S=22时，满足进入循环的条件，执行完循环体后，S=24，k=4；当S=24时，满足进入循环的条件，执行完循环体后，S=216，k=5；当S=216时，不满足进入循环的条件，故输出结果为：5，故选：C【思路点拨】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量k 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【题文】5．已知某几何体的正视图与侧视图都是边长为1的正方形，且体积为．则该几何体的俯视图可以是（）【知识点】简单空间图形的三视图．G2【答案解析】A 解析：由题意可知当俯视图是A时，即每个视图是变边长为1的正方形，那么此几何体是立方体，显然体积是1，注意到题目体积是，知其是立方体的一半，可知选A．【思路点拨】结合选项，正方体的体积否定C，推出正确选项A即可．【题文】6．将函数f（x）=2sin（+）的图象向左平移个单位，再向下平移1个单位，得到函数g（x）的图象，则g（x）的解析式为（）A． g（x）=2sin（+）﹣1 B． g（x）=2sin（﹣）+1C． g（x）=2sin（﹣）+1 D． g（x）=2sin（﹣）﹣1【知识点】函数y=Asin（ωx+φ）的图象变换．C4【答案解析】A 解析：函数y=2sin（+）的图象先向左平移个单位，可以得到函数y=2sin[（x+）+]=2sin（+）的图象再向下平移1个单位后可以得到y=2sin（+）﹣1的图象故选：A．【思路点拨】根据平移变换的法则﹣﹣“左加右减，上加下减”，我们先求出将函数y=2sin （+）的图象先向左平移个单位的图象对应的函数的解析式，再求出再向下平移1个单位后得到图象的解析式即可得到答案．【题文】7．已知等差数列{an}的公差为2，若前17项和为S17=34，则a12的值为（）A． 8 B． 6 C． 4 D． 2【知识点】等差数列的前n项和；等差数列的通项公式．D2【答案解析】A 解析：∵等差数列{an}的前17项和为S17=34，∴=34∴a1+a17=4，∵a1+a17=2a9，∴a9=2，，等差数列{an}的前17项和为S17=34∴a12=a9+（12﹣9）×2，∴a12=8，故答案选A。

绝密★启用前2021年秋季高三数学开学摸底考试卷01（浙江专用）考生须知：1．本试题满分150分，考试时间120分钟。

2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号。

3．所有答案必须写在答题卷上，写在试卷上无效。

4．考试结束后，只需上交答题卷。

选择题部分一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}2680M x x x =-+≤，{}13N x x =<<，则M N =（ ）．A ．{}23x x <≤ B ．{}23x x ≤< C ．{}14x x ≤< D ．{}14x x <≤【答案】B 【分析】根据一元二次不等式的解法得出{}24M x x =≤≤，结合集合交集的运算即可得出结果. 【详解】因为{}24M x x =≤≤，{}13N x x =<<， 所以{}23M N x x ⋂=≤<， 故选：B ．2．如图是一个空间几何体的三视图，则该几何体的体积为（ ）A ．23B ．43C ．2D ．83【答案】B 【分析】根据三视图还原几何体即可求解. 【详解】解：该几何体的直观图为如图所示的三棱锥，底面是等腰直角三角形，高为2，则体积114222323V ⎛⎫=⨯⨯⨯⨯= ⎪⎝⎭.故选：B.3．若a ，b ∈R ，直线l ：y ax b =+，圆C ：221x y +=．命题p ：直线l 与圆C 相交；命题q ：a p 是q 的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B 【分析】由直线与圆相交，求出命题p 为真时,a b 的关系，再由充分、必要条件的定义，即可得出结论. 【详解】直线l ：y ax b =+，圆C ：221x y +=，命题p 为真：即直线l 与圆C1<，即221a b >-.当命题q 成立时，即a 221a b >-成立， 命题p 成立，p 是q 的必要条件；而当命题p 成立时，取1,0a b ==，此时命题q 不成立，p 不是q 的充分条件.所以p 是q 的必要不充分条件. 故选：B.4．在平面直角坐标系xOy 中，若双曲线2221(0)y x b b-=>经过点(，则该双曲线的渐近线方程为（ ）A ．y =B ．2y x =±C ．43y x =±D ．3y x =±【答案】A 【分析】把点代入双曲线方程求出b 的值，从而根据双曲线的渐近线方程公式求出答案. 【详解】因为双曲线2221(0)y x b b-=>经过点(，所以代入得248251b-=，解得22b =，即b =所以双曲线的渐近线方程为y =. 故选：A.5．已知m ､n 是两条不同的直线，α､β是两个不同的平面，则一定能使//m n 成立的是（ ）A ．//αβ，m α⊂，n β⊂B ．m ､n 与平面α所成角相等C ．αβ⊥，m α⊥，//n βD ．//αβ，m α⊥，n β⊥【答案】D 【分析】分别举出每个选项的反例即可选出正确选项． 【详解】对于选项A ，m 与n 还可能是异面直线；对于选项B ，m 与n 还可能是相交直线、异面直线； 对于选项C ，m 与n 可能是相交直线、异面直线；对于选项D ，若//αβ，m α⊥，n β⊥，则一定有//m n 成立． 故选：D.6．已知函数()2sin cos 66f x x x ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭，则下列说法错误的是（ ）A ．函数()f x 的最小正周期为πB ．12x π=-是函数()f x 图象的一条对称轴C ．函数()f x 的图象关于点,03π⎛⎫⎪⎝⎭中心对称D ．将函数()22cos sin g x x x =-的图象向右平移512π个单位后得到函数()f x 的图象 【答案】C 【分析】先根据二倍角公式化简()f x 的解析式， A ．根据最小正周期计算公式进行求解； B ．根据12f π⎛⎫-⎪⎝⎭是否为最值进行判断； C ．根据3f π⎛⎫⎪⎝⎭是否为0进行判断； D ．先求解出平移后的函数解析式，然后进行判断. 【详解】()2sin cos 2sin cos sin 266663f x x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=--=--=- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，A ．最小正周期22T ππ==，故正确； B ．因为sin 11263f πππ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭为最小值，所以12x π=-是()f x 图象的一条对称轴，故正确； C．因为sin 203332πππf ⎛⎫⎛⎫=⨯-=≠ ⎪ ⎪⎝⎭⎝⎭，所以()f x 的图象不关于点,03π⎛⎫ ⎪⎝⎭中心对称，故错误；D ．()22cos sin cos2g x x x x =-=，()g x 的图象向右平移512π个单位后得到： 5cos 2cos 2cos 2sin 21232233y x x x x ππππππ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=--=--=- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦，故正确； 故选：C.7．某中学高一年级和高二年级进行篮球比赛，赛制为3局2胜制，若比赛没有平局，且高二队每局获胜的概率都是112p p ⎛⎫<< ⎪⎝⎭，记比赛的最终局数为随机变量X ，则（ ）A ．2(2)P X p ==B ．(3)(1)P X p p ==-C ．5()2E X < D ．1()4D X >【答案】C 【分析】根据实际意义得2X =或3．求得概率后判断AB ，由期望公式计算出期望可判断C ，由均值求出方差可判断D ． 【详解】赛制为3局2胜制，比赛没有平局，因此随机变量X 的可能值为2或3，222(2)(1)221P X p p p p ==+-=-+，A 错；222(3)(1)(1)(1)(1)(1)22P X p p p p p p p p p p p p ==-+-+-+--=-+，B 错；222215()2(221)3(22)2222()22E X p p p p p p p =-++-+=-++=--+，因为112p <<，所以5()(2,)2E X ∈，C 正确；记2222p p t -++=，5(2,)2t ∈，2222()4(221)9(22)1010456E X p p p p p p t =⨯-++⨯-+=-++=-，222251()()()56()24D XE X E X t t t =-=--=--+，因为5(2,)2t ∈，所以1()4D X <，D 错． 故选：C ． 【点睛】结论点睛：本题考查随机变量的概率分布列与数学期望、方差等概念．随机变量的期望与方差之间有关系：[]22()()()D X E X E X =-．8．设数列{a n }满足113,34n n a a a n +==-，若21485n n n n n b a a +++=，且数列{b n }的前n 项和为n S ，则n S =（ ） A ．2169n n ⎛⎫+⎪+⎝⎭B ．42369n n ++ C ．1169n n ⎛⎫+⎪+⎝⎭D ．2169n n ⎛⎫+⎪+⎝⎭【答案】D 【分析】由已知可求得21n a n =+，再利用裂项相消法可求得. 【详解】由134n n a a n +=-可得()()132123n n a a n n +⎡⎤=-+-⎣+⎦，13a =，()12110a -⨯+=∴，则可得数列(){}21n a n -+为常数列0，即()210n a n -+=，21n a n ∴=+，∴()()()()()()()()221232485211112123212321232123n n n n n b n n n n n n n n +++++===+=+-++++++++，11111111355721229336321n n n n n n S n n ⎛⎫∴=+-+-++-=+-=⎛⎫+ ⎪+⎝ ⎪+++⎝⎭⎭. 故选：D.9．已知F 是椭圆2221(1)x y a a+=>的左焦点，A 是该椭圆的右顶点，过点F 的直线l（不与x 轴重合）与该椭圆相交于点M ，N ．记MAN α∠=，设该椭圆的离心率为e ，下列结论正确的是（ ）A ．当01e <<时，2πα<B ．当0e <<2πα>C ．当122e <<时，23πα> D 1e <<时，34πα> 【答案】A 【分析】设M 在x 轴上方，N 在x 轴下方，设直线AM 的倾斜角为θ，直线AN 的倾斜角为β，联立直线AM 的方程与椭圆方程可求M 的坐标，同理可求N 的坐标，利用,,M F N 三点共线可得()12211e k k a e -=+，利用离心率的范围可得121k k >-，从而可判断α为锐角.【详解】不失一般性，设M 在x 轴上方，N 在x 轴下方，设直线AM 的斜率为1k ，倾斜角为θ，直线AN 的斜率为2k ，倾斜角为β， 则210,0k k ><，,2πθπ⎛⎫∈⎪⎝⎭，0,2πβ⎛⎫∈ ⎪⎝⎭，且()0,απθβπ=-+∈.又()2121tan tan tan tan 1+tan tan 1k k k k βθαπθββθ--=-+==+.又直线AM 的方程为()1y k x a =-，由()12222y k x a x a y a⎧=-⎨+=⎩可得22232422111(1)20a k x a k x a k a +-+-=， 故42212211M a k a x a a k -⨯=+，所以3212211M a k ax a k -=+，故122121M ak y a k -=+， 同理3222221N a k ax a k -=+，故222221Nak y a k -=+， 因为,,M F N 共线，故21222221323221222221221111ak ak a k a k a k a a k ac c a k a k --++=--++++，整理得到()()()()21212210a a c k k k k c a k k +-+--=即()122c ak k a a c -=+，若01e <<，()()122211c a e k k a a c a e --==++，因为()1211,011e e e -=-∈-++，21a >，故121k k >-，所以2121tan 01k k k k α-=>+， 故2πα<.故选：A. 【点睛】思路点睛：与椭圆有关的角的计算，一般利用其正切来刻画，因为角的正切与直线的斜率相关，注意运算结果的准确性.10．设a ∈R ，函数22cos(22).()2(1)5,x a x a f x x a x a x a ππ-<⎧=⎨-+++≥⎩，若()f x 在区间(0,)+∞内恰有6个零点，则a 的取值范围是（ ）A ．95112,,424⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦B ．5711,2,424⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭C ．9112,,344⎛⎤⎡⎫⋃ ⎪⎥⎢⎝⎦⎣⎭D ．11 ,2,3447⎛⎫⎡⎫⋃ ⎪⎪⎢⎝⎭⎣⎭【答案】A【分析】由()222150x a x a -+++=最多有2个根，可得()cos 220x a ππ-=至少有4个根，分别讨论当x a <和x a ≥时两个函数零点个数情况，再结合考虑即可得出. 【详解】()222150x a x a -+++=最多有2个根，所以()cos 220x a ππ-=至少有4个根，由22,2x a k k Z ππππ-=+∈可得1,24k x a k Z =++∈，由1024k a a <++<可得11222a k --<<-，（1）x a <时，当15242a -≤--<-时，()f x 有4个零点，即7944a <≤；当16252a -≤--<-，()f x 有5个零点，即91144a <≤；当17262a -≤--<-，()f x 有6个零点，即111344a <≤；（2）当x a ≥时，22()2(1)5f x x a x a =-+++，()()22Δ4(1)4582a a a =+-+=-，当2a <时，∆<0，()f x 无零点； 当2a =时，0∆=，()f x 有1个零点；当2a >时，令22()2(1)5250f a a a a a a =-+++=-+≥，则522a <≤，此时()f x 有2个零点； 所以若52a >时，()f x 有1个零点. 综上，要使()f x 在区间(0,)+∞内恰有6个零点，则应满足7944522a a ⎧<≤⎪⎪⎨⎪<≤⎪⎩或91144522a a a ⎧<≤⎪⎪⎨⎪=>⎪⎩或或1113442a a ⎧<≤⎪⎨⎪<⎩， 则可解得a 的取值范围是95112,,424⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦.【点睛】关键点睛：解决本题的关键是分成x a <和x a ≥两种情况分别讨论两个函数的零点个数情况.非选择题部分二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分． 11．复数z 满足()134i z i -=+，则z 的虚部为______，z =______．【答案】722【分析】利用复数的除法法则可化简复数z ，利用复数的模长公式可求得z . 【详解】 由已知可得()()()()341341717111222i i i i z i i i i +++-+====-+--+， 所以， 复数z 的虚部为72，2z == 故答案为：72；2. 12．已知角α的终边上有一点坐标是133⎛- ⎝⎭，，则cos α=________；tan α=_______【答案】13-- 【分析】根据三角函数的定义求解. 【详解】因为角α的终边上有一点坐标是133P ⎛⎫- ⎪ ⎪⎝⎭，，所以1OP == 1cos 3x OP α==-，3tan 13y x α===--故答案为: 13-；-13．已知51(1)a x x ⎛⎫++ ⎪⎝⎭展开式中的所有项的系数和为64，则实数a =___________；展开式中常数项为___________. 【答案】1 6 【分析】由题意令1x =，可得二项式的各项系数和，求出a 的值，再利用二项展开式的通项公式，求得展开式的常数项. 【详解】令1x =，可得51(1)a x x ⎛⎫++ ⎪⎝⎭展开式中的 所有项的系数和为()32164a +=，则实数1a =.展开式中常数项为0155156a C C ⨯+=+=，故答案为：1；6.14．已知a ，b R +∈，当()21ab a b +=时，ab 的最大值为___________，2+a b 的最小值为___________. 【答案】122 【分析】利用基本不等式求解即可，由于(2)1(ab a b ab +=≥，从而可求出ab 的最大值，由于1(2)2(2)2ab a b a b a b +=⋅⋅+212(2)22a b a b +⎫⎛≤+⋅ ⎪⎝⎭，从而可求出2+a b 的最小值【详解】(2)1(ab a b ab +=≥，解得12≤ab ，等号当且仅当1a =，12b =时成立； 1(2)2(2)2ab a b a b a b +=⋅⋅+212(2)22a b a b +⎫⎛≤+⋅ ⎪⎝⎭，所以3(2)8a b +≥，进而22a b +≥，等号当且仅当1a =，12b =时成立.故答案为：12，2 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方15．已知等比数列{}n a 的公比为q ，且116a ，24a ，3a 成等差数列，则q 的值是___________. 【答案】4 【分析】根据三数成等差数列列等式，再将2a ，3a 用含1a 和q 的式子表示，代入等式求解. 【详解】因为{}n a 为等比数列，且公比为q ， 所以21a a q =⋅，231a a q =⋅且10a ≠，0q ≠. 因为116a ，24a ，3a 成等差数列， 所以1321624a a a +=⨯，有21111624a a q a q +⋅=⨯⋅，28160q q -+=， 解得4q =. 故答案为：4.16．已知有5男5女共10名记者参加2021年的两会新闻报道，现从中选取8人分配到A ，B 两个组，每个组4人，其中A 组的4人中，要求女性的人数多于男性，B 组的4人中，要求至少有1名女性，则不同的分配方法数为___________. 【答案】750 【分析】首先把分配情况分为三类，①A 组3女1男，B 组1女3男；①A 组3女1男，B 组2女2男；①A 组4女0男，B 组1女3男.然后再计算每一类的分配方法数. 【详解】 分三类：第一类：A 组3女1男，B 组1女3男，此时分配方法有：31135524400C C C C =；第二类：A 组3女1男，B 组2女2男，此时分配方法有：31225524300C C C C =； 第三类：A 组4女0男，B 组1女3男，此时分配方法有：41351550C C C =，所以分配方法共有40030050750++=. 故答案为：750.17．设O 是ABC 的外心，满足1324CO t CA t CB →→→⎛⎫=+- ⎪⎝⎭，若||3AB →=，则ABC 面积的最大值为___________. 【答案】9 【分析】设D 为BC 边中点，化简已知得3cos 4b C a =，由余弦定理得22218b a -=，再利用基本不等式求解. 【详解】1324CO t CA t CB →→→⎛⎫=+- ⎪⎝⎭1324CO CB C C O t A B D →→→→→⎛⎫⇔-=-= ⎪⎝⎭，其中D 为BC 边中点，所以304BC CA C D B B O C →→→→→⎛⎫⋅=-⋅= ⎪⎝⎭，所以234CB CB CA →→→⋅=,所以233cos ,cos 44ab C a b C a =∴= 又222cos 9b a ab C +-=，所以联立得22218b a -=， 因为in 12s S ab C =, 所以()2222222291cos (1)4416a b a b a S C b=-=- ()22222144()1442816464a aa a +--=≤= 所以ABC 面积的最大值为9. 故答案为：9 【点睛】关键点睛：解答本题的关键有两点，其一是，化简已知得到3cos 4b C a =，其二是转化为求2S 的最大值，利用基本不等式求最大值.三、解答题：本大题共5小题，共74分．解答应写出文字说明、证明过程或演算步骤． 18．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，其面积为S ，且（c ﹣a ）（c +a ）+ab cos CS . （1）求角A 的大小；（2）若4cos B •cos C ＝1，且a ＝，求S 的值. 【答案】（1）3π;（2）【分析】（1）边化角即可；（2）通过角得关系求出B ，进一步即可获解 【详解】 （1）222221()()cos ,sin 22a b c c a c a ab C c a ab bc A ab +--++=∴-+⨯=()()2222222211sin sin 22c a a b c A b c a A ⇔-++-=⇔+-=所以cos 3A A =，即tan A =0A π<<， ∴3A π=（2）()cos cos[()]cos(),,A B C c A B C A B A B πππ++=∴=-+=-+=-+∴1cos cos cos cos sin sin cos 3332C B B B B B πππ⎛⎫=-+=-+=- ⎪⎝⎭214cos cos 4cos sin cos 2cos sin 22B C B B B B B B ⎛⎫=-=-+ ⎪ ⎪⎝⎭1cos 222sin 211sin 2166,B B B B ππ⎛⎫⎛⎫=--=--=∴-= ⎪ ⎪⎝⎭⎝⎭22702,2,33666623B C B B B B ππππππππ⎛⎫+=∴<<-∈-∴-== ⎪⎝⎭ ①ABC 为等边三角形所以211sin 12232S a π=⨯=⨯⨯=19．如图，在四棱锥P ABCD -中，PC ⊥底面,ABCD ABCD 是直角梯形，,//AD DC AB DC ⊥，222AB AD CD ===，点E 是PB 的中点.（1）证明：直线BC ⊥平面PAC ；（2）者直线PB 与平面PAC 所成角的正弦值为3，求三棱锥P ACE -的体积. 【答案】（1）证明见解析；（2）13. 【分析】（1）由PC ⊥平而ABCD ，证得PC BC ⊥，再由222AC BC AB +=，得到AC BC ⊥，结合线面垂直的判定定理，即可证得BC ⊥平面PAC ；（2）由（1）得到BPC ∠为PB 与平面PAC 所成角，在直角BPC △中，可求得PB =得到2PC =，结合12P ACEP ACB V V --=，即可求解.【详解】（1）因为PC ⊥平而ABCD ，BC ⊂平面ABCD ，所以PC BC ⊥， 又由2,1,AB AD CD AD DC ===⊥，且ABCD 是直角梯形，可得AC BC ==222AC BC AB +=，所以AC BC ⊥，又因为PC AC C ⋂=，且,PC AC ⊂平面PAC ，所以BC ⊥平面PAC .（2）由（1）知BC ⊥平面PAC ，所以BPC ∠即为直线PB 与平面PAC 所成角， 在直角BPC △中，可得sin BC BPC PB ∠===，所以PB =2PC =， 所以11111(122)22323P ACE P ACB V V --==⨯⨯⨯⨯⨯=. 20．已知数列{}n a 中，112a =，()*123nn n a a n N a +=∈+. （1）求证：11n a ⎧⎫+⎨⎬⎩⎭是等比数列，并求数列{}n a 的通项公式； （2）已知数列{}n b 满足()312n nn nn b a -=.△求数列{}n b 的前n 项和n T ；△若不等式(1)2nn n nT λ-<+对一切*n N ∈恒成立，求实数λ的取值范围. 【答案】(1)证明见解析；131n n a =-；(2)①222n n n T +=-；①3(1)2-，【分析】(1)由题意推出11113(1)n na a ++=+，进而可以证明11n a ⎧⎫+⎨⎬⎩⎭是以3为首项，3为公比的等比数列，由此即可得出数列的通项公式. (2)①：由(1)得2n nnb =，结合错位相减法即可求出n T ； ①：由①得2(1)22nn λ-<-，设222nnc =-，则{}n c 是递增数列，由此求得λ的取值范围.【详解】(1)因为111==()223n n n a a a n N a *+∈+，，， 所以113=2n na a ++，所以111+1=3(1)n n a a ++， 又111=3a +， 所以11n a ⎧⎫+⎨⎬⎩⎭是以3为首项，3为公比的等比数列， 故111+1=333n n n a -+⨯=， 即1=31n n a -； (2)①：由(1)知2n n nb =， 所以231232222nnnT ， 234111231222222n n n n nT +-=+++++， 两式相减，得23111231222222n n n nT +=++++- 1111[1()]222112212n n n n n ++-+=-=--， 所以222n n n T +=-；①：由①得22(1)22222nn n n n n λ+-<-+=-，设222n n c =-，则{}n c 是递增数列，当n 为偶数时，222n λ<-恒成立，又232c =，所以32λ<；当n 为奇数时，222n λ-<-恒成立，又11c =，所以1λ-<，所以1λ>-，综上诉述，λ的取值范围是3(1)2-，.21．已知点P 在抛物线2:4C y x =上，过点P 作圆()(222:30M x y rr -+=<≤的两条切线，与抛物线C 分别交于A ､B (A ､B 异于点P )两点，切线PA ､PB 与圆M 分别相切于点E ､F .（1）若点P 到圆心M 的距离与它到抛物线C 的准线的距离相等，求点P 的坐标； （2）若点P 的坐标为(1，2)，设线段AB 中点的纵坐标为t ，求t 的取值范围. 【答案】（1）(2,或(2,-；（2）[)10,6--. 【分析】（1）设出P 点的坐标，根据题目所给条件列方程组，解方程组求得P 点坐标. （2）设出切线的方程，由圆心到切线的距离等于半径列等量关系式，求得两条切线斜率的关系式，联立切线的方程和抛物线的方程，求得,A B 两点的纵坐标，进而求得t 的表达式，由r 的取值范围求得t 的取值范围. 【详解】（1）设点P 的坐标为(x ，y )，则241y x x ⎧==+，解得2x y =⎧⎪⎨=⎪⎩2x y =⎧⎪⎨=-⎪⎩， 即点P 的坐标为(2,或(2,-；（2）由题意知切线P A ､PB 的斜率均存在且不为零，设切线方程为()21y k x -=-，由r =，得()2224840r k k r -++-=，记切线P A ､PB 的斜率分别为1k ､2k ，则12212841k k r k k ⎧+=⎪-⎨⎪=⎩，由于切线P A ､PB 的方程分别为()121y k x -=-､()221y k x -=-， 联立()21421y x y k x ⎧=⎪⎨-=-⎪⎩，消去x ，得2114840k y y k -+-=，设()11,A x y ､()22,B x y ，则1142y k +=，故1142y k =-.同理2242y k =-， 于是()1212212122221622224k k y y t k k k k r ++==+-=-=--，因为0r <≤202r <≤，2442r -<-≤-，2111244r -≤<--，216844r -≤<--， 21610264r -≤-<--.所以[)216210,64r -∈---.即t 的取值范围是[)10,6--. 【点睛】直线和圆相切，可利用圆心到直线的距离等于半径来列方程. 22．已知函数()212xf x xe ax ax =++，()()21ln 2g x ax a x a =-∈R ． （1）讨论()f x 在区间()0,∞+上的单调性；（2）若关于x 的不等式()()f x g x >在区间()0,∞+上恒成立，求a 的取值范围． 【答案】（1）当1a ≥-时，()f x 在()0,∞+上单调递增，当1a <-时，()f x 在()()0,ln a -上单调递减，在()()ln ,a -+∞上单调递增；（2）(],0e -． 【分析】（1）通过求导，分1a ≥-、1a <-讨论即可得到单调性；（2）要使()()f x g x >在区间()0,∞+上恒成立，通过变形、换元，则ln t a t >-即可，进而可求出a 的取值范围． 【详解】 （1）()212xf x xe ax ax =++，求导得：()()()()11x xf x x e ax a e a x =+++=++'． 当1a ≥-时，0x e a +≥，10x +>，()0f x '≥，()f x 在()0,∞+上单调递增． 当1a <-时，令()0f x '>，得x e a >-，()ln x a >-，()f x 单调递增； 令()0f x '<，得x e a <-，()ln x a <-，()f x 单调递减． 综上，当1a ≥-时，()f x 在()0,∞+上单调递增；当1a <-时，()f x 在()()0,ln a -上单调递减，在()()ln ,a -+∞上单调递增． （2）由()()f x g x >得，()ln ln xxxe ax a x xe a x x +>-⇒>-+．令(),0,xt xe t =∈+∞，则()ln ln ln xx x xet +==，上式变为ln t a t >-．①当0a =时，上式恒成立；①当0a >时，0t →时，ln a t -→+∞，不成立；①当0a <时，()1ln t h t a t ->=，求导得：()21ln 0t h t t e t-==⇒='， 所以，()()max1h t h e e ==，则11a e->，即e a -<<0．综上，(],0a e ∈-． 【点睛】本题难点在于第（2）问中，对()()f x g x >做等价处理成“()ln xxe a x x >-+”，进而借助换元进行分类讨论．。

2021年秋季高三数学开学摸底考试卷01一、单选题1．设集合{}1,1,2,3,5A =-，{}2,3,4B = ，{|13}C x R x =∈< ，则()A C B =A ．{2}B ．{2，3}C ．{-1，2，3}D ．{1，2，3，4}【答案】D 【分析】 先求AC ，再求()A C B ．【详解】 因为{1,2}AC =，所以(){1,2,3,4}A C B =.故选D ． 【点睛】集合的运算问题，一般要先研究集合中元素的构成，能化简的要先化简，同时注意数形结合，即借助数轴、坐标系、韦恩图等进行运算．2．设复数12,z z 在复平面内的对应点关于实轴对称，134,z i +＝则12z z ＝（ ） A ．25 B ．25-C ．724i -D ．724i --【答案】A 【分析】由题意可得234z i -＝，根据复数的乘法运算即可求解. 【详解】复数12,z z 在复平面内的对应点关于实轴对称，134,z i +＝则234z i -＝，所以()()12343491625z z i i +-=+=＝. 故选：A3．已知直三棱柱111ABC A B C -2AB =，1AC =，60BAC ∠=︒，则该球的表面积为（ ）A ．4πB ．C ．8πD ．32π【答案】C 【分析】利用三棱柱111ABC A B C -2AB =，1AC =，60BAC ∠=︒，求出1AA ，再求出ABC ∆外接圆的半径，即可求得球的半径，从而可求球的表面积.【详解】∵三棱柱111ABC A B C -的侧棱垂直于底面，2AB =，1AC =，60BAC ∠=︒，∴1121sin 602AA ⨯⨯⨯︒⨯=12AA =∵2222cos604123BC AB AC AB AC =+-⋅︒=+-=，∴BC =. 设ABC ∆外接圆的半径为R ，则2sin 60BCR =︒，∴1R =.=248ππ⨯=.故选：C. 【点睛】本小题主要考查根据柱体体积求棱长，考查几何体外接球有关计算，属于基础题.4．函数2()sin cos f x x x x =的图象的一条对称轴为（ ） A ．12x π=B ．6x π=C ．3x π=D ．2x π=【答案】A 【分析】先化简得()sin 23f x x π⎛⎫=+ ⎪⎝⎭232x k πππ+=+，k Z ∈求出对称轴即可判断. 【详解】211cos 2()sin cos sin 2sin 2223x f x x x x x x π+⎛⎫=+==+ ⎪⎝⎭令232x k πππ+=+，k Z ∈，解得122k x ππ=+，k Z ∈， 则可得12x π=是()f x 的一条对称轴. 故选：A.5．椭圆221259x y +=上一点M 到焦点1F 的距离为2，N 是1MF 的中点，则||ON 等于（ ）A ．2B ．4C ．6D ．1.5【答案】B 【分析】设椭圆另一焦点为2F ,根据椭圆定义12210MF MF a +==，故28MF =，再结合中位线定理即可得答案. 【详解】设椭圆另一焦点为2F ,根据椭圆定义12210MF MF a +==，故28MF =，12MF F △中, N 是1MF 的中点，O 是12F F 的中点，故ON 是中位线，2118422ON MF ==⨯=. 故选：B.6．已知0,2πα⎛⎫∈ ⎪⎝⎭，2sin 2cos 21αα-=，则cos α的值为（ ）A ．15B C ．3D 【答案】D 【分析】利用二倍角公式化简得到2sin cos ,αα=再利用同角的平方关系求解. 【详解】由题得24sin cos 12cos 1,ααα+-= 所以24sin cos 2cos ,ααα= 因为0,2πα⎛⎫∈ ⎪⎝⎭，所以2sin cos ,αα=因为22221sin cos 1,cos cos 14αααα+=∴+=，所以24cos ,(0,),cos 52πααα=∈∴=故选：D 【点睛】方法点睛：三角函数求值常用的方法有：三看（看角、看名、看式）三变（变角、变名、变式）. 7．若ln ln ln 1a a b b c c >>=，则（ ） A ．ln ln ln b c c a a b e a e b e c +++>> B ．ln ln ln c a b c a b e b e a e c +++>> C ．ln ln ln a b c a b c e c e b e a +++>> D ．ln ln ln a b b c c a e c e a e b +++>>【答案】C 【分析】构造函数()ln f x x x =，利用导数得出1a b c >>>，构造函数ln ()x x g x e =，利用导数证明ln ln ln a b c a b ce e e<<，从而得出ln ln ln a b c a b c e c e b e a +++>>. 【详解】令()ln f x x x =，则()1ln f x x '=+ 当10x e<<时，()0f x '<，当1x e >时，()0f x '>即函数()f x 在10,e ⎛⎫ ⎪⎝⎭上单调递减，在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增()()()1f a f b f c >>=，由图象易知，1a b c >>>令ln ()x x g x e=，则1ln ()xxx g x e -'= 由于函数1ln y x x=-在(0,)+∞上单调递减，1ln c c =，111ln 0c c c c -=-=则1ln 0x x-=在(0,)+∞上有唯一解c ，故()0g x '=在(0,)+∞上有唯一解c 即当x c >时，()0g x '<，则函数()g x 在(,)c +∞上单调递减 即()()()g a g b g c <<，即ln ln ln a b c a b ce e e<< ln ln ,ln ln b a c b e a e b e b e c ∴<<ln ln ,ln ln ln ln ln b c a c a c b c b c a c b c e a e b e b e c e a e b e c +++++++∴<<⇒<<故选：C 【点睛】关键点睛：解决本题的关键在于构造函数，利用导数得出函数的单调性，进而得出函数值的大小关系. 8．算盘是中国传统的计算工具，是中国人在长期使用算筹的基础上发明的，是中国古代一项伟大的、重要的发明，在阿拉伯数字出现前是全世界广为使用的计算工具．“珠算”一词最早见于东汉徐岳所撰的《数术记遗》，其中有云：“珠算控带四时，经纬三才．”北周甄鸾为此作注，大意是：把木板刻为3部分，上、下两部分是停游珠用的，中间一部分是作定位用的．下图是一把算盘的初始状态，自右向左，分别是个位、十位、百位、……，上面一粒珠（简称上珠）代表5，下面一粒珠（简称下珠）是1，即五粒下珠的大小等于同组一粒上珠的大小．现从个位、十位、百位和千位这四组中随机拨动2粒珠（上珠只能往下拨且每位至多拨1粒上珠，下珠只能往上拨），则算盘表示的整数能够被3整除的概率是（ ）A ．38B ．58C ．29D ．12【答案】D 【分析】从个位、十位、百位和千位这四组中随机拨动2粒珠，利用列举法列出整数共有32个，其中能够被3整除的整数有16个，进而根据古典概型的概率计算公式可解．解：从个位、十位、百位和千位这四组中随机拨动2粒珠，得到的整数共有32个，分别为： 11，15，51，55，101，105，501，505，110，150，510，550，1001，1005，5001，5005，1010，1050，5010，5050，1100，1500，5100，5500， 2，20，200，2000，6，60，600，6000，其中算盘表示的整数能够被3整除的整数有16个，分别为：15，51，105，501，150，510，1005，5001，1050，5010，1500，5100，6，60，600，6000， 则算盘表示的整数能够被3整除的概率为161322P ==． 故选：D ． 【点睛】关键点点睛：本题的解题关键点是利用列举法把从个位、十位、百位和千位这四组中随机拨动2粒珠所得到的整数列举出来.二、多选题9．已知在数学测验中，某校学生的成绩服从正态分布()110,81N ，其中90分为及格线，则下列结论中正确的有（附：随机变量ξ服从正态分布()2,N μσ，则()220.9545P μσξμσ-<<+=）（ ）A ．该校学生成绩的期望为110B ．该校学生成绩的标准差为9C ．该校学生成绩的标准差为81D ．该校学生成绩及格率超过95%【答案】ABD 【分析】根据正态分布的数字特征可判断ABC 选项的正误，计算出()900.97725P ξ≥>，可判断D 选项的正误. 【详解】因为该校学生的成绩服从正态分布()110,81N ，则110μ=，方差为281σ=，标准差为9σ=，21102992μσ-=-⨯=，()()()()11909222222P P P P ξξξμσμσξμσ≥>≥=≥-=+-<<+110.95450.977250.9522=+⨯=>. 所以，该校学生成绩的期望为110，该校学生成绩的标准差为9，该校学生成绩及格率超过95%. 所以，ABD 选项正确，C 选项错误.10．ABC 中，D 为边AC 上的一点，且满足12AD DC =，若P 为边BD 上的一点，且满足()0,0AP mAB nAC m n =+>>，则下列结论正确的是（ ）A ．21m n +=B ．mn 的最大值为112C ．41m n+的最小值为6+ D ．229m n +的最小值为12【答案】BD 【分析】根据平面向量共线定理可知A 错误； 根据()133mn m n =⋅，利用基本不等式可求得最大值，知B 正确； 由()41413m n m n m n ⎛⎫+=++ ⎪⎝⎭，利用基本不等式可求得最小值，知C 错误； 利用基本不等式可得()222392m n m n ++≥，知D 正确.【详解】对于A ，3AP mAB nAC mAB nAD =+=+，,,B P D 三点共线，31m n ∴+=，A 错误；对于B ，31m n +=，()21131333212m n mn m n +⎛⎫∴=⋅≤⨯= ⎪⎝⎭（当且仅当3m n =时取等号），B 正确；对于C ，()4141123777n m m n m n m n m n ⎛⎫+=++=++≥+=+ ⎪⎝⎭12n m m n =，即m =时取等号），C 错误； 对于D ，()22231922m n m n ++≥=（当且仅当3m n =时取等号），D 正确.故选：BD. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：一正二定三相等.（1）“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.11．古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名．他发现：“平面内到两个定点A，B的距离之比为定值λ（λ≠1）的点的轨迹是圆”．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆，在平面直角坐标系xOy中，A（﹣2，0），B（4，0），点P满足12PAPB=．设点P的轨迹为C，下列结论正确的是，（）A．C的方程为（x+4）2+y2＝9B．在x轴上存在异于A，B的两定点D，E，使得12 PDPE=C．当A，B，P三点不共线时，射线PO是∠APB的平分线D．在C上存在点M，使得|MO|＝2|MA|【答案】BC【分析】设P（x，y），运用两点的距离公式，化简可得P的轨迹方程，可判断A；假设在x轴上存在异于A，B的两定点D，E，使得12PDPE=，设出D，E的坐标，求得轨迹方程，对照P的轨迹方程可得D，E，可判断B；当A，B，P三点不共线时，由12OA PAOB PB==，由角平分线定理的逆定理，可判断C；若在C上存在点M，使得|MO|＝2|MA|，可设M（x，y），运用两点的距离公式，可得M的轨迹方程，联立P 的轨迹方程，即可判断D．【详解】在平面直角坐标系xOy中，A（﹣2，0），B（4，0），点P满足12 PAPB=，设P （x ，y ），则12=， 化简可得（x +4）2+y 2＝16，故A 错误；假设在x 轴上存在异于A ，B 的两定点D ，E ，使得12PDPE =， 可设D （m ，0），E （n ，0）= 化简可得3x 2+3y 2﹣（8m ﹣2n ）x +4m 2﹣n 2＝0，由P 的轨迹方程为x 2+y 2+8x ＝0，可得8m ﹣2n ＝﹣24，4m 2﹣n 2＝0，解得m ＝﹣6，n ＝﹣12或m ＝﹣2，n ＝4（舍去），即存在D （﹣6，0），E （﹣12，0），故B 正确； 当A ，B ，P 三点不共线时，由12OA PAOBPB==，可得射线PO 是∠APB 的平分线，故C 正确； 若在C 上存在点M ，使得|MO |＝2|MA |，可设M （x ，y ）=化简可得x 2+y 2163+x 163+=0，联立x 2+y 2+8x ＝0，可得方程组无解，故不存在M ，故D 错误． 故选：BC ． 【点睛】本题考查轨迹方程的求法，考查圆方程的求法和运用，以及两点距离公式的运用，考查化简运算能力，属于中档题．12．如图，在棱长为2的正方体ABCD A B C D ''''-中，M 为BC 边的中点，下列结论正确的有（ ）A ．AM 与DB ''B ．过三点A 、M 、D的正方体ABCD A B C D ''''-的截面面积为92C ．四面体A C BD ''的内切球的表面积为3πD ．正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动并且使MAC PAC ''∠=∠，那么点P 的轨迹是椭圆 【答案】AB 【分析】构建空间直角坐标系，由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误；同样设(,,0)P x y 结合向量夹角的坐标表示，且由等角的余弦值相等可得=P 的轨迹知D 的正误；由立方体的截面为梯形，分别求,,,MN AD AM D N ''，进而得到梯形的高即可求面积，判断B 的正误；由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ，进而求内切球表面积，判断C 的正误. 【详解】A ：构建如下图所示的空间直角坐标系：则有：(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D ''， ∴(1,2,0),(2,2,0)AMD B ''==-，cos ,10||||5AM D B AM D B AM D B ''⋅''<>===''，故正确.B ：若N 为CC '的中点，连接MN ，则有//MN AD '，如下图示，∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面，而MNAD AM D N ''===，可得梯形的高为2，∴梯形的面积为1922S =⨯=，故正确. C ：如下图知：四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积，∴118848323V =-⨯⨯⨯=，而四面体的棱长都为有表面积为14sin 23S π=⨯⨯=，∴若其内切圆半径为r ，则有1833r ⨯=，即r =2443r ππ=.故错误. D ：正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动且MAC PAC ''∠=∠，即P 的轨迹为面A B C D ''''截以AM 、AP 为母线，AC’为轴的圆锥体侧面所得曲线，如下图曲线GPK ，构建如下空间直角坐标系，(0,0,2),(22A M C '-，若(,,0)P x y ，则232(,,0),(0,22,2),(,,2)22AM AC AP x y '=-=-=-，∴cos ||||5AM AC MAC AM AC '⋅'∠==='，cos ||||AP AC PAC AP AC x '⋅'∠=='5=22(9216(0)y x y +-=>，即轨迹为双曲线的一支，故错误.故选：AB 【点睛】关键点点睛：应用向量的坐标表示求异面直线的夹角，并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹，综合立方体的性质求截面面积，分割几何体应用等体积法求内切球半径，进而求内切球的表面积.三、填空题13．已知()f x 是定义在R 上的周期为3的奇函数，且(1)2(10)3f f -=+，则(2021)f =___________. 【答案】1 【分析】利用函数的周期性得(2021)(1)f f =-，由已知条件可知(1)2(1)3f f -=--+，即可求值. 【详解】由题意知：(2021)(36741)(1)f f f =⨯-=-，而(1)2(10)3f f -=+， ∴(1)2(331)32(1)32(1)3f f f f -=⨯++=+=--+，即3(1)3f -=， ∴()11f -=，故(2021)1f =. 故答案为：114．已知抛物线()2:20C y px p =>的焦点为F ，过F l 交抛物线C 与A 、B 两点，若线段AB C 的方程是________. 【答案】26y x = 【分析】本题首先可设()11,A x y 、()22,B x y ，则2112y px =、2222y px =，然后两式相减，可得()()()1212122y y y y p x x -+=-，再然后根据A 、B l )122y y p +=，最后根据线段AB . 【详解】设()11,A x y ，()22,B x y ，则2112y px =，2222y px =，两式相减得22121222y y px px -=-，即()()()1212122y y y y p x x -+=-，因为A 、B l 上，所以12123y y x x ，()()()1212122y y y y p x x -+=-)122y y p +=，因为线段AB 12y y +=2p =，3p =，抛物线C 的方程是26y x =， 故答案为：26y x =. 【点睛】关键点点睛：本题考查抛物线方程的求法，考查直线与抛物线相交的相关问题的求解，考查中点坐标的相关性质，考查直线斜率的应用，考查计算能力，是中档题.15．已知函数()ln(1)f x x x =+-，()ln g x x x =，若1()12ln f x t =+，22()g x t =，则122()ln x x x t -的最小值为___________. 【答案】12e- 【分析】先证明据121ln x x -=，结合222ln x x t =，求出2122()ln ln x x x t t t -=，令2ln ()(0)h t t t t =>，根据函数的单调性求出代数式的最小值即可． 【详解】111()ln(1)12ln f x x x t =+-=+，即1121111ln(1)ln ln[(1)]x x x t e x --+-==⋅-，1121(1)x t e x -∴=-①，20t >， 2ln 22222()ln ln x g x x x t e x ===⋅②，又x y x e =⋅在[0，)+∞上单调递增，故由①②得()121ln 12121ln 1ln x xe x e x x x --=⋅⇒-=，故212222()ln ln ln ln x x x t x x t t t -=⋅=， 令2ln ()(0)h t t t t =>，则()2ln h t t t t '=+，令()0h t '>，解得：12t e ->，令()0h t '<，解得：120t e -<<， 故()h t 在12(0,)e -递减，在12(e -，)+∞递增，故12min 1()()2h t h e e-==-， 故答案为：12e-． 【点睛】利用导数解答函数最值的一般步骤：第一步：利用()0f x '>或()0f x '<求单调区间；第二步：解()0f x '=；第三步：比较方程的根同区间端点的大小；第四步：求极值；第五步：比较区间端点的函数值与极值的大小．16．格点是指平面直角坐标系中横纵坐标均为整数的点.一格点沿坐标线到原点的最短路程为该点到原点的“格点距离”（如：(2,1)P -，则点P 到原点的格点距离为213+=）.格点距离为定值的点的轨迹称为“格点圆”，该定值称为格点圆的半径，而每一条最短路程称为一条半径.当格点半径为6时，格点圆的半径有______条（用数字作答）. 【答案】252 【分析】由题设，易知格点圆上的格点都在||||6x y +=上，其中每个象限有5个，且相互关于x 、y 轴或原点对称，分析可得每个格点半径条数为||||||x x y C +，进而可求所有格点的半径条数. 【详解】设格点为(,)x y ，格点半径为6，则||||6x y +=， ∴对应格点圆图象如下，每条边上有(不含端点)5个格点，以第一象限为例，格点有(1,5),(2,4),(3,3),(4,2),(5,1)，其中(1,5)的半径有6条，(2,4)的半径有15条，(3,3)的半径有20条，(4,2)的半径有15条，(5,1)的半径有6条，∴共有62条，即对于任意格点，其半径条数有||||||x x y C +条， ∴由上，四个象限共有12345666664()248C C C C C ⨯++++=条半径，另外数轴上有(6,0),(0,6),(6,0),(0,6)--四个点，半径共有0644C =条，综上，格点半径为6时，格点圆的半径有2484252+=条. 故答案为：252. 【点睛】关键点点睛：画出格点圆的图象，确定各象限中格点坐标，分析格点半径条数与坐标值之间的关系，应用对称性求格点圆半径总条数即可.四、解答题17．已知等差数列的首项为2，前n 项和为S n ，正项等比数列{b n }的首项为1，且满足，前n 项和为a 3＝2b 2，S 5＝b 2＋b 4．（1）求数列{a n }，{b n }的通项公式；（2）设()331log log nn n n c S b =-+，求数列{c n }的前26项和．【答案】（1）2n a n =，13n n b -=；（2）328.【分析】（1）根据题设可得关于公差和公比的方程组，求出其解后可得两个数列的通项公式. （2）利用裂项相消法和分组求和可求{}n c 的前26项和. 【详解】（1）由题意得：113111225452a d b q a d b q b q +=⎧⎪⎨⨯+=+⎪⎩即32221010d q d q q +=⎧⎨+=+⎩， ∴390q q -=，∵{}n b 是正项等比数列，∴3q =，则2d =，∴()2212n a n n =+-=，11133n n n b --==.（2）()()12212n S n n n n =+=+， 则()()()()()13331log 1log 31log 1log 11nn nn n c n n n n n -⎡⎤=-++=-+-++-⎡⎤⎣⎦⎣⎦∴{}n c 的前26项和为：()()()26333333log 1log 20log 2log 31log 3log 42T =--+++++--++()()3333log 25log 2624log 26log 2725+--++++()3326025log 1log 2733253282⨯+=-++=+=.【点睛】思路点睛：数列求和关键看通项的结构形式，如果通项是等差数列与等比数列的和，则用分组求和法；如果通项是等差数列与等比数列的乘积，则用错位相减法；如果通项可以拆成一个数列连续两项的差，那么用裂项相消法；如果通项的符号有规律的出现，则用并项求和法.18．潍坊市为切实保障疫情防控期间全市食品质量安全，采取食品安全监督抽检和第三方托管快检室相结合的方式，全面加强食品安全检验检测据了解，滩坊市市场监管部门组织开展对全市部分生产企业、农贸市场、大型商超、餐饮服务场所生产经营的小麦粉、大米、食用油、调味品、肉制品、乳制品等与人民群众日常生活关系密切且消费量大的食品进行监督抽检组织抽检400批次，抽检种类涵盖8大类31个品种全市各快检室快检60209批次，其中不合格53批次．某快检室在对乳制品进行抽检中，发现某品牌乳制品质量不合格，现随机抽取其5个批次的乳制品进行质量检测，已知其中有1个批次的乳制品质量不合格下面有两种检测方案：方案甲：逐批次进行检测，直到确定质量不合格乳制品的批次；方案乙：先任取3个批次的乳制品，将他们混合在一起检测．若结果不合格，则表明不合格批次就在这3个批次中，然后再逐个检测，直到能确定不合格乳制品的批次；若结果合格，则在另外2批次中，再任取l 个批次检测．（1）方案乙中，任取3个批次检测，求其中含有不合格乳制品批次的概率； （2）求方案甲检测次数X 的分布列；（3）判断哪一种方案的效率更高，并说明理由． 【答案】（1）35；（2）答案见解析；（3）方案乙的效率更高．理由见解析. 【分析】（1）由题意即可求解；（2）先求出X 的可能取值，然后求出对应的概率，进而可以求解；（3）设方案乙的检测次数为Y ，求出Y 的可能取值，然后求出对应的概率，再求出方案甲和乙的数学期望，比较大小即可求解． 【详解】解：（1）由方案乙可知含有不合格乳制品批次的概率243535C P C ==，（2）依题意知检测次数X 的可能取值为1，2，3，4，()445511 5A P X A ===，()445512 5A P X A ===，()445513 5A P X A ===，()444455245A A P X A +===， 故方案甲检测次数X 的分布列为：（3）设方案乙检测次数为Y ，则Y 的可能取值为2，3．当2Y =时的情况为先检测3个批次为不合格，再从中逐一检测时，恰好1次检测出，或先检测3个批次为合格，再从其他2个批次中取出1个批次检测．则()2331434231325352132 5C A A A P Y A A A A ⨯⨯==⨯+=， 所以()235P Y ==． 故方案乙检测次数Y 的分布列为：()555E Y =+=， 则()12381455555E X =+++=，因为()()E Y E X<，所以方案乙的效率更高．19．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且cos cos 2cos b A a B c A +=． （1）求A ；（2）若2a =，ABC ABC 的周长． 【答案】（1）3A π=；（2）6．【分析】（1）根据cos cos 2cosb A a Bc A +=，利用正弦定理，结合两角和的正弦公式得到()sin 2sin cos A B C A +=，又A B C π+=-，由sin 2sin cos C C A =求解；（2）根据3A π=，ABC 4bc =，再结合余弦定理求得b c +即可.【详解】（1）因为cos cos 2cos b A a B c A += 所以sin cos sin cos 2sin cos B A A B C A +=，所以()sin 2sin cos A B C A +=， 因为A B C π+=-， 所以sin 2sin cos C C A =， 因为sin 0C ≠， 所以1cos 2A =． 因为0A π<<， 所以3A π=．（2）因为3A π=，ABC所以1sin 23ABC S bc π==△ 解得4bc =，由余弦定理2222cos a b c bc A =+-，得()22243b c bc b c bc =+-=+-，所以4b c +=， 所以6a b c ++=． 所以ABC 的周长为6． 【点睛】方法点睛：（1）在解有关三角形的题目时，要有意识地考虑用哪个定理更适合，或是两个定理都要用，要抓住能够利用某个定理的信息，一般地，如果式子中含有角的余弦或边的二次式，要考虑用余弦定理；如果遇到的式子中含有角的正弦或边的一次式时，则考虑用正弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到．（2）解题中注意三角形内角和定理的应用及角的范围限制． 20．如图，四棱锥P ABCD -中，底面ABCD 是菱形，3BAD π∠=，M 是棱PB 上的点，O 是AD 中点，且PO ⊥底面ABCD ，OP =.（1）求证：BC ⊥OM ；（2）若35PM PB =，求二面角B OM C --的余弦值.【答案】（1）证明见解析；（2【分析】 (1)由底面ABCD 是菱形，3BAD π∠=，可得ABD △为等边三角形，再加上点O 是AD 中点可证OB AD ⊥，进而可得OB BC ⊥，再由PO ⊥底面ABCD ，可得OP BC ⊥，结合线面垂直的判定定理及性质定理，即可求证所求证；(2)由题意及(1)可以，以点O 为原点，,,OA OB OP 所在的直线分别为,,x y z 轴，建立空间直角坐标系，再利用向量法即可求解.【详解】证明：在菱形ABCD 中，3BAD π∠=，ABD ∴为等边三角形.又O 为AD 的中点，∴OB AD ⊥.AD //BC ，∴OB BC ⊥.PO ⊥底面ABCD ，BC ⊂平面ABCD ，∴OP BC ⊥.OP OB O =，,OP OB ⊂平面POB ，∴BC ⊥平面POB .M 是棱PB 上的点，∴OM ⊂平面POB .∴BC ⊥OM .（2）解：PO ⊥底面ABCD ，OB AD ⊥，∴建立如图所示空间直角坐标系O xyz -，设1OA =，则==OP OB(0,0,0)O，(1,0,0)A ，B ，(C -，P ，∴(OC →=-. 由35PM PB =，得35OM OP PB →→→=+=. 设(,,)m x y z →=是平面OMC 的法向量，由00OM m OC m →→→→⎧⋅=⎪⎨⎪⋅=⎩，得320,20,y z x +=⎧⎪⎨=⎪⎩ 令2y =，则3x z ==-，则3)m →=-. 又平面POB 的法向量为(1,0,0)n →=，∴cos ,m n m n m n →→→→→→⋅===. 由题知，二面角B OM C --为锐二面角，所以二面角B OM C --的余弦值为4【点睛】本题考查线线垂直的证明及空间向量法求二面角，考查考生的逻辑推理能力、空间想象能力、运算求解能力及方程思想，属于中档题. 21．已知等轴双曲线C ：22221x y a b-=(a >0，b >0)经过点，12). （1）求双曲线C 的标准方程；（2）已知点B (0，1).①过原点且斜率为k 的直线与双曲线C 交于E ，F 两点，求∠EBF 最小时k 的值；②点A 是C 上一定点，过点B 的动直线与双曲线C 交于P ，Q 两点，APAQ k k +为定值λ，求点A 的坐标及实数λ的值.【答案】（1）221x y -=；（2）①0k =；②),Aλ=(),A λ=. 【分析】（1）由题意a b =，代入已知点建立方程，解之可得双曲线C 的标准方程.（2）①由对称性可设()(),,,E x y F x y --，且1≥x ，运用向量数量积的坐标运算表示221BE BF x y ⋅=--+，又由221y x =-可得()2210BE BF x ⋅=-≤，由此可得EBF ∠最小时，k 的值.②设(),,A m n 过点B 的动直线为： 1.y tx =+设()()1122,,,,P x y Q x y 与双曲线的方程联立得()221220t x tx ---=，根据根的判别式和根与系数的关系可求得22t <且21t ≠，由直线的斜率公式得121211tx n tx n x m x mλ+-+-+=--，再由恒等式的思想可求得点A 的坐标及实数λ的值. 【详解】解：（1）由题意a b =，且2251441a b -=解得1a b ==， 所以双曲线C 的标准方程为22 1.x y -=（2）①由对称性可设()(),,,E x y F x y --，且1≥x ，则()()22,1,11BE BF x y x y x y ⋅=-⋅---=--+， 因为E 点在双曲线C 上，所以221x y -=，所以221y x =-，所以()2210BE BF x ⋅=-≤， 当1x =时，0,BE BF EBF ∠⋅=为直角， 当1x >吋，0,BE BF EBF ∠⋅<为钝角.因此，EBF ∠最小时，1,0x k ==.②设(),,A m n 过点B 的动直线为： 1.y tx =+设()()1122,,,,P x y Q x y 联立2211x y y tx ⎧-=⎨=+⎩得()221220t x tx ---=， 所以()22212212210Δ48102 121t t t t x x t x x t ⎧-≠⎪=+->⎪⎪-⎨+=-⎪-⎪⎪=--⎩，由210t -≠且Δ0>，解得22t <且21t ≠，AP AQ k k λ+=，即1212,y n y n x m x m λ--+=--即121211tx n tx n x m x mλ+-+-+=--， 化简得()()()2121221220t x x mt n m x x m mn m λλλ-+-+-++-+-=，所以()()222222122011t t mt n m m mn m t tλλλ--+-+-+-+-=--， 化简得()()2222212220m mn t m n t m mn m λλλλ-+--+-+-=， 由于上式对无穷多个不同的实数t 都成立，所以2220102220m mn m n m mn m λλλλ⎧-=⎪--=⎨⎪-+-=⎩如果0,m =那么1,n =-此时()0,1A -不在双曲线C 上，舍去.因此0,m ≠从而22,m n =代入21m n =+解得1,n m ==.此时()A 在双曲线C 上.综上，),A λ=或者(),A λ=. 【点睛】 关键点点睛：本题考查直线与双曲线位置关系之定值问题，属于较难题，关键在于将直线与双曲线的方程联立，得出根与系数的关系，继而将目标条件转化到曲线上的点的坐标上去.22．已知函数()()()2ln 1002x f x ax a x x -=+->≥+，. （1）当12a =时，讨论函数()y f x =的单调性； （2）若不等式()1f x ≥在[0,)x ∈+∞时恒成立，求实数a 的取值范围；（3）证明：()()*11111ln 1357212n n N n ++++<+∈+. 【答案】（1）在区间()02，上单调递减；在区间()2+∞，上单调递增；（2）[1，)+∞；（3）证明见解析.【分析】（1）求出()f x 的导数，根据导数的正负即可判断单调性；（2）求出()f x 的导数，根据a 的范围讨论单调性，求出()f x 的最小值，满足()min 1f x ≥即可求出a 的取值范围；（3）由（2）可知当1a =时，不等式()1f x >在(0,)x ∈+∞时恒成立，可得11[ln(1)ln ]122k k k <+-+，即可得证.【详解】 解：（1）当12a =时，()()()221142122212x f x x x x -'=⋅-=+++， 当()0,2x ∈时，()0f x '<，()f x 单调递减；当()2,x ∈+∞时，()0f x '>，()f x 单调递增；所以()y f x =在区间()0,2上单调递减；在区间()2,+∞上单调递增；（2）()2224441(2)(1)(2)a ax a f x ax x ax x +-'=-=++++， 当1a ≥时，()0f x '≥，∴函数()y f x =在[)0+∞，上单调递增； 当01a <<时，由()0f x '>可得x > ∴函数在⎡⎫∞⎪⎢⎪⎣⎭上单调递增，在⎡⎢⎣上单调递减； ①当1a ≥时，函数()y f x =在[)0+∞，上单调递增， ()()01f x f ∴≥=，即不等式()1f x ≥，在[)0x ∈+∞，时恒成立， ②当01a <<时，函数在0⎡⎢⎣上单调递减，存在00x ⎡∈⎢⎣使得()()001f x f <=，所以不合题意，舍去. 综上可知实数a 的取值范围为[)1,+∞；（3）由（2）得当1a =时，不等式()1f x >在(0,)x ∈+∞时恒成立，即2ln(1)2x x x +>+，12ln(1)12k k ∴+>+，*()k N ∈. 即11[ln(1)ln ]122k k k <+-+， ∴11(ln 2ln1)32<-，11(ln3ln 2)52<-，11(ln 4ln3)72<-，11[ln(1)ln ]212n n n ⋯<+-+， 将上述式子相加可得()()()111111ln 1ln1ln 13572122n n n ++++<+-=++ 原不等式得证.【点睛】 结论点睛：本题考查不等式的恒成立问题，一般按如下规则转化，（1）对于[],x a b ∀∈，都有()f x m ≥恒成立，则()min f x m ≥；（2）对于[],x a b ∀∈，都有()f x m ≤恒成立，则()max f x m ≤.。

顶级名校2021届高三数学上学期开学摸底考试试题 文〔含解析〕第I 卷一、选择题：此题一共12小题，每一小题5分，在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的.{}1A x x =≤，{}0B x x =>，那么A B =〔 〕A. []1,0-B. []1,0-C. (]0,1D. []0,1【答案】C 【解析】 【分析】可以求出集合A ，然后进展交集的运算即可． 【详解】解：{}|1A x x =≤{}11A x x ∴=-≤≤，{}0B x x =>， {}01A B x x ∴⋂=<≤.应选：C .【点睛】考察描绘法的定义，绝对值不等式的解法，以及交集的运算，属于根底题． z 满足21iz i=-，其中i 为虚数单位，那么z 的虚部为〔 〕 A. i - B. iC. 1-D. 1【答案】D 【解析】 【分析】根据复数代数形式的除法运算将复数化成HY 形式即可得解；【详解】解：()()()2122211112i i i i z i i i i +-====-+--+，z ∴的虚部为1.应选：D.【点睛】此题考察复数的根本概念，关键是将其分母实数化，化为(,)a bi a b R +∈的形式，进展判断，属于根底题．{}n a 中，2100a a +=，684a a +=-，那么其公差为〔 〕A. 2B. 1C. 1-D. 2-【答案】D 【解析】 【分析】等差数列{}n a 中，根据下标和性质解得：6a 、7a ，即可得出公差． 【详解】解：在等差数列{}n a 中，210620a a a +==，60a ∴=，又68724a a a +==-，72a ∴=-，∴公差为762d a a =-=-.应选：D.【点睛】此题考察了等差数列的通项公式及性质，考察了推理才能与计算才能，属于根底题． 4.()2sin 3πα-=，那么sin(2)cos απα+=〔 〕 A. 43-B. 34-C.43D.34【答案】A 【解析】 【分析】由题意利用诱导公式、二倍角公式，化简要求的式子，可得结果． 【详解】解：()2sin 3πα-=，2sin 3α∴=， ()sin 2sin 22sin cos 42sin cos cos cos 3απααααααα+-∴==-=-=-.应选：A.【点睛】此题主要考察诱导公式、二倍角公式的应用，属于根底题．ABC ∆中，点D 、E 分别在边BC 、AD 上，且BD DC =.2ED AE =，那么向量AE =〔 〕A.1133AB AC + B.1166AB AC + C.1566AB AC + D.1233AB AC + 【答案】B 【解析】 【分析】根据题目条件，结合平面向量运算的三角形法那么，进展推导即可． 【详解】解：AD AB BD =+，AD AC CD =+，又BD DC =，BD CD ∴=-，()12AD AB AC ∴=+， 又2ED AE =，13AE AD ∴=， 111366AE AD AB AC ∴==+. 应选：B.【点睛】此题考察了平面向量运算的三角形法那么，难度不大，属于根底题．6.在?九章算术?中将四个面都是直角三角形的四面体称之为鳖臑.假设某个鳖臑的三视图均为直角边长为1的等腰直角三角形〔如下图〕.那么该鳌臑的中最大面积为〔 〕A.22B. 12 D. 12+【答案】A 【解析】 【分析】利用三视图画出几何体的直观图，判断各个面的面积的最大者，求解即可得到结果． 【详解】解：根据三视图画出该几何体的直观图为如下图的四面体P ABC -，其中PA 垂直于等腰直角三角形ABC 所在的平面.将其放置于正方体中〔如下图〕，可知该正方体的棱长为1，所以111122ABC PAB S S ∆∆==⨯⨯=， 122122PBC PAC S S ∆∆==⨯⨯=，所以外表中最大面的面积为22. 应选：A.【点睛】此题考察的知识要点：三视图的应用，几何体的体积公式的应用，主要考察学生的运算才能和转化才能，属于根底题．()f x 是定义在()(),00,-∞⋃+∞上的偶函数，假设当()0,x ∈+∞时，()ln f x x =，那么满足()0f x >的x 的取值范围为〔 〕 A. ()(),11,-∞-+∞ B. ()()1,00,1- C. ()(),10,1-∞D.()()1,01,-⋃+∞【答案】A 【解析】 【分析】根据函数奇偶性和单调性的关系，分两种情况讨论，然后结合函数单调性的性质进展转化求解即可．【详解】解：由题易知()f x 在()0,x ∈+∞上单调递增，且()10f =，那么由()0f x >，得1x >，又因为()f x 为偶函数，所以当(),0x ∈-∞时，()f x 单调递减，且有()10f -=，那么由()0f x >，得1x <-，所以满足()0f x >的x 的取值范围为()(),11,-∞-+∞.应选：A.【点睛】此题主要考察不等式的求解，结合函数单调性和奇偶性的关系，将不等式进展转化是解决此题的关键，属于根底题．()()2sin 2f x x πωϕϕ⎛⎫=+< ⎪⎝⎭，()0f =()f x 的图象关于直线712x π=对称，那么ω的取值可以为〔 〕 A. 1 B. 2C. 3D. 4【答案】B 【解析】 【分析】由(0)f =ϕ，可得函数的解析式，再利用正弦函数的图象的对称性，求出ω的值．【详解】解：()0f =，sin ϕ∴=，又2πϕ<，3πϕ∴=，从而()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭.()f x 的图象关于直线712x π=对称，71232k πππωπ∴⨯+=+，k Z ∈，即21277k ω=+，k Z ∈， 令1k =，得2ω=. 应选：B.【点睛】此题主要考察正弦函数的图象的对称性，属于根底题，,,A B C 所处的位置恰好位于三角形的三个顶点处，且6,8,10AB km BC km AC km ===.如今ABC ∆内任取一点M 建一大型的超，那么M 点到三个村庄,,A B C 的间隔 都不小于2km 的概率为〔 〕B.12πD.1212π- 【答案】D 【解析】 【分析】采用数形结合，计算ABC S ∆，以及“M 点到三个村庄,,A B C 的间隔 都不小于2km 〞这局部区域的面积S ，然后结合几何概型，可得结果. 【详解】由题可知：222AB BC AC += 所以该三角形为直角三角形分别以,,A B C 作为圆心，作半径为2的圆 如图所以那么 “M 点到三个村庄,,A B C 的间隔 都不小于2km 〞 该局部即上图阴影局部，记该局部面积为S11682422ABC S AB BC ∆=⨯⨯=⨯⨯=又三角形内角和为π，所以2122422ABC S S ππ∆=-⨯=- 设M 点到三个村庄,,A B C 的间隔 都不小于2km 的概率为P 所以242122412ABCS P S ππ∆--=== 应选：D【点睛】此题考察面积型几何概型问题，重点在于计算面积，难点在于计算阴影局部面积，考验理解才能，属根底题.ABCD -A 1B 1C 1D 1中，点M 为棱A 1B 1的中点，那么异面直线AM 与BD 所成角的余弦值为〔 〕A.32B.34C.105D.1010【答案】D 【解析】 【分析】取A 1D 1的中点N ，连结MN ，B 1D 1，易得MN ∥BD ，故异面直线AM 与BD 所成角的余弦值为直线AM 与MN 所成角的余弦值.【详解】如下图，取A 1D 1的中点N ，连结MN ，B 1D 1，∵M 为棱A 1B 1的中点，∴MN ∥B 1D 1， 在正方体ABCD -A 1B 1C 1D 1中，BD ∥B 1D 1，∴异面直线AM 与BD 所成角的余弦值为直线AM 与MN 所成角的余弦值， 连结AN ，那么∠AMN 〔或者其补角〕为异面直线AM 与BD 所成的角， 设正方体ABCD -A 1B 1C 1D 1棱长为2a ， 那么AM =AN 5a ，MN 2a ，在△AMN 中，由余弦定理得：cos∠AMN 222252a a ⨯⨯=1010．故答案为D【点睛】此题考察异面直线所成角的求法，考察空间中线线、线面、面面间的位置关系等根底知识，考察空间想象才能与计算才能，属于常考题型.11.O 为坐标原点，点()1,2P 在抛物线2:4C y x =，过定点P 作两直线分别交抛物线C 于点A 、B ，假设0PA PB k k +=，那么AB OP k k ⋅的值是〔 〕 A. 1- B. 2-C. 3-D. 4-【答案】B 【解析】【分析】设1(A x ，1)y ，2(B x ，2)y ，求得124AB k y y =+，再求出PA 、PB 的斜率，由斜率和为0求得12y y +的值，进一步求出AB 的斜率，那么答案可求．【详解】解：设()11,A x y ，()22,B x y ，那么212122212112444AB y y y y k y y x x y y --===-+-，1121112241214PA y y k y x y --===-+-，同理242PBk y =+. 因为0PA PB k k +=，所以1244022y y +=++，124y y ∴+=-，所以414AB k ==--，又221OP k ==，所以122AB OP k k ⋅=-⨯=-. 应选：B.【点睛】此题考察抛物线的简单性质，考察直线与抛物线位置关系的应用，表达了整体运算思想方法，属于中档题．0,ln 0x x x x a >--≥恒成立，那么实数a 的取值范围是〔 〕A. (,1]-∞-B. (,1]-∞C. [1,)-+∞D.[1,)+∞【答案】A 【解析】 【分析】构造函数()ln f x x x x a =--，利用导数研究函数()f x 在()0,∞+单调性，并计算()min 0f x ≥，可得结果.【详解】令()ln f x x x x a =--，()0,x ∈+∞ 那么()'ln fx x =，令()'01f x x =⇒=假设01x <<时，()'0fx <假设1x >时，()'0fx >所以可知函数()f x 在()0,1递减，在()1,+∞递增 所以()()min 11f x f a ==--由对任意的实数0,ln 0x x x x a >--≥恒成立 所以()min 101f x a a =--≥⇒≤- 应选：A【点睛】此题考察利用导数解决恒成立问题，关键在于构建函数，通过导数研究函数性质，属根底题.第II 卷二、填空题：此题一共4小题，每一小题5分.ABC ∆中，1AB =，2AC =，60A =︒，那么ABC S ∆=________.【解析】 【分析】由利用三角形的面积公式即可计算得解．【详解】解：1AB =，2AC =，60A =︒，11sin 12sin 6022ABC S AB AC A ∆∴==⨯⨯⨯︒=故答案为 【点睛】此题主要考察了三角形的面积公式在解三角形中的应用，属于根底题．:10l x my +-=与圆22:3O x y +=，假设圆心到直线的间隔 为2，那么m =________. 【答案】±1 【解析】 【分析】由点到直线的间隔 公式可知，圆心O 到直线的间隔 为d =，结合可求m ．【详解】解：由点到直线的间隔 公式可知，圆心O 到直线的间隔 为21221d m ==+， 解可得，1m =±， 故答案为：±1．【点睛】此题主要考察了利用点到直线的间隔 公式解决直线与圆的位置关系，属于根底题．x 、y 满足约束条件210100x y x y y -+≥⎧⎪+-≤⎨⎪≥⎩，那么2z x y =+的最大值为_________.【答案】53【解析】 【分析】作出可行域后,根据斜率关系找到最优解,代入最优解的坐标即可求得最大值. 【详解】作出可行域如下图:由2z x y =+可得122z y x =-+, 由图可知最优解为M ,联立21010x y x y -+=⎧⎨+-=⎩ ,解得13x =,23y =,所以最优解为12(,)33M , 所以max 1252333z =+⨯=.故答案为:53. 【点睛】此题考察了线性规划求最大值,利用斜率关系找到最优解是答题关键,属于根底题. 16.如下分组的正整数对：第1组为(){1,2，()2,1}，第2组为(){1,3，()3,1}，第3组为(){1,4，()2,3，()3,2，()4,1}，第4组为(){1,5，()2,4，4,2，()5,1}，⋯，那么第40组第21个数对为______． 【答案】()22,20 【解析】 【分析】由题意可得第n 组各个数和为n 2+，且各个数对无重复数字，按照顺序排列，即可得到所求数对．【详解】由题意可得第一组的各个数和为3，第二组各个数和为4， 第三组各个数和为5，第四组各个数和为6，，第n 组各个数和为n 2+，且各个数对无重复数字， 可得第40组各个数和为42，那么第40组第21个数对为()22,20． 故答案为()22,20．【点睛】此题主要考察了归纳推理的应用，注意总结各组数对的特点，考察简单的归纳推等根底知识，考察判断才能、推理才能、数据处理才能，考察函数与方程思想，是根底题．， 三、解答题：解容许写出文字说明、证明过程或者演算步骤.{}n a 的前n 项和22n n nS +=．〔1〕求数列{}n a 通项公式； 〔2〕令11n n n b a a +=，求数列{}n b 的前n 项和n T . 【答案】〔1〕n a n =；〔2〕1n nT n =+ . 【解析】【分析】〔1〕根据{}n a 和n S 关系得到答案.〔2〕首先计算数列{}n b 通项，再根据裂项求和得到答案. 【详解】解：〔1〕当1n =时，111a S ==当2n ≥时，()11n n n n a S S n n a n -=-==∴=时符合 〔2〕()11111n b n n n n ==-++11111111223111n n T n n n n ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭【点睛】此题考察了{}n a 和n S 关系，裂项求和，是数列的常考题型.18.为进步产品质量，某企业质量管理部门经常不定期地抽查产品进展检测，如今某条消费线上随机抽取100个产品进展相关数据的比照，并对每个产品进展综合评分〔满分是100分〕，将每个产品所得的综合评分制成如下图的频率分布直方图.记综合评分为80分及以上的产品为一等品.〔1〕求图中a 的值，并求综合评分的中位数；〔2〕用样本估计总体，以频率作为概率，按分层抽样的思想，先在该条消费线中随机抽取5个产品，再从这5个产品中随机抽取2个产品记录有关数据，求这2个产品中恰有一个一等品的概率.【答案】(1) 0.040a =；中位数为82.5. (2) 35【解析】 【分析】〔1〕根据频率之和为1，结合频率分布直方图对应矩形区域面积求解即可；先结合数值预判中位数所在组距应在80到90之间，设综合评分的中位数为x ，结合频率计算公式求解即可；〔2〕先结合分层抽样计算出一等品所占比例，再采用列举法表示出所有根本领件，结合古典概率公式求解即可【详解】〔1〕由频率和为1，得(0.0050.0100.0250.020)101a ++++⨯=，0.040a =； 设综合评分的中位数为x ，那么(0.0050.0100.025)100.040(80)0.5x ++⨯+⨯-=，解得82.5x =，所以综合评分的中位数为82.5.〔2〕由频率分布直方图知，一等品的频率为(0.0400.020)100.6+⨯=，即概率为0.6； 所以100个产品中一等品有60个，非一等品有40个，那么一等品与非一等品的抽样比为3：2；所以现抽取5个产品，一等品有3个，记为a 、b 、c ，非一等品2个，记为D 、E ； 从这5个产品中随机抽取2个，根本领件为：ab 、ac 、aD 、aE 、bc 、bD 、bE 、cD 、cE 、DE 一共10种；抽取的这2个产品中恰有一个一等品的事件为：aD 、aE 、bD 、bE 、cD 、cE 一共6种，所以所求的概率为63105P ==. 【点睛】此题考察频率分布直方图中详细数值的求解，中位数的计算，求解详细事件对应的概率，属于中档题19.如下图，在四棱锥A BCDE -中，底面BCDE 2BC =，4AB =， 25AC AE ==.〔1〕证明：AB ⊥平面BCDE ；〔2〕假设点P 在线段AD 上，且2DP AP =，求三棱锥P ABC -的体积. 【答案】〔1〕详见解析；〔2〕89.【解析】 【分析】〔1〕推导出AB BC ⊥，AB BE ⊥，由此能证明AB ⊥平面BCDE ．〔2〕由AB BE ⊥，BE BC ⊥，得BE ⊥平面ABC ，过点P 作//PF CD ，交AC 于点F ，推导出PF 为点P 到平面ABC 的间隔 ，由此能求出三棱锥P ABC -的体积． 【详解】解：〔1〕因为底面BCDE 为正方形，且2BC =，4AB =，25AC AE ==， 所以222AC AB BC =+，222AE AB BE =+， 所以AB BC ⊥，AB BE ⊥， 又BCBE B =，BC ⊂平面BCDE ，BE ⊂平面BC DE -，所以AB ⊥平面BCDE .〔2〕由〔1〕知，AB BE ⊥，又底面BCDE 为正方形， 所以BE BC ⊥， 又AB BC B ⋂=，AB平面ABC ，BC ⊂平面ABC ，所以BE ⊥平面ABC .过点P 作//PF CD 交AC 于点F . 因为//CD BE ，所以//PF BE ，所以PF ⊥平面ABC ， 所以PF 为点P 到平面ABC 的间隔 . 由2DP AP =，知1233PF CD ==， 所以1111128423323239P ABCABC V S PF AB BC PF -∆=⨯⨯=⨯⨯⨯=⨯⨯⨯⨯=. 【点睛】此题考察线面垂直的证明，考察三棱锥的体积的求法，考察空间中线线、线面、面面间的位置关系等根底知识，考察运算求解才能，属于中档题．()2222:10x y C a b a b+=>>的中心为原点O ，过O 作两条互相垂直的射线分别交椭圆于P 、Q两点. 〔1〕证明：2211OPOQ+为定值；〔2〕假设椭圆22:143x y C +=，过原点O 作直线PQ 的垂线，垂足为D ，求OD .【答案】〔1〕详见解析；〔2〕7. 【解析】 【分析】〔1〕分类讨论，当OP ，OQ 斜率存在且不为0时，设直线OP 的方程，代入椭圆方程，求得||OP ，同理求得||OQ ，即可求证2211||||OP OQ +为定值；〔2〕根据〔1〕及三角形的面积相等，即可求得||OD 的值． 【详解】解：〔1〕当射线OP 或者OQ 在x 轴上时，显然有22221111a b OPOQ+=+； 当射线OP ，OQ 不在x 轴上时，设:OP y kx =，(),P P P x y ，联立方程22221y kx x y a b =⎧⎪⎨+=⎪⎩，()222222k a b x a b ∴+=， 222222Pa b x k a b=+∴， 那么2222222Pk a b y k a b =+，所以()222222211k a b k a bOP +=+. 用1k-是代替上式中的k ，可得()222222211a k b k a b OQ +=+，所以()()22222222222222222222111111k a b a k b a b a b a bk a b k a b OP OQ ++++=+==+++. 综上22221111a bOPOQ+=+为定值. 〔2〕由〔1〕的证明，可知22111174312OPOQ+=+=， 即2222712OP OQ OP OQ+=⋅， ()22712PQ OP OQ ∴=⋅ 所以1122OPQ S OP OQ OD PQ ∆=⋅=⋅所以7OP OQ OD PQ===. 【点睛】此题考察直线与椭圆的位置关系，考察椭圆中定值问题，考察三角形的面积相等，考察计算才能，属于中档题．()322f x x ax a x =+-.〔1〕当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程.〔2〕当0a ≥时，假设对任意的[]0,1x ∈，都有()11f x ≥-，务实数a 的取值范围. 【答案】〔1〕43y x =-；〔2〕[]0,4. 【解析】 【分析】〔1〕求得1a =时()f x 的导数，可得切线的斜率和切点，由点斜式方程可得所求切线方程； 〔2〕求得()f x 的导数，讨论0a =，0a >，()f x 的单调区间，考虑()f x 在[0，1]的单调性，求得最小值，可令其不小于11-，解不等式可得所求范围． 【详解】解：〔1〕当1a =时，()32f x x x x =+-，所以()2321f x x x '=+-，所以曲线()y f x =在点()()1,1f 处的切线斜率()14k f '==，又()11f =，所以曲线()y f x =在点()()1,1f 处的切线方程为()141y x -=-，即43y x =-.〔2〕由()322f x x ax a x =+-，得()()223233a f x x ax a x x a ⎛⎫'=+-=-+ ⎪⎝⎭.当0a =时，()0f x '≥，()f x 在[]0,1上单调递增， 那么()()min 0011f x f ==>-，显然成立； 当0a >时，由()0f x '>，得(),,3a x a ⎛⎫∈-∞-+∞ ⎪⎝⎭； 由()0f x '<，得,3a x a ⎛⎫∈- ⎪⎝⎭，所以()f x 在,3a a ⎛⎫- ⎪⎝⎭上单调递减，在(),a -∞-和,3a ⎛⎫+∞ ⎪⎝⎭上单调递增.①3a ≥时，13a≥，()f x 在[]0,1上单调递减， 所以()()2min 11f x f a a ==+-，所以对任意的[]0,1x ∈，都有()11f x ≥-等价于2111a a +-≥-， 即2120a a --≤， 解得34a -≤≤，又3a ≥，所以34a ≤≤； ②当0<<3a 时，013a<<， 所以()f x 在[]0,1上的最小值为32325333327a a a a a f a a -⎛⎫⎛⎫⎛⎫=+⨯-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.又当0<<3a 时，351127a ->-，显然成立.综上，实数a 的取值范围为[]0,4.【点睛】此题考察导数的运用：求切线方程和单调性、极值和最值，考察分类讨论思想和化简运算才能，属于中档题．请考生在第22、23题中任选一题答题，假如多做，那么按所做的第一题计分.xOy 中，直线l 的参数方程为12x ty t =+⎧⎨=⎩〔t 为参数〕，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2sin 4cos 0ρθθ-= 〔1〕求直线l 的普通方程和曲线C 的直角坐标方程； 〔2〕假设直线l 与曲线C 相交于A ，B AB 【答案】〔1〕22y x =-.24y x =；〔2〕5.【解析】 【分析】〔1〕将12x ty t =+⎧⎨=⎩〔t 为参数〕中的参数t 消去，即可求得直线l 的普通方程，再根据极坐标与直角坐标的互化公式，即可求得曲线C 的直角坐标方程；〔2〕令5t '=，得到直线的参数方程1,,x y ⎧=+⎪⎪⎨''⎪=⎪⎩〔t '为参数〕，代入24y x =，结合直线参数方程中参数的几何意义，即可求解.【详解】〔1〕由题意，将12x ty t =+⎧⎨=⎩〔t 为参数〕中的参数t 消去，可得22y x =-即直线l 的普通方程为22y x =-，由2sin 4cos 0ρθθ-=，可得22sin 4cos ρθρθ=， 又由cos ,sin x y ρθρθ==，代入可得24y x =，所以曲线C 的直角坐标方程为24y x =.〔2〕令t '=，那么有1,,5x y ⎧=⎪⎪⎨''⎪=⎪⎩〔t '为参数〕. 将其代入方程24y x =中，得24405t ''-=，其中245∆=-4⨯⨯(-4)>0.设点A ，B 对应的参数分别为1t '，2t '，那么12t t ''+=，125t t ''⋅=-，所以125AB t t ''=-===. 【点睛】此题主要考察了参数方程与普通方程的互化，极坐标方程与直角坐标方程的互化，以及直线参数方程的应用，其中解答中熟记互化公式，纯熟应用直线的参数方程中参数的几何意义是解答的关键，着重考察了推理与运算才能，属于根底题.()21f x x =+.〔1〕求不等式()1f x ≤的解集； 〔2〕假设x R ∀∈，()2f xa x ≥恒成立，务实数a 的最大值.【答案】〔1〕[]1,0-；〔2〕【解析】 【分析】〔1〕由()1f x ≤，可得211x +≤，即可求得不等式的解集； 〔2〕由x R ∀∈，()2f x a x ≥恒成立，转化为x ∀∈R ，221xa x +≥恒成立，分类讨论，即可求解.【详解】〔1〕根据题意，函数()21f x x =+，由()1f x ≤，可得211x +≤，即1211x -≤+≤，解得10x -≤≤， 所以原不等式的解集为[]1,0-. 〔2〕由x R ∀∈，()2f x a x ≥恒成立，即为x R ∀∈，221xa x +≥恒成立，当0x =时，a R ∈；当0x ≠时，22112x a x x x+≤=+，因为12x x +≥12x x =，即2x =时等号成立，所以a ≤综上可得a ≤a 的最大值为.【点睛】此题主要考察了含绝对值不等式的求解，以及不等式的恒成立问题的解答，着重考察了推理与运算才能，属于根底题.。

2021年秋季高三数学开学摸底考试卷01班级___________ 姓名___________ 分数____________（考试时间：120分钟 试卷满分：150分）一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的． 1．设10i3iz =+，则z 的共轭复数在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】D 【详解】()()()10i 3i 10i 13i 3i 3i 3i z -===+++-，所以z 的共轭复数13i z =-， 它对应的点落在第四象限. 故选：D.2．设集合{}1A x x =≥，{}12B x x =-<<，则()RA B =（ ）A ．{}1x x >- B ．{}1x x ≥C ．{}11x x -<<D ．{}12x x ≤<【答案】C 【详解】由题意，集合{}1A x x =≥，{}12B x x =-<<， 根据补集的运算，可得R{|1}A x x =<，所以(){}R 11A B x x ⋂=-<<.故选：C.3．若抛物线22y x =上的一点M 到其焦点的距离为1，则点M 的纵坐标是（ ） A ．1 B ．98C ．12D ．78【答案】D 【详解】解：抛物线22y x =焦点在y 轴上，焦点坐标为1(0,)8，准线方程为：18y =-，设(,)M x y ，由抛物线的定义可知：||MF =118y +=，解得：78y =， 故选：D ．4．我国南北朝时期的数学家祖暅提出了一条原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等．这个原理能够帮助人们计算3D 打印时的材料耗费问题.3D 打印属于快速成形技术的一种，是将粉末状金属或塑料等可粘合材料，通过逐层喷涂，逐渐堆叠累积的方式来构造物体的技术，可以用来制造结构复杂的物件．根据祖暅原理，对于3D 打印制造的零件，如果能找到另一个与其高相等，并在所有等高处的水平截面的面积均相等的几何体，就可以通过计算该几何体的体积得到打印的零件的体积．现在要用3D 打印技术制造一个零件，其在高为h 的水平截面的面积为()()24,02S h h h π=-≤≤，则该零件的体积为（ ） A ．43πB ．83π C ．163πD ．323π【答案】C 【详解】解：由祖暅原理可知，该零件在高为h 的水平截面的面积为()()24S h h π=-，恰好与一个半径为2的半球在高为h 处的水平截面面积一致， 所以该零件的体积为半球的体积314162233ππ⨯⨯=， 故选：C5．已知三棱柱的侧棱垂直于底面，所有棱的长都为6，项点都在一个球面上，则该球的表面积为（ ） A ．36π B ．84πC ．132πD ．180π【答案】B 【详解】由题意三棱柱111ABC A B C -是正三棱柱，设,N M 是上下底面中心，MN 的中点O 是三棱柱111ABC A B C -外接球的球心，6AM ==111322OM MN AA ===，r =OA ===，所以24S r π=2484ππ=⨯=． 故选：B ．6．某物理量的测量结果服从正态分布()210,N σ，下列结论中不正确的是（ ）A ．σ越小，该物理量在一次测量中在(9.9,10.1)的概率越大B ．σ越小，该物理量在一次测量中大于10的概率为0.5C ．σ越小，该物理量在一次测量中小于9.99与大于10.01的概率相等D ．σ越小，该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等 【答案】D 【详解】对于A ，2σ为数据的方差，所以σ越小，数据在10μ=附近越集中，所以测量结果落在()9.9,10.1内的概率越大，故A 正确；对于B ，由正态分布密度曲线的对称性可知该物理量一次测量大于10的概率为0.5，故B 正确；对于C ，由正态分布密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等，故C 正确；对于D ，因为该物理量一次测量结果落在()9.9,10.0的概率与落在()10.2,10.3的概率不同，所以一次测量结果落在()9.9,10.2的概率与落在()10,10.3的概率不同，故D 错误. 故选：D. 7．设54a =，3log 4b =，4log 5c =，则（ ） A ．c b a >> B ．b a c >> C ．c a b >> D ．a b c >>【答案】B【详解】5435log 34a ==∵3log y x =在()0,∞+上单调递增，且455433243⎛⎫== ⎪⎝⎭，44256=，∵243256<，∵5434< ∵5433log 3log 4<，即a b <；5445log 44a ==∵4log y x =在()0,∞+上单调递增，且4554441024⎛⎫== ⎪⎝⎭，45625=，∵1024625>，∵5445> ∵5444log 4log 5>，∵a c >故c a b <<. 故选：B.8．已知函数()f x 在定义域R 上单调，且(()2)1f f x x +=，则(2)f -的值为（ ） A ．3 B ．1C ．0D ．﹣1【答案】A 【详解】因为函数()f x 在定义域R 上单调，且(()2)1f f x x +=， 所以()2f x x +为常数，不妨设()2f x x t +=，则()2f x t x =- 由(()2)1f f x x +=得()21f t t t =-=，解得：1t =-， 所以()21f x x =--， 所以(2)2(2)13f -=---=. 故选：A二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得3分，有选错的得0分．9．某教练组为了比较甲、乙两名篮球运动员的竞技状态，选取了他们最近10场常规赛得分制成如图的茎叶图，则从最近10场比赛的得分看（ ）A ．甲的中位数大于乙的中位数B ．甲的平均数大于乙的平均数C ．甲的竞技状态比乙的更稳定D ．乙的竞技状态比甲的更稳定【答案】AC 【详解】由茎叶图知：甲的得分为8,12,15,21,23,25,26,28,30,34；乙的得分为7,13,15,18,22,24,29,30,36,38， A ：甲、乙中位数分别为2325242+=、2224232+=，即甲的中位数大于乙的中位数，正确； B ：甲的平均数812152123252628303422.210+++++++++=，乙的平均数713151822242930363823.210+++++++++=，甲的平均数小于乙的平均数，错误；C ：甲的方差1022111(22.2)61.5610i i s x ==-=∑，乙的方差1022211(23.2)92.5610i i s x ==-=∑，即2212s s <，甲的竞技状态比乙的更稳定，正确，故D 错误. 故选：AC.10．设α为平面，a ，b 为两条不同的直线，则下列命题正确的是（ ） A ．若//a α，//b α，则a ∵b B ．若a α⊥，a b ⊥，则//b α C ．若a α⊥，a ∵b ，则b α⊥ D ．若a ∵α，b ∵α则a //b【答案】CD 【详解】解：对于A ，//a α，//b α时，直线a ，b 可能相交，也可能异面，也可能平行，所以A 错误； 对于B ，当a α⊥，a b ⊥时，直线b 有可能在平面α内，所以B 错误； 对于C ，由线面垂直的判定理的推论可知是正确的；对于D ，由线面垂直的性质定理可知是正确的， 故选：CD11．已知直线:20l kx y k -+=和圆22:16O x y +=，则（ ） A ．直线l 恒过定点()2,0B ．存在k 使得直线l 与直线0:220l x y -+=垂直C ．直线l 与圆O 相交D ．若1k =-，直线l 被圆O 截得的弦长为4 【答案】BC 【详解】解：对于A 、C ，由:20l kx y k -+=，得(2)0k x y +-=，令200x y +=⎧⎨-=⎩，解得2x y =-⎧⎨=⎩，所以直线l 恒过定点(2,0)-，故A 错误；因为直线l 恒过定点(2,0)-，而()2220416-+=<，即(2,0)-在圆22:16O x y +=内，所以直线l 与圆O 相交，故C 正确； 对于B ，直线0:220l x y -+=的斜率为12，则当2k =-时，满足直线l 与直线0:220l x y -+=垂直，故B 正确；对于D ，1k =-时，直线:20l x y ++=，圆心到直线的距离为d ==所以直线l 被圆O截得的弦长为==D 错误.故选：BC.12．函数()()2sin f x x ωϕ=+(0>ω，ϕπ<)的部分图像如图所示，则下列结论正确的是（）A ．()12sin 36x f x π⎛⎫=-⎪⎝⎭B ．若把函数()f x 的图像向左平移2π个单位，则所得图像对应的函数是奇函数 C ．若把()f x 的图像上所有点的横坐标变为原来的23倍，纵坐标不变，得到图像对应的函数在[],ππ-上是增函数D ．,33x ππ⎡⎤∀∈-⎢⎥⎣⎦，若()332f x a f π⎛⎫+≥ ⎪⎝⎭成立，则a 【答案】AB 【详解】解析：由题图，知1732422T πππ=-=， ∵6T π=，∵2163πωπ==.∵()222sin 23f ππϕ⎛⎫=+=⎪⎝⎭，即2sin 13πϕ⎛⎫+= ⎪⎝⎭， ∵2232k ππϕπ+=+(k ∈Z )，即26k πϕπ=-+(k ∈Z )， ∵ϕπ<，∵6πϕ=-，∵()12sin 36x f x π⎛⎫=-⎪⎝⎭，故A 正确；把()f x 的图像向左平移2π个单位，所得图像对应的函数解析式为12sin 2sin 3263x y x ππ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦，是奇函数，故B 正确：把()f x 的图像上所有点的横坐标变为原来的23，纵坐标不变， 得到图像对应的函数解析式为12sin 26y x π⎛⎫=-⎪⎝⎭，∵[],x ππ∈-，∵12sin 26y x π⎛⎫=- ⎪⎝⎭在[],ππ-上不是增函数，故C 错误；,33x ππ⎡⎤∀∈-⎢⎥⎣⎦，令()()332x f f x g π⎛⎫=- ⎪⎝⎭2sin 2sin 2sin 2666x x ππππ⎛⎫⎛⎫⎛⎫=---=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，,33x ππ⎡⎤∈-⎢⎥⎣⎦，()12g x ≤≤，所以a 2，故D 错误.故选：AB.三、填空题：本题共4小题，每小题5分，共20分．13．写出一个与双曲线2214y x -=共渐近线的双曲线的标准方程___________.(不同于原双曲线)【答案】22128x y -=(答案不唯一)【详解】与双曲线2214y x -=共渐近线的双曲线为()2204y x λλ-=≠，即()22104x y λλλ-=≠，所以可以填22128x y -=. 故答案为：22128x y -=(答案不唯一)14．函数()y f x =的图象在点()()2,2M f 处的切线方程是28y x =-，则()()22f f ='__________. 【答案】-2 【详解】解：由题意，()22f '=， 又()22284f =⨯-=-，∵()()24222f f -==-'. 故答案为：2-.15．已知向量()222,2,,,4a ab b a a b π==-=⋅，则b =___________.【答案】4 【详解】由题设，22b a a b -=⋅知：22||||||cos ,||0b a b a b a -<>-=， ∵()2,2,,4a ab π==，∵2||2||80b b --=，解得||4=b 或||2b =-(舍)∵||4=b . 故答案为：416．已知奇函数()f x 的定义域为R ，且当()0,x ∈+∞时，()2021f x m x=--，若()()202102f f -+=，则实数m =________． 【答案】1 【详解】解：由()f x 为R 上的奇函数，得()()f x f x -=-且()00f =， 所以()()20212021202112021f f m m ⎛⎫-=-=---=+ ⎪⎝⎭，又()()202102f f -+=，所以102m ++=，得1m =． 故答案为：1四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．已知数列{}n a 的前n 项和122n n S +=-.（1）求数列{}n a 的通项公式；（2）设100n n b a =-，求数列{}n b 的前10项和10T . 【详解】解：（1）当1n =时，112a S ==； 当2n ≥时，()()1122222n n n n n n a S S +-=-=---=，经验证12a =满足上式；所以{}n a 的通项公式为2n n a =.（2）由（1）可知，1002,16,1002100,7,n n n n n b a n ⎧-≤≤=-=⎨-≥⎩其中*n N ∈，故{}n b 的前10项和为()()()()()267101010021002100221002100T =-+-++-+-++-()()1267891010620022222222002S S =-+++++++=+-… 117200222(22)1994=+---=.18．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知tan cos tan sin A B A B =+. （∵）若8a c +=，ABC 的面积为6，求sin B ； （∵）若2252b a =，求sin 23B π⎛⎫- ⎪⎝⎭.【详解】解：（∵）tan cos tan sin A B A B =+，sin sin cos sin cos sin()sin A A B B A A B C ∴=+=+=，∴由正弦定理可得a c =，又8a c +=，4a c ∴==，ABC 的面积为116sin 44sin 22ac B B ==⨯⨯⨯，∴解得：3sin 4B =． （∵）由（∵）可得a c =，又2252b a =， ∴由余弦定理可得2222222512cos 224a a a a cb B ac a +-+-===-， (0,)B π∈，sin 4B ∴==，sin 22sin cos 8B B B ==-，27cos 22cos 18B B =-=-，∴17sin(2)sin 2cos cos2sin (()33328B B B πππ-=-=⨯--=19．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，AD DC ⊥，PA PD PB ===122BC DC AD ===，E 为AD 的中点.（∵）求证：PE ⊥平面ABCD ；（∵）求二面角A PB C --的正弦值；（∵）记BC 的中点为M ，若N 在线段PE 上，且直线MN 与平面PAB 段EN 的长.【详解】（∵）连接BE ，则12BC AD DE ==，因为//AD BC ，所以四边形BCDE 为平行四边形；所以2BE CD ==，因为4,PA AD AD ===且E 为AD 的中点，所以PE AD ⊥，所以4PE ===，所以222PE BE PB +=，即PE BE ⊥，又因为AD BE E =，所以PE ⊥平面ABCD ；（∵）以E 为原点，EA 为x 轴，EB 为y 轴，EP 为z 轴建立如图所示的空间直角坐标系，则()()()()2,0,0,0,2,0,2,2,0,0,0,4A B C P -,所以()()()2,2,0,0,2,4,2,0,0AB PB BC =-=-=-,设平面PAB 的法向量为()111,,m x y z =，则00m AB m PB ⎧⋅=⎨⋅=⎩，即1111220240x y y z -+=⎧⎨-=⎩，取()2,2,1m =，设平面PBC 的法向量为()222,,n x y z =，则00n BC n PB ⎧⋅=⎨⋅=⎩，即22220240x y z -=⎧⎨-=⎩，取()0,2,1n =，所以2cos ,32m nm n m n ⋅====⋅， 所以二面角A PB C --23=； （∵）设()()0,4EN t t =∈，则()0,0,N t ，而()1,2,0M -，所以()1,2,NM t =-，由（∵）知平面PAB 的法向量为()2,2,1m =，设直线与平面PAB 所成的角为θ，则sin cos ,NM m θ===，化简得2524190t t -+=，解得：1t =或195t =，故线段EN 的长度为1或195. 20．已知椭圆2222:1(0)x y C a b a b +=>>，离心率为2，点(1,2P -在椭圆C 上． （1）求椭圆C 的标准方程；（2）若()11,0F -，()21,0F ，过1F 直线l 交椭圆C 于M 、N 两点，且直线l 倾斜角为45︒，求2MF N 的面积．【详解】（1）因为椭圆()2222:10x y C a ba b +=>>的离心率c e a ==， 所以a =，点(1,2P -代入椭圆C 得：221112a b +=；联立解得a =1c =， 所以1b ==，所求椭圆方程为2212x y += （2）直线l 的斜率tan 451k =︒=，故直线l 的方程为：1y x =+，．与椭圆方程联立，消去x 得：23210y y --=， ∵1y =或13y =-． ∵2MF N 的面积为12121423F F y y ⋅-= 21．某商场拟在周年店庆进行促销活动，为吸引消费者，特别推出“玩游戏，送礼券”的活动，游戏规则如下：每轮游戏都抛掷一枚质地均匀的骰子（形状为正方体，六个面的点数分别为1，2，3，4，5，6），若向上点数不超过4点，获得1分，否则获得2分，进行若干轮游戏，若累计得分为9分，则游戏结束，可得到200元礼券，若累计得分为10分，则游戏结束，可得到纪念品一份，最多进行10轮游戏．（1）当进行完3轮游戏时，总分为X ，求X 的数学期望；（2）若累计得分为i 的概率为i p ，（初始分数为0分，记01p =）．（i ）证明数列{}1i i P P --()1,2,,9i =⋅⋅⋅⋅⋅⋅是等比数列； （ii ）求活动参与者得到纪念品的概率．【详解】解：（∵）由题意得每轮游戏获得1分的概率为23，获得2分的概率为13，X 可能取值为3，4，5，6， ()3283327P x ⎛⎫=== ⎪⎝⎭，()2132144339P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， ()2231225339P x C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，()3116327P X ⎛⎫=== ⎪⎝⎭， ∴X 的分布列：()842134564279927E X =⨯+⨯+⨯+⨯=； （∵）（i ）（证明：1i =，即累计得分为1分，是第1次掷骰子，向上点数不超过4点的概率123p =，则10p p -=13-，累计得分为i 分的情况有两种： （1）()22i i =-+，即前一轮累计得2i -分，又掷骰子点数超过4点其概率为213i p -，（2）前一轮累计得分为1i -分，又掷骰子点数没超过4点得1分其概率为123i p -， ∴211233i i i p p p --=+()2,3,,9i =⋅⋅⋅⋅⋅⋅， ∴()11213i i i i p p p p ----=--()2,3,,9i =⋅⋅⋅⋅⋅⋅， ∴数列{}1i i P P --，()1,2,,9i =⋅⋅⋅⋅⋅⋅是首项为13-，公比为13-的等比数列． （ii ）数列{}1i i P P --，()1,2,,9i =⋅⋅⋅⋅⋅⋅是首项为13-，公比为13-的等比数列． ∴113i i i p p --⎛⎫=- ⎪⎝⎭， ∴1013p p -=-，22113p p ⎛⎫=- ⎪⎝⎭-，……，113i i i p p --⎛⎫=- ⎪⎝⎭， 各式相加，得：011143i i p p ⎡⎤⎛⎫=---⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-， ∴311443i i p ⎛⎫=+- ⎪⎝⎭，()1,2,,9i =⋅⋅⋅⋅⋅⋅， ∴活动参与者得到纪念品的概率为：891081131111133443443p p ⎡⎤⎛⎫⎛⎫==⨯+⨯-=+⨯⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦． 22．已知函数221()(1)2x f x x a e ax a x =---+. （1）讨论()f x 的单调性； （2）若()f x 在(,0)-∞上只有一个极值，且该极值小于1a e --，求a 的取值范围.【详解】（1）由题意，函数221()(1)2x f x x a e ax a x =---+， 可得()2()()()x x f x x a e ax a x a e a '=--+=--，当0a ≤时，0x e a ->，令()0f x '<，解得x a <；令()0f x '>，解得x a >， 故()f x 在(,)a -∞递减，在(,)a +∞递增，当0a >时，令()0f x '=，解得1x a =或2ln x a =，设()ln g a a a =-，可得1()a g a a-'=，当1a >时，()0g a '>；当01a <<时，()0g a '<，故min ()(1)10g x g ==>，故ln a a >，由()0f x '>，解得x a >或ln x a <，由()0f x '<，解得ln a x a <<，故()f x 在(,ln )a -∞递增，在(ln ,)a a 递减，在(,)a +∞递增， 综上可得：当0a ≤时，()f x 在(,)a -∞递减，在(,)a +∞递增， 0a >时，()f x 在(,ln )a -∞递增，在(ln ,)a a 递减，在(,)a +∞递增； （2）当0a <时，由（1）知，()f x 在(,)a -∞递减，在(,)a +∞递增，故()31()12a a f x f a e a e ==-+<--极小值，解得a < 当01a <<时，ln 0a <，由（1）知()f x 在ln x a =处取极大值， 设221()(ln )(ln 1)ln ln 2h a f a a a a a a a a ==---+21ln 1ln 2a a a a a a ⎛⎫=-+-- ⎪⎝⎭， 则21()ln 2ln 2h a a a a a '=-+-， 因为01a <<，可得ln 0a <，所以()0h a '<，()h a 在(0,1)递减， 所以()(1)21ah a h e >=->--，所以01a <<不合题意， 当1a ≥时，ln 0a ≥，由（1）知()f x 在(,0)-∞递增，此时()f x 在(,0)-∞无极值，不符合题意，综上可得，实数a 的取值范围是(,-∞.扫码关注学科网数学服务号，获取优质数学教育资源↓↓↓。