清华大学-理论力学-习题解答-2-34
- 格式:pdf
- 大小:96.97 KB
- 文档页数:1



CA(a)ωO(a)第10章动能定理及其应用10-1计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A、B 两点的速度方向如图示,B 点的速度为v B ,θ =45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v (图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.2222221632(2121)2(212121B B B C C C mv r v mr v m J mv T =⋅+=+=ω2.222122222214321(21212121vm v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )BA T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕω⋅⋅+⋅++++=l g W l l v l v l g W v g W ]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。

(b)第2篇 工程运动学基础第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环 A的运动规律。
解:Rv a a 2ns in ==θ,θs in 2R v a =θθt an co s d d 2tR v a tv a ===,⎰⎰=t v v t R v v 02d t an 1d 0θ t v R R v t s v 00t an t an d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0t an t an ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324t t y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2ar cco s 213ar cs i n y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π== t,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮A习题4-1图习题4-2图习题4-3图e e -t (c)e e -t υ (b)R t R +υ (a)习题4-6图以匀角速度ω转动,如图所示。

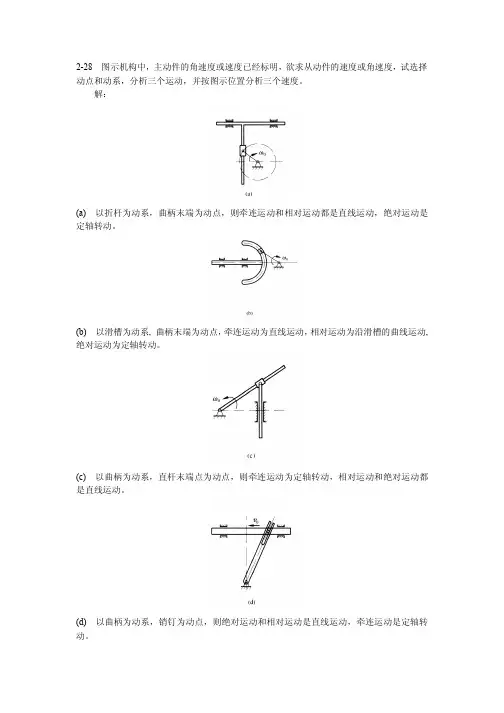
2-28 图示机构中,主动件的角速度或速度已经标明,欲求从动件的速度或角速度,试选择动点和动系,分析三个运动,并按图示位置分析三个速度。
解:
(a) 以折杆为动系,曲柄末端为动点,则牵连运动和相对运动都是直线运动,绝对运动是定轴转动。
(b) 以滑槽为动系, 曲柄末端为动点,牵连运动为直线运动,相对运动为沿滑槽的曲线运动,绝对运动为定轴转动。
(c) 以曲柄为动系,直杆末端点为动点,则牵连运动为定轴转动,相对运动和绝对运动都是直线运动。
(d) 以曲柄为动系,销钉为动点,则绝对运动和相对运动是直线运动,牵连运动是定轴转动。
(e) 以曲柄为动系,半圆的圆心为动点。
则绝对运动和相对运动都是直线运动,牵连运动是定轴转动。
(f) 以曲柄为动系,铰结点为动点,则绝对运动为定轴转动,相对运动为直线运动,牵连运动为定轴转动。
(g) 以曲柄为动系,销钉为动点,则相对运动为直线运动,绝对运动为定轴转动,牵连运动也为定轴转动。
(h) 以较长的曲柄为动系,滑块铰结点为动点,分别讨论联立求解。
第一组,绝对运动为定轴转动,第二组绝对运动为直线运动。
相对运动都为直线运动,牵连运动为定轴转动。
平面运动,牵连运动为定轴转动。
平面运动,牵连运动为定轴转动。


第三章思考题解答3.1 答:确定一质点在空间中得位置需要3个独立变量,只要确定了不共线三点的位置刚体的位置也就确定了,故须九个独立变量,但刚体不变形,此三点中人二点的连线长度不变,即有三个约束方程,所以确定刚体的一般运动不需3n 个独立变量,有6个独立变量就够了.若刚体作定点转动,只要定出任一点相对定点的运动刚体的运动就确定了,只需3个独立变量;确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量,确定任一点在平面上的位置需二个独立变量,共需三个独立变量;知道了定轴转动刚体绕转动轴的转角,刚体的位置也就定了,只需一个独立变量;刚体的平动可用一个点的运动代表其运动,故需三个独立变量。
3.2 答物体上各质点所受重力的合力作用点即为物体的重心。
当物体的大小远小于地球的线度时物体上各质点所在点的重力加速度都相等,且方向彼此平行即重力场为均匀场,此时质心与重心重合。
事实上但物体的线度很大时各质点所在处g 的大小是严格相等,且各质点的重力都指向地心,不是彼此平行的,重心与质心不和。
答 当物体为均质时,几何中心与质心重合;当物体的大小远小于地球的线度时,质心与重心重合;当物体为均质且大小远小于地球的线度时,三者都重合。
3.4 答 主矢F 是力系各力的矢量和,他完全取决于力系中各力的大小和方向,故主矢不随简化中心的位置而改变,故而也称之为力系的主矢;简化中心的位置不同,各力对简化中心的位矢i r 也就不同则各力对简化中心的力矩也就不同,故主矩随简化中心的位置而变,被称之为力系对简化中心的主矩。
分别取O 和O '为简化中心,第i 个力i F 对O 和O '的位矢分别为i r 和i r ',则i r =i r '+O O ',故()()iii ii i O F O O r F r M ⨯'-'=⨯'=∑∑'()∑∑⨯'-⨯'=ii ii i F O O F r ∑⨯'+=ii o F O O M即o o M M ≠'主矢不变,表明刚体的平动效应不变,主矩随简化中心的位置改变,表明力系的作用对刚体上不同点有不同的转动效应,但不改变整个刚体的转动规律或者说不影响刚体绕质心的转动。


第3章部分习题解答1. 列出下列集合的元素.(1) {x | x 是小于5的非负整数}(2) {x | x 是大于0的偶数}(3) {x |(x 是整数) ∧(2<x <10)}(4) { x | x ∈N˄∃ t ( t ∈{2,3}˄x=2t )}(5) { x | x ∈R˄x 2-1=0˄x>3}解:(1){0,1,2,3,4} (2){2,4,6,…,} (3){3,4,5,6,7,8,9} (4){4,6}(5)∅2. 判断下列集合是否相等。
(1) {1, 2, 1, 3, 1, 2}, {2, 3, 1}(2) {{1}}, {1, {1}}(3) ∅ , {∅ }解:(1)相等 (2)不相等 (3)不相等3. 假定 A , B , 和 C 是集合, 若 A ⊆ B 且 B ⊆C . 证明 A ⊆ C .证明:对任意x ∈A ,因为A ⊆ B ,有x ∈B ,又因为 B ⊆C ,有x ∈C ,所有A ⊆ C .4. 判定下列各题的正确与错误:(1)a ∈{{a }};(2){a }⊆{ a ,b ,c };(3)∅∈{∅ };(4)∅⊆{ a ,b ,c };(5) ∅∈∅;(6)∅⊆∅ ;(7){{a },1,3,4}⊂{{a },3,4,1};(8){a ,b }⊆{a ,b ,c ,{ a ,b }};(9){a ,b }∈{a ,b ,{ a ,b }};(10){a ,b }∈{a ,b ,{{ a ,b }}}。
解:正确:2、3、4、6、8、9错误:1、5、7、105.设 E ={a ,b ,c ,d ,e },A ={a ,d },B ={a ,b ,e } 和 C ={b ,d }.试求出下列的集合:(1) ~A B ⋂(2) ()~A B C ⋃⋂(3) ~()A B ⋂(4)(A ⋃C )-B(5) A ⊕B ⊕C解:(1){d} (2){a,e} (3) {b,c,d,e} (4) {b} (5) {e}6.给定自然数集合 N 的下列子集:A ={1,2,7,8}B ={i |i ⨯i <50}C ={i |i 可被 3 整除且 0≤i ≤30}D ={i |i =2k ,k ∈I ,0<k <6}试求出下列集合:(1)A⋃ (B⋃ (C⋃D))(2)A⋂ (B⋂ (C⋂D))(3)B-(A⋃C)(4)(~A⋂B) ⋃D(5)A⊕B解:(3) {4,5}(4) {0,2,3,4,5,6,8,10}(5) {0,3,4,5,6,8}7.给定正整数集合I+的下列子集:A={n|n<12}B={n|n≤8}C={n|n=2k,k∈I+}D={n|n=3k,k∈I+}F={n|n=2k-1,k∈I+}试用集合A,B,C,D和F表达下列集合:(1){2,4,6,8}(2){3,6,9}(3){10}(4){n|n是偶数,n>10}(5){n|n是正偶数且n≤10,或n是正奇数且n >= 9}解:(1)B (2)A⋂D (3)(A-B)⋂C (4)C-B (5)(C⋂A)⋃(F-B)8.设A,B和C是全集E的子集,下列关系是否成立?(A⋃B) ⋂~(B⋃C)⊆A⋂~B解:成立(A⋃B) ⋂~(B⋃C)⊆A⋂~B9.设A,B是全集E的子集,证明下列恒等式:(1)(A⋂B) ⋃ (A⋂~B)=A(2)B⋃~((~A⋃B) ⋂A)=E(3)(A⋃~B)⋂(~A⋃B)=(A⋂B)⋃(~A⋂~B)。

理论⼒学思考题习题答案第⼀章质点⼒学矿⼭升降机作加速度运动时,其变加速度可⽤下式表⽰:?-=T t c a 2sin1π式中c 及T 为常数,试求运动开始t 秒后升降机的速度及其所⾛过的路程。
已知升降机的初速度为零。
解:由题可知,变加速度表⽰为-=T t c a 2sin1π由加速度的微分形式我们可知dtdv a =代⼊得 dt T t c dv ??? ??-=2sin 1π对等式两边同时积分dt T t c dv t v-=002sin 1π可得:D T t c T ct v ++=2cos 2ππ(D 为常数)代⼊初始条件:0=t 时,0=v ,故c T D π2-=即??-+=12cos 2T t T t c v ππ⼜因为dtds v =所以 =ds dt T t T t c??-+12cos 2ππ对等式两边同时积分,可得:ω绕其焦点F 转动。
求此直线与椭圆的焦点M 的速度。
已知以焦点为坐标原点的椭圆的极坐标⽅程为()θcos 112e e a r +-=式中a 为椭圆的半长轴,e 为偏⼼率,常数。
解:以焦点F 为坐标原点题1.8.1图则M 点坐标 ??==θθsin cos r y r x 对y x ,两式分别求导+=-=θθθθθθcos sin sin cos &&&&&&r r yr r x 故()()22222cos sin sin cos θθθθθθ&&&&&&r r r r y x v ++-=+=222ωr r +=&如图所⽰的椭圆的极坐标表⽰法为()θcos 112e e a r +-=对r 求导可得(利⽤ωθ=&)⼜因为()()221cos 111ea e e a r -+-=θ即 ()rer e a --=21cos θ所以()()2222221211cos 1sin e r e ar r ea --+--=-=θθ故有 ()2222224222sin 1ωθωr e a r e v +-=()2224221e a r e -=ω()()]1211[2222222e r e ar r e a --+--22ωr +()()??--+-?-=2222222221121e e ar r r e e a r ω()r r a b r -=2222ω即 ()r a r br v -=2ω(其中()b a e b ,1222-=为椭圆的半短轴)质点作平⾯运动,其速率保持为常数。
2-37 OA 杆以等角速度绕轴转动,半径为0ωO r 的滚轮在OA 杆上作纯滚动,已知r 3B O 1=,图示瞬时、O B 在同一水平线上,O 在铅垂位置,B 1°=∠30AOB ,求在此瞬时(1)O 杆的角速度与角加速度;(2)滚轮的角速度与角加速度;(3)滚轮上B 1P 点的速度与加速度。
B nBn Bτ解:建立如图所示的动系Ox 。
由于滚轮在OA 杆上作纯滚动,在动系上看,滚轮上的P 点与在杆OA 上相应点的相对速度为0。
从而,11y0101P OP r ω==νj j(1)以点B 为基点分析P 点运动,得到:B 1+P B r ω=ννi(2)又:111112B O B B O B O B O B r r ωω==ντi 11j (3)将(1),(3)代入(2),得到:110111112O B O B B r r r ωω=+r j i j i 得到:102O B ωω=(逆时针 ) 03ωω=−B (顺时针 ) (4)B 点加速度为:111112211111332222B O B O B O B O B O B O B O B O B r r r r εωεωω=+=+−+a τn i 121j i j (5) 利用加速度合成公式,得到P 点加速度:P e r c =++a a a a其中:201e r =a i 0c =,a ,1r r a =a j从而:2011P r a =+i r a j(6)以B 点为基点分析P 点加速度为:a a(7)21P B B B r r ωε=++j 1i (5),(6)代入(7)得到:111122011111132O B O B O B B B r r r r r εωε=++i i j j j 2r i (8) 将(4)代入(8)得到:1203O B ε=(逆时针), 0ε=B (9)答:(1),021ωω=B O ( 203321ε=B O 0=轮ε(2), 03ωω=轮(3)103j ωr p =v ,()1120163j i a +−=ωr p。
清华⼤学版理论⼒学课后习题答案⼤全_____第6章刚体平⾯运动分析汇总6章刚体的平⾯运动分析6-1 图⽰半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等⾓加速度α绕轴O 转动,当运动开始时,⾓速度0ω= 0,转⾓0?= 0。
试求动齿轮以圆⼼A 为基点的平⾯运动⽅程。
解:?c o s )(r R x A += (1) ?sin )(r R y A +=(2)α为常数,当t = 0时,0ω=0?= 0 221t α?=(3)起始位置,P 与P 0重合,即起始位置AP ⽔平,记θ=∠OAP ,则AP 从起始⽔平位置⾄图⽰AP 位置转过θ??+=A因动齿轮纯滚,故有?=CP CP 0,即θ?r R = ?θr R =, ??rr R A += (4)将(3)代⼊(1)、(2)、(4)得动齿轮以A 为基点的平⾯运动⽅程为:+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A α?αα6-2 杆AB 斜靠于⾼为h 的台阶⾓C 处,⼀端A 以匀速v 0沿⽔平向右运动,如图所⽰。
试以杆与铅垂线的夹⾓θ表⽰杆的⾓速度。
解:杆AB 作平⾯运动,点C 的速度v C 沿杆AB 如图所⽰。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬⼼。
则⾓速度杆AB 为hv AC v AP v ABθθω2000cos cos ===轮A 和垫滚B 与地⾯之间以及垫滚B 与拖车之间⽆滑动。
解:R v R v A A ==ωR vR v B B 22==ωB A ωω2=6-4 直径为360mm 的滚⼦在⽔平⾯上作纯滚动,杆BC ⼀端与滚⼦铰接,另⼀端与滑块C 铰接。
设杆BC 在⽔平位置时,滚⼦的⾓速度ω=12 rad/s ,θ=30?,?=60?,BC =270mm 。
试求该瞬时杆BC 的⾓速度和点C 的速度。
习题6-1图习题6-2图习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬⼼在点P ,滚⼦O 的瞬⼼在点D BDv B ?=ωBPBD BP v B BC ?==ωω =30sin 27030cos 36012 rad/s 8=PC v BC C ?=ωm/s 87.130cos 27.08=??=6-5 在下列机构中,那些构件做平⾯运动,画出它们图⽰位置的速度瞬⼼。