物理化学第六章
- 格式:doc
- 大小:102.50 KB
- 文档页数:5




第六章相平衡一.基本要求1.掌握相平衡的一些基本概念,会熟练运用相律来判断系统的组分数、相数和自由度数。
2.能看懂单组分系统的相图,理解相图中的点、线和面的含义及自由度,知道相图中两相平衡线的斜率是如何用Clapeyron方程和Clausius-Clapeyron方程确定的,了解三相点与凝固点的区别。
3.能看懂二组分液态混合物的相图,会在两相区使用杠杆规则,了解蒸馏与精馏的原理,知道最低和最高恒沸混合物产生的原因。
4.了解部分互溶双液系和完全不互溶双液系相图的特点,掌握水蒸汽蒸馏的原理。
5.掌握如何用热分析法绘制相图,会分析低共熔相图上的相区、平衡线和特殊点所包含的相数、相的状态和自由度,会从相图上的任意点绘制冷却时的步冷曲线。
了解二组分低共熔相图和水盐相图在湿法冶金、分离和提纯等方面的应用。
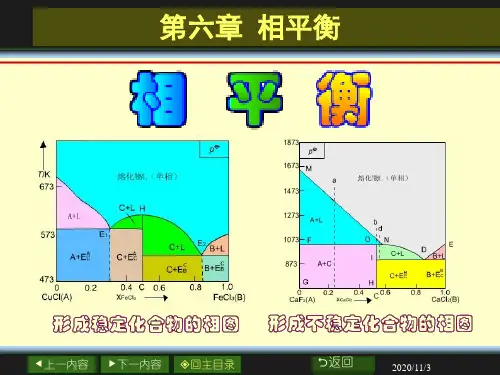
6.了解生成稳定化合物、不稳定化合物和形成固溶体相图的特点,知道如何利用相图来提纯物质。
二.把握学习要点的建议相律是本章的重要内容之一,不一定要详细了解相律的推导,而必须理解相律中各个物理量的意义以及如何求算组分数,并能熟练地运用相律。
水的相图是最简单也是最基本的相图,要把图中的点、线、面的含义搞清楚,知道确定两相平衡线的斜率,学会进行自由度的分析,了解三相点与凝固点的区别,为以后看懂相图和分析相图打好基础。
超临界流体目前是分离和反应领域中的一个研究热点,了解一些二氧化碳超临界流体在萃取方面的应用例子,可以扩展自己的知识面,提高学习兴趣。
二组分理想液态混合物的相图是二组分系统中最基本的相图,要根据纵坐标是压力还是温度来确定气相区和液相区的位置,理解气相和液相组成为什么会随着压力或温度的改变而改变,了解各区的条件自由度(在二组分相图上都是条件自由度),为以后看懂复杂的二组分相图打下基础。
最高(或最低)恒沸混合物不是化合物,是混合物,这混合物与化合物的最根本的区别在于,恒沸混合物含有两种化合物的分子,恒沸点的温度会随着外压的改变而改变,而且两种分子在气相和液相中的比例也会随之而改变,即恒沸混合物的组成也会随着外压的改变而改变,这与化合物有本质的区别。






第六章相平衡6.1指出下列平衡系统中的组分数C,相数P及自由度F。
(1)I2(s)与其蒸气成平衡;(2)CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡;(3)NH4HS(s)放入一抽空的容器中,并与其分解产物NH3(g)和H2S(g)成平衡;(4)取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡。
(5)I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡(凝聚系统)。
解:(1)C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.(2)C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1.(3)C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.(4)C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2.(5)C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2.6.2 常见的Na2CO3(s)水合物有Na2CO3∙H2O(s),Na2CO3∙7H2O(s)和Na2CO3∙10H2O(s).(1)101.325kPa下,与Na2CO3水溶液及冰平衡共存的水合物最多能有几种?(2)20℃时,与水蒸气平衡的水合物最多可能有几种?解:(1)C = S – R - R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0,即P-2≤1,那么能与Na2CO3水溶液及冰平衡共存的水合物最多只有一种。
(2)C = S – R - R' = 2 – 0 – 0 =2F = C – P + 1 =2 –P + 1= 3 – P ≥0,即P-1≤2,那么与水蒸气平衡的水合物最多可能有两种。
6.4 单组分系统碳的想吐(示意图)如附图所示。
第六章统计热力学初步一、选择题1. 体积为1cm3,质量为m克的单原子分子气体,在温度为T时,对一般的物理过程,分子的配分函数为:( )(A) × 1055(mT)3/2 ;(B) × 1020(mT)3/2;(C) × 1026(mT)3/2 ;(D) × 1049(mT)3/2。
2. 在相同条件下,对于He与Ne单原子分子,近似认为它们的电子配分函数相同且等于1,则He与Ne单原子分子的摩尔熵是:( )(A) S m(He) > S m(Ne);(B) S m(He) = S m(Ne);(C) S m(He) < S m(Ne);(D) 以上答案均不成立。
3. 巳知CO和N2分子的质量相同,转动特征温度基本相等,若电子均处于非简并的基态,且振动对熵的贡献可忽略,那么:( )(A) S m(CO) < S m(N2) ;(B) S m(CO) 与S m(N2) 大小无法比较;(C) S m(CO) = S m(N2) ;(D) S m(CO) > S m(N2) 。
4. HI的转动特征温度Θr = K,300K时HI的摩尔转动熵为:( )(A) J·K-l·mol-1;(B) J·K-l·mol-1;(C) J·K-l·mol-1;(D) J·K-l·mol-1。
5. O2的转动惯量J = × 10-47 kg·m2,则O2的转动特征温度是:( )(A) 10K ;(B) 5K ;(C) ;(D) 8K 。
6. 单原子理想气体在室温下的物理过程,通过配分函数求过程热力学函数的变化:( )(A) 必须知道q t、q R、q v、q n各配分函数;(B) 只须知道q t一个配分函数;(C) 必须知道q t、q n配分函数;(D) 必须知道q t、q R、q v配分函数。
7. 下面哪组热力学性质的配分函数表达式与体系中粒子的可别与否无关:( )(A) S、G、F、C V;(B) U、H、P、C V;(C) G、F、H、U;(D) S、U、H、G8. 各种运动形式的配分函数中与压力有关的是:( )(A) 电子配分函数;(B) 平动配分函数;(C) 转动配分函数;(D) 振动配分函数。
9. 分子运动的振动特征温度Θv是物质的重要性质之一,下列正确的说法是:( )(A) Θv越高,表示温度越高;(B) Θv越高,表示分子振动能越小;(C) Θv越高,表示分子处于激发态的百分数越小;(D) Θv越高,表示分子处于基态的百分数越小。
10. I2分子的振动能级间隔是× 10-20J,则在298K时某一振动能级和其较低能级上分子数之比为:( )(A) 1 ;(B) × 10-20;(C) ;(D) 无法计算。
11. 温度T,某种粒子的能级εj = 2εi,简并度g i = 2g j,则εj和εi上分布的粒子数之比为:( )(A) ½exp(εj/2kT) ;(B) 2exp(-εj/2kT) ;(C) ½exp(-εj/2kT) ;(D) 2exp(-2εj/kT) 。
12. 如分子第一激发态的能量为400 kJ·mol-1,则体系中10%的分子被激发到第一激发态时,体系的温度(K)是:( )(A) × 104;(B) × 104;(C) × 103 ;(D) × 10513. I2的振动特征温度ΘV = 307K,相邻两振动能级上粒子数之n(v + 1)/n(v) = ½的温度是:( )(A) 306K;(B) 443K;(C) 760K;(D) 556K14. 下面有关统计热力学的描述,正确的是:( )(A) 统计热力学研究的是大量分子的微观平衡体系;(B) 统计热力学研究的是大量分子的宏观平衡体系;(C) 统计热力学是热力学的理论基础;(D) 统计热力学和热力学是相互独立互不相关的两门学科。
15. 在统计热力学中,物系的分类常按其组成的粒子能否被辨别来进行,按此原则,下列说法正确的是:( )(A) 晶体属离域物系而气体属定域物系;(B) 气体和晶体皆属离域物系;(C) 气体和晶体皆属定域物系;(D) 气体属离域物系而晶体属定域物系。
16. 在研究N、V、U有确定值的粒子体系的统计分布时,令∑n i = N,∑n iεi = U,这是因为所研究的体系是:( )(A) 体系是孤立的,粒子是独立的; (B) 体系是孤立的,粒子是非独立的;(C) 体系是封闭的,粒子是独立的; (D) 体系是封闭的,粒子是非独立的。
17. 对双原子分子理想气体的一般物理过程,下面关于体系熵函数和各运动形式对熵的贡献描述错误的是:( )(A) S = S t + S r + S v;(B) S t = k B ln((q t)N/N!) + Nk B T(∂ln q/∂T) ;(C) S r = k B ln[(q r)N/N!] + Nk B(∂ln q/∂T) ;(D) S v = Nk B ln q v + Nk B T(∂ln q v/∂T)。
18、对于玻尔兹曼分布定律n i =(N /q )g i exp(-εi /kT )的说法:⑴ n i 是第i 能级上的粒子分布数;⑵ 随着能级升高,εi 增大,n i 总是减少的;⑶ 它只适用于可区分的独立 粒子体系;⑷ 它适用于任何的大量粒子体系。
其中正确的是: ( ) (A) ⑴ ⑶; (B) ⑶ ⑷;(C) ⑴ ⑵;(D) ⑵ ⑷19. 对于分布在某一能级εi 上的粒子数n i ,下列说法中正确是: ( )(A) n i 与能级的简并度无关; (B) εi 值越小,n i 值就越大;(C) n i 称为一种分布;(D) 任何分布的n i 都可以用波尔兹曼分布公式求出。
20、麦克斯韦 - 玻尔兹曼分布定律,要求粒子数N 很大,这是因为在推出该定律时:( )(A) 假定粒子是可别的;(B) 应用了斯特林近似公式; (C) 忽略了粒子之间的相互作用;(D) 应用拉氏待定乘因子法。
21、玻耳兹曼分布:( )A.就是最概然分布,也是平衡分布;C.不是最概然分布,也不是平衡分布;B.只是最概然分布,但不是平衡分布;D.不是最概然分布,但是平衡分布。
22、不同运动状态的能级间隔不同,对于分子平动、转动和振动的能级间隔大小顺序为:( ) A .v t r εεε∆>∆>∆ B.v r t εεε∆>∆>∆C. t v r εεε∆>∆>∆D.r t v εεε∆>∆>∆ 23、一定量纯理想气体,恒温变压时:( ) A.转动配分函数q r 变化;B.振动配分函数q v 变化;C.平动配分函数q t 变化。
D.电子配分函数q e 变化 二、填空题1、按子之间有无相互作用,统计系统可分为系,既子之间相互作用及系,既子之间相互作用。
2、假设晶体上被吸附的气体分子间无相互作用,则可把该系统视为 3.非理想气体是 4、温度愈高,配分函数之值愈。
(选填大,小)在相同温度下,粒子的配分函数之值最大,粒子的配分函数之值最小。
(填平动、转动、振动) 5、N 2与CO 的r 分别为K 及 K ,在相同温度下,N 2与CO 的转动配分函数之比为6、 线形刚体转子转动能级的简并度为,一维简谐振子振动能级的简并度为。
7、微观粒子在各能级上的分布,既每一个能级上分布的粒子数与该能级的高低有关,这种分布称为分布。
8、一定量纯理想气体等温变压时,其配分函数发生变化,而配分函数保持不变。
(选填平动、转动、振动) 9、粒子配分函数的析因子性质可表达为q=。
10、粒子转动惯量大,转动特征温度 r;谐振频率大,振动特征温度v(填高,低)11、分子仅利用旋转方法绕对称轴旋转一周所产生的相同位形数目,称为分子的。
12、玻耳兹曼分布公式的形式为,式中的叫分子分配函数。
13、CO 与N 2的质量、转动温度的数值基本相同,若电子均处于非简并的最低能级,且设振动对熵的贡献可忽略,则相同温度下,S (CO)S (N 2) 。
(选填 > ,< )14、平动、转动、振动运动对熵的贡献是不同的,运动的贡献最大,运动的贡献最小。
15、用统计热力学得到N 2O 气体在25℃时标准摩尔熵为22011J K mol --⋅,由热力学第三定律得到是11J K mol --⋅。
作为热力学数据使用,较为可靠的是。
两者之差称为。
16、有1molHCl ,1molN 2均处于25℃,101325Pa 下,二者的摩尔平动熵之差可以表示为m,t m,t 2(HCl)-S (N )S = (HCl ,N 2的摩尔质量分别为M (HCl )和M (N 2)17、纯物质完整晶体在0K T →在时,系统的总微观状态数为。
当热力学系统的熵增加K 时,系统的微观状态数增加倍数为 多少(已知231.3810J K k -=⨯⋅。
s J 100.662633⋅⨯=-h )18、298K 时,当分布在J=1转动能级上的分子数是J=0能级上的21-e 倍时,其分子的转动特征温度是 多少19、1000K 时,AB 双原子分子的振动配分函数q V ,0= ,(q V ,0为振动基态能量规定为零的配分函数),振动特征温度为 ,处于振动基态能级上的分布分数 n 0/N = 三、计算题 1、试()V V U C T∂=∂由2ln ()V q U NkT T∂=∂和出发,推证单原子分子理想气体V,m 32C R =。
2、用统计热力学方法证明:1 mol 单原子理想气体在等温条件下,体系的压力由p 1变到p 2时,其熵变ΔS = R ln(p 1/p 2) 。
3、四种分子有关参数如下:分子 M r k r /Θk V /ΘH 2 2 5976 HBr 81 12 3682 I 2 254 HI1283209在同温同压下,哪种气体的,,t m r m S S 最大?那种气体的最大?哪种分子的振动频率最小? 四、判断题1、对于一个N 、U 、V 确定的体系, 沟通宏观和微观、热力学与统计力学的桥梁是 S = k ln 。
2、定域子和离域子的配分函数的单位不同。
3、任意相邻振动两能级的差值都是一恒值,振动量子数只能是正整数(包括零)4、在N 个NO 分子组成的晶体中,•每个分子都有两种可能的排列方式,即NO 和ON ,也可将晶体视为NO 和ON 的混合物。
在绝对零度时该系统的熵值为S=kln2。
5、研究统计热力学的基本方法是对微观粒子的微观量求统计平均值。