圆截面偏压计算
- 格式:xls
- 大小:178.00 KB
- 文档页数:1

C.O.2沿用边均匀配筋的圆形截面钢筋混凝土偏心受压构件,其正截面抗压承载力可用查表法(表C.0.2)并按下列规定计算求得:1当对构件承载力进行复核验算时1)由本规范公式(5.3.9-1)和(5.3.9-2)解得轴向力的偏心距:'0'g cd sd cd sd Bf D f e r Af C f ρρ+=+(C.0.2-1)2)已知cd f 、'sd f 、ρ、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式(C.0.2-1)计算0e 值。
若此0e 值与实际计算偏心距/d d M N η相符(允许偏差在2%以内),则设定的ξ值为所求者;若不相符,重新设定ξ值,重复上述计算,直到相符为止;3)将最后确定的ξ相应的A、B、C、D值代入规范公式(5.3.9-1)或(5.3.9-2)进行构件正截面承载力的复核验算。
2当对构件进行配筋设计时1)由公式(C.0.2-1)变换得截面配筋率:0'cd sd o f Br Ae f Ce Dgr ρ−=•−(C.0.2-2)2)已知cd f 、'sd f 、0e 、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式( C.0.2-2)计算ρ值,计算时式中的0e 应乘以偏心距增大系数η;再再把ρ和A、C值直代入规范公式(5.3.9-1)算得轴向力值。
若此轴向力值与实际作用的轴向力设计值相符(允许偏差在2%以内),则该ξ值及依此计算的ρ值为所求者;若不相符,重新设定ξ值,重复上述计算,直至相符为止。
3)以最后确定的ρ值代入下列公式计算纵向钢筋截面面积:2s A r ρπ=(C.0.2-3)所得钢筋配筋率应符合最小配筋率的要求。
表C.O.2圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数ξA B C D ξA B C DξA B C D0.200.32440.2628-1.52961.4216 0.210.34810.2787-1.46761.4623 0.220.37230.2945-1.40741.5004 0.230.39690.3103-1.34861.5361 0.240.42190.3259-1.29111.5697 0.250.44730.3413-1.23481.6012 0.260.47310.3566-1.17961.6307 0.270.49920.3717-1.12541.6584 0.280.52580.3865-1.07201.6843 0.290.55260.4011-1.01941.7086 0.300.57980.4155-0.96751.7313 0.310.60730.4295-0.91631.7524 0.320.63510.4433-0.86561.7721 0.330.66310.4568-0.81541.7903 0.340.69150.4699-0.76571.8071 0.350.72010.4828-0.71651.8225 0.360.74890.4952-0.66761.8366 0.370.77800.5073-0.61901.8494 0.380.80740.5191-0.57071.8609 0.390.83690.5304-0.52271.8711 0.400.86670.5414-0.47491.8801 0.410.89660.5519-0.42731.8878 0.420.92680.5620-0.379818943 0.430.95710.5717-0.33231.8996 0.440.98760.5810-0.28501.9036 0.451.01820.5898-0.23771.9065 0.461.04900.5982-0.19031.9081 0.471.07990.6061-0.14291.9084 0.481.11100.6136-0.09541.9075 0.491.14220.6206-0.04781.9053 0.501.17350.6271-0.00001.9018 0.51 1.20490.63310.0480 1.8971 0.52 1.23640.63860.0963 1.8909 0.53 1.26800.64370.1450 1.8834 0.54 1.29960.64830.1941 1.8744 0.55 1.33140.65230.2436 1.8639 0.56 1.36320.65590.2937 1.8519 0.57 1.39500.65890.3444 1.8381 0.58 1.42690.66150.3960 1.8226 0.59 1.45890.66350.44851,8052 0.60 1.49080.66510.5021 1.78560.64 1.61880.66610.7373 1.67630.65 1.65080.66510.8080 1.63430.66 1.68270.66350.8766 1.59330.67 1.71470.66150.9430 1.55340.68 1.74660.6589 1.0071 1.51460.691.77840.6559 1.06921.47690.70 1.81020.6523 1.1294 1.44020.71 1.84200.6483 1.1876 1.40450.72 1.87360.6437 1.2440 1.36970.73 1.90520.6386 1.2987 1.33580.74 1.93670.6331 1.3517 1.30280.75 1.96810.6271 1.4030 1.27060.76 1.99940.6206 1.4529 1.23920.77 2.03060.6136 1.5013 1.20860.78 2.06170.6061 1.5482 1.17870.79 2.09260.5982 1.5938 1.14960.80 2.12340.5898 1.6381 1.12120.81 2.15400.5810 1.6811 1.09340.82 2.18450.5717 1.7228 1.06630.83 2.21480.5620 1.7635 1.03980.84 2.24500.5519 1.8029 1.01390.85 2.27490.5414 1.84130.98860.86 2.30470.5304 1.87860.96390.87 2.33420.5191 1.91490.93970.88 2.36360.5073 1.95030.91610.89 2.39270.4952 1.98460.89300.90 2.42150.4828 2.01810.87040.91 2.45010.4699 2.05070.84830.92 2.47850.4568 2.08240.82660.93 2.50650.4433 2.11320.80550.94 2.53430.4295 2.14330.78470.95 2.56180.4155 2.17260.76450.96 2.58900.4011 2.20120.74460.97 2.61580.3865 2.22900.72510.98 2.64240.3717 2.25610.70610.99 2.66850.3566 2.28250.68741.002.69430.3413 2.30820.66921.012.71120.3311 2.33330.65131.022.72770.3209 2.35780.63371.032.74400.3108 2.38170.61651.042.75980.3006 2.40490.59971.082.82000.26092.49240.53561.092.83410.25112.51290.52041.102.84800.24152.53300.50551.112.86150.23192.55250.49081.122.87470.22252.57160.47651.132.88760.21322.59020.46241.142.90010.20402.60840.44861.152.91230.19492.62610.43511.162.92420.18602.64340.42191.172.93570.17722.66030.40891.182.94690.16852.67670.39611.192.95780.16002.69280.38361.202.96840.15172.70850.37141.212.97870.14352.72380.35941.222.9886O.13552.73870.34761.232.99820.12772.75320.33611.243.00750.12012.76750.32481.253.01650.11262.78130.31371.263.02520.10532.79480.30281.273.03360.09822.80800.29221.283.04170.09142.82090.28181.293.04950.08472.83350.27151.303.05690.07822.84570.26151.313.06410.07192.85760.25171.323.07090.06592.86930.24211.333.07750.06002.88060.23271.343.08370.05442.89170.22351.353.08970.04902.90240.21451.363.09540.04392.91290.20571.373.10070.03892.92320.19701.383.10580.03432.93310.18861.393.11060.02982.94280.18031.403.11500.02562.95230.17221.413.11920.02172.96150.16431.423.12310.01802.97040.15661.433.12660.01462.97910.14911.443.12990.01152.98760.14171.453.13280.00862.99580.13451.463.13540.00613.00380.12751.473.13760.00393.01150.12061.483.13950.00213.01910.11400.61 1.52280.66610.5571 1.76360.62 1.55480.66660.6139 1.73870.63 1.58680.66660.6734 1.7103 1.05 2.77540.2906 2.42760.58321.06 2.79060.2806 2.44970.56701.07 2.80540.2707 2.47130.5512 1.49 3.14080.007 3.02640.10751.503.14160.00003.03340.10111.513.14160.00003.04030.09505.3.9沿周边均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件(图5.3.9),其正截面抗压承载力计算应符合下列规定:图5.3.9沿周边均匀配筋的圆形截面偏心受压构件计算22'0d cd sdN Ar f C r f γρ≤+(5.3.9-1)33'00d cd sd N e Br f D gr f γρ≤+(5.3.9-2)式中0e ——轴向力的偏心距,0/d d e M N =,应乘以偏心距增大系数η,η可按第5.3.10条的规定计算;A、B——有关混凝土承载力的计算系数,按附录C 的迭代法由表C.O.2查得;C、D——有关纵向钢筋承载力的计算系数,按附录C 的迭代法由表C.O.2查得;r ——圆形截面的半径;g ——纵向钢筋所在圆周的半径s r 与圆截面半径之比,/s g r r =;ρ——纵向钢筋配筋率,2/s A r ρπ=。
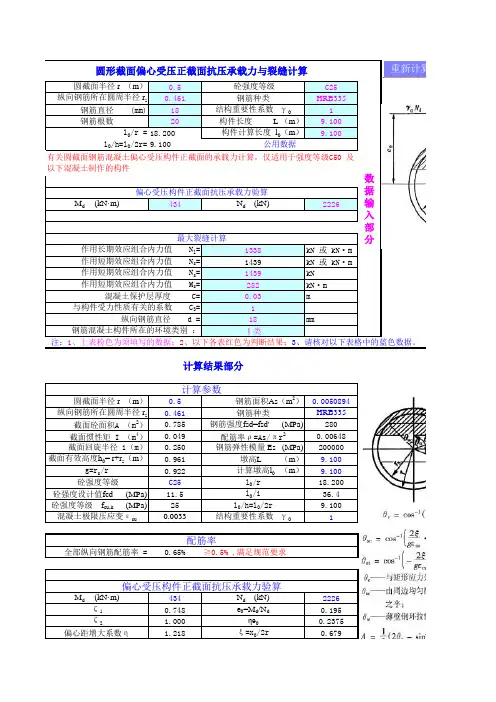
计算结果部分1.744507717(2)1338kN 或 kN·m 1439kN 或 kN·m 1439kN 282kN·m 0.5m0.00648025MPa 0.196m1.0000钢筋应力-35.3Mpa 钢筋应力≤24MPa,不必验算裂缝200000Mpa 30mm1.01.46518mm 偏心距 e 0=Ms/Ns=裂缝宽度计算 (JTG D62-2004 第6.4.5条)作用长期效应组合内力值 N l =作用短期效应组合内力值 N s =作用短期效应组合内力值 N s =作用短期效应组合内力值 M s =纵向受拉钢筋配筋率 ρ=As/πr 2=混凝土立方体抗压强度标准值 f cu,k =使用阶段轴向力偏心距增大系数钢筋弹性模量 E s =作用长期效应影响系数 =纵向钢筋直径 d=构件截面半径 r=混凝土保护层厚度 C=钢筋表面形状系数 C 1=210.5lsN C N =+=+=2000)(/140011hl h e s η=∙⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛-=-320,265.10.180.2πr 42.59ρησr e f N s k cu S SS最大裂缝宽度0.003mm < 0.2 mm,满足Ⅰ类0.20mm钢筋混凝土构件所在的环境类别 :最大裂缝宽度限值 :=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=C d E C C w SSSk f 52.104.003.021ρσ钢筋应力≤24MPa,不必验算裂缝宽度根据“C.0.2-1 的e0=εe0”用excel菜单"工具->单变量求解" 可快速解得ξ< 0.2 mm,满足规范要求。



Vol121No13公路交通科技2004年3月JOURNAL OF HIGHWAY AND TRANSPORTATION RESE ARCH AND DE VELOPMENT文章编号:1002O0268(2004)03O0040O04钢筋混凝土圆环截面偏心受压构件极限强度计算及程序黄平1,陈平2,李立3(11广东省公路勘察规划设计院,广东广州510507;21湖南环达路桥总公司,湖南长沙410001;31北京建达道桥咨询有限公司,北京100101)摘要:在文献[1]沿周边均匀配置钢筋的圆形偏心受压构件强度计算的基础上,运用叠加原理推导出内外圆周均匀配置双层钢筋的圆环截面偏心受压构件的极限强度计算公式,所得公式具有一般性,并编写相应的计算程序,程序在数家设计院经多年使用,证明是正确可靠的,可供工程设计应用。
关键词:圆环截面构件;偏心受压;极限强度;计算程序中图分类号:U444118文献标识码:AThe Limit Strength Calculation and Program for Circu lar Section ReinforcedConcrete Members under Eccentric Pressu resH U ANG Ping1,C H E N Ping2,LI li3(11Guangdon g Highway Desi gn Institute,Guangdong Guangzhou510507,China;21Hunan Huanda Road and Bridge En g ineering Company,Hunan Changsha410001,Chian;31Beijing Jianda Jianda Road and Bridge Consultant Company,Beijing100101,China)Abstract:This paper employs superposi tion theory to deduce formulations for limit strength calculation of eccen trically pressured circular sections wi th evenly placed double deck reinforcemen ts along inner and outer circles1Works i n this paper are based upon former works in strength theory of evenly reinforced circular secti ons under eccentric pressure1These formulations were attested to be accurate enough and sufficient for engineering applications by incorporating into a computer program that has been used by several design ins titutes for many years1Key words:Circular section member;Eccentric pressure;Limit strength;Computer program0引言钢筋混凝土圆环偏心受压构件具有重量轻、刚度大、受力合理、节约材料等优点,应用较为广泛。
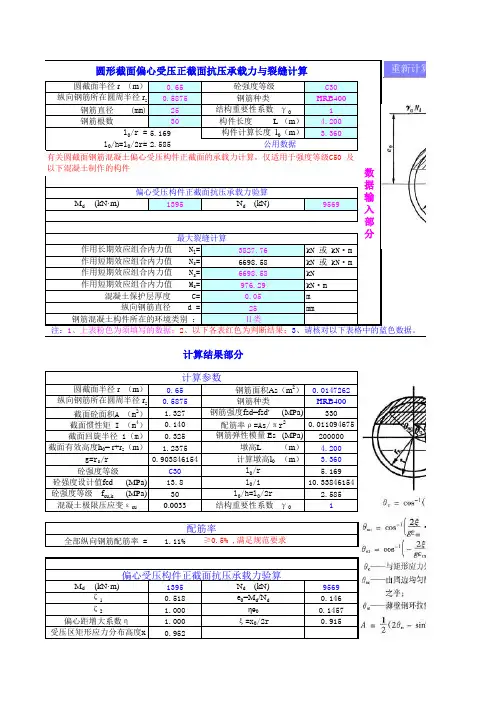
计算结果部分2.4640738410.4635307782546.2(2)3827.76kN 或 kN·m 6698.58kN 或 kN·m 6698.58kN 976.29kN·m 0.65m0.01109530MPa 0.146m1.0142钢筋应力-106.2Mpa 钢筋应力≤24MPa,不必验算裂缝200000Mpa 50mm 1.01.28625mm 钢筋弹性模量 E s =混凝土保护层厚度 C=钢筋表面形状系数 C 1=作用长期效应影响系数 =纵向钢筋直径 d=作用短期效应组合内力值 M s =构件截面半径 r=纵向受拉钢筋配筋率 ρ=As/πr 2=混凝土立方体抗压强度标准值 f cu,k =偏心距 e 0=Ms/Ns=使用阶段轴向力偏心距增大系数裂缝宽度计算 (JTG D62-2004 第6.4.5条)作用长期效应组合内力值 N l =作用短期效应组合内力值 N s =作用短期效应组合内力值 N s =210.5lsN C N =+=+=2000)(/400011hl h e s η=∙⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-=-320,265.10.180.2πr 42.59ρησr e f N s k cu S SS最大裂缝宽度-0.019mm < 0.2 mm,满足Ⅱ类0.20mm最大裂缝宽度限值 :钢筋混凝土构件所在的环境类别 :=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++=C dE C C w S SS k f 52.1004.003.021ρσ钢筋应力≤24MPa,不必验算裂缝宽度根据“C.0.2-1 的e0=ηe0”用excel菜单"工具->单变量求解" 可快速解得ξ< 0.2 mm,满足规范要求。
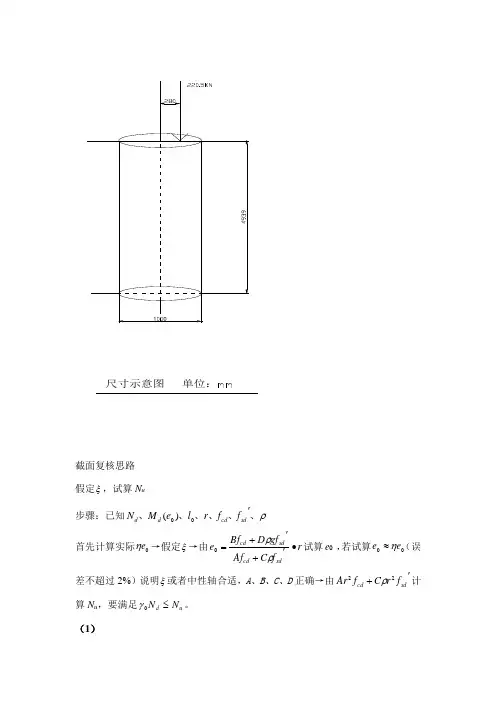
尺寸示意图 单位:截面复核思路假定ξ,试算N u步骤:已知ρ、、、、、、'sd cd d d f f r l e M N 00)(首先计算实际0e η→假定ξ→由r f C Af gf D Bf e sdcd sd cd •'+'+=ρρ0试算e 0 ,若试算00e e η≈(误差不超过2%)说明ξ或者中性轴合适,A 、B 、C 、D 正确→由'+sd cd f r C f Ar 22ρ计算N u ,要满足u d N N ≤0γ。
(1)其中圆柱的高度为:m 939.45.30439.35=∇-∇=l其半径为:m 5.0mm 50021000===r 混凝土保护层的厚度为50mm ;竖向轴力:由5根梁组成,每根重16t ,由两根柱承担其重量,故单根柱所受轴向力简化为KN 5.2208.925218=⨯⨯=d N 偏心距:0.28m 280mm 0==e对于C30混凝土轴心抗压强度设计值: MPa 5.11=cd fⅡ级钢筋:抗压强度设计值MPa 280='sd f ,构件的计算长度,按《公桥规》表5.3.1注,当一端固定,一端自由时,取2l ,故计算长度m 878.9939.4220=⨯==l l对于轴压构件的长细比:i l 0=λ A I i = 对于圆形截面面积:441422πππ=⨯==D A 对于圆形截面惯性矩:646416464444ππππ=⨯===D D I 故其回转半径:41644===ππA I i 所以,其长细比:5.17512.3941878.90>===i l λ 对于长细比5.170>i l 的构件,应考虑构件在弯矩作用平面内的挠曲对轴向力偏心距的影响,此时,应将轴向力对截面重心轴的偏心距e 0 乘以偏心距增大系数η。
圆形截面的偏心受压构件的偏心距增大系数可由下式确定:212000140011ζζη⎪⎭⎫ ⎝⎛+=h l h e 17.22.0001≤+=h e ζ 101.015.102≤-=hl ζ 对于圆形截面,截面有效高度h 0 :m 95.045.05.00=+=+=s r r h对于圆形截面,截面高度h :m 0.12==r h由上式可得:0.19958.095.028.07.22.01≤=⨯+=ζ 0.10512.11878.901.015.101.015.102>=⨯-=-=h l ζ 故取0.19958.021==ζζ;。

§5 圆形截面偏心受压构件承载力计算在桥梁工程中,钢筋混凝土圆形受压柱应用很广,例如桥墩、钻孔灌注桩基础等桥梁下部结构。
除了前一章学过的轴心受压柱以外,大量使用的还是偏心受压柱,。
我们知道,轴心受压构件计算简单,而偏心受压构件计算则复杂得多。
由于圆形偏心受压构件得截面及布筋不同于矩形截面构件,因此和矩形截面的公式也就不同,需要另外建立公式,本节就讲基本公式怎么建立,以及公式怎么应用。
柱的类型轴心受压柱桥墩偏心受压柱钻孔灌注桩⎧⎪⎧⎨⎨⎪⎩⎩在讲公式之前,先讲一下柱的构造。
我们知道,在规范中,构造规定与计算公式同等重要,偏心受压时的构造规定大部分与轴心受压相同。
纵筋沿圆周均匀布置;纵筋直径不小于 12,纵筋要伸入基础和盖梁, 混凝土保护层C 不小于30~40㎜,此外还规定了最小配筋率、最大配筋率,对箍筋也作了规定。
对于钻孔灌注桩,由于它的直径大,又处于地下,所以它的主筋比一般的柱要粗,保护层也相应要大些,具体看教材、规范对应条款。
max min min max6125035030~40 mm 0.0045156,40010.84纵筋沿圆周均匀布置,不少于根纵筋,水平净距不小于,不大于纵筋要伸入基础和盖梁构造、,纵筋=,=%直径箍筋,封闭式;不小于(柱直径)灌注桩,保护层要大一些v mm mm C d mm S mm d D φρρρρ⎧⎪⎪⎪⎪≥⎪⎪⎪⎪≥⎨⎪⎪⎪≤⎧≥⎧⎪⎪⎪≤⎨⎨⎪⎪⎪⎪≤⎩⎩⎪⎪⎩一、 基本假定根据试验研究分析,规范引入以下假定作为计算基础: 1、 截面变形符合平面假定2、 受压区混凝土最大压应变εcu =0.00333、 混凝土压应力图采用等效矩形应力图,应力达到f cd ,等效区高度00()为实际受压区高度x x x β=,002值随而变,=x x D rβξξ=(ξ实际受压区高度与截面直径的比值),即1,0.81 1.5, 1.0670.267当时当<时ξβξβξ≤=≤=-4、忽略受拉区混凝土拉力,拉力全部由钢筋承担。


盖梁圆形墩柱偏心受压计算方法**《盖梁圆形墩柱偏心受压计算方法,听我给你唠唠》**嘿,朋友!今天我要跟你分享一个超级实用,但可能有点复杂的盖梁圆形墩柱偏心受压计算方法。
别担心,跟着我,咱们一步一步来,保证让你搞明白!首先呢,咱们得搞清楚一些基本的概念。
就好比你要去一个陌生的地方,得先知道路名对吧?这盖梁圆形墩柱偏心受压计算,简单来说,就是看看这个柱子能不能承受住偏了心的压力。
想象一下,柱子就像一个大力士,压力就是要它举的重物,但是这重物不在正中间,有点偏,咱们就得算算大力士能不能撑住。
接下来,进入第一步,收集数据。
这就像买菜做饭,你得先知道有啥食材。
咱们要知道墩柱的直径、混凝土的强度、钢筋的配置等等。
这些数据就像是做菜的原料,缺了可不行。
我跟你说,我有一次算这个,数据没搞全,结果算得乱七八糟,就像做饭没放盐,那味道,简直没法吃!第二步,确定计算模型。
这一步就像是给大力士设计一个比赛场地。
我们要根据柱子的实际情况,确定是按照短柱还是长柱来计算。
这可不能马虎,要是搞错了,那后面的计算可就全错啦。
第三步,计算偏心距。
这个偏心距就像是重物偏离中心的距离。
咱们得通过各种公式和数据算出来。
这一步可得细心,一个数字错了,那结果可能差十万八千里。
我之前有次算偏心距,不小心把小数点弄错了,算出的结果简直能把人吓一跳,还以为这柱子要被压垮了呢!第四步,进行承载力验算。
这就好比检查大力士到底能不能举起这个偏了心的重物。
通过一系列复杂的公式和计算,看看柱子能不能扛得住。
在这一步,要是发现柱子扛不住,那可就得重新设计或者加强柱子啦,不然万一出问题,那可就糟糕了。
最后一步,整理结果和分析。
算出结果后,咱们得看看是不是合理,要是不合理,就得回头检查前面的步骤,看看哪里出错了。
整个计算过程就像一场战斗,每一步都要小心谨慎。
不过别害怕,多练几次,你就能熟练掌握啦!朋友,记住这几个步骤,多练习练习,相信你也能轻松搞定盖梁圆形墩柱偏心受压计算!加油,你一定行!。

1圆形截面偏心受压构件计算书1基本信息1.1尺寸信息圆形截面构造尺寸及钢筋示意图几何长度l=12 m,半径r=750 mm,约束方式为:两端铰结。
根据规范《JTG 3362-2018 公路钢筋混凝土及预应力混凝土桥涵设计规范》附录E可知,计算长度换算系数k=1.0,计算长度l0=kl=1.0×12=12.00 m,混凝土的面积A=πr2=π×750 2=1767145.87 mm2。
1.2材料信息混凝土的等级为:C30,抗压强度f cd=13.8 MPa;纵向钢筋的等级为:HRB400,抗拉强度f sd=330 MPa ,直径d s=28 mm,根数n=28 根,钢筋重心所在圆周半径r s=680 mm,钢筋面积为A s=0.25πd s2n=0.25×π×28 2×28=17241.06 mm2。
不考虑骨架焊接,钢筋表面没有环氧树脂涂层。
1.3设计信息结构的重要性系数γ0=1.1;环境类别:Ⅰ类;计算类型:一般计算;弯矩的基本组合:M d=1680 kN∙m 轴力的基本组合:N d=3590 kN 弯矩的频遇组合:M s=1500 kN∙m 轴力的频遇组合:N s=2000 kN轴力的准永久组合:N l=2000 kN2极限状态承载能力验算截面高度ℎ=2r=2×750=1500.0 mm截面有效高度ℎ0=r+r s=750+680=1430.0 mm 纵向钢筋配筋率ρ=A sπr2=17241.06π×750 2×100%=0.98%基本组合下的初始偏心距e0=M dd=1000×1680=468.0 mmi=0.5×r=0.5×750=375.0 mmψ=l0i⁄=12.00 ×1000 375.0⁄=32.00>17.5所以要考虑偏心距增大系数的影响。
计算偏心距系数时,e0=max (468.0 ,1500.030,20)=468.0 mm荷载偏心率系数ζ1=0.2+2.7e0ℎ0=0.2+2.7×468.01430.0=1.0836且需满足ζ1≤1.0,所以ζ1=1.0000长细比系数ζ2=1.15−0.01l0ℎ=1.15−0.01×1000×12.001500.0=1.0700且需满足ζ2≤1.0,所以ζ2=1.0000偏心距增大系数η=1+11300e0ℎ0⁄(l0ℎ)2ζ1ζ2=1+11300×468.0 1430.0⁄(12.00×1000.01500.0)2×1.0000×1.0000=1.1504所以偏心距e=ηe0=1.1504 × 468.0=538.4 mm沿圆周均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件,当截面内纵向普通钢筋数量不少于8根时,其承载力计算应符合下列规定:γ0N d≤N ud=αf cd A(1−sin2πα2πα)+(α−αt)f sd A sγ0N dηe0≤M ud=23f cd Arsin3παπ+f sd A s r ssinπα+sinπαtπαt=1.25−2α,当α大于0.625时,取αt=0。