3.正截面承载力计算(T形截面)

T形截面受弯构件正截面承载力计算首先，我们需要确定T形截面的几何形状参数。

T形截面由两个部分组成，一部分是腿部，另一部分是横梁。

我们需要测量腿部和横梁的宽度b和高度h，以及腿部和横梁的厚度t1和t2接下来，我们需要确定材料的特性参数。

材料的特性参数包括弹性模量E和抗弯强度fy。

弹性模量表示材料在受应力作用下产生的变形程度，抗弯强度表示材料在受弯应力作用下的最大承载能力。

然后，我们需要确定加载方式。

T形截面受弯构件可以分为两种加载方式：一种是在腿部施加荷载，另一种是在横梁施加荷载。

对于腿部受载的情况，我们可以先假设T形截面的两个腿部均受到均匀荷载q的影响。

然后利用梁的理论计算方法，根据T形截面的几何形状和材料特性，计算出腿部的正截面承载力。

根据梁的理论计算方法，腿部受均匀荷载q的最大弯矩应为最大正截面弯矩M。

根据梁的力学方程M=E·I/y，其中E为弹性模量，I为截面的惯性矩，y为截面上其中一点的距离截面重心的垂直距离。

梁的截面惯性矩I可以根据截面几何形状的性质计算得到。

腿部的正截面承载力可以根据下式计算：P = fy·A = fy·(h1·t1 + h2·t2)其中，fy为材料的抗弯强度，A为截面的面积，h1和h2为腿部的高度，t1和t2为腿部的厚度。

最后，我们还需要根据截面几何形状的性质计算出腿部的扭转常数J和抗扭矩Wt。

扭转常数J表示截面抵抗扭转变形的能力，抗扭矩Wt表示截面的最大承载能力。

通过计算这两个参数，我们可以得到T形截面的抗扭矩Wt。

综上所述，我们可以通过测量T形截面的几何形状参数，确定材料的特性参数，采用梁的理论计算方法，计算出T形截面受弯构件的正截面承载力。

这将有助于工程师评估T形截面受弯构件的结构安全性，并进行合理的设计和优化。

T形截面受弯构件正截面承载力计算对于T形截面受弯构件正截面承载力的计算，我们需要考虑以下几个因素：1.材料的力学性能：首先我们需要知道构件所使用的材料的弹性模量和屈服强度。

这些参数通常可以从材料的规格书或实验数据中获得。

2.受力分析：我们要确定在构件上产生最大弯矩的位置。

通常情况下，T形截面受弯构件在底部和侧面承受的弯矩是最大的。

根据受力分析，我们可以得出最大弯矩值。

3.截面形状：T形截面由顶横梁和底翼板组成。

我们需要确定这些截面的几何参数，例如顶横梁的宽度、厚度和底翼板的高度、厚度。

4.应力分布：根据受力分析，我们可以绘制出T形截面受弯构件的应力分布图。

根据构件上的应力分布，我们可以确定任意截面上的应力值。

5.截面承载力计算：正截面承载力的计算通常包括弯曲抗力和剪切抗力两个方面。

-弯曲抗力：根据截面形状和应力分布，我们可以计算出截面所能承受的最大弯矩。

根据材料的弹性模量和屈服强度，我们可以计算出构件所能承受的最大应力。

然后，我们可以通过应力与强度的比较来确定截面的弯曲抗力。

-剪切抗力：T形截面的底横梁和侧面翼板之间存在剪力作用。

根据剪力的大小，我们可以计算出截面上的剪应力。

同样，我们通过应力与强度的比较来确定截面的剪切抗力。

6.结构稳定性考虑：在计算截面承载力时，还需要考虑到结构的稳定性。

这包括了截面的屈曲和扭曲稳定性等。

需要注意的是，以上步骤只是一个大致的计算方法，具体的计算过程还需要根据具体的情况进行调整和修改。

在实际工程中，通常会根据设计规范和标准进行计算，确保构件的安全可靠。

第四章钢筋混凝土受弯构件正截面承载力计算本章学习要点：1、掌握单筋矩形截面、双筋矩形截面和T形截面承载力的计算方法；2、了解配筋率对受弯构件破坏特征的影响和适筋受弯构件在各阶段的受力特点；3、熟悉受弯构件正截面的构造要求。

§4-1 概述一、受弯构件的定义同时受到弯矩M和剪力V共同作用，而轴力N可以忽略的构件（图4-1）。

梁和板是土木工程中数量最多，使用面最广的受弯构件。

梁和板的区别：梁的截面高度一般大于其宽度，而板的截面高度则远小于其宽度。

受弯构件常用的截面形状如图4-2所示。

图4-1二、受弯构件的破坏特性正截面受弯破坏：沿弯矩最大的截面破坏，破坏截面与构件的轴线垂直。

斜截面破坏：沿剪力最大或弯矩和剪力都较大的截面破坏。

破坏截面与构件轴线斜交。

进行受弯构件设计时，要进行正截面承载力和斜截面承载力计算。

图4-3 受弯构件的破坏特性§4-2 受弯构件正截面的受力特性一、配筋率对正截面破坏性质的影响配筋率：为纵向受力钢筋截面面积A s与截面有效面积的百分比。

sAbh式中sA——纵向受力钢筋截面面积。

b——截面宽度，h——截面的有效高度（从受压边缘至纵向受力钢筋截面重心的距离）。

构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素，但配筋率的影响最大。

受弯构件依配筋数量的多少通常发生如下三种破坏形式：1、少筋破坏当构件的配筋率低于某一定值时，构件不但承载力很低，而且只要其一开裂，裂缝就急速开展，裂缝处的拉力全部由钢筋承担，钢筋由于突然增大的应力而屈服，构件立即发生破坏。

图4-4 受弯构件正截面破坏形态2、适筋破坏当构件的配筋率不是太低也不是太高时，构件的破坏首先是受拉区纵向钢筋屈服，然后压区砼压碎。

钢筋和混凝土的强度都得到充分利用。

破坏前有明显的塑性变形和裂缝预兆。

3、超筋破坏当构件的配筋率超过一定值时，构件的破坏是由于混凝土被压碎而引起的。

受拉区钢筋不屈服。

破坏前有一定变形和裂缝预兆，但不明显，。

单筋T形梁正截面承载力计算首先，单筋T形梁的截面形状决定了其抗弯性能。

截面一般包括上翼缘、下翼缘和腹板三个部分。

上翼缘主要承担拉力，下翼缘和腹板主要承担压力。

根据材料的强度和构件尺寸，可以计算出单筋T形梁的截面性能指标，如截面面积、截面惯性矩、截面模量等。

其次，单筋T形梁的承载力计算还要考虑由荷载引起的应力。

常见的荷载包括自重、活载、风载和地震载等。

这些荷载可以综合考虑，并转化为梁的等效荷载作用于梁上。

根据不同的受力情况，可以采用弹性理论或塑性理论进行计算。

弹性理论假设材料的应力和应变满足胡克定律，可以解析地计算出梁的最大应力和变形情况。

而塑性理论假设材料达到屈服应变时，应力保持不变，可以通过平衡条件和塑性转化准则进行计算。

在设计和计算中，还需要考虑梁的安全性。

常见的安全系数包括抗弯强度安全系数、极限状态安全系数和服务状态安全系数等。

抗弯强度安全系数是指梁的抗弯强度与设计荷载之比，一般要求大于1.5、极限状态安全系数是指梁在极限状态下的荷载与承载力之比，要求大于1.0。

而服务状态安全系数是指梁在使用过程中的荷载与承载能力之比，要求大于 1.0。

最后，计算单筋T形梁的承载力还需要考虑构件的受限状况。

单筋T形梁的受限状态一般有局部屈曲、整体侧扭和挤压等。

这些受限状态会影响梁的承载能力。

为了确保梁的良好工作性能，需要对梁的限制状态进行合理的分析和计算。

综上所述，单筋T形梁的承载力计算是一个综合考虑材料、截面形状、荷载、安全性和受限状况等多个因素的过程。

只有在合理选择计算方法和参数的基础上，才能保证梁的设计符合规范，并能满足工程实际需求。

因此，在设计和计算单筋T形梁的承载力时，需要根据具体情况进行详细分析，并结合相关理论和规范进行计算，以保证构件的安全可靠性。

T型截面正截面承载力计算周佳（西南科技大学城市学院土木工程与建筑系，四川绵阳621000）[摘要] 由于T型截面梁具有更经济更轻质的功能，这种构造被广泛用于桥梁工程及大荷载工程，以下根据自己在学习过程中的总结和计算列出一般单筋T型截面梁正截面抗弯承载能力计算的简单过程。

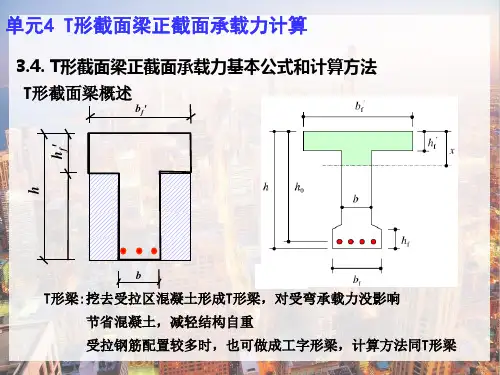
（本文仅错位自己在钢筋混凝土设计课程学习后对一般单筋T型截面梁正截面抗弯承载能力计算过程的总结与复习）[关键词] T型截面梁正截面承载力0 引言T型截面梁由矩形截面梁衍生出来，其截面形式如图1所示。

阴影部分面积为混凝土，为减轻自重可以抠除同时基本不会影响该梁的抗弯承载能力。

建筑工程中受弯构件正截面承载力计算的基本假定：1）截面应保持平面；2）不考虑混凝土的抗拉强度；3）给出混凝土受压的应力—应变关系曲线按下列规定取用：图1 图2T型截面梁分为两类（如图2）：一类如图2（a）：中和轴在翼缘内，即受压区宽度小于等于翼缘厚度。

二类如图2（b）：中和轴在翼缘下部，即受压区厚度大于等于翼缘厚度。

给出两类截面梁的判别式文献[1]：2 T 型截面梁正截面抗弯承载力的计算：一、基本公式（一）第一类T 形梁2．第一类T 形梁的基本计算公式这一类梁的截面虽为T 形，但由于中和轴通过翼缘，即'f h x ≤，s y f c A f x b f ='1α⎪⎭⎫ ⎝⎛-'=≤201x h x b f M M f c u α 3．基本公式的适用条件是：1）0h x b ξ≤由于T 形截面的翼缘厚度h f ′一般都比较小，既然x ≤h f ′，因此这个条件通常都能满足，故不必验算。

2）0/bh A s =ρ应不小于min ρ（具体计算时，bh A A s S min min ,ρ=≥）（二）第二类T 形梁1．计算图式2．第二类T 形梁的基本计算公式这一类梁截面的中和轴通过肋部，即x > h f ′，故受压区为T 形。

于是第二类T 形梁正截面受弯承载力的基本计算公式可以写成： s y f f c c A f h b b f bx f ='-'+)(11αα()⎪⎪⎭⎫ ⎝⎛'-'-'+⎪⎭⎫ ⎝⎛-=≤220101f f f c c u h h h b b f x h bx f M M αα3．基本公式的适用条件1）为防止发生超筋破坏，应当满足： 0h x b ξ≤或 b ξξ≤或 y c b s f f bh A //1011αξρ≤=或 ()b b c u bh f M ξξα5.012011-≤2）bhA A s s min min ,ρ=≥由于第二类T 形梁受压区较大，相应受拉钢筋也就较多，故一般均能满足此条件，可不必验算。