电路原理课后习题答案-2

习题22.1在图2.18所示的电路中，求各理想电流源的端电压、功率及各电阻上消耗的功率。

解答：由节点方程得I3=I2-I1=1A，U1=I3R1=1A×20Ω=20V，U2=U1+I2R2=20V+2A×10Ω=40V，P1= U1I1=20V×1A=20W，P2=-U2I2=-80W，电阻上的功率P R1=20V×1A=20W，P R2=20V×2A=40W。

2.2求图2.19所示电路中各支路电流，并计算理想电流源的电压Ｕ１。

已知Ｉ１＝３Ａ，Ｒ２＝１２Ω，Ｒ３＝８Ω，Ｒ４＝１２Ω，Ｒ５＝６Ω。

电压和电流的参考方向如图中所示。

解答：节点方程I1+I2+I3=0，I3=I4+I5，网孔方程I2R2=I3R3+I4R4，I4R4=I5R5，联立上述方程得I2=I3=-1.5A，I4=-0.5A，I5=-1A，U1=I2R2=-1.5A×12Ω=-18V。

2.3试用支路电流法求图2.20所示电路中各支路电流，并求三个电源的输出功率和负载电阻ＲＬ上的取用功率。

解答：节点方程I1+I2+10=I，网孔方程0.8I1+116=0.4I2+120，0.8I1+4I=120，联立三方程得I1=75/8A，I2=35/4A，I=225/8A，三个电源的输出功率分别为1125W，1015W，1125W；负载电阻上的取用功率为3164.0625W。

2.4用网孔电流法求解习题2.3。

解答：将电流源与负载电阻的位置互换形成三个网孔，网孔参考电流方向均为顺时针方向，网孔电流方程如下1.2I A-0.4I B=120-116，4.4I B-0.4I A-4I C=116，I C=-10A，解得I A=75/8A，I B=145/8A，于是I1=I A=75/8A，I2=I B-I A=35/4A，I=I B-I C=225/8A。

2.5图2.21所示电路，网孔电流如图中所标，试列写可用来求解该电路的网孔方程。

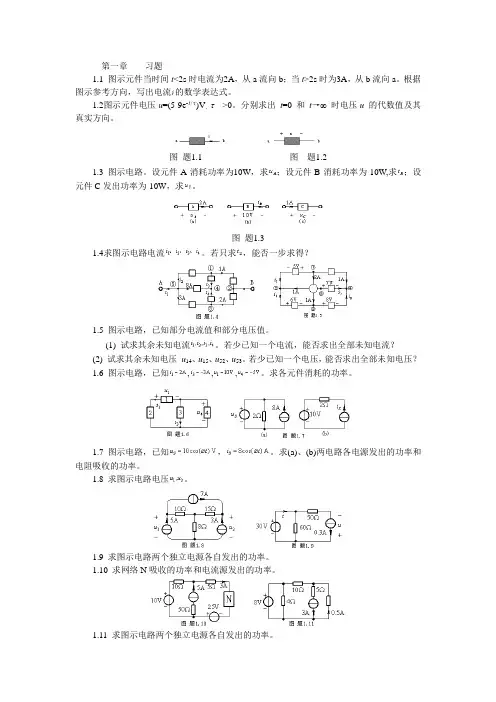
第一章习题1.1 图示元件当时间t<2s时电流为2A，从a流向b；当t>2s时为3A，从b流向a。

根据图示参考方向，写出电流的数学表达式。

1.2图示元件电压u=(5-9e-t/τ)V，τ>0。

分别求出t=0 和t→∞时电压u的代数值及其真实方向。

图题1.1 图题1.21.3 图示电路。

设元件A消耗功率为10W，求；设元件B消耗功率为-10W,求；设元件C发出功率为-10W，求。

图题1.31.4求图示电路电流。

若只求，能否一步求得？1.5 图示电路，已知部分电流值和部分电压值。

(1) 试求其余未知电流。

若少已知一个电流，能否求出全部未知电流？(2) 试求其余未知电压u14、u15、u52、u53。

若少已知一个电压，能否求出全部未知电压？1.6 图示电路，已知,,,。

求各元件消耗的功率。

1.7 图示电路，已知，。

求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。

1.8 求图示电路电压。

1.9 求图示电路两个独立电源各自发出的功率。

1.10 求网络N吸收的功率和电流源发出的功率。

1.11 求图示电路两个独立电源各自发出的功率。

1.12 求图示电路两个受控源各自发出的功率。

1.13 图示电路，已知电流源发出的功率是12W，求r的值。

1.14 求图示电路受控源和独立源各自发出的功率。

1.15图示电路为独立源、受控源和电阻组成的一端口。

试求出其端口特性，即关系。

1.16 讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响，加深对独立源特性的理解。

第二章习题2.1 图(a)电路，若使电流A,，求电阻；图(b)电路，若使电压U=(2/3)V，求电阻R。

2.2 求图示电路的电压及电流。

2.3 图示电路中要求，等效电阻。

求和的值。

2.4求图示电路的电流I。

2.5 求图示电路的电压U。

2.6 求图示电路的等效电阻。

2.7 求图示电路的最简等效电源。

图题2.72.8 利用等效变换求图示电路的电流I。

第一章电路模型和电路定律电路理论主要研究电路中发生的电磁现象，用电流i、电压u和功率p等物理量来描述其中的过程。

因为电路是由电路元件构成的，因而整个电路的表现如何既要看元件的联接方式，又要看每个元件的特性，这就决定了电路中各支路电流、电压要受到两种基本规律的约束，即：（1）电路元件性质的约束。

也称电路元件的伏安关系（VCR），它仅与元件性质有关，与元件在电路中的联接方式无关。

（2）电路联接方式的约束（亦称拓扑约束）。

这种约束关系则与构成电路的元件性质无关。

基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）是概括这种约束关系的基本定律。

掌握电路的基本规律是分析电路的基础。

1-1说明图（a）,（b）中,（1）u,i的参考方向是否关联？（2）ui乘积表示什么功率？（3）如果在图（a）中u0,i0；图（b）中u0,i0，元件实际发出还是吸收功率？解：（1）当流过元件的电流的参考方向是从标示电压正极性的一端指向负极性的一端，即电流的参考方向与元件两端电压降落的方向一致，称电压和电流的参考方向关联。

所以（a）图中u,i的参考方向是关联的；（b）图中u,i的参考方向为非关联。

（2）当取元件的u,i 参考方向为关联参考方向时，定义pui为元件吸收的功率；当取元件的u,i参考方向为非关联时，定义p ui为元件发出的功率。

所以（a）图中的ui乘积表示元件吸收的功率；（b）图中的ui乘积表示元件发出的功率。

（3）在电压、电流参考方向关联的条件下，带入u,i数值，经计算，若p ui0，表示元件确实吸收了功率；若p0，表示元件吸收负功率，实际是发出功率。

（a）图中，若u0,i0，则p ui0，表示元件实际发出功率。

在u,i参考方向非关联的条件下，带入u,i数值，经计算，若pui0，为正值，表示元件确实发出功率；若p0，为负值，表示元件发出负功率，实际是吸收功率。

所以（b）图中当u0,i0，有pui0，表示元件实际发出功率。

电路第四版课后习题答案第一章：电路基础1. 确定电路中各元件的电压和电流。

- 根据基尔霍夫电压定律和电流定律，我们可以列出方程组来求解未知的电压和电流值。

2. 计算电路的等效电阻。

- 使用串联和并联电阻的计算公式，可以求出电路的等效电阻。

3. 应用欧姆定律解决实际问题。

- 根据欧姆定律 \( V = IR \)，可以计算出电路中的电压或电流。

第二章：直流电路分析1. 使用节点电压法分析电路。

- 选择一个参考节点，然后对其他节点应用基尔霍夫电流定律，列出方程组并求解。

2. 使用网孔电流法分析电路。

- 选择电路中的网孔，对每个网孔应用基尔霍夫电压定律，列出方程组并求解。

3. 应用叠加定理解决复杂电路问题。

- 将复杂电路分解为简单的子电路，然后应用叠加定理计算总的电压或电流。

第三章：交流电路分析1. 计算交流电路的瞬时值、有效值和平均值。

- 根据交流信号的表达式，可以计算出不同参数。

2. 使用相量法分析交流电路。

- 将交流信号转换为复数形式，然后使用复数运算来简化电路分析。

3. 计算RLC串联电路的频率响应。

- 根据电路的阻抗，可以分析电路在不同频率下的响应。

第四章：半导体器件1. 分析二极管电路。

- 根据二极管的伏安特性，可以分析电路中的电流和电压。

2. 使用晶体管放大电路。

- 分析晶体管的共发射极、共基极和共集电极放大电路，并计算放大倍数。

3. 应用场效应管进行电路设计。

- 根据场效应管的特性，设计满足特定要求的电路。

第五章：数字逻辑电路1. 理解逻辑门的工作原理。

- 描述不同逻辑门（如与门、或门、非门等）的逻辑功能和电路实现。

2. 使用布尔代数简化逻辑表达式。

- 应用布尔代数的规则来简化复杂的逻辑表达式。

3. 设计组合逻辑电路。

- 根据给定的逻辑功能，设计出相应的组合逻辑电路。

第六章：模拟集成电路1. 分析运算放大器电路。

- 根据运算放大器的特性，分析电路的增益、输入和输出关系。

2. 设计滤波器电路。

电路原理第二版课后答案1. 电路原理课程是电子工程专业的基础课程，对于学生来说，课后习题是检验自己对知识掌握程度的重要途径。

因此，本文档将为大家提供电路原理第二版课后答案，希望能够帮助大家更好地学习和理解电路原理课程。

2. 第一章电路基本概念。

1. 什么是电路？电路是由电源、导线和负载组成的电气网络，用于传输电能和信号。

2. 什么是电流？电流是电荷在单位时间内通过导体横截面的数量，通常用符号I表示，单位是安培(A)。

3. 什么是电压？电压是电荷单位正电荷所具有的电位能，通常用符号U表示，单位是伏特(V)。

4. 什么是电阻？电阻是导体对电流的阻碍作用，通常用符号R 表示，单位是欧姆(Ω)。

5. 什么是电路的基本分类？电路可以分为直流电路和交流电路两种基本类型。

3. 第二章电路分析基础。

1. 什么是基尔霍夫定律？基尔霍夫定律是电路分析中常用的方法，它包括基尔霍夫电压定律和基尔霍夫电流定律。

2. 基尔霍夫电压定律是什么？基尔霍夫电压定律指出，电路中任意闭合回路的电压代数和为零。

3. 基尔霍夫电流定律是什么？基尔霍夫电流定律指出，电路中任意节点处，进入节点的电流等于离开节点的电流之和。

4. 什么是戴维南定理？戴维南定理是电路分析中的重要方法，它可以将电路中的任意两点简化为等效电压源和等效电阻。

4. 第三章电路定常状态分析。

1. 什么是电路的定常状态？电路的定常状态是指电路中各元件参数不随时间变化的状态。

2. 什么是节点分析法？节点分析法是一种电路分析方法，通过对电路中各节点电压进行分析，得到电路的解。

3. 什么是支路电流分析法？支路电流分析法是一种电路分析方法，通过对电路中各支路电流进行分析，得到电路的解。

5. 第四章交流电路分析。

1. 什么是交流电路？交流电路是指电源为交流电的电路，其特点是电压和电流随时间变化。

2. 什么是交流电路中的阻抗？阻抗是交流电路中元件对交流电的阻碍作用，它包括电阻、电感和电容。

高频电路原理与分析第五版课后习题答案曾兴雯刘乃安陈健付卫红编[日期]NEUQ西安电子科技大学出版社第一章 绪论1－1 画出无线通信收发信机的原理框图，并说出各部分的功用。

答：上图是一个语音无线电广播通信系统的基本组成框图，它由发射部分、接收部分以及无线信道三大部分组成。

发射部分由话筒、音频放大器、调制器、变频器（不一定必须）、功率放大器和发射天线组成。

低频音频信号经放大后，首先进行调制后变成一个高频已调波，然后可通过变频，达到所需的发射频率，经高频功率放大后，由天线发射出去。

接收设备由接收天线、高频小信号放大器、混频器、中频放大器、解调器、音频放大器、扬声器等组成。

由天线接收来的信号，经放大后，再经过混频器，变成一中频已调波，然后检波，恢复出原来的信息，经低频功放放大后，驱动扬声器。

1－2 无线通信为什么要用高频信号？“高频”信号指的是什么？ 答：高频信号指的是适合天线发射、传播和接收的射频信号。

采用高频信号的原因主要是： （1）频率越高，可利用的频带宽度就越宽，信道容量就越大，而且可以减小或避免频道间的干扰；（2）高频信号更适合电线辐射和接收，因为只有天线尺寸大小可以与信号波长相比拟时，才有较高的辐射效率和接收效率，这样，可以采用较小的信号功率，传播较远的距离，也可获得较高的接收灵敏度。

1－3 无线通信为什么要进行凋制？如何进行调制？ 答：因为基带调制信号都是频率比较低的信号，为了达到较高的发射效率和接收效率，减小天线的尺寸，可以通过调制，把调制信号的频谱搬移到高频载波附近；另外，由于调制后的音频放大器调制器激励放大输出功率放大载波振荡器天线开关高频放大混频器中频放大与滤波解调器音频放大器话筒本地振荡器扬声器变频器信号是高频信号，所以也提高了信道利用率，实现了信道复用。

调制方式有模拟调调制和数字调制。

在模拟调制中，用调制信号去控制高频载波的某个参数。

在调幅方式中，AM 普通调幅、抑制载波的双边带调幅（DSB ）、单边带调幅（SSB ）、残留单边带调幅（VSSB ）；在调频方式中，有调频（FM ）和调相（PM ）。

第二章电路分析基础2-1 电路如图所示，已知US1=24V，US2=16V，IS=1A，R1=R2=8Ω，R3=4Ω。

试用支路电流法求各支路电流。

解：该题有四条支路其中一条支路是恒流源（设恒流源两端电压为U IS），应列四个方程。

有两个节点，按KCL定理可列一个节点方程： I1+I2 =I S+I3有三个网孔按KVL定理可列三个回路方程：I1R1 =U S1+U ISI2R2 =U S2+U IS I2R2+I3R3 =U S2 U IS=I3R3 解之 I1=2A I2=1A I3=2A U S=8V2-2 电路如图所示。

已知I S=2A，U S=6V，R1=R2=3Ω，R3=R4=6Ω，用叠加原理求a、b两点之间电压U ab。

解：当电压源U S单独作用时，题图变如右图：Uab1=当电流源I S单独作用时，题图变如右图Uab2=3V Uab=Uab1+Uab2=2-3 电路如图所示。

已知R1=6Ω，R2=12Ω，R3=8Ω，R4=4Ω，R5=1电路中流经R3的电流I当电流源I S单独作用时，题图变如右图)(13844434AIRRRI=⨯+=+=''I=)(211AII=+=''+'2-4 在图示电路中，当U S=24V时，Uab=8v. 试用叠加原理求U S=0时的UabIs。

解：当电压源U S单独作用时，题图变如右图)(1841243ARRUI S=+=+='解：以知U S=24V时，Uab=8v.当U S、、I S1、I S2、单独作用时题图分别变作变作下图1、图2、图3由图1可得：Uab1=)(64244VRRUS-=-=⨯；由图2可得：Uab2=)(212411VRIRRISS=⨯；由图3可得：Uab3=)(41422VRIRISS=⨯；UabIs=Uab2+Uab3=8+6=14（V）2-5 用电源等效变换法求图示电路中6Ω电阻中的电流I。

电路原理课后答案电路原理是电子工程专业的一门重要课程，它涉及到电路的基本概念、分析方法和设计技术。

通过学习电路原理，我们可以掌握电路的基本工作原理，为日后的电子电路设计和实际应用打下坚实的基础。

下面是一些电路原理课后习题的答案，希望能够帮助大家更好地理解和掌握这门课程。

1. 电路原理中，最基本的电路元件是什么？答，最基本的电路元件是电阻、电容和电感。

2. 什么是欧姆定律？它的数学表达式是什么？答，欧姆定律是指在恒定温度下，电流与电压成正比，即I=U/R，其中I为电流，U为电压，R为电阻。

3. 什么是串联电路？并写出串联电路的等效电阻公式。

答，串联电路是指电路中的电阻依次连接在一起，电流依次通过每一个电阻。

串联电路的等效电阻公式为R=R1+R2+...+Rn。

4. 什么是并联电路？并写出并联电路的等效电阻公式。

答，并联电路是指电路中的电阻同时连接在一起，电流分别通过每一个电阻。

并联电路的等效电阻公式为1/R=1/R1+1/R2+...+1/Rn。

5. 什么是电压分压原理？并写出电压分压电路的计算公式。

答，电压分压原理是指在串联电路中，电压与电阻成正比，即U=IR。

电压分压电路的计算公式为U1=U(R1/(R1+R2))，U2=U(R2/(R1+R2))。

6. 什么是电流合流原理？并写出电流合流电路的计算公式。

答，电流合流原理是指在并联电路中，电流与电阻成反比，即I=U/R。

电流合流电路的计算公式为I=I1+I2。

通过以上习题的答案，我们可以更好地理解电路原理中的基本概念和计算方法。

希望大家能够通过认真学习和练习，掌握好这门课程，为将来的学习和工作打下坚实的基础。

电路原理(邱关源)习题答案(dá àn)第二章-电阻电路的等效变换练习电路原理(邱关源)习题(xítí)答案第二章-电阻电路的等效变换练习第二章电阻电路(diànlù)的等效变换“等效(děnɡ xiào)变换”在电路理论中是很重要的概念，电路等效变换的方法是电路问题分析(fēnxī)中经常使用的方法。

所谓两个电路是互为等效的，是指（1）两个结构参数不同的电路再端子上有相同的电压、电流(diànliú)关系，因而可以互相代换；（2）代换的效果是不改变外电路（或电路中未被代换的部分）中的电压、电流和功率。

由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。

等效的对象是外接电路（或电路未变化(biànhuà)部分）中的电压、电流和功率。

等效变换的目的是简化电路，方便地求出需要求的结果。

深刻地理解“等效变换”的思想，熟练掌握“等效变换”的方法在电路分析中是重要的。

2-1 电路如图所示，已知。

若：（1）；（2）；（3）。

试求以上3种情况下电压和电流。

解：（1）和为并联(bìnglián)，其等效电阻，则总电流(diànliú)分流(fēn liú)有（2）当，有（3），有2-2 电路如图所示，其中(qízhōng)电阻、电压源和电流源均为已知，且为正值。

求：（1）电压2u和电流(diànli ú)；（2）若电阻增大，对哪些元件的电压、电流有影响？影响如何？解：（1）对于2R和3R来说，其余部分的电路可以用电流源等效代换，如题解图（a）所示。

因此有（2）由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源，如题解图（b ）所示。

因此当1R 增大，对及的电流和端电压都没有影响。

但1R 增大(z ēn ɡ d à)，1R 上的电压(di àny ā)增大，将影响电流源两端的电压，因为显然(xi ǎnr án)随1R 的增大(z ēn ɡ d à)而增大。

电路原理练习题一及答案一、选择题1、已知ab 两点之间电压为10V ，电路如下图所示，则电阻R 为（）R — 10V +A 、0ΩB 、—5ΩC 、5ΩD 、10Ω2、在下图1示电阻R 1和R 2并联电路中，支路电流I 2等于（）+ R 2 10V Ω——图1 A 、I R R R 211+ B 、I R R R 212+ C 、I R R R 121+ D 、I R R R 221+ 3、在上图2示电路中，发出功率的是（）A 、电阻B 、电压源和电流源C 、电压源D 、电流源4、叠加定理用于计算（）A 、线性电路中的电压、电流和功率；B 、线性电路中的电压和电流；C 、非线性电路中的电压、电流和功率；D 、非线性电路中的电压和电流。

5I S 和电阻R 为（）A 、1A ，1ΩB 、1A ，2ΩC 、2A ，1ΩD 、2A ，2Ω6 ）A 、有电流，有电压B 、无电流，有电压C 、有电流，无电压D 、无电流，无电压7、在电路的暂态过程中，电路的时间常数τ愈大，则电流和电压的增长或衰减就（）A 、愈慢B 、愈快C 、先快后慢D 、先慢后快8、有一电感元件，X L =5Ω,其上电压u=10sin(ωt+600)V,则通过的电流i 的相量为（）A 、A I015050∠= B 、A I 015022∠= C 、A I0302-∠= D 、A I 0302∠= 9、下面关于阻抗模的表达式正确的是（）A 、i u Z =B 、I U Z =C 、I U Z =D 、IU Z = 10、u=102sin(ωt-300)V 的相量表示式为（）A 、03010-∠=UV B 、030210-∠=U V C 、03010∠=UV D 、030210∠=U V 11、已知电路如下图所示，则电压电流的关系式为（）R — E +A 、U= —E+RIB 、U= —E —RIC 、U= E+RID 、U=E —RI12、在下图示电路中，电压U 的值等于（）1ΩA 、11VB 、12VC 、13VD 、14V）A 、6W+ B 、12W— C 、30W— D 、35W14、下列关于戴维宁定理描述不正确的是（）A 、戴维宁定理通常用于含独立电源、线性电阻和受控源的一端口网络；B 、戴维宁等效电阻q R e 是指有源一端口内全部独立电源置零后的输入电阻；C 、在数值上，开路电压OC U 、戴维宁等效电阻q R e 和短路电流SC I 于满足OC U =q R e SC I ；D 、求解戴维宁等效电阻q R e 时，电流源置零时相当于短路，电压源置零时相当于开路。

电路原理第四版课后练习题含答案介绍电路原理是电工电子工程的基础课程，是理解电子电路，掌握电子技术的必备基础。

电路原理第四版是一本经典的教材。

本文将提供该教材的课后练习题及答案，以供读者学习和练习。

课后练习题第一章电路基本定理1.四个1Ω的电阻分别连在电源的正极和负极，求它们之间的总电阻。

2.两个串联的电容C1=10μF，C2=20μF，两端的电压分别为50V和100V，求总电容。

3.RC电路充电后，电容器电压的夹角为45度，某一时刻电容器电压为6V，充电电阻R=2kΩ，电容C=0.1μF，求该时刻电容充电所经过的时间。

第二章电路简化技术1.简化下列电路：simplify_circuit2.已知电路中R1=3Ω，R2=4Ω，R3=5Ω，求R4使得电路平衡。

第三章交流电路基本理论1.已知某电路中电感为5mH，电容为8μF，电源交流电压为60V，频率为50Hz，求电流的有效值和相位角。

2.有一个平衡电桥电路，其两端分别为220V和200V，电桥中R1=100Ω，R2=50Ω，C1=0.1μF，C2=0.02μF，求电桥平衡时C3和R3的阻值。

答案第一章电路基本定理1.总电阻为4Ω。

2.总电容为6.67μF。

3.电容充电所经过的时间为2.2ms。

第二章电路简化技术1.简化后的电路如下：simplified_circuit2.R4=15Ω。

第三章交流电路基本理论1.电流的有效值为1.202A，相位角为-53.13度。

2.R3=5.52kΩ，C3=0.16μF。

总结本文提供了电路原理第四版课后练习题及答案，供读者学习和练习。

电路原理是电子电路的基本理论，掌握了该理论，才能更好的理解和应用电子电路技术。

同时，也希望本文的内容能对读者有所帮助。

1-4． 电路如图所示,试求支路电流I.IΩ12解：在上结点列KCL 方程：A I II I I 6.301242543-==+-++解之得： 1-8．求图示电路中电压源发出的功率及电压xU 。

53U解：由KVL 方程：V U U U 5.2,53111=-=-得 由欧姆定律，A I I U 5.0,5111-=-=得所以是电源）（电压源的功率：,05.251123)52(151<-=-⨯-===⨯+=W I P VI U V X1-10．并说明是发出还是消耗源功率试求图示电路两独立电,。

10A解：列KVL 方程：A I I I I 5.0010)4(11101111==++⨯+⨯+-，得电路两独立电源功率：，发出）（，发出。

W I P W I P A V 38411051014110-=⨯⨯+-=-=⨯-= 2-6如图电路：R1=1Ω ，R2=2Ω，R3=4Ω，求输入电阻Rab=？解：含受控源输入电阻的求法，有外施电压法。

设端口电流I ，求端口电压U 。

Ω====+-=+=+=9945)(21131211211I UR IU II I R I I R I I I R I IR U ab 所以，得，2-7应用等效变换方法求电流I 。

解：其等效变化的过程为，根据KVL 方程，AI I I I 31,08242-==+++ 3—8．用节点分析法求电路中的xI 和xU.6A3ΩV解：结点法：A I V U U I U U U U U U U U U U U U U UU U U X X X n n n n X n n n n n n n n n 5.16.72432242)212141(21411321)212111(214234121)4121(3121321321321==-⨯=--==+=+++--=-+++--=--+，解之得：，，补充方程：网孔法：网孔电流和绕行方向如图所示：323132132112224123221212242223m x x m x m m m m m m m m m IU I U I I I I U I I I U I I I I ++-==-⨯=-=+++⨯-⨯-=-+++-=，），（补充方程：）（）（3—17．电路如图，试用网孔分析法求解电路中受控源发出的功率。

电路原理第二版课后答案
1. 答案: 在电路中，电源是提供电流的设备，电阻是阻碍电流
流动的设备，电流是电子在电路中的流动。

2. 答案: 串联电路中，电流在电路中只有一条路径可以流动，
因此串联电路中的电流相同，而电压会分配到各个电阻上。

3. 答案: 并联电路中，电流在电路中有多条路径可以流动，因
此并联电路中的电压相同，而电流会分配到各个支路上。

4. 答案: 电阻是阻碍电流流动的物体或装置。

它的单位是欧姆，常被用来衡量电阻的大小。

5. 答案: 正常运转的电路中，电流在导线中的流动是由电源驱
动的，而不是自己产生的。

电流的流动方向取决于电子的运动方向（从负极流向正极）。

6. 答案: 电能是电流通过电路时所携带的能量，可以通过电功
公式 P = VI 来计算，其中 P 表示功率，V 表示电压，I 表示电流。

7. 答案: 电流的大小与电压和电阻之间的关系可以由欧姆定律
表示，即 I = V/R，其中 I 表示电流，V 表示电压，R 表示电阻。

8. 答案: 电阻可以通过串联和并联的方式进行连接。

串联方式
是将电阻依次连接在一起，而并联方式是将电阻同时连接到电
路中。

9. 答案: 电路中的电阻可以通过改变电阻的材料、长度和截面积来改变。

材料的电阻率越大，电阻就越大。

长度越长，电阻越大。

截面积越小，电阻越大。

10. 答案: 电阻可以用来调节电路中的电流和电压。

当电阻增大时，电流会减小，而电压会增大。

当电阻减小时，电流会增大，而电压会减小。

电路原理习题习题作业1大题一二三成绩一、单项选择题：在下列各题中，有四个备选答案，请将其中唯一正确的答案填入题干的括号中。

(本大题共3小题，总计29分)1、(本小题6分)电路如图所示, 若R、U S、I S均大于零，, 则电路的功率情况为A. 电阻吸收功率, 电压源与电流源供出功率B. 电阻与电压源吸收功率, 电流源供出功率C. 电阻与电流源吸收功率, 电压源供出功率D. 电阻吸收功率, 电流源供出功率，电压源无法确定答( )U S R I S2、(本小题9分)若电流表A读数为零, 则R与I的值分别为A. 6 Ω, 2.5 AB. 8 Ω, -2.5 AC. 6 Ω, 1 AD. 0.66 Ω, 15 A答( )abcd 6Ω15.Ω1ΩA4ΩRI2Ω10V3、(本小题14分)用叠加定理可求得图示电路中ab 端的开路电压U ab 为A. 8.5 VB. 7.5 VC. 6 VD. 6.5 V答()2V2Ω2A 1Ω2Ω3ΩU ab︒︒1Ω4A1V+-二、填充题：在下列各题中，请将题止所要求的解答填入题干中的各横线上方内。

(本大题共2小题，总计31分) 1、(本小题12分)图示电路中的电流=I A ,电压=U V .10Ω5Uo3.0U Ω5AoU2、(本小题19分)图示正弦交流电路，已知t u 310cos 2100=V ，电源向电路提供功率P =200W ，L u 的有效值为50V ，求R 和L 。

iL +-Lu R+︒︒三、非客观题( 本 大 题40分 )电路及外施电压波形如图所示，求电感贮能的最大值，并表明t >2s 时电阻所消耗的能量等于该值。

uO10H5Ωu Vt s210习题作业2一、单项选择题：在下列各题中，有四个备选答案，请将其中唯一正确的答案填入题干的括号中。

(本大题共3小题，总计34分) 1、(本小题9分)电路如图所示, 若R 、U S 、I S 均大于零，, 则电路的功率情况为 A. 电阻吸收功率, 电压源与电流源供出功率 B. 电阻与电流源吸收功率, 电压源供出功率 C. 电阻与电压源吸收功率, 电流源供出功率 D. 电阻吸收功率，供出功率无法确定答( )U SRI S2、(本小题8分)用叠加定理可求得图示电路中电压u 为A. ()1+cos t VB. ()5-cos t VC. ()53-cos t VD. 513-⎛⎝ ⎫⎭⎪cos t V答( )1A 9V 4Ω3cos t V6Ω3Ω︒︒u+-3、(本小题17分)图示电路中a 、b 端的等效电阻R ab 为A. 83 ΩB. 3 ΩC. 4 ΩD. 6 Ω答()︒︒a4Ω4Ω4Ω4Ω4Ω4Ω二、填充题：在下列各题中，请将题止所要求的解答填入题干中的各横线上方内。

大学电路原理习题答案【篇一：华南理工大学网络教育电路原理作业1-13、16章全答案】s=txt>1-1说明题1-1图（a）、（b）中：（1）u、i的参考方向是否关联？（2）ui乘积表示什么功率？（3）如果在图（a）中u0、i0；图（b）中u0、i0，元件实际发出还是吸收功率？（a）（b）题1-1图解：（1）题1-1图（a），u、i在元件上为关联参考方向：题1-1图（b）中，u、i在元件上为非关联参考方向。

（2）题1-1图（a）中，p=ui表示元件吸收的功率；题1-1图（b）中，p=ui表示元件发出的功率。

（3）题1-1图（a）中，p=ui0表示元件吸收负功率，实际发出功率：题1-1图（b）中，p=ui0，元件实际发出功率。

1-4 在指定的电压u和电流i的参考方向下，写出题1-4图所示各元件的u和i的约束方程（即vcr）。

（a）（b）（c）（d）（e）（f）题1-4图1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率（须说明是吸收还是发出）。

（a）（b）（c）题1-5图解：题1-5图（a）中流过15v电压源的2a电流与激励电压15v为非关联参考方向，因此，题1-5图（b）中电压源中的电流ius=(2-5/15)a=－1a，其方向与激励电压关联，15v的2a电流源两端的电压为15v，与激励电流2a为非关联参考方向，电阻消耗功率pr=152/5=45w，电路中pus+pr=pis发功率平衡。

题1-5图（c）中电压源折中的电流ius=(2+15/5)a=5a方向与15v激励电压非关联，电流源两端的电压为15v，与激励电流2a为关联参考方向，电阻消耗功率pr=152/5=45w，电路中pus发=pis吸+pr功率平衡。

1-16 电路如题1-16图所示，试求每个元件发出或吸收的功率。

i1（a）（b）题1-16图解：题1-16图（a）中，应用kvl可得方程：解得：u=－1v电流源电压u与激励电流方向为非关联，因此电流源发出功率为：电阻功率为：vcvs两端的电压2u与流入电流方向关联，故吸收功率为显然，pis发=pus吸+pr题1-16图（b）中，在结点a应用kcl可得：i2=i1+2i1-3i1再在左侧回路应用kvl可得：2i1+3i1=2解得：i1=0.4a根据各电流、电压方向的关联关系，可知，电压源发出功率为：pus发=2i1=0.8wcccs发出功率为：2?电阻消耗功率：1?电阻消耗功率：显然，pus发+pcs发=pr1+pr21-20 试求题1-20图所示电路中控制量u1及电压u。